
An Empirical Research on the Investment Strategy of Stock Market
based on Deep Reinforcement Learning model
Yuming Li
1,2
, Pin Ni
1,2
and Victor Chang
3,4
1
Department of Computer Science, University of Liverpool, Liverpool, U.K.
2
Department of Computer Science and Software Engineering, Xi’an Jiaotong-Liverpool University, Suzhou, China
3
International Business School Suzhou, Xi’an Jiaotong-Liverpool University, Suzhou, China
4
Research Institute of Big Data Analytics (RIBDA), Xi’an Jiaotong-Liverpool University, Suzhou, China
Keywords:
Deep Reinforcement Learning (DRL), Stock Market Strategy, Deep Q-Network.
Abstract:
The stock market plays a major role in the entire financial market. How to obtain effective trading signals
in the stock market is a topic that stock market has long been discussing. This paper first reviews the Deep
Reinforcement Learning theory and model, validates the validity of the model through empirical data, and
compares the benefits of the three classical Deep Reinforcement Learning models. From the perspective of the
automated stock market investment transaction decision-making mechanism, Deep Reinforcement Learning
model has made a useful reference for the construction of investor automation investment model, the con-
struction of stock market investment strategy, the application of artificial intelligence in the field of financial
investment and the improvement of investor strategy yield.
1 INTRODUCTION
1.1 Background
Deep Reinforcement Learning (DRL) is a model that
integrates Deep Learning (DL) and Reinforcement
Learning (RL). The network model has an ability to
learn and control strategies directly from high dimen-
sional raw data, and achieve end-to-end learning from
perception to action. This model simulates human
cognition and learning styles, inputting visual and
other sensory information (high dimensional data),
and then directly outputting actions through brain pro-
cessing(simulated with Deep Neural Networks) with-
out external supervision.
Dimensionality reduction is the most prominent
feature of Deep Learning. The DNN (Deep Neural
Networks) could automatically discover correspond-
ing representations of low dimension by extracting
the input data of high dimension. By incorporat-
ing respondent biases into the hierarchical neural net-
work architecture, Deep Learning has strong percep-
tual ability and feature extraction ability, but it lacks
decision-making ability. And Reinforced Learning
has decision-making ability, but it has a problem of
perception. Therefore, Deep Reinforcement Learn-
ing combines the two and complement each other, and
provides a solution for the construction of the cogni-
tive decision system of complex systems.
Traditional quantitative investment often con-
structed on technical indicators, it has a short life
span and poor self-adaptability. This research applies
the Deep Reinforcement Learning model to the finan-
cial investment field, which can better adapt to the
large-scale data of the financial market, strengthen the
data processing power, enhance the ability to extract
feature from trading signals and improve the self-
adaptability of the strategy. In addition, this research
applies the theory of Deep Learning and Reinforce-
ment Learning in machine learning to the field of fi-
nancial investment, and applies the ability to grasp
and analyze the information characteristics of big data
to finance. For example, stock trading is a sequence
decision process, for the Reinforcement Learning sys-
tem, the goal is to learn a multi-stage behavioral strat-
egy. The system can determine the current best price
limit order, so that the transaction cost of all orders is
the lowest. Therefore, the investment field has great
practical significance.
52
Li, Y., Ni, P. and Chang, V.
An Empirical Research on the Investment Strategy of Stock Market based on Deep Reinforcement Learning model.
DOI: 10.5220/0007722000520058
In Proceedings of the 4th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2019), pages 52-58
ISBN: 978-989-758-366-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

1.2 Organization
The following sections are listed as follows: Section
2 provides the related work from the perspective of
theory and application; Section 3 describes the ex-
periment and introduces the environment and device
of the experiment, the related theoretical knowledge
and the process and the existing problems; Section 4
shows the experimental results, including images and
tables. Section 5 discusses the experimental results
from the perspective of consequence, actual impact
and critical reflection. Section 6 briefly summarizes
the full text.
2 LITERATURE REVIEW
The main viewpoint of early Deep Reinforcement
Learning is by using neural networks for dimension-
ality reduction of high-dimensional data to facilitate
data processing. Shibata et al. (Shibata and Okabe,
1997)(Shibata and Iida, 2003) combined the shallow
neural network with Reinforcement Learning to pro-
cess the visual signal input during the construction
of neural network, and then controlled the robot to
complete specific task of pushing the box. Lange et
al. (Lange and Riedmiller, 2010) proposed the appli-
cation of efficient deep autoencoder to visual learn-
ing control, and proposed “visual motion learning” to
make the agent have similar perception and decision-
making ability. Abtahi et al. (Abtahi et al., 2015)
introduced the Deep Belief Networks into Reinforce-
ment Learning during the construction of the model,
replacing the traditional value function approximator
with a Deep Belief Networks, and successfully apply-
ing the model to the task of character segmentation in
license plate images. In 2012, Lange et al. (Lange
et al., 2012) applied Reinforced Learning based on
visual input to vehicle control, a technique known as
Deep Q-Learning. Koutnik et al. (Koutn
´
ık et al.,
2014) combined the Neural Evolution (NE) method
with Reinforcement Learning and applied the model
to the video racing game TORCS (Wymann et al.,
2000) to achieve the automatic driving of the car.
In the Deep Reinforcement Learning stock decision
model, the DL section voluntarily perceives the real-
time market environment of feature learning, and the
RL section builds the interaction with deep character-
ization and makes exchanging decisions to cumulate
final rewards of the current new environment.
Mnih et al. (Mnih et al., 2013) is the pioneer of
DRL. In the paper, the pixel of the original picture of
the game is taken as the input data (S), and the di-
rection of the joystick is used as the action space (A)
to solve the Atari game decision problem. Then he
demonstrated that the agent of Deep Q-Network was
able to exceed all the existing algorithms in terms of
performance in 2015 (Mnih et al., 2015).Later, many
authors improved DQN. Van Hasselt et al. (Van Has-
selt et al., 2016) proposed Double-DQN, using a Q
network for selecting actions, and another Q network
for evaluating actions, alternating work, and achiev-
ing results in solving the upward-bias problem. In
2016, Silver et al. (Schaul et al., 2015) added a
priority-based replay mechanism based on Double-
DQN, which speeds up the training process and adds
samples in disguise. Wang et al. (Wang et al., 2015)
put forward the Dueling Network based on DRN,
which divides the network into an output scalar V(s)
and another output action on the advantage value,
and finally synthesizes the two Q values. Silver et
al. (Silver et al., 2014) demonstrated Deterministic
Policy Gradient Algorithms (DPG), then DDPG pa-
per by Google (Lillicrap et al., 2015) combined DQN
and DPG above to push DRL into continuous motion
space control. In the paper from Berkeley University
(Schulman et al., 2015), the core of which is the credi-
bility of learning and improve the stability of the DRL
model. Gabriel et al. (Dulac-Arnold et al., 2015) in-
troduced action embedding concept, embedding dis-
crete actions into successive small spaces, making
reinforcement learning methods applicable to large-
scale learning problems. It can be verified that the
Deep Reinforcement Learning algorithm is progres-
sively improving and perfecting in order to adapt to
more situations.
Recently, researchers have been more interested
in evolutionary algorithms such as genetic algo-
rithm (Cheng et al., 2010) (Chien and Chen, 2010)
(Berutich et al., 2016), and artificial neural networks
(Chang et al., 2011), to decide stock trading strat-
egy. The Reinforcement Learning algorithm was
previously used as a method of quantify financing
(Almahdi and Yang, 2017). The superiority in ap-
plying Reinforcement Learning concepts in financial
field is that the agent can automatically process real-
time data with high-frequency, and carry out trans-
actions efficiently. The enhanced learning algorithm
of optimized trading system by JP Morgan Chase
(jpmorgan, ) uses both Sarsa (On-Policy TD Con-
trol) and Q-learning (Off-Policy Temporal Difference
Control Algorithm). League Champion Algorithm
(LCA) (Alimoradi and Kashan, 2018) used in the
stock trading rules extraction process, which extracts
and holds diversiform stock trading rules for diver-
siform stock market environment. Krollner et al.
(Krollner et al., 2010) review different types of stock
market forecasting papers based on machine learn-
An Empirical Research on the Investment Strategy of Stock Market based on Deep Reinforcement Learning model
53

ing, such as neural network based models, evolu-
tion and optimization mechanics, multiple and com-
pound methods, ect. Most researchers use the Artifi-
cial Neural Network to predict the stock market trend
(Wang et al., 2011)(Liao and Wang, 2010). Guresen
et al.(Guresen et al., 2011) forecast NASDAQ Stock
Index using Dynamic Artificial Neural Network and
Multi-Layer Perceptron (MLP) Model. Vanstone et
al. (Vanstone et al., 2012) design a trading system
based on MLP to provide trading signals for stock
market in Australia. Due to the limitations of a single
model, a mainstream which use hybrid machine learn-
ing models to resolve financial trading points based
on time sequence gradually emerge. J.Wang et al.
(Wang et al., 2016) propose a hybrid Support Vec-
tor Regression model connecting Principal Compo-
nent Analysis with Brainstorm optimization to pre-
dict trading prices. Mabu et al.(Mabu et al., 2015)
propose an integrated learning mechanism combining
MLP with rule-based evolutionary algorithms which
can determine trading points in stock market. Tra-
ditional quantitative investments are often based on
technical indicators. These strategies usually have
longevity and poor self-adaptation. The application of
machine learning algorithms in the field of financial
investment can significantly enhance strategic data.
The processing power of the machine can improve
the ability to extract feature information from trading
signals, and can also improve the adaptability of the
strategy.
3 DESCRIPTION OF THE
EXPERIMENT
For purpose of verifying the feasibility of Deep Rein-
forcement Learning in stock market investment deci-
sions, we randomly selected ten stocks in the ‘Histori-
cal daily prices and volumes of all US stocks’ data set
for experiments. We selected the three classic models
in DRL, which are Deep Q-Network (DQN), Dou-
ble Deep Q-Network (DDQN), and Dueling Double
Deep Q-Network (Dueling DDQN) for performance
comparison. Each stock is split into training set and
testing set in advance, and then fed into three Deep
Reinforcement Learning models. Finally, the training
results and test results are compared and analyzed.
3.1 Experimental Environment
The running environment of this experiment is in
python 3.5 version based on Tensorflow learning
framework, with Windows 7 64-bit system.
3.2 Methods
We introduced three classic Deep Reinforcement
Learning models as follows:
3.2.1 Deep Q Network
DQN is one of the algorithms of DRL. This algorithm
combines the Q-Learning algorithm with the neu-
ral network and has the experience replay function.
There are two networks in DQN, Q estimated network
named MainNet and predicted Q realistic neural net-
work named TargetNet, which have the same struc-
ture but different parameters. The input of MainNet
is raw data (as state State), and output is value eval-
uation (Q value) corresponding to each action. Then
passing the Q value from MainNet to TargetNet to get
the Target Q and update the MainNet parameters ac-
cording to the Loss Function, thus completing a learn-
ing process. The experience pool can store the trans-
fer samples (s
t
, a
t
, r
t
, s
t+1
) obtained by each time step
agent and the environment to the memory unit, and
randomly take some minibatch for training when nec-
essary. The experience replay function can solve the
correlation and non-static distribution problems. The
update formula of Q-Learning:
Q
0
(s, a) = Q(s, a)+ [r + γmax
a
0
Q(s
0
, a
0
) − Q(s, a)]
The loss function of DQN is as follows:
L(θ) = E[(TargetQ − Q(s, a; θ))
2
]
TargetQ = r
t+1
+ γmax
a
0
Q(s
0
, a
0
;θ)
(a represents an action of the Agent, s represents a
state of the Agent, r is a real value representing the
reward of the action, θ indicates the mean square error
loss of the network parameter, and Q
0
, s
0
, a
0
represents
the updated value of Q, s and a. )
3.2.2 Double DQN
Double DQN combines Double Q-learning with
DQN. Van Hasselt et al. (Van Hasselt et al., 2016)
found and proved that traditional DQN generally
overestimates the Q value of action, and the estimated
error increases with the number of actions. If the over-
estimation is not uniform, it will lead to a subopti-
mal Action overestimated Q value that exceeds the Q
value of optimal action, and will never find the opti-
mal strategy. Based on the Double Q-Learning pro-
posed by him in 2010 (Lange and Riedmiller, 2010)
the author introduced the method into DQN. The spe-
cific operation is to modify the generating of the Tar-
get Q value.
TargetDQ = r
t+1
+ γQ(s, argmax
a
0
Q(s
0
, a
0
;θ); θ
0
)
COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk
54

3.2.3 Dueling DQN
Dueling DQN combines Dueling Network with
DQN.The dueling net offloads the abstract features
extracted from the convolutional layer into two
branches. The upper path is the state value func-
tion V (s;θ, β), which represents the value of the static
state environment itself; the lower path is the ac-
tion advantage function A(s, a; θ, α) of the dependent
state, which indicates the extra value of an Action. Fi-
nally, the two paths are re-aggregated together to get
the final Q value. Theoretically, the calculation for-
mula of the action Q value is:
Q(s, a; θ, α, β) = V (s; θ, β) + A(s, a; θ, α)
(a represents an action of the Agent, s represents a
state of the Agent, θ is the convolutional layer param-
eter and α and β are the two-way fully connected layer
parameters.)
In practice, the action dominant flow is generally set
to the individual action advantage function minus the
average of all action advantage functions in a certain
state:
Q(s, a; θ, α, β) = V (s; θ, β)+
A(s, a; θ, α) −
1
|A|
∑
a
0
A(s, a
0
;θ, α)
This can ensure that the relative order of the dom-
inant functions of each action is unchanged in this
state, and can narrow the range of Q values, remove
redundant degrees of freedom, and improve the sta-
bility of the algorithm.
3.3 Experimental Steps
The experimental steps are in the following sequences
as follows:
• Import data and process it, split the data into
training-set and testing-set by time, and set related
parameters.
• Use Deep Reinforcement Learning strategy, buy-
and-hold strategy in the selected 10 stocks, then
sum and average the historical strategies of 10
stocks for comparison.
• Feed The processed data into the Deep Reinforce-
ment Learning model, and the output is obtained
after iterative training.
• Analyze and discuss the outputs
3.4 Problems
Since the amount of data in the data set is enormous,
the data size has a wide range of differences. Hence,
randomly pumping too small data for training will re-
sult in less intuitive results. Due to the difference in
the issuance time of stocks, the ten stocks conduct-
ing experiments are not uniform in time dimension.
Although time is not used as an input parameter to
influence the results in the whole experiment, it still
leads to some external influences in the actual market.
4 RESULTS
The training profit and test profit of the ten stocks in
the three Deep Reinforcement Learning models are
shown in Table 1.
We randomly selected one of the ten experimental
stocks. Figure 1 shows the time-market value pro-
file of the three models. The gray part indicates that
the “stay” action is selected at this moment; the cyan
portion indicates that “buy” action is selected at that
moment; and the magenta portion indicates that “sell”
action is selected at that moment. “Stay” refers to
a wait-and-see attitude toward the current situation,
neither buying nor selling, “buy” refers to the trad-
ing means that investors take against the bullish fu-
ture price trend, and “sell” refers to the trading means
that investors take against the bearish trend of future
prices. Visualizing the decision process through the
matplotlib package in Python can make the decision
distribution of different DRL models clear and com-
parable.
Figure 1: Time-market value profile.
An Empirical Research on the Investment Strategy of Stock Market based on Deep Reinforcement Learning model
55
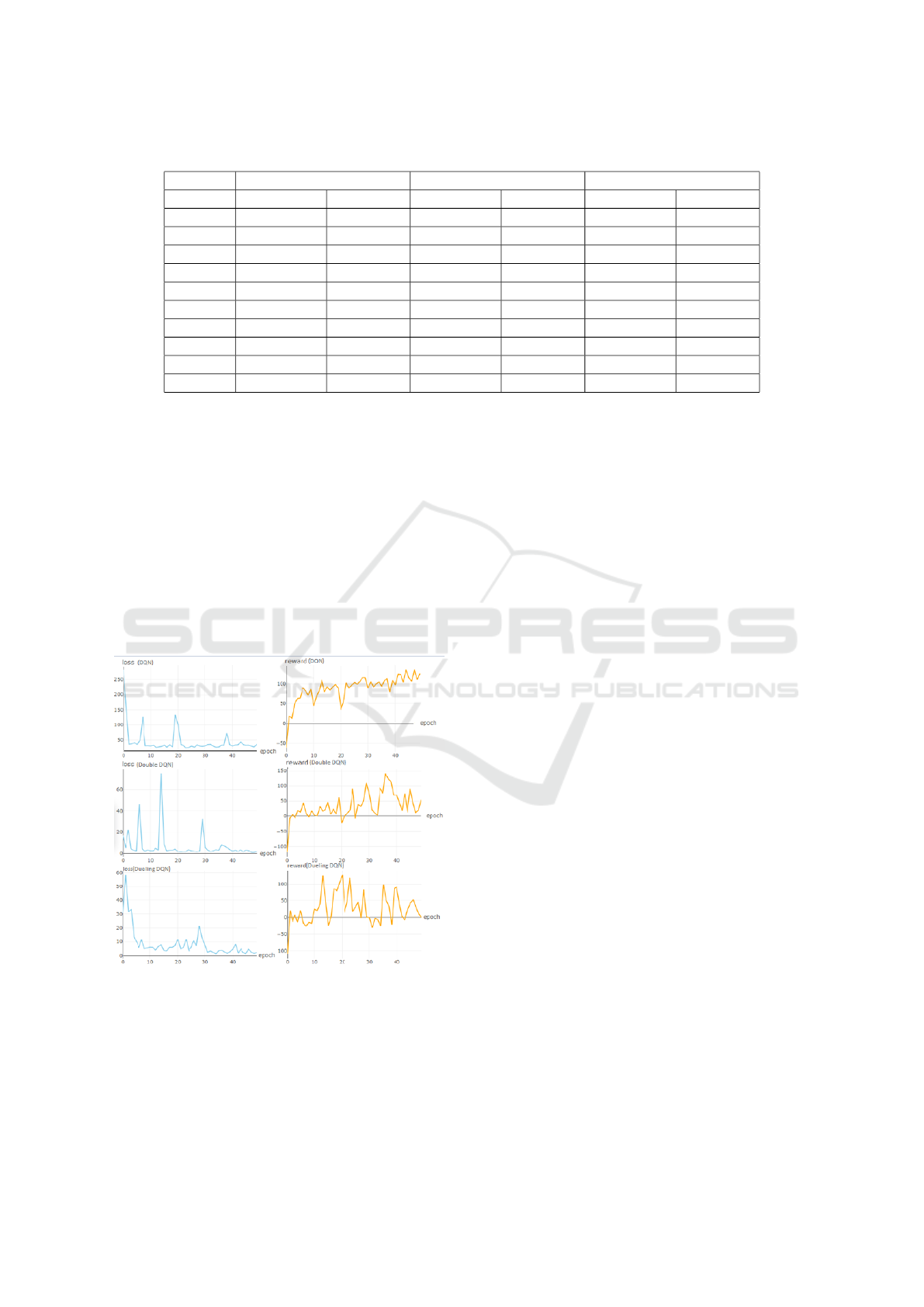
Table 1: Profit Statement Table.
DQN DDQN Dueling DDQN
Name Train-Profit Test-Profit Train-Profit Test-Profit Train-Profit Test-Profit
a.us 490 916 296 551 173 285
kdmn.us -9 -7 1 15 1 8
ibkco.us 20 9 11 12 10 5
eght.us 57 198 18 15 13 38
nbh.us 48 56 4 9 16 24
int.us 958 1029 100 166 10 22
rbcaa.us 418 519 312 425 353 418
intx.us 88 184 39 149 91 334
rlje.us 37 38 138 147 47 349
pool.us 179 336 42 66 7 27
Figure 2 shows the Loss function and the Reward
function of the stock under the three models. A Loss
function is a function that maps an event to a real
number that expresses the economic cost associated
with its event. The experiment compares the loss
functions of the three DRL models in order to mea-
sure and compare the economic benefits of these mod-
els in strategy making. Reward function refers to the
reward brought by the change of the environmental
state caused by the sequence of actions. It is an in-
stant reward that can measure the pros and cons of the
actions.
Figure 2: The Loss Function and the Reward Function of
the stock.
5 DISCUSSION
From the perspective of individual stocks, as shown
in Table 1, the Deep Reinforcement Learning strategy
does not work well for all stocks, but it is effective for
most of the stocks. For example, kdmn.us has a nega-
tive profit when making decisions using DQN, while
the profit of the remaining stocks through the three
Deep Reinforcement Learning model is positive. Af-
ter the training of the model, most stocks have a Test-
Profit higher than the Train-Profit value, which is due
to the testing set use the optimal Q value from the
training set output. The result of using the optimal Q
value is better than the Reinforcement Learning result
in the unsupervised mode. At the same time, compar-
ing the three Deep Reinforcement learning models, it
can be seen that the profit brought by DQN in stock
decision is generally greater than Double DQN and
Dueling DQN. Even though Double DQN and Duel-
ing DQN is an improved version based on DQN, the
double Q network and the dueling network are not
suitable for stock market decision making due to the
characteristics of the training data set.
Figure 1 illustrates the decision sequences of dif-
ferent Deep Reinforcement Learning models are dif-
ferent. It can be seen from the test part of the three
models that the training results tend to be on Constant
Mix Strategy, which means “sell when the stock price
rises and buy when the stock price declines”. From
DQN to Dueling DQN, the discrimination accuracy is
getting higher and higher, which is determined by the
calculation method of Q value in the model. The Dou-
ble DQN main network chooses the optimum action,
and the target network fits the Q value; The Q value
of Dueling DQN is added by the state value and the
action value (the specific process can be learned from
Section 3), Double DQN and Dueling DQN is more
accurate than DQN in calculating the optimal Q value,
therefore, the strategy switching is more frequent and
the recognition accuracy is higher in testing set.
Figure 2 is a graph of the loss function and re-
ward function for three Deep Reinforcement Learn-
ing models. The loss function is used to measure the
COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk
56

“gap” between the model output and the real value.
The goal of the training process is to make the loss
function get its minimum value. It can be seen from
the figure that although there are extreme values in the
middle, the overall trend of the loss function of the
three models is it gradually decreases and approaches
infinity to zero. The trend of the Dueling DQN model
is the most gradual, which is due to the characteristics
of the dueling network that can improve the stability
of the algorithm. The decision process of the Deep
Reinforcement Learning model is generally regarded
as a Markov decision process. Based on the Markov
setting, the next possible state s
i+1
only depends on
the current state s
i
and the behavior a
i
, and the previ-
ous status and behavior are irrelevant. Therefore, the
Reward values of the three models are independent at
the current time, and their charts fluctuate greatly, and
there is no obvious trend.
The experimental results show the feasibility of
Deep Reinforcement Learning in the field of stock
market decision-making, which can be used by subse-
quent practitioners to invest in the real market. In ad-
dition, as shown in Table 1, the best-performing Deep
Reinforcement Learning model is DQN, not Double
DQN and Dueling DQN which improved on the basis
of DQN. This shows that we can not make empiri-
cal errors in practical applications. The subsequent
new method not always be better than the original
method. Each method has its own suitable field. For
instance, Double DQN is obviously better than DQN
in the game, but the opposite is true in stock market
decision making. Hence, decisions must always be
proven through scientific experiments.
It can be seen from the experimental results that
the Deep Reinforcement Learning model does not
profit well in all stocks. Therefore, in the actual in-
vestment, the strategy should be used to reduce the in-
compatibility of the strategy to individual stocks and
reduce the risk of the strategy. The empirical evidence
demonstrates the diversified risk of diversified invest-
ment to a certain extent, and also shows that deep in-
tensive learning strategies need to spread risk to be
profitable.
6 CONCLUSION AND FUTURE
WORK
This paper mainly applied DRL to the aspect of stock
investment strategy, proved the feasibility of DRL to
the field of financial strategy, and compared three
classic DRN models. Our results showed that the
DQN model works the best in the decision-making
of stock market investment, which is slightly differ-
ent from the inertia thinking result. As the improved
algorithm based on DQN, Double DQN and Dueling
DQN in this experiment were not as effective as the
traditional DQN, therefore, we could identify that the
improved algorithm was not always applicable to all
fields. The working principle of DRL was to simu-
late the learning mechanism between humans and an-
imals of higher intelligence, emphasizing ”trial and
error and its improvement” in the constant interaction
with the environment. The main advantage of this ap-
proach was the realization of unsupervised learning
without the need for a supervising agent or method.
Since the predecessors’ work is mainly focused on
theoretical research, the application of financial in-
vestment is relatively new or even just beginning.
This research demonstrated the application field of
Deep Reinforcement Learning and also the decision-
making tools of financial investment. Reinforcement
Learning as a prominent method of artificial intelli-
gence applied in financial transactions in recent years,
our contribution is mainly to make an innovative at-
tempt to apply Deep Reinforcement Learning, a new
variant of Reinforcement Learning, to financial trans-
actions. And compare the performance of three kinds
of Deep Reinforcement Learning models, which are
Deep Q Network (DQN), Double Deep Q-Network
(Double DQN) and Dueling Deep Q-Network (Duel-
ing DQN) in the same transaction data, and ultimately
obtain DQN as a strategy to maximize stock returns
for reference.
The theory of Deep Reinforcement Learning has
been widely used in all major fields. However, there
are still many problems to be improved, such as ex-
ploring and utilizing the balance problem, the slow
convergence, and the ”dimensional disaster” etc. We
plan to improve on all the major shortcomings, and
ensure we can produce better quality and accuracy
for our research outputs and predictions in our future
work.
REFERENCES
Abtahi, F., Zhu, Z., and Burry, A. M. (2015). A deep re-
inforcement learning approach to character segmenta-
tion of license plate images. In Machine Vision Appli-
cations (MVA), 2015 14th IAPR International Confer-
ence on, pages 539–542. IEEE.
Alimoradi, M. R. and Kashan, A. H. (2018). A league
championship algorithm equipped with network struc-
ture and backward q-learning for extracting stock trad-
ing rules. Applied Soft Computing, 68:478–493.
Almahdi, S. and Yang, S. Y. (2017). An adaptive portfolio
trading system: A risk-return portfolio optimization
using recurrent reinforcement learning with expected
An Empirical Research on the Investment Strategy of Stock Market based on Deep Reinforcement Learning model
57

maximum drawdown. Expert Systems with Applica-
tions, 87:267–279.
Berutich, J. M., L
´
opez, F., Luna, F., and Quintana, D.
(2016). Robust technical trading strategies using gp
for algorithmic portfolio selection. Expert Systems
with Applications, 46:307–315.
Chang, P.-C., Liao, T. W., Lin, J.-J., and Fan, C.-Y.
(2011). A dynamic threshold decision system for
stock trading signal detection. Applied Soft Comput-
ing, 11(5):3998–4010.
Cheng, C.-H., Chen, T.-L., and Wei, L.-Y. (2010). A hybrid
model based on rough sets theory and genetic algo-
rithms for stock price forecasting. Information Sci-
ences, 180(9):1610–1629.
Chien, Y.-W. C. and Chen, Y.-L. (2010). Mining associative
classification rules with stock trading data–a ga-based
method. Knowledge-Based Systems, 23(6):605–614.
Dulac-Arnold, G., Evans, R., van Hasselt, H., Sunehag,
P., Lillicrap, T., Hunt, J., Mann, T., Weber, T., De-
gris, T., and Coppin, B. (2015). Deep reinforcement
learning in large discrete action spaces. arXiv preprint
arXiv:1512.07679.
Guresen, E., Kayakutlu, G., and Daim, T. U. (2011). Us-
ing artificial neural network models in stock market
index prediction. Expert Systems with Applications,
38(8):10389–10397.
jpmorgan. jpmorgan. https://www.businessinsider.com/jpm
organ-takes-ai-use-to-the-next-level-2017-8.
Koutn
´
ık, J., Schmidhuber, J., and Gomez, F. (2014). Online
evolution of deep convolutional network for vision-
based reinforcement learning. In International Con-
ference on Simulation of Adaptive Behavior, pages
260–269. Springer.
Krollner, B., Vanstone, B., and Finnie, G. (2010). Financial
time series forecasting with machine learning tech-
niques: A survey.
Lange, S. and Riedmiller, M. (2010). Deep auto-encoder
neural networks in reinforcement learning. In The
2010 International Joint Conference on Neural Net-
works (IJCNN), pages 1–8. IEEE.
Lange, S., Riedmiller, M., and Voigtlander, A. (2012). Au-
tonomous reinforcement learning on raw visual input
data in a real world application. In Neural Networks
(IJCNN), The 2012 International Joint Conference on,
pages 1–8. IEEE.
Liao, Z. and Wang, J. (2010). Forecasting model of global
stock index by stochastic time effective neural net-
work. Expert Systems with Applications, 37(1):834–
841.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-
uous control with deep reinforcement learning. arXiv
preprint arXiv:1509.02971.
Mabu, S., Obayashi, M., and Kuremoto, T. (2015). En-
semble learning of rule-based evolutionary algorithm
using multi-layer perceptron for supporting decisions
in stock trading problems. Applied soft computing,
36:357–367.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Schaul, T., Quan, J., Antonoglou, I., and Silver, D.
(2015). Prioritized experience replay. arXiv preprint
arXiv:1511.05952.
Schulman, J., Levine, S., Abbeel, P., Jordan, M., and
Moritz, P. (2015). Trust region policy optimization.
In International Conference on Machine Learning,
pages 1889–1897.
Shibata, K. and Iida, M. (2003). Acquisition of box
pushing by direct-vision-based reinforcement learn-
ing. In SICE 2003 Annual Conference, volume 3,
pages 2322–2327. IEEE.
Shibata, K. and Okabe, Y. (1997). Reinforcement learn-
ing when visual sensory signals are directly given as
inputs. In Neural Networks, 1997., International Con-
ference on, volume 3, pages 1716–1720. IEEE.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and
Riedmiller, M. (2014). Deterministic policy gradient
algorithms. In ICML.
Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep rein-
forcement learning with double q-learning. In AAAI,
volume 2, page 5. Phoenix, AZ.
Vanstone, B., Finnie, G., and Hahn, T. (2012). Creating
trading systems with fundamental variables and neu-
ral networks: The aby case study. Mathematics and
computers in simulation, 86:78–91.
Wang, J., Hou, R., Wang, C., and Shen, L. (2016). Improved
v-support vector regression model based on variable
selection and brain storm optimization for stock price
forecasting. Applied Soft Computing, 49:164–178.
Wang, J.-Z., Wang, J.-J., Zhang, Z.-G., and Guo, S.-P.
(2011). Forecasting stock indices with back propa-
gation neural network. Expert Systems with Applica-
tions, 38(11):14346–14355.
Wang, Z., Schaul, T., Hessel, M., Van Hasselt, H., Lanc-
tot, M., and De Freitas, N. (2015). Dueling network
architectures for deep reinforcement learning. arXiv
preprint arXiv:1511.06581.
Wymann, B., Espi
´
e, E., Guionneau, C., Dimitrakakis, C.,
Coulom, R., and Sumner, A. (2000). Torcs, the
open racing car simulator. Software available at
http://torcs. sourceforge. net, 4:6.
COMPLEXIS 2019 - 4th International Conference on Complexity, Future Information Systems and Risk
58
