The Experiential Heterogeneous Earliest Finish Time Algorithm for

Task Scheduling in Clouds

Artan Mazrekaj

, Arlinda Sheholli

, Dorian Minarolli

and Bernd Freisleben

Faculty of Contemporay Sciences and Technologies, SEEU University, Tetovo, Republic of North Macedonia

Faculty of Electrical and Computer Engineering, University of Prishtina, Prishtina, Kosovo

Faculty of Information Technology, Polytechnic University of Tirana, Tirana, Albania

Department of Mathematics and Computer Science, University of Marburg, Marburg, Germany

Keywords: Cloud Computing, Task Scheduling, Resource Allocation.

Abstract: Task scheduling in cloud environments is the problem of assigning and executing computational tasks on the

available cloud resources. Effective task scheduling approaches reduce the task completion time, increase the

efficiency of resource utilization, and improve the quality of service and the overall performance of the

system. In this paper, we present a novel task scheduling algorithm for cloud environments based on the

Heterogeneous Earliest Finish Time (HEFT) algorithm, called experiential HEFT. It considers experiences

with previous executions of tasks to determine the workload of resources. To realize the experiential HEFT

algorithm, we propose a novel way of HEFT rank calculation to specify the minimum average execution time

of previous runs of a task on all relevant resources. Experimental results indicate that the proposed experiential

HEFT algorithm performs better than HEFT and the popular Critical-Path-on-a-Processor (CPOP) algorithm

considered in our comparison.

1 INTRODUCTION

The Infrastructure-as-a-Service (IaaS) service model

in cloud computing can be used to adjust the capacity

of cloud resources depending on changing demands

of applications. This feature is known as auto-scaling

(Malawski et al., 2012).

Task scheduling in cloud infrastructures is the

problem of assigning tasks to appropriate resources

(Bailin et al., 2014). Task scheduling can have a

significant impact on the performance of the system

and is particularly challenging when the cloud

resources are heterogeneous in terms of their

computation, memory, and communication

characteristics, due to different execution speeds,

memory capacities, and communication rates

between processors.

Typically, the scheduling process in the cloud

consists of several phases (Choudhary and Peddoju,

2012): resource discovery and filtering, where a

broker discovers the resources in the network and

collects their status information; resource selection,

where the target resources are selected, based on the

main parameters of the task and the resources; task

submission, where tasks are submitted to selected

resources. Task scheduling algorithms select and

allocate suitable resources to tasks such that the

overall execution can be completed to satisfy

objective functions specified by users or cloud

providers (Singh and Singh, 2013; Cui and Xiaoqing,

2018). For example, to improve Quality of Service

(QoS) for users and maximize profit for cloud

providers, parameters such as resource utilization,

throughput, performance, execution times,

computational cost, bandwidth, energy consumption,

and Service Level Agreements (SLAs) may be

considered (Dubey et al., 2018).

The task scheduling problem can be classified into

static and dynamic scheduling. In static scheduling,

all information about tasks such as execution and

communication costs for each task and the

relationship with other tasks are known in advance. In

dynamic scheduling, there is no prior information,

i.e., decisions are made at runtime (Arabnejad and

Barbosa, 2014).

In this paper, we present a novel dynamic task

scheduling algorithm for cloud environments with

heterogeneous resources. It extends the

Heterogeneous Earliest Finishing Time (HEFT)

algorithm by utilizing past experiences with task

Mazrekaj, A., Sheholli, A., Minarolli, D. and Freisleben, B.

The Experiential Heterogeneous Earliest Finish Time Algorithm for Task Scheduling in Clouds.

DOI: 10.5220/0007722203710379

In Proceedings of the 9th International Conference on Cloud Computing and Services Science (CLOSER 2019), pages 371-379

ISBN: 978-989-758-365-0

371

executions, hence we call it the experiential HEFT

(EHEFT) algorithm. It uses an additional parameter

that calculates the minimum average execution time

of previous runs of a task on all relevant resources.

This parameter equips the proposed EHEFT with the

ability to take the workload and processing power of

resources into account when assigning a task to a

processor. It gives priority to a resource that in the

past has executed the task faster than others.

Experimental results show that our EHEFT algorithm

performs better and is more efficient than other than

the original HEFT and the popular Critical-Path-on-

a-Processor (CPOP) algorithm considered in our

comparison.

This paper is organized as follows. Section 2

describes related work on task scheduling. In Section

3, the task scheduling problem is formulated. HEFT

and CPOP are described in Section 4. Our novel

EHEFT algorithm is introduced in Section 5.

Experimental results are presented in Section 6.

Section 7 concludes the paper and outlines areas for

future work.

2 RELATED WORK

Several approaches have been presented in the

literature to solve the problem of task scheduling. The

general task scheduling problem is NP-hard (Garey

and Johnson, 1979). Thus, research in this field

focuses on finding suitable low-complexity heuristics

that perform well.

Parsa and Entezari-Maleki (2009) have proposed

a task scheduling algorithm called RASA (Resource

Aware Scheduling Algorithm) that takes the

scalability characteristics of resources into account.

RASA is compared to two traditional scheduling

algorithms, Max-Min and Min-Min, making use of

their advantages and avoiding their disadvantages.

RASA is more efficient in task scheduling and

achieves better load balancing.

To achieve better results than RASA, an improved

version of the Max-Min algorithm has been proposed

Elzeki et al., (2012). Their improved Max-Min

algorithm is based on the expected execution time as

a basis for selecting tasks instead of completion time.

This approach has resulted in better load balancing

and smaller makespans than other algorithms used for

comparison.

Hu et al., (2009) have proposed a probability

dependent priority algorithm to determine the

allocation strategy that requires the smallest number

of servers to execute tasks.

Pandey et al., (2010) have proposed a scheduling

strategy that is based on a Particle Swarm

Optimization (PSO) algorithm to schedule

applications to cloud resources. It takes computation

cost and data transmission into account. The

algorithm is compared to the existing heuristic

algorithm ’Best Resource Selection’ (BRS) where

PSO can achieve three times of cost savings

compared to BRS, and the best distribution of the

workload to resources.

To schedule large-scale workflows with various

QoS parameters, Chen and Zhang (2009) have

proposed an Ant Colony Optimization (ACO)

algorithm. The algorithm intends to find a solution

that meets all QoS constraints and optimizes the user

preferred QoS parameters.

Malawski et al., (2012) have addressed the issue

of efficient management under budget and deadline

constraints in IaaS clouds. They propose various

static and dynamic algorithms for both task

scheduling and resource provisioning. From the

results it is evident that an admission procedure based

on workflow structure and the task’s estimated

execution time can improve quality and performance.

Their work considers only a single type of virtual

machines (VM) and does not take heterogeneity of

IaaS clouds into account.

Byun et al., (2011) have proposed an architecture

for automatically executing large-scale workflow

applications on dynamically and elastically

provisioned computing resources. The authors

describe an algorithm that estimates the optimal

number of resources to execute a workflow within a

user specified finish time. The algorithm also

generates a task to resource mapping and is designed

to run online. This approach considers the elasticity

of cloud resources, but does not consider the

heterogeneity of computing resources.

Rodriguez and Buyya (2014) have proposed a

resource provisioning and scheduling strategy for

scientific workflows in cloud infrastructures. The

authors model this strategy through Particle Swarm

Optimization, to optimize the total execution cost

while meeting deadline constraints. In their model,

there are some IaaS cloud properties such as

heterogeneity, elasticity, and dynamicity of

resources. Moreover, performance variations and VM

boot time parameters are considered.

Canon et al., (2008) have analyzed 20 directed

acyclic graph (DAG) scheduling heuristics by

investigating how robustness and makespan are

correlated. The authors address the issue whether

dynamically changing the order of tasks on their

processors can improve robustness. The authors

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

372

conclude that the HEFT algorithm is one the best

algorithms in terms of robustness and schedule

length.

In contrast to the existing task scheduling

approaches presented above, we propose a novel

approach as an extended version of the HEFT

algorithm that takes the workload of resources

depending on experiences with previous executions

of tasks into account. In the following sections, we

explain task scheduling in general and the CPOP and

HEFT algorithms in particular to motivate the design

of our novel algorithm.

3 TASK SCHEDULING

To divide an application into tasks with appropriate

sizes, we use DAGs. Each task of a DAG corresponds

to the sequence of operations and a directed edge

represents the dependency between the tasks.

More precisely, a DAG is represented by the

graph G = (V, E), where V is the set of v tasks and E

is the set of e edges between the tasks. Each edge (i,



E represents the dependency such that task n

should complete its execution before task n

starts.

If a task has no a parent task, this task is defined

as the entry task of a workflow of tasks. If a task has

no a child, this task is defined as the exit task of a

workflow of tasks.

From the DAG, we derive a matrix W that is a v x

p computation cost matrix, where v is the number of

tasks and p is the number of processors; w

i,j

represents

the estimated execution time to complete task v

processor v

. The average execution time of task v

defined in Equation (1) (Llavarasan and Thambidurai,

2007; Arabnejad and Barbarosa, 2014):

,ij







(1)

Each edge (i, j)



E is associated with a non-negative

weight c

i,j

which represents the communication cost

between task v

and v

. The average communication

cost of an edge (i, j) is defined in Equation (2):

data



(2)

is the average communication startup time, and

is the average transfer rate among the processors;

data

i,j

is the amount of data required to be transmitted

from task v

to task v

. In cases when tasks v

and v

are scheduled to run on the same processor, the

communication cost is considered to be zero, because

the intra-processor communication cost is negligible

compared to the inter-processor communication cost.

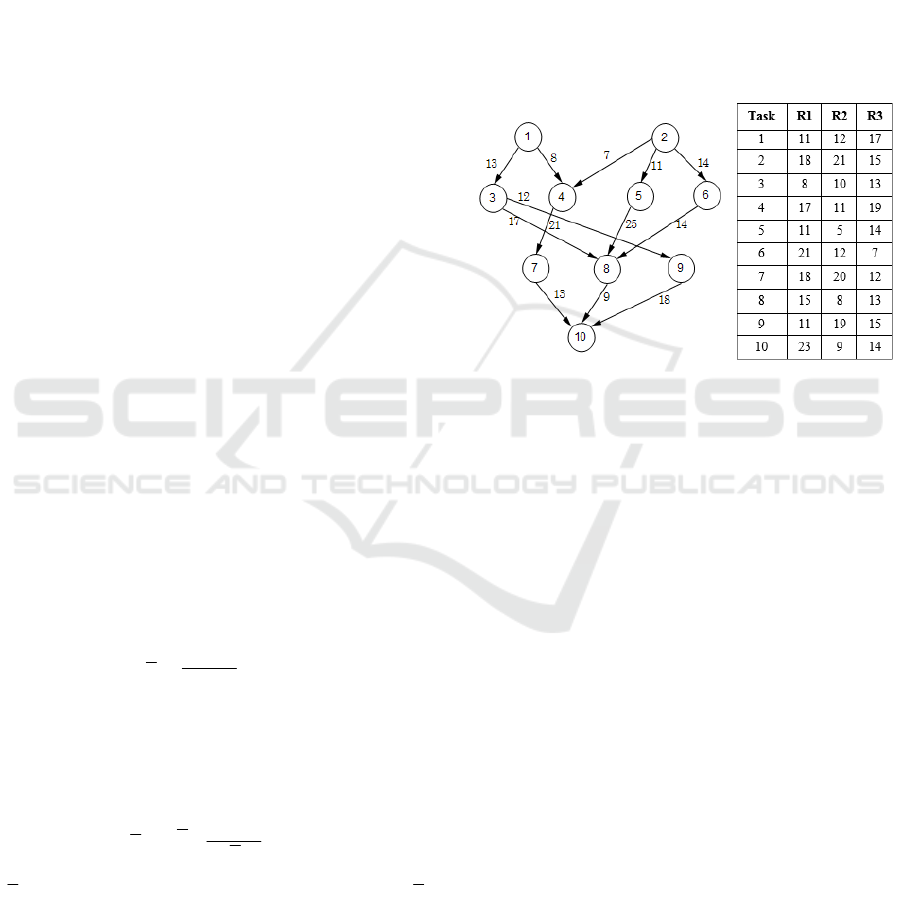
A task workflow example and a computation cost

matrix of tasks 1-10 for the resources R1, R2, R3 is

shown in Figure 1.

An popular metric in task scheduling is the

makespan or schedule length, which defines the finish

time of the last task in the given DAG. The makespan

is defined in Equation (3):

max{ ( )}

exit

makespan AFT n



(3)

where AFT(n

exit

) represents the Actual Finish Time of

the exit node.

Figure 1: An example of a task graph and a computation

time matrix of the tasks for each resource.

Furthermore, the Earliest Start Time EST (n

, p

)

of a node n

on a processor p

is defined in Equation

(4):

()

( , ) max{ ( ), max ( ( ) )}

i j avail j m m i

npredn

EST n p T p AFT n c







(4)

where T

avail

is the earliest time at which processor p

is ready to execute the task. pred(ni) is the set of

immediate predecessor tasks of task n

. The inner max

block in the EST equation denotes the time at which

all data needed by n

arrive at processor p

. The

communication cost c

m,i

is zero if the predecessor

node n

is assigned to processor p

Finally, EFT(n

) defines the Earliest Finish

Time of a node n

on a processor p

, which is defined

in Equation (5):

(, ) (, )

ij ij ij

FT n p EST n p w





(5)

4 CPOP AND HEFT

In this section, we describe two popular algorithms

for task scheduling, namely the Critical-Path-On-a-

Processor (CPOP) and the Heterogeneous-Earliest-

The Experiential Heterogeneous Earliest Finish Time Algorithm for Task Scheduling in Clouds

373

Finish-Time (HEFT) algorithms (Topcuoglu et al.,

2002; Arabnejad and Barbosa, 2014).

Canon et al., (2008) have compared 20 scheduling

algorithms and have concluded that both algorithms

perform well, but the HEFT algorithm is the best

algorithm in terms of makespan. Topcuoglu et al.

(Topcuoglu et al., 2002) also consider the HEFT

algorithm among the best list-based heuristic

algorithms, and use the CPOP algorithm, among

others, for comparison.

In both algorithms, the tasks are ordered based on

a scheduling priority defined by a ranking function.

The rank value for an exit task n

is:

()

rank n w

(6)

For other tasks, the rank values are computed

recursively based on the Equations (1), (2) and (6), as

defined in Equation (7):

()

() ( ())

max

ii ij j

nsuccn

rank n w c rank n



 

(7)

where succ(n

) is the set of immediate successors of

task n

,ij

is the average communication cost of

edge (i, j), and

is the average execution time of

task n

4.1 CPOP

The CPOP algorithm consists of two phases: task

prioritization and processor selection.

The task prioritization phase assigns the priority

of each task by computing the rank values for all

tasks. In CPOP, for a given application the graph uses

a critical path, where the length of this path is the sum

of the communication costs of the tasks on the path

and the communication costs between the tasks along

the path. The sum of rank values set the priority of

each task. Initially, the entry task is the selected task

and marked as a critical path task. An immediate

successor (of the selected task) that has the highest

priority value is selected and is marked as a critical

path. This process is repeated until the exit node is

reached (Topcuoglu et al., 2002). In the processor

selection phase, the task that has the highest priority

is selected for execution. If the selected task is on the

critical path, it will be scheduled on the critical path

processor. Otherwise, the task is assigned to a

processor that minimizes the earliest execution finish

time. The CPOP algorithm has O (v

x p) time

complexity, where v is the number of tasks and p is

the number of processors (Llavarasan and

Thambidurai, 2007; Arabnejad and Barbosa, 2014).

4.2 HEFT

Similarly, the HEFT algorithm also has the same two

phases: task prioritization and processor selection

(Topcuoglu et al., 2002; Arabnejad and Barbosa,

2014).

In the task prioritization phase, HEFT assigns the

priorities of all tasks by computing the rank for each

task, which is based on mean computation time and

mean communication cost. The task list is ordered by

decreasing of their rank values.

The processor selection phase schedules the tasks

on the processors that give the Earliest Finish Time

(EFT) for the task. The algorithm uses an insertion

policy that tries to insert a task at the earliest idle time

between two already scheduled tasks on a processor.

The slot should have enough capacity to

accommodate the task.

The HEFT algorithm also has O (v

x p) time

complexity, where v is the number of tasks and p is

the number of processors (Topcuoglu et al., 2002;

Llavarasan and Thambidurai, 2007; Arabnejad and

Barbosa, 2014).

5 EXPERIENTIAL HEFT

We now present a novel task scheduling algorithm,

called experiential HEFT (EHEFT), which gives the

original HEFT algorithm the ability to take the

workload and computational power of resources into

account when assigning a task to processor. In the

EHEFT algorithm, the average execution time of a

task is calculated by the definition given in Equation

(1). Furthermore, the calculation of the average

communication cost is performed according to

Equation (2). As an extension of Equation (7), we

have added a parameter that calculates the rank by

considering the minimum average execution time of

the task on each relevant resource. This novel rank

calculation is shown in Equation (8):

()

() ( ())min

max

ii ij j

nsuccn

rank n w c rank n





  



(8)

where R represents the set of processors; j is a

processor of the set of processors. The execution time

of the task i on processor j is defined by w

i,j

, while the

number of previous executions of the task in

processor j is defined by n

The proposed EHEFT algorithm is shown in

Algorithm 1.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

374

To prioritize processors that have executed a

given task in a more efficient manner in the past, a

sum and a count of previous execution times of tasks

for each of the resources in the cloud is stored. When

there is no such data, the EHEFT algorithm performs

exactly as the HEFT algorithm itself. Therefore, the

EHEFT algorithm we propose is highly dependent on

the values of the past execution times of tasks.

Algorithm 1: Experiential HEFT Algorithm.

1: Compute the computation cost for each

task according to Eq.(1)

2: Compute the communication cost of

edges according to Eq.(2)

3: Compute the average execution time of

previous runs:

for each task

for each machine do

sum up the time of the task’s

previous executions in the

assigned processor

end for

4: Calculate the minimum as the

proportion of the sum of Step 3 and

the number of executions of a task

in the assigned processor

5: end for

6: Compute the rank value for each task

according to Equation (8)

7: Sort the tasks in a scheduling list by

decreasing order of task rank values

8: while there are unscheduled tasks in

the list

9: Select the first task i from the

list

for each processor m do

Compute the EFT(i,m) value

end for

Assign task i to processor m that

minimized EFT of task i.

10: end while

Assuming a high heterogeneity between cloud

resources, variable processing powers, and

workloads, as well as taking into account that some

tasks are better suited for a particular processor

architecture than others, by including the minimum

average execution time of previous runs of a task in

the resources of the cloud, the EHEFT algorithm

gives precedence to a processor that has performed

better in executing a given task in the past.

6 EXPERIMENTAL RESULTS

We now present experimental results of our proposed

EHEFT algorithm compared to the existing HEFT

and CPOP algorithms. The tests were conducted on

an Intel Core i7-6500U CPU with a 2.50 GHz × 4

speed, 16 GB of RAM, on Ubuntu 16.04 LTS.

To evaluate the performance of the EHEFT

algorithm, task graphs that were generated randomly

are considered. We have implemented and simulated

the three algorithms using the Python programming

language. Our simulator has five input parameters:

the number of resources (i.e., processors) in the cloud,

the number of DAG nodes (i.e., tasks), connections

between tasks, resource heterogeneity, and previous

run statistics for each task. For simplicity, constant

values are set for the average computational and

communication costs. The simulator defines a set of

virtual resources with heterogeneous processing

powers, as well as current computational workloads

and communication costs for the given input DAG.

Resource heterogeneity is achieved by setting the

Beta parameter in the simulator. Its value defines the

ratio of the differences of processing powers between

resources in the cloud.

The simulator is fed with different input values to

test the variance of the algorithm in terms of

makespan and runtime under different conditions.

During our tests, the following parameters were used:

Beta = {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}

Number of DAG Tasks = {5, 10, 15, 20, 25}

Connectivity = {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8,

0.9, 1.0}

Number of Processors = {2, 3, 4, 5, 6}

Our experiments are run for each of the tasks in each

of the processors. Such test runs were performed to

collect statistics for the execution times that were then

used to calculate the minimum average execution

time for past runs of a given task on all cloud

resources. To avoid that this additional parameter

biases the ranking function, a scaling parameter is

used. This scaling parameter determines the weight of

the minimum average execution time for past runs in

the overall calculation of the rank. For all compared

algorithms, the simulation conditions were the same.

We use the following performance metrics for our

evaluation of the proposed approach.

6.1 Scheduling Length Ratio (SLR)

To evaluate a schedule for a single DAG, the most

commonly used metric is the makespan. The

makespan represents the finish time of the last task in

the scheduled DAG, as shown in Equation (3).

Considering that a large set of task graphs with

different properties is used, the schedule length

should be normalized to a lower bound, which is

known as the Schedule Length Ratio (SLR), defined

in Equation (9).

The Experiential Heterogeneous Earliest Finish Time Algorithm for Task Scheduling in Clouds

375

min { }

iMIN

Qij

nCP

makespan

SLR







(9)

The denominator in the SLR metric is the minimum

computation cost of the critical path tasks,

represented as CP

MIN

Figures 2-5 show the makespan of the three

algorithms calculated by the example task graph and

computation time matrix of the tasks in each

processor of Figure 1.

The calculation of the makespan is performed for

(a) Number of Tasks (Figure 2), (b) Connectivity

(Figure 3), (c) Number of Processors (Figure 4), and

(d) Processor Range (Figure 5).

In Figure 2, the simulations are run for five

different DAG nodes, with an increasing number of

nodes. As expected, the makespan increases with the

number of nodes for each of the algorithms we

evaluated. EHEFT performs better than the other

algorithms, because it considers the heterogeneity of

resources when calculating the rank for a task. It

assigns the execution of a task to a resource that not

only has the best present conditions to achieve the

earliest finish time, but that has also shown to do so

in the past.

Figure 2: Makespan for Number of Tasks.

Figure 3 shows that increasing the connectivity

between nodes of the input DAG also increases the

makespan of the algorithms linearly. The higher the

number of dependent tasks on the graph, the more

time it takes for the algorithm to assign and execute

the tasks.

Therefore, it is important to assign tasks that are

part of critical paths to resources that can execute

them in the fastest manner. In our simulations, we

have put more load on the tasks in the critical path.

Thus, the results indicate the ability of EHEFT to

assign such tasks to resources with the highest

processing power.

Figure 3: Makespan for Connectivity.

Figure 4 shows that increasing the number of

processors and a constant node number for the input

DAG decreases the makespan. The improvement in

performance of the EHEFT algorithm is due to the

variance in the calculation of the rank that the

statistics of previous runs provide.

Figure 4: Makespan for Number of Processors.

The main advantage of EHEFT over HEFT and

CPOP is the processor range parameter Beta, as

shown in Figure 5. EHEFT considers the processing

efficiency of a resource for a task, given its previous

run statistics. The performance of EHEFT improves

with the increase of the processor range, because it is

the factor that makes the highest difference with

respect to the average past execution time parameter.

Figure 5: Makespan for Processor Range.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

376

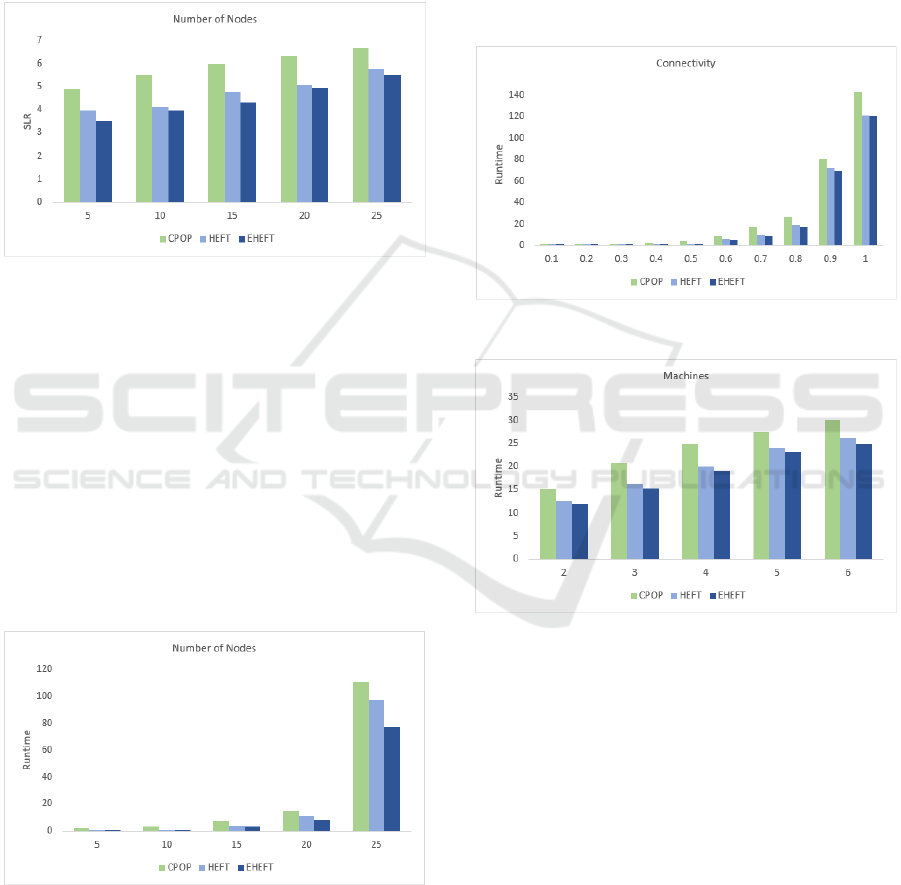
In Figure 6, we present the SLR value for each of

algorithms calculated from the number of nodes. The

graph shows that the SLR value for EHEFT is lower

than for the HEFT and CPOP algorithms.

6.2 Runtime

The runtime metric represents the execution time to

obtain the output of a schedule for a given task graph.

Figure 6: Scheduling Length Ratio.

The results for the runtimes of our performed

experiments are shown in the graphs below.

Figures 7-10 show the runtimes of each of the

algorithms calculated for the parameters (a) Number

of Tasks (Figure 7), (b) Connectivity (Figure 8), (c)

Number of Processors (Figure 9), and (d) Processor

Range (Figure 10).

Figure 7 shows that for small numbers of DAG

nodes the difference in runtime between EHEFT and

HEFT is small. The improvement in performance that

the minimum average execution time of the task for

each resource gives is only apparent when the number

of nodes in the input DAG increases.

Figure 7: Runtime for Number of Tasks.

Figure 8 shows that increasing the connectivity

between the nodes in the graph results in an increased

runtime for the algorithms. The small difference in

performance between EHEFT and HEFT is due to the

difference in the handling of critical path tasks in the

overall runtime. The CPOP algorithm takes more

time to execute due to its two phase rank calculation.

As shown in Figure 9, task assignment and

execution are performed in a faster manner with an

increasing number of simulated virtual resources, as

indicated by the decrease in the runtimes of the

algorithms. The EHEFT algorithm gains an edge in

performance due to its ability to assign the heavy

loaded tasks and the ones in the critical path to better

performing resources.

Figure 8: Runtime for Connectivity.

Figure 9: Runtime for Number of Processors.

Figure 10 shows that increasing the processor

range improves the performance of all the algorithms

that we evaluated. Since the CPOP algorithm assigns

only tasks on the critical path to critical path

processors, the EHEFT and HEFT algorithms show

better results due to the fact that not only critical path

tasks may be assigned to high performance resources.

Tasks that take more time to process and that are not

on the critical path of the graph are better assigned to

resources through the HEFT and EHEFT algorithms.

The difference in performance between the EHEFT

and HEFT algorithm lies in the fact that EHEFT

assigns tasks to resources that were better suited to

execute such tasks in the past.

The Experiential Heterogeneous Earliest Finish Time Algorithm for Task Scheduling in Clouds

377

Figure 10: Runtime for Processor Range.

7 CONCLUSION

In this paper, we have presented a novel task

scheduling algorithm for cloud environments, called

Experiential Heterogeneous Earliest Finish Time

(EHEFT) algorithm. In EHEFT, we have modified

the rank calculation of the original HEFT algorithm

by adding a parameter that specifies the minimum

average execution time of a task on each relevant

resource. The EHEFT algorithm performs better than

the original HEFT and CPOP algorithms in terms of

scheduling length ratio and runtime.

There are several areas for future research. First,

we will investigate and experimentally evaluate other

heuristic algorithms for task scheduling that consider

the priority of tasks. Second, for more efficient task

scheduling, other factors such as availability and

scalability should be considered. Finally, it would be

interesting to investigate multi-criteria and other

workflow-aware strategies in cloud environments,

including multiple virtual machine types and cloud

deployment models.

REFERENCES

Arabnejad, H., and Barbosa, J. G. (2014). List Scheduling

Algorithm for Heterogeneous Systems by an Optimistic

Cost Table. IEEE Transactions on Parallel and

Distributed Systems, 25(3), pages 1-14.

Bailin, P., Yanping, W., Hanxi, L., and Jie Q. (2014). Task

Scheduling and Resource Allocation of Cloud

Computing Based on QoS. Advanced Materials

Research, Vols. 915-916, pages 1382-1385.

Byun, E. K., Kee, Y. S., Kim, J. S., and Maeng, S. (2011).

Cost Optimized Provisioning of Elastic Resources for

Application Workflows. Future Generation Computer

Systems, 27(8), pages 1011–1026.

Canon, L.C., Jeannot, E., Sakellariou, R. and Zheng, W.

(2008). Comparative Evaluation of the Robustness of

DAG Scheduling Heuristics. Grid Computing -

Achievements and Prospects, edited by Sergei

Gorlatch, Paraskevi Fragopoulou and Thierry Priol,

pages 73-84. Springer.

Chen, W. N. and Zhang, J. (2009). An Ant Colony

Optimization Approach to a Grid Workflow Scheduling

Problem with Various QoS Requirements. IEEE

Transactions on Systems, Man, and Cybernetics, Part

C: Applications and Reviews, 39(1), pages 29-43.

Choudhary, M., and Peddoju, S. K. (2012). A Dynamic

Optimization Algorithm for Task Scheduling in Cloud

Environment. Journal of Engineering Research and

Applications (IJERA), 2(3), pages 2564-2568.

Cui, Y., and Xiaoqing, Z. (2018). Workflow Tasks

Scheduling Optimization Based on Genetic Algorithm

in Clouds. 3rd IEEE International Conference on

Cloud Computing and Big Data Analysis (ICCCBDA),

pages 6-10. IEEE.

Dubey, K., Kumar, M., and Sharma, S.C. (2018). Modified

HEFT algorithm for Task Scheduling in Cloud

Environment. Procedia Computer Science, Volume

125, pages 725-732. Elsevier.

Elzeki, O. M., Reshad, M.Z., and Elsoud, M.A. (2012).

Improved Max-Min Algorithm in Cloud Computing.

International Journal of Computer Applications,

50(12):22-27.

Garey, M. R., and Johnson, D. S. (1979). Computers and

Intractability; A Guide to the Theory of NP-

completeness. 1979.

Hu, Y., Wong, J., Iszlai, G., and Litoiu M. (2009). Resource

Provisioning for Cloud Computing. Conference of the

Centre for Advanced Studies on Collaborative

Research, CASCON ’09, pages 101-111. ACM.

Llavarasan, E., and Thambidurai, P. (2007). Low

Complexity Performance Effective Task Scheduling

Algorithm for Heterogeneous Computing

Environments. Journal of Computer Sciences, 3(2),

pages 94-103.

Malawski, M., Juve, G., Deelman E., and Nabrzyski J.

(2012). Cost- and Deadline-Constrained Provisioning

for Scientific Workflow Ensembles in IaaS Clouds.

Proceedings of the International Conference on High

Performance Computing, Networking, Storage and

Analysis, pages 1–11.

Pandey, S., Wu, L., Guru, S. M., and Buyya, R. (2010). A

Particle Swarm Optimization-based Heuristic for

Scheduling Workflow Applications in Cloud

Computing Environments. In 24th IEEE International

Conference on Advanced Information Networking and

Applications (AINA). IEEE.

Parsa, S., and Entezari-Maleki, R. (2009). RASA: A New

Task Scheduling Algorithm in Grid Environment.

World Applied Sciences Journal

, 7 (Special Issue of

Computer & IT), pages 152-160.

Rodriguez, M. A., and Buyya, R. (2014). Deadline Based

Resource Provisioning and Scheduling Algorithm for

Scientific Workflows on Clouds. IEEE Transactions on

Cloud Computing, 2(2), pages 222-235.

Singh, L., and Singh, S. (2013). A Survey of Workflow

Scheduling Algorithms and Research Issues.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

378

International Journal of Computer Applications,

74(15), pages 21-28.

Topcuoglu, H., Hariri, S., Wu, W. Min-You. (2002).

Performance-Effective and Low-Complexity Task

Scheduling for Heterogeneous Computing. IEEE

Transactions on Parallel and Distributed Systems,

13(3), pages 260-274.

The Experiential Heterogeneous Earliest Finish Time Algorithm for Task Scheduling in Clouds

379