A Semantic Approach for Handling Probabilistic Knowledge of Fuzzy

Ontologies

Ishak Riali, Messaouda Fareh and Haﬁda Bouarfa

LRDSI Laboratory, Faculty of Science, University Blida 1, Soumaa BP 270, Blida, Algeria

Keywords:

Fuzzy Ontologies, Fuzzy Bayesian Networks, Uncertainty, Vagueness, Semantic Web.

Abstract:

Today, there is a critical need to develop new solutions that enable classical ontologies to deal with uncertain

knowledge, which is inherently attached to the most of the real world’s problems. For that need, several

solutions have been proposed; one of them is based on fuzzy logic. Fuzzy ontologies were proposed as

candidate solutions based on fuzzy logic. Indeed, they propose a formal representation and reason in presence

of vague and imprecise knowledge in classical ontologies. Despite their indubitable success, they cannot

handle the probabilistic knowledge, which is presented in most of the real world’s applications. To address

this problem, this paper proposes a new solution based on fuzzy Bayesian networks, which aims at enhancing

the expressivity of the fuzzy ontologies to handle probabilistic knowledge and beneﬁts from the highlights of

the fuzzy Bayesian networks to provide a fuzzy probabilistic reasoning based on vague knowledge stored in

fuzzy ontologies.

1 INTRODUCTION

Ontologies provide an important key factor for rep-

resenting, reasoning, sharing, and reusing the knowl-

edge of domains. They provide the key to machine-

processbale data and permit to use it in more efﬁcient

way. They have been successfully used in order to

represent and reasoning with the knowledge in sev-

eral areas such semantic Web, artiﬁcial intelligence,

etc. Despite the great success of the classical ontolo-

gies, they were deemed inappropriate and fail when

handling uncertain knowledge that can appear inher-

ently in most of the real world’s problems. Indeed, the

uncertainty is a ubiquitous aspect of most real world

problems. It exists in almost every aspect of ontology

engineering(Pan et al., 2005).

To cope with uncertainty in ontologies, great deals

of efforts have been carried out. Fuzzy ontologies

were proposed in this context as promising solu-

tion, they beneﬁt from the power of fuzzy logic to

cope with vagueness in classical ontologies (Zadeh,

1975). Fuzzy ontologies handle effectively the lin-

guistic vagueness, which is attached inherently to the

most of the natural language. Moreover, they permit

to make lots of reasoning tasks based on vague con-

cepts and assertions in fuzzy ontologies using some

reasoners such as(Bobillo et al., 2012)(Bobillo and

Straccia, 2016). Despite the fact that fuzzy ontologies

were successfully applied in many challenging tasks,

they suffer from their inability to handle the proba-

bilistic knowledge.

Besides, Fuzzy Bayesian Networks (FBNs) have

been proposed as an extension of the classical ones to

cope with vagueness that may be attached to the ran-

dom variables. They can deal with probabilistic and

vague knowledge at the same time and execute proba-

bilistic reasoning based on fuzzy evidences. However,

they cannot represent the probabilistic knowledge in

a semantic formal way that is treatable by machine.

In fact, uncertainty is present in most of the real

world’s problems, and it becomes a serious challenge

to model and resonate with it in ontologies. Espe-

cially, when semantic Web agents are dealing with

open data such in Internet, where information is com-

bined from different sources and is often incomplete,

vague, etc. Indeed, imperfection is a common prop-

erty of the most real world applications. Therefore,

it is important to develop hybrid models that allow

handling these uncertainties simultaneously in on-

tologies. Thus, this paper proposes a novel solution

that tackles this problem, it combines fuzzy ontolo-

gies with fuzzy bayesian networks in order to bene-

ﬁt from the advantages of the both, where fuzzy on-

tologies allow handling vagueness in ontologies and

fuzzy Bayesian networks permit to cope with proba-

bilistic knowledge and make probabilistic reasoning

Riali, I., Fareh, M. and Bouarfa, H.

A Semantic Approach for Handling Probabilistic Knowledge of Fuzzy Ontologies.

DOI: 10.5220/0007724104070414

In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 407-414

ISBN: 978-989-758-372-8

 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

407

over vague knowledge.

The rest of this paper is organized as follows. In

Section 2, we brieﬂy introduce fuzzy ontologies then

we give a summary about Fuzzy Bayesian Networks.

In Section 3, we present our proposed approach. In

section 4 we discuss the related work and section 5

concludes this paper and talks about future works.

2 BACKGROUND

In this section, some background knowledge is pre-

sented including fuzzy ontologies and fuzzy Bayesian

networks.

2.1 Fuzzy Ontologies

Several deﬁnitions have been presented in the scien-

tiﬁc literature for what is a fuzzy ontology, but there

is no common deﬁnition. Indeed, many researchers

have proposed to extend ontologies with fuzzy logic.

The most shared characteristic of these propositions

is that they extend the components of the classical

ontologies in order to allow them representing vague

and imprecise knowledge. Refereeing to (Bobillo and

Straccia, 2011) , a fuzzy ontology is an ontology that

uses fuzzy logic to represent the world in a natu-

ral representation of imprecise and vague knowledge.

Therefore, eases reasoning over it.

A fuzzy ontology consists of a set of components:

• Fuzzy Concepts: are the concepts that have no

clear boundaries, they can be used to represent

fuzzy sets of individuals and allow representing a

gradual belonging of individuals to their classes;

• Fuzzy Roles: are divided into two classes, Fuzzy

object properties that are fuzzy binary relations

among concepts or individuals. They permit to

assign some degree to the association among the

instances of concepts (crisp or fuzzy). And fuzzy

data properties that permit to assign a degree to

the association among a data value and an instance

of fuzzy concept;

• Fuzzy Data Types: fuzzy data types are used to

fuzzify attributes values of concepts, such as the

range of data properties. They can also be at-

tached to a concept instance;

• Fuzzy Modiﬁers: are generally used in order to

change the interpretation of fuzzy concepts and

fuzzy datatypes.

2.2 Fuzzy Bayesian Networks

Fuzzy Bayesian networks proposed as hybrid models

that enhance the classical ones in order to cope with

vague and imprecise knowledge that may be attached

to the random variables. They combine the capabili-

ties of Bayesian networks and fuzzy logic to beneﬁt

from the advantages of the two models.

FBN is a Bayesian network extension that con-

sists of two types of nodes; crisps nodes are the nodes

whose meaning is precise, and the fuzzy nodes are the

nodes whose meaning is vague. Many experiments

have proved the beneﬁts of FBNs in wide diversity do-

mains and applications. Nonetheless, there is no uni-

ﬁed model which deﬁnes fuzzy Bayesian networks. In

fact, many solutions have been proposed in the scien-

tiﬁc literature in order to incorporate the membership

degrees with probabilities, which are:

• First, the weighted method (Mrad et al., 2012):

the main idea of this method is to extend the dif-

ferent rules used in the Bayesian networks by as-

sociating a membership degree value to each rule

as weight; then the fuzzy Bayesian rules can be

deﬁned to support the fuzzy Bayesian inference

in FBN model.

• Second, fuzzy distribution method (Ryhajlo et al.,

2013): in this method, the fuzzy membership de-

grees will be integrated directly in the probability

distribution, where in the ﬁrst step the fuzzy mem-

bership degree must be represented like a proba-

bility distribution, then this later will be integrated

in the probability distribution in order to gener-

ate the Fuzzy Probability Distribution. The Fuzzy

Probability Distribution is a hybrid representation

of the fuzzy membership degree and the probabil-

ity distribution.

• Finally, virtual evidence method (Li, 2009)(Peng

et al., 2010): this method consists to add new

nodes in the bayesian network called virtual evi-

dence nodes. Then incorporate the fuzzy evidence

in these latters, the fuzzy evidence will be rep-

resented as a probability distribution in the con-

ditional probability table (CPT) of each virtual

node. Then the fuzzy probabilistic inference can

be done by setting the evidences on the virtual

nodes and applying classical algorithms of infer-

ence.

3 THE PROPOSED APROACH

The study of the literature has showed that existing

works, when dealing with uncertainty residing in on-

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

408

tologies are not enough expressive and suffer from the

inability to deal with rich-uncertainty domains; where

vague, imprecise and probabilistic knowledge appears

simultaneously. Indeed, probabilistic knowledge and

fuzzy knowledge have been treated separately in on-

tologies and unfortunately, there is no efforts have

been devoted to cope with the two simultaneously in

the ontologies. In this paper, we consider this prob-

lem; we propose a probabilistic extension of fuzzy on-

tologies, which provides a strong mean foundation to

enable the fuzzy ontologies to cope with the proba-

bilistic knowledge based on fuzzy Bayesian networks.

It permits to handle both probabilistic knowledge and

fuzzy knowledge at the same time in ontologies.

The main idea behind our proposal is to deal with

the probabilistic knowledge in fuzzy ontologies by

creating an FBN based on an existing fuzzy ontol-

ogy in order to capture the probabilistic knowledge

involved within. In addition, incorporate this proba-

bilistic knowledge in the fuzzy ontology using a high-

level ontology in order to represent it in a formal way.

The proposed solution is described by a general pro-

cess that eases creating probabilistic fuzzy ontologies.

It refers to the phases illustrated in the Fig1.

The input of the proposed process is an fuzzy on-

tology (F1) that must confront probabilistic knowl-

edge which is involved in its elements.

3.1 Phase 1 (Speciﬁcation of

Requirements)

This phase aims to specify explicitly the purpose

that must be achieved by constructing a probabilis-

tic fuzzy ontology. In this step, the ontology engineer

must justify the needs and the requirements behind

the creation of ProbFuzzOnto ontology for the studied

domain. This step serves to identify the probabilistic

components of the fuzzy ontology that are relevant

for the considered problem and must be modeled in

the next steps.Thus, the main objectives of this step

are:

• To specify the objectives and the needs for creat-

ing probabilistic fuzzy ontology.

• To identify the probabilistic components of the

fuzzy ontology that are relevant to the studied do-

main.

3.2 Phase 2 (Probabilistic Knowledge

Design)

This phase is the core of our proposed solution, it

aims to model the probabilistic knowledge involved

in the fuzzy ontology using an Fuzzy Bayesian Net-

work. This is done by constructing an FBN based on

the requirements speciﬁed in the previous step, which

captures the probabilistic knowledge of the studied

domain. Therefore, the probabilistic knowledge de-

sign goes through three steps:

3.2.1 Constructing Structure of Bayesian

Networks.

In this step ontology engineer has to represent the

probabilistic components of the fuzzy ontology se-

lected in the previous phase in an FBN. The main

tasks of this step are:

• Node creation. Each selected concept will be rep-

resented by a node in the FBN.

• The ontology engineer must deﬁne the states of

each created node.

• Arcs creation. Each probabilistic role will be rep-

resented by an arc in the FBN.

3.2.2 Estimate the Conditional Probability

Tables (CPTs)

The aim of this step is to estimate the conditional

probability tables of the Bayesian network (parame-

ters). The most efﬁcient solution is to use machine-

learning algorithms in order to estimate the proba-

bility distributions from available data. However, in

practical cases, the data are incomplete and usually

contain missing values, where some random variables

are observed only partially or never.

For this reason, we propose the use of the most

applied method of estimating parameters with incom-

plete data. It is based on the iterative Expectation-

Maximization (EM) algorithm proposed by Dempster

in (Dempster et al., 1977). The EM algorithm al-

ternates between executing an expectation (E) step,

which creates a function for the expectation of the

log-likelihood evaluated using the current estimate for

the parameters, and maximization (M) step, which

computes parameters maximizing the expected log-

likelihood found on the E step. These parameter-

estimates are then used to determine the distribution

of the latent variables in the next E step.

3.2.3 Fuzzify the States of each Fuzzy Node

The objective of this step is to attribute to each state

of each fuzzy node a membership function, which is

already deﬁned in the fuzzy data types represented in

the fuzzy ontology.

A Semantic Approach for Handling Probabilistic Knowledge of Fuzzy Ontologies

409

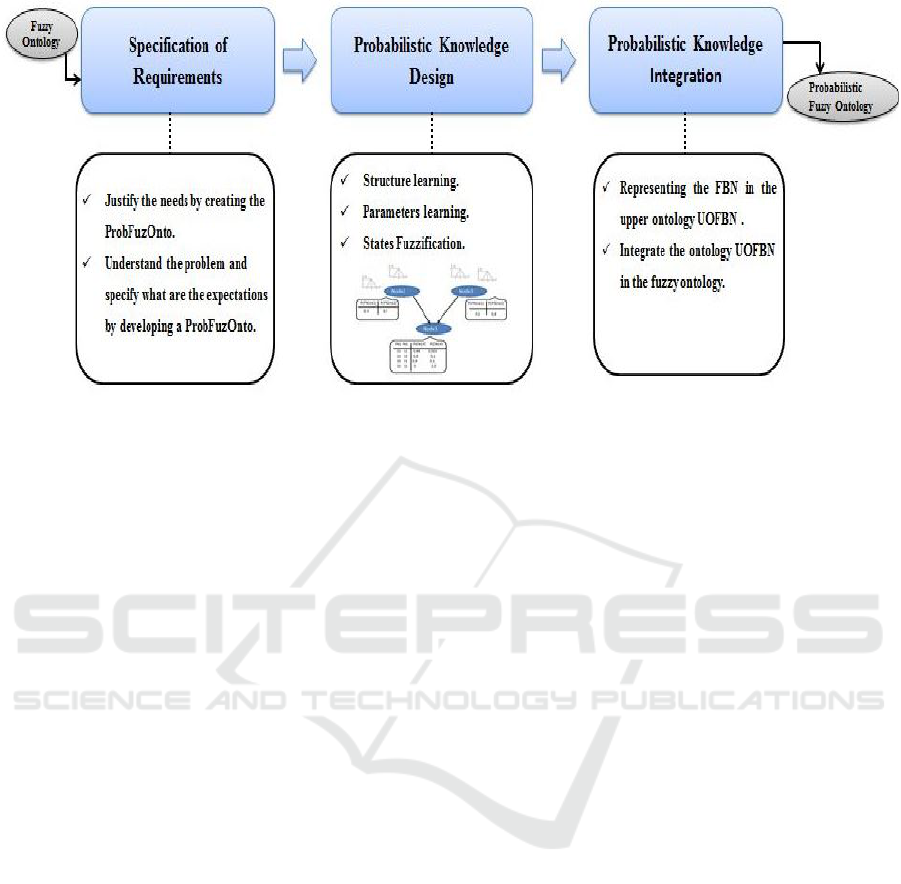
Figure 1: The proposed process for constructing Probabilistic Fuzzy Ontologies.

3.3 Phase 3 (Probabilistic Knowledge

Integration)

Despite the probabilistic knowledge involved in the

fuzzy ontology has been modeled and represented

in the previous steps in an Fuzzy Bayesian network

model. Nevertheless, this knowledge needs to be rep-

resented and formalized in a way that it can be read

and processable by machine. In other words, it needs

to be represented semantically. For this purpose, we

propose a high level ontology of FBN that permits to

represent semantically the fuzzy Bayesian networks

and then incorporate it in the fuzzy ontology.

Besides, the fuzzy Bayesian network created in

the previous step will be represented and described

in this high level ontology, which facilitates the

integration of the probabilistic knowledge in the

fuzzy ontology.

Deﬁnition 1. Fuzzy Bayesian Networks. An

Fuzzy Bayesian Network is deﬁned by 3-tuple

F =≺ G, M, P 

, where:

1. G= (N, A) is an acyclic graph.

(a) N = {n

,...,n

} is the set of the nodes

that constitute G. Where, N= Φ ∪ Ψ.

(b) Φ = { f n

, f n

,..., f n

} is the list of the

fuzzy nodes of F with size of k, with Φ ⊆ N.

,cn

,...,cn

} is the list of the

crisp nodes of F with size of j, with Ψ ⊆ N.

(d) A = {(n

)/n

∈ Nandn

∈ N} is a set of arcs,

each (n

) ∈ A represents a dependency link

between n

and n

(i.e, n

inﬂuences directly on

2. M = {m

,...,m

} is a ﬁnite set of the mem-

bership functions used to fuzzify fuzzy nodes.

3. P is the probability distribution of F.

Furthermore, each node n

∈ N has a set of ﬁnite

states S={s

,...,s

} , when n

∈ Φ. i.e., is fuzzy,

per each s

∈ S, a membership function m

∈ M will

be associated to s

in order to fuzzify this last.

Deﬁnition 2. Membership Function. Let Ω

be the universe of the discourse of s.

Then, a membership function m is deﬁned in Ω as

follows:

m: Ω → [0, 1].

Per each x ∈ Ω, the value m(x) is called the degree

of membership of x in s .

Deﬁnition 3. Mapping Function. A mapping

function Γ is a function that maps to each state s, its

membership function m.

Formally, Γ: S x M → False, True.

Property 1. Let s ∈ S and m ∈ M. Then Γ(s, m) =

True if only if m is the membership function used to

fuzzify s.

Each nodes n

∈ N has a probabilistic distribu-

tion, when a node is a root node (without parents)

its probabilistic distribution called Prior Probability

represented in prior table, when a node has parents its

probabilistic distribution is named Conditional Proba-

bilistic Table represented by a set of conditional prob-

abilities.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

410

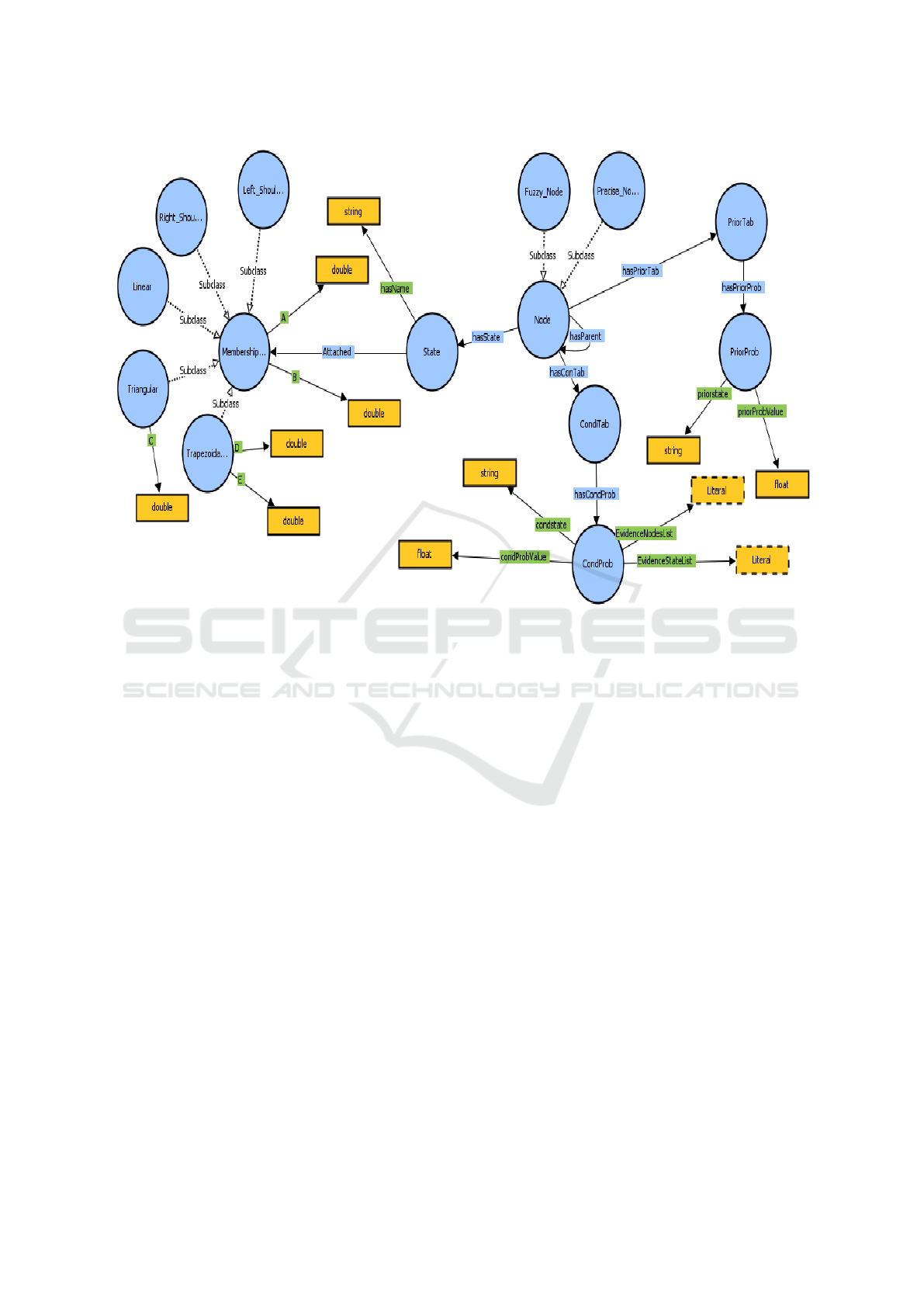
Figure 2: The upper ontology UOFBN.

Deﬁnition 4. A Prior Table. A prior table of a node

n ∈ N is a set of couples (s, P) that link to each state

with its prior probability Prior

. Formally:

PriorTab (n) = {Prior

,...,Prior

} , with a is the

number of states of the node n.

Prior

= (s

, P

), where,

∈ S: represents a state of the node n.

∈ [0, 1] : represents the prior value.

Deﬁnition 5. A Conditional Probabilistic Table. A

Conditional Probabilistic Table of a node n ∈ N is a

set of conditional probabilities, it is deﬁned as:

CondTab (n) = {Cond

,...,Cond

}, with b is the

number of states of the node n.

Cond

= (s

,ne

,se

), with :

∈ S : represents the state of the node n.

: represents the nodes of the evidence (observed

nodes).

: represents the states of the evidences nodes .

∈ [0, 1] : represents the conditional probability

value.

The UOFBN allows representing the semantic of

FBN and it is illustrated in the Fig. 2. It consists of a

set of class and properties:

1. Node Class. The nodes of the FBN will be rep-

resented by individuals of the class Node. In fact,

the nodes in an FBN can be crisp or fuzzy, for this

purpose, we created two subclasses of the class

Node in order to make a distinction between the

two types. The Fuzzy Node class, which includes

all the fuzzy nodes of the FBN, each fuzzy node

f n

∈ Φ, will be represented by an individual I f

of the class FuzzyNode. The Crisp Node class,

which includes all the crisp nodes of the FBN,

each crisp node cn

∈ Ψ will be represented by an

individual Ic

of the class CrispNode. Moreover,

the arcs between nodes can be represented by the

object property ”hasParent”.

2. State Class. The elements of this class are the

states related to each node n

, thus, per each state

∈ S, an individual I

will be created to represent

that state. Moreover, I

will be linked with

the node n

via the object property ”hasState”.

Moreover, when n

is fuzzy, all its states will be

fuzziﬁed using membership functions, for this

reason. An object property named ”Attached” is

deﬁned, which links each state with its member-

ship function m

A Semantic Approach for Handling Probabilistic Knowledge of Fuzzy Ontologies

411

3. Membership Function Class. This class rep-

resents the membership functions, it contains

ﬁve sub-classes (left-shoulder, right-shoulder,

triangular, linear function, and trapezoidal),

each membership function sub-class has a set

of arguments represented by data properties (A,

B, C, D, E). Thus, to each membership function

, an individual of the class ”Membership func-

tion” Im

will be created to represent that function.

4. The probabilistic table of each node will be rep-

resented using the classes ”CondTab” and ”Pri-

orTab”.

(a) CondTab. For each root node, an instance

”pr” of this class will be created to repre-

sent its probabilistic table. Moreover, a set of

prior probabilities P= {Prior

,...,Prior

} will

be created as instances of the class “PriorProb”.

These instances will be linked with their table

”pr” via the object property ”hasPriorTab”.

(b) PriorTab. For each node with parents, an

instance ”cpt” of this class will be created

to represent its probabilistic table. More-

over, a set of conditional probabilities C=

{Cond

,....,Cond

} will be created as instances

of the class ”CondiTab”. These instances will

be linked with their conditional table ”cpt” via

the object property ”hasCondTab”.

At the end of the proposed process, the fuzzy ontol-

ogy F1 will be augmented and enriched with proba-

bilistic knowledge; it can represent both fuzzy knowl-

edge and probabilistic one and make a probabilistic

reasoning based on fuzzy evidences stored in the on-

tology.

4 RELATED WORK AND

DISCUSSION

Many solutions have been provided in the scientiﬁc

literature to cope with uncertainty in ontologies; in

this section we investigate the most relevant works.

Authors in (Yang and Calmet, 2005), proposed

an extension of the ontology Web language (OWL),

which is named Bayes OWL; it allows a set of rules

for translating OWL ontology to a Bayesian network.

It also provides a method for incorporating avail-

able probability constraints when constructing the

Bayesian network especially when constructing the

conditional probability tables.

In (Ding et al., 2006), the authors proposed an

extension called OntoBayes. It enhances knowledge

representation in OWL and enables agents to act un-

der uncertainty; the authors deﬁned additional OWL

classes that can be used to markup probabilities and

dependencies in OWL. Both OntoBayes and Bayes

OWL are unable to cope with the vague an imprecise

knowledge.

In (Costa et al., 2008) (Carvalho et al., 2017),

PROWL was proposed as an extension that enables

ontologies represented in OWL to model and res-

onate under uncertain knowledge in complex real-

world applications. It can encode probabilities dis-

tributions on the interpretation of an associated ﬁrst-

order theory as well as repeated structure based on

the Multi-Entity Bayesian Network (MEBN) formal-

ism (Laskey, 2008). Despite its robustness in terms

of expressivity, its use remains very complicated for

non-expert users of its modeling details. Moreover, it

is based on MEBN. However, the MEBN community

is not broad enough to consider it as a new standard

for modeling uncertainty (Setiawan et al., 2015).

In (Ishak et al., 2011), an extension of ontolo-

gies based on Oriented Object Bayesian Networks

(OOBNs) has been developed. In this approach, au-

thors deﬁned a set of mapping rules in order to con-

struct an OOBN based on ontology. Despite the fact

that this extension can cope with complex problems

based on OOBNs, the vague and imprecise knowl-

edge is not taken into account by this extension.

In (Emna et al., 2016a)(Emna et al., 2016b), a

probabilistic extension of OWL 2 Meta-Model is

presented which is named Probabilistic Ontology

Deﬁnition Meta-Model (PODM). This is done by

adding some new components such as Probabilis-

tic Class, Probabilistic Individual, Probabilistic Data

Property. . . etc. The main defect of this approach is

that it cannot cope with the vague knowledge in the

ontology.

Lately, in (Mohammed et al., 2016), an extension

named hybrid probabilistic ontology based on the hy-

brid Bayesian networks is proposed. The merit of

this extension is that it allows handling simultane-

ously distributions over discrete and continuous quan-

tities in the ontology. Nevertheless, it cannot deal

with vague and imprecise knowledge in the ontolo-

gies, neither reason with it.

Recently, a method to construct the probabilis-

tic ontologies is developed in (Hlel et al., 2018), it

is based on the classical Bayesian networks to cope

with probabilistic knowledge in the classical ontolo-

gies, this method focuses on converting only the com-

ponents of ontology that can support uncertainty in

a BN graph(focus on instances and roles of the on-

tology). However, when constructing the CPTs, this

method does not consider the missing data and it ig-

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

412

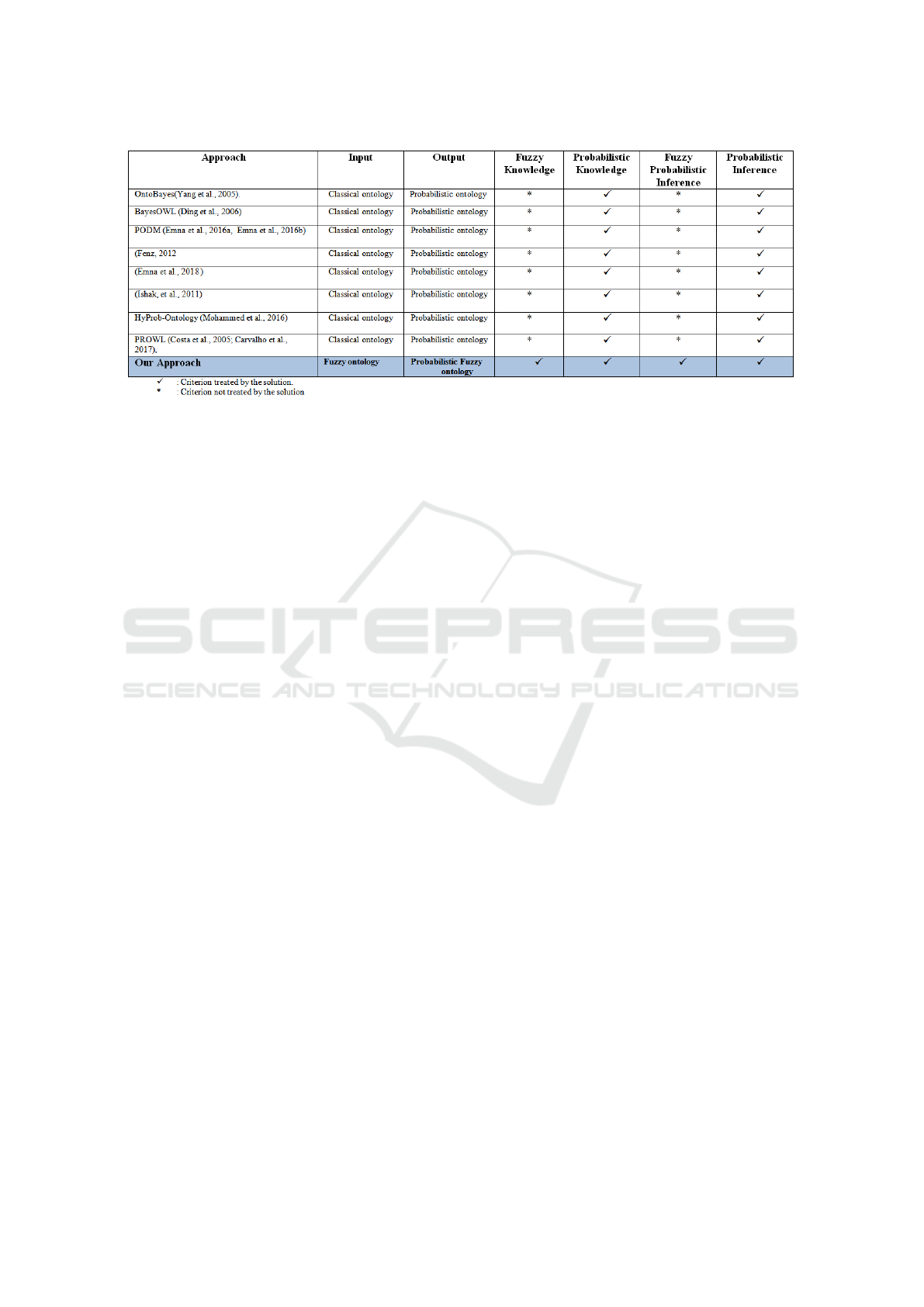
Figure 3: The differences between our approach and the related work.

nores vague and imprecise knowledge.

Based on the study of the related work, we can see

clearly that most of the related work are based on clas-

sical Bayesian networks and their extensions to deal

with probabilistic knowledge in classical ontologies.

Unfortunately classical BNs fail to handle the vague

knowledge that may be attached to the nodes of these

networks and their inference is based on certain evi-

dence.

Indeed, the proposed solution in this paper aims

to model probabilistic knowledge in fuzzy ontolo-

gies, it combines the advantages of fuzzy ontologies

and fuzzy Bayesian networks to beneﬁts from both of

them. Indeed, Fuzzy Bayesian networks allow deal-

ing with probabilistic events based on fuzzy evidence

to perform a fuzzy probabilistic inference. Neverthe-

less, they cannot model this knowledge in a formal

way that is treatable automatically by machine.

Fuzzy ontologies on the other side allow repre-

senting and make some reasoning tasks such as in-

dividual classiﬁcation based on vague knowledge.

The table 1 compares between the different proposed

solutions in the literature, according to their provided

mechanisms in terms of modeling and reasoning.

In the table 1:

• The Inputs Column: represents the input taken

by each solution, it can be classical ontology or

fuzzy ontology.

• Fuzzy Knowledge Column: it indicates if the so-

lution treats Fuzzy Knowledge and provides alter-

natives in order to represent vagueness in ontolo-

gies.

• Probabilistic Knowledge Column: it indicates

if the solution considers Probabilistic Knowledge

and provides alternatives in order to represent it

semantically in ontologies.

• Probabilistic Inference Column: it indicates if

the solution provides probabilistic reasoning or

not.

• Fuzzy Probabilistic Inference Column: it indi-

cates if the solution provides probabilistic reason-

ing (Fuzzy Probabilistic inference) based on fuzzy

evidences or not.

• The Outputs Column: Represents the results

given by the solutions. It can be probabilistic on-

tology or probabilistic fuzzy ontology.

Indeed, most of the proposed solutions in the lit-

erature focus on exploiting the classical BNs in order

to deal with the probabilistic knowledge in classical

ontologies. Unfortunately, classical BNs fail to han-

dle the vague knowledge that may be attached to the

nodes of these latters.

Moreover, all the probabilistic extensions are

based on extending OWL language to deal only with

the probabilistic knowledge. These extensions are

limited to handle just the probabilistic knowledge and

do not consider the vague and imprecise one.

In the contrary, our solution aims to combine the

advantages of fuzzy ontologies and FBs. Thus, the

underlying key of our proposed solution is that:

• It is a probabilistic extension of fuzzy ontologies,

which is expressive enough to cover the needs of

most of real world’s problems. So far, it allows

handling and representing formally vague, impre-

cise and probabilistic knowledge simultaneously

in ontologies.

• It introduces a process for building ProbFuzOnto

based on fuzzy ontologies.

• It provides several reasoning tasks, where all the

tasks of reasoning that can be applied on fuzzy

ontologies are still valid in our extension.

A Semantic Approach for Handling Probabilistic Knowledge of Fuzzy Ontologies

413

5 CONCLUSIONS

In this paper, we introduced a new solution that aims

to improve the knowledge representation and rea-

soning with uncertain knowledge in fuzzy ontolo-

gies. The proposed solution is described by a gen-

eral process, which takes as an input a fuzzy ontol-

ogy and outputs a probabilistic fuzzy ontology. The

merit of our proposal is that it can represent and rea-

son with rich-uncertainty domains, where it models

the vague, imprecise and probabilistic knowledge si-

multaneously and combines the ontological inference

with the fuzzy probabilistic inference.

As future works, we are looking to present real cases

studies with our proposed approach to show its poten-

tial applicability in terms of modeling and reasoning.

Moreover, we are looking to implement an interactive

prot

e-plugin in order to help ontology developers to

follow our proposed process.

REFERENCES

Bobillo, F., Delgado, M., and G

omez-Romero, J. (2012).

Delorean: A reasoner for fuzzy owl 2. Expert Systems

with Applications, 39(1):258–272.

Bobillo, F. and Straccia, U. (2011). Fuzzy ontology rep-

resentation using owl 2. International Journal of Ap-

proximate Reasoning, 52(7):1073–1094.

Bobillo, F. and Straccia, U. (2016). The fuzzy ontology

reasoner fuzzydl. Knowledge-Based Systems, 95:12–

34.

Carvalho, R. N., Laskey, K. B., and Costa, P. C. (2017).

Pr-owl–a language for deﬁning probabilistic ontolo-

gies. International Journal of Approximate Reason-

ing, 91:56–79.

Costa, P. C., Ladeira, M., Carvalho, R. N., Laskey, K. B.,

Santos, L. L., and Matsumoto, S. (2008). A ﬁrst-order

bayesian tool for probabilistic ontologies. In Proceed-

ings of the Twenty-First International Florida Artiﬁ-

cial Intelligence Research Society Conference, pages

631–636.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the em

algorithm. Journal of the Royal Statistical Society:

Series B (Methodological), 39(1):1–22.

Ding, Z., Peng, Y., and Pan, R. (2006). Bayesowl: Uncer-

tainty modeling in semantic web ontologies. In Soft

computing in ontologies and semantic web, pages 3–

29. Springer.

Emna, H., Salma, J., Mohamed, T., and Abdelmajid, B. H.

(2016a). Building probabilistic ontologies based on

meta-model podm. In International Conference on

Hybrid Intelligent Systems, pages 288–297. Springer.

Emna, H., Salma, J., Mohamed, T., and Abdelmajid,

B. H. (2016b). Probabilistic ontology deﬁnition meta-

model. In Intelligent Decision Technologies 2016,

pages 243–254. Springer.

Hlel, E., Jamoussi, S., and Hamadou, A. B. (2018). A new

method for building probabilistic ontology (prob-ont).

In Information Retrieval and Management: Concepts,

Methodologies, Tools, and Applications, pages 1409–

1434. IGI Global.

Ishak, M. B., Leray, P., and Amor, N. (2011). Ontology-

based generation of object oriented bayesian net-

works. In Bayesian Modeling Applications Workshop

(BMAW-11). Citeseer.

Laskey, K. B. (2008). Mebn: A language for ﬁrst-order

bayesian knowledge bases. Artiﬁcial intelligence,

172(2-3):140–178.

Li, X. (2009). On the use of virtual evidence in conditional

random ﬁelds. In Proceedings of the 2009 Conference

on Empirical Methods in Natural Language Process-

ing: Volume 3-Volume 3, pages 1289–1297. Associa-

tion for Computational Linguistics.

Mohammed, A.-W., Xu, Y., and Liu, M. (2016).

Knowledge-oriented semantics modelling towards un-

certainty reasoning. SpringerPlus, 5(1):706.

Mrad, A. B., Delcroix, V., Maalej, M. A., Piechowiak, S.,

and Abid, M. (2012). Uncertain evidence in bayesian

networks: Presentation and comparison on a simple

example. In International Conference on Informa-

tion Processing and Management of Uncertainty in

Knowledge-Based Systems, pages 39–48. Springer.

Pan, R., Ding, Z., Yu, Y., and Peng, Y. (2005). A bayesian

network approach to ontology mapping. In Inter-

national Semantic Web Conference, pages 563–577.

Springer.

Peng, Y., Zhang, S., and Pan, R. (2010). Bayesian network

reasoning with uncertain evidences. International

Journal of Uncertainty, Fuzziness and Knowledge-

Based Systems, 18(05):539–564.

Ryhajlo, N., Sturlaugson, L., and Sheppard, J. W. (2013).

Diagnostic bayesian networks with fuzzy evidence. In

2013 IEEE AUTOTESTCON, pages 1–8. IEEE.

Setiawan, F. A., Wibowo, W. C., and Ginting, N. B. (2015).

Handling uncertainty in ontology construction based

on bayesian approaches: A comparative study. In

International Conference on Soft Computing, Intel-

ligence Systems, and Information Technology, pages

234–246. Springer.

Yang, Y. and Calmet, J. (2005). Ontobayes: An ontology-

driven uncertainty model. In International Conference

on Computational Intelligence for Modelling, Control

and Automation and International Conference on In-

telligent Agents, Web Technologies and Internet Com-

merce (CIMCA-IAWTIC’06), volume 1, pages 457–

463. IEEE.

Zadeh, L. A. (1975). The concept of a linguistic variable

and its application to approximate reasoning-iii. In-

formation sciences, 9(1):43–80.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

414