
Accelerating Urban Modelling Algorithms with Artificial Intelligence
Richard Milton
1
and Flora Roumpani
2
1
Centre for Advanced Spatial Analysis, University College London, 90 Tottenham Court Road, WC1E 6BT, U.K.
2
The Alan Turing Institute, The British Library, London, U.K.
Keywords:
Urban Modelling, Spatial Interaction Modelling, Artificial Intelligence, 3D Visualisation.
Abstract:
In this paper, we demonstrate that developments in computer hardware to support the increasingly complex
artificial intelligence workflows for Deep Learning networks can be adapted for urban modelling and visual-
isation. The hypothesis here is that by leveraging the current practice of AI as a Service (AIaaS), then this
enables Urban Modelling as a Service (UMaaS) to be developed. The starting point for this paper is a 3D vi-
sualisation of the Queen Elizabeth Olympic Park, developed using a web-based spatial interaction modelling
system which calculates population metrics on the fly, capable of showing the results of interventions by urban
planners in real-time. We take the web application that powers the interactive visualisation and use Google’s
TensorFlow AI library to accelerate the matrix operations required to run the spatial interaction model, making
the web application fast enough to be used interactively.
1 INTRODUCTION
This work takes our existing ‘QUANT’ website for
spatial interaction modelling (figure 1) and uses its
core modelling services in an interactive 3D planning
scenario based around housing requirements for the
Queen Elizabeth Olympic Park. Our stated aim is to
use AI hardware acceleration to build an ‘urban mod-
elling as a service’ system to provide urban planners
with the ability to build their own applications, exper-
iment and see immediate results. This then allows us
to take a step further, and we test a number of neural
spatial interaction models, asking the question about
which mathematical model best fits the data.
Figure 1: The QUANT Website, http://quant.casa.ucl.ac.uk,
showing the travel to work flows.
While the links between artificial neural net-
works (ANNs) and spatial interaction models have
been cited in the literature as far back as (Fischer
and Sucharita, 1994), (Black, 1995) and (Openshaw,
1997), recent advances in specialised computing ar-
chitectures designed to accelerate the matrix opera-
tions required to train a large-scale deep neural net
have now become mainstream. As a consequence of
this, open-source libraries such as TensorFlow (Abadi
et al., 2016), Keras (Chollet, 2015), PyTorch (Paszke
et al., 2017) and Caffe (Jia et al., 2014), can rou-
tinely deal with ANNs that are orders of magnitudes
larger than a previous generation. These libraries are
designed to work on conventional CPUs for small-
scale work, in addition to utilising the multiple par-
allel cores of graphics processing units (GPUs) for
large-scale networks. Add to this the Tensor Process-
ing Units (TPUs), designed by Google for AI work-
flows at the level of warehouse scale computing, plus
a myriad of other custom hardware for vision and
speech processing ‘at the edge’ (e.g. MOVIDIUS
Neural Compute Stick (Intel, 2019)) and the poten-
tial exists to make use of this high performance cloud
and desktop processing capability. The natural ques-
tion to ask is how to make a symbiotic link between
the current advances in AI and existing urban mod-
els? This paper sets out to put urban modelling into
the context of mainstream AI to both accelerate the
current computer models and to suggest new avenues
Milton, R. and Roumpani, F.
Accelerating Urban Modelling Algorithms with Artificial Intelligence.
DOI: 10.5220/0007727201050116
In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 105-116
ISBN: 978-989-758-371-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
105

for future research. Existing applications of “AI as
a Service” can be cited which relate to object and
speech recognition, natural language processing and
other artificially intelligent systems, but there is an
absence of applications relating to urban modelling.
While one discipline seeks to give computers human
abilities, the other seeks to explain and predict hu-
man behaviour. A commonality exists where the pat-
tern matching abilities of ANNs are compared and
contrasted with the calibration and ‘model parameter
fitting’ phase common in many types of urban mod-
elling. In effect, both are seeking to minimise an error
term and find the best fit for the data available.
The decision to focus on spatial interaction mod-
elling is based on the already established theoretical
links with ANNs, which are expanded upon in section
2. The initial work on QUANT developed a website
for spatial interaction modelling using 7,201 zones
for England and Wales. This is introduced in sec-
tion 3 and provides the real-life urban planning sce-
narios used to test the algorithmic and architectural
improvements. The urban datasets used in QUANT,
for example the travel times between zones and trip
matrices, are re-used in this paper, which extends the
urban modelling system beyond the current capabili-
ties of the QUANT system. This is a step-change in
performance, as, while QUANT takes around 10 sec-
onds to run a model, the system presented here takes
just 0.28 seconds. The modular and web-based design
of the system means that these improvements can be
easily incorporated and used with both 2D and 3D vi-
sualisation workflows. As an application of the the-
ory, we present the Queen Elizabeth Olympic Park
(QEOP) urban planning example, which is a Unity
application that requires the immediate urban mod-
elling enabled by the work in this paper. Unity is a
3D game engine development environment, which is
introduced in, “Unity 3D Game Development by Ex-
ample” (Creighton, 2010). While this serves as a vi-
sual front-end for planners who use the system, by
improving the performance of the spatial interaction
modelling algorithms, we demonstrate a step in per-
formance that makes the immediate urban modelling
required by the 3D application possible.
2 RELATED WORK
In his 1997 book, “Artificial Intelligence in Geogra-
phy” (Openshaw, 1997), Openshaw demonstrates the
application of an ANN to a spatial interaction mod-
elling problem involving flows of people. Following
on from this, in “Building an Automated Modeling
System to Explore a Universe of Spatial Interaction
Models” (Openshaw, 1998a), a ‘universe’ of mod-
elling equations is fitted to calibration data in an at-
tempt to find the equation that describes the data with
the lowest error. The interesting result here is that
the traditional gravity model equations do not give the
best fit with the training set. In all of these examples,
the inputs to the models are the origin and destination
attractions, derived from the flows, and the distance
between zones. For the purposes of the following
discussion, a singly constrained spatial interaction, or
gravity model, is defined by the following equation:
T
i j
= A
i
O
i
D
j
e
−βc
i j
(1)
A
i
=
1
∑
j
D
j
e
−βc
i j
(2)
i, j = origin and destination zone numbers,
c
i j
= cost of travel between them,
β = parameter for willingness to travel given cost,
O
i
= origin attraction,
D
j
= destination attraction,
A
i
= balancing factor
An important distinction to make concerns the
number of degrees of freedom of the model and the
method of training or calibration. In a spatial inter-
action model, the calibration involves fitting a pa-
rameter, β, that defines how far people are willing
to travel. In Openshaw’s neural spatial interaction
model, the net has been trained to predict flow from
origin (O
i
) and destination (D
j
) attractions at the in-
put layer. The β parameter is learnt by the network
as a ‘black box’, which could explain why neural spa-
tial interaction modelling techniques are not widely
adopted. However, the point being made here is one
of equivalence and some of the beliefs of neural nets
as being black boxes that defy explanation are chal-
lenged in the remainder of this paper. Here we argue
that black boxes are not the only option, advocating a
different approach which leads to “Urban Modelling
as a Service” for the exploration and explanation of
different scenarios. By way of comparison with equa-
tion 1, a simple ‘feed forward’ neural network is de-
fined as follows:
v
k
=
∑
j
w
k j
h
j
(3)
y
k
= ϕ(v
k
) + θ
k
(4)
v
k
= neuron k internal state,
w
k j
= weight between input j and neuron k,
h
j
= input to neuron j,
y
k
= neuron output,
ϕ = activation function,
θ
k
= bias value
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
106

In “Spatial Interaction Models: From the Gravity
to the Neural Network Approach” (Fischer and Reg-
giani, 2005), Fischer and Reggiani discuss different
forms of spatial interaction models, from singly and
doubly constrained through to a singly constrained
neural spatial interaction model, including the choice
of activation function (ϕ(v
k
) in equation 3). Their
conclusion states that the classic gravity model equa-
tions (equation 1) are the preferred choice because
of the “simplicity of their mathematical form and the
theoretical nature of their underlying assumptions”.
However, they go on to say that the neural network
approach is attractive in “data-rich environments” and
where “little is known about the form of the spatial
interaction function to be approximated”. In “Why
does deep and cheap learning work so well?” (Lin
et al., 2017), Lin shows how a three layer continu-
ous input feed forward network can be made to ap-
proximate a gate multiplier to any degree of accuracy.
Their analysis of the types of functions that deep neu-
ral networks can be made to approximate is impor-
tant in the context of modelling when the function
underlying the observed data is under investigation.
This final point fits with our statement in the intro-
duction about discovering new avenues of research.
The initial research with our previous QUANT model
was to see whether a large-scale model covering the
whole of England and Wales was possible. One of the
difficulties with spatial interaction modelling is that
the algorithm is of order O(n
2
), while the number of
zones, n, can be in the thousands in order to combat
edge effects and demonstrate the finer grain detail of
the model. It should be noted that the QUANT sys-
tem currently runs equation 1 in 1.23 seconds on an
8 core CPU using parallel optimisations
1
, while a test
using OpenCL achieved the same result, but taking
only 0.25 seconds. This test was using dual NVIDIA
GTX 980 Ti GPUs, each with 640 cores clocked and a
quoted speed of 1306 GFLOPS. This evidence forms
our basis for believing that urban modelling can be
influenced by the current pace of AI research. One
thing stands out about equation 1 above all else. It is
‘pure parallel’, in that there are no loop dependencies
between different i or j indexes, so every T
i j
can be
calculated independently without having to wait for
a prior dependency. This fact, which is backed by
the evidence in the following results section, is the
cornerstone of our argument. The re-formulation of
the spatial interaction model equations into a parallel
form enables maximum usage of all available process-
ing cores on any massively parallel architecture.
1
The gravity model formula in equation1 needs to exe-
cute n x n times to compute every value in the matrix where
n = 7201 zones, giving rise to ≈ 52million iterations.
The final point to note regards the number of zones
in the model. While Black’s example (Black, 1995)
had 9 zones, Openshaw’s example of Durham had
73 zones. The example here has 7,201 zones for the
whole of England and Wales, so the goodness of fit of
a neural spatial interaction model of this size is one
metric to be investigated, as it is possible that the net-
work might not train on a model of this size. Also, the
observed matrix contains 51, 854, 401 training sam-
ples.
In the following sections we demonstrate our cur-
rent work on building a web-based urban modelling
framework. The key consideration influencing the de-
sign is for immediate results, rather than having to
wait hours for a simulation to run, as was the case in
the past. This focuses our work on urban modelling
for experimentation and exploration.
3 OVERVIEW
Previously, it has not been possible to create models
with the number of zones we require and that also run
fast enough on the hardware to make “Urban Mod-
elling as a Service” (UMaaS) a viable proposition.
Our method enables this through a set of web ser-
vices acting as a “model view controller” and provid-
ing the client with a REST API for the urban mod-
elling functions. As this is a real-time modelling ser-
vice, the main requirement is to provide the user with
model outputs fast enough to be interactive. In or-
der to achieve this, we use the software and hardware
improvements being driven by “AI as a Service” to
power “Urban Modelling as a Service”.
While equation 1 introduced the basic gravity
model equation, there are four variants that are de-
fined as follows: unconstrained, singly constrained
origin, singly constrained destination and doubly con-
strained. A complete description can be found in
“A Family of Spatial Interaction Models” (Wilson,
1971). For simplicity, the results presented here fo-
cus on the singly constrained origin model, but the
results are directly applicable to all four variants.
Of paramount importance to our case for ‘urban
modelling as a service’ is the quantity and variety of
data required to build a real urban model, as opposed
to a theoretical example. The data required for the
model are: zone boundaries, zone centroids, network
graphs for each mode of travel (e.g. road, rail, bus),
cost function between zones per mode of travel (c
i j
),
resident population, workplace population, travel to
work flow matrix per mode (T
i j
), land use (building
constraints on space), green belt, parks and protected
areas.
Accelerating Urban Modelling Algorithms with Artificial Intelligence
107

Figure 2: Single Source Shortest Path runs on random networks with varying numbers of vertices. The graph on the right is
for a sparse network (e = 0.9v), while the left graph is more highly connected (e = 5v). The relative positions of the rail, bus
and road networks are shown on the graph to give a sense of scale.
Figure 3: Left: road network (8.4M edges), Centre: bus network (0.42M edges) and Right: rail network (10,269 edges).
The cost function is required for every zone pair
and mode, yielding an n x n matrix that matches the
dimensions of the flow matrix. This is significant
undertaking computationally when n = 7201 =⇒
51, 854, 401 trips, where each trip requires running
a shortest path algorithm to obtain the minimum trip
time on a network graph containing 8 million edges.
Figure 3 shows the three transport networks behind
how the cost matrices are calculated. The two graphs
in figure 2 show the application of Nvidia’s nvGraph
library to this problem. While the cost matrices used
in this paper use the real transport network for Eng-
land and Wales (figure 3), the tests in figure 2 are for
randomised networks with two variations on the ratio
of the number of edges to the number of vertices.
4 APPLICATION
The current release of QUANT, simulates the im-
pact of changes in population, employment and travel
costs in UK Cities, using a simple model of how
workers choose where to live in respect to the attrac-
tiveness of those places and the cost of traveling to
their workplaces. By building this as a set of web ser-
vices, the core modelling component can be re-used
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
108

Figure 4: The Unity 3D Olympic Park application. A scenario built using the QUANT web services core (figure 5).
in other scenarios. The following sections describe
how the QUANT urban modelling services are used
in a 3D interactive planning application for the Queen
Elizabeth Olympic Park (figure 4). The application
tests scenarios online by assigning proposed increase
in employment, and by calculating flows of popula-
tion based on a singly constrained spatial interaction
model. These are based on three means of transporta-
tion: tube, buses and trains. As such it can calculate
inter-city flows that come from not only within Lon-
don, but from all of the UK.
This is very useful for the evaluation of master-
plans for areas in metropolitan cities such as Lon-
don. For example, The London Legacy Development
Corporation (LLDC) is now using the opportunity of
the London 2012 Games and the opening of Queen
Elizabeth Olympic Park (QEOP) to create “a dynamic
new metropolitan centre for London, and develop an
inspiring and innovative place where people want –
and can afford – to live, work and visit” (LLDC,
2011). The plans include large scale residential de-
velopments and supralocal commercial centres such
as Westfield London, that are programmed to attract
people from all over London and beyond. As such
it cannot be studied in isolation, and would be useful
to include a regional model that calculates flows of
employment and population in order to program the
capacities needed for transportation, housing and ser-
vices.
We will use QUANT MSOA zones as the regional
zones (I,J), whose modelling outputs can be accessed
real time using requests from the web server using
QUANT’s REST API, and develop a fine scale plan-
ning zone system for the Olympic Park in the Unity
3D graphics package. Essentially, we develop a sys-
tem, in which we design new developments, these will
be translated into floorspace, and then to population.
This means, that it is possible to create scenarios by
calculating the total of employment and population
from all planning zones within each MSOA in the
Olympic Park and then send it back to QUANT to
calculate flows on a regional level. This loop will en-
sure the stability of the planning scenarios, and allow
QUANT and the planning model to communicate by
exchanging information back and forth.
To create the fine-scale planning zones we use
the official planning policies of the QEOP as set by
LLDC. These indicators will essentially inform the
design scenarios with permissions set by the different
urban authorities. We can then develop a calibrated
urban planning model as an internal pre-model which
will take the role of assigning population flows from
Accelerating Urban Modelling Algorithms with Artificial Intelligence
109

the QUANT regional model to the designed planning
zones. This follows the initial work visualising com-
plex urban models in procedural 3D environments
(Roumpani et al., 2013) ,(Hudson-Smith, 2014). In
this case we have linked building floorspace and land
uses with population figures. e.g. A housing unit of
300m
2
hosts maximum 10 people. The result of this
work, is then a composite interactive 3D plan of the
Olympic Park, which links floorspace as designed in
Unity3D with population projections from QUANT.
Starting with the existing conditions of the Park and
adding the projected developments of the LCS, we
set out to show how the assigned development types
would affect growth over the projected period, and to
compare alternative development strategies. We have
developed this as an android application, which uses
the 3D model as an interface (figure 4). This will al-
low the user to experiment with different policies and
test scenarios within a 3D model of the Olympic park
and use QUANT to evaluate these scenarios in terms
of population distribution.
5 IMPLEMENTATION
In this section we present our architecture for running
urban modelling experiments, followed by an analysis
of the achieved performance in the ‘Results’ section.
At the top level, this consists of a collection of web
services using a ‘model view controller’ pattern. The
structure of this can be seen in figure 5. Below the
web services layer are the libraries that perform the
actual modelling functions. This enables us to sep-
arate the functionality from the web protocol frame-
work and test the performance of the urban modelling
library in isolation. By exposing the modelling func-
tions as a set of web services, different clients can be
used for exploration and visualisation. In the process
of our testing we used both conventional 2D maps and
a 3D client written using the Unity framework. For
the purposes of this paper, though, only the “QUANT
Model” and “Web Services” boxes are considered as
these deal with the calibration and the running of the
model.
The rest of this section describes the implementa-
tion of the modelling library as follows:
1. CPU based spatial interaction model
2. GPU based spatial interaction model (OpenCL)
3. AI optimised spatial interaction model (Tensor-
Flow)
4. AI optimised neural spatial interaction model
(Keras/Tensorflow)
5. AI alternative model structure (radial basis, gener-
ative adversarial networks, neurodynamic models
(Milton et al., 2018))
This methodology allows 1, 2 and 3 to be com-
pared for speed as they are functionally identical,
while 4 and 5 are interesting from a research point
of view as they explore modelling equations them-
selves. The implementation is using Python 3.6 as
it allows for a TensorFlow implementation with the
trained model able to be run on the CPU or GPU for
benchmarking.
We start with an origin constrained spatial inter-
action model of commuter flow in England and Wales
using data from the 2011 Census. Data is available at
the ‘Middle level Super Output Area (MSOA)’ geog-
raphy, where there are 7201 zones in the model.
T
i j
= O
i
B
j
D
j
e
−βc
i j
∑
j
B
j
D
j
e
−βc
i j
(5)
O
i
=
i<n
∑
i=0
T
i j
, D
j
=
j<n
∑
j=0
T
i j
(6)
The variables in equation 5 follow the same pat-
tern as equation 1, earlier, with the exception of B
j
,
which is a constraints factor, used to prevent build-
ing in zones where none is possible, for example on
green belt land, parks, or areas of outstanding natural
beauty. In terms of the system diagram in figure 5,
this fits into the box labelled “QUANT Model”.
While commuter flows have been used as the ini-
tial example (travel to work), other types of flow are
also considered such as retail (travel to shop). As
long as there is some type of flow matrix, T
i j
, then
anything can be simulated. In addition to this, flows
can be disaggregated by type, so, in the case of travel
to work, the flows are broken down into three modes
‘road (mode=0)’, ‘bus and tube (mode=1)’ and ‘heavy
rail (mode=2)’. This results in one order n x n matrix
T
i j
and one trip cost matrix c
i j
for each of the three
transport modes. The final result is then given by the
following equation:
T
total
i j
=
m<3
∑
m=0
T
m
i j
, {m = mode} (7)
Learning in this respect is seen as fitting the β pa-
rameter to achieve the optimal goodness of fit mea-
sured over D
j
for singly constrained, or both O
i
and
D
j
for doubly constrained. The β parameter repre-
sents the willingness of a commuter to travel the dis-
tance between i and j, which is where the functional
difference between the conventional spatial interac-
tion model and the neural spatial interaction model
can be measured.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
110

Figure 5: QUANT system diagram showing the server/client split. The box labelled “QUANT Model” contains the code
outlined in this paper. This is the section that is critical to the speed of the entire system.
For the TensorFlow version of the conventional
spatial interaction model, the operations required to
run the model are defined by an execution graph. This
graph is shown in figure 6, which shows the paral-
lelism achievable in the flows of dependencies. The
C
bar
calculation (mean trips) from T
i j
(trips matrix) is
visible, along with the O
i
and D
j
row and column sum
reductions. Other than the trips matrix, the only other
inputs to the system are C
i j
(cost matrix) and the β
parameter which is the variable to be calibrated. This
execution graph only shows a single run of the model
equation, with no adaptaion of the β parameter to fit
the data to the observed values (T
i j
). The reason for
this is that this is the execution graph that was used for
the benchmark tests between the regular Python code
and the TensorFlow code to measure both speed of ex-
ecution and equivalence of numerical results. Adding
the β calibration to the graph is added in the produc-
tion version of the class, while the simplification here
is to make direct testing possible.
All the code for this paper can be found
on GitHub under the following project:
https://github.com/maptube/UMaaS.
5.1 Neural Model
The neural spatial interaction model follows the pre-
vious work of Openshaw (Openshaw, 1997, pp174),
Black (Black, 1995) and (Fischer and Sucharita,
1994), using [O
i
, D
j
,C
i j
] as inputs to the model with
T
i j
as the target. Openshaw included an additional ‘in-
trazonal flag’, used to indicate when i = j and travel
is within the same zone. This has not been used here,
but one advantage of the neural model over the con-
ventional spatial interaction model is that additional
parameters can be added as inputs to explore their
significance, as discussed in (Openshaw, 1998a). An-
other problem concerns the scaling of the inputs and
outputs, which need to be in the range [0..1] for the
neural network type used here. The practice adopted
in the literature is used, with the inputs and outputs
being scaled linearly. This introduces a problem, as
the maximum O
i
value is 24, 061, resulting in a scal-
ing factor of
1
max(O
i
)
= 4.15x10
−5
. This needs to
be applied to the loss function, used to establish the
model’s goodness of fit when training.
Having defined the inputs and outputs, the next
problem concerns the network structure itself. While
three inputs and one output is fixed, the number of
hidden layers in between can be varied, as can the
number of neurons in each layer. This introduces an
optimisation problem where too few layers and neu-
rons results in the model not fitting the observed data
to a high enough level of accuracy, while too many
will result in over-fitting the model. Black (Black,
1995) used a single hidden layer, obtaining results
better than the conventional formulation of the model,
which suggests that one layer is adequate. Fischer
(Fischer and Sucharita, 1994) evaluated ten different
network architectures, varying the number of hidden
neurons in order to find the optimum for his telecom-
munications data. Our zonal model is an order of
magnitude bigger than any in the literature (Black 9
zones, Openshaw 73 zones), so the structure of the
network is under investigation. Finally, the activation
function, ϕ() in equation 3, needs to be chosen. In
Accelerating Urban Modelling Algorithms with Artificial Intelligence
111
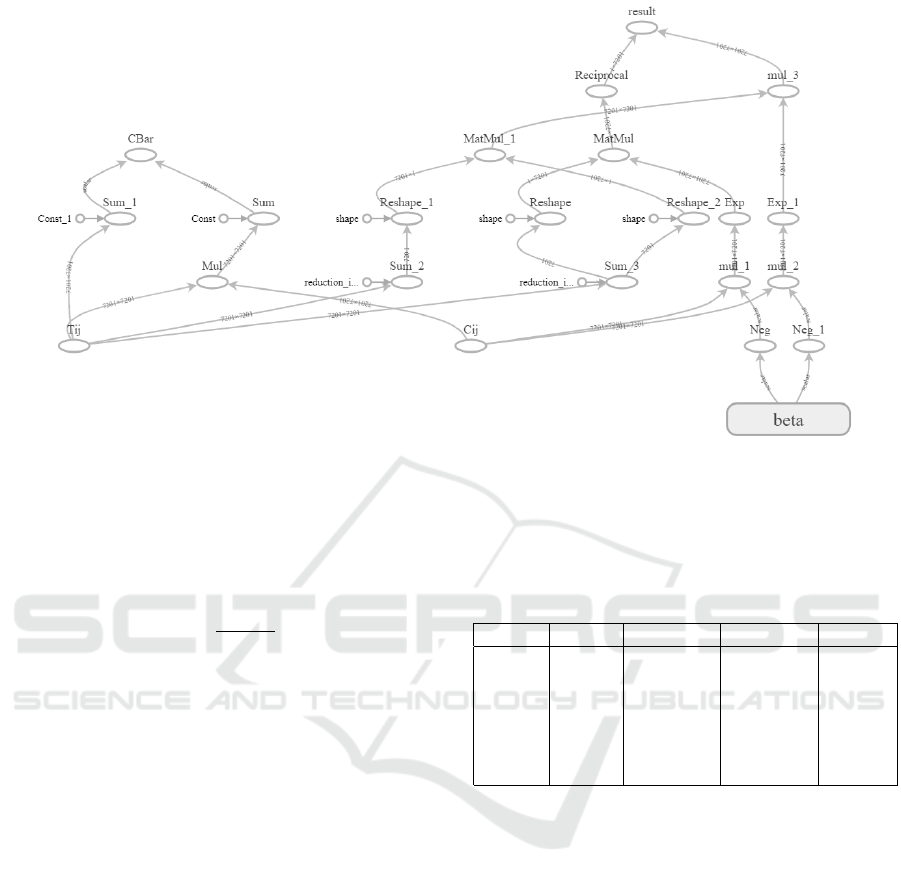
Figure 6: Tensorflow execution graph for the TFSingleOrigin code to run the conventional model of equation 5 on the GPU.
“Spatial Interaction Models: From the Gravity to the
Neural Network Approach” (Fischer and Reggiani,
2005), Fischer and Reggiani use the sigmoid, or lo-
gistic function, defined as follows:
ϕ(x) =
1
1 + e
−x
(8)
The ANN model is implemented using the Keras
library. While this could be implemented directly us-
ing TensorFlow, the advantage of using a higher level
library over the lower level TensorFlow library is the
ease with which different neural network architec-
tures can be explored. In the older literature cited
at the beginning of this section, three layer networks
with a single hidden layer were used. Here, we inves-
tigate the effect of adding additional hidden layers on
the prediction performance using a parameter sweep
of number of layers and number of neurons. During
training the error is taken as mean square error be-
tween output and target summed over the batch. A
single epoch represents all of the trips data available
being applied in batches.
The following data is an example from the training
set, which contains 1,960,428 non-zero patterns from
original census data, or 3.78% of the full 7201x7201
matrix.
[ Oi, Dj, Cij ] ---> Tij
[ 24061.0 , 165.0 , 1.0 ] ---> 19.0
[ 24061.0 , 1006.0 , 13.0 ] ---> 8.0
[ 24061.0 , 1645.0 , 11.0 ] ---> 11.0
[ 24061.0 , 1248.0 , 13.0 ] ---> 13.0
[ 24061.0 , 1419.0 , 11.0 ] ---> 18.0
[ 24061.0 , 1241.0 , 12.0 ] ---> 9.0
For the purposes of evaluating the performance of
the neural model, six different network architectures
were tested, as shown in table 1.
Table 1: Network architecture.
Model Inputs Hidden 1 Hidden 2 Output
1 3 64 0 1
2 3 32 0 1
3 3 16 0 1
4 3 8 0 1
5 3 4 0 1
6 3 4 4 1
The network architectures were chosen as follows:
model 1 is larger than Openshaw’s test in (Openshaw,
1998b), which had a maximum of 50 hidden neurons,
while model 5 is smaller than his minimum of 7. This
is included as a test to allow a fast executing model to
be trained for longer. Finally, model 6 is a deep net-
work, included as a comparison with the single hidden
layer architectures. While the conventional spatial in-
teraction model can be approximated to any degree
using a single hidden layer, the deep network is to test
whether a more complex function can be discovered
which fits the data more closely.
Benchmark tests were run on a cropped version of
the England and Wales data, consisting of a 500 zone
segment of London. This was necessary to reduce
the training time and allow a parameter sweep of the
number of hidden neurons, number of layers, batch
size and number of training epochs. With the full
England and Wales, data, there are 51, 854, 401 in-
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
112

put/target training pairs compared to 250, 000 for the
smaller subset of London, so this represents a signifi-
cant reduction in compute time. Training is based on
minimisation of “mean square error” over the batch,
with a batch size of 200, 000 to fit inside GPU mem-
ory. Batches are presented for training in a random
order, which is a technique designed to prevent over-
fitting the data.
Following the parameter sweep with the test
model, experiments were then conducted using the
full 7201 zone model for direct comparison with the
conventional gravity model.
6 RESULTS
This section presents the results of testing the fi-
nal evolution of the code optimisations. The com-
puter used to do the tests is an Alienware Area 51
computer, i7 5960X @ 3GHz, 32GB RAM, dual
NVIDIA GTX980 Ti GPUs. For the Google Tensor-
Flow tests, this used TensorFlow version 1.12 with
NVIDIA CUDA Toolkit 9.0. For the purposes of test-
ing, figure 7 shows the results of executing the main
spatial interaction model given by equation 5. This is
the base equation used in both the calibration (train-
ing) phase and later for inference, or testing scenarios.
Where a multi-modal model is concerned, each mode
is computed separately using the same equation, so
this serves as a representative test.
The TensorFlow model class
2
is used to build the
graphs for the O
i
and D
j
inputs to the model equa-
tion, which are row and column sums computed using
a reduction kernel. One of the problems with measur-
ing GPU performance is that there is significant setup
time compared to the CPU, the effects of which have
been minimised by timing batches of 1000 runs of the
code.
For comparison, a C# implementation was con-
structed to match the Python implementation. This
runs the benchmark test on a matrix of size 7201 in
1.23 seconds, compared to the Python implementa-
tion presented here, which takes 1.54 seconds on the
same test.
6.1 Neural Model Results
While Tensorflow and GPU hardware has been used
to accelerate the evaluation of the conventional grav-
ity model, this section presents the results of training
an artificial neural network (ANN) on identical trips
2
TFSingleOrigin: https://github.com/maptube/UMaaS/
blob/master/models/TFSingleOrigin.py
Figure 7: Model execution time graph showing the effect
that changing the matrix size has on the model run time.
Timings are in seconds for a single model run, based on an
average of 1000 runs on the CPU or GPU.
Table 2: Training time for 10,000 epochs and final error.
NOTE: this is for the 500 x 500 test matrix.
Model Net Training
Time
Min Error
(
¯
C)
1 3-64-0-1 55min 0.65
2 3-32-0-1 33min 0.80
3 3-16-0-1 23min 0.18
4 3-8-0-1 19min 0.017
5 3-4-0-1 17min 0.19
6 3-4-4-1 19min 0.033
data. Firstly, the ANN has more degrees of freedom
than the β parameter of the gravity model. Here, the
model has three inputs, one or more hidden layers and
an output layer containing a single neuron. For a hid-
den layer with h hidden neurons, there are 3h weights
in the hidden layer and h weights in the output layer.
This makes calibration time longer than in the gravity
model case as shown in table 2.
In order to measure the goodness of fit of the mod-
els, the
¯
C metric is used, which is a measure of the to-
tal trip time recorded in the original observation data.
During the calibration phase of the conventional grav-
ity model, the β value is adjusted until the mean trip
times factor,
¯
C is within 0.1 of the observed value.
Equation 9 defines how
¯
C is calculated, with the val-
ues for each of the models shown in table 2.
¯
C =
∑
i, j
T
i j
C
i j
∑
i, j
T
i j
(9)
Training only needs to be performed once, though,
while speed of inference is the main metric of inter-
est. The test here is to see whether the mathematically
complicated ANN can be used to infer the data for the
entire N × N trips matrix in a time comparable to the
gravity model by using the hardware acceleration pro-
vided by the GPU.
Accelerating Urban Modelling Algorithms with Artificial Intelligence
113

Then, as a secondary test, the results are compared
with the conventional gravity model to see whether
they are consistent. Table 3 shows the inference times
for the full 7201 matrix data.
Table 3: Inference times for the full 7201 element matrix
data on the six models.
Inference Time (secs)
Model Net GPU CPU
1 3-64-1 1.156 74.937
2 3-32-1 1.025 14.523
3 3-16-1 1.214 5.314
4 3-8-1 0.900 3.240
5 3-4-1 0.929 2.152
6 3-4-4-1 0.996 3.590
Now, the goodness of fit between the ANN model
and the observed data is measured. However, with
the neural model, training uses the mean square er-
ror between predicted and target as the loss function,
so the back-propagation algorithm seeks to minimise
this factor instead. This marks an important differ-
ence of the neural model, as the
¯
C calculation requires
the entire predicted matrix for its evaluation, while the
neural model operates at the level of batches of indi-
vidual predicted/target pairs. This leads to the result
that the neural model’s mean square error is not di-
rectly comparable with
¯
C, the usual measure of fit for
a gravity model. The
¯
C metric is trips weighted by
travel time, while the ANN’s loss algorithm only op-
timises for the raw number of trips. The mean square
error provides an upper bound on
¯
C, which can be
seen in the data if
¯
C is plotted against mean square
error.
Looking at the training data in figure 8, any of the
models with a final error below 0.1 would be accept-
able in the context of the conventional gravity model,
which is calibrated to this accuracy. In other words,
we have a universe of models that provide a differ-
ent way of fitting the observed flow data. While fig-
ure 8 shows the training on a test matrix of 500x500
for speed, this is still only a subset of the full data.
The faster training speed on this smaller data set en-
ables a parameter sweep which then translates into
faster training on the full 7201x7201 data set, which
is a factor of 207 times bigger. Although the smaller
matrix size was used as a test, it still constitutes real
data and could, in theory, be used to ‘seed’ the train-
ing with the full data. This has not been attempted
here, with the full training performed starting from
randomised weights. Using the graph in figure 8 and
timings obtained from running the software, the “3-
64-1” model was rejected on the grounds that train-
ing would need at least 10,000 epochs at 30 seconds
each (83 hours), similarly for “3-32-1” and “1-16-1”.
The “1-4-1” model was rejected for being too small to
generalise the data, leaving the “1-8-1” and “1-4-4-1”
(approx 0.5s per epoch) models. The “1-4-4-1” model
would make for an interesting comparison being a two
layer deep network, but, unfortunately, it proved too
difficult to train, requiring over 40,000 epochs.
3
Of
the remaining “1-8-1” model, after 12,000 epochs of
training the
¯
C mean tips length is 23.8, when the ob-
served data is 12.5, this is with a mean square error of
4.16x10
−6
. The main lesson learned from the train-
ing exercise is to train with the full data and update
the weights at the end of the epoch, rather than using
small batches and updating more frequently.
7 CONCLUSIONS
In this paper we showed how the performance of a
gravity model is speeded up using the TensorFlow ar-
tificial intelligence library and GPU hardware. We
compared the CPU performance of the model with the
GPU accelerated model and showed how large mod-
els approaching 10,000 zones can be handled at in-
teractive speeds. We termed this, “Urban Modelling
as a Service”, leveraging “AI as a Service” for urban
modelling. The immediacy of the results is important
here due to the interactive nature of the visualisation
and exploration of modelling scenarios through a real-
time, web-based, user interface. The power of this ar-
chitecture is that it opens up the possibility of testing
modelling scenarios to the general public. Data like
the trips and cost matrices, zone boundaries, and con-
straints can be held and curated on the server, thereby
providing all the data required for modelling in one
place.
A secondary result is the comparison of a neural
spatial interaction model with a conventional model.
Here, the scaling of inputs to fit the sigmoid activa-
tion function and extended training times on the data
are shown to be a problem. This is unfortunate, as
the logical extension to this work is to continue with
the comparison between the neural spatial interaction
models and the conventional model and show that
the neural network is not a “black box”. The same
methodological testing can be applied to both types
of model in order to assess their function. The future
direction of this research is to investigate the ensem-
ble of models provided by this method when applied
to the same scenario.
3
The estimates of how long training would take are
based on analysing the drop in error over time.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
114
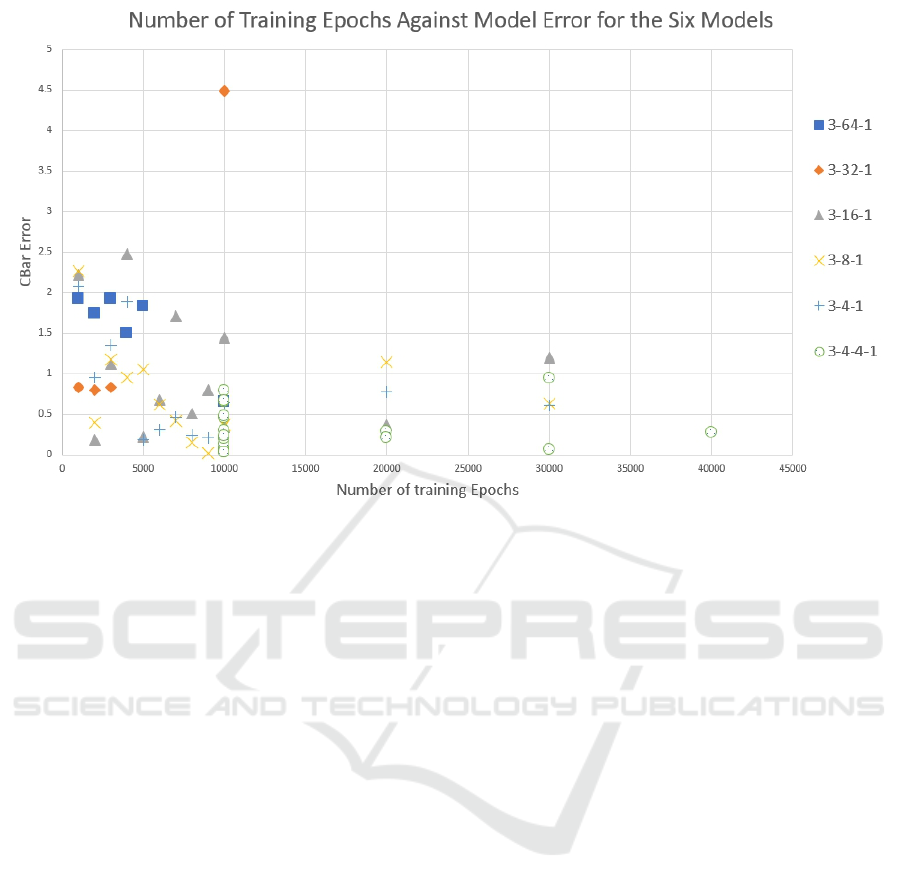
Figure 8: Number of training epochs and goodness of fit (
¯
C), this is for 500 x 500 matrix test data.
ACKNOWLEDGEMENTS
The authors would like to thank Prof. Andrew
Hudson-Smith for supervising the Queen Elizabeth
Olympic Park Unity 3D, Prof. Mike Batty for the
QUANT project and Prof. Alan Wilson (Alan Turing
Institute). We would like to thank EPSRC for fund-
ing the QEOP work under PhD grant number EPSRC
DTG 2012-2016.
REFERENCES
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,
J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,
Kudlur, M., Levenberg, J., Monga, R., Moore, S.,
Murray, D. G., Steiner, B., Tucker, P., Vasudevan, V.,
Warden, P., Wicke, M., Yu, Y., and Zheng, X. (2016).
Tensorflow: A system for large-scale machine learn-
ing. In 12th USENIX Symposium on Operating Sys-
tems Design and Implementation (OSDI 16), pages
265–283.
Batty, M. (1976). Urban Modelling: Algorithms, Calibra-
tions, Predictions. Cambridge University Press.
Black, W. R. (1995). Spatial interaction modeling using
artificial neural networks. Journal of Transport Geog-
raphy, 3(3):159 – 166.
Chollet, F. (2015). keras. https://github.com/fchollet/keras.
Creighton, R. H. (2010). Unity 3D Game Development by
Example Beginner’s Guide. Packt Publishing.
Fischer, M. M. and Reggiani, A. (2005). Spatial interac-
tion models: From the gravity to the neural network
approach. In Capello, R. and Nijkamp, P., editors, Ur-
ban Dynamics and Growth: Advances in Urban Eco-
nomics, Contributions to Economic Analysis, volume
266, chapter 11, pages 319–346. Elsevier.
Fischer, M. M. and Sucharita, G. (1994). Artificial neural
networks. a new approach to modelling interregional
telecommunication flows. Journal of Regional Sci-
ence, 34(4):503–527.
Hudson-Smith, A. (2014). Tracking, tagging and scanning
the city. Architectural Design, 84(1):40–47.
Intel (2019). Intel movidius neural compute stick. url
= https://software.intel.com/en-us/movidius-ncs. Ac-
cessed: Jan 2019.
Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J.,
Girshick, R., Guadarrama, S., and Darrell, T. (2014).
Caffe: Convolutional architecture for fast feature em-
bedding. In Proceedings of the 22Nd ACM Inter-
national Conference on Multimedia, MM ’14, pages
675–678, New York, NY, USA. ACM.
Lin, H. W., Tegmark, M., and Rolnick, D. (2017). Why
does deep and cheap learning work so well? Journal
of Statistical Physics, 168(6):1223–1247.
LLDC (2011). LLDC legacy communities scheme. url
= http://www.queenelizabetholympicpark.co.uk/our-
story/transforming-east-london/legacy-communities-
scheme. Accessed: March 12 2018.
Milton, R., Hay, D., Gray, S., Buyuklieva, B., and Hudson-
Smith, A. (2018). Smart IoT and Soft AI. IET Con-
ference Proceedings, pages 16 (6 pp.)–16 (6 pp.)(1).
Openshaw, S. (1997). Artificial Intelligence in Geography.
John Wiley and Sons.
Accelerating Urban Modelling Algorithms with Artificial Intelligence
115

Openshaw, S. (1998a). Building an automated modeling
system to explore a universe of spatial interaction
models. Geographical Analysis, 20(1):31–46.
Openshaw, S. (1998b). Neural network, genetic, and fuzzy
logic models of spatial interaction. Environment and
Planning A: Economy and Space, 30(10):1857–1872.
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E.,
DeVito, Z., Lin, Z., Desmaison, A., Antiga, L., and
Lerer, A. (2017). Automatic differentiation in pytorch.
In NIPS-W.
Roumpani, F., O’Brien, O., and Hudson-Smith, A. (2013).
Creating, visualizing and modelling the realtime city.
In Proceedings of Hybrid City II ‘Subtle rEvolutions’
Conference.
Wilson, A. G. (1971). A family of spatial interaction mod-
els, and associated developments. Environment and
Planning A: Economy and Space, 3(1):1–32.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
116
