
Detecting Influencers in Very Large Social Networks of Games
Leonardo Mauro Pereira Moraes and Robson Leonardo Ferreira Cordeiro
Institute of Mathematics and Computer Sciences, University of S
˜
ao Paulo,
Keywords:
Data Mining, Social Networks of Games, Player Modeling, Classification, Feature Extraction, Data Streams.
Abstract:
Online games have become a popular form of entertainment, reaching millions of players. Among these play-
ers are the game influencers, that is, players with high influence in creating new trends by publishing online
content (e.g., videos, blogs, forums). Other players follow the influencers to appreciate their game contents.
In this sense, game companies invest in influencers to perform marketing for their products. However, how to
identify the game influencers among millions of players of an online game? This paper proposes a framework
to extract temporal aspects of the players’ actions, and then detect the game influencers by performing a clas-
sification analysis. Experiments with the well-known Super Mario Maker game, from Nintendo Inc., Kyoto,
Japan, show that our approach is able to detect game influencers of different nations with high accuracy.
1 INTRODUCTION
The digital game market is in constant ascendancy,
both in the production and in the consumption. This
industry moves billions of dollars per year (Lucas,
2009). According to Newzoo
1
, a specialist company
of game marketing, the estimated value for 2018 is
US$ 134.9 billion. Only in the first quarter of 2018,
players produced more than 260 million hours of on-
line videos related to game contents on Twitch and
YouTube platforms.
Online games are dynamic environments, in
which the players interact with the game and with
other players all over the world (Yannakakis and To-
gelius, 2015). The interactions performed by each
player represent relationships of several types; they
can relate to other players (e.g., friend, sharing games)
or to the game itself (e.g., play, like) (Lee et al., 2012).
These relationships form a social network, i.e., in this
context a Social Network of Games.
For example, the well-known Super Mario Maker
game (SMM), from Nintendo Inc., Kyoto, Japan,
forms a very large social network. According to Nin-
tendo
2
, it has more than 3.5 million players, and 7.2
million courses (or maps) that were already played
1
Newzoo. “Insights”. https://newzoo.com/insights/ (ac-
cessed December 18, 2018).
2
NintendoAmerica. “If you played every level
in #SuperMarioMaker for 1 minute each, it would
take you nearly 14 years to play them all!”.
https://twitter.com/NintendoAmerica/status/732624228428750848/
more than 600 million times. In this game, a player
can play, give a star, break a record or comment on
online courses created by other players, besides cre-
ating his/her own courses to share with the world.
Influencer users in the digital field exist since
the popularization of social media (Pei et al., 2018).
They produce digital contents (e.g., online videos)
that arouse the attention of other users with similar
tastes. Among them, there are the game influencers
that produce contents related to digital games (Gros
et al., 2018; Hilvert-Bruce et al., 2018). Players fol-
low the game influencers looking for entertainment
and credible information on the universe of the games
(Sj
¨
oblom and Hamari, 2017; Gros et al., 2018).
Game influencers get recognition from the play-
ers who follow them. Consequently, game companies
invest in influencers to endorse and perform market-
ing for their products (Sj
¨
oblom and Hamari, 2017).
Hence, an influencer has direct relevance in such phe-
nomena as viral marketing, innovation diffusion and
behavior adoption (Pei et al., 2018). To detect game
influencers is therefore almost mandatory when look-
ing for popular preferences, new trends, and the like
(Sj
¨
oblom and Hamari, 2017; Hilvert-Bruce et al.,
2018).
This paper proposes a novel framework to de-
tect game influencers in Social Networks of Games.
Given the actions of millions of players in an online
game, how to detect the game influencers? It is obvi-
(accessed November 10, 2018).
Moraes, L. and Cordeiro, R.
Detecting Influencers in Very Large Social Networks of Games.
DOI: 10.5220/0007728200930103
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 93-103
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
93
ously necessary to model the players’ characteristics.
We express the problem as a classification task, and
propose a player modeling heuristic based on tempo-
ral aspects of their courses analyzing the history of
“likes” over time. To validate our proposal, we stud-
ied the famous Super Mario Maker game, from Nin-
tendo Inc., Kyoto, Japan, and report experimental re-
sults to show that our framework detects game influ-
encers of different nations with high accuracy.
The rest of this paper is organized as follows: it
starts with background concepts (Section 2), followed
by the related work (Section 3), the proposed method-
ology (Section 4), the experiments (Section 5) and the
conclusion (Section 6). Table 1 lists the main symbols
of our notation.
Table 1: Definitions.
Symbols Definitions
Graph
G
dev
= {V,E
dev
} Developer network
G
star
= {V,E
star
} Stars network
g(n) | n ∈ V Degree centrality
Modeling
T = [t
1
,t
2
,. ..] Timestamps
c = [ε
1
,ε
2
,. ..] Stars stream
C
p
= {c
1
,c
2
,. ..} Player’s courses
Extractor
LR(p,L) Algorithm 1
DR(p,L) Algorithm 2
CA(p,L) Algorithm 3
F
ALL
(p,L) Ensemble method
2 BACKGROUND CONCEPTS
This section discusses Social Networks of Games and
presents the problem definition.
2.1 Social Networks of Games (SNG)
Social networks describe interactions and relations
among users (Barab
´
asi and P
´
osfai, 2016). In a social
network, the users represent their relations by links.
There are many types of links, e.g., links determined
by individual opinions on other individuals, links de-
noting collaboration, links resulting from behavioral
interactions, and so on (Savi
´
c et al., 2019).
Social links may also be present in digital games,
where the players interact, compete and relate among
each other (Lee et al., 2012). A real-world example is
the Super Mario Maker game (SMM). In this game,
players can elaborate their own Super Mario courses
and share their courses with the world. A Super Mario
course is a map of the game that players play. Besides
playing and developing courses, a player can also give
a star to (i.e., similar to “like”) a course elaborated by
another player.
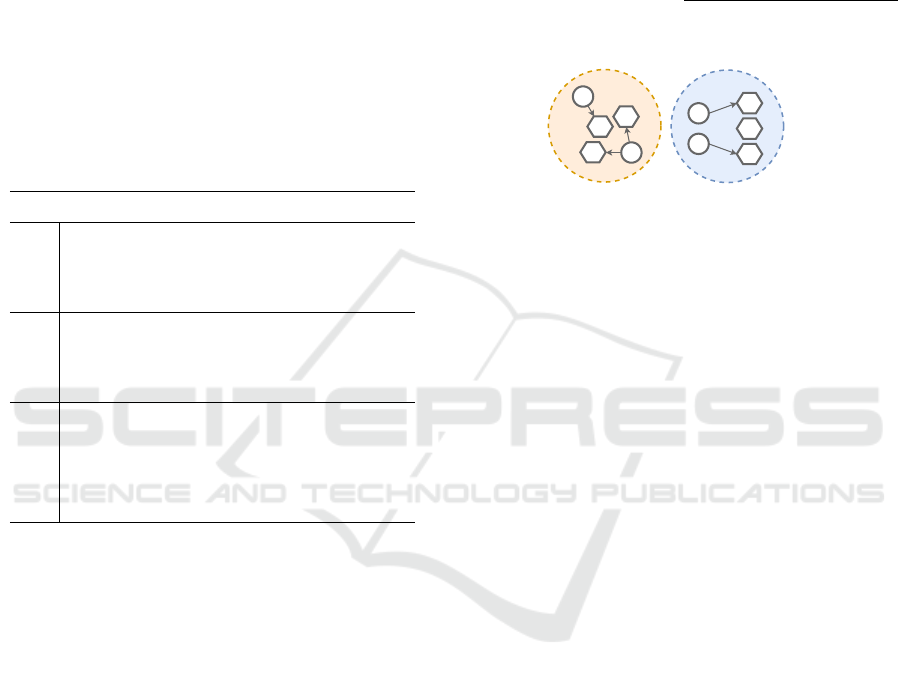
Figure 1 illustrates two players p
1
and p
2
inter-
acting (develop, star, etc.) with three courses c
1
, c
2
and c
3
. Such relationships form a social network. In
this sense, online games have their intrinsic social net-
works; we coin the term Social Networks of Games
(or simply SNG) to refer to them in this paper.
p1
c1
p2
c2
c3
p1
c3
p2
c1
c2
Gstar
Gdev
...
Figure 1: Graphs of different types of interactions (develop,
star, etc.) in a Social Networks of Games.
2.2 Network and Problem
In the SMM game, players can elaborate and share
their courses. In this sense, the SMM network in-
cludes a directed bipartite graph G
dev
= {V, E
dev
}
with edges e ∈ E
dev
of players p ∈ V sharing courses
c ∈ V . Additionally, graph G
dev
changes over time.
Thus, in time t
i
, graph G
dev,i
presents a determined
topology, while new nodes (i.e., new players and/or
courses) and new edges can arrive in graph G
dev,i+1
,
in time t
i+1
, where t
i
< t
i+1
. Thus, since there exists
a stream of graphs [G
dev,1
,G
dev,2
,. ..] as a function of
time, it is a dynamic network (Westaby, 2012).
Figure 2(a) illustrates this network. The initial
graph G
dev,i
has nodes V = {p
1
, p
2
,c
1
,c
2
,c
3
}, i.e.,
two players and three courses. The corresponding
edges are E
dev
= {(p
1
,c
3
),(p
2
,c
1
),(p
2
,c
2
)}, defining
the courses shared by each player. In G
dev,i+1
, player
p
1
shares a new course c
4
. In G
dev,i+2
, there appears
a new player p
3
without sharing any course. At last,
in G
dev,i+3
, nothing changes. Thus, the network can
only grow over time.
Besides creating new courses, a player can also
star courses of others players in SMM. In this sense,
the SMM network has also another directed bipartite
graph G
star
= {V,E
star
} with edges e ∈ E
star
of play-
ers p ∈ V that give stars to courses c ∈ V . Note that
the nodes in V are the same for both graphs G
dev,i
and
G
star,i
, considering a time instant t
i
. Similarly to graph
G
dev
, graph G
star
is also a dynamic network.
Figure 2(b) illustrates this network. In time t
i
,
graph G
star,i
has nodes V = {p
1
, p
2
,c
1
,c
2
,c
3
} and
edges E
star
= {(p
1
,c
1
),(p
2
,c
3
)} indicating players
that starred courses. In G
star,i+1
, player p
1
stars
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
94

p1 c3
p2
c1
c2
c4 c4
p3 p3
Gdev
Time
ti ti+1 ti+2 ti+3
p1 c3
p2
c1
c2
p1 c3
p2
c1
c2
c4
p1 c3
p2
c1
c2
(a) Graph G
dev
= {V,E
dev
}
p1
c1
p2
c2
c3
Time
ti ti+1 ti+2
c4
p3
c4
p3
c4
Gstar
ti+3
p1
c1
p2
c2
c3
p1
c1
p2
c2
c3
p1
c1
p2
c2
c3
(b) Graph G
star
= {V,E
star
}
Figure 2: Graphs G
dev
and G
star
changing over time.
course c
2
, and there appears a new course c
4
with no
star. In G
star,i+2
, there appears a new player p
3
that
stars course c
3
; also, player p
2
stars course c
4
. At
last, in G
star,i+3
, player p
3
stars courses c
2
and c
4
.
According to this discussion, the SMM game can
be represented by two dynamic networks, G
dev
and
G
star
, whose topologies are correlated and evolve as a
function of time. To analyze such correlated evolution
is essential when spotting game influencers, since the
courses that they develop become popular right after
they advertise them in other media, like Twitch and
YouTube, while the other players’ courses gain pop-
ularity gradually. The correlated evolution is proba-
bly even more important than looking for static graph
topologies in individual time stamps. With that in
mind, the main problem that we tackle in this paper
is: how to spot game influencers by evaluating the
correlated evolution of graphs G
dev
and G
star
?
Obviously, there exist other types of interactions
that lead to additional dynamic networks describing
the SMM game, such as, play, break time record, etc.
Nevertheless, without loss of generality, we only con-
sider G
star
and G
dev
in this paper, and show that they
are enough to accurately identify game influencers.
The next section describes existing works focused
on identifying influencer users in social networks.
3 INFLUENCER DETECTION
To the best of our knowledge, there is no research on
detecting influencers in Social Networks of Games;
the existing approaches to detect influencers in other
types of social networks are thus the closest related
works. In this section, we outline the state-of-the-art.
The na
¨
ıve approaches to detect digital influencers
are based on selecting the top-ranked nodes identi-
fied by some centrality indices; more advanced strate-
gies are greedy methods and heuristic methods (Wang
et al., 2017; Al-Garadi et al., 2018). The centrality-
based methods find a set of the most influential nodes
based on the network topology (Barab
´
asi and P
´
osfai,
2016). In (Morone et al., 2016), it is presented an al-
gorithm that ranks nodes based on collective influence
propagation, which quantifies the nodes’ “influences”
in the network. Meanwhile, another research infers
the influential nodes based on spreading paths (i.e.,
the links) (Wang et al., 2017).
Unfortunately, these algorithms work only on ho-
mogeneous networks (i.e., a single type of node),
while our problem refers to heterogeneous/bipartite
networks (i.e., nodes of two types, players and
courses). Also, we need to correlate two dynamic net-
works, and analyze their evolution over time. In this
sense, it is difficult to use centrality indices because
they infer knowledge only based on the topology of
a single static network. To tackle our problem, one
must observe the nodes’ features, so to model game
influencers’ characteristics instead of ranking them.
In (Chino et al., 2017), a dynamic graph of com-
ments and online reviews was analyzed to detect sus-
picious users, like spammers. The authors model the
temporal aspect of the volume of activity (e.g., num-
ber of characters in a review) to detect an anomaly in
a social media. The proposed temporal aspect mod-
eling is interesting and inspiring, but this research
works with only one dynamic network and specific
application-related features of the contents, besides
detecting suspicious users; not, influential users.
Other approaches extract features to describe so-
cial media users; then, they use the features to train
Machine Learning (ML) algorithms to identify the
most influential ones. ML-based approaches have
great potential to identify influential users in large net-
works and complex networks (Al-Garadi et al., 2018).
In (Liu et al., 2014), temporal features are extracted
based on microblog posts (post-features) to train an
ML method to identify influential users in a tempo-
ral microblog network. The authors infer features for
a user according to his/her number of followers, the
number of microblog posts, the number of responses
received and the number of comments over time.
In (Qi et al., 2015), the aforementioned work is
extended by identifying domain-topics of influential
users so to improve the microblog’s search engines.
The improved work uses temporal post-features com-
bined with microblog text to fit the domain-topics of
each influential user. Unfortunately, both works (Liu
et al., 2014) and (Qi et al., 2015) use a single dynamic
graph and heavily depend on the post-features, so it is
not clear how to use them to tackle our problem.
Finally, let us summarize the state-of-the-art on
influencer detection. Some techniques use central-
Detecting Influencers in Very Large Social Networks of Games
95

ity metrics to rank influential users based on graph
topology (Morone et al., 2016; Wang et al., 2017).
Other methods are designed to work with dynamic
networks; they commonly perform feature extraction
from the network and from the users’ external con-
tents to train ML algorithms (Liu et al., 2014; Qi
et al., 2015). Also, user modeling based on temporal
aspects has been applied (Chino et al., 2017). How-
ever, these works cannot tackle our problem mainly
because they do not correlate more than one dynamic
network and/or fail to quantify the changes/evolution
over time. In the next section, we present a novel
framework to tackle the problem.
4 PROPOSED METHODOLOGY
This section presents a new framework to detect influ-
encers in very large Social Networks of Games. The
main question here is: how to model the correlated
evolution of players’ actions on the dynamic networks
G
dev
of developers and G
star
of stars? To answer it,
we propose a new player modeling heuristic based on
temporal aspects of their courses by extracting fea-
tures from the history of players’ actions over time.
4.1 Main Idea
Individually, neither network G
dev
nor G
star
has in-
trinsic characteristics that are truly useful to spot
game influencers. For example, by using an outdegree
centrality ranking algorithm on G
dev
we simply rank
the players by the number of shared courses; note that
it does not help much. Similarly, network G
star
would
lead to a ranking of players by the number of stars
given, which does not help either. Both rankings fail
to present relevant characteristics of the players that
would help identifying the influencers. Unfortunately,
the same problem happens when using more elabo-
rated analytical techniques, simply because there is
not enough information in any of the networks alone;
they must be analyzed combined.
As it was described before, we need to capture
relevant information from the correlated evolution of
both G
dev
and G
star
over time. To make it possible,
we propose to model this correlated evolution using
data streams, and to extract relevant features from the
streams to be used by a classification ML algorithm.
4.2 Stream Modeling
In this sense, we obtain from G
star
the quantity ε
i
of
stars received by each course c by applying degree
centrality g(c) | c ∈ V in each instant of time t
i
. Thus,
a course is represented here by a stream of star count-
ing events c = [ε
1
,ε
2
,. ..], where each event ε
i
refers
to a pair (star
i
,t
i
) with a number of stars star
i
and
a time stamp t
i
. Figure 3 illustrates this idea for the
toy graph G
star
shown in Figure 2(b). The number of
stars is constant over time for course c
1
, as it is shown
in Figure 3(a). Course c
2
received one star from p
1
in
time t
i+1
, and another one from p
3
in time t
i+3
(Figure
3(b)). Course c
3
received one star from p
3
in time t
i+2
(Figure 3(c)). At last, course c
4
received a new star in
each time instant after it arises in time t
i+1
(Figure
3(d)).
In this way, each course has a star counting stream
through time instants T = [t
1
,t
2
,. ..]. In addition,
by observing G
dev
, for each player p its elaborated
courses are extracted, so C
p
= {c
1
,c
2
,. ..}. There-
fore, we have for each player p a set C
p
of elaborated
courses and their stars counting stream over time.
Now, we need to extract temporal features from
each player. Note that each player p develops courses
c ∈ C
p
, and each course c has a star counting stream.
Thus, how to model the players based on their
courses? To accomplish this goal, we extract tem-
poral features of the courses and ensemble them to
model the players, as it is detailed in the next section.
4.3 Temporal Feature Extraction
This section describes our temporal aspects mod-
els. We developed three temporal features extractors.
Each extractor captures a specific characteristic of the
star counting stream. They use the players’ courses
and their stars counting streams to infer the features.
4.3.1 Linear Regression (LR)
The first feature extractor, called Linear Regression
(LR) extractor, infers features related to the stars as-
cension of the courses, i.e., the growth of star count-
ing over time. The linear regression model is widely
used in social sciences; it can model the statistical re-
lation between the variables.
We used the well-known Least Squares method
for estimating the unknown parameters in the linear
model. Since each event ε
i
in the stream has only two
attributes (i.e., stars
i
and t
i
), the linear function can
be simplified to a vector (α,β) (Equation 1).
f (t
i
) = α + β ·t
i
= (α, β) (1)
In this sense, f (t
i
) represents an estimated star
counting for time t
i
. The parameters (α, β) are in-
ferred by the stars stream c = [ε
1
,ε
2
,. ..]. Considering
that stars is the average number of stars and t is the
average time, the parameters are defined as follows:
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
96

(a) c
1
stream (b) c
2
stream (c) c
3
stream (d) c
4
stream
Figure 3: Stream Modeling on the toy graph G
star
shown in Figure 2(b).
β =
∑
t
i
stars
i
−
1
|c|
∑
t
i
∑
stars
i
∑
t
2
i
−
1
|c|
(
∑
t
i
)
2
α = stars − β ·t
(2)
Figure 4 illustrates an example of linear regres-
sion for a star counting stream c = [0, 1,4, 6,6,7,7]
between time instants t
1
and t
7
. The LR extractor finds
the linear function and extracts the angle ]
c
and the
coefficient of determination R
2
c
of the course c. In this
example, ]
c
= 51.34
o
and R
2
c
= 0.88.
curvature
Figure 4: Linear Regression for a star counting stream.
The angle ]
c
represents how ascending are the
events of a star counting stream c. Meanwhile, the co-
efficient of determination R
2
c
is the proportion of the
variance from the linear regression prediction, rang-
ing from 0 to 1. In this range, R
2
c
= 1 is the best pre-
diction for a stream c. The extractor uses coefficient
R
2
c
to estimate a “curvature” on the stream; low R
2
c
represents how large the “curvature” is.
The LR extractor is in Algorithm 1. It infers for
each player’s course c ∈ C
p
(Line 8) the linear func-
tion model
c
, angle ]
c
and coefficient of determination
R
2
c
(Line 9). In addition, the average angle coefficient
] (Line 15) and the corresponding standard deviation
σ
]
(Line 16) are extracted from the player’s courses.
How ascending is each player p? We measure the
angle ]
p
(Line 14) of a player p by the average vector
model
p
(Line 13) of the linear function of the courses
(Equation 3):
model
p
=
1
|C
p
|
∑
c∈C
p
model
c
]
p
= angle(model
p
)
(3)
Additionally, it measures the entropy S
]
of
courses’ angles (Line 17). Entropy is a measure of
the randomness in the information, ranging from 0 to
∞ as the randomness increases. Thus, entropy veri-
fies the tendency of player’s courses to have similar
ascension patterns, i.e., similar angles.
In Line 18, it is obtained the bottom-L lower co-
efficients of determination R
2
c
of the courses, repre-
sented by R
2
rank
= [min
1
(R
2
),. ..,min
L
(R
2
)]. Also, the
top-L great angle ]
c
of courses is computed in Line
19, represented by ]
rank
= [max
1
(]),. ..,max
L
(])].
Thus, the extractor uses a parameter L ∈ N to deter-
mine the top-L and bottom-L.
Note the algorithm captures the bottom-L lower
coefficients of determination R
2
rank
to identify “cur-
vatures”, whereas top-L angles ]
rank
to represent the
greatest star counting stream of a player.
Algorithm 1: LR Extractor.
1: procedure LR-MAP(c) Course Modeling
2: model
c
← LinearRegression(c)
3: ]
c
← angle(model
c
)
4: R
2
c
← R
2
(model
c
,c)
5: return model
c
, ]
c
, R
2
c
6: procedure LR(p,L) Player Modeling
7: Initialize models, ], R
2
with
/
0
8: for c ∈ C
p
do
9: model
c
, ]
c
, R
2
c
← LR-MAP(c)
10: models ← models ∪ {model
c
}
11: ] ← ] ∪ {]
c
}
12: R
2
← R
2
∪ {R
2
c
}
13: model
p
← mean(models)
14: ]
p
← angle(model
p
)
15: ] ← mean(])
16: σ
]
← std(])
17: S
]
← entropy(])
18: R
2
rank
← bottom(R
2
,L)
19: ]
rank
← top(], L)
20: return ]
p
, ], σ
]
,S
]
,R
2
rank
,]
rank
Detecting Influencers in Very Large Social Networks of Games
97
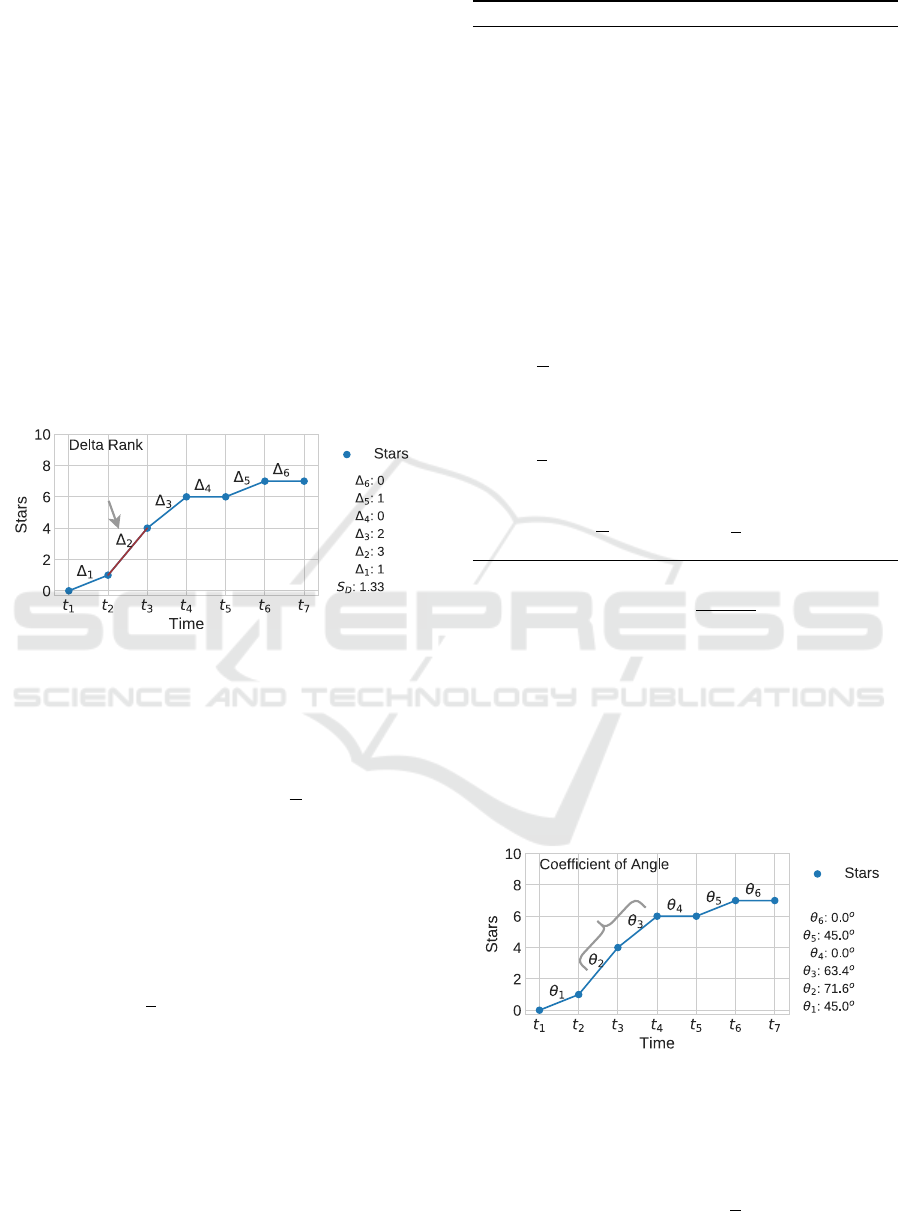
4.3.2 Delta Rank (DR)
The Delta Rank (DR) extractor infers features related
to star counting differences in time. The difference
∆ ∈ N between two sequential events ε
i
,ε
i+1
is:
∆ = stars
i+1
− stars
i
(4)
∆ means how many new stars a course c received
in a short temporal interval t
i+1
− t
i
. In this way, a
set D of star counting differences is extracted for a
course c, so D = {∆
1
,∆
2
,. ..}. Figure 5 illustrates this
idea. Course c has six pairs of sequential events, so
D = {∆
1
,. ..,∆
6
} with the values 1, 3,2,0,1 and 0, re-
spectively. By ranking the values in D it is possible
to identify the greatest ∆; it is ∆
2
= 3 in this example.
Also, we measure the entropy S
D
of D values. In this
example, it is S
D
= 1.33.
greatest value
Figure 5: Delta Rank for a star counting stream.
The DR extractor is in Algorithm 2. It represents a
player p as the union of D for all its courses (Line 12),
so D
p
= D
1
∪ ... ∪ D
|C
p
|
. A set S
p
of entropy values
S
D
for the courses (Line 13) is also collected. Then
we use D
p
and S
p
to infer features for player p.
In this analysis, we compute: ∆ that is the av-
erage of D
p
values (Line 14); σ
∆
that is the cor-
responding standard deviation (Line 15), and; S
∆
that is the entropy of D
p
values (Line 16). Also,
the extractor obtains the top-L great star count-
ing differences ∆ of the player, represented by
∆
rank
= [max
1
(∆),. ..,max
L
(∆)] (Line 17).
Additionally, the extractor analyzes the entropy
values S
D
of the player’s courses. It calculates the
average entropy
S of the courses (Line 18), and
the corresponding standard deviation σ
S
(Line 19).
Also, the extractor obtains the top-L great entropy
values S
D
of the player’s courses, represented by
S
rank
= [max
1
(S
D
),. ..,max
L
(S
D
)] (Line 20).
4.3.3 Coefficient of Angle (CA)
The Coefficient of Angle (CA) extractor infers fea-
tures related to the angles between events. The angle
θ between two sequential events ε
i
,ε
i+1
is:
Algorithm 2: DR Extractor.
1: procedure DR-MAP(c) Course Modeling
2: Initialize D with
/
0
3: for i ← 1 to |c| − 1 do
4: ∆ ← stars
i+1
− stars
i
5: D ← D ∪ {∆}
6: S
D
← entropy(D)
7: return D, S
D
8: procedure DR(p,L) Player Modeling
9: Initialize D
p
, S
p
with
/
0
10: for c ∈ C
p
do
11: D, S
D
← DR-MAP(c)
12: D
p
← D
p
∪ D
13: S
p
← S
p
∪ {S
D
}
14: ∆ ← mean(D
p
)
15: σ
∆
← std(D
p
)
16: S
∆
← entropy(D
p
)
17: ∆
rank
← top(D
p
,L)
18: S ← mean(S
p
)
19: σ
S
← std(S
p
)
20: S
rank
← top(S
p
,L)
21: return ∆, σ
∆
, S
∆
, ∆
rank
, S, σ
S
, S
rank
θ = tan
−1
∆
t
i+1
−t
i
(5)
θ means the star counting ascension between an in-
terval t
i+1
− t
i
. For each course, it is extracted a set
T = {θ
1
,θ
2
,. ..} of coefficients of angle. Note that θ
varies within interval [0
o
,90
o
); high values indicate
high star counting growth in two sequential events.
Figure 6 illustrates this idea. Course c has six pairs
of sequential events, so T = {θ
1
,. ..,θ
6
} with values
45.0
o
,71.6
o
,63.4
o
,0.0
o
,45.0
o
and 0.0
o
, respectively.
high grown
Figure 6: Coefficient of Angle for a star counting stream.
The CA extractor is in Algorithm 3. It represents a
player p as the union of T for all its courses (Line 12),
so, T
p
= T
1
∪ ... ∪ T
|C
p
|
. Then it analyzes T
p
to infer
features for player p.
In the analysis, we obtain: θ that is the average
of values in T
p
(Line 13), and; σ
θ
that is the corre-
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
98

sponding standard deviation (Line 14). We also cal-
culate the player’s top-L high growth θ, represented
as θ
rank
= [max
1
(θ),. ..,max
L
(θ)] (Line 15).
Algorithm 3: CA Extractor.
1: procedure CA-MAP(c) Course Modeling
2: Initialize T with
/
0
3: for i ← 1 to |c| − 1 do
4: ∆ ← stars
i+1
− stars
i
5: θ ← tan
−1
(∆)/(t
i+1
−t
i
)
6: T ← T ∪ {θ}
7: return T
8: procedure CA(p,L) Player Modeling
9: Initialize T
p
with
/
0
10: for c ∈ C
p
do
11: T ← CA-MAP(c)
12: T
p
← T
p
∪ T
13: θ ← mean(T
p
)
14: σ
θ
← std(T
p
)
15: θ
rank
← top(T
p
,L)
16: return θ, σ
θ
, θ
rank
4.3.4 The F
ALL
Feature Extractor
Each feature extractor, i.e., LR, DR, and CA, infers a
series of features for a player p. They are then com-
bined into a single feature extractor F
ALL
:
F
ALL
(p,L) = LR(p,L) + DR(p,L) +CA(p,L) (6)
The three feature extractors have an input param-
eter L ∈ N that determines the quantity of ranked val-
ues to be extracted, each one with its particularities.
Note that, whenever L exceeds the number of values
available to rank some characteristic of a player, the
missing values are assumed to be zeros.
4.4 Framework
This section summarizes our proposed strategy to de-
tect game influencers in Social Networks of Games.
Given the actions of millions of players in an online
game, how to detect the game influencers? It is ob-
viously necessary to model the players’ characteris-
tics, but how can it be done? So far we have no-
ticed that neither graph G
dev
nor G
star
has intrinsic
characteristics that are truly useful to spot game in-
fluencers, since we need to capture relevant informa-
tion from the correlated evolution of both graphs over
time. Then, we described how to model this corre-
lated evolution using data streams, from which we ex-
tract relevant features that properly represent the play-
ers’ characteristics. Now, we propose to simply ex-
press the game influencer detection problem as a clas-
sification ML task, using the features of our extractors
as input. In the next section, we validate our proposal
with the famous SMM game; specifically, we report
experimental results to show that our framework de-
tects game influencers of different nations with high
accuracy.
5 EXPERIMENTS
We performed a series of experiments to validate our
proposal. They are described in the following:
1. In the first experiment, we analyzed each feature
extractor individually, considering players from
one country only, i.e., Canada;
2. In the second experiment, we analyzed the ensem-
ble of the three feature extractors, also consider-
ing Canadian players.
3. We then performed input parameter tuning in the
classifiers to improve their results.
4. At last, we validated the best classifier on data
from another country, i.e., France, so to demon-
strate the generality of our framework.
In the first two experiments, we applied a set of 28
classification algorithms. They are: AdaBoostClas-
sifier, BaggingClassifier, BernoulliNB, Calibrated-
ClassifierCV, ComplementNB, DecisionTreeClassi-
fier, ExtraTreeClassifier, ExtraTreesClassifier, Gaus-
sianNB, GaussianProcessClassifier, GradientBoost-
ingClassifier, KNeighborsClassifier, LinearDiscrim-
inantAnalysis, LinearSVC, LogisticRegression, Lo-
gisticRegressionCV, MLPClassifier, MultinomialNB,
NearestCentroid, NuSVC, PassiveAggressiveClas-
sifier, Perceptron, QuadraticDiscriminantAnalysis,
RandomForestClassifier, RidgeClassifier, RidgeClas-
sifierCV, SGDClassifier, and SVC.
The algorithms are implemented in Python 3 with
the sklearn package. We used the standard input pa-
rameter values of each algorithm. For reproducibility,
our code is open-sourced at GitHub
3
, We present how
to use it and the performed experiments.
5.1 Dataset Collection
We crawled data from the Super Mario Maker game
on the SMM Bookmark website
4
continuously over
3
GitHub. “Detecting Influencers in Very Large SNG”
https://github.com/leomaurodesenv/paper-2019-iceis
4
SMM Bookmark. https://supermariomakerbookmark.
nintendo.net (accessed December 03, 2018).
Detecting Influencers in Very Large Social Networks of Games
99
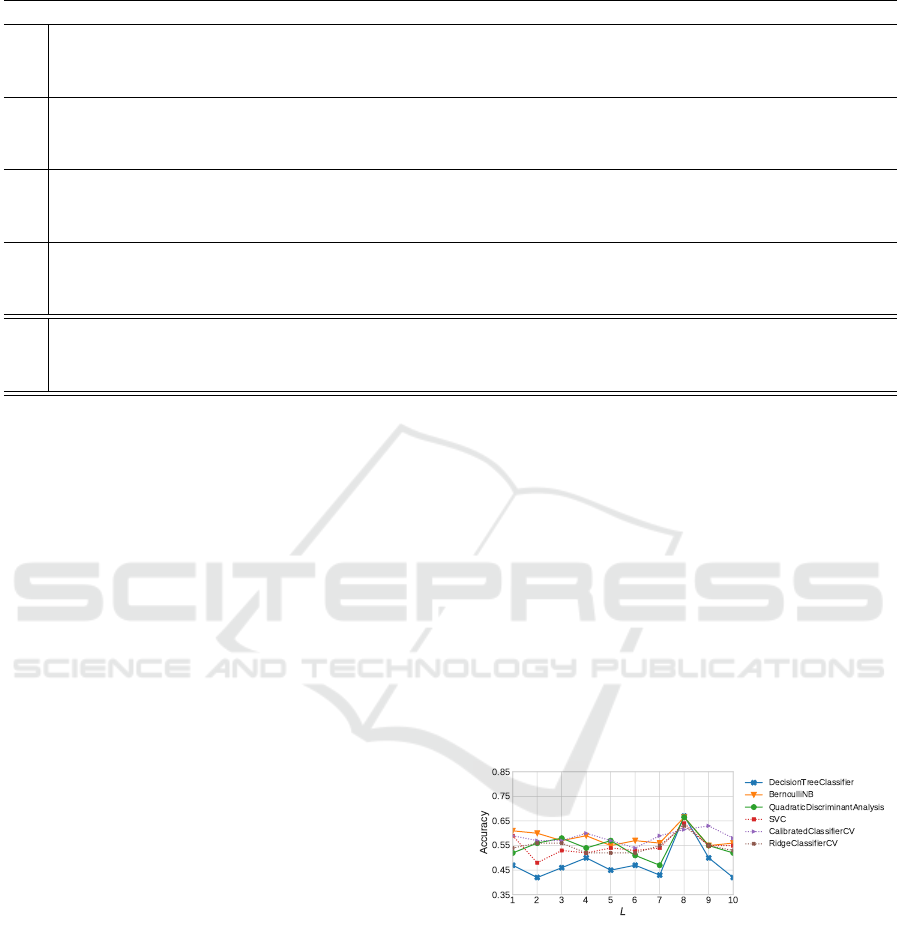
Table 2: Experiments: results of the top-3 best classifiers in each experiment.
Algorithm Accuracy Precision Recall F1-score
LR
DecisionTreeClassifier 0.670 (±0.079) 0.621 (±0.109) 0.645 (±0.100) 0.595 (±0.100)
BernoulliNB 0.665 (±0.106) 0.432 (±0.145) 0.600 (±0.100) 0.489 (±0.131)
QuadraticDiscriminantAnalysis 0.665 (±0.106) 0.432 (±0.145) 0.600 (±0.100) 0.489 (±0.131)
DR
DecisionTreeClassifier 0.690 (±0.065) 0.680 (±0.089) 0.658 (±0.070) 0.632 (±0.073)
ExtraTreeClassifier 0.670 (±0.067) 0.616 (±0.101) 0.653 (±0.075) 0.607 (±0.087)
GradientBoostingClassifier 0.670 (±0.055) 0.593 (±0.102) 0.613 (±0.058) 0.579 (±0.077)
CA
GradientBoostingClassifier 0.740 (±0.069) 0.745 (±0.068) 0.766 (±0.076) 0.722 (±0.072)
BaggingClassifier 0.696 (±0.090) 0.648 (±0.104) 0.675 (±0.106) 0.640 (±0.096)
ExtraTreeClassifier 0.680 (±0.071) 0.650 (±0.086) 0.687 (±0.091) 0.644 (±0.079)
F
ALL
LogisticRegression 0.808 (±0.108) 0.808 (±0.108) 0.733 (±0.157) 0.745 (±0.142)
RidgeClassifierCV 0.775 (±0.105) 0.733 (±0.131) 0.675 (±0.155) 0.685 (±0.144)
LinearSVC 0.750 (±0.113) 0.750 (±0.111) 0.683 (±0.154) 0.688 (±0.139)
Tuning
LogisticRegression 0.8709 (±0.066) 0.9029 (±0.053) 0.8588 (±0.080) 0.8573 (±0.076)
RidgeClassifierCV 0.8064 (±0.220) 0.7903 (±0.270) 0.8225 (±0.212) 0.7849 (±0.255)
LinearSVC 0.8387 (±0.094) 0.8596 (±0.097) 0.8306 (±0.103) 0.8266 (±0.099)
a three-months period, collecting information about
74,915 courses, and 884,302 players in which 32,055
are makers (i.e., players who elaborated courses).
These courses were developed by Canadian and
French makers and received more than 380,000 stars.
The data was split into Canadian makers (CAN
dataset) that elaborated 34,479 courses, and French
makers (FRA dataset) that elaborated 40,436 courses.
The idea is to use the CAN dataset in a train/test step,
and the FRA dataset in a validation step.
To make it possible, we had to create ground truth
for the CAN dataset. Specifically, we first ranked the
top-100 makers from CAN dataset based on the total
count of stars received by all of their courses. In this
sense, we selected graph G
star, f
of the last timestamp
t
f
to get the degree centrality (Barab
´
asi and P
´
osfai,
2016, ch.2) of each course , so it is the stars counting
of course c in G
star, f
. Also, graph G
dev, f
was used to
identify the maker’s courses.
Then, we manually labeled the top-100 makers
into two classes, non-influencer and influential player,
by checking their social activities searching the Web
with Google and also sites of the communities of
games. In total, 41% (41) influential and 59% (59)
non-influencer players were identified.
Our consensus to determine whether a player is an
influencer is if the player markets/publish its courses
in popular sites of the communities of SMM, they
are: Reddit, GameFAQs, Twitch, YouTube, Face-
book, NintendoLife, and Makers of Mario.
5.2 Feature Extractors Experiments
In the first experiment, we evaluated each feature ex-
tractor individually, i.e., LR, DR and CA. Here, the
CAN dataset was used with a 5-fold cross-validation
strategy. We evaluated the LR extractor with L rang-
ing from 1 to 10. Figure 7 reports accuracy results
for the top-6 classifiers. In this interval, the LR
(L = 8) extracting 20 attributes presented the best av-
erage accuracy. The results of the best classifiers for
the LR extractor (L = 8) are shown in Table 2. The
DecisionTreeClassifier algorithm had the best perfor-
mance with accuracy of 67.0% and f1-score of 59.5%.
Figure 7: Accuracy of the top-6 classifiers using the LR
feature extractor with parameter L ranging from 1 to 10.
Figure 8 reports the accuracy of the top-6 classi-
fiers using the DR extractor with L ranging from 1
to 10. First, we observe that the average accuracy
of classifiers grows with L. However, if L becomes
higher than the number of values ranked, nonexistent
attributes will be filled with zeros. In this sense, L
cannot be so great. Second, the experiment shows
that L = 10 present the best average accuracy with
25 attributes. Table 2 reports the evaluation of the 3
best classifiers for the DR extractor (L = 10). The De-
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
100
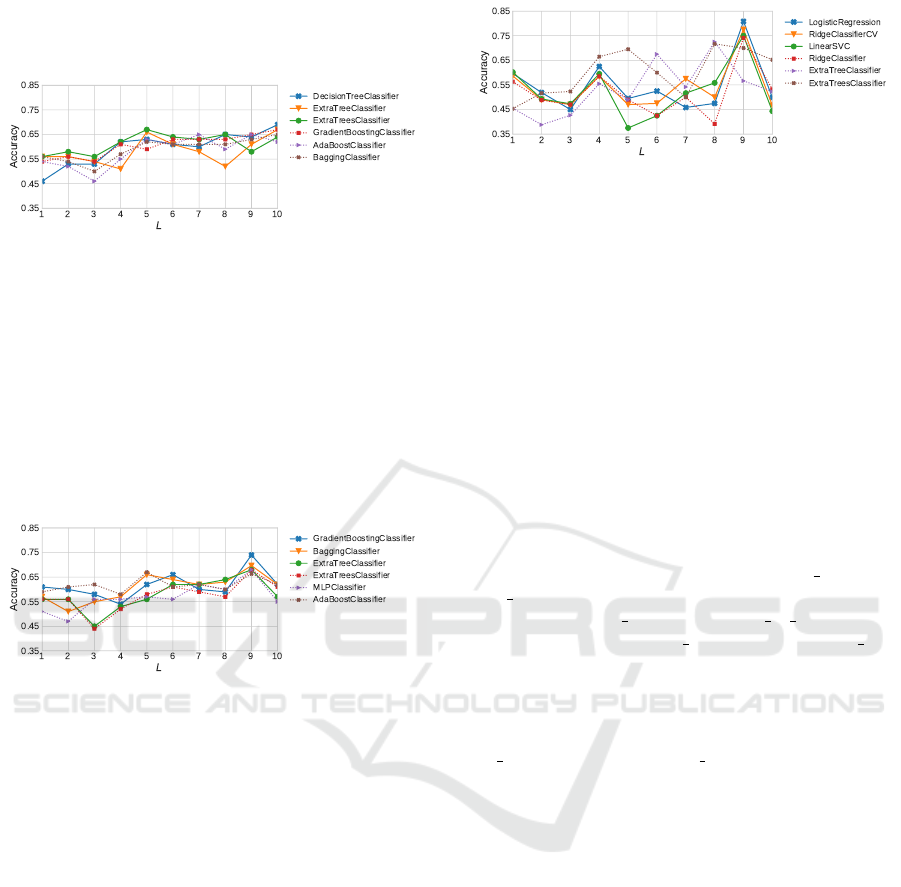
cisionTreeClassifier had the best performance again,
with 69.0% accuracy and 63.2% f1-score.
Figure 8: Accuracy of the top-6 classifiers using the DR
feature extractor with parameter L ranging from 1 to 10.
At last, we evaluated the CA extractor with L rang-
ing from 1 to 10. Figure 9 reports results from the
top-6 classifiers with the highest accuracy. The best
average accuracy was obtained with L = 9, using 11
attributes only. The results of the 3 best classifiers
for the CA extractor (L = 9) are shown in the Ta-
ble 2. Here, we highlight the GradientBoostingClas-
sifier with 74.0% accuracy and 72.2% f1-score.
Figure 9: Accuracy of the top-6 classifiers using the CA
feature extractor with parameter L ranging from 1 to 10.
In summary, the three feature extractors presented
average results in a classification task, with approxi-
mately 70% accuracy.
5.3 Framework Experiments
In this section, we analyze the F
ALL
feature extractor,
i.e., the ensemble of the three feature extractors that
we proposed. Once more, we used the CAN dataset
with a 5-fold cross-validation strategy.
Figure 10 reports the accuracy of the top-6 classi-
fiers using F
ALL
with L ranging from 1 to 10. In this
experiment, L = 9 clearly leads to the best average
accuracy, using 56 attributes. Table 2 reports results
for the 3 best classifiers with F
ALL
extractor (L = 9).
We highlight the LogisticRegression with the 80.8%
accuracy and 74.5% f1-score.
Note that the framework F
ALL
presented better re-
sults than the feature extractors individually. In addi-
tion, the top algorithms that were similar to the feature
extractors also changed, as well as the performance of
the LogisticRegression. F
ALL
(L = 9) presented great
Figure 10: Accuracy of the top-6 classifiers using the F
ALL
feature extractor with the L ranging from 1 to 10.
results using 56 attributes, meanwhile the LR (L = 8),
DR (L = 10) and CA (L = 9) used 20, 25 and 11 fea-
tures, respectively. However, LogisticRegression us-
ing F
ALL
(L = 9) obtained the best accuracy (80.8%),
precision (80.8%), and f1-score (74.5%).
5.4 Parameter Tuning
In this step, we focused on improving the top-3 classi-
fiers of the framework experiments (F
ALL
(L = 9)) us-
ing a grid search, that is, an exhaustive search through
the hyperparameter space of the classifiers.
The grid search on each classifier’s parameters,
i.e., LogisticRegression (C, dual, f it intercept,
max iter, penalty, solver), RidgeClassifierCV
(al phas, cv, f it intercept, store cv values) and
LinearSVC (C, dual, f it intercept, loss, max iter,
penalty), also used the CAN dataset with a 5-fold
cross-validation strategy.
Table 2 reports the best results of each classi-
fier. The LogisticRegression (C = 0.9, dual = True,
f it intercept = True, max iter = 100, penalty =
l2, solver = warn) using F
ALL
(L = 9) obtained the
best accuracy (87.1%), precision (90.3%), recall
(85.9%), and f1-score (85.7%). The performance of
RidgeClassifierCV and LinearSVC also improved.
5.5 Validation
The validation experiment evaluated the generality of
our framework. Here, we used the best configuration,
i.e., F
ALL
(L = 9) plus LogisticRegression with the
fine tuned parameter values of Section 5.4, taking the
whole CAN dataset for training and the FRA dataset
for testing. At first, we ranked the top-100 makers
from the FRA dataset based on their total number of
stars received. Then, we used F
ALL
(L = 9) to infer the
players’ features and the LogisticRegression classifier
to label the game influencers. Thanks to our proposed
framework, the algorithm labeled 27 players as game
influencers, automatically, in which 21 were manu-
ally confirmed as true influencers. Thus, our proposed
model presented 77.8% precision to find influencers
Detecting Influencers in Very Large Social Networks of Games
101

with a classifier trained in data from another coun-
try. These results indicate that our proposal is generic
enough to accurately model the behaviour of game in-
fluencers from different nationalities.
6 CONCLUSION
This paper presented a novel framework to detect
game influencers in Social Networks of Games.
Given the actions of millions of players in an online
game, how to detect the most influential users? It was
obviously necessary to model the players’ character-
istics, but how can it be done? To tackle the prob-
lem, we needed to capture relevant information from
the correlated evolution of more than one dynamic
network over time, which could not be performed
with the existing works. Then, we described how
to model this correlated evolution using data streams,
from which we extracted relevant features to properly
represent the players’ characteristics, and mapped the
game influencer detection problem into a classifica-
tion ML task that uses our features as input. Finally,
we validated our proposal by studying the famous Su-
per Mario Maker game, from Nintendo Inc., Japan.
The novel framework includes three feature ex-
tractors, i.e., Linear Regression, Delta Rank and Co-
efficient of Angle. They are unsupervised and based
on the temporal aspects of the players’ actions on
the social network. In the experimental evaluation,
28 classification algorithms were studied. Using our
features as input, the LogisticRegression classifier ob-
tained the bests results with accuracy (87.1%), preci-
sion (90.3%), recall (85.9%) and f1-score (85.7%).
We also demonstrated that the proposed framework
automatically detects game influencers with high ac-
curacy even when using data from distinct nations for
testing and training.
Analyzing Other Types of Social Networks: in
theory, our methodology can also be used in non-
game-related applications, such as to spot influencers
in other types of social networks by analyzing the
“likes” received by posts over time. Minor adapta-
tions may be needed, due to domain specificities. Ba-
sically, two dynamic networks are the only require-
ment; one to store the creator of digital content and
another to represent positive reactions (e.g., “like”) of
users to the content, as it is formalized in the paper.
Further Research: (1) analyze influencers’
games to discover popular games’ characteristics,
e.g., platform games’ characteristics, such as general
monsters, course size, challenges, traps, and so on;
(2) apply this framework in other domains to spot in-
fluencers; (3) also, use regression modeling to study
different degrees of influence over the players.
ACKNOWLEDGEMENTS
This work was supported by the Brazilian National
Council for Scientific and Technological Develop-
ment (CNPq); Coordination for the Improvement of
Higher Education Personnel - Brazil (CAPES) [grant
001]; Sao Paulo Research Foundation (FAPESP)
[grant 2018/05714-5]; and AWS Cloud Credits for
Research.
REFERENCES
Al-Garadi, M. A., Varathan, K. D., Ravana, S. D., Ahmed,
E., Mujtaba, G., Khan, M. U. S., and Khan, S. U.
(2018). Analysis of online social network connections
for identification of influential users: Survey and open
research issues. ACM Comput. Surv., 51(1):16:1–
16:37.
Barab
´
asi, A.-L. and P
´
osfai, M. (2016). Network science.
Cambridge university press, Cambridge, USA.
Chino, D. Y. T., Costa, A. F., Traina, A. J. M., and Falout-
sos, C. (2017). VolTime: Unsupervised Anomaly De-
tection on Users’ Online Activity Volume, pages 108–
116. SIAM International Conference on Data Mining.
Gros, D., Hackenholt, A., Zawadzki, P., and Wanner, B.
(2018). Interactions of twitch users and their usage
behavior. In Meiselwitz, G., editor, Social Computing
and Social Media. Technologies and Analytics, pages
201–213, Cham. Springer International Publishing.
Hilvert-Bruce, Z., Neill, J. T., Sj
¨
oblom, M., and Hamari, J.
(2018). Social motivations of live-streaming viewer
engagement on twitch. Computers in Human Behav-
ior, 84:58 – 67.
Kamber, M., Han, J., and Pei, J. (2012). Data mining: Con-
cepts and techniques. Elsevier, Amsterdam.
Lee, J., Lee, M., and Choi, I. H. (2012). Social network
games uncovered: Motivations and their attitudinal
and behavioral outcomes. Cyberpsychology, Behav-
ior, and Social Networking, 15(12):643–648. PMID:
23020746.
Liu, N., Li, L., Xu, G., and Yang, Z. (2014). Identify-
ing domain-dependent influential microblog users: A
post-feature based approach. In AAAI, pages 3122–
3123.
Lucas, S. M. (2009). Computational intelligence and ai
in games: A new ieee transactions. IEEE Transac-
tions on Computational Intelligence and AI in Games,
1(1):1–3.
Morone, F., Min, B., Bo, L., Mari, R., and Makse, H. A.
(2016). Collective influence algorithm to find influ-
encers via optimal percolation in massively large so-
cial media. Scientific reports, 6:30062.
Pei, S., Morone, F., and Makse, H. A. (2018). Theories for
Influencer Identification in Complex Networks, pages
125–148. Springer International Publishing, Cham.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
102

Qi, L., Huang, Y., Li, L., and Xu, G. (2015). Learning to
rank domain experts in microblogging by combining
text and non-text features. In 2015 International Con-
ference on Behavioral, Economic and Socio-cultural
Computing (BESC), pages 28–31.
Savi
´
c, M., Ivanovi
´
c, M., and Jain, L. C. (2019). Introduction
to Complex Networks, pages 3–16. Springer Interna-
tional Publishing, Cham.
Sj
¨
oblom, M. and Hamari, J. (2017). Why do people watch
others play video games? an empirical study on the
motivations of twitch users. Computers in Human Be-
havior, 75:985 – 996.
Strang, G., Strang, G., Strang, G., and Strang, G. (2016).
Introduction to Linear Algebra, volume 5. Wellesley-
Cambridge Press Wellesley, MA.
Wang, X., Zhang, X., Yi, D., and Zhao, C. (2017). Identify-
ing influential spreaders in complex networks through
local effective spreading paths. Journal of Statistical
Mechanics: Theory and Experiment, 2017(5):053402.
Westaby, J. D. (2012). Dynamic network theory: How so-
cial networks influence goal pursuit. American Psy-
chological Association.
Yannakakis, G. N. and Togelius, J. (2015). A panorama
of artificial and computational intelligence in games.
IEEE Transactions on Computational Intelligence and
AI in Games, 7(4):317–335.
Yannakakis, G. N. and Togelius, J. (2018). Artificial Intelli-
gence and Games. Springer International Publishing,
Cham.
Detecting Influencers in Very Large Social Networks of Games
103
