
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent
Systems
Ashalatha Kunnappiilly, Simin Cai, Raluca Marinescu and Cristina Seceleanu
Mälardalen University, Västerås, Sweden
Keywords:
Cyber-physical Systems, Ambient Assisted Living, Multi-Agent Systems, Architecture Analsysis And Design
Language, Model Checking, PRISM.
Abstract:
Modern cyber-physical systems usually assume a certain degree of autonomy. Such systems, like Ambient As-
sisted Living systems aimed at assisting elderly people in their daily life, often need to perform safety-critical
functions, for instance, fall detection, health deviation monitoring, communication to caregivers, etc. In many
cases, the system users have distributed locations, as well as different needs that need to be serviced intel-
ligently and simultaneously. These features call for intelligent, adaptive, scalable and fault-tolerant system
design solutions, which are well embodied by multi-agent architectures. Analyzing such complex architec-
tures at design phase, to verify if an abstraction of the system satisfies all the critical requirements is beneficial.
In this paper, we start from an agent-based architecture for ambient assisted living systems, inspired from the
literature, which we model in the popular Architecture Analysis and Design Language. Since the latter lacks
the ability to specify autonomous agent behaviours, which are often intelligent, non deterministic or prob-
abilistic, we extend the architectural language with a sub-language called Agent Annex, which we formally
encode as a Stochastic Transition System. This contribution allows us to specify behaviours of agents involved
in agent-based architectures of cyber-physical systems, which we show how to exhaustively verify with the
state-of-art model checker PRISM. As a final step, we apply our framework on a distributed ambient assisted
living system, whose critical requirements we verify with PRISM.
1 INTRODUCTION
Equipped with various sensors, actuators and com-
putation units, modern cyber-physical systems have
evolved into increasingly intelligent, autonomous and
adaptive systems. A representative category is Am-
bient Assisted Living (AAL) systems, which monitor
the conditions of elderly people and their surround-
ings, in order to provide them with intelligent and
timely assistance, autonomously. Due to such charac-
teristics, as well as the possibly distributed locations
of users and service providers, the multi-agent ar-
chitecture is deemed appropriate for designing multi-
user AAL systems. In a multi-agent system (MAS),
each agent is an autonomous entity that can perform
actions individually and intelligently, while adapting
to the environment. For instance, a pulse agent may
monitor an elderly user’s pulse, and decide whether
an alert should be sent to the caregiver. Multiple
agents can be distributed geographically, and cooper-
ate by exchanging network messages to achieve com-
plex tasks, such as a proper reaction to the fall caused
due to a sudden drop of pulse, via the cooperation of a
pulse agent and a fall-detection agent. In many cases,
such system behaviours are often probabilistic due
to random component failures, communication fail-
ures, arbitrary service connection requests, user inter-
actions, etc.
In order to guarantee the system’s safety and
achieve the desired quality of service (QoS), it is ben-
eficial to ensure the correctness of the AAL system
design, with respect to the real-time, fault-tolerant
and probabilistic behaviors of agents, both individu-
ally and in cooperation. To achieve this, specification
and rigorous analysis of such behaviors are necessary,
which should go hand-in-hand with the specification
and analysis of the entire architecture in which the
agents are integrated. Existing techniques either do
not support the integrated specification and analysis
of architecture and agent behaviors, or lack reason-
ing capabilities of combined real-time, fault-tolerant
and probabilistic behaviors that are essential to many
AAL systems (Kunnappilly et al., 2018; Rodrigues
et al., 2012).
In this paper, based on existing solutions (Tapia
114
Kunnappiilly, A., Cai, S., Marinescu, R. and Seceleanu, C.
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems.
DOI: 10.5220/0007730201140126
In Proceedings of the 14th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2019), pages 114-126
ISBN: 978-989-758-375-9
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

et al., 2009), we propose a MAS architecture for
AAL, comprising simple reflex agents based on if-
then-else rules, and complex intelligent agents with
self-learning based on Reinforcement Learning (RL)
(Sutton et al., 1998). As our basis for specification,
we choose a commonly-used architecture specifica-
tion language, that is, the Architecture Analysis and
Design Language (AADL) (Feiler et al., 2006). We
use the original AADL constructs to specify the ar-
chitecture including the agent components, their in-
terfaces and communication. However, since the core
AADL language lacks the ability to specify emergent
agent behaviours, which may be both probabilistic
and non deterministic, we propose an annex exten-
sion to the core AADL, referred to as Agent Annex.
Unlike the existing Behaviour Annex specification of
AADL (Dissaux et al., 2006), usually used for encod-
ing component behavior, the Agent Annex allows one
to describe the combined real-time, fault-tolerant and
probabilistic behaviors. We formulate the new annex
by extending the AADL meta model, and define its
semantics as a stochastic transition system. To en-
able formal verification, we also provide formal se-
mantics to the AADL architectural model, in terms of
Stochastic Transition Systems (STS). We employ the
state-of-the-art probabilistic model checker, PRISM
(Kwiatkowska et al., 2002), to formally verify a set of
crucial functional and quality-of-service properties of
an illustrative AAL use case.
The rest of the paper is organized as follows.
Section 2 overviews the basics of AADL, STS and
PRISM. In Section 3, we describe our AAL system
architecture based on MAS. We present the AADL
modeling constructs and the Agent Annex extension
in Section 4. Section 5 describes the formal encod-
ing of the AADL model, and in Section 6, we present
the verification results applying the PRISM model-
checker on a representative AAL system. Related
work is described in Section 7. Some discussion
points are presented in Section 8 and conclusions and
future work in Section 9.
2 PRELIMINARIES
In this section, we give an overview of AADL, STS
and PRISM, in Sections 2.1, 2.2 and 2.3, respectively.
2.1 Architecture Analysis and Design
Language
The Architecture Analysis and Design Language
(AADL) (Feiler et al., 2006) is a textual and graph-
ical language for modeling and analyzing a real-time
system’s hardware and software architecture as hier-
archies of components at various abstraction levels.
AADL component categories like Application
Software, Execution Platform and System are used
to represent the run-time architecture of the system,
whereas a more generalized representation is also
possible by specifying it as abstract. A component
in AADL can be defined by its type and implemen-
tation; the first defines the interface of the compo-
nent and its externally-observable attributes, whereas
the second defines its internal structure. AADL al-
lows possible component interactions via ports/fea-
tures, shared data, subprograms, and parameter con-
nections, whereas a communication protocol over a
network connection is modeled by a bus. The com-
ponents can also be associated with various proper-
ties, like period, execution time, and dispatch proto-
col. The dispatch protocol specifies if the component
trigger is periodic or aperiodic. We also employ vari-
ous user-defined properties for representing the prob-
abilistic distribution of an aperiodic event and the rate
at which a component recovers from the failure. All
the AADL declarations are declared in packages and
are therefore accessible to other packages, or they can
be declared directly in an AADL specification and not
be accessible to packages.
The AADL core language is designed to be ex-
tensible and can be extended via user-defined proper-
ties and annex sub-languages. User-defined proper-
ties are relatively simpler extensions, when compared
to sub-languages, and can be associated with model-
ing elements as simple values, for instance, integers
or strings. However, sub-languages allow more com-
plex structures to be added to an AADL model. A
sub-language can be standardized and published as an
AADL annex. Several such annexes have been de-
fined, for example, the behavior annex to model the
component’s behaviour, and the error annex for mod-
eling the error behaviour of the system. Annex sub-
languages are included into AADL specifications as
annex libraries or annex subclauses. An annex library
is used to define classifiers defined in an anonymous
namespace, or in a public or private part of a pack-
age. Annex subclauses are inserted into component
types and component implementations and can refer-
ence the classifiers declared in the annex library. In
AADL, annexes are considered to be separate from
the core AADL, i.e., if we remove all the annex li-
braries, subclauses, and annex-related property asso-
ciations, the resulting model is a valid core AADL
model. For further details, the reader can refer to the
work (Feiler et al., 2006).
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
115

2.2 Stochastic Transition Systems
Stochastic transition systems (STS) (De Alfaro, 1998)
are transition systems that support non determinism,
and transitions with unspecified delay distributions,
providing concise and compositional means to rep-
resent systems in terms of probability, waiting-time
distributions, non determinism, and fairness.
A stochastic transition system is defined by a tuple
S =< V, Θ, T >, where V = V
l
∪V
g
, V
l
is a finite set
of local state variables with finite domain, and V
g
is the finite set of global variables of the system. In
case a subset of V
g
is used in a particular module,
i.e., V
g
∩V
l
6=
/
0, implies that V
g
also contributes to
the state-space of the module. We denote by s[[v]] the
value in state s ∈ S of v ∈ V
l
(the interpretation of
function [[·]] is extended to terms in the obvious way).
Θ is an assertion over V
l
denoting the set {s ∈ S | s |=
Θ} of initial states, and the assertions over V
g
. T
is a set of transitions. The following quantities are
associated with each transition τ ∈ T:
• An assertion ε
τ
over V
l
, which specifies the set of
states {s ∈ S | s |= ε
τ
} on which τ is enabled.
• A number m
τ
of transition modes, where each
transition mode i ∈ {1, . . . , m
τ
} corresponds to a
possible outcome of τ. Each transition mode i is
specified by V
l
: (i) a set of assignments {v
0
:=
f
τ
i,v
}
v∈V
l
, where each f
τ
i,v
is a term over V
l
and
f
τ
i
: S 7→ S is a function that maps every state s ∈ S
to a successor s
0
= f
τ
i
(s) such that s
0
[[v]] = s[[ f
τ
i,v
]]
for all v ∈ V
l
, and (ii) the probability p
τ
i
∈ [0, 1]
with which mode i is chosen, where
∑
m
τ
i=1
p
τ
i
= 1.
The set of transitions T is partitioned into
the set of immediate transitions T
i
and the set
of delayed transitions T
d
. Immediate transitions
must be taken as soon as they are enabled, and
a subset of these transitions T
f
⊆ T
i
is the set of
f air transitions. In turn, the set of delayed tran-
sitions is partitioned into: (i) the set of transi-
tions with exponential delay distribution T
e
, where
for each τ ∈ T
e
there is an associated transition
rate γ
τ
> 0, and (ii) the set of transitions with
unspeci f ied delay distributions T
u
that are taken with
non-zero delay, but the probability distribution of the
delay and the possible dependencies between this dis-
tribution and the system’s state or past history are not
specified.
Given a state s ∈ S, we indicate by T (s) = {τ ∈ T |
s |= ε
τ
} the set of transitions enabled by s. To ensure
that T (s) 6=
/
0 for all s ∈ S, an idle transition τ
idle
is
added to every STS defined by ε
τ
idle
= true, m
τ
idle
=
1, p
τ
idle
1
= 1, γ
τ
idle
= 1 and by the set of assignments
{v
0
:= v}
v∈V
.
2.3 Probabilistic Timed Automata and
PRISM
To analyze our multi-agent systems, in this paper we
use the PRISM model checker (Kwiatkowska et al.,
2002). Among other supported formal notations,
PRISM provides symbolic model checking of sys-
tems modeled as networks of Probabilistic Timed Au-
tomata (PTA), which are semantically described by
Timed Probabilistic Systems (TPS)(Norman et al.,
2013). De Alfaro shows that an STS can be straight-
forwardly translated into (fair) TPS, yielding the same
state space (De Alfaro, 1998).
In PRISM, a PTA is represented by a module,
which is defined as a tuple M =< Var,Clock,C >,
in which Var is a set of local finite-valued variables,
Clock is a set of local clock variables that progress
with step of 1, and C is a set of commands. The state
of a PTA is the valuation of Var ∪ Clock. The com-
mands, which define the transitions of the system, are
specified as guarded probabilistic updates of states in
the following form: [a] g → p
1
: u
1
+ ... + p
n
: u
n
.
Here, guard g is a predicate over the variables that
enable the transition. Variables p
1
, ..., p
n
are proba-
bilities within the interval (0,1], whose values sum up
to 1. Each u
i
is an update of the state by assigning
new values to variables, or by resetting clocks. The
update of a variable v is specified as v
0
= n, where n
is the new value. A command is enabled if the guard
of the command evaluates to true. If multiple com-
mands are enabled, one command is selected non-
deterministically, and one of its updates is executed
probabilistically. In the brackets, a is a labeled action.
Commands with same actions are forced to be taken
simultaneously. We can also augment the model with
rewards, which are real values associated with states
or transitions. Rewards can be both positive or nega-
tive depending on the system behaviour.
A system is defined as a network of modules via
parallel composition: Sys = M
1
||...||M
n
. A global
state is the valuation of all variables of all modules.
A module can both read and write its own local vari-
ables, but only has read access to the local variables of
other modules. Synchronized transitions of modules
are identified by the commands with the same labels.
The property specification language of PRISM
for PTA is based on Probabilistic Computation Tree
Logic (PCTL) (Hansson et al., 1994). The model
checker can verify whether the probability of a path
property pp is within a bound b, which is specified
as: P b [ pp]. Here, b can be any of >= p, > p,
<= p or < p, where p is a double within [0,1]. A
path property pp is a formula that evaluates to either
true or false for a single path in the model, in which
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
116
one can apply the following operators: X (next), U
(until), F (eventually), G (always), W (weak until), R
(release). PRISM can also compute the minimum and
maximum probabilities of a path property, in the form
of: Pmin =?[ pp ], and Pmax =? [ pp ], respectively. In
order to check a path property for paths that start from
multiple states, filters are used to identify the starting
states. For instance, the “forall” filter returns true if
the property is true for all states satisfying the filter.
In the following section, we present a multi-agent
system (MAS) architecture for the AAL domain.
3 A MULTI-AGENT SYSTEM
ARCHITECTURE FOR AAL
Our proposed architecture consists of multiple agents,
and ensures improved fault-tolerance, scalability and
adaptability, compared to centralized architectures in
the domain, such as CAMI (Kunnappilly et al., 2017).
The architecture is inspired from similar existing ar-
chitectures in literature (Tapia et al., 2009). How-
ever, existing solutions usually suffer from additional
overhead encountered during agent synchronization
for collective decision-making and data consistency
maintenance. This overhead can sometimes hamper
the real-time behavior of the system. Hence, we in-
vestigate how we can use these systems for develop-
ing integrated solutions that ensure a safe trade off
between autonomous behavior and consistency over-
heads. This is challenging since agents are interde-
pendent, and have only a limited view of the envi-
ronment. Concretely, the agent-based solution should
ensure a consistent view of the environment, in terms
of processed data and events, as well as an inter-
agent communication overhead that should not result
in breaching the real-time system demands. We en-
sure this by allowing each agent to cater for a partic-
ular functionality, respectively; for instance, a health-
monitoring agent detects health-parameter variations
and raises a notification to caregiver. However, in
order for the agents to cooperate in real time, each
agent maintains the dependencies it can have with
other agents, in a list that can change at run time
1
.
The architecture is described briefly in the follow-
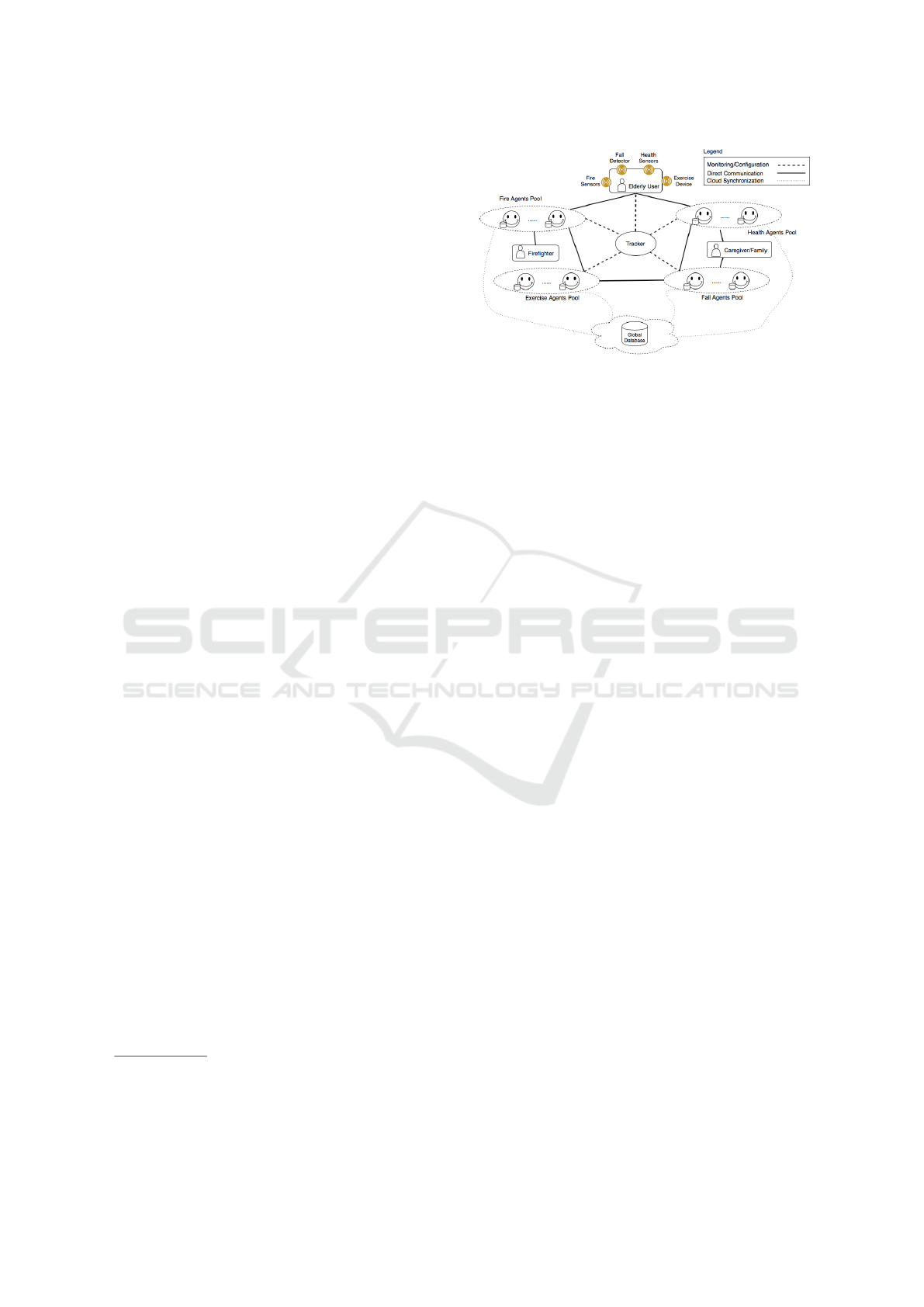
ing, and is shown in Fig. 1. It consists of the following
components:
• Agents: In our solution, each agent tackles a
particular functionality, in response to the sensor
1
This claim is based on the simulation of the AADL
model of the architecture for end-to-end latency according
to the process detailed here: https://github.com/ashalatha-
0504/Real-time-behvaiour-of-MAS
Figure 1: A MAS Architecture for AAL.
data, that is, the fire agent deals with detecting fire
events from fire sensors and sends a notification to
firefighters, the pulse agent detects the pulse data
variations and sends a notification to the caregiver,
the fall agent detects the user fall and alerts the
caregiver, the exercise agent schedules and mon-
itors the exercise session of the user, etc. These
agents can belong to different categories, ranging
from simple reflex agents to complex intelligent
agents. In our case, we use the exercise agent
as an example of an intelligent agent with em-
bedded reinforcement learning (RL) algorithms.
This provides an optimized exercise session for
the user, taking into account his/her health con-
dition, preferences and exercise trends. All other
agents are modelled as reflex agents encoded us-
ing “if-then-else” rules to handle the particular
scenario. To be able to cooperate efficiently in real
time (by reducing extra overheads), each agent
is equipped with a list of possible dependencies
with other agents. For instance, a fall agent has
a dependency relation with a pulse agent. If a
heavy fall occurs, the fall is first communicated to
the caregiver, and then the fall agent synchronizes
with the pulse agent to see if there are any pulse
deviations (like a low pulse). If a low pulse is de-
tected, the fall agent updates its notification to the
caregiver indicating that the fall may be due to a
low pulse. Each agent also maintains a small lo-
cal database to store the individual data and keep
track of the processed events and the decisions
taken. The dependency lists are also maintained
in the local database.
• Tracker: The system has a tracker that keeps the
record of the IP addresses of all the agents in the
system. The user’s connections to the agents are
established via the tracker. If the tracker fails at
any point in time, the system continues to func-
tion via direct connections between user requests
and agents. As shown in Fig 1, we have multi-
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
117

ple agents of each category, which can accept re-
quests from multiple users, arbitrarily, based on
availability.
• Cloud Database: We also maintain a large-scale
database in the cloud. All the local databases of
the agents eventually synchronize with this cloud
database. The cloud database also maintains the
domain information about the user, like age, dis-
ease history, user preferences, etc.
• End Users of the System: There are two types
of users, elderly users and the service providers
(caregivers, firefighters, etc.).
We assume the following: (i) Each of the agents
can accept a maximum of m connections, and
there is a maximum of n users of the system,
(ii) The number of accepted connections is al-
ways smaller than or equal to the number of users,
that is, m ≤ n, (iii) The system components com-
municate via various network protocols, (iv) The
communication between agents is mediated by the
tracker and is assumed instantaneous; however, if
the tracker fails, then the agents can communicate
to each other with an assumed delay.
3.1 Reinforcement Learning in Exercise
Agents
The interaction between the exercise agent and its
environment is modeled as an RL problem as fol-
lows: An exercise agent proposes 2 kind of exercise
categories for its user - Low-intensity, and Medium-
intensity, specifically tailored for cardiac patients, and
normal users, respectively. Each category has a set
of individual exercises. If a calendar notification is
raised for the start of the exercise session, the ex-
ercise agent becomes operational and communicates
with the health agent to see if the user has a normal
pulse range. If the pulse level is normal, the health
agent is ready to propose an optimized exercise ses-
sion for the user. At any point in time, the exercise
agent has 2 choices to make: a) choose an exercise
category out of the 2 options, and b) suggest an ex-
ercise duration. The choice is made initially by con-
sidering user preferences and health condition. For
simplicity, we assume that both options for exercise
sessions are initially set to 10 minutes. The exercise
duration is subdivided into intervals of 5 minutes. In
these sub-intervals, the user gets an exercise recom-
mendation of the same category. If the user quits
in between (or not satisfied), the exercise category is
re-adjusted in the next sub-interval. For each of the
action that the agent suggests, it gets a reward back,
based on the utility of the suggested action. The util-
ity is calculated as a weighted sum of the following
parameters: (i) user satisfaction for the prescribed ex-
ercise (u_st), based on a user feedback recorded and
(ii) session completion, that is, if the user has com-
pleted the prescribed exercise duration (ss_com):
Utility = w1 ∗ (u_st) + w2 ∗ (ss_com), (1)
where w1, w2 are the respective weights, where
w1>w2. In this case, we assume that these weights
are assigned to 0.6 and 0.4.
u_st =
(
1 if user satisfied
−1 if user not satisfied
(2)
ss_com =
(
1 if exercise duration completed
−1 if exercise duration not completed
(3)
In this paper, we consider that the reward signal
is directly proportional to system utility, i.e, we get a
higher reward for taking an action with higher utility.
For this purpose, the initial system reward is calcu-
lated as its utility. After this, we always add up the
successive reward values to determine the cumulative
reward. In our case, we calculate the cumulative re-
ward for each of the chosen exercise category, and the
best action is considered as the one that has the max-
imum cumulative reward at any time point. In addi-
tion to the reward function, we also take into account
the domain knowledge to make the choice of the ex-
ercise. The domain knowledge in our case consists
of the user disease history, and preferences. It should
be noted that the initial choice of exercise is made
based on domain knowledge and thereafter, the choice
is made by comparison of the reward variables., i.e.,
an exercise of a higher reward is always weighted over
the other choice.
3.2 Use-Case Scenarios and System
Requirements
In this paper, we consider a MAS consisting of a pulse
agent, a fire agent, a fall agent, and an exercise agent,
each with its replica, respectively. Each agent can ac-
cept a maximum of 2 connections, while the system
is simultaneously utilized by two elderly adults, say
Jim and Mary, living independently in their respec-
tive homes. Jim is also a cardiac patient. We consider
the following two scenarios where the AAL system
assists its users.
• Scenario 1: Fall due to a Low Pulse: The pulse-
detection sensor worn by Jim detects the low
pulse, and the wearable fall-sensor detects the fall.
The sensors forward the sensed data to the tracker,
which assigns a pulse agent and a fall agent to user
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
118

1 (arbitrarily, based on availability). The agents
communicate with each other and reach the con-
clusion that the fall is due to a low pulse, and send
a notification alert to the caregiver.
• Scenario 2: Fire and Fall Occurring Simultane-
ously: Mary is cooking dinner, and suddenly she
feels dizzy and falls. The cooker is still on, start-
ing a fire at home. In this case, the sensors alert
the tracker of the respective events, and the former
assigns a fire agent and a fall agent to Mary. The
agents communicate with each other, synchronize
the simultaneous occurrences of both events, and
alert both the firefighter and the caregiver.
• Scenario 3: Health Abnormality during the Ex-
ercise Session: Jim gets a calendar notification to
start the exercise session. The tracker then assigns
an exercise agent to Jim to schedule and moni-
tor the exercise session. The exercise agent com-
municates with the health agent and identifies that
Jim’s health is normal and suggests the medium-
complexity exercise for cardiac patients based on
his preferences and health condition. In the mid-
dle of the exercise session, Jim’s health agent in-
dicates a sudden increase in pulse and hence the
exercise agent suggests an exercise of lower com-
plexity in the next sub-interval. The following
system requirements are formulated for the above
scenarios:
– R1: If a fall occurs due to low pulse, then raise
an alert to caregiver indicating fall due to low
pulse within 20 s. It relates to Scenario 1.
– R2: If a fire and a fall event occur simultane-
ously, then raise an alert to both caregiver and
firefighter indicating the issue, within 20 s. This
requirement relates to Scenario 2.
– R3: The exercise session is scheduled only if
the health agent indicates a normal pulse.
– R4: The initially suggested exercise is based on
user preferences and health condition.
– R5: If any health abnormality is detected in
the first sub-session of the exercise, a different
set of exercises of lower intensity is prescribed.
Requirements R3, R4 and R5 are formulated
based on Scenario 3. It should be noted that
R1-R5 are safety-critical requirements.
In addition, the system has quality-of-service
(QoS) requirements as follows:
– R6: If the tracker fails, the system continues its
functionality.
– R7: If one of the agent fails, its function is car-
ried out by the back-up.
4 MODELING MULTI-AGENT
SYSTEMS IN AADL
In this section, we illustrate the AADL modeling
of our MAS, depicted in Fig 1. The components
are modeled as follows: the agents and tracker are
modeled as abstract components, which can be ex-
tended to suit a hardware or software implementa-
tion, at later stages of design. The sensors are mod-
eled as hardware devices. The databases are modeled
as data components in AADL. All the components
have their respective component type and implemen-
tation defined. The component type defines the com-
ponent features and properties. We use bus connec-
tions to represent the respective communication pro-
tocols used by the components. The bus access is
modeled as a feature of the component. We restrict to
only using properties like dispatch protocol, period,
execution time and user-defined properties to specify
the scope of global variables in the system. However,
based on the requirements, certain user-defined prop-
erties can also be added to specify the rate of occur-
rence of an aperiodic event or so (Kunnappilly et al.,
2018). In the component implementation, we define
the sub-components and connections.
Listing 1 shows an excerpt of the AADL model of our
system with an exercise agent, and a bus component;
the Agent Communication Protocol (ACP) models
the communication protocol between multiple agents.
For simplicity, we assume that the communication
protocols defined here work via shared variables. The
Agent component is modeled as an abstract compo-
nent in AADL (Lines 1-8), which can be later refined
towards a particular hardware or software, based on
the application. We also show a system-level rep-
resentation (Lines 10-26) with its sub-components,
user-defined properties (some of which needs asser-
tion in the respective agent annex, where the property
is applied) and their connections defining the commu-
nication.
Listing 1: An excerpt of the system modeling in AADL.
1 a b s t r a c t Ex c_Ag ent1
2 f e a t u r e s
3 BA1 : r e q u i r e s bu s a c c e s s ACP ;
4 BA2 : r e q u i r e s bu s a c c e s s SA_comm1 ;
5 p r o p e r t i e s
6 D i s p a t c h _ P r o t o c o l => A p e r i o d i c ;
7 C o m pu t e _Ex e c ut i o n_ t i me => 2ms . . 2 ms ;
8 en d Exc_ Agen t1 ;
9 b u s ACP . . . end ACP ;
10 s ys t e m a g e n t _ s y s t e m
11 p r o p e r t i e s
12 m y p r o p e t r i e s : : w1= 0. 6 a p p l i e s t o Exc_A gent 1 ;
13 m y p r o p e t r i e s : : w2= 0. 4 a p p l i e s t o Exc_A gent 1 ;
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
119
14 m y p r o p e r t i e s : : u t i l i t y
=> " The v a l u e n e e d s a s s e r t i o n i n annex ! "
15 a p p l i e s t o Ex c_Ag ent1 ;
16 m y p r o p e r t i e s : : r e wa r d =>
17 " The va l u e n e ed s a s s e r t i o n i n annex ! "
18 a p p l i e s t o Ex c_Ag ent1 ;
19 en d a g e n t _ s y s t e m ;
20 s ys t e m i m p l e m e n t a t i o n a g e n t _ s y s t e m . i mpl
21 s u b com p o n e nts
22 A1 : a b s t r a c t Exc _Age nt1 ;
23 Agent_Comm_Proto : bus ACP ;
24 c o n n e c t i o n s
25 BAsys1 : bu s a c c e s s Agent_Comm_Proto <−>A1 . BA1 ;
26 en d a g e n t _ s y s t e m . i m p l ;
After specifying the components and their inter-
faces, the next step is to specify the behaviour of the
agent system. In the following sub-section, we pro-
pose an AADL annex specification tailored to mod-
eling the autonomous behaviours of multi-agent sys-
tems and their learning algorithms.
4.1 Modeling Behaviours of Agents in
AADL: Agent Annex
We present the syntax and semantics of our proposed
Agent Annex, the AADL extension that we introduce
in order to encode behaviors of agents.
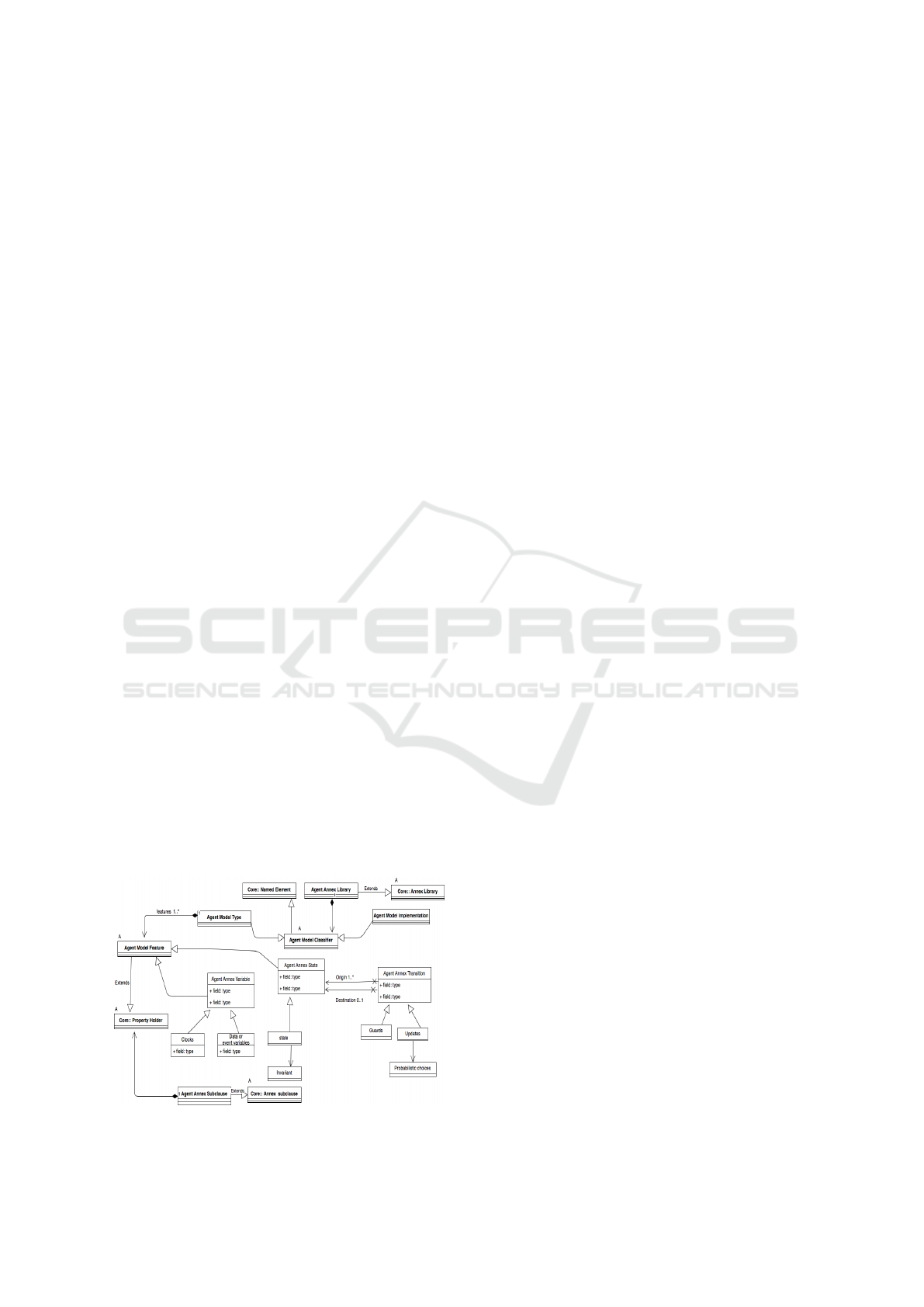
Metamodel Extension of AADL. The structure of
our Agent Annex is defined by extending the AADL
metamodel (Society of Automotive Engineers, 2006),
represented as UML2 class diagrams. All classes in
the Agent Annex metamodel are defined as subclasses
of class AObject, the root class of the AADL meta-
model. Named objects in the Agent Annex model is
a subclass of the Property Holder class, allowing an
object to have a name and associated AADL prop-
erties. Abstract classes in the metamodel are tagged
by an “A”. The Agent Model Annex is formulated
Figure 2: Agent Annex Metamodel.
by extending the AADL abstract classes, Annex Li-
brary and Annex subclause. All the expressions of
the Agent Annex are introduced as subclasses of these
abstract classes. The Annex Library is used to de-
clare classifiers of our Agent Annex in packages. The
Annex Library concepts are attached to an AADL
model by using the Annex subclause within a compo-
nent type or component implementation declaration.
An Annex subclause can refer to items in the Annex
Library, and to basic AADL model elements. The
Agent Annex metamodel is presented in Fig. 2.
Like all other components, Agent Annex also has
a type and an implementation classifier. The Agent
Model feature includes the definitions of annex vari-
ables, states and transitions. Any specific kind of
variable, including clocks, can be declared in the
Agent Annex. The state of an Agent Annex can also
be associated with an invariant. The transitions are
defined by using guards and updates. The updates
support probabilistic choices.
Semantics and Syntax of Agent Annex. The
Agent Annex (AA) is formally encoded as an STS,
as follows:
AA = hVar, Init, T ti (4)
• where: Var represents the set of local and global
variables defined in the AA ;
• Init is the assertion over Var denoting the set of
initial states, formulas and also specifies associa-
tion of reward values to a state or transition ;
• T t is the set of state transitions, defined accord-
ingly as in Section 2.3.
An excerpt of the Agent Annex subclause of the exer-
cise agent is defined in Listing 2. As shown in Listing
2, the annex defines a probabilistic transition system
with 7 states - Idle, Op, Comm, Exc_sc, Ex1, Ex2
and Fail, and a clock variable x. Idle represents the
initial state. It also defines a probabilistic transition
from state Idle. The transition is enabled aperiodi-
cally based on the calendar schedule for exercise and
it has a probability of 0.999 to reach the state Op, and
of 0.001 to reach the state Fail. Lines 11-21 define
the other transitions specific to exercise agent. For
instance, Lines 11-13 define the transitions for initi-
ating communication with the user’s pulse agent. If
the agent reaches the Comm state, it will initiate com-
munication with the pulse agent and the exercise ses-
sion starts only if the user pulse is normal. Lines 16-
23 illustrate the exercise recommendation based on
RL. Upon reaching the Exc_sc state initially, an ex-
ercise recommendation is made to the user based on
the user preferences and disease history. The exer-
cise duration is 10 min split in 2 intervals of 5 min
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
120

each. Upon an initial recommendation (say category
1), the agent moves to the state Exc1 (Lines 14-16).
The agent stays in this state until the completion of
split duration of 5 min or until the user has decided to
quit the exercise session. If the exercise split interval
is less than 2 and greater than 0 (assuming the dura-
tion is 10 min), the exercise schedule has to continue
and in the next split interval the agent recommends
the action with the highest reward (Lines 20-21). The
associated variables and their assertions are defined
in the variables section Lines 22-30. Lines 28-30 in-
dicates that the sys_rew1 is associated with the state
Exc1 depending on user satisfaction or session com-
pletion and also with the transition r1 defined by lines
17-19. Similarly, there is sys_rew2 calculated for ex-
ercise 2, however due to space constraints, we do not
show transitions for exercise category 2.
Listing 2: An example of Agent Model Annex Subclause
attached to Exercise Agent.
1 s ys t e m i m p l e m e n t a t i o n exc . a g e n t
2 s u b com p o n e nts
3 e x e r c i s e _ s e n s o r : d e v i c e e x c _ s e n s o r ;
4 annex Agent_Model {∗∗
5 s t a t e s
6 I d l e , Op , Comm, Exc _sc , Exc1 , Exc2 , F a i l ;
7 I d l e : i n i t i a l s t a t e ;
8 t r a n s i t i o n s
9 [ ] s t a t e = I d l e & c a l _ e x c =1 − >0.999:
10 ( s t a t e ’ = Op & x ’ = 0 ) + 0 . 0 0 1 : ( s t a t e ’= F a i l ) ;
11 [ ] s t a t e =Op & x= exe −> s t a t e ’ = Comm & x ’ = 0 ;
12 [ ] s t a t e = Comm & h _ s t a t = 1 −> s t a t e ’
13 = E x c _ s c h & x ’ = 0 ;
14 [ ] s t a t e = Exc_sch & u _p r e =1 & d _ h i s =0 &
15 e x c _ s p l i t =0−> ( s t a t e ’ = Exc1 ) & ( ex c _r e c ’=1) &
16 & ( e x c _ s p l i t ’ = 2 ) & ( x ’ = 0 ) ;
17 [ r 1 ] s t a t e = Exc1 & ( x = 5 | u _ q u i t =1 ) & h _ s t a t =1
18 & e x c _ s p l i t < 2 −> ( s3 ’ = 5 ) & ( e x c _ s p l i t ’=
19 e x c _ s p l i t + 1 ) & ( x ’ = 0 ) ;
20 [ ] s t a t e =Ex c _ s c h & e x c _ s p l i t <2 & e x c _ s p l i t >0
21 &s y s_rew1 > ( s ys_ r e w 2 ) −> ( s t a t e ’= Exc1 ) ;
22 v a r i a b l e s
23 b o ol c a l _ e x c ; bo o l u _ q u i t ; b o o l ss_com ;
24 i n t ex c _ r e c ; c l o c k x ;
25 f o r m u l a u t i l i t y 1 = w1∗ ( u _ s t )+w2 ∗ ( ss_com ) ;
26 f o r m u l a sys _ r e w1 = u t i l i t y 1 ;
27 f o r m u l a sys _ r e w1 = s y s_r e w 1 + u t i l i t y 1 ;
28 r e w a r d _ a s s s t a t e =Exc1 & ( u _ s a t = 0 | u _ s a t =1)&
29 ( ss_ com = 1 | ss_com =0 ) : sy s _ r ew1 ;
30 r e w a r d _ a s s [ r 1 ] t r u e : s y s _ rew 1 ; ∗ ∗} ;
31 en d Exc . a g e n t ;
In the following section, we define the syntax and
semantic encoding of a complete AADL component,
consisting of its interface and agent annex, and dis-
cuss its semantic mapping to an STS.
5 FORMAL ENCODING OF MAS
The first step of encoding our multi-agent architecture
formally is to assign formal semantics to the specific
AADL components that we utilize for modeling our
system. An AADL component employed in this paper
is defined by the following tuple:
AADL
Comp
= hComp
type
,Comp
imp
, AAi, (5)
where Comp
type
is the component type, Comp
imp
rep-
resents the component implementation, and AA, the
agent annex specification.
• Comp
type
is in turn defined as a tuple: Comp
type
=
hFeatures, Propi, where:
– Features model the bus access that abstracts the
communication protocol utilized by the system.
– Prop lists the associated properties of the
component, like Deployment, Communication,
Timing, T hread-related properties, user-
de fined properties, etc. In this work, we
only consider a subset of Timing, T hread-
related properties, user-de fined properties as
follows: Prop = {T
p
, T
e
, Dispatch protocol},
where T
p
and T
e
represent the period and exe-
cution time of the component, respectively, T
p
,
T
e
∈ Timing properties, Dispatch protocol ∈
{P, AP}, where P and AP represent periodic ac-
tivation and aperiodic activation, respectively.
User-de fined properties are used to declare
global variables.
• Comp
imp
is defined as Comp
imp
= hSC,Coni,
where:
– SC represents the sub-components of the sys-
tem,
– Con represents the set of connections. The
function F
con
: Con → Features assigns
Features to Con.
• Agent Annex AA follows the semantics defined in
Section 4.1.
Definition 1. The AADL component defined by Equa-
tion (2) is formally encoded as an STS. The MAS ar-
chitecture is represented as a parallel composition
of all the STS modules: MAS = ||
n
i=0
ST S_module
i
,
where n is the number of AADL components of the
system, excluding data components and bus compo-
nents, if defined in the system. The STS_module
i
ele-
ments are defined as follows:
• V
l
is defined the set of AA variables that con-
tribute to the state space of STS_module
i
, local
and possibly global variables.. The clock vari-
ables values are given by the component’s period
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
121

Table 1: Encoding of AADL Component as STS.
AADL comp STS
hComp
type
,Comp
imp
, AAi ST S
T
p
Invariant + Guard
T
e
Invariant + Guard
User-defined properties Variables
Bus Variable
Data Variable
A sub-component ST S
AA states Variable values
AA transitions Transitions
AA variables Variables
AA formulas Variable assertions
AA reward association Variable assertions
and execution-time properties of Comp
type
defini-
tion. V
g
is defined by the global variables that do
not contribute to the state of the system.
• Θ
i
denotes assertion over V
l
and V
g
.
• T
i
represents the set of transitions defined in the
AA of an agent.
The formal encoding is tabulated in Table 1. We
now present an example of the above formal encod-
ing, by applying it on a exercise agent of our use case.
The excerpt of the exercise agent (EA) presented in
Listings 1 and 2 is formally encoded as an STS mod-
ule, where:
• V
EA
(where by EA we denote the exercise agent)
: {(s1, cal_exc, ss_com, exc_rec, exc_split, x,
sys_rew1) ∪ (utlity1, w1, w2)}
• θ
EA
: {s0 |= (s1 = 0 ∧ cal_exc = 0 ∧ ss_com =
0 ∧ exc_rec = 0 ∧ exc_split = 0 ∧ x =
0 ∧ sys_rew1 = 0), weights |= (w1 =
0.6 ∧ w2 = 0.4), utility |= (utlility1 =
w1∗u_st +w2 ∗ ss_com), reward |= ((sys_rew1 =
utility1) ∪ (sys_rew1 = sys_rew1 + utility1),
reward association |= (s1 = 4&(u_sat =
0|u_sat = 1)&(ss_com = 1|ss_com = 0) :
sys_rew1) ∧ ([r1]true : sys_rew1)}
• T
EA
is defined by the transitions as follows
2
:
T
EA
: {τ1 : {(s1 = 0 ∧ cal_exc = 1 ∧ ss_com =
0 ∧ exc_rec = 0 ∧ exc_split = 0 ∧ x =
0 ∧ sys_rew1 = 0) −→ (s1
0
= 1 ∧ cal_exc
0
=
1 ∧ ss_com
0
= 0 ∧ exc_rec
0
= 0 ∧ exc_split
0
=
0 ∧ x
0
= 0 ∧ sys_rew1
0
= 0), P = 0.999 ∪ (s1
0
=
6 ∧ cal_exc
0
= 1 ∧ ss_com
0
= 0 ∧ exc_rec
0
=
0 ∧ exc_split
0
= 0 ∧ x
0
= 0), P = 0.001},
τ2 : {(s1 = 1 ∧ cal_exc = 1 ∧ ss_com =
2
Due to space constraints, we only illustrate the first two
transitions according to Listing 2, however all other transi-
tions can be enlisted in a similar way.
0 ∧ exc_rec = 0 ∧ exc_split = 0 ∧ x =
2 ∧ sys_rew1 = 0) −→ (s1
0
= 2 ∧ cal_exc
0
=
1 ∧ ss_com
0
= 0 ∧ exc_rec
0
= 0 ∧ exc_split
0
=
0 ∧ x
0
= 0 ∧ sys_rew1
0
= 0), P = 1}
Similarly, all other AADL components are encoded
as STS modules, respectively. In the next section, we
describe our formal analysis approach with PRISM.
6 SYSTEM ANALYSIS WITH
PRISM
The STS modules are encoded as a set of PTA mod-
ules in PRISM. The architecture is a parallel compo-
sition of the PTA modules. Each agent can accept at
most 2 connections, and each has a redundant copy.
Therefore, in order to ensure parallel processing, we
assume 4 PTA for a single category of agent. Thus,
we have 16 agent PTA that deal with pulse moni-
toring, fall monitoring, exercise monitoring and fire
monitoring. In addition, we have one tracker PTA,
through which connections between the agents are
established. The sensor data and internal databases
are modeled as variables, and their communication is
modeled via shared data access. For simplicity, we
have not chosen to model the cloud database.
Listing 3 shows an excerpt of exercise agent en-
coding in PRISM. Since PTA is a subset of STS,
the encoding of STS as PTA modules is a one-to-
one mapping, with the syntax adapted to match the
PRISM input language. All the global variables and
their assertions (weights, utility and rewards) are de-
fined outside the module definition of the exercise
agent. Apart from these, the exercise agent module
uses a set of local variables. Variable s represent the
state, s = 0 (Idle), s = 1 (Op), s = 2 (Comm), s = 3
(Exc_sc), s = 4 (Exc1), s = 5 (Exc2), s = 6 (Fail).
There are variables that represent the user’s calendar
exercise input (cal_exc_u1: [0..1]), user quit u1_quit:
[0..1]), session completion (ss_comp: [0..1], where 0
indicates that the event has not occurred, whereas 1
indicates the opposite. There are also variables to rep-
resent the exercise split sessions ( exc_split[0..2]), 0
representing the initial value and 1 and 2 representing
the two split sessions respectively, and the exercise
recommendations (exc_rec [0..2]) where 0 represent
the initial condition and 1 indicating that exercise cat-
egory 1 is chosen and 2 indicates that category 2 is
chosen. Variable x is a clock variable. The invari-
ant associated with the states (Lines 15-17) depend
on the component’s execution time (defined at the in-
terface of the AADL component’s model). The in-
variant of state Op is x ≤ Exec_time. The transitions
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
122

defined in Lines 18-27 follow the transitions defini-
tion of the Agent Annex specification of the exercise
Agent. Finally, in Lines 29-33, we show the asso-
ciation of rewards to the respective states or transi-
tions. After modeling the respective PTA modules,
we can perform exhaustive probabilistic verification
of the model, and generate probabilistic guarantees
for the satisfaction of the functional and QoS require-
ments listed in Section 3.1.
The verification results are tabulated in Table 2.
The requirements are formulated as PCTL queries
and the model-checking method is Digital Clocks.
Since PRISM, by default, returns the value for
the (single) initial state of the model while model
checking, we employ filters to verify our properties
over all states. Requirement R1 ensures that if a fall
event occurs due to a low pulse for user1 (Jim), and
the tracker is operational, then the tracker initiates
the communication between the respective fall and
pulse agents associated with user Jim (the request can
be assigned to any of the agent sockets depending
on availability), and the probability that one of them
sends an alert to caregiver indicating that there is “fall
due to low pulse” is greater than 0.999 provided that
at least one of the sockets of each agent is functional.
Assuming that the communication via tracker takes
less time, the requirement is satisfied within 10
time units. Similarly, for R2, we verify for user2
(Mary) that in case of fire and fall events occurring
simultaneously, an alert indicating both events is
raised and sent within 10 time units, provided that the
tracker has not failed. In case of R3, R4 and R5, we
verify the functionality of the exercise agent serving
Jim. By R3, we establish that the exercise session
is scheduled only if the corresponding health agent
indicates that the user’s pulse level is normal. R4
indicates that the initial exercise category is chosen
based on user preferences and health condition. By
verifying R5, we show that if a high pulse devia-
tion occurs during the exercise sub-session, a low
intensity exercise is chosen in the next sub-session,
irrespective of user preferences. In R6, we illustrate
a similar function as in R2, but assuming that the
tracker has failed. In this case, the functionality is
met by direct communication between the agents,
which takes more time than the communication via
tracker (it is shown that this requirement is satisfied
within 20 time units). Next, in R7, we assume a fall
event of user2, and one failed fall agent; then, a fall
alert is raised and sent to the caregiver by either one
of the redundant fall agents. PRISM shows that this
requirement is satisfied within 20 time units.
Listing 3: An excerpt of the PRISM Model of an Exercise
Agent.
1 p t a
2 co n s t d o u b le w1 = 1 . 0 ;
3 co n s t d o u b le w2 = 1 . 0 ;
4 f o r m u l a u t i l i t y 1 = w1 ∗ ( u _ s a t ) +w2 ∗ ( ss_ comp ) ;
5 f o r m u l a sys _ r e w 1 = u t i l i t y 1 ;
6 f o r m u l a sys _ r e w 1 = s y s_r e w 1 + u t i l i t y 1 ;
7 mod ule E x c _ a g e n t1
8 s : [ 0 . . 6 ] i n i t 0 ;
9 / / s t a t e s 0 −I d l e , 1−Op , 2−Comm, 3−Ex c_ sc , 4−Ex1 ,
10 5− Ex2 , 6− F a i l
11 c a l _ e x c _ u 1 : [ 0 . . 1 ] i n i t 0 ; u 1 _ q u i t : [ 0 . . 1 ] i n i t 0;
12 ss_ com : [ 0 . . 1 ] i n i t 0 ; e x c _ s p l i t : [ 0 . . 2 ] i n i t 0 ;
13 e x c _ r e c : [ 0 . . 2 ] i n i t 0 ;
14 x : c l o c k ;
15 i n v a r i a n t
16 ( s =1 => x <=2 )
17 e n d i n v a r i a n t
18 [ 1 ] s =0 & c a l _ e x c _ u 1 =1 −> 0 . 9 9 9 : ( s ’ = 1 ) & ( x ’= 0 ) +
19 0 . 0 0 1 : ( s ’ = 6 ) &(x ’ = 0 ) ;
20 [ 2 ] s =1 & x=2 −> ( s ’ = 2 ) & ( x ’ = 0 ) ;
21 [ 3 ] s =2 & h _ s t a t _ u 1 =1 −> ( s ’ = 3 ) & ( x ’ = 0 ) ;
22 [ 4 ] s =3 & u 1 _ p r e f =1 & u 1 _ d i s _ h i s =1 &e x c _ s p l i t =0
23 −> ( s ’ = 4 ) & ( e x c _ r e c ’ = 1 ) & ( e x c _ s p l i t ’ = 2 ) & ( x ’ = 0 ) ;
24 [ r 1 ] s =4 &(x = 5 | u 1 _ q u i t =1) & h _ s t a t _ u 1 =1 & e x c _ s p l i t
25 < 2 −> ( s ’ = 3 ) & ( e x c _ s p l i t ’ = e x c _ s p l i t +1) & ( x ’ = 0 ) ;
26 [ 5 ] s =3 & e x c _ s p l i t >0 & e x c _ s p l i t <2 & sy s_r ew1 >
27 sy s _r e w2 −> ( s ’ = 3 ) & ( e x c _ s p l i t ’= e x c _ s p l i t +1 ) & ( x ’ = 0 ) ;
28 en dm od ule
29 r e w a r d s
30 s =4 & ( u 1 _ s a t =0 | u 1 _ s a t =1) &(s s_ com = 1 | ss_co m = 0 ) :
31 s y s_r e w 1 ;
32 [ r 1 ] t r u e : s y s _ r ew1 ;
33 e n d r e war d s
7 RELATED WORK
Modern AAL systems are designed to tackle numer-
ous functions, and to cater for multiple, distributed
users, which makes the system design more complex,
and calls for design-time formal analysis.
Some related work is directed towards provid-
ing formalisms for agents in terms of various log-
ics (Che et al., 2006; Luo et al., 2005). However,
some others have proceeded further to develop spec-
ification languages/methodologies for agent systems.
Some examples include CASL (Shapiro et al., 2002),
DESCARTES (Medina and Urban, 2007), etc. These
methodologies employ different formalisms, however
some of them are complex and are not expressive
enough, like in case of CASL. For DESCARTES,
tool support for executing the specifications is also
provided. Although the approach is promising, the
DESCARTES language is still missing constructs to
specify adaptive capabilities of agents, nor it provides
an analysis framework for MAS. One of the other
common approaches, popular in industry also, is the
Agent UML (Bauer et al., 2001) one. The approach
does not specify the architectural constructs of the
system, and lacks formal analysis, unlike the frame-
work that we present in this paper. Few works have
considered the specification and formal analysis of
agent behavior in architecture description languages
(Oquendo, 2004). The AADL-based modeling frame-
work for multi-agent systems, which we propose in
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
123
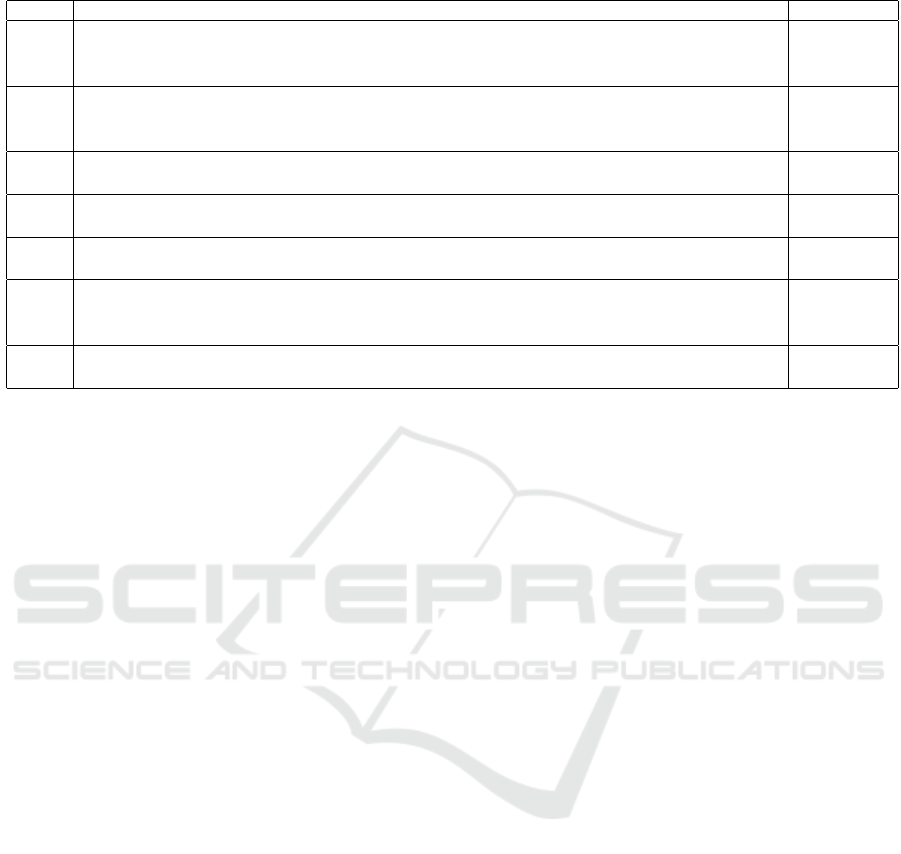
Table 2: Verification results.
Req. Query Result
R1
f ilter( f orall, f all_user1 = 1&pulse_user1 ≤ 50&tracker_ f ail = 0 → P ≥ 0.999
[F((pulse_alert0_u1 = 3|pulse_alert1_u1 = 3| pulse_alert2_u1 = 3|pulse_alert3_u1 = 3)
& (y ≤ 10)&( f all_ f ail = 0) &(pulse_ f ail = 0))] satisfied
R2
f ilter( f orall, f all_user2 = 1& f ire_user2 = 1&tracker_ f ail = 0 → P ≥ 0.999
[F(( f ire f all_alert0_u2 = 2| f ire f all_alert1_u2 = 2| f ire f all_alert2_u2 = 2|
f ire f all_alert3_u2 = 2)&(y ≤ 10) &( f all_ f ail = 0)&( f ire_ f ail = 0))] satisfied
R3
f ilter( f orall, cal_notexc_user1 = 1&tracker_ f ail = 0&(pulse_user1 ≥ 60
&pulse_user1 ≤ 120) → P ≥ 0.999 [F(exc_sch_u1 = 1))] satisfied
R4
f ilter( f orall, exc_sch_u1 = 1&u1_disease_history = 1&u1_pre f = 2
→ P ≥ 0.999 [F(exc_u1_int1 = 2)] satisfied
R5
f ilter( f orall, exc_sch_u1 = 1&interval = 1 &y ≤ 5 &pulse_user1 ≥ 200
→ P ≥ 0.999 [F(exc_u1_int2 = 1)] satisfied
R6
f ilter( f orall, f all_user2 = 1& f ire_user2 = 1&tracker_ f ail = 1 → P ≥ 0.999
[F(( f all_alert0_u2 = 2| f all_alert1_u2 = 2| f all_alert2_u2 = 2| f all_alert3_u2 = 2)
&(y ≤ 20) & ( f all_ f ail = 0)&( f ire_ f ail = 0))] satisfied
R7
f ilter( f orall, f all_user2 = 1&tracker_ f ail = 0& f ail1_ f all = 1 & f all2_ f all = 0
→ P ≥ 0.999 [F(( f all_alert2_u2 = 1| f all_alert3_u2 = 1)&y ≤ 20)] satisfied
this paper, has the benefit of being integrated into a
popular framework that also provides tool support.
There are also some approaches that focus on
the formal verification of AAL systems. An inter-
esting related work is that of Rodrigues et al. (Ro-
drigues et al., 2012), who perform dependability anal-
ysis of AAL architectures using UML and PRISM.
Other interesting research work uses temporal reason-
ing (Magherini et al., 2013) to formally verify the
reliability of AAL systems. However, the above fo-
cus only on QoS requirements, and do not look into
the critical functions of AAL systems, which require
decision making. Unlike these approaches, we carry
out our analysis on an agent-based AAL system ar-
chitecture, focusing on both functional and QoS re-
quirements, and propose a complete modeling and
verification framework for distributed AAL systems
that involve real-time, fault-tolerant and probabilis-
tic behaviours. As an advantage if compared to an-
other work (Kunnappilly et al., 2018), the verification
results obtained with PRISM are exhaustive. In the
mentioned work, the authors have proposed a formal
assurance framework for AAL system architectures
described in AADL, and showed how to verify them
in UPPAAL SMC. As different from the work in this
paper, the approach assumes a centralized system ar-
chitecture, and the only probabilistic behaviour con-
sidered in the system is component failure, which can
occur arbitrarily. In addition, the statistical analysis
with UPPAAL SMC, is not exhaustive, but it relies
instead on a finite number of simulations.
8 DISCUSSION
This paper presents an architecture for MAS, which
we model in the architecture language AADL that
we extend with an agent annex intended to model
real-time, fault-tolerant and probabilistic behavior of
agents, in a unified manner. This approach allows an
agent to synchronize only with a limited number of
agents in the system (according to its dependency),
unlike the traditional case where each agent has to
communicate with every other agent in the system
to achieve a consistent view of the environment be-
fore making a decision (Kunnappilly et al., 2017).
We show the design of our MAS architecture applied
to AAL domain with 2 agent categories- simple re-
flex agents, that use if-then-else rules and complex in-
telligent agents that employ learning techniques, like
Reinforcement Learning. Although we have demon-
strated the use-case of Ambient Assisted Living in the
paper, the approach fits well for any other applications
employing MAS for handling multiple safety criti-
cal applications in real-time, e.g., those of automotive
systems for which earlier stage analysis is beneficial.
The modeling framework used in this paper is re-
lying on the Architecture Analysis and Design Lan-
guage (AADL), one of the best-suited architecture de-
scription languages to describe real-time embedded
systems (Feiler et al., 2006). Although MAS spec-
ifications based on logics and domain specific lan-
guages do exist and are popular, they are mostly lim-
ited to specification of properties at the agent level
and also do not have tool support (see Section 7).
AADL, on the other hand, allows us to focus on the
component level (here agents) and also at the system
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
124

level (MAS architecture) and can effectively model
agents’ real-time characteristics. With our proposed
extension to AADL using Agent Annex, a user can
also specify the intelligent agent behaviours (which
are often probabilistic) and their failures. AADL also
supports a graphical plug-in in OSATE tool to visual-
izethe model and supports analysis with respect to la-
tency, schedulability, resource utilization, etc. (Feiler
and Gluch, 2012).
In this work, we encode the semantics of the
AADL model and its agent annex as Stochastic Tran-
sition Systems. The encoding is suitable due to
the probabilistic behaviour of such systems and al-
lows it to be model-checked exhaustively by proba-
bilistic model checkers, like PRISM, or statistically
by simulation-based model checkers like UPPAAL
SMC. This paper shows a reduced and abstract archi-
tecture with only 4 types of agents and hence can be
verified exhaustively with PRISM.
9 CONCLUSIONS AND FUTURE
WORK
In this paper, we have proposed an architecture mod-
eling and formal analysis framework for agent-based
AAL systems characterized by intelligent, probabilis-
tic, and real-time behaviours. The intelligence is in-
corporated by using learning algorithms, in our case,
the Reinforcement Learning algorithm. The model-
ing framework is based on one of the well-established
architecture description languages for modeling real-
time embedded systems, called AADL. As the core
AADL does not suffice to represent the probabilis-
tic and non-deterministic behavior of our system, we
propose an annex extension to AADL, the so-called
Agent Annex that we formally encode as a stochas-
tic transition system. In order to verify a set of criti-
cal functional and QoS requirements like timeliness,
fault-tolerance etc., we use an exhaustive probabilistic
model-checking method, using the state-of-art model
checker PRISM.
Our contribution paves the way for the devel-
opment of formally assured distributed, adaptable,
scalable, fault-tolerant systems, with intelligent be-
haviours and autonomy. The scalability of the pro-
posed framework is supported by the semantic def-
inition of AADL elements that allows an encoding
in UPPAAL SMC for instance, for statistical model
checking of models that exceed the boundaries of ex-
haustive model checking. As future work, we intend
to extend our architecture with multiple categories
of agents and integrate the Agent Annex to the core
AADL.
ACKNOWLEDGEMENTS
This work is supported by the EU Celtic Plus /Vin-
nova project, Health
5G
- Future eHealth powered by
5G, which is gratefully acknowledged.
REFERENCES
Bauer, B. et al. (2001). Agent UML: A formalism for speci-
fying multiagent software systems. International jour-
nal of software engineering and knowledge engineer-
ing, 11(03):207–230.
Che, H.-y. et al. (2006). A Description Logic Method of
Formalizing the Specification of Multi-Agent System.
In Machine Learning and Cybernetics, 2006 Interna-
tional Conference on, pages 61–65. IEEE.
De Alfaro, L. (1998). Stochastic transition systems. In
International Conference on Concurrency Theory,
pages 423–438. Springer.
Dissaux, P., Bodeveix, J.-P., Filali, M., Gaufillet, P., and
Vernadat, F. (2006). Aadl behavioral annex. In Pro-
ceedings of DASIA conference, Berlin, volume 32.
Feiler, P. H. et al. (2006). The architecture analysis & design
language (AADL): An introduction. Technical report,
Carnegie-Mellon Univ Software Engineering Inst.
Feiler, P. H. and Gluch, D. P. (2012). Model-based engi-
neering with AADL: an introduction to the SAE archi-
tecture analysis & design language. Addison-Wesley.
Hansson, H. et al. (1994). A logic for reasoning about
time and reliability. Formal aspects of computing,
6(5):512–535.
Kunnappilly, A. et al. (2017). A Novel Integrated Archi-
tecture for Ambient Assisted Living Systems. In 41st
COMPSAC, pages 465–472. IEEE.
Kunnappilly, A. et al. (2018). Assuring intelligent ambient
assisted living solutions by statistical model checking.
In International Symposium on Leveraging Applica-
tions of Formal Methods, pages 457–476. Springer.
Kwiatkowska, M. et al. (2002). PRISM: Probabilistic sym-
bolic model checker. In International Conference on
Modelling Techniques and Tools for Computer Perfor-
mance Evaluation, pages 200–204. Springer.
Luo, J. et al. (2005). Multi-agent cooperation: A description
logic view. In Pacific Rim International Workshop on
Multi-Agents, pages 365–379. Springer.
Magherini, T. et al. (2013). Using temporal logic and model
checking in automated recognition of human activi-
ties for ambient-assisted living. IEEE Transactions
on Human-Machine Systems, 43(6):509–521.
Medina, M. A. and Urban, J. E. (2007). An approach to
deriving reactive agent designs from extensions to the
descartes specification language. In Eighth Interna-
tional Symposium on Autonomous Decentralized Sys-
tems (ISADS’07), pages 363–367. IEEE.
Norman, G. et al. (2013). Model checking for probabilistic
timed automata. Formal Methods in System Design,
43(2):164–190.
Architecture Modelling and Formal Analysis of Intelligent Multi-Agent Systems
125

Oquendo, F. (2004). π-ADL: an Architecture Description
Language based on the higher-order typed π-calculus
for specifying dynamic and mobile software architec-
tures. ACM SIGSOFT Software Engineering Notes,
29(3):1–14.
Rodrigues, G. N. et al. (2012). Dependability analysis in the
ambient assisted living domain: An exploratory case
study. JSS, 85(1):112–131.
Shapiro, S. et al. (2002). The cognitive agents specifica-
tion language and verification environment for multia-
gent systems. In Proceedings of 1st international joint
conference on Autonomous agents and multiagent sys-
tems, pages 19–26. ACM.
Society of Automotive Engineers, Warrendale, P. U. (2006).
AE-AS5506/1, SAE Architecture Analysis and De-
sign Language (AADL) Annex Volume 1, Annex C:
AADL Meta-Model and Interchange Formats.
Sutton, R. S., Barto, A. G., et al. (1998). Introduction to
reinforcement learning. 135.
Tapia, D. I. et al. (2009). An ambient intelligence based
multi-agent system for Alzheimer health care. Inter-
national Journal of Ambient Computing and Intelli-
gence, 1(1):15–26.
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
126
