
Decision Support for Planning Maritime Search and Rescue
Operations in Canada
Irène Abi-Zeid, Michael Morin and Oscar Nilo
Operations and Decision Systems, Université Laval, Québec, Canada
Keywords: Search and Rescue, Decision Support System, Search Theory, Design Science Research, Optimal Search
Planning.
Abstract: In this project we constructed and evaluated research artifacts to support Search and Rescue (SAR) mission
coordinators in planning searches for missing persons or objects at sea. An iterative heuristic based
optimization model was formulated and implemented in a prototype that is integrated in a Decision Support
System. Using representative examples, we show that the new planning method can help coordinators with
the complex task of allocating search resources to search areas in a way that maximizes the chances of finding
survivors quickly. Although developed for the Canadian Coast Guard, our method can be used in other
countries. We followed Design Science Research guidelines and our design process was according to the
Design Science Research Methodology. The research entry point was client and context initiated and beta
testing with users is planned in the spring of 2019. It is expected that our innovative artifacts will contribute
to improving the SAR system and saving more lives.
1 INTRODUCTION
Search and Rescue (SAR) comprises “the search for,
and provision of aid to, persons who are, or who are
feared to be, in distress” (Canadian Coast Guard,
2014). The Canadian government is responsible for
providing SAR in an area covering over 18 million
square kilometers of land and water and the Canadian
Coast Guard is involved in an average of 6000
incidents per year (Quadrennial SAR review, 2013).
Maritime SAR operations are under the control of
three joint rescue coordination centres and two
marine rescue sub-centres where SAR mission
coordinators (SMC) are responsible for planning,
coordinating, controlling and directing the response
to incidents. They are decision-makers who must
make timely decisions in situations where lives are at
risk. Search planning is a complex task where time is
a crucial factor for survivors who must be found
quickly. SAR operations are among the most critical
responsibilities of the Canadian Coast Guard and can
be difficult to carry out. Each situation is unique:
Particular constraints limit the choice of the search
resources and their deployment, difficult climatic and
weather conditions may be present and operations are
often carried out in remote and unfamiliar areas. It is
therefore of the utmost importance to plan searches
that ensure the best use of available search resources
in order to maximize the chances of finding survivors.
The Canadian Coast Guard (CCG) is currently
working on developing the Advanced Search
Planning Tool (ASPT), the next generation decision
support system (DSS) to replace CANSARP
(Canadian Coast Guard, 1998), its current SAR
planning system. During the requirements
specification phase, the need for an intelligent search
planning module, that can recommend search plans
designed to ensure the optimal use of available search
resources, was identified and confirmed. This led our
research team to formulate the following research
question:
RQ: How can optimal or near-optimal search
operations be planned in reasonable time and
decision support provided to assist maritime search
mission coordinators?
The research presented in the paper was
conducted within the Design Science Research (DSR)
paradigm defined by Hevner and Chatterjee (2010),
as“a research paradigm in which a designer answers
questions relevant to human problems via the
creation of innovative artifacts, thereby contributing
new knowledge to the body of scientific evidence. The
designed artifacts are both useful and fundamental in
understanding that problem.”
328
Abi-Zeid, I., Morin, M. and Nilo, O.
Decision Support for Planning Maritime Search and Rescue Operations in Canada.
DOI: 10.5220/0007730303280339
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 328-339
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In order to answer the research question relevant
to the human problem of searching for and quickly
finding missing persons or objects at sea, we created
a method consisting of innovative artifacts as follows:
we first formulated a search planning model
involving simulation and optimization based on
search theory (Stone, 2004). Search theory can be
seen as the application of Bayesian statistics to the
question of where to search for a missing object. We
refer the reader interested in learning about search
theory to the seminal work of L. D. Stone (Stone,
2004).
Our model was then translated into an algorithm
and further implemented in Search Planner, a
prototype that provides optimal or satisficing (Simon,
1956) feasible search plans to the SMC. The figures
of merit, probability of success, associated with the
resulting search plans are obtained via simulation of
moving search objects and available search and
rescue units. Although a standalone application,
Search Planner has been integrated within the ASPT
DSS and beta testing with the users is planned in the
spring of 2019. The work presented here was carried
out over a span of three years, from 2016 to 2018.
The rest of this paper is structured as follows: In
Section 2, we address the research background along
with related work and research design. In Section 3,
we describe and explain our search planning model,
algorithm and present the implemented prototype.
Using representative application examples in Section
4, we show some results. In Section 5 we provide a
discussion as well as limitations. Finally, we conclude
in Section 6.
2 BACKGROUND
Following the receipt of an alert pertaining to a
maritime incident, SAR mission coordinator must
gather information in order to establish whether a
search is to be conducted, in which case he/she must
begin the search planning process by verifying the
search resources available, choosing the resources,
determining the area to be searched and developing a
search plan. A search plan is a distribution of the
search resources over a search area, also called effort
allocation. Optimal search planning may be defined
as the allocation of the available search resources in
such a way to maximize the chances of locating and
rescuing survivors, subject to operational constraints.
Over the years, manual methods and procedures
have been devised to develop search plans. However,
these methods do not in general take advantage of
today’s computer power and advances in search
theory and simulation, and may not be specifically
tailored to the search equipment on hand, which may
result in plans that do not have the highest success
probabilities.
Nonetheless, it has been known since the Second
World War that search theory-based planning can
result in significant gains in search effectiveness. It is
now recognized that the use of search theory and
organized planning results in higher success rates and
a significant increase in the number of lives preserved
(Frost and Stone, 2001; Abi-Zeid and Frost, 2005;
Ferguson, 2008; Abi-Zeid et al., 2011). Furthermore,
Stone et al. (2016) give examples of some high profile
cases including the response to the submarine threat
in the Atlantic, the search for a lost H-bomb in the
Mediterranean, the search for the US nuclear
submarine Scorpion, the clearing of unexploded
ordnance in the Suez Canal, the search for the sunken
treasure ship, the SS Central America, and more
recently the locating of the wreckage of AF 447. The
authors further identify two unsuccessful searches
that might have benefited from better planning. In
more recent years, search theory has also been applied
in the area of autonomous searching by robots in
structured environments, and by unmanned air
vehicles for outdoor searching of large areas
(Ablavsky and Snorrason, 2000; Lau et al., 2008; Sato
and Royset, 2010; Kriheli et al., 2016; Venkatesan,
2016; Bernardini et al., 2017).
The need for specific decision support systems
that can assist a SMC has long been identified in the
scientific literature (Abi-Zeid and Frost 2005; Hillier,
2008; Aronica et al., 2010; Kratzke et al., 2010; Stone
et al., 2014; Małyszko and Wielgosz, 2016;
Bellantuono et al., 2016). Various SAR information
systems are currently available in various countries
(Vidan et al., 2016), including the widely used SARIS
(sold by BMT ships & Coastal Dynamics product),
SARMAP (sold by RPS ASA), SAR (sold by
TRANSAS), SARGIS (Guoxiang and Maofeng,
2010), and CANSARP (Canadian Coast Guard,
1998). However, at the present time, only SAROPS,
a maritime SAR DSS developed for the US Coast
Guard, provides capabilities for search theory-based
search planning (Kratzke et al. 2010). Our research
project was therefore created as an answer to an
expressed requirement of the Canadian Coast Guard
to fill an existing gap. Nonetheless, the knowledge
created and our designed artifacts can benefit the
whole international SAR community, since there is
willingness on the part of the Canadian Coast Guard
to share knowledge with other countries.
In the next subsection, we describe our research
design and provide methodological context.
Decision Support for Planning Maritime Search and Rescue Operations in Canada
329
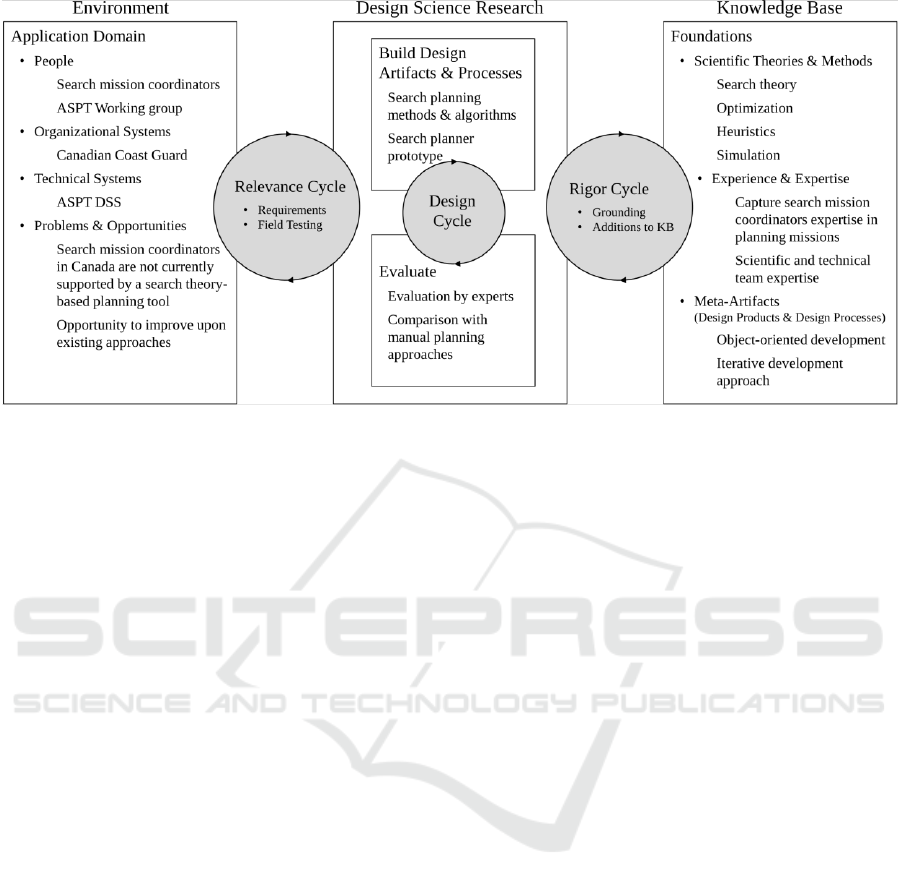
Figure 1: The three design research cycles (adapted from Hevner and Chatterjee, 2010, Fig. 2.2).
2.1 Research Design
Our project was conducted following
recommendations from Hevner and Chatterjee (2010)
who proposed three design research cycles, where the
aim is to ensure that the research is both rigorous and
relevant, and provided design science research
guidelines. Figure 1 shows the three research cycle
while providing additional context-specific
information. Table 1 provides context-specific
information to design science research guidelines.
Based on our research question, our objective and
design requirement was to develop and implement
methods and algorithms for optimal search planning
that would provide results in reasonable time. Our
artifacts are therefore, the search planning method,
the algorithms and the resulting prototype. These are
viable since they are compatible with existing
technical systems, were transferred to an operational
system in the organizational environment, and will be
supported by training and technical teams.
The relevance of our research is established since
the requirements were expressed by the organization
responsible for search planning, namely the Canadian
Coast Guard and by future users of our artifacts.
Operations and management had identified problems
with the current methods and foreseen opportunities
to remedy this situation by taking advantage of
advances in computing power and in simulation. As
for rigor, our approach was based on search theory, a
well-established theory for search and detection
(Stone et al., 2016). We conducted a thorough
literature review and had exchanges with other search
theory experts. Furthermore, we have extensive
experience with search theory for SAR, since two of
the authors have been conducting research on this
topic for over 20 years, and the third for over 10 years.
In fact, we had previously developed SARPlan for
overland search planning, a DSS that had won awards
for innovative technology on the national level.
Our design process was iterative, as we defined
and refined our artifacts. All along the project, there
were regular meetings and exchanges with
practitioners, technical staff and intended users and
their representatives, who provided input, criticism,
requests for modifications, constraints, etc. Five
versions of the model and optimization algorithms
were developed, compared and tested before adopting
the current version. The aim of these iterations was to
increase the solution’s quality and reduce
computation time. The acceptance of our artifacts was
an ongoing process where we produced various
documents, demonstrated the prototype, and had
multiple meetings with the stakeholders.
Furthermore, external scientific experts have been
tasked to evaluate our methods and artifacts.
During the design process, we followed the
Design Science Research Methodology as shown in
Figure 2 (Peffers et al., 2007). Our research entry
point was client/context centered. The problem
identified was how to plan search operations for
moving objects simulated using Monte Carlo based
drift models. Our objective was to demonstrate a
search planning method, which led us to design and
develop search theory based artifacts that were
implemented and demonstrated in a prototype. The
client integrated the artifacts in their operational
system. Evaluation and communication are on-going.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
330
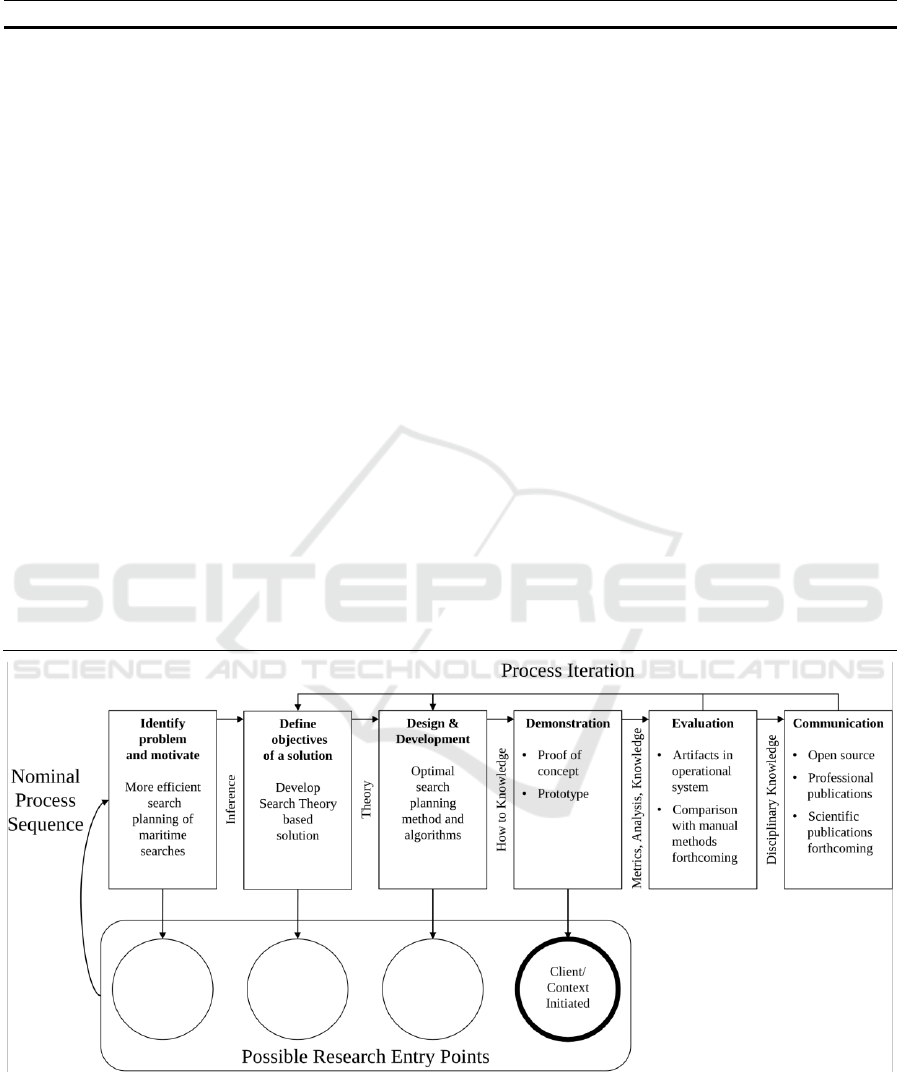
Table 1: Design research guidelines (adapted from Hevner and Chatterjee, 2010, Table 2.1).
Guideline
Description (Hevner and Chatterjee, 2010)
Specific context
1. Design as an
Artifact
Design science research must produce a viable
artifact in the form of a construct, a model, a
method, or an instantiation.
Search planner prototype for ASPT
2. Problem relevance
The objective of design science research is to
develop technology-based solutions to important
and relevant business problems.
Relevant problem: maritime search and
rescue operations planning
3. Design evaluation
The utility, quality, and efficacy of a design artifact
must be rigorously demonstrated via well-executed
evaluation methods.
Comparison with search mission
coordinators manual planning
(forthcoming)
4. Research
contributions
Effective design science research must provide clear
and verifiable contributions in the areas of the
design artifact, design foundations, and/or design
methodologies.
Proof of concept and prototype in
response to search mission
coordinators needs
5. Research rigor
Design science research relies upon the application
of rigorous methods in both the construction and
evaluation of design the artifact.
Agile development approach,
implementation of search theory
concepts, optimization approaches,
search mission coordinators expertize
6. Design as a search
process
The search for an effective artifact requires utilizing
available means to reach desired ends while
satisfying laws in the problem environment.
Development of a prototype
compatible with existing systems,
algorithms and simulator short
response time needed
7. Communication of
research
Design science research must be presented
effectively to both technology-oriented and
management-oriented audiences.
Open source, professional and
scientific publications
Figure 2: Our process iteration following the Design Science Research Methodology.
Decision Support for Planning Maritime Search and Rescue Operations in Canada
331
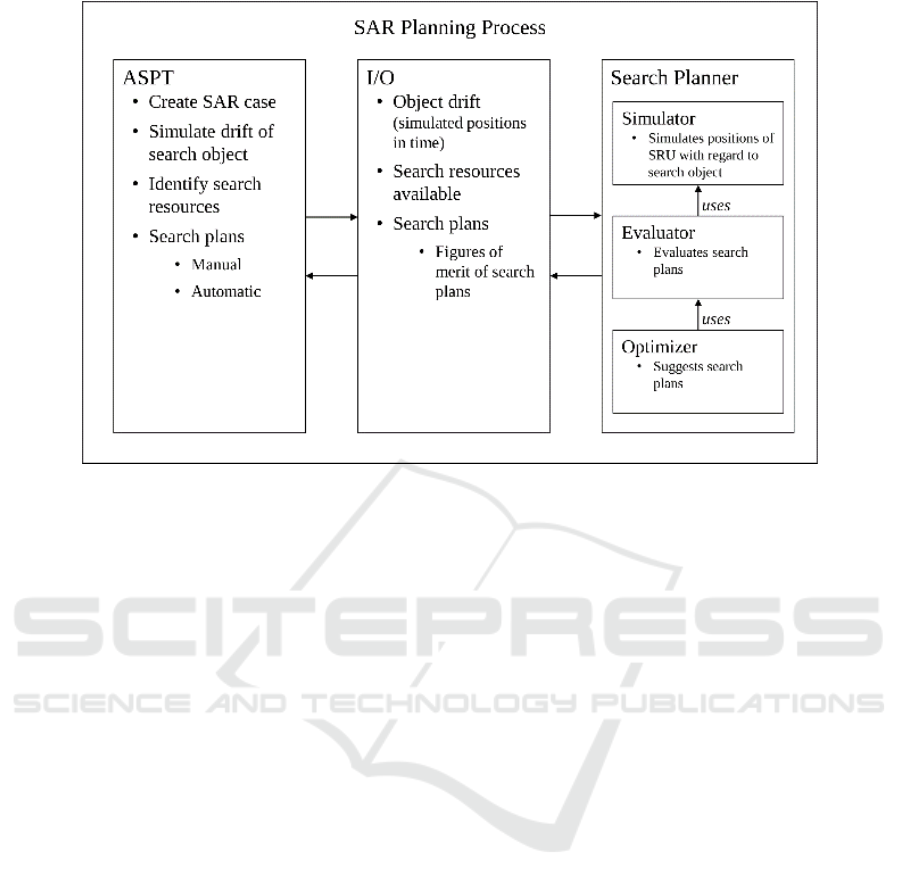
Figure 3: The SAR Planning process.
3 SEARCH PLANNER
When a SMC begins the process of planning a
maritime search mission, he/she starts by creating a
SAR case containing all the available information
concerning the emergency, the characteristics of the
vessel, the number of persons involved, the last
known point, possible sightings, relevant
communications, etc. The next step is to run, in
ASPT, a Monte Carlo (MC) based stochastic drift
simulation (particle filter) for computing probability
distributions of the search object location. The first
step in the simulation is to seed, in space, a certain
number of particles (typically 5000), equally likely to
be the search object, using a 2D Gaussian distribution
with a standard deviation specified by the user. The
locations where the particles are seeded in the
simulation represent plausible last known positions of
the search object. The particles are then moved, by
simulation, in time and space, according to a drift
model, as a function of surface currents and winds.
The drift model calculates, over a simulation horizon,
the positions of the particles at each time step. Each
set of particle’s positions in time represents a search
object’s likely trajectory (Breivik and Allen, 2008).
The simulation’s output, the MC drift file containing
the particles’ positions at each time step, is an input
to Search Planner.
Subsequently, the SMC must identify available
search resources that will be tasked to conduct the
search operations. This is also an input to Search
Planner. At this point, the SMC can either manually
produce a search operation and send it to Search
Planner for evaluation purposes, i.e. computing its
probability of success, or request that Search Planner
suggest a search operation in which case the
Optimizer module is invoked. Planning a search
operation (SO) consists of assigning search plans to
the available search resources (SRU). A search plan
(SP) is defined for a SRU by a search pattern over a
search rectangle. A search area (SA) is a rectangular
region where SRUs are tasked. It is defined over a
drift simulation time horizon and is based on the
simulated particles’ positions.
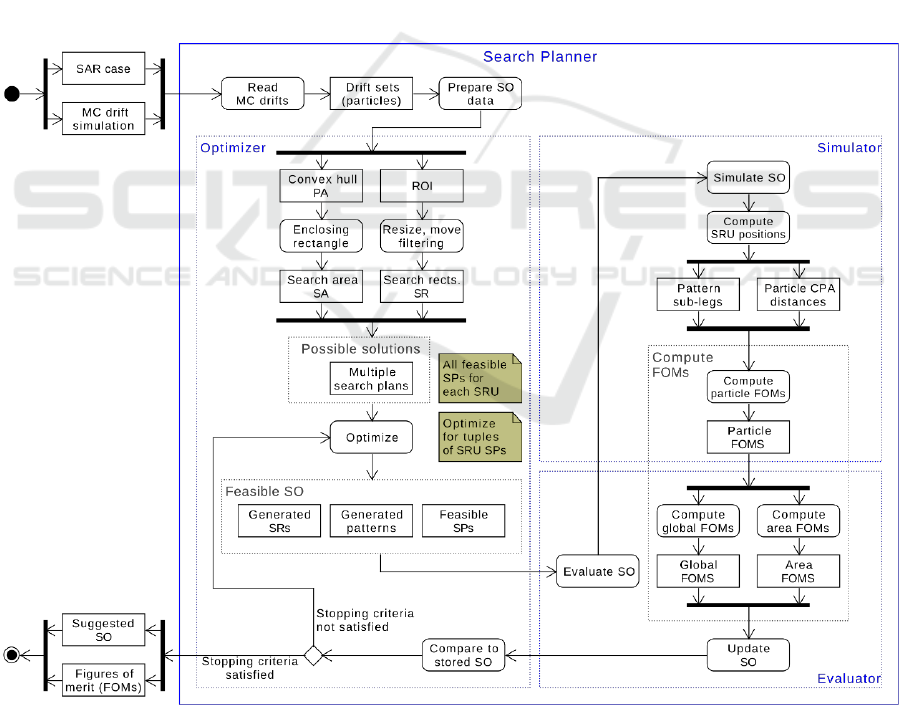
Our prototype Search Planner contains three
submodules, a Simulator (to simulate the positions of
the SRU), an Evaluator, and an Optimizer. The
Optimizer uses the Evaluator that in turns uses the
SRU Simulator. The maritime SAR planning process
using ASPT along with Search Planner is presented
in Figure 3.
Our objective in designing and implementing the
Optimizer is to provide a tool that recommends
feasible search operations with the highest probability
of success (POS). A POS is a figure of merit,
associated with a search operation, loosely defined as
the probability of finding the search object.
In order to illustrate the concepts used, Figure 4
presents an example of a search area containing a 12-
hour simulated drift.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
332
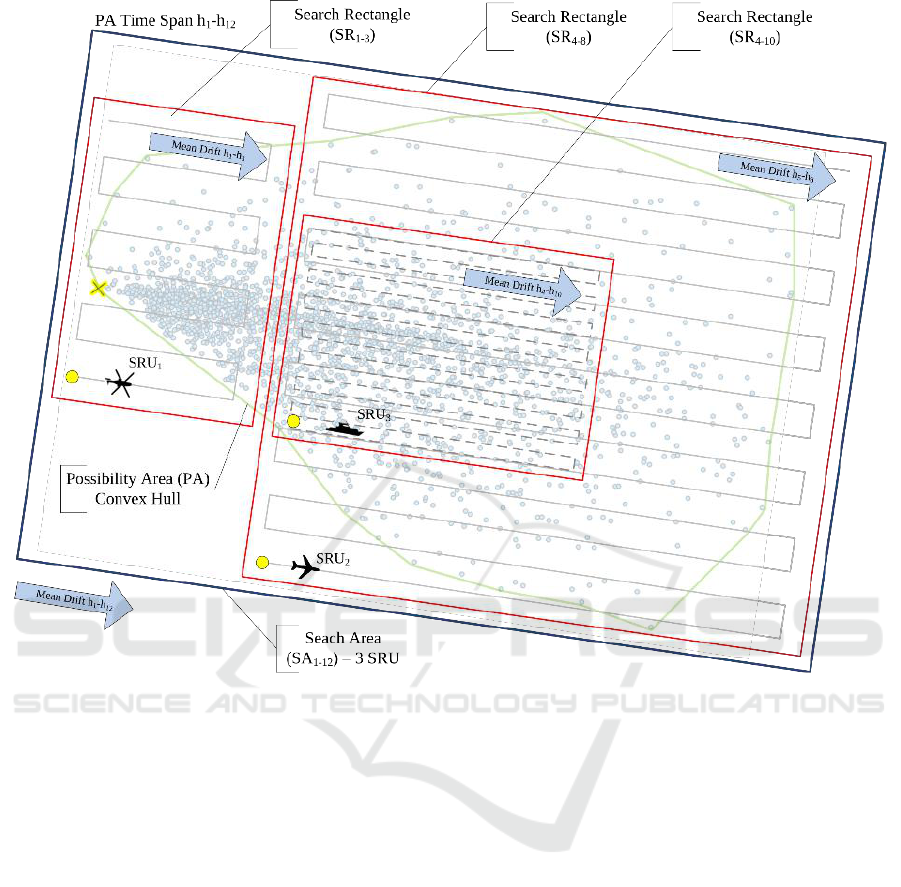
Figure 4: An example of a Search Operation.
The points are positions of drifting particles in time.
The green polygon is the possibility area, a convex
hull containing all search particles positions over the
12-hour period. The Search operation is composed of
three SRUs each having their own search pattern over
their search rectangle. A helicopter (SRU
1
) is present
on-scene between hours 1 and 3 of the simulation. A
fixed wing aircraft (SRU
2
) is present between hours 4
and 8 and a vessel (SRU
3
) is present between hours 4
and 10. The patterns shown are parallel search
patterns. Our artifacts are designed to recommend the
search plans of a search operation, namely identify
the best combination of search rectangles (in red) and
the enclosed patterns.
We describe below the algorithm, based on search
theory, implemented in the Optimizer module.
3.1 The Optimizer
We developed a heuristic based optimization
algorithm that provides feasible optimal or near-
optimal search plans, given appropriate input
parameters, operational constraints and data. It takes
into account the various characteristics of the SRUs
namely their endurance, speed, altitude, and detection
capability as a function of the environment and of the
search object type. The activity diagram depicting the
Search Planner process for suggesting a search
operation is presented in Figure 5.
Given a SAR case, the optimal search planning
problem or SRU allocation problem can be viewed in
terms of the global problem of identifying a search
area, and then locally defining a search plan for each
SRU by assigning it to its optimal or satisfactory
feasible search rectangle, yielding a feasible optimal
or near-optimal search operation. This division of the
optimization task is similar to the approach used by
the SMCs. They tend to define the general SA first
and then position the search patterns of various SRUs
inside that large SA. The optimization procedure we
propose uses a simulation-based evaluation of the
POS of the candidate SO at each iteration.
Decision Support for Planning Maritime Search and Rescue Operations in Canada
333
3.1.1 Evaluating a Search Operation
Optimizing search operations requires that we find
the best combination of search plans for the available
SRUs. The figure of merit used to compare candidate
search operations is the probability of success
associated with the SRUs and a search object
(Kratzke et al., 2010). This is the probability of
detecting the object It is obtained via the Simulator
and the Evaluator.
Suppose that we have P particles. Let O(p) be the
probability that particle p is the search object (prior to
searching) and let pfail(p) be the probability that
particle p has not been detected. Before any search is
conducted, this probability is 1. Consider a SRU u
searching along K straight-line legs where d
k
is the
distance at the closest point of approach between the
SRU u on leg k and the particle p. Let f
u
(d
k
) be the
probability that SRU u detects particle p when the
distance, at the closest point of approach, between the
particle and the SRU is d
k
. This is computed from
lateral range curves developed following extensive
experiments under various weather and search
conditions (Frost, 2002). It is a function of the search
object and of the SRU. The probability the SRU u
fails to detect the particle on the k
th
leg is: 1−f
u
(d
k
).
Detections are assumed to be independent along
different search legs. The probability of SRU u not
detecting particle p is therefore:
(1)
Suppose now that U SRUs are searching, then the
probability of particle p not being detected is:
(2)
and the probability of a particle being detected is
(3)
Figure 5: The Activity Diagram for optimization in Search Planner.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
334

The probability of success of a search operation S is
then defined as:
(4)
After an unsuccessful search, the prior probability
O(p) is updated in a Bayesian fashion and the
posterior probability (after the search) O
a
(p), used as
an a priori probability for the subsequent search, is
computed as follows:
(5)
3.1.2 The Optimization Algorithm
We begin by receiving, from ASPT, drift data
containing the particle’s position in space and time.
Next, we create a convex hull (called a possibility
area or PA) containing all the particles during the
whole MC simulation. There are many algorithms to
generate convex hulls from a set of 2D points. We use
Andrew's monotone chain algorithm (Andrew, 1979)
that has a O(n log n) complexity. We then compute a
search area, a minimum spanning rectangle around
the convex hull. The SA can be oriented according to
the mean drift vector, or following the convex hull’s
longest side. Using the information about the
available resources such as time on-scene, duration
on-scene, detection capability as a function of the
search object, operational constraints on track spacing
in search patterns, etc., the next step is to generate, for
each SRU, a region of interest (ROI), a rectangle
enclosing the convex hull of particles present during
a given time period, normally its on-scene duration.
This uses the same procedure as computing a SA but
with a subset of the particles. We then apply a sub-
optimization filtering procedure: For each SRU, we
modify its ROI by shrinking it or enlarging it and by
moving its centre, within the operational constraints
related to the SRU’s capabilities. Each modified
version of the ROI is a possible search plan (rectangle
and search pattern). We only retain feasible search
plans. We then evaluate all combinations of feasible
search plans for all SRUs and we obtain a POS
evaluation of the SO (Equation 4). The algorithm is
iterative, we continue until we have evaluated all the
combinations or until we reach a given stopping
criterion such as a time limit or minimum global POS
improvement. The pseudo-algorithm is summarized
in Algorithm 1.
Algorithm 1: The optimization pseudo-algorithm.
Search operations are successive in time (Alpha,
Bravo, Charlie, etc.) and are planned as a function of
the previous search operations. Consider for example
an Alpha search that was conducted over N hours
starting at time T. If it is unsuccessful, a subsequent
search operation Bravo, must be planned over M
hours, starting at time T+N. This is done by redrifting
Input:
U SRUs, search object, the
drifted particles positions in
time
Output:
A best POS Search Operation
containing a search rectangle
and pattern for each of the U
SRUs
Steps:
1 - Let z(u) be the total amount of
available search effort for SRU
u (hours)
2 - For each SRU u = 1 to U:
i. Construct the convex hull
containing the particles
during the on-scene
period of the SRU u
ii. Construct its ROI: A(u)
iii. Run the sub-optimization
procedure to generate
SR(u), a set of feasible
search rectangles. This
set is constructed by
varying the location, the
size and the orientation
of A(u).
3 - Add the sets SR(u) to a
candidate SO
4 - Simulate (Simulator) and
evaluate (Evaluator) to obtain
the SO’s POS
5 - Let S be the POS value of the
current candidate SO. Let S* be
the POS value of the best so
far incumbent SO. If S is
strictly better than S* then
the candidate SO becomes the
best so far incumbent SO and S*
is updated
6 - If the stopping criteria are
not met, return to step 4.
Otherwise recommend the best so
far incumbent SO.
Decision Support for Planning Maritime Search and Rescue Operations in Canada
335

the particles starting at simulation time T for a
duration of M+N hours and by re-evaluating the
Alpha search as a function of the real environmental
conditions observed between T and T+N. Re-
evaluating the Alpha search produces more realistic
figures of merit to update the probability that a given
search particle is the actual search object, depending
on whether it came within detection range of a SRU
during the Alpha search. The optimized Bravo search
is then obtained by maximizing Equation 4, between
T+N and T+N+M, where O (p) are replaced by the
updated particles probabilities, O
a
(p). Particles with
lower O
a
(p), ones that came within detection range,
are less likely to be the search object and their
importance in planning subsequent searches are
thereby reduced. Furthermore, the cumulative
probability of success is computed for successive
search operations. This information is very useful for
the search reduction process. At some point, the
commander will have to decide to reduce and stop the
search. This happens when he/she is reasonably
convinced that the chances of finding survivors are
practically nil, reflected by many hours of
unsuccessful search operations that had a very high
theoretical cumulative POS. The rationale is, if
survivors were to be found, they would have been
found by the end of these well-planned searches.
Other factors to take into account in the reduction
decision include the average survival times of persons
in water under the given environmental conditions.
4 APPLICATION EXAMPLES
In order to illustrate the applicability of our method,
we present two representative examples of realistic
maritime SAR cases. The first incident, described in
Section 4.1, pertains to a person in water (PIW) and
the second one, in Section 4.2, to a fishing vessel
(FV). The drift model in ASPT is used to estimate the
particles positions at time steps of 15 minutes.
Currents and winds and last known points are entered
in the MC module of ASPT. A total of 5000 particles
are seeded. The corresponding lateral range curves
for computing detection probabilities are used. The
results are presented using the geographic
information system QGIS (QGIS development team,
2019). It is important to note that both the search
object and the SRUs are moving. Detection
opportunities depend on both positions being
synchronized. The heat maps presented correspond to
the position of all particles during the whole search.
They do not necessarily convey a good idea of the
movement of the particles. The ability of our search
planning method to take into account the particles’
movements is one of its main advantages over the
current manual planning method using deterministic
drift. In fact, a person manually developing a plan will
be tempted to position the search pattern over the heat
map. Although a good starting heuristic, it does not
automatically produce the best probabilities of
success since it is not possible to synchronize in one’s
head the positions of the particles and of the SRU.
This can only be done by simulation, as in our
Simulator component. The white triangle shows the
direction of the drift. The solution for both examples
was obtained in under one minute. The area searched
is much larger for the FV because its search duration
is longer.
4.1 Case 1: Person in Water
A person has gone overboard in water and is assumed
to have a survival suit. Two SRUs are available: One
helicopter with endurance (time on-scene) of 2 hours
and one fixed wing with endurance of 4 hours. The
visibility is of 10 nautical miles (NM). The waves are
5 m high. The Search Planner results are presented in
Figure 6 where we see the search rectangles and
corresponding search patterns (expanding square in
blue and parallel in purple) assigned to the two SRUs.
The helicopter, flying at 50 knots at an altitude of 750
ft, has a recommended search rectangle of 6 by 9
(NM) (smaller rectangle). The fixed wing has a
recommended search rectangle of 11 by 14 (NM)
(larger rectangle). Its search speed is 100 knots and
altitude is 1000 feet. The combined probability of
success is 31%. This may seem not very high but the
probability of detecting a person in water is very
small because of the size of the person. The total area
searched is 154 NM
2
and represents a 4 hour drift.
Deconfliction between SRUs is based on altitudes.
Figure 6: The proposed search operation for the PIW.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
336

4.2 Case 2: Fishing Vessel
A fishing vessel is missing. Two SRUs are available:
One helicopter with endurance (time on-scene) of 2
hours and one fixed wing with endurance (time on-
scene) of 6 hours. The visibility is of 10 nautical miles
(NM). The results are presented in Figure 7 where we
see both search rectangles (in red) and corresponding
search patterns (parallel patterns, dotted blue and
purple lines). The helicopter, flying at 50 knots at an
altitude of 100 ft, has a recommended search
rectangle of 17 by 20 (NM). The fixed wing, flying at
120 knots and an altitude of 1500 feet, has a search
rectangle of 38 by 45 (NM). All particles were
covered (came within detection range). Under these
conditions, the probability of success is very high:
99%. This can be explained by the fact that the object
has high detectability. The total search area is 1710
NM
2
and represents a 6 hour drift. Deconfliction
between SRUs is based on altitudes.
Figure 7: The proposed search operation for the FV.
5 DISCUSSION
The two examples presented above illustrate how, by
designing Search Planner, we were able to answer our
research question. Our new method, implemented in
a prototype and integrated in a DSS, can assist search
mission coordinators in planning optimal or near-
optimal search operations in reasonable time. As
required, Search Planner produces search plans for
each available SRU that have the best combined POS
within a limited computation time defined by the user.
The software has been verified in the sense that it
meets the specifications of the designed method. Its
validation, i.e. ensuring that the software meets the
requirements of the users is planned in the spring of
2019. However, the evaluation of the results produced
(search plans quality) is an ongoing process that
requires some months, and is planned as follows:
First, “beat the DSS” sessions where experienced
SMCs are asked to provide manual plans will be
conducted. The POS of the manually produced plans
will be compared with the automatically produced
plans. It is expected that the DSS will compete
advantageously with the human operator. In all cases,
this experiment will contribute to improving the
algorithm’s heuristics based on practical human
experience and knowledge. Second, past solved SAR
incidents will be used to validate the artifacts. They
will be defined as new cases, and the search plans
produced by the DSS will be evaluated as a function
of the locations where the search objects were
actually found in the past incidents. DSS-produced
search plans will be considered valid if they contain
the locations of the found search objects. Third, to
help validate their drift simulation module,
experiments are planned by the Canadian Coast
Guard where buoys will be released in water and
tracked. Their actual physical trajectories will be
compared to the simulated particles positions.
Comparing the output of our DSS with existing
similar systems could further validate our artifacts.
However, at the current time, we do not have access
to the only other DSS, developed in the US, that has
similar optimal search planning functionalities
(Kratzke et al., 2010).
Our search planning method has limitations. The
main one is related to the model itself. Any model is
a simplified assumption of reality based on
underlying hypotheses. In our case, in order to use
theoretical search theory and lateral range curves to
compute probabilities of detection and of success, we
make the assumption of independent detections along
infinitely long parallel search tracks. This a
reasonable assumption when the tracks are longer
than the detection range. Furthermore, the lateral
range curves, constructed and validated in
experiments (US unpublished reports, 1998; 2005),
are simplified detection models. However, both the
underlying hypotheses and the lateral range curves
are behind a DSS that has been operational and is
successfully used for over 10 years in the US (Stone
et al., 2016).
Another limitation is related to scaling up. Drift
simulation may imply the use of thousands of
particles that drift for many hours. Their positions can
be computed at various time steps ranging from 1
minute to 30 minutes. This has great implications on
the size of the problem. Computing, using step by step
search pattern simulation, probabilities of detections
Decision Support for Planning Maritime Search and Rescue Operations in Canada
337

of millions of particles, in order to evaluate a possible
search operation, can be very time consuming.
Alternatives including particle random sampling and
evaluating a subset of particles can reduce
computation time. Working with larger simulation
time steps is another option. Intensive sensitivity
analyses are necessary to arrive to a compromise in
terms of solution quality and computation time.
One of the challenges we face is the acceptance of
the DSS by the users as this implies a new way of
working and a new way of thinking. Furthermore, this
will imply extensive training (already planned) before
we can be confident that the tool is used to its full
capability. Moreover, the real ability of the proposed
method to increase the number of lives saved can be
assessed only after it has been in operation for a few
years when it is established that the average number
of lives saved has actually increased. Finally, search
operations with very high success probabilities do not
guarantee that the search objects will be found. There
have been many examples of SRUs flying over a
missing object and not seeing it. Although the POS is
accepted as a figure of merit for a search plan, it
remains only a probability.
6 CONCLUSION
We have designed research artifacts to support SAR
mission coordinators in planning searches for missing
persons or objects at sea. An iterative heuristic based
optimization model was formulated and implemented
in a prototype that is integrated in a DSS. Following
the identified limitations in the discussion section,
further research is needed to improve the quality and
performance of the heuristic optimization algorithm,
and to measure the real gains obtained in an
operational setting. For example, in order to try to
reduce computation time related to evaluating the
POS of each candidate search rectangle by
simulation, we are currently exploring machine-
learning techniques from Artificial Intelligence to
automatically “learn” then estimate, without having
to simulate the whole search pattern, the POS of a
search rectangle from a set of previously evaluated
similar rectangles in a similar area. This could result
in a significant decrease in computation time.
Future planned research includes the development
and evaluation of clustering algorithms that divide the
drifted particles set in clusters, which kernels can be
used as a starting centre points for the candidate
search rectangles. Another possible avenue is to
explore the influence of the search pattern type and its
starting point as a function of the drift’s direction.
Further algorithm enhancements could also be
achieved by adding some degrees of freedom in
designing the search plans: the initial convex hull
defining the possibility area could be constructed
using the rotating callipers algorithm to obtain the
most promising orientation of the search area
(Toussaint, 1983). In addition, the candidate search
rectangles could be rotated within the search area in
an attempt to improve the POS. Most importantly,
data on the DSS use in an operational context must be
gathered to continuously improve its acceptability
and performance over the next years.
In the future, as the users become more
comfortable with the new DSS, it is expected that
they will require additional functionalities, such as for
example, simultaneous planning for multiple search
objects, or planning with concurrent unequally likely
scenarios related to what might have happened in the
SAR incident and where.
ACKNOWLEDGEMENTS
The authors wish to thank the ASPT Working group
and the SMCs for their support during the project.
Special thanks to the project manager and the
technical team from the Canadian Coast Guard
College in Sydney. This project was funded by the
Canadian Government, contract number FP802-
150046 to Neosoft Technologies. Research and any
resulting information/theory gathered or compiled
during employment of the author of this published
work by the Government of Canada is licensed for
publication by the Department of Fisheries and
Oceans, and Canadian Coast Guard. No transfer of
Intellectual Property (IP) is implied by the granting of
said license.
REFERENCES
Abi-Zeid, I. and Frost, J.R., 2005. SARPlan: A decision
support system for Canadian Search and Rescue
Operations. European Journal of Operational Research,
162(3), pp.630-653.
Abi-Zeid, I., Nilo, O. and Lamontagne, L., 2011. A
constraint optimization approach for the allocation of
multiple search units in search and rescue operations.
INFOR: Information Systems and Operational
Research, 49(1), pp.15-30.
Ablavsky, V. and Snorrason, M., 2000, August. Optimal
search for a moving target-A geometric approach. In
AIAA Guidance, Navigation, and Control Conference
and Exhibit (p. 4060).
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
338

Andrew, A.M., 1979. Another efficient algorithm for
convex hulls in two dimensions. Information
Processing Letters, 9(5), pp.216-219.
Aronica, S., Benvegna, F., Cossentino, M., Gaglio, S.,
Langiu, A., Lodato, C., Lopes, S., Maniscalco, U. and
Sangiorgi, P., 2010. An Agent-based System for
Maritime Search and Rescue Operations. In WOA.
Bellantuono, N., Camarda, P., Lisi, S., Caneva, P.,
Pontrandolfo, P., Romano, V., Striccoli, D., Scozzi, B.,
SpA, C. and Selex, E.S., 2016. Emergency management
at sea: A decision support system for Search and Rescue
operations. Journal of Software & Systems
Development.
Bernardini, S., Fox, M. and Long, D., 2017. Combining
temporal planning with probabilistic reasoning for
autonomous surveillance missions. Autonomous
Robots, 41(1), pp.181-203.
Breivik, Ø. and Allen, A.A., 2008. An operational search
and rescue model for the Norwegian Sea and the North
Sea. Journal of Marine Systems, 69(1-2), pp.99-113.
Canadian Coast Guard/Department of Fisheries and Oceans
Canada, 2014. Canadian Aeronautical and Maritime
Search and Rescue Manual, Combined Edition –
Volumes I, II and III, B-GA-209-001/FP-001.
Canadian Coast Guard College, 1998. A brief guide to
CANSARP, TP 11718E.
Ferguson, D., 2008, February. GIS for wilderness search
and rescue. In Proceedings of ESRI Federal User
Conference.
Frost, J.R. and Stone, L.D., 2001. Review of search theory:
advances and applications to search and rescue decision
support (No. CG-D-15-01). SOZA AND COMPANY
LTD FAIRFAX VA.
Frost, J.R., 2002. Elements, Modules and Algorithms for
Planning Optimal Searches - A High Level Overview.
Prepared for. U. S. Coast Guard Office of Search and
Rescue. Potomac Management group Inc. Alexandria,
Virginia.
Hevner, A. and Chatterjee, S., 2010. Introduction to design
science research. In Design Research in Information
Systems (pp. 1-8). Springer, Boston, MA.
Hillier, L.E., 2008. Validating and improving the Canadian
coast guard search and rescue planning program
(CANSARP) ocean drift theory (Masters dissertation,
Memorial University of Newfoundland).
Guoxiang, L. and Maofeng, L., 2010, May. Sargis: A gis-
based decision-making support system for maritime
search and rescue. In E-Business and E-Government
(ICEE), 2010 International Conference on (pp. 1571-
1574). IEEE.
Kratzke, T.M., Stone, L.D. and Frost, J.R., 2010, July.
Search and rescue optimal planning system. In
Information Fusion (FUSION), 2010 13th Conference
on (pp. 1-8). IEEE.
Kriheli, B., Levner, E. and Spivak, A., 2016. Optimal
search for hidden targets by unmanned aerial vehicles
under imperfect inspections. American Journal of
Operations Research, 6(02), p.153.
Lau, H., Huang, S. and Dissanayake, G., 2008. Discounted
mean bound for the optimal searcher path problem with
non-uniform travel times. European journal of
operational research, 190(2), pp.383-397.
Małyszko, M. and Wielgosz, M., 2016. Decision support
systems in search, rescue and salvage operations at sea.
Zeszyty Naukowe/Akademia Morska w Szczecinie, (45
(117)), pp.191-195.
Peffers, K., Tuunanen, T., Rothenberger, M.A. and
Chatterjee, S., 2007. A design science research
methodology for information systems research. Journal
of management information systems, 24(3), pp.45-77.
QGIS Development Team (2019). QGIS Geographic
Information System. Open Source Geospatial
Foundation Project. http://qgis.osgeo.org. Visited on
21/2/2019.
Quadrennial SAR Review, available at:
https://www.publicsafety.gc.ca/cnt/rsrcs/pblctns/archiv
e-nss-qdrnnl-rvw/index-en.aspx. Visited on
30/12/2018.
Simon, H.A., 1956. Rational choice and the structure of the
environment. Psychological review, 63(2), p.129.
Sato, H. and Royset, J.O., 2010. Path optimization for the
resource constrained searcher. Naval Research
Logistics (NRL), 57(5), pp.422-440.
Stone, L. D. ,2004.Theory of Optimal Search. Academic
Press, New York, 2
nd
edition.
Stone, L.D., Keller, C.M., Kratzke, T.M. and Strumpfer,
J.P., 2014. Search for the wreckage of Air France Flight
AF 447. Statistical Science, pp.69-80.
Stone, L.D., Royset, J.O. and Washburn, A.R., 2016.
Optimal Search for Moving Targets, International
Series in Operations Research & Management Science.
Reston and Monterey, CA. doi, 10, pp.978-3.
Toussaint, G.T., 1983, May. Solving geometric problems
with the rotating calipers. In Proc. IEEE Melecon (Vol.
83, p. A10).
Venkatesan, S., 2016, November. AUV for Search &
Rescue at sea-an innovative approach. In Autonomous
Underwater Vehicles (AUV), 2016 IEEE/OES (pp. 1-
9). IEEE.
Vidan, P., Hasanspahić, N. and Grbić, T., 2016.
Comparative Analysis of Renowned Softwares for
Search and Rescue Operations. NAŠE MORE:
znanstveno-stručni časopis za more i pomorstvo, 63(2),
pp.73-80.
Decision Support for Planning Maritime Search and Rescue Operations in Canada
339
