Formal Approach to Dynamic SoS Design

Hela Kadri

1,2

, Simon Collart-Dutilleul

, Philippe Bon

and Samir Ben Ahmed

IFSTTAR/ESTAS, Universit

e Lille Nord de France, 20 rue Elis

ee Reclus, France

Universit

e de Tunis El Manar, Campus Universitaire Farhat Hached, Tunisia

Keywords:

System of Systems, Petri Nets, Discrete-event Systems, Operating Modes, Control Design, Reconﬁguration,

Supervisory Control Theory.

Abstract:

This paper deals with the problem of System-of-Systems (SoS) modeling whose structure change due to the

dynamics of its constituent systems as they are developed in different operating modes. Designed by using

multi-model approach, each operating mode represents a process functioning of its system, depending on the

resources to activate and requirements to enforce. Studied as a Discrete-Event System (DES), we propose a

hierarchical framework for designing suitable switching control for dynamic SoS using the High Level Petri

Nets (HLPN). Following a bottom up approach, we model each component ﬁrst in a separate sheet and then

the operating modes. Next, systems are designed by integrating a switching mechanism to commit to different

operating modes when switching events occur. Finally, a mechanism for managing systems dependencies

inside the SoS is proposed. Algorithms are provided to generate the different layers of HLPN permitting easy

implementation of our framework and a ﬂexible manufacturing SoS is used to illustrate our approach.

1 INTRODUCTION

In recent years, complex systems have seen an in-

creasing interest; they became large and work to-

gether to achieve common goals. In this context, the

concept of a System-of-Systems (SoS) has been pro-

posed. It offers a high-level viewpoint encompass-

ing the interactions between the constituent systems

(Jamshidi, 2008). The SoS concept has applied in

many ﬁelds including military (Huynh and Osmund-

son, 2006), robotics (Jamshidi, 2008), transportation

(Caballini et al., 2012) and crisis management (Kadri

et al., 2018). As the malfunction of a single system

can have some serious consequences on the perfor-

mance of the whole SoS, it’s important that the de-

sign of SoSs takes into account the reliability and ro-

bustness requirements of its operation safety. Start-

ing from this necessity, the objective of this paper is

the design in a formal way of SoSs with maintain-

ing an acceptable SoS operation despite failures oc-

curring. To reduce complexity, we adopt a hierar-

chical bottom-up design approach using High Level

Petri Nets (HLPN). First, we model all components

of an SoS in different models. Next and to avoid

to handle the whole process and the whole speciﬁ-

cation, we adopt the multi-model approach to design,

for each system of the SoS, the behavior of its op-

erating modes in separate models. In this step, we

handle the problem of common components between

operating modes, especially that of states. Then, we

present a framework devoted to operating mode man-

agement under speciﬁc control based on supervisory

control theory (Ramadge and Wonham, 1989). In this

theory, systems are allowed to switch from one oper-

ating mode to another one, when exceptional events

occur. Such events may be a failures, failed resource

recoveries, maintenance, etc. Finally, we introduce,

in an upper layer, a framework for modeling inter-

actions and dependencies between systems in order

to maintain acceptable SoS operation despite failures

occurring. In the following sections, we present the

developed work in its different stages and aspects.

2 PRELIMINARY

2.1 SoS Concept

The (ISO/IEC/IEEE 15288 Annex G (ISO, 2015) de-

ﬁnes an SoS as ”[...] a set of systems [brought to-

gether] for a task that none of the systems can ac-

complish on its own. Each constituent system keeps

its own management, goals, and resources while co-

ordinating within the SoS and adapting to meet SoS

goals.” However, several deﬁnitions, which are not

Kadri, H., Collart-Dutilleul, S., Bon, P. and Ben Ahmed, S.

Formal Approach to Dynamic SoS Design.

DOI: 10.5220/0007730903770384

In Proceedings of the 14th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2019), pages 377-384

ISBN: 978-989-758-375-9

377

universally accepted, appeared before. For exam-

ple, (Checkland, 1999) deﬁnes SoS as ”two or more

systems that are separately deﬁned but operate to-

gether to perform a common goal”. The Depart-

ment of Defense American (DoD, 2008) consider an

SoS as ”a set or arrangement of systems that results

when independent and useful systems are integrated

into a larger system that delivers unique capabilities.”

(Maier, 1998) proposes ﬁve traits, known as Maier’s

criteria, for distinguishing SoSs: Operational Inde-

pendence of Elements, Managerial Independence of

Elements, Evolutionary Development, Emergent Be-

havior, and Geographical Distribution of Elements.

2.2 Operating Mode Management for

SoS

In this paper and to study its dynamic, SoS is studied

as a Discrete-Event System (DES). There are several

methods proposing safe control and able to cope with

systems complexity in the DES domain. Among these

methods, Supervisory Control Theory (SCT) seems to

be more convenient for mode management by distin-

guishing process and speciﬁcations. Initiated by (Ra-

madge and Wonham, 1989), SCT is the theory of ana-

lyzing discrete event control systems and it allows the

deﬁnition of different control strategies for each oper-

ating mode based on operating modes management.

This technology aims to ensure the switching from

one operating mode to another one according to the

user input and safety requirements and it is the sub-

ject of several researches (Kamach et al., 2003; Kadri

et al., 2013; Kadri et al., 2017).

In order to deﬁne separate behavior of each sys-

tem of an SoS, we consider the multi-model approach.

This approach assumes that only one operating mode

is activated at a time for each system, while the oth-

ers are deactivated. This allows us to deﬁne separate

models for each system. Each model is a process

functioning description represented by a HLPN and

the process is made up of several components.

2.3 High Level Petri Net (HLPN)

HLPNs are a graphical and mathematical modeling

tool. Among the types of HLPN, we use particu-

larly the Hierarchical Prioritized Colored Petri Net

(HPCPN).

2.3.1 Prioritized Colored Petri Net (CPN)

A CPN is a 7-tuple < P,T,K,W

−

,Φ,M

,Π >

where P is a set of places; T is a set of transitions

(P ∩ T =

0 , P ∪ T 6=

0); K is a color domain func-

tion deﬁned from P∪T into ﬁnite and non-empty sets;

−

, deﬁned on P × T → IN, are the backward

and forward incidence functions, respectively, which

specify the arcs connecting places and transitions; Φ

is a guard function, it is a boolean expression attached

to a transition t ∈ T and by default Φ(t) is evaluated to

true; M is a function deﬁned on P describing the ini-

tial marking; Π is a priority function. It maps transi-

tions into non-negative natural numbers representing

their priority level.

2.3.2 Hierarchical Colored Petri Net (HCPN)

HPN allows to split models of large systems into man-

ageable modules with well-deﬁned. HCPN allows to

split models of large systems into manageable sub-

modules with well-deﬁned. It permits to work at dif-

ferent abstraction levels and have the model reﬂect the

structure of the system. It also allows to create build-

ing submodels that are used repeatedly in the HCPN

model.

3 HIERARCHICAL SOS

DESIGNING

3.1 Proposed Approach

The proposed approach has the purpose to provide an

bottom up approach to SoS design with all its systems

and with the actions of reconﬁguration in a hierarchi-

cal way. The ﬁrst step is Components Design in which

components are modeled in separate HLPN sheets in

according to their speciﬁcations. The second step is

called Modes Design and it consists to study indepen-

dently and separately each operating mode with ap-

plying conventionally the SCT. In fact, in any system,

operating modes engage a set of components and ful-

ﬁl requirements that may be very different from other

ones. In the proposed approach, and through the use

of hierarchical Petri nets, an operating mode model

is a top layer to component models containing substi-

tution transitions, each one is associated with a com-

ponent’s subnet. Furthermore, a notion of common

component is presented in this step to reduce the size

of the global model. The third step is Systems Design

and it allows to model each system with its actions of

reconﬁguration. Each system model is a top layer of

its operating mode models and it integrates a switch-

ing mechanism allowing to commit from one mode to

another. The last step is SoS Design in which the de-

pendencies between the systems are modeled follow-

ing a request for reconﬁguration. This step models of

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

378

the upper layer of the presented model.

Next subsections detail each step. But ﬁrst, let de-

note S = {S

,..,S

|S|

} the set of all systems of an

SoS where |S| > 1, M

= {M

i,1

i,2

,..,M

i,|M

} the set

of operating modes of a system S

, i ∈ {1..|S|} where

| ≥ 1 and C

= {C

i,1

i,2

,..,C

i,|C

} the set of com-

ponents of S

where |C

| ≥ 1. Let also C

i, j

⊆ C

be the set of components that made up the mode

i, j

, M = {M

,..,M

|S|

} be the set of all operat-

ing modes and C = {C

,..,C

|S|

} be the set of all

components.

3.2 Components Design

Each system is made up by several components

whose behavior is the same regardless of the system

mode and it includes possible failures and recoveries

and communication ports. At this stage, we aim

to model components in separate pages. So, for

each component, we associate a CPN describing its

component behavior.

Deﬁnition 1. Let S be the set systems of an SoS

and let C

be the set of components of a system S

where S

∈ S. A component C

i, j

where i ∈ {1..|S|}

and j ∈ {1..|C

|} is modeled by a CPNs with <

i, j

−

i, j

,Φ

i, j

> where:

i, j

= P

i, j



∪ P

i, j



with P

i, j



∩ P

i, j



0. P

i, j



and

i, j



are, respectively, internal places and fusion

(shared) places of the component C

i, j

= T

i, j



∪ T

i, j



with T

i, j



∩ T

i, j



0. T

i, j



and

i, j



are, respectively, internal transitions and

switching transitions of the component C

i, j

3.3 Modes Design

The objective of this section is to ensure the internal

behavior of the operating modes and that they are

well-built and reliable according to the requirements.

The commutation from one operating mode to an-

other leads to change of the process model structure

by engaging new components and by releasing others

ones. Therefore, each mode has to ﬁx the set of com-

ponents necessary to perform its tasks according to

the speciﬁcation. It has also to differentiate between

its own components, used in only one operating

mode, and its common components, used in two or

more operating modes of the same system. Formally,

Deﬁnition 2. Let S

∈ S and M

i, j

∈ M

A component C

i,k

, k ∈ 1..|C

|, is called own to M

i, j

i,k

∈C

i, j

and ∀M

i,p

∈ M

, such as p 6= j, C

i,k

/∈C

i,p

A component C

i,k

, k ∈ 1..|C

|, is called common to

i, j

and M

i,p

if C

i,k

∈ C

i, j

∩C

i,p

with j 6= p.

Let denote C

i, j

= C



i, j

∪C

⇔

i, j

where:

• C



i, j

is the set of its own components;

• C

⇔

i, j

is the set of its common components.

Conceptually, we aims to model the operating

modes by applying the multi-model approach, which

involves designing a process model structure for each

operating mode through the use of hierarchical CPN

bottom-up. Each mode model is a superpage con-

taining substitution transitions, each of which is as-

sociated to a subpage representing one model com-

ponent. Superpages and subpages are connected by

substitution transitions and by equating places on the

two pages.

For common components, substitution transitions re-

fer to the same subpage. So other instances of the

selected component are created. Then, each place of

the different instances is fused with the corresponding

one to ensure an instances identical functioning repre-

senting the same common component. Accordingly,

any state change made to one instance applies to all

other instances as well. This keeps the behavior of

common components when switching from one mode

to another.

In the following Algorithm 1, we present the different

steps to create mode models. First, for simplicity rea-

sons, we confuse the notation M

i, j

of a mode identity

and its associated HCPN and the notation of C

i, j

of a

mode identity and its associated CPN.

Nevertheless, these mode models are not intercon-

nected, and this is the main focus of the next section.

3.4 Systems Design

This section focuses on the design of all the systems

comprising the SoS. Each system is designed and

developed separately by taking the behavior that

could lead to switching between modes into account.

This guarantees a functioning under failure, whilst

causing degraded production. The proposed frame-

work allows to model each system as a superpage for

its mode pages in which we handle the commutation

problem and we add substitution transitions, each

of which is associated to a subpage representing an

operating mode.

In the presented framework, the switching mech-

anism is modeled by the T

i,k



transitions where

i ∈ {1..|S|} and k ∈ {1..|C

|}. Firing such transition

must disable the transitions of their corresponding

HCPL mode and enable ﬁring the transitions of

Formal Approach to Dynamic SoS Design

379

the destination HCPN mode. To distinguish this

type of transitions, we deﬁne an application noted

target mode whose role is to associate with each

transition its destination mode.

Algorithm 1: Pseudo-algorithm generating HCPN of the

operating modes.

Input: the set S of systems; the set M of

modes; the set C

i, j

of M

i, j

components (i = 1..|S|, j = 1..|M

|);

the set of CPN C;

Output: the set of HCPN M

i, j

foreach system, i ← 1to |S| do

foreach mode, j ← 1to |M

| do

Create page M

i, j

;

foreach component C

i,k

∈ C

i, j

Add substitution transition, T

i, j,k

in M

i, j

associated with C

i,k

;

foreach P

i,k

∈ P

i,k



Add P

i,k

in M

i, j

;

Add port-type tag on C

i,k

;

Add arc connecting P

i, j

i, j,k

;

end

if C

i,k

∈ C

⇔

i, j

then

foreach M

i,p

, p ← 1to j do

if C

i,k

∈ C

⇔

i,p

then

Fusion P

i,k



instances of M

i, j

and

i,p

;

end

Deﬁnition 3. Let S

∈ S, M

i, j

∈ M

and T

i, j

be the

related set of transitions.

Let target mode : T

i, j

→ M

be a mapping such that

target mode(t) indicates the active operating mode

after ﬁring t,∀t ∈ T

i, j

Remark 1. Let T

i, j



⊂ T

i, j

be the related set of

switching transitions. ∀t ∈ T

i, j



, t corresponds to a

switching mechanism of mode M

i, j

leading to mode

target mode(t).

Moreover, new elements must be added to each

system S

in order to ensure the switching mechanism:

• Class color Mode

• Place Mode Mgt S

marked by one token repre-

senting the initial mode;

• Arcs connecting Mode Mgt S

to non-switching

transitions and labelled by M, where M is a vari-

able deﬁned on Mode

• ∀C

i,k

∈ C

⇔

i, j

and ∀t ∈ T

i,k



, a predicate is as-

signed and it is satisﬁed as soon as the token of

Mode Mgt S

has the value of a mode including

the component.

• ∀C

i,k

∈ C



i, j

and ∀t ∈ T

i,k



, a predicate is assigned

and it is satisﬁed only when the appropriate token

is in Mode Mgt S

• ∀C

i,k

∈ C

i, j

and ∀t ∈ T

i,k



, t is connected to

Mode Mgt S

with an input label M, and with an

output label set to its target mode.

Algorithm 2 describes the necessary steps to create a

HCPN allowing the operating mode management of

each S

3.5 SoS Design

In this section, we create the top-level net of the

HCPN in which we guarantee a coherent behavior of

the whole SoS despite failures occurring. Indeed, we

aim to maintain an acceptable SoS operation when a

system switches to a degraded mode. We therefore

develop the following idea: if a system goes into de-

graded mode, a subset of systems will be affected and

will have to switch off or to switch to another de-

graded in which a minimum operation is ensured un-

der a revised control policy.

First, a systems decomposition of the SoS should be

modeled and veriﬁed checked against the speciﬁca-

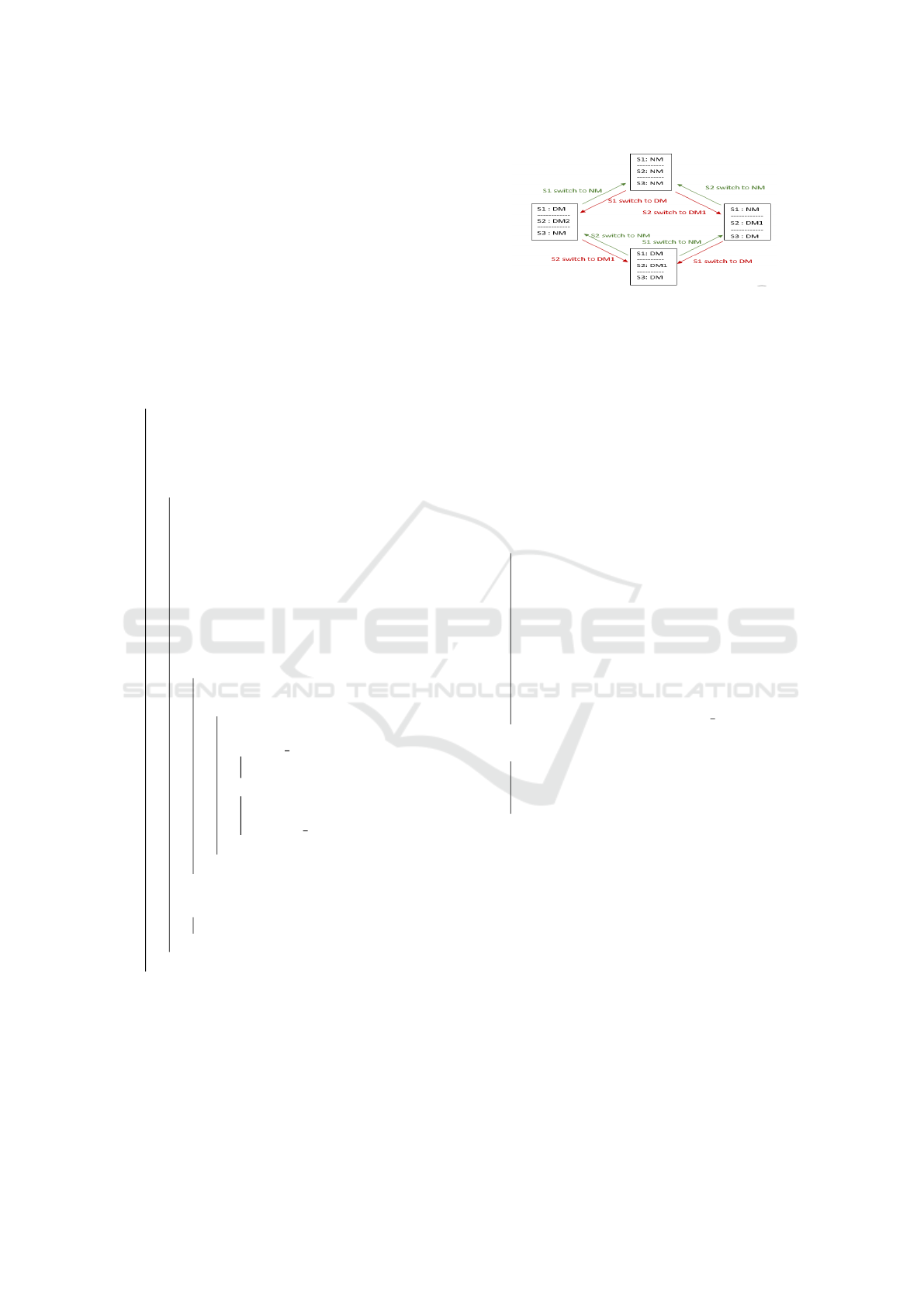
tion. Figure1 illustrates an example of systems de-

composition. There are three systems: S1, S2 and S3.

S1 and S3 are composed of two modes: NM for nom-

inal mode and DM for degraded mode while S2 is

composed of three modes: NM for nominal mode and

DM1 and DM2 for its two degraded modes. Initially,

all the three systems are in NM. When S1 (resp. S2)

switches to DM (resp. DM1), S2 (resp. S3) also has

to switch to DM2 (resp. DM1). And when S1 (resp.

S2) reverts to the initial mode, S2 (resp. S3) also has

to return to MN. If S2 is in DM, the switching of S1

from NM to DM and vice versa does not inﬂuence

the SoS. However, if S1 is in DM and S2 switches to

DM1, then S3 should switch to DM; and if S2 return

to DM2, S1 should return to NM.

At this top layer, a dependency mechanism is

ensured through a new set of high priority transitions,

called set of dependency transitions and noted T

Each transition of the layer level SoS has the role

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

380

of associating with a subset of systems their new

operating modes according to an internal change of

mode in one system. We deﬁne an application noted

dependency whose role is to ensure reconﬁguration

relations between systems:

Algorithm 2: Pseudo-algorithm generating HCPN of sys-

tems.

Input: the set S of systems; the set M of

modes; the set of HCPN M

i, j

(i = 1..|S|, j = 1..|M

|); the set of

CPN C;

Output: the set of HCPN S

foreach system, i ← 1to |S| do

Create page S

;

K = K ∪ Mode;

Add place Mode Mgt S

;

(Mode Mgt S

) = M

i,1

;

foreach mode, j ← 1to |M

| do

Add substitution transition, T

i, j

associated with M

i, j

in S

;

Add arc connecting Mode Mgt S

i, j

Add place Mode Mgt S

in M

i, j

;

Add arc connecting Mode Mgt S

i,k



in C

i,k

;

Add port-type tag on M

i, j

;

foreach C

i,k

, k ← 1to |C

| do

Add place Mode Mgt S

in C

i,k

;

foreach t ∈ T

i,k

i,t

−

(Mode Mgt S

,t) = M;

if target mode(t) = M

i, j

then

i,t

(Mode Mgt S

,t) = M

else

i,t

(Mode Mgt S

,t) =

target mode(t)

end

foreach t ∈ T

i,k



Φ(t) = Φ(t) ∧ [M = M

i, j

]

end

Deﬁnition 4. Let S

⊆ S be a subset of system,

⊆ M be its set of related operating mode and T

be the set of dependency transitions. Let dependency

: T

→ M

be a mapping such that dependency(t)

indicates the activated operating mode of each S

after ﬁring t.

Figure 1: Example of systems decomposition inside an SoS.

Algorithm 3: Pseudo-algorithm generating HPCPN of SoS.

Input: the set S of systems; the set M of

modes; the set of HCPN M

i, j

(i = 1..|S|, j = 1..|M

|);

Output: the ﬁnal HPCPN SoS

Create page SoS;

K = K ∪ ModeSoS;

Add place SoS Mode Mgt ;

Add transitions T

;

Add arcs SoS Mode Mgt to T

;

(SoS Mode Mgt) = empty;

foreach system, i ← 1to |S| do

(SoS Mode Mgt) =

(SoS Mode Mgt) + +(S

i,1

);

Add substitution transition, T

associated with S

in SoS;

Add place Mode Mgt S

in SoS;

Add arc connecting Mode Mgt S

to T

;

Add arc connecting Mode Mgt S

to T

;

−

(Mode Mgt S

,t) = M

i,1

;

(Mode Mgt S

,t) = target mode(t);

end

foreach t ∈ T

(SoS Mode Mgt,t) =

(SoS Mode Mgt);

−

(SoS Mode Mgt,t) = dependency(t);

end

Some new elements also are added to this layer to en-

sure the dependency mechanism:

• Class color ModeSoS such as ModeSoS =

∪(S

,Mode);

• Place SoS Mode Mgt marked by as many tokens

as systems in the SoS and each one contains the

identity of its corresponding system and its initial

mode;

• Transitions T

;

• ∀t ∈ T

, t is connected to the place

SoS Mode Mgt with an input label set of

systems current modes, and with an output label

set to their new modes; t is connected to a

Formal Approach to Dynamic SoS Design

381

Restart_M11

M11

1`P11

Produce_M11

M11

Buffer1

Out

Product

Mode Mgt

System 1

In/Out

Mode

In/Out

Raw Materials Receipt_M11

[M=N]

Place Workpiece_M11

[M=N]

Faillure

Repair

P11

Out

(a) HLPN of M11.

Restart_M12

M12

1`P12

Produce workpiece_M12

M12

Buffer1

Out

Product

Mode Mgt

System 1

In/Out

Mode

Raw materials receipt _M12

[M=D]

Place workpiece M12

[M=D]

P12

In/Out

Out

(b) HLPN of M12.

Restart_M13

Fusion R13

M13

1`P13

Fusion R13

Produce workpiece_M13

Fusion P13

M13

Fusion P13

Buffer1

Product

Mode Mgt

System 1

In/Out

Mode

Picks up workpiece _M13

[M=D orelse M=N]

End production _M13

[M=D orelse M=N]

P13

In/Out

Restart_M21

M21

1`P21

Produce_M21

M21

Buffer

Out

Product

Mode Mgt

System 2

In/Out

Mode

Raw materials receipt_M21

[M=N]

Place workpiece_M21

[M=N]

P21

In/Out

Out

(d) HLPN of M21.

Restart_M22

Fusion R22

M22

1`P22

Fusion R22

Produce workpiece_M22

Fusion P22

M22

Buffer

Out

Product

Mode Mgt

System 2

In/Out

Mode

Raw materials receipt _M22

[M=N orelse M=D]

Place workpiece M22

[M=N orelse M=D]

P22

Fusion P22

Out

In/Out

(e) HLPN of M22.

Restart_M23

M23

1`P23

Produce workpiece_M23

M23

Buffer

Product

Mode Mgt

System 2

In/Out

Mode

Picks up workpiece _M23

[M=N orelse M=D]

End production _M23

[M=N orelse M=D]

P23

In/Out

(f) HLPN of M23.

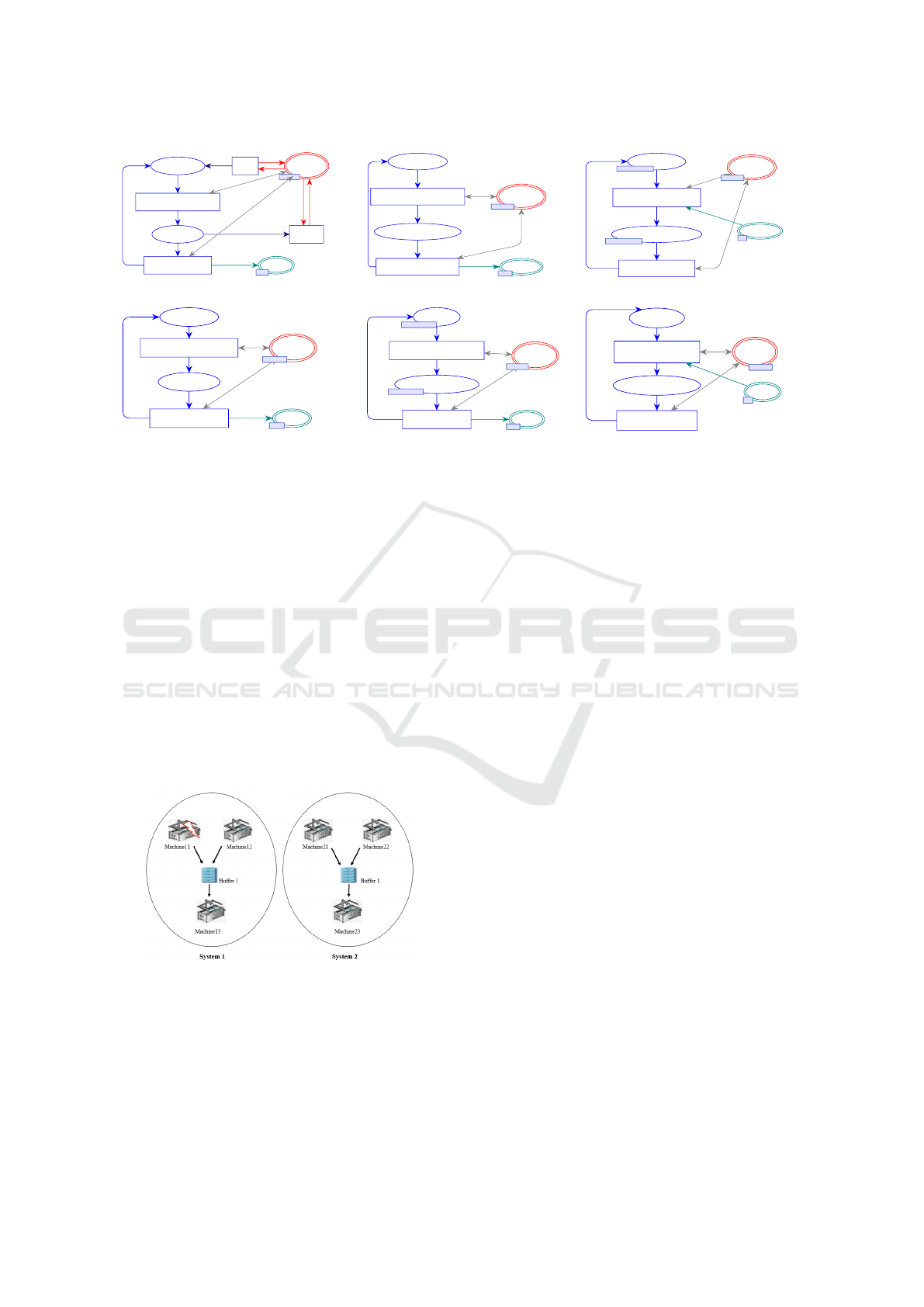
Figure 3: vHLPN of the SoS components.

Mode Mgt S

with an input/output label M, where

M is a variable deﬁned on Mode.

Algorithm 3 creates the last layer of our framework

that represents the whole management of the SoS.

4 CASE STUDY

4.1 System Description

We illustrate our contribution with a manufacturing

SoS inspired from literature. This SoS features two

systems, each one is composed by three components

and one buffer as shown in Figure 2. System1

Figure 2: Manufacturing SoS.

treats workpieces type A. Thereafter, these work-

pieces are delivered to System2 in order to be used

in the treatment of workpieces type B. The function-

ing of System1 is as follows: M

1,1

takes one by one

workpieces from an upstream stock, achieves a treat-

ment and then deposits it in an intermediate buffer.

1,3

takes one by one workpieces from the buffer,

achieve a treatment and then deposit it in a down-

stream stock. Once workpieces type A arrive to

system2, M

2,1

and M

2,2

, which are quite similar, take

two workpieces of which one is type type A from an

upstream stock, achieves a treatment and then deposit

in an intermediate buffer. Afterwards, the workpieces

type B product is treated by the machine M

2,3

It is assumed System1 can break down on M

1,1

and be

repaired. If a failure occurs, M

1,2

, which is less efﬁ-

cient than the defective machine, replaces it and the

concerned system goes into degraded mode. A tran-

sition to a degraded mode of System1 inﬂuences the

operation of the entire SoS: System2 will no longer

be supplied with adequate quantities and will then go

into degraded mode: M

2,2

goes into sleep mode.

The functioning of the example studied enables us to

deﬁne for each system two operating modes: nominal

and degraded. Formally, an S = {System1,System2}

where System1 = {M

1,1

1,2

1,3

} and System2 =

2,1

2,2

2,3

}. The stock is not considered a

component but rather as a system speciﬁcation. This

corresponded to a classic choice of SCT (Ramadge

and Wonham, 1989) constraint because the stock is

no generator events that its own.

4.2 Components Model

In our studied SoS of the Figure 2, there

are 6 components spread over two systems.

C = {M

1,1

1,2

1,3

2,1

2,2

2,3

For system

, the functioning of M

1,1

is represented by the state machine of

Figure3(a) made up of places P

M11



{StartM11,TreatmentM11}, transitions T

M11



{TakeWorkpieceM11, PlaceWorkpieceM11}, and

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

382

the related arcs labelled by the P

1 that is deﬁned by

the colour class M11 = P11. M

(StartM11) = 1‘P11

(one token P11). T

M11



= {Failure,Repair}, is the

switching transitions. As in the following component

models, place P

M11



= {Bu f f er1} is a communica-

tion places, it aims to store workpieces produced; and

the place ”Mode Management System S1” is added

in the system design step.

The functioning of M

1,2

(Figure 3(b))

is represented by places P

M12



{StartM12,TreatmentM12}, transitions T

M12



{TakeWorkpieceM12, PlaceWorkpieceM12} and the

arcs labelled by P12 deﬁned on M12 = {P12}.

The behavior of M

2,2

(Figure 3(e))

is represented by places P

M22



{StartM22,TreatmentM22}, transitions

M22



= {TakeWork pieceM22,EndTreatmentM22}

and arcs labelled by P22 deﬁned on M22 = P22.

The behavior of M

2,3

(Figure3(f))

is represented by places P

M23



{StartM23,AssemblageM23}, transitions T

M23



{TakeWorkpiecesM23, PlaceWorkpieceM23} and

arcs labelled by PM23 deﬁned on M23 = P23;

4.3 Modes Model

At this layer, we can notice, for System1 that M

engaged in its two operating modes, while M

does

not contribute to production in Nominal1 but it in-

tervenes when a commutation to Degraded1 is per-

formed. And for System2 that all machines are en-

gaged in Nominal2, however only M

and M

are

engaged in Degraded2. We then get C



Nominal1

M11, C



Degraded1

= M12, C

⇔

Nominal1

= C

⇔

Degraded1

M13, C



Nominal2

= M22 and C

⇔

Nominal2

= C

⇔

Degraded2

M21,M23.

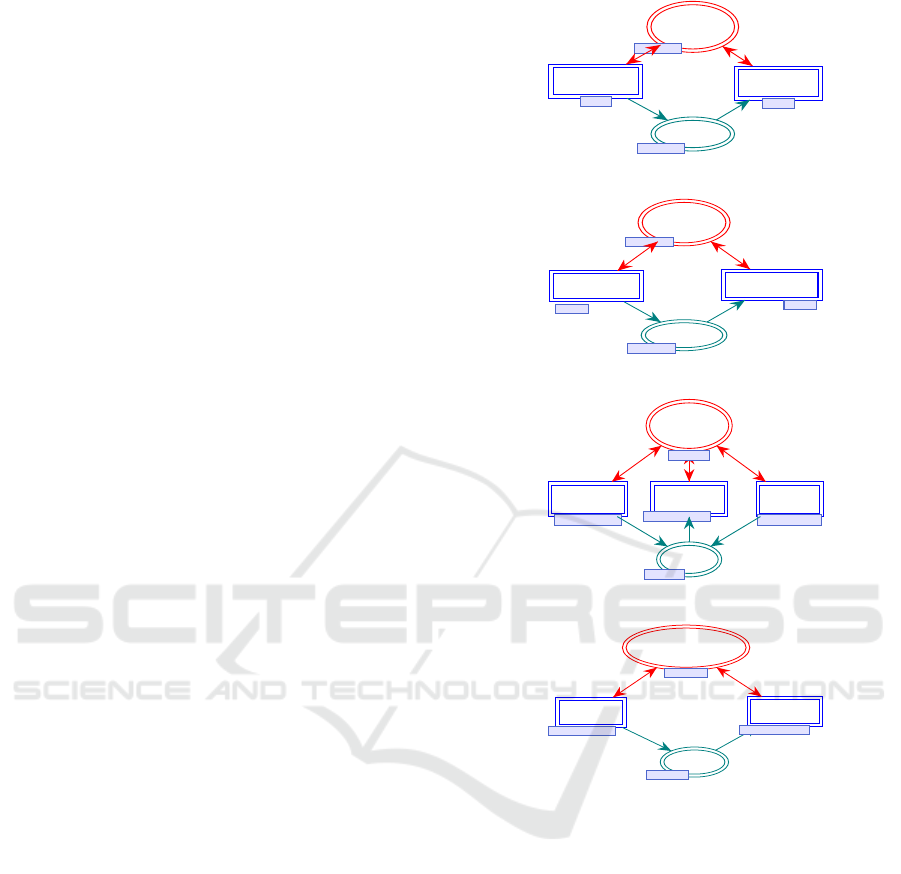
By applying Algorithm 1, we obtain four HCPNs,

each one represents an operating mode of the stud-

ied SoS: Figure4(a) and Figure4(b) represent the

operating modes of System1, while Figure4(a) and

Figure4(b) represent those of System2.

4.4 Systems Model

For System1, Nominal1 mode is composed of the

components M

and M

. From this mode, a

switch is possible to Degraded1, by the switch event

”Failure” generated if the component M

breaks

down, Degraded1 is composed of the components

, common component with Nominal1, and M

When M

generates the event ”recovery”, System1

switches to the ﬁrst mode.

In the same way, For System2, Nominal1 mode is

Mode Mgt

System 1

In/Out

Mode

In/Out

Buffer1

In/Out

Product

In/Out

Machine11

M11M11

Machine13

M13M13

(a) HLPN of System1 nominal mode.

Mode Mgt

System 1

In/Out

Mode

In/Out

Buffer1

In/Out

Product

In/Out

Machine12

M12M12

Machine13

M13M13

(b) HLPN of System1 degraded mode.

Mode Mgt

System 2

In/Out

Mode

Buffer S1

In/Out

Product

Machine1

Machine 21Machine 21

Machine2

Machine 23Machine 23

Machine3

Machine22Machine22

In/Out

Mode

Management

System2

In/Out

Mode

Buffer

In/Out

Product

Machine3

Machine22

Machine2

Machine 23

Machine22

Machine 23

In/Out

(d) HLPN of system2 degraded mode.

Figure 4: HLPN of the SoS modes.

composed of the components M

, M

and M

. A

switch is possible from Nominal2 to Degraded2 if a

request for switching happens. Likewise, a switch to

Nominal2 from Degraded2 can be performed follow-

ing a switching request.

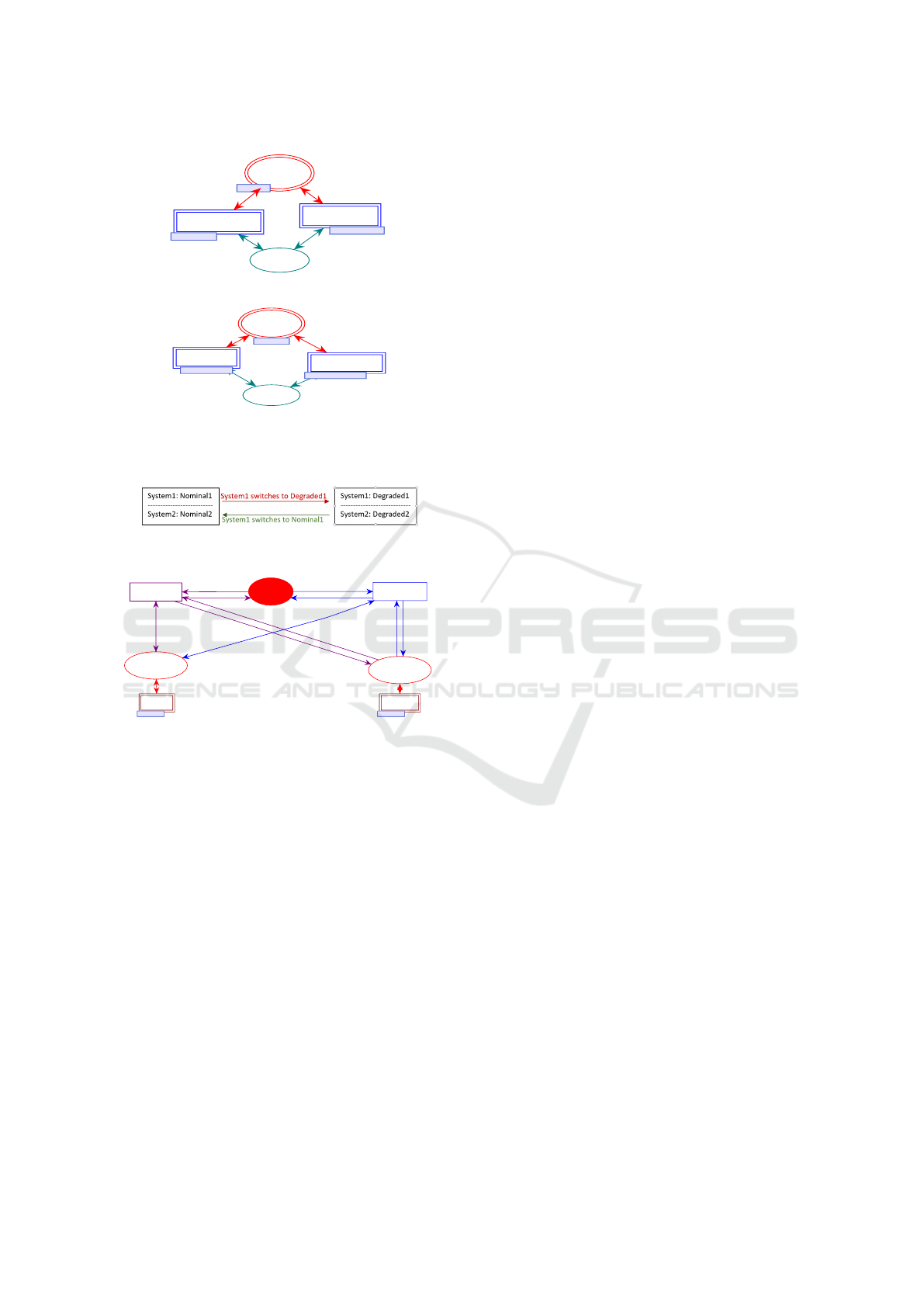
The third HCPN layers obtained is represented in

Figure5(a) and 5(b).

4.5 SoS Model

Figure6 shows systems dependencies inside our stud-

ied SoS: a switching of System1 to its degraded mode

imposes on System2 a commutation to degraded mode

and and vice versa.

The ﬁnal layer of the study example is represented

in Figure7 and it is obtained after generating Algo-

rithm 3.

Formal Approach to Dynamic SoS Design

383

Mode Mgt

System 1

In/Out

Mode

In/Out

Buffer1

Product

Nominal1

Nominal1Nominal1

Degraded1

Degraded1Degraded1

(a) A modal decomposition of System1.

Mode Mgt

System2

In/Out

Mode

Buffer

Product

Nominal2

Nominal 2

Degraded2

Degraded 2

Nominal 2

Degraded 2

In/Out

(b) A modal decomposition of System2.

Figure 5: A modal decomposition of each system of the

studied SoS, with the components used in each mode.

Figure 6: Systems decomposition.

SoS

Mode Mgt

ModeSoS

1`(S1,N)++1`(S2,N)

Mode Mgt

System 2

Mode

Mode Mgt

System 1

Mode

Failure System1

P_HIGH

Recover System1

P_HIGH

System1

System1System1

System2

System2System2

1`(S1,N)++1`(S2,N)

1`(S1,D)++1`(S2,D)

1`(S1,N)++1`(S2,N)

Figure 7: SoS design layer.

5 CONCLUSION

The contribution of this paper is to present a hierarchi-

cal framework using HLPN and allowing to control

the dynamic inside and between systems of an SoS

whose systems are modeled using multimodel ap-

proach. In fact, when an exceptional event occur in a

system, it switches to another operating mode in order

to maintain an acceptable functioning. This switching

causes a reconﬁguration inside the SoS. The proposed

framework decomposes the systems of an SoS in sev-

eral operating modes and each one is decompose in

components. The ﬁrst step of the framework is the

component design where each component is designed

independently. The second step is the mode design

where operating modes are studied and also modeled

independently on formal way. The third step focuses

system design with all operating modes including its

different switch dynamics by using SCT. The last step

is to model the dependencies between the systems.

Current research involves deﬁning strategies when the

similarities between components and modes can be

noticed in order to reduce the complexity of the SoS.

REFERENCES

Caballini, C., Sacone, S., and Siri, S. (2012). The port as

a system of systems: A system dynamics simulation

approach. Proc. 7th Int. Conf. Syst. Syst, Genoa, Italy.

Checkland, P. B. (1999). Systems thinking, systems prac-

tice. Chichester, UK: John Wiley and Sons Ltd.

DoD (2008). System of systems engineering. In Defense

Acquisition Guidebook (DAG). Washington, DC: Pen-

tagon.

Huynh, T. V. and Osmundson, J. S. (2006). A systems en-

gineering methodology for analyzing systems of sys-

tems using the systems modeling language (sysml).

Proc. 2nd Syst. Syst. Eng. Conf.

ISO/IEC/IEEE 15288 Annex G (ISO, . (2015). Systems and

software engineering – system life cycle processes. In

Geneva, Switzerland: International Organisation for

Standardisation / International Electrotechnical Com-

missions / Institute of Electrical and Electronics Engi-

neers.

Jamshidi, M. (2008). Systems of systems engineering: Prin-

ciples and applications. New York, NY, USA: Taylor

& Francis.

Kadri, H., Ahmed, S. B., and Collart-Dutilleul, S. (2017).

Formal approach to control design of complex and

dynamical systems. In Procedia Computer Science

108C:2512-2516, pages: 2512-2516. Elsevier B.V.

Kadri, H., Schleiner, S., Collart-Dutilleul, S., Bon, P.,

Ahmed, S. B., Steyer, S., Gabriel, F., and Aim

e, A. O.

(2018). Proposition of a formal model for crisis man-

agement in the context of high-speed train networks in

border areas. In the proceeding of Transport Research

Arena 2018 (TRA 2018), 16-19th April, Vienna, Aus-

tria.

Kadri, H., Zairi, S., and Zouari, B. (2013). Global model for

the management of operating modes in discrete event

systems. In 6th IFAC Conference Management and

Control of Production and Logistics, Volume 6 — Part

1, Fortaleza, Brazil, September 11-13.

Kamach, O., Pietrac, L., and Niel, E. (2003). Multi-

model approach for discrete event systems: applica-

tion to operating mode management. In Multiconfer-

ence Computational Engineering in Systems Applica-

tions, CESA, Lille.

Maier, M. W. (1998). Architecting principles for systems-

of-systems. In Systems Engineering, vol. 1, no. 4, pp.

267–284.

Ramadge, P. and Wonham, W. (1989). The control of dis-

crete event systems. In Proceedings IEEE, vol.77,

num 1, pp. 81-98.

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

384