Expert Competitive Trafﬁc Light Optimization with Evolutionary

Algorithms

Yann Semet

, Benoit Berthelot

, Thierry Glais

, Christian Isb

erie

and Aur

elien Varest

Thales Research and Technology, 1 avenue Augustin Fresnel, Palaiseau, France

CDVIA, 2 Rue Suchet, Maisons-Alfort, France

Thales Communications and Security, Rue de la Mare aux Joncs, Br

etigny-sur-Orge, France

Keywords:

Trafﬁc Lights, Optimization, Evolutionary Algorithms, Genetic Algorithms, Artiﬁcial Intelligence, Simula-

tion, Calibration, Experts.

Abstract:

We present a complete system to optimize trafﬁc lights green phases and temporal offsets based on a combina-

tion of microscopic simulation and black box, evolutionary algorithms. We also report the outcome of an AI

versus experts comparison workshop conducted with our algorithm and seasoned experts from a specialized

trafﬁc engineering ofﬁce. Experimental results indicate that the proposed algorithmic scheme signiﬁcantly

outperforms expert efforts. Our system entails a memetic (genetic+gradient) calibration module to adapt the

Origin/Destination (O/D) matrix to current trafﬁc conditions, an inoculation procedure to incorporate exist-

ing trafﬁc light programs, genetic multi-objective optimization capabilities and sound metrics. Experiments

are conducted over several real world datasets of operational sizes from the Paris outskirts and various other

French urban areas. Our experimental outcome is threefold. First, we report the success of the memetic

calibration module in adjusting the simulator’s O/D matrix to a point with variation levels corresponding to

recorded sensor data. Second, we conﬁrm the ability of the system to obtain signiﬁcant gains on that sound

basis: gains ranging from 15% to 35% are consistently reached on both trafﬁc jams reduction and pollutant

emissions. Most importantly, we report the outcome of the comparison workshop: a formalized methodology

followed by experts to manually optimize trafﬁc lights, iterative experimental logs tracing the application of

that methodology to two real world cases and comparable results obtained by the algorithm on the same cases.

Results indicate that the AI module performs signiﬁcantly better than experts in both speed and ﬁnal solution

quality.

1 INTRODUCTION

Urban planning is a daunting task. Trafﬁc light opti-

mization is one lever to improve the quality of life for

all citizens: less trafﬁc jams means more time, less

stress and cleaner air. But the task is ludicrously difﬁ-

cult and infrastructure managers or specialized engi-

neering ofﬁces need help to reduce the costs and in-

crease the efﬁciency of trafﬁc light plans design. Ar-

tiﬁcial Intelligence can help by providing computa-

tional support in exploring the space of possibilities.

Trafﬁc engineers are usually equipped with so-

phisticated command and control systems that pro-

vide them with substantial data streams and action

possibilities. They are also pressured to pursue var-

ious, varying and sometimes antagonistic objectives

dictated by the needs of the local population, the par-

ticularities of their trafﬁc network and political leader-

ship or sustainable concerns. Making a smart an efﬁ-

cient mapping between complex objectives and com-

plex decision variables with hidden relationships or

correlations is precisely what evolutionary algorithms

can offer. This artiﬁcial intelligence technique, com-

ing from the ﬁelds of optimization and machine learn-

ing can indeed quickly and reliably ﬁgure out the right

elements of solution necessary to achieve what the in-

frastructure engineers want.

In this paper, we present an integrated, global ap-

proach to help experts optimize trafﬁc light settings

on a sound, validated basis. It is organized as fol-

lows: after a brief literature review, we detail the var-

ious components of our system and then present ex-

perimental results on real-world benchmarks. Most

importantly, we conclude with the report of a compet-

itive comparison workshop between actual trafﬁc ex-

perts and our algorithm in order to conﬁrm the ability

Semet, Y., Berthelot, B., Glais, T., Isbérie, C. and Varest, A.

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms.

DOI: 10.5220/0007732701990210

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 199-210

ISBN: 978-989-758-374-2

199

of this AI-based approach to outperform humans on

this speciﬁc mathematical but very complex and sub-

tle task.

2 LITERATURE REVIEW

Many attempts at optimizing trafﬁc light settings with

various ﬂavors of evolutionary algorithms have been

made, underlining both how promising the approach

is and how important the problem has always been.

Two early examples can be found in (Foy et al., ;

Rouphail et al., 2000). As early as 1992 indeed, Foy,

Benekohal and Goldberg (Foy et al., ) applied bit-

string Genetic Algorithms to the optimization of sig-

nal timing and obtained consistent results in decreas-

ing wait time on variants of a small test case with

four junctions. In 2000, (Rouphail et al., 2000) tried

to minimize queue lengths on a Chicago,IL test case

with 9 signalized intersections using CORSIM and

Transyt.

More recently, (Stevanovic et al., 2008) conducted

a rigorous study with genetic algorithms searching a

sophisticated, complete representation of trafﬁc light

plans tried against a trafﬁc model run by microscopic

simulator VISSIM. Experiments were conducted on

two US benchmarks: Park City, UT and Albany, NY.

One particular focus of the study was to see how op-

timizing parameters in sequence or all at once inﬂu-

enced ﬁnal solution quality. Optimized plans were fa-

vorably compared to existing plans and to plans pro-

duced by SYNCHRO but with gains limited in ampli-

tude.

(Sanchez-Medina et al., 2008) applied evolution-

ary algorithms to the trafﬁc light optimization prob-

lem with a sophisticated gray-code based encoding

of phases. Plan quality was evaluated with an ad

hoc Cellular Automaton based microscopic simulator

built after the Kraus car following model and run on a

Beowulf cluster. Two rather large test cases and asso-

ciated data were procured from the local councils of

Saragossa and Santa Cruz de Tenerife and signiﬁcant

gains were obtained with respect to existing trafﬁc

light plans : around 10% on the ﬁrst benchmark even

though it had little trafﬁc and therefore room for im-

provement and up to 30% on the second one although

with very signiﬁcant variance between solutions.

Very recently, (P

eres et al., 2018), following sev-

eral studies over preceding years (e.g. see (Garc

ıa-

Nieto et al., 2011) or (Garc

ıa-Nieto et al., 2013))

tackled real-world cases with evolutionary algorithms

with a particular focus on multiobjective optimiza-

tion and sustainable concerns. Using SUMO, an

open-source trafﬁc simulator, as the objective func-

tion provider, they obtain large and consistent gains

on three real-world benchmarks in Montevideo. They

offer an interesting benchmark comparison of var-

ious classical Multi-Objective Evolutionary Algo-

rithms applied to the problem and shed interesting

light on edge prioritization.

Other studies worth citing (Hu et al., 2015;

Garc

ıa-Nieto et al., 2011; Jin et al., 2017; Jin and

Ma, 2014) make use of various computational tech-

niques related to evolutionary algorithms such as Par-

ticle Swarm Optimization in varied operational con-

texts.

There are many ways in which trafﬁc regulation

can be approached with computational support. With

the recent rise of global interest in Machine Learn-

ing, on can note observe an increasing number of at-

tempts at using Reinforcement Learning to approach

the problem with a more dynamic orientation (e.g.

see (Chin et al., 2012; Fakult

at, 2006; Marsetic et al.,

2014; Salkham et al., 2008) and obtain very encourag-

ing results with Q-learning, policy gradients or actor

critic methods.

Most aforementioned approaches make use of

microscopic simulation as the objective function

provider. For any operational application to be con-

sidered or more generally, for any trust to be placed

in the results, care must be taken that simulators and

their models are realistic enough. To that end, cal-

ibration is necessary. Calibration is the problem of

adjusting simulation parameter values so as to maxi-

mize the predictive capability of the simulator. Simu-

lation parameters include physical variables (e.g. ve-

hicle weights and length), behavioral and kinetic vari-

ables and, most importantly, demand modeling with

O/D matrices and dynamic routing parameters. Cal-

ibration is absolutely critical but is often overlooked

in studies that are focused on the main optimization

problem that is difﬁcult enough in itself. There is,

however a signiﬁcant but rather separate body of work

on that issue. (Paz et al., 2015; Chu et al., 2003) for

example, offer very interesting systematic methodolo-

gies to address all aspects of the calibration problem.

Other approaches, such as (Toledo and Kolechkina,

2013), focus on speciﬁc calibration subproblems with

adequate mathematical tooling.

Overall, although many trafﬁc light optimization

studies have been conducted, most of them, while of-

fering interesting insight and convincing results, seem

to be lacking in at least one aspect of this deceptively

complex problem: validation benchmarks, particu-

larly in early studies, are often small and/or unreal-

istic, simulators may have weak or no calibration and

optimization sometimes lack essential aspects such as

multi-objective capabilities or statistical validation of

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

200

its results. We try to offer a comprehensive algorith-

mic proposal with at least one form of answer for all

key aspects of the problem.

3 SYSTEM OUTLINE AND

ALGORITHMS

3.1 Overview

Our system’s purpose is to try to ﬁnd optimal or

near optimal values for trafﬁc light plan settings. To

that end, we follow the classical evolutionary black-

box approach which consists in associating a genetic

search engine with a simulator that provides objec-

tive function values. Having a well calibrated simula-

tor is extremely important in such a context because

by providing short term world evolution prediction

for particular individuals to feed the objective func-

tion, the simulator is ultimately and almost entirely

responsible for solution quality. That is the reason

why, as outlined in ﬁgure 1, our system is composed

of three main separate boxes whose underlying prin-

ciples and implementation we detail below : simula-

tor, optimizer and calibrator. The input data comes

from the ﬁeld (sensors providing ﬂow or occupancy

rate measurements and/or existing trafﬁc light plans).

The output is of course, a suggested near optimal traf-

ﬁc light plan for the input trafﬁc model. More detailed

design information, along with experimental valida-

tion of choices can be found in (Damay, 2015).

Figure 1: Global system architecture.

3.2 Genetic Search and Multi-objective

Capabilities

Genetic and Evolutionary Algorithms (Goldberg,

1989; Eiben and Smith, 2003) are mathematical pro-

cedures created in the ﬁeld of Artiﬁcial Intelligence

to solve complex problems by following a biological

metaphor with a few essential aspects : genetic en-

coding, random variations (mutation and crossover)

and survival of the ﬁttest. By using selection pres-

sure to intelligently explore the spaces of possible so-

lutions, engineers have created very powerful algo-

rithms which can favorably solve very difﬁcult real

world problems. Evolutionary algorithms, besides be-

ing mathematically efﬁcient, happen to have several

practical advantages: they provide “anytime” solu-

tions, are highly paralellisable, straightforward to im-

plement, need very little information about the prob-

lem and can be hybridized naturally with speciﬁc al-

gorithms or expert knowledge.

Another key advantage of evolutionary algorithms

is that, being population based, they are naturally ﬁt

for multi-objective search in the Pareto sense. By that

we mean the ability to provide the entire set of so-

lutions, or a good approximation of that set, which

are non Pareto-dominated. Practically, it means that

the algorithm is able to identify in a single run all

good solutions which represent interesting compro-

mises for the decision maker facing antagonistic ob-

jectives (e.g. cost vs. engine power when consid-

ering a new car). Very well-known multi-objective

variants of evolutionary algorithms such as NSGA-

II (Deb et al., 2002), SPEA2 (Zitzler et al., 2001),

IBEAx (Zitzler and K

unzli, 2004) or MOEAD (Zhang

and Li, 2007) can indeed provide that service very ef-

ﬁciently.

Trafﬁc light plan design is a typical optimization

problem : variables are green phases durations and

temporal offsets, constraints are given by law or se-

curity considerations and limit the possible values for

the variables and objective functions are straightfor-

wardly given by trafﬁc ﬂuidity metrics (waiting time,

timeloss, queue length, etc.) or pollutant emissions

measurements (CO, CO2, NOx, PMx, HC, fuel con-

sumption, noise, etc.). Experimenting directly in the

ﬁeld is of course impossible for obvious security and

public relations reasons so one has to resort to mathe-

matical models or simulators. Vehicular trafﬁc being

a very complex process with signiﬁcant human and

cognitive components, microscopic simulation is of-

ten the most reasonable option to be sure to take intri-

cate interaction phenomena properly into account.

We therefore have a classical black-box setting,

which we tackle straightforwardly with an evolution-

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms

201

ary algorithm and simulator combination. So as not to

reinvent the wheel and beneﬁt from good implemen-

tation and out of the box parallel computing, we use

the excellent DEAP library (Distributed Evolutionary

Algorithms in Python (Fortin et al., 2012)).

Our particular choice of basis algorithm went to

NSGA-II after an extensive experimental campaign

with statistical signiﬁcance testing for algorithmic

variants, components and parameter settings. The

fundamental multi-objective mechanism of NSGA-

II uses a combination of crowding distance non-

dominated sorting of its population to ensure diver-

sity preserving and exploration in the Pareto sense.

We use a traditional evolutionary sequence and the

structure of our algorithm follows the NSGA-II ba-

sis, which we use in either mono-objective or multi-

objective mode.

3.3 Problem Representation, Variation

Operators, Metrics

We adopt a very straightforward solution encoding

strategy. As detailed in ﬁgure 2, we just use vec-

tors of integer values that represent, junction by junc-

tion successively, green phases durations and tempo-

ral offsets.

Figure 2: Problem representation. The small schematic

zone above contains three junctions (A,B and C) situated

along and aside a main axis of trafﬁc. The corresponding

genome encodes green phase durations for A’s 3 phases and

B and C’s two phases as well as relative temporal offsets for

all 3 junctions.

Variation operators work on that representation di-

rectly. Crossover is a classical two point scheme.

Our mutation is a Gaussian variation whose standard

deviation is controlled dynamically with a sigmoid

swap scheme as introduced in (Semet and Schoe-

nauer, 2006) and used in (Marceau Caron, 2014).

This allows to tune the exploration/exploitation trade-

off by controlling how ”disruptive” the mutation ra-

dius (in our case the standard deviation of the Gaus-

sian variation) shall be over the course of evolution:

mutation

(

α if t < t

β + 2 × (α − β) ×

1+exp

γ(t−t

)

if t ≥ t

Initialization ﬁnally, although not technically a

variation operator, is, as outlined in (Semet and

Schoenauer, 2006), an essential building block of the

overall algorithm. We found that using an “inoc-

ulant”, which means a heuristically built individual

based on the existing trafﬁc light plan was useful to

achieve rapid early search, which is a particularly de-

sirable trait in this fast paced operational context. The

initial population is therefore built as a mix of inoc-

ulants varied with mutation and purely random indi-

viduals.

3.4 Microscopic Simulation and

Calibration

3.4.1 Simulator

To substantiate the objective function, we use the

open-source microscopic trafﬁc simulator SUMO

(Krajzewicz et al., 2012) developed by DLR. In

their own words, taken from SUMO’s homepage

(http://http://sumo.sourceforge.net/) :

”Simulation of Urban MObility”, or ”SUMO”

for short, is an open source, microscopic,

multi-modal trafﬁc simulation. It allows to

simulate how a given trafﬁc demand which

consists of single vehicles moves through a

given road network. The simulation allows

to address a large set of trafﬁc management

topics. It is purely microscopic: each vehicle

is modeled explicitly, has an own route, and

moves individually through the network.

SUMO is a very powerful and versatile tool that

provides rigorous trafﬁc representation and easy inte-

gration with computational support algorithms. It is

also very fast, which is particularly precious for pop-

ulation based stochastic search, which requires many

computations of the objective function.

Our SUMO trafﬁc model is an O/D matrix that

is turned into individual routes by shortest path rout-

ing utilities provided with the software (od2trips and

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

202

duarouter). Some attempts at dynamic equilibrium

ﬁnding and routing optimization have also been found

useful and were performed with the duaIterate script

and the Cadyts external utility (Flotterod et al., 2011).

Our GIS based road network was imported and ad-

justed, which is a long, tedious, but absolutely critical

step for any realism to be achieved, with netconvert

and netedit.

3.4.2 Memetic Calibration

One speciﬁcity of our algorithmic system is the cal-

ibrator module. Achieving realistic simulation is

extremely important, both for fundamental solution

quality and as a caution of trust for the end-user who

wants guarantees about how well her ﬁeld is mod-

eled by the computer. To that end, much effort was

spent in trying to procure the best possible O/D ma-

trix. Beyond dynamic routing and calibration outlined

above, speciﬁc R&D efforts were conducted to de-

velop an optimization module for that purpose. Ex-

periments, reported in (Damay, 2015) revealed that

the best solution was an hybrid algorithm combining

genetic search and a speciﬁc, state-of-the-art gradient

algorithm. Such an hybrid is usually called a Memetic

algorithm and typically tries to combine the beneﬁts

of global stochastic search with local optimization to

reﬁne the solution.

Uncharacteristically, this particular ﬂavor uses

gradient to optimize the starting point (either a zero

or heuristically provided O/D matrix) and produce an

inoculant for the genetic search that will ﬁnd both lo-

cal and global improvements. The genetic part of the

calibrator is a standard (λ + µ) evolutionary scheme

with Gaussian mutation. The gradient part is an ex-

tended version of the algorithm introduced in (Toledo

and Kolechkina, 2013), which performs steepest de-

scent on matrix coefﬁcients in the error space. For

both parts, error or ﬁtness is measured by comparing

obtained simulated counts with sensor history. Impor-

tantly, considered sensor values can either be averages

or speciﬁc values. This allows to serve, at will, two

functional purposes: aiming for robust values with

good generalization ability or being as precisely close

as possible to what is currently happening in the ﬁeld.

4 EXPERIMENTAL RESULTS

4.1 Benchmarks

Validation experiments have been conducted on sev-

eral real-world benchmarks corresponding to regula-

tion zones of medium size, usually a well delimited

neighborhood, portion of the dense center of a city.

Our main test cases were :

• A portion of the downtown area in Rouen, with a

mesh-like network of 10 signalized intersections

• A portion of the downtown area in Strasbourg,

with 9 signalized junctions, one of them being

shared with a tramway line with absolute priority

• A large linear portion of the immediate north-

ern outskirts of Paris with three intersecting high

speed axes of trafﬁc which has 12 to 20 signalized

intersections, depending on the instances.

A screen capture of the typical Rouen benchmark

is given in ﬁgure 3 with sensors and O/D source/sinks.

All benchmarks were complete with digitized road

network, sensor data over several months and/or turn-

ing proportion studies and currently used trafﬁc light

plans.

Figure 3: The downtown Rouen benchmark map. Blue dots

represent O/D entry/exit points, red ones sensors.

4.2 Calibration Results

The ﬁrst O/D matrix we used for the Rouen bench-

mark was constructed heuristically using a few mea-

sured ﬂow rates and turning proportions studies. In

order to reﬁne it against historical sensor data, we

deﬁned a realism goal by computing statistics on a

carefully chosen subset of sensors. We observed that

within the considered morning peak hours, values for

individual sensors varied within a plus or minus 30

% range over average values. We therefore set as an

objective that the optimized O/D matrix should pro-

duce simulated counts, not only as close as possible

to the average corresponding counts (for each sen-

sor) on average (over all sensors) but that the aver-

age of variances for all sensors should be below the

30% limit as observed in the data. This simple cri-

terion proved difﬁcult to reach and only the memetic

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms

203

hybrid algorithm we proposed was able to reach that

target with a 28% average variance. The heuristic ma-

trix alone yielded

60% variance, gradient alone (as in

(Toledo and Kolechkina, 2013)) yielded 41% and ge-

netic search alone yielded 32%.

Figure 4 illustrates the result obtained by the

memetic algorithm with a star diagram: each branch

of the star shows a speciﬁc sensor and the point on

that axis represents the obtained simulated count for

that sensor on a normalized scale valued at 1 if sim-

ulated count exactly equals the average of historical

sensor data. According to our criterion, points should

therefore lie between 0.7 and 1.3 on all axes, which is

represented by the blue and black circles respectively,

the red circle representing the ideal solution. As can

be seen in the ﬁgure, while correct on average over all

sensors, our solution has room for improvement on

several underused sensors.

Figure 4: Calibration results star diagram. Each branch rep-

resents a sensor, whose simulated count should reach the

red circle (normalized value of 1) corresponding to the av-

erage measured value. This solution, the best we obtained,

corresponds to an average variance of 28%.

4.3 Optimization Results

4.3.1 Experimental Setup

In order to assess the ability to produce substantial

and reliable gains, we follow the following experi-

mental guidelines:

• All evolutionary algorithm run results are aver-

aged over at least 11 random seeds

• All simulator runs are averaged over 10 random

seeds, a value empirically determined to trigger

sufﬁciently low variance

• Simulator runs usually have a warm-up time of 5

minutes and metric measuring time window of 20

minutes

• Algorithmic variants, components or parameter

settings are chosen from using the Wilcoxon

signed test for statistical signiﬁcance

Typical parameter values are as follows: popula-

tion size 12, mutation probability 0.5, crossover prob-

ability 0.25, 100 generations, minimum variable value

1, maximum 120, initial sigma value 10.

4.3.2 Mono-Objective Results

In the following section, we report results obtained on

the Rouen benchmark. Similar results have been ob-

tained on the other test zones. The main objective of

trafﬁc light optimization being to reduce trafﬁc jams,

mono-objective results are related to trafﬁc ﬂuidity

metrics. Many possibilities exist to quantify this, we

chose to use a weighted average of waiting time (total

amount of time spent by vehicles under epsilon speed)

and total number of processed vehicles so as to avoid

solutions where trafﬁc is prevented from entering the

zone by over-saturating entry junctions.

Figure 5 illustrates the typical optimization curve

we obtain on both morning and evening peak hours,

with average and maximum gain (which means min-

imum metric value). Gains of up to 28% in waiting

time are obtained for the morning peak at end of the

run. One notices that variance is limited, making for a

robust result and that, thanks to the anytime property

of evolutionary algorithms, strong gains of 15 to 20

% can be obtained very quickly, as soon as generation

10. As one can see, the evening peak is much more

difﬁcult, maximum gain is only around 12% in that

case.

4.3.3 Multi-objective Results

Thanks to the HBEFA and Harmonoise models pro-

vided with SUMO, one can pursue other objectives

than trafﬁc ﬂuidity: pollutant emissions (CO, CO2,

NOx, PMx, HC, fuel consumption) and noise. Some

of these objectives are correlated, some are antago-

nistic with varying degrees. See (Damay, 2015) for

extensive analysis and experimental results on all ob-

jectives. For the sake of brevity and simplicity, we

report results obtained on the illustrative waiting time

/ CO2 couple. The top-right corner of ﬁgure 6 shows

the evolution path followed by the population towards

the Pareto front obtained at the end of the run, one

clearly sees both a strong direction, aiming at the bot-

tom left corner, and a maintained variety of choices

along the front.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

204

Figure 5: Mono-Objective (waiting time) results obtained

on morning and evening peak hours.

Zooming in on the obtained Pareto front in ﬁg-

ure 6, one can pick four distinct illustrative solutions

A,B,C and D. A and B are extremal solutions, respec-

tively excellent in waiting time and CO2. C and D

offer two different compromises.

Figure 6: Zoom on the Pareto fronts. 4 representative points

are chosen along it: 2 extremal ones (A and B) and 2 com-

promises (C and D).

Finally, one gives corresponding gain ﬁgures : up

to 38% in waiting time (point A) and 24% in CO2

(point B). Point C has 32% gain in waiting time and

13% in CO2. Point D offers 16% and 18% respec-

tively. One notices that optimizing seems to be sig-

niﬁcantly harder and that going from C to D for ex-

ample has a huge cost in waiting time for a limited

CO2 beneﬁt.

4.3.4 Drawing Lessons with Reverse

Engineering

A very interesting characteristic of straightforward

black-box search, where one manipulates decision

variables directly, is that the result can be interpreted

immediately by experts, who can start an analysis pro-

cess to try to understand why the settings proposed

by the algorithm are efﬁcient. This process, based

on the fact that the outcome of the optimization algo-

rithm is interesting in itself, can bring a lot of useful

information by shedding light on the speciﬁcs of the

ﬁeld or by experimentally conﬁrming counterintuitive

ideas. All that can help improve or adjust heuristics

and expert thinking. This reverse engineering process

is not always easy or necessary but it is almost sys-

tematically informative. We give here a simple ex-

ample of solution interpretation to illustrate both the

surprisingly accurate ability of evolutionary search to

detect opportunities in the objective function search

landscape and the type of methodological conclusion

one may draw from observing, a posteriori, building

blocks of the optimized solutions.

Our example focuses on a speciﬁc junction in the

benchmark. It is situated along an important axis

of trafﬁc and has three main successive phases in

its trafﬁc light plan. The ﬁrst one is for the main

north/south axis, going straight in both directions, the

second phase is for vehicles turning left coming from

that main axis and onto the perpendicular, secondary

axis and the last phase is for the secondary axis, go-

ing straight. The initial, expert provided, trafﬁc light

plan had values, for the respective phases, of [29 12

21]. The optimized plan suggests [20 5 20]. By ob-

serving trafﬁc, one quickly understands why. First

and foremost, there is a signiﬁcant loss of green time

on the ﬁrst phase : the light remains green long af-

ter all vehicles have been processed. Secondly, very

few vehicles use the left turn phase. Finally, the ﬂow

of vehicles on the secondary axis is steady and prop-

erly handled. The algorithm has therefore managed

to make the right decisions both by implicitly making

these observations and by adequately sizing the cor-

responding changes.

The methodological conclusion for experts, which

conﬁrms what we have seen on other similar cases is

that one of the most efﬁcient optimization lever, as

opposed to focusing on green splits, consists in re-

ducing unnecessarily long green times to decrease cy-

cle length so as to process more cycles and therefore

more vehicles in a given time window. In our small

example, saving 17 seconds of cycle length procures 3

additional full cycles over the metric measuring time

window.

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms

205

4.4 Additional Results

In order to further substantiate and illustrate the com-

parison between expert and algorithmically computed

settings, we synthetically report below results ob-

tained in other studies we conducted on strongly re-

lated trafﬁc problems.

4.4.1 Trafﬁc Conditions Classiﬁcation

A critical problem in trafﬁc regulation is to be able to

identify the currently ongoing type of trafﬁc episode

in order to trigger the right plan in a portfolio of pre-

computed options. This is essential in order to avoid

incorrect regulation, which means using a peak hour

plan during off peak hours or vice-versa, and the ensu-

ing consequences on waiting time and pollutant emis-

sions.

As can be seen in ﬁgure 7, our algorithm, in that

case a patented combination of optimization and ma-

chine learning, is able to produce a surprisingly com-

pact and accurate decision tree which performs better

than expert provided classiﬁcation criteria based on

ﬁeld observation and experience. Estimated gains are

indeed of 264 hours of incorrect regulation over reg-

ular work days in a year, which correspond to more

than 10% of the total regulation time. Through re-

verse engineering analysis, this result also allowed to

correct signiﬁcant misconceptions about peak hours

starting and end times.

Figure 7: Compact and accurate algorithmically produced

classiﬁcation tree for trafﬁc episode classiﬁcation.

4.4.2 Adaptive Trafﬁc Lights

Adaptive trafﬁc lights are based on modern con-

trollers that adjust their plans dynamically according

to on-line sensor feedback. This form of dynamic

regulation is very efﬁcient when allowed by available

equipment but rather difﬁcult to parametrize properly.

In a separate preliminary study, publication pending,

we proposed to genetically optimize such dynamic

controllers based on decision trees. As a preliminary

trial, we only optimized thresholds (on sensor data)

and green phases adjustment values on an otherwise

ﬁxed tree. We intend to apply Genetic Programming

on tree structure exploration in further work.

Experiments were conducted on a benchmark of

three successive intersections with a three hours sim-

ulation time line enriched with three events (simu-

lated accidents obstructing lanes for a certain dura-

tion at distinct timestamps) to assess the adaptive ca-

pacity of the dynamic controller. Comparisons, re-

ported in ﬁgure 8 were made between a static plan,

a dynamic plan whose weights and thresholds were

set manually by an expert, and the genetically en-

gineered plan. Results show that the expert tuned

plan performs only slightly better than the static, non-

adaptive plan, while the the decision tree with geneti-

cally optimized thresholds procures a very signiﬁcant

and promising gain of 34% in waiting time.

Figure 8: Results of the comparative benchmark for dy-

namical control: algorithmically optimized decision trees

largely outperform expert provided trees. The x-axis shows

simulation time steps, the y-axis total accumulated waiting

time. The blue and green curve (top) show the static and

expert plans respectively and the red curve (bottom) shows

the results of the genetically optimized tree.

5 EXPERTS VERSUS

ALGORITHMS

This section details the benchmarking experiment we

conducted to compare the efﬁciency of trafﬁc light

setting efforts as they are usually performed by ex-

perts to those automatically obtained with our algo-

rithm. We introduce the actual experts who com-

mendably accepted to do this with us, outline their

methodology and report comparative results on two

test zones.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

206

5.1 Meet the Experts

This work was conducted with three experts from CD-

VIA, a French trafﬁc engineering ofﬁce specialized in

mobility, trafﬁc analysis and optimization, measure-

ment and modeling. Created in 1984 by Christian Is-

berie, M. Eng., it now employs a total of 35 engineers

with several ofﬁces across the country. CDVIA works

with town councils, cities, local communities or in-

frastructure managers to help them analyze, predict

and design in all mobility related matters. CDVIA is

particularly specialized in trafﬁc ﬂow modeling and

regulation based on macro, micro or mesoscopic sim-

ulation. In constant search of innovative tools and

approaches, CDVIA uses both cutting-edge technol-

ogy and ﬁeld-honed expertise to tackle large scale

study cases such as the airport platform for Charles

de Gaulle in Paris or the Conakry peninsula project

for the Guinean ministry of transportation.

Christian Isb

erie, M. Eng., CDVIA founder and

trafﬁc regulation expert has 35 years of experience in

mobility engineering. After founding the company

as a local, individual consulting business, he gradu-

ally modernized it and steered its growth into a full

ﬂedged engineering company with contracts all over

the country. Besides management duties, he provides

trafﬁc-related expertise and encourages innovation as

well as the adoption of modern technologies particu-

larly in data collection and trafﬁc simulation.

Benoit Berthelot, M. Eng., project manager, has

10 years of experience in mobility and trafﬁc regula-

tion related studies and has command over all aspects

of CDVIA’s business areas : ﬁeld based trafﬁc mea-

surement, mobility modeling tools and urban trafﬁc

simulation.

Aur

elien Varest, M. Eng., senior consultant, has

5 years of experience. He graduated with and M. Eng.

from the National School of Geographical Science

Engineers and obtained an additional M. Sc. in Ur-

ban Planning and Information Sciences from the City

of Paris Engineering School. Specialized in trafﬁc en-

gineering and GIS based trafﬁc simulation, he is also

contributing to internal research and development ef-

forts. He has conducted over 70 mobility studies for

CDVIA so far.

5.2 Formalized Expert Methodology

The experts shared their methodology for optimizing

trafﬁc lights in a medium sized urban area with us. It

was formalized through an extensive, procedure ori-

ented discussion to produce this unique set of explicit

steps that is most likely largely followed, more or less

consciously, by numerous other experts. This knowl-

edge is widely transverse but it is usually guarded

or encapsulated by personal ﬁeld-based expertise or

intuition and oral tradition, leading to pitfalls such

as subjectivity, variability or wishful thinking. The

coarse grained methodology is as follows. Intricate

details, speciﬁc principles or tools cannot be shared

for obvious industrial secrecy reasons.

5.2.1 Preamble

We suppose that three aspects of the problem are

kept constant: the infrastructure cannot be modiﬁed

to achieve better trafﬁc (e.g. by adding a lane), the

type of ongoing trafﬁc is considered unique and ﬁxed

(e.g. morning peak hours) and trafﬁc light plans are

considered static (no on-line adaptation in relation to

sensors) and ﬁxed in structure, which means that no

changes are allowed besides green phase durations

and relative temporal offsets (phases cannot be added

or removed or see their order changed for example).

The methodology proceeds in four major steps,

usually in the following order, although all steps are

not systematically used and loops can be necessary

: 1) Global Static Analysis, 2) Cycle Length Opti-

mization, 3) Green Split Optimization, 4) Temporal

Offsets and Junction Coordination.

5.2.2 Global Static Analysis

A global analysis is conducted for each individual

ﬂow controlled by a trafﬁc light by comparing theo-

retical demand (vehicle ﬂows pondered by the kind of

movement (straight, turn left, etc.)) and ﬂow capac-

ity, which is a product of current corresponding green

time and number of implicated lanes. The resulting

vector provides a coarse grain analysis of which ﬂows

are in need of more green time and those who have

too much. This step can also be used to provide a ﬁrst

heuristic trafﬁc light plan based on making, at each

intersection, green splits proportional to relative de-

mands for each ﬂow.

5.2.3 Cycle Length Optimization

If the considered junction is under capacity, shorten-

ing the cycle will help reduce queues and will increase

ﬂuidity. On the contrary, saturated junctions can ben-

eﬁt from longer cycle durations to prevent transmis-

sion of part of the queue from one cycle to the next.

When modifying cycle length, care must be taken

to keep green splits unmodiﬁed. In dense urban ar-

eas, shorter cycles are preferred, notably to facilitate

pedestrian trafﬁc.

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms

207

5.2.4 Green Split Optimization

To adjust green split within an intersection, one usu-

ally goes through the following steps:

1. Check all lanes and order them by degree of con-

gestion (queue length, number of unprocessed ve-

hicles in one cycle, etc.)

2. Relate ordered lanes to existing green phases in

the current plan

3. Identify phase couples with one “rich phase” (un-

der capacity) phase and one “poor” phase (satu-

rated) to move green time from the former to the

latter without affecting cycle length.

4. Repeat previous step until no signiﬁcant couple

can be found

5.2.5 Temporal Offsets and Junction

Coordination

To coordinate junctions with each other, the follow-

ing principles are useful : cycle lengths should be ho-

mogenized, try to ensure that upstream junctions will

not deliver more ﬂow than downstream ones can han-

dle, do not hesitate to limit output ﬂow if necessary to

preserve global ﬂuidity even at the cost of a little local

congestion. Finally, try to create green waves by :

1. Identifying major axes

2. Identifying main direction of trafﬁc for the current

conditions (can be opposite between morning and

evening peak hours)

3. Compute corresponding temporal offsets by ob-

serving actual run times between junctions with

the considered conditions (use simulation or sen-

sor data) as opposed to theoretically calculated

run times.

5.3 Experimental Setup and Results

The experts followed the methodology outlined above

to try to increase trafﬁc ﬂuidity metrics (a combina-

tion of waiting time and total number of processed

vehicles) as given by our simulator. They also used

visual analysis and iterative trial and error to achieve

the best possible result.

5.3.1 First Area

The ﬁrst optimization session focused on a small trial

zone made of two signalized intersections of medium

complexity. It lasted for two hours and the experts

produced a ﬁnal gain of 13.68%.

Figure 9 gives, as an illustration of the tedious,

iterative character of the methodology, the last trial

and error steps followed by the experts to get to the

best possible setting they could reach.

Figure 9: Sample of steps followed by experts on the small

test case. The two junctions are named N (North) and S

(South) respectively. Nk means phase number k of junction

In contrast, and as can be seen in ﬁgure 10 be-

low, the algorithm managed to reach much better so-

lutions, achieving a ﬁnal gain of 23.9%. That level

of gain is reached in 37 minutes on a regular laptop

computer without parallel computing and the cross-

ing point with experts in terms of gain amplitude (

percent) is reached after 2 minutes only.

Figure 10: Gains obtained by the experts and the algorithm

respectively, on the small test zone.

5.3.2 Second Area

In order to assess whether this result extended to

cases of operational size and complexity, we orga-

nized a second session with a full-ﬂedged zone ex-

tracted from a real world benchmark with 12 signal-

ized intersections in the immediate northern outskirts

of Paris. As can be seen in ﬁgure 11, it has one major

north/south axis and two intersecting highways.

Experts tried very hard to manually optimize traf-

ﬁc on this zone under the arbitrage of the simulator.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

208

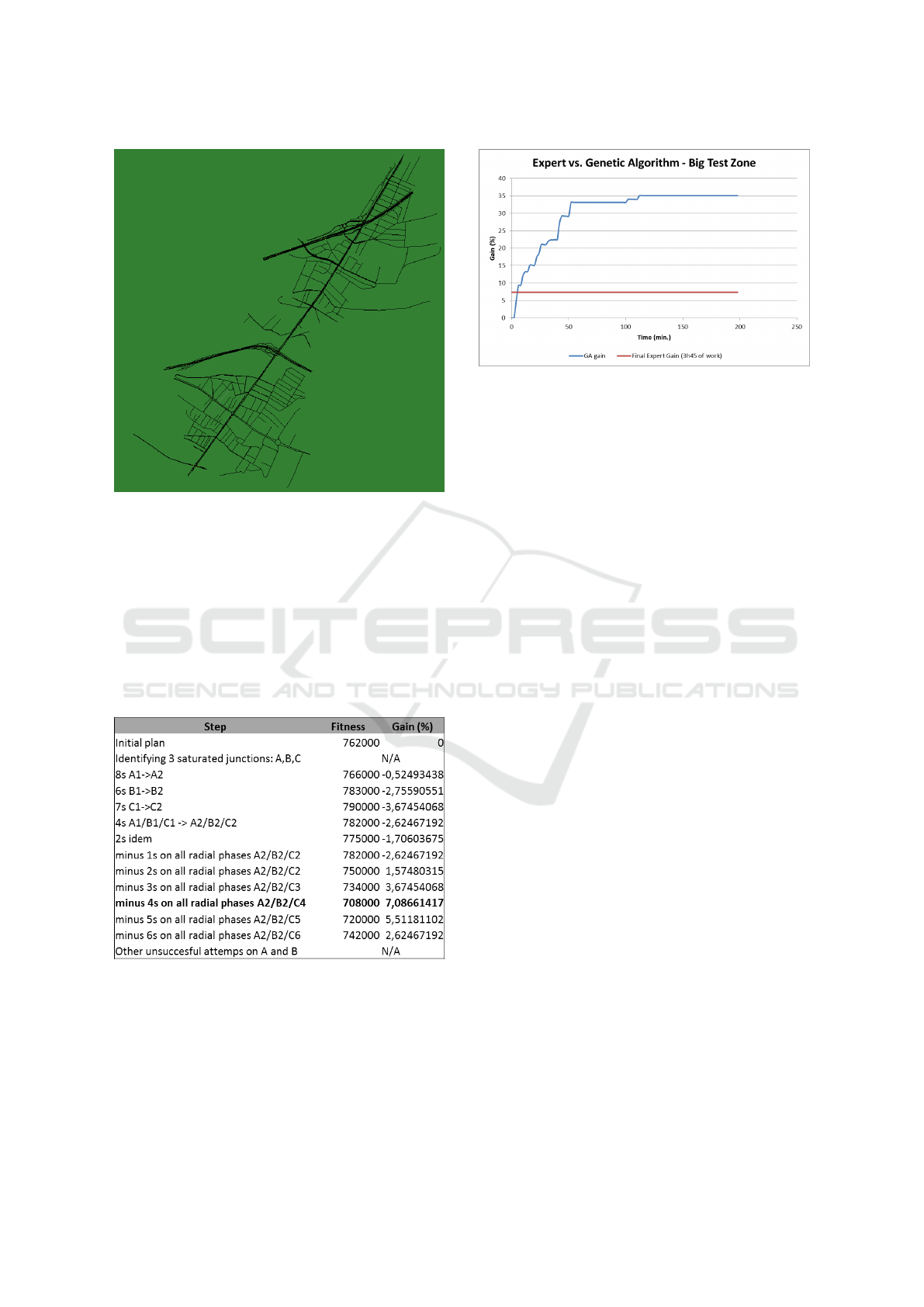
Figure 11: Second testing area: a large portion of a dense

urban area situated along a major trafﬁc north/south axis

with 12 signalized intersections and crossed by two high-

ways.

The experiment lasted for 3 hours and 45 minutes and

while the task proved very hard, the experts managed

to achieve 7.08% gain.

Part of the analysis and of the numerous attempts

they made is traced if ﬁgure 12 for illustrative pur-

poses, notably to underline how rigged and counter-

intuitive the search space of this problem can be.

Figure 12: Sample of the steps followed by experts to try to

optimize the large test zone.

Again in striking contrast (see ﬁgure 13), the ge-

netic algorithm reached a ﬁnal gain of 35.06 % in

around 1h42. The crossing point with manual expert

gain was reached in under 6 minutes.

Figure 13: Gains obtained by the experts and the algorithm

respectively, on the large test zone.

6 CONCLUSIONS

We introduced an algorithmic system based on evolu-

tionary algorithms and calibrated microscopic simula-

tion to optimize trafﬁc light green phase durations and

relative temporal offsets in order to reduce trafﬁc jams

and pollutant emissions simultaneously. Our experi-

mental results are threefold. First, we report success

of the calibration module to reach statistically realis-

tic vehicle counts with respect to historical data. Sec-

ondly, we conﬁrm the ability of the introduced sys-

tem to consistently produce signiﬁcant optimization

gains on real-world benchmarks with respect to expert

provided solutions. Finally, and most importantly, se

report the results of a competitive comparison work-

shop between trafﬁc engineering experts and our algo-

rithm. The results indicate that the evolutionary algo-

rithm performs substantially better in both speed and

ﬁnal solution quality.

While the results reported here suggest that AI

based optimization modules perform signiﬁcantly

better than experts at these particular tasks, we ﬁrmly

believe that there is much to gain from hybridizing

expert knowledge with stochastic search algorithms.

The former indeed have both precious insights and

heuristics as well as an uncapturable ability to think

globally. The latter, conversely, are uncannily apt at

quickly ﬁguring out the right numerical decisions. We

sincerely think the future belongs to those who will

know how to use both in synergy.

ACKNOWLEDGEMENTS

The authors would like to thank the LaSDIM project

and BPIFrance for funding part of this work under the

20th FUI call. The authors would also like to thank

Expert Competitive Trafﬁc Light Optimization with Evolutionary Algorithms

209

Nicolas Damay for his remarkable Master’s degree in-

ternship work.

REFERENCES

Chin, Y. K., Kow, W. Y., Khong, W. L., Tan, M. K., and

Teo, K. T. K. (2012). Q-learning trafﬁc signal opti-

mization within multiple intersections trafﬁc network.

In 2012 Sixth UKSim/AMSS European Symposium on

Computer Modeling and Simulation, pages 343–348.

Chu, L., Liu, H. X., Oh, J.-S., and Recker, W. (2003).

A calibration procedure for microscopic trafﬁc sim-

ulation. In Proceedings of the 2003 IEEE Interna-

tional Conference on Intelligent Transportation Sys-

tems, volume 2, pages 1574–1579 vol.2.

Damay, N. (2015). Multiple-objective optimization of traf-

ﬁc lightsusing a genetic algorithm and a microscopic

trafﬁc simulator. Master’s thesis, KTH, School of

Computer Science and Communication (CSC).

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

Nsga-ii. IEEE Transactions on Evolutionary Compu-

tation, 6(2):182–197.

Eiben, A. and Smith, J. (2003). Introduction to Evo-

lutionary Computation. Natural Computing Series.

Springer.

Fakult

at, S. R. A. L. U. F. (2006). Learning road trafﬁc

control : Towards practical trafﬁc control using policy

gradients diplomarbeit.

Flotterod, G., Bierlaire, M., and Nagel, K. (2011). Bayesian

demand calibration for dynamic trafﬁc simulations.

Transportation Science, 45(4):541–561.

Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A., Parizeau,

M., and Gagn

e, C. (2012). DEAP: Evolutionary algo-

rithms made easy. Journal of Machine Learning Re-

search, 13:2171–2175.

Foy, M. D., F., B. R., and Goldberg, D. E. Signal timing

determination using genetic algorithms.

Garc

ıa-Nieto, J., Alba, E., and Olivera, A. C. (2011).

Enhancing the urban road trafﬁc with swarm intel-

ligence: A case study of c

ordoba city downtown.

In 2011 11th International Conference on Intelligent

Systems Design and Applications, pages 368–373.

Garc

ıa-Nieto, J., Olivera, A. C., and Alba, E. (2013). Opti-

mal cycle program of trafﬁc lights with particle swarm

optimization. IEEE Transactions on Evolutionary

Computation, 17(6):823–839.

Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-

timization, and Machine Learning. Addison-Wesley,

New York.

Hu, W., Wang, H., Liping, Y., and Du, B. (2015). A swarm

intelligent method for trafﬁc light scheduling: appli-

cation to real urban trafﬁc networks. Applied Intelli-

gence, 44.

Jin, J. and Ma, X. (2014). Implementation and optimiza-

tion of group-based signal control in trafﬁc simula-

tion. pages 2517–2522.

Jin, J., Ma, X., and Kosonen, I. (2017). A stochastic op-

timization framework for road trafﬁc controls based

on evolutionary algorithms and trafﬁc simulation. Ad-

vances in Engineering Software, 114.

Krajzewicz, D., Erdmann, J., Behrisch, M., and Bieker-

Walz, L. (2012). Recent development and applications

of sumo - simulation of urban mobility. International

Journal On Advances in Systems and Measurements,

3 and 4.

Marceau Caron, G. (2014). Optimization and uncertainty

handling in air trafﬁc management. PhD thesis. Th

ese

de doctorat dirig

ee par Schoenauer, Marc et Sav

eant,

Pierre Informatique Paris 11 2014.

Marsetic, R., Semrov, D., and Zura, M. (2014). Road artery

trafﬁc light optimization with use of the reinforcement

learning. PROMET - Trafﬁc and Transportation, 26.

Paz, A., Molano, V., and Sanchez-Medina, J. (2015). Holis-

tic Calibration of Microscopic Trafﬁc Flow Models:

Methodology and Real World Application Studies,

pages 33–52.

eres, M., Ruiz, G., Nesmachnow, S., and Olivera, A. C.

(2018). Multiobjective evolutionary optimization of

trafﬁc ﬂow and pollution in montevideo, uruguay. Ap-

plied Soft Computing, 70:472 – 485.

Rouphail, N., Park, B., and Sacks, J. (2000). Direct sig-

nal timing optimization: Strategy development and re-

sults. pages 195 – 206.

Salkham, A., Cunningham, R., Garg, A., and Cahill, V.

(2008). A collaborative reinforcement learning ap-

proach to urban trafﬁc control optimization. In 2008

IEEE/WIC/ACM International Conference on Web In-

telligence and Intelligent Agent Technology, volume 2,

pages 560–566.

Sanchez-Medina, J., J. Gal

an Moreno, M., and Rubio, E.

(2008). Evolutionary Computation Applied to Urban

Trafﬁc Optimization.

Semet, Y. and Schoenauer, M. (2006). On the Beneﬁts of

Inoculation, an Example in Train Scheduling. In et al.,

M. C., editor, GECCO-2006, pages 1761–1768, Seat-

tle, United States. ACM Press.

Stevanovic, J., Stevanovic, A., Martin, P. T., and Bauer, T.

(2008). Stochastic optimization of trafﬁc control and

transit priority settings in vissim. Transportation Re-

search Part C: Emerging Technologies, 16(3):332 –

349. Emerging Commercial Technologies.

Toledo, T. and Kolechkina, T. (2013). Estimation of dy-

namic origin–destination matrices using linear assign-

ment matrix approximations. Intelligent Transporta-

tion Systems, IEEE Transactions on, 14:618–626.

Zhang, Q. and Li, H. (2007). Moea/d: A multiob-

jective evolutionary algorithm based on decomposi-

tion. IEEE Transactions on Evolutionary Computa-

tion, 11(6):712–731.

Zitzler, E. and K

unzli, S. (2004). Indicator-based selection

in multiobjective search. In PPSN.

Zitzler, E., Laumanns, M., and Thiele, L. (2001). Spea2:

Improving the strength pareto evolutionary algorithm.

Technical report.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

210