On Improved Verification of Reconfigurable Real-Time Systems
Yousra Hafidi
1,2,3,4
, Laid Kahloul
3
, Mohamed Khalgui
1,2
and Mohamed Ramdani
1,2,3,4
1
LISI Laboratory, National Institute of Applied Sciences and Technology, University of Carthage, Tunis 1080, Tunisia
2
School of Electrical and Information Engineering, Jinan University, China
3
LINFI Laboratory, Computer Science Department, Biskra University, Algeria
4
University of Tunis El Manar, Tunis, Tunisia
Keywords:
Real-time System, Reconfiguration, Formal verification, Model-checking, CTL.
Abstract:
This paper deals with formal modeling and verification of reconfigurable real-time systems under reconfigura-
bility and real-time constraints. To deal with the modeling, we enrich the formalism, named reconfigurable
timed net condition event systems (R-TNCESs), with new reconfiguration forms such as the ability to update
the earliest/latest firing time on the intervals which are associated to flow arcs. To handle the verification of the
new extended formalism, an algorithm is defined to generate a timed accessibility graph for timed net condition
event systems (TNCESs). We control the verification complexity of R-TNCESs using a new method which
accelerate the generation of accessibility graphs, where redundancies, repetitions, and unnecessary compu-
tations are avoided as much as possible. An experimentation is carried out and a performance evaluation is
achieved to demonstrate the advantages of the proposed contribution compared with related works.
1 INTRODUCTION
Several critical systems such as medical, aerospace
and manufacturing systems are facing challenges like
dealing with the technology process updating, fault-
tolerance, response in time, flexibility, modularity,
etc. Systems had to comprise new abilities in order
to efficiently answer today’s requirements. Actually,
any problem that a critical system may face during
its execution can cause serious consequences. Most
problems of critical systems are due to a faulty and
an unreliable design. To deal with those problems,
many academic researchers as well as industrial com-
panies tackle systems reliability by formal verifica-
tion (Ramdani et al., 2018).
Formal verification methods exploit techniques
based on mathematical and logical proofs to check
whether a system meets the requirements of its initial
specification. Indeed, system requirements are usu-
ally specified in a temporal logic like computational
tree logic (CTL), and/or its extensions: extended CTL
(eCTL), timed CTL (TCTL), etc. The system de-
sign is carried out using one of the existing formal
languages such as Petri Nets and their extensions.
Many system properties including safety, deadlock-
freedome and liveness that are specified by a tempo-
ral logic can be verified using model-checking (Baier
et al., 2008). Model-checking is the process that takes
as inputs a model (typically a state/transition system)
and a property (typically written in a temporal logic),
then proves that the system satisfies the given prop-
erty or provides a counterexample of the execution
that falsifies it.
Reconfigurability is the ability of systems to trans-
form their selves and their working process in or-
der to adapt to a changed inner/outer environment,
respond to user requirements, prevent malfunctions
when hardware failures occur during the process,
etc. Reconfigurable real-time systems are systems
that encompass reconfigurability constraints (Lyke
et al., 2015) and they subject to real-time require-
ments (Lakhdhar et al., 2018).
By the inclusion of some new skills, reconfig-
urable real-time systems become more complex, i.e.,
their design includes more details, and their verifica-
tion becomes more expensive in terms of computa-
tion time and memory. Researchers have tried to deal
with the formal modeling and verification of discrete
event systems using Petri nets and their extensions.
(Badouel and Oliver, 1998) proposed reconfigurable
Petri nets which are considered as high level Petri nets
with special abilities of self reconfiguration. (Bier-
mann and Modica, 2008) proposed reconfigurable ob-
ject Petri nets (RONs) that are used to design recon-
394
Hafidi, Y., Kahloul, L., Khalgui, M. and Ramdani, M.
On Improved Verification of Reconfigurable Real-Time Systems.
DOI: 10.5220/0007736603940401
In Proceedings of the 14th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2019), pages 394-401
ISBN: 978-989-758-375-9
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

figurable manufacturing systems. RONs formalism
has two types of places (1) net places that contain or-
dinary Petri nets as tokens, and (2) rule places that
contain rules as tokens. Also, two types of transi-
tions (1) firing transitions that model the simple fir-
ing of Petri nets, and (2) transform transitions that
model the reconfiguration of the system. (Rausch and
Hanisch, 1995) proposed net condition/event systems
(NCESs) formalism which is a modular Petri nets
extension enriched with event/condition signals that
models interactions among system modules. NCESs
are developed through the last years to timed net
condition/event systems (TNCESs) (Hanisch et al.,
1997) involving time constraints on arcs. (Zhang
et al., 2017) proposed reconfigurable timed net condi-
tion/event systems (R-TNCESs) which is an enriched
extension of Petri nets formalism that supports recon-
figuration constraints. In R-TNCESs formalism, the
system is represented by a couple Sys(B
sys
, R
sys
) such
that (1) B
sys
is a set of TNCESs that represent the be-
havior module, and (2) R
sys
is a set of reconfigura-
tion rules that represent the control module. All of
those research works are important because they are
building convenient formal models. However, these
models face important problems when they are used
to verify complex reconfigurable real-time systems.
The formal verification of reconfigurable real-time
systems is a hard computationally problem that re-
quires so much time and memory, and it is identified
as a very expensive task. Consequently, proposing
a new methodology for ensuring the safety of these
systems as well as controlling the complexity of their
verification is an important research area. In this pa-
per, we model reconfigurable real-time systems using
R-TNCESs formalism. In fact, R-TNCESs formal-
ism is like the well-known formalism timed net con-
dition/event systems (TNCESs) (Hanisch et al., 1997)
such that R-TNCESs formalism does not change the
semantic of TNCESs but it just gives functional struc-
ture and a pattern for reconfigurable systems in terms
of (B
sys
, R
sys
). R-TNCES is a suitable model because
it provides modularity, time and reconfiguration abil-
ities. However, many computations and redundan-
cies can be encountered during R-TNCESs verifica-
tion process. To deal with the complexity problem,
we propose a method that benefits from the similari-
ties between the system’s configurations to avoid un-
necessary and repetitive calculations. Indeed the pa-
per proposes a method that generates an accessibil-
ity graph from another one according to the system’s
reconfiguration. Given an R-TNCES Sys(B
sys
, R
sys
),
where (1) B
sys
=
{
C
1
, C
2
}
is the set of system con-
figurations, (2) R
sys
=
{
rule
C
1
C
2
}
is the set of pos-
sible reconfiguration rules such that rule
C
1
C
2
trans-
forms the configuration C
1
to C
2
, and (3) tAG(C
0
) is
the timed accessibility graph of the configuration C
0
.
The proposed method, in this paper, shows how to
generate tAG(C
2
) from tAG(C
1
) according to rule
C
1
C
2
, (i.e., rather than computing the whole accessibil-
ity graph tAG(C
2
) from zero, the new method ap-
plies the corresponding graph modifications such as
adding/removing a state/arc in tAG(C
1
) in order to ob-
tain tAG(C
2
)).
(Hafidi et al., 2018) propose a methodology that
improves the modeling and the verification of re-
configurable discrete event control systems using R-
TNCESs formalism. The authors main contribution
is efficient for the verification of functional proper-
ties in R-TNCESs. However, the suggested methodol-
ogy cannot be used for systems under reconfigurabil-
ity and real-time constraints. The main difference be-
tween the paper’s methodology and the one presented
in (Hafidi et al., 2018) is that it shows how to gener-
ate an accessibility graph from another one when a re-
configuration on real-time constraints occurs which is
not considered in other works. The paper’s contribu-
tion will complete the work presented in (Hafidi et al.,
2018). Therefore, we assume that functional proper-
ties are already verified in the system, we focus on
real-time properties, reconfiguration properties, their
modeling in R-TNCES formalism and their efficient
verification.
The main contributions of this paper are summa-
rized as:
• The enrichment of R-TNCESs with new real-time
reconfiguration forms such that modifying the ear-
liest/latest firing times on the timed arcs are in-
cluded, i.e., new structure modification instruction
for the new reconfiguration forms;
• The proposition of new rewriting rules that gen-
erate a new graph from a given one, according to
the reconfiguration on time applied by the system,
i.e., this is used to control the complexity of the
verification task.
The originality of this research work can be founded
from two general parts, i.e., the formal modeling and
the improved verification of reconfigurable real-time
systems using R-TNCESs. To the best of our knowl-
edge, this is the first study that deals with the enrich-
ment of R-TNCESs modeling by the new reconfigu-
ration form of real-time systems, i.e., the modification
of time constraints on timed arcs. In addition, no pre-
vious research works have tackled with the complex-
ity control and optimization of the verification task.
The performance evaluation proves that the complex-
ity of the verification task increases exponentially if
it is not controlled such as in the blind method which
constructs the whole accessibility graph of the system
On Improved Verification of Reconfigurable Real-Time Systems
395

after each reconfiguration step. However, by using
the proposed method in this paper, significant gains
in computation time are achieved for the same verifi-
cation result as in the classical algorithm. The exper-
imentation and the performance evaluation results are
compared using the model checker SESA (Patil et al.,
2015) which analyses TNCESs models and computes
their accessibility graphs.
The remainder of the paper is organized as fol-
lows. Section 2 outlines the definition of R-TNCES
formalism and explains its enrichment with the new
time reconfiguration forms. Section 3 defines the pro-
posed method for improving the verification of real-
time and reconfiguration properties in R-TNCESs.
Section 4 shows the performance of the proposed
method on a case study. Section 5 concludes the pa-
per with the limitations of the current work and the
perspectives for future works.
2 PRELIMINARIES:
RECONFIGURABLE TIMED
NET CONDITION/EVENT
SYSTEMS (R-TNCESs)
Reconfigurable timed net condition/event systems
(R-TNCESs) are an extension of Petri nets (Zhang
et al., 2017), used for formal specification of recon-
figurable discrete event control systems (RDECSs).
An RDECS may encompass a set of configurations,
where each one is modeled by a TNCES. A TNCES
is a set of modules graphically represented as depicted
in Fig. 2. To model an RDECS, we use the concept
of control components (CCs) introduced in (Khalgui
et al., 2011), i.e., the interconnected modules com-
municating with signals that compose each TNCES
are called control components (CCs). The syntax and
semantics of the previous structures are explained in
this subsection.
2.1 Syntax
R-TNCESs are formally defined in as a couple
RT N = (B, R) where B (respectively, R) is the behav-
ior (respectively, the control) module of a reconfig-
urable discrete event control system (RDECS). B is a
union of multi-TNCESs represented by
B = (P, T, F, W, CN, EN, DC, V, Z
0
)
where, (1) P (respectively, T ) is a finite
set of places (respectively,transitions), (2)
F ⊆ (P × T ) ∪ (T × P) is a superset of flow
arcs, (3) W : (P × T ) ∪ (T × P) −→
{
0, 1
}
maps a
weight to a flow arc, (4) W (x, y) > 0 if (x, y) ∈ F,
and W (x, y) = 0 otherwise, where x, y ∈ P ∪ T ,
(5) CN ⊆ (P × T ) (respectively, EN ⊆ (T × T ))
is a superset of condition signals (respectively,
event signals), (6) DC : F ∩ (P × T ) → {[l
1
, h
1
], . . . ,
[l
|F∩(P×T)|
, h
|F∩(P×T)|
]} is a superset of time
constraints on transition’s input flow arcs, where
∀i ∈ [1, | F ∩(P × T ) |], l
i
, h
i
∈ N and l
i
< h
i
,
(7) V : T −→
{
∨, ∧
}
maps an event-processing
mode (AND or OR) for every transition, and (8)
Z
0
= (M
0
, D
0
), where M
0
: P −→
{
0, 1
}
is the initial
marking, and D
0
: P −→
{
0
}
is the initial clock
position.
R is a set of reconfiguration rules such that rule r
is a structure represented by
r = (Cond, s, x)
where, (1) Cond →
{
True, False
}
is the pre-
condition of r, i.e., r is executable only if Cond =
True, (2) s : T N(
•
r) → T N(r
•
) is the structure-
modification instruction such that T N(
•
r) (respec-
tively, T N(r
•
)) represents the structure before (re-
spectively, after) applying the reconfiguration r, and
(3) x : last
state
(
•
r) → initial
state
(r
•
) is the state pro-
cessing function.
In this paper, we denote by r
i j
the reconfiguration
rule that transforms T NCES
i
to T NCES
j
.
As reported in (Zhang et al., 2017), the ba-
sic possible structure-modification instructions for R-
TNCESs are summarized by adding/removing signals
(i.e., condition signals or event signals) between or
among modules. However, other possible reconfigu-
ration forms should be considered in this paper to ex-
press the transformation of time constraints. There-
fore, we present in Table. 1 A new time structure-
modification instructions for R-TNCESs. We denote
by p a place, t a transition, e f t the earliest firing time,
l f t the latest firing time, N
+
=
{
1, 2, ...
}
the set of
positive natural numbers, and N = N
+
∪
{
0
}
the set
of all natural numbers.
Table 1: Time structure-modification instructions.
Instruction Symbol
Modify the earliest
or/and the latest
mtime((p, t), [e f t, l f t])
firing time value in
the time interval
of the flow arc (p, t).
e f t ∈ N
+
∧ l f t, ω ∈
N ∧ e f t < l f t < ω
mtime: symbol of the instruction that modifies
time constraints.
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
396

2.2 Semantics
An R-TNCES RT N(B
RT N
, R
RT N
) behavior is de-
scribed by the dynamism of tokens inside of each
T NCES ∈ B
RT N
, and the transformations applied by
each reconfiguration rule rule ∈ R
RT N
. There exist
two types of transitions in TNCESs formalism: (1)
forced transitions have at least an incoming signal arc
(2) spontaneous transitions have no incoming signal
arcs. Enabled forcing transitions with input flow arcs
associated by time interval [e f t, l f t] should fire af-
ter a duration d since it became enabled such that
e f t ≤ d ≤ l f t.
A reconfiguration rule rule(cond, s, x) has the pri-
ority to be applied first when its condition is veri-
fied, i.e., cond = True. In this case, the enability
of transitions falls down and only the reconfiguration
rule is applied. A reconfiguration rule r
st
transforms
a TNCES source T NS
s
to a TNCES target T NS
t
.
last
state
(
•
r
st
) denotes the last state where the simula-
tion among T NS
s
ends (i.e., the dynamism of tokens),
it also denotes the source state where the reconfigura-
tion rule is applied. initial
state
(r
•
st
) denotes the initial
state where the simulation among T NS
t
starts, it also
denotes the target state after applying the reconfigura-
tion rule.
3 VERIFICATION OF TIME
CONSTRAINTS IN
RECONFIGURABLE SYSTEMS
USING TAG
This section deals with the checking whether the
modeled system (R-TNCES) meets the temporal re-
quirements. In this task, we specify system proper-
ties using TCTL, we compute the accessibility graphs,
and we use model-checking to check whether tempo-
ral properties are satisfied or not. Classical accessi-
bility graphs (AGs) are extended to timed accessibil-
ity graphs (TAGs) and a new method is proposed to
optimize the calculation of these last ones.
3.1 Timed Accessibility Graph
Timed accessibility graph (TAG) of a TNCES TNS is
a structure tAG given by
tAG(St, Ed, s
0
)
where, (1) St denotes the set of reachable states, (2)
Ed : St → St denotes the set of edges that defines
state-transitions such that each edge is labeled by the
executed step, and (3) s
0
denotes the initial state.
A state s ∈ St is a structure given by
State(Mp, Pclocks, D)
where, (1) M p is the set of marked places in T NS,
(2) Pclocks is a vector of integers representing places
clock positions, and (3) D is the delay of the state
which denotes the minimal number of time units after
which at least one step becomes enabled.
3.2 TAG Generation from a Graph
(Contribution)
Given two TNCESs T NCES
1
and T NCES
2
such
that T NCES
2
is obtained from T NCES
1
by ap-
plying a time modification instruction. Classi-
cally, tAG(T NCES
1
) (respectively, tAG(T NCES
2
))
the timed accessibility graph of T NCES
1
(respec-
tively, T NCES
2
) is computed using the classical algo-
rithm explained in (Murata, 1989), where the whole
accessibility graph of each structure is computed
from zero (Fig. 1(a)). Actually, tAG(TNCES
1
) and
tAG(T NCES
2
) share some similar parts (sub-graphs)
that should not be recomputed again while generat-
ing tAG(T NCES
2
). Consequently, the complexity of
the accessibility graphs generation can be optimized
if these repetitive computations are avoided. In this
paper as depicted in Fig. 1(b), we propose an im-
proved graph-generation method iGG that computes
tAG(T NCES
2
) from the graph tAG(TNCES
1
) rather
than computing tAG(T NCES
2
) from the model. The
proposed iGG method then, considers the already
computed parts and does not recalculate them.
TNCES
1
TNCES
2
tAG(TNCES
1
) tAG(TNCES
2
)
TAG Generation
from the model
Reconfiguration
TAG Generation
from the model
(a) TAG generation from
model..
TNCES
1
TNCES
2
tAG(TNCES
1
) tAG(TNCES
1
)
TAG Generation
from the model
Reconfiguration
TAG Generation
from the graph
iGG
(b) TAG generation from
graph.
Figure 1: TAG generation from graph.
3.3 The Improved Graph-generation
Method iGG (Contribution)
In order to verify system properties in an R-TNCES
model RTN(B, R), the timed accessibility graph of
each TNCES T S ∈ B should be generated using the
classical method described in (Murata, 1989), i.e., the
algorithm is therefore executed | B | times. Conse-
quently, the operation requires more time and mem-
ory.
On Improved Verification of Reconfigurable Real-Time Systems
397

Table 2: Rewriting rules on TAG.
SMI Rewriting rules on TAGs Comments
mtime((p, t), [e f t, l f t])
a) ∀e ∈ Ed, t ⊂ Label(e) ::= St ← St \
{
sc(e)
}
;
a) Remove all source states of
edges
labeled by t in TAG ;
b) ∀s ∈ St ::= SimulationFrom(s).
b) Continue the simulation
from each state.
Given two TNCESs structures T NCES
a
,
T NCES
b
, where tAG
a
is the timed accessibility
graph of T NCES
a
. The TNCES T NCES
b
is obtained
from T NCES
a
after applying a transformation of
time constraints which is described by the structure
modification instruction SMI in Tables 1 and 2.
The new proposed method iGG (improved graph
generation) takes as an input tAG
a
then transforms
it into a new graph tAG
b
by adding/removing some
states/edges from tAG
a
. Therefore, the complexity
of iGG is O (1) in its best case where O(1) is the
complexity of each instruction of modification on the
graph. The complexity in the worst case is O (e
m
),
such that O(e
m
) is the complexity of accessibility
graphs computations as reported in (Murata, 1989).
The resulting graph is exactly the timed accessibility
graph of T NCES
b
except that by using iGG method,
there are less computed states, i.e., no repetitive
calculations for the similar parts.
Table 2 introduces the proposed rewriting rules on
timed accessibility graphs (TAGs) related to the new
time structure modification instructions (SMI) pro-
posed in this paper. We denote by e a TAG edge, t
a transition, Ed the set of edges in a TAG, s a state in
a TAG, St the set of states in a TAG, sc(e) the func-
tion that returns the source state of an edge e in a TAG,
and Label(e) the function that returns the label of the
edge e in a TAG. iGG method is applied in the case of
having n SMIs to get tAG
b
as follows.
Step
0
Copy tAG
a
to tAG
b
, i.e., initially, tAG
b
is
a copy of tAG
a
;
Step
1
For every structure modification instruc-
tion SMI apply the indicated rewriting
rules (Table 2) on tAG
b
;
Step
2
Delete all unreachable states in tAG
b
.
3.4 iGG
generalized
: iGG for R-TNCESs
(Contribution)
Algorithm 1 deals with the application of iGG in the
case when having n TNCESs. The proposed algo-
rithm is recursive and composed of a parallel part
that computes the TAGs of reachable TNCESs in the
same time when possible. The algorithm stops in
Algorithm 1: iGG
Generalized
.
Input: RT N(B : Set of TNCESs, R : Set of
Reconfiguration Rules): R-TNCES;
tAG
current
: TAG; p: Set of Properties;
Variables : tAG: TAG; isCorrect: Boolean;
ToVeri f y: Set of TNCESs;
1 tAG ← tAG
current
;
2 ToVeri f y ← NextCon f igs(tAG, R);
3 foreach TNCES
i
∈ ToVeri f y in parallel do
4 if newTN(T NCES
i
) /* New TNCES: if
its TAG has not been computed
yet */
5 then
6 tAG
i
← iGG(tAG, T NCES
i
);
7 isCorrect ←
veri f yPropertiesIn(tAG
i
, p);
8 if isCorrect == True then
9 iGG
Generalized
(RTN(B, R), tAG
i
,
p);
10 end
11 end
12 end
two cases: (1) if the behavior of a configuration is
not validated by the verification, or (2) if it reaches
a configuration that has been already verified be-
fore, i.e., to avoid redundant computations. In Al-
gorithm 1, we denote by: (1) NextCon f igs(tAG, R)
the function that from the TAG tAG of the cur-
rent TNCES and a set of possible reconfiguration
rules R returns the set of reachable TNCESs re-
sulted from reconfigurations (2) newTN(T NCES
i
)
the Boolean function that returns True if T NCES
i
has not been verified before, otherwise it returns
False, (3) iGG(tAG, T NCES
i
) the function that gen-
erates and returns the TAG of TNCES
i
from the TAG
tAG (already explained in previous subsections), and
(4) veri f yPropertiesIn(tAG
i
, p) the Boolean function
that returns True if the system indicated properties p
are verified on tAG
i
, otherwise it returns False.
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
398

TNCES
1
t
4
t
5
p
5
p
6
Module
1
Module
2
[1, 4]
j
t
1
t
2
[3, 4]
p
2
p
3
t
3
r
12
TNCES
2
r
12
p
1
p
7
p
8
p
9
t
7
t
8
t
9
p
4
t
6
Module
3
t
4
t
5
p
5
p
6
Module
1
Module
2
[0, 4]
j
t
1
t
2
[3, 4]
p
2
p
3
t
3
p
1
p
7
p
8
p
9
t
7
t
8
t
9
p
4
t
6
Module
3
Figure 2: RTN Graphical model.
s
1
s
2
s
4
s
3
s
11
s
10
s
12
s
5
s
8
s
9
s
7
s
6
(a) tAG(T NCES
1
).
s
1
s
2
s
4
s
3
s
11
s
10
s
12
s
5
s
6
s
13
s
15
s
14
s
16
s
17
s
18
(b) tAG(T NCES
2
).
Figure 3: RT N timed accessibility graphs.
4 EXPERIMENTATION
In this section, we experiment the proposed approach
on a running example, and we evaluate its perfor-
mance on large scale systems.
4.1 Running Example
Given an R-TNCES RT N(B
RT N
, R
RT N
) such that
B
RT N
=
{
T NCES
1
, T NCES
2
}
is the behavior mod-
ule containing all possible configurations and R
RT N
=
{
r
12
, r
21
}
is the control module containing all possi-
ble reconfigurations. The graphical model of RT N is
depicted in Fig. 2.
The reconfiguration rules in R
RT N
are described in
Table 3.
Reconfigurations run spontaneously when their
conditions are fulfilled, i.e., there are no time con-
straints on reconfiguration scenarios. Therefore, the
control module R
RT N
is not considered by the verifi-
cation of real-time properties. Contrarily, the behav-
ior module B
RT N
contains a set of TNCESs which are
timed and should be validated by checking real-time
properties. Note that in the behavior module B
RT N
,
there exist similar parts between both configurations
T NCES
1
and T NCES
2
, e.g., module
1
in T NCES
1
is similar to module
1
in T NCES
2
and module
2
in
T NCES
1
is similar to module
2
in T NCES
2
. The
repetitive calculations on those similar parts are con-
sidered as redundancies that make of the verification
a complex task.
In this subsection, we try to apply the proposed
method to verify the R-TNCES RT N(B
RT N
, R
RT N
)
efficiently by avoiding as much as possible necessary
computations. The timed accessibility graph of the
initial structure T NCES
1
is computed classically us-
ing SESA tool. The resulted graph tAG(T NCES
1
)
is depicted in Fig.3(a). To compute tAG(T NCES
2
)
from tAG(T NCES
1
) we use the improved graph-
generation method iGG as following:
Step
0
Copy tAG(T NCES
1
) to tAG(T NCES
2
);
Step
1
Apply the rewriting rules (Table 2) on
tAG
b
as in Step
11
and Step
12
;
Step
1.1
(∀e ∈ Ed
2
, t
6
⊂ Label(e) ::= St
2
← St
2
\
{
s
6
}
) ⇒ St
2
← St
2
\
{
s
6
}
. Ed
2
(respec-
tively, St
2
) represents the set of edges (re-
spectively, states) in tAG(T NCES
2
);
Step
1.2
∀s ∈ St ::=SimulationFrom(s). By the
simulation, new states are created: St
2
←
St
2
∪
{
S
6
, S
13
S
14
S
15
S
16
S
17
S
18
}
;
Step
2
Delete all unreachable states in tAG
b
:
St
2
← St
2
\
{
S
7
, S
8
S
9
S
15
}
.
After following the previous steps, tAG(T NCES
2
)
the new accessibility graph of T NCES
2
is achieved.
tAG(T NCES
2
) is depicted in Fig. 3(b) where the col-
ored states among it denote the new computed ones.
Note that the studied system RT N has 12 states
in the configuration T NCES
1
, and 15 states in the
configuration T NCES
2
where only 7 states are com-
puted using the improved graph-generation method
iGG, i.e., the other states are kept from the first
TAG tAG(TNCES
1
). Therefore, iGG has avoided the
unnecessary repetitive computations and optimized
RT N accessibility graphs generation by more than
50% calculations.
4.2 Concept of Redundancies
We define the function RRedun(TNCES
a
, T NCES
b
)
that takes two TNCESs T NCES
a
, T NCES
b
and gives
the redundancy rate between them.
RRedun(T NCES
a
, T NCES
b
) is computed as follows
RRedun(T NCES
a
, T NCES
b
) =
#similarStates
#States
where (1) #similarStates is the number of similar
states that appear in both graphs tAG(T NCES
a
) and
On Improved Verification of Reconfigurable Real-Time Systems
399

Table 3: RT N reconfiguration rules.
Rule Condition s x
r
12
True
{
mtime((p
6
, t
6
), [0, 4])
} {
(S
9
, T NCES
1
), (S
1
, T NCES
2
)
}
r
21
True
{
mtime((p
6
, t
6
), [1, 4])
} {
(S
16
, T NCES
2
), (S
1
, T NCES
1
)
}
Table 4: States marking and clocks positions.
State P
1
P
2
P
3
P
4
P
5
P
6
P
7
P
8
P
9
D
S
1
M p 1 0 0 1 0 0 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
2
M p 0 1 0 1 0 0 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
3
M p 0 0 1 1 0 0 1 0 0
2
Pclocks 0 0 0 0 0 0 0 0 0
S
4
M p 1 0 0 0 1 0 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
5
M p 0 1 0 0 0 1 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
6
M p 0 0 1 0 0 1 1 0 0
1
Pclocks 0 0 0 0 0 0 0 0 0
S
7
M p 0 0 1 1 0 0 0 1 0
0
Pclocks 0 0 1 0 0 0 0 0 0
S
8
M p 0 0 1 1 0 0 0 0 1
0
Pclocks 0 0 1 0 0 0 0 0 0
S
9
M p 0 0 1 1 0 0 1 0 0
2
Pclocks 0 0 1 0 0 0 0 0 0
S
10
M p 1 0 0 0 0 1 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
11
M p 0 1 0 0 1 0 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
12
M p 0 0 1 0 1 0 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
13
M p 0 1 0 1 0 0 0 1 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
14
M p 0 0 1 1 0 0 0 0 1
0
Pclocks 0 0 0 0 0 0 0 0 0
S
15
M p 0 1 0 1 0 0 0 0 1
0
Pclocks 0 0 0 0 0 0 0 0 0
S
16
M p 0 0 1 1 0 0 0 1 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
17
M p 0 0 1 0 0 1 1 0 0
0
Pclocks 0 0 0 0 0 0 0 0 0
S
18
M p 1 0 0 1 0 0 0 1 0
0
Pclocks 0 0 0 0 0 0 0 0 0
tAG(T NCES
b
), and (2) #States is the total number of
states in tAG(T NCES
b
).
We denote by: low redundancy rate LRR the
systems with RRedun ≤ 30%, medium redundancy
rate MRR the systems with 30% < RRedun < 80%,
and high redundancy rate HRR the systems with
RRedun ≥ 80%, e.g. in the example of the experi-
mentation part RRedun
T NCES
1
T NCES
2
=
8
15
= 53% is
the redundancy rate of RT N which denotes that RT N
is in MRR systems.
4.3 Evaluation of Performance
The proposed method has proven benefits in the ex-
perimentation of the previous running example. We
want to study its efficiency in larger systems by mea-
suring computed states where a parameter namely re-
dundancy rate is used as a factor to held the perfor-
mance evaluation in different kinds of problems.
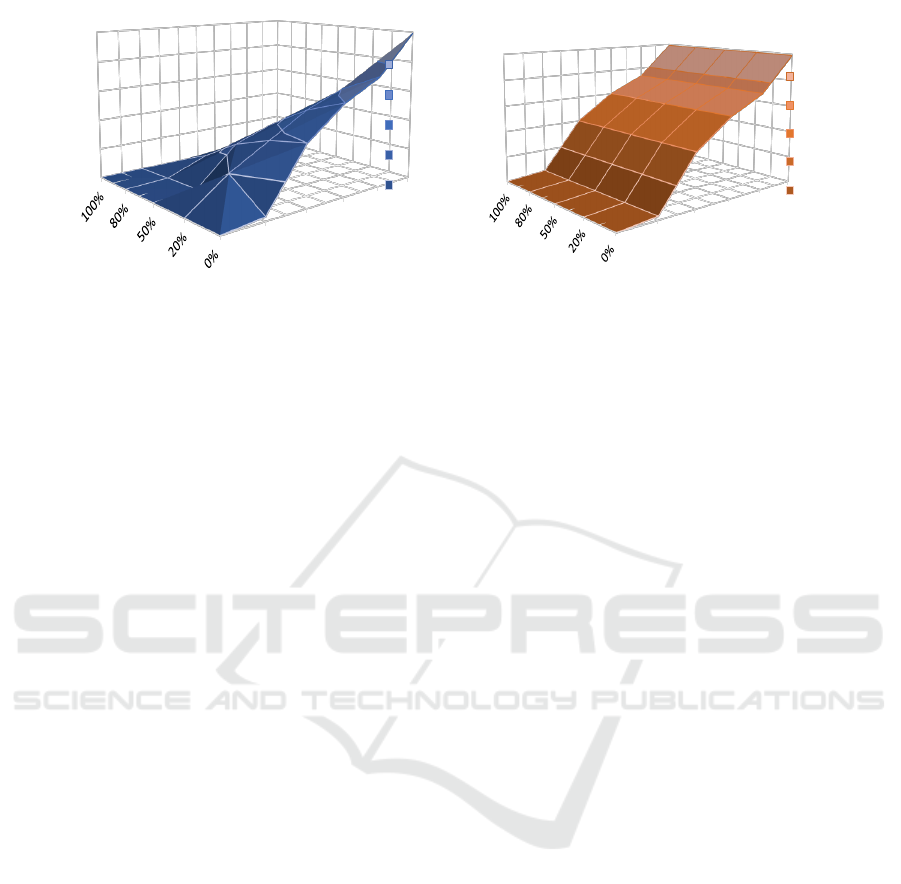
The 3D surfaces in Fig. 4 depict the number of
computed states resulted from the analyzes held on R-
TNCESs with: (1) different redundancy rates, and (2)
different numbers of nodes. The study is performed
in two cases, the former by using the proposed iGG
method while computing the TAGs, the latter using
the classical method and without any improvement.
The surfaces show that the number of computed states
using iGG reduces when the RRedun is higher, i.e., in
HRR systems. Therefore, iGG method performs best
for HRR systems verification regardless the number
of nodes. The surface presented in Fig. 4(a) matches
to the surface depicted in Fig. 4(b) when RRedun =
0. Thus, iGG method turns to classical verification
methods when the redundancy rate is very low, i.e.,
the method is in its worst case.
5 CONCLUSION
This research work deals with the formal modeling
and verification of reconfigurable real-time systems
such as reconfigurable discrete event control systems
RDECSs. The modeling is enriched with new pos-
sible reconfiguration forms: the modification of the
earliest/latest firing time in the intervals associated to
flow arcs. The proposed method iGG showed how to
generate a TAG from another one to avoid repetitive
computations when the two TAGs have some similar
parts.
According to the formal running example and
the performance evaluation results, it is shown that
the verification task of temporal properties has been
improved in terms of computing time and mem-
ory. In addition, it is proved that the proposed
method performs best for HRR systems. The pro-
posed method is less beneficial in LRR systems. Actu-
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
400

0
200
400
600
800
1000
0
35
150
250
370
500
RRedun (%)
#Computed srates
#Nodes in the system
Verification with iGG method
800-1000
600-800
400-600
200-400
0-200
(a) IGG method.
0
200
400
600
800
1000
0
35
150
250
370
500
RRedun (%)
#Computed States
#Nodes in the system
Verification without iGG method
800-1000
600-800
400-600
200-400
0-200
(b) Classical method.
Figure 4: iGG efficiency.
ally in RDECSs reconfigurations, the transformation
includes only some modules and others will still be
identical as those in the source model, which gives
a high similarity between models and makes most of
them HRR systems. Therefore, the proposed method-
ology is suitable for RDECSs improved verification.
Compared with the previous related works, this work
presents a new reconfiguration form to the R-TNCES
formalism, a method to verify real-time properties
where the correctness of the system is considered and
also the complexity of its verification is controlled.
Future works will (1) provide a formal proof of
correctness proving that information on the system’s
behavior are not lost or corrupted after applying the
proposed improvement method, (2) consider proba-
bilistic constraints in the verification task, and (3) in-
volve new techniques to reduce the system properties
and TAGs in order to improve the model-checking on
R-TNCESs, and (4) include the proposed improve-
ment method in a model-checker in order to automa-
tize it and profit from its gain. Finally the proposed
techniques will be generalized to be considered in
other formalisms like reconfigurable Petri nets (Pad-
berg and Kahloul, 2018).
REFERENCES
Badouel, E. and Oliver, J. (1998). Reconfigurable nets,
a class of high level Petri nets supporting dynamic
changes within workflow systems. PhD thesis, INRIA.
Baier, C., Katoen, J., and Larsen, K. (2008). Principles of
Model Checking. MIT Press.
Biermann, E. and Modica, T. (2008). Independence analysis
of firing and rule-based net transformations in recon-
figurable object nets. Electronic Communications of
the EASST, 10.
Hafidi, Y., Kahloul, L., Khalgui, M., Li, Z., Alnowibet, K.,
and Qu, T. (2018). On methodology for the verifica-
tion of reconfigurable timed net condition/event sys-
tems. IEEE Transactions on Systems, Man, and Cy-
bernetics: Systems, (99):1–15.
Hanisch, H.-M., Thieme, J., Luder, A., and Wienhold, O.
(1997). Modeling of PLC behavior by means of timed
net condition/event systems. In Proc. 6th Interna-
tional Conference on Emerging Technologies and Fac-
tory Automation Proceedings, pages 391–396. IEEE.
Khalgui, M., Mosbahi, O., Li, Z., and Hanisch, H. M.
(2011). Reconfigurable multiagent embedded control
systems: From modeling to implementation. IEEE
Transactions on Computers, 60(4):538–551.
Lakhdhar, W., Mzid, R., Khalgui, M., Li, Z., Frey, G., and
Al-Ahmari, A. (2018). Multiobjective optimization
approach for a portable development of reconfigurable
real-time systems: From specification to implementa-
tion. IEEE Transactions on Systems, Man, and Cyber-
netics: Systems.
Lyke, J. C., Christodoulou, C. G., Vera, G. A., and Edwards,
A. H. (2015). An introduction to reconfigurable sys-
tems. Proceedings of the IEEE, 103(3):291–317.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Padberg, J. and Kahloul, L. (2018). Overview of reconfig-
urable petri nets. In Graph Transformation, Specifica-
tions, and Nets, pages 201–222. Springer.
Patil, S., Vyatkin, V., and Pang, C. (2015).
Counterexample-guided simulation framework
for formal verification of flexible automation systems.
In Proc. IEEE 13th International Conference on
Industrial Informatics (INDIN), pages 1192–1197.
Ramdani, M., Kahloul, L., and Khalgui, M. (2018). Au-
tomatic properties classification approach for guiding
the verification of complex reconfigurable systems. In
Proc. Proceedings of the 13th International Confer-
ence on Software Technologies - Volume 1: ICSOFT,,
pages 591–598. INSTICC, SciTePress.
Rausch, M. and Hanisch, H.-M. (1995). Net condition/event
systems with multiple condition outputs. In Proc.
Emerging Technologies and Factory Automation, vol-
ume 1, pages 592–600. IEEE.
Zhang, J., Frey, G., Al-Ahmari, A., Qu, T., Wu, N., and
Li, Z. (2017). Analysis and control of dynamic recon-
figuration processes of manufacturing systems. IEEE
Access.
On Improved Verification of Reconfigurable Real-Time Systems
401