A First Approach on Big Data Missing Values Imputation

Besay Montesdeoca, Juli

an Luengo

, Jes

us Maillo, Diego Garc

ıa-Gil, Salvador Garc

ıa

and Francisco Herrera

Dept. of Computer Science and Artiﬁcial Intelligence, University of Granada, Granada, E-!8071, Spain

Keywords:

Big Data, Missing Values, Imputation, k-Means, Fuzzy k-Means.

Abstract:

Albeit most techniques and algorithms assume that the data is accurate, measurements in our analogic world

are far from being perfect. Since our capabilities of storing and processing data are growing everyday, these

imperfections will accumulate, generating poorer decisions and hindering any knowledge extraction process

carried out over the raw data. One of the most disturbing imperfections is the presence of missing values.

Many inductive algorithms assume that the data is complete, thus if they face missing data they will not work

properly or the quality of the knowledge extracted will be poorer. At this point there is no sophisticated missing

values treatment implemented in any major Big Data framework. In this contribution, we present two novel

imputation methods based on clustering that achieve better results than simply removing the faulty examples

or ﬁlling-in the missing values with the mean that can be easily ported to Spark’s MLlib.

1 INTRODUCTION

We are currently surrounded by immense amounts of

data. On the Internet data is generated at an expo-

nential rate at an increasingly reduced cost thanks

to the great development of storage and network re-

sources (Ram

ırez-Gallego et al., 2018). The vol-

ume of data has exceeded the processing capabili-

ties of the systems. We have entered the era of Big

Data (John Walker, 2014), which is deﬁned as of the

presence of great volume, speed and variety in the

data, three characteristics that were introduced by D.

Laney (Laney, 2001) with the requirement of new

high-performance processing systems.

In all areas of data science, including Big Data,

quality of extra-knowledge depends to a large extent

on the quality of the data. It is demonstrated that a

low quality of the data leads to a low quality of ex-

tracted knowledge. In some cases, preprocessing of

data is used to improve data quality, resulting in an

increased performance of learning algorithms (Garc

ıa

et al., 2015). However, the preprocessing algorithms

are also affected by the problem of scalability and

they must be redesigned for use with new technolo-

gies (Gupta et al., 2016).

https://orcid.org/0000-0003-3952-3629

https://orcid.org/0000-0003-4494-7565

https://orcid.org/0000-0002-7283-312X

This challenging scenario has motivated the term

Smart Data (Triguero et al., 2018), which lies around

two important characteristics, the veracity and the

value of the data. Smart Data objective is to clean

out imperfect data and maintain valuable data (Iafrate,

2014), which can be used for smart decision making.

The presence of missing values (MVs) is one chal-

lenging kind of imperfect data, where several val-

ues of input attributes are lost due to different rea-

sons. In spite of being easily identiﬁable, MVs pose

a more severe impact in learning models, as most

of the techniques assume that the training data pro-

vided is complete (Garc

ıa-Laencina et al., 2010). Un-

til recently, practitioners opted to discard the exam-

ples containing MVs, but this praxis often leads to

severe bias in the inference process (Little and Ru-

bin, 2014). Several techniques have been developed

to cope with MVs without discarding examples, but

they were originally devised for standard Data Min-

ing frameworks (Luengo et al., 2012). In the Big Data

framework, the attention has been recently drawn to

cope with this problem, either by taking advantage

of the iterative capabilities of Spark by using a re-

peated approximated clustering algorithm to impute

MVs (Kaliamoorthy and Bhanu, 2018) or the usage of

artiﬁcial distributed neural networks to compute the

numerical MVS (Petrozziello et al., 2018). This work

is on the line of the latter, offering a scalable solution

that can be exploited by posterior learning algorithms.

Montesdeoca, B., Luengo, J., Maillo, J., García-Gil, D., García, S. and Herrera, F.

A First Approach on Big Data Missing Values Imputation.

DOI: 10.5220/0007738403150323

In Proceedings of the 4th International Conference on Internet of Things, Big Data and Security (IoTBDS 2019), pages 315-323

ISBN: 978-989-758-369-8

315

The main goal of this work is to propose two

Big Data preprocessing techniques to impute MVs.

We will use the K-Means and Fuzzy-K-Means algo-

rithms as imputation techniques where we will gen-

erate the MVs through the information of the clus-

ters (Li et al., 2004). These two approaches will be

implemented under Spark (Zaharia et al., 2016), re-

designing the original algorithms to take full advan-

tage of the MapReduce paradigm. The proposed tech-

niques will be validated using different well-known

data sets for Big Data classiﬁcation benchmarking. In

particular, we will simulate different amount of MVs

to check whether our proposal behave correctly in low

to high missing data scenarios and we will evaluate

the effect of the number of centroids selected in the

performance and running times.

The rest of this contribution is organized as fol-

lows. Section 2 will introduce the background on MV

imputation. Section 3 describe the two imputation

techniques proposed. Section 4 contains the experi-

mental analysis carried out with the proposals and the

compared techniques. Finally, Section 5 presents the

conclusions of our work.

2 MISSING VALUES

TREATMENT

In the last few decades, a great deal of progress has

been made in our capacities to generate and store data,

basically due to the great power of the processing of

the machines in addition to its low cost of storage.

However, within these huge volumes of data, there is a

large amount of hidden information, of great strategic

importance. The discovery of this hidden information

is possible thanks to Big Data techniques, which ap-

plies machine learning algorithms to ﬁnd patterns and

relationships within the data, allowing the creation of

models and abstract representations of reality.

To ensure that extracted models are accurate, the

quality of the source data must be as high as possi-

ble. Sadly, real-world data sources are often subject

to imperfections that will diminish such quality. It is

in this scenario where data preprocessing techniques

are demanded, by cleaning and transforming the data

to increment its quality.

Among the main problems of real-world data,

MVs are one of the most challenging problems, as

the majority of Big Data techniques assume that the

data is complete. In such a way, the presence of MVs

will disallow any practitioner to utilize a large set of

techniques. Hence, the treatment of MVs is one of the

main paradigms within imperfect data treatment.

Before deciding applying any preprocessing tech-

nique, we must acknowledge the type of missingness

we are facing. The statistical dependencies among the

corrupted and clean data will dictate how the imper-

fect data can be handled. Originally, Little and Ru-

bin (Little and Rubin, 2014) described the three main

mechanisms of MVs introduction. When the MV

distribution is independent of any other variable, we

face Missing Completely at Random (MCAR) mech-

anism. A more general case is when the MV appear-

ance is inﬂuenced by other observed variables, con-

stituting the Missing at Random (MAR) case. These

two scenarios enable the practitioner to utilise imputa-

tors to deal with MVs. Inspired by this classiﬁcation,

enay and Verleysen (Fr

enay and Verleysen, 2014)

extended this classiﬁcation to noise data, analogously

deﬁning Noisy Completely at Random and Noisy at

Random. Thus, noise ﬁlters can only be safely ap-

plied with these two scenarios.

Alternatively, the value of the attribute itself can

inﬂuence the probability of having a MV or a noisy

value. These cases were named as Missing Not at

Random (MNAR) and Noisy Not at Random for MVs

and noisy data, respectively. Blindly applying im-

putators in this case will result in a data bias. In

these scenarios, we need to model the probability dis-

tribution of the missigness mechanism by using ex-

pert knowledge and introduce it in statistical tech-

niques as Multiple Imputation (Royston et al., 2004).

To avoid improperly application of correcting tech-

niques, some test have been developed to evaluate the

underlying mechanisms (Little, 1988) but still careful

data exploration must be carried out ﬁrst.

Once we acknowledge the kind of MVs we are

facing, there are different ways to approach the prob-

lem of MVs. For the sake of simplicity, we will focus

on the MCAR and MAR cases by using imputation

techniques, as MNAR will imply a particular solution

and modeling for each problem. When facing MAR

or MCAR scenarios, the simplest strategy is to discard

those instances that contain MVs. However, these in-

stances may contain relevant information or the num-

ber of affected instances may also be extremely high,

and therefore, the elimination of these samples may

not be practical or even bias the data.

Instead of eliminating the corrupted instances, the

imputation of MVs is a popular option (Little and

Rubin, 2014). The simplest and most popular esti-

mate used to impute is the average value of the whole

dataset, or the mode in case of categorical variables.

Mean imputation would constitute a perfect candidate

to be applied in Big Data environments as the mean of

each variable remains unaltered and can be performed

in O(n). However, this procedure presents drawbacks

that discourage its usage: the relationship among the

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

316

variables is not preserved and that is the property that

learning algorithms want to exploit. Additionally, the

standard error of any procedure applied to the data

is severely underestimated (Little and Rubin, 2014)

leading to incorrect conclusions.

Further developments in imputation are to

solve the limitations of the two previous strate-

gies. Statistical techniques such as Expectation-

Maximization (Schneider, 2001) or Local Least

Squares Imputation (Kim et al., 2004) were applied in

bioinformatics or climatic ﬁelds. Note that imputing

MVs can be described as a regression or classiﬁca-

tion problem, depending on the nature of the missing

attribute. Shortly after, computer scientists propose

the usage of machine learning algorithms to impute

MVs (Luengo et al., 2012).

Nowadays, data imputation in Big Data frame-

works is being explored more and more. Qu et al. (Qu

et al., 2016) proposed the usage of a distributed Apri-

ori to estimate nominal attributes over a single dataset.

Petrozziello et al. (Petrozziello et al., 2018) on the

other hand tackled the MV problem by using dis-

tributed artiﬁcial neural networks over a sales travel

industry problem, showing a good performance with

numerical attributes. If we take into account clus-

tering algorithms for imputation, Kaliamoorthy et

al. (Kaliamoorthy and Bhanu, 2018) created a multi-

ple imputation algorithm with an approximate version

of fuzzy k-means, but without any prior knowledge

about the data distribution.

In this work we deepen in the last approach, by

proposing two novel techniques to deal with MVs in

Big Data, as shown in the next section. Instead of

comparing the performance of the proposals in terms

of imputation accuracy, we want to explore the im-

pact of a correct imputation in the latter learning al-

gorithms applied.

3 BIG DATA MISSING VALUES

IMPUTATION

This section presents the two proposed techniques

for Big Data MVs imputation. Section 3.1 is de-

voted to describe the K-means imputation. Section

3.2 presents the Fuzzy K-means imputation.

3.1 Big Data K-means Imputation

The implementation of the two proposed MVs impu-

tation methods is enclosed under MLib. MLib is the

machine learning library offered by Spark. Among

its methods, K-means clustering is available at

https://github.com/apache/spark/blob/master/mllib/

src/main/scala/org/apache/spark/mllib/clustering/

KMeans.scala. Such implementation will be used as

a basis to develop the Big Data K-Means Imputation

(BD-KMI).

First of all, MLlib K-means algorithm is intended

for data complete, i.e. for data that do not have miss-

ing values. Instead of using the Dense Vector to rep-

resent the examples, we modiﬁed the implementation

to work with the Sparse Vector class. In such a way,

we can detect whether an example contains a MV by

comparing the number of stored values with the num-

ber of indices actually used.

The distance calculation had to be modiﬁed as

well, since the original implementation only ac-

counted for complete instances. To take into account

the presence of MVs, the distance calculation is based

on normalized instances (done in a previous step).

Thanks to such normalization, when a MV is found,

the difference between the attribute’s values is set to

1.0, the largest possible.

Once these modiﬁcations have been introduced to

deal with MVs, BD-KMI is divided into two main

steps: (i) the clustering stage and (ii) the imputation

step.

The clustering stage is composed of the following

steps, executed repeatedly until convergence is found,

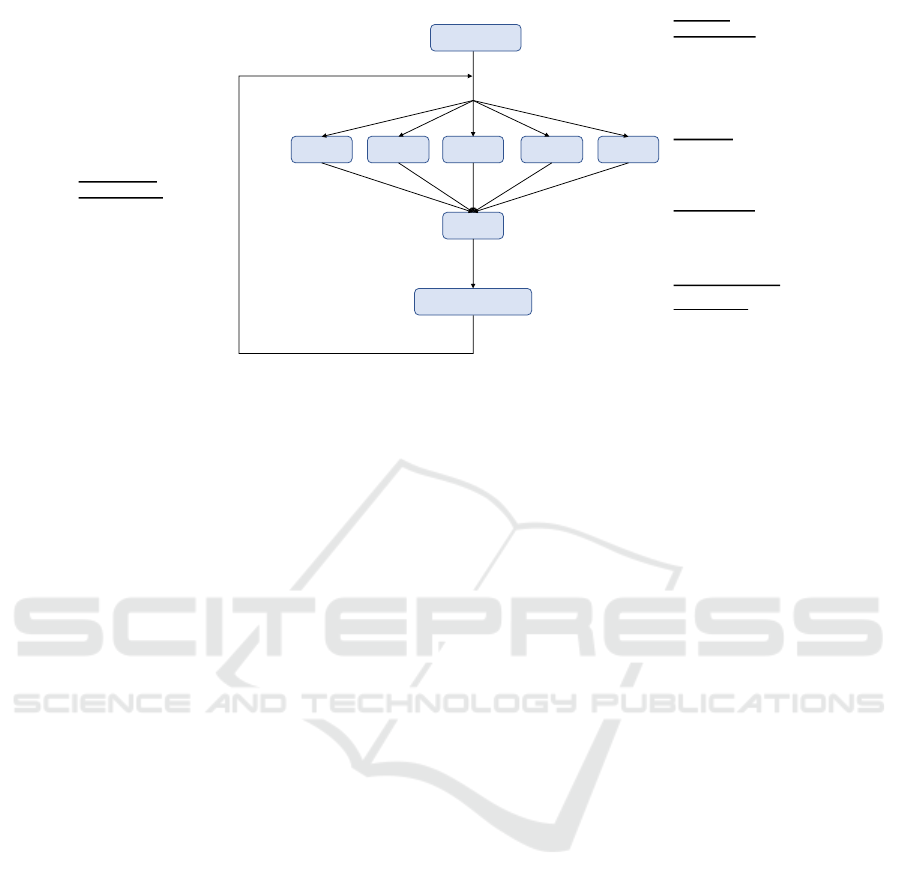
as shown in Figure 1:

1. Initialization of the Centroids: The ﬁrst process

that takes place is the establishment of the initial

centroids. In this process, the following are cho-

sen from a random selection of the data, in ad-

dition we should take special care not to choose

elements that contain values lost.

2. Map Phase: The next process that takes place is

the mapping phase, where the mapPartition func-

tion is used to split the data in different partitions.

In each partition and for each data of the same

one, we calculate the nearest centroid and then we

carry out two operations. On the one hand we in-

crease in one the counter that indicates the number

of elements that belong to a centroid. On the other

hand we add that data to the cumulative sum of the

cluster data represented by the centroid. For each

partition, we will obtain an array of Kx2(K rep-

resents the number of centroids) and where each

represents a cluster with the number of elements

that belong to that cluster and the sum of the vec-

tors of all those elements.

3. Reduce Phase: In the next stage of reduction we

group the results of each one of the partitions, in

such a way that when nalizar the stage reduces we

have the sums of the different counters and the

sum of vectors but for the entire dataset.

A First Approach on Big Data Missing Values Imputation

317

Map Map Map MapMap

Reduce

Centroid update

Inicialization

Centroid

inicialization

Random selection of

centroids from examples in

the dataset

Map step

Data partition

Computation per cet roid : [no. of

points, sum of points]

Reduce step

Grouping of [total no. of points,

total sum of points]

Centroid Update

New centroid =

!"! #$% &'(%")%*"+,!&

!"! #$ %," .")%*"+ ,!&

Repeat until

convergence

Repeat until there is little or no

change to centroids

Figure 1: Big Data K-means Imputation outline.

4. Centroid Update: Once obtained the information

on the centroids, we proceed to update it. For it

we will use the two data on the centroids obtained

in the previous phases. To obtain the new centroid

we divide the vector resulting from the sum of the

data that belong to the cluster by the number of

elements of the same, in this way the centroid will

be readjusted and placed at the midpoint accord-

ing to the elements that belong to the cluster it

represents.

Steps 2 to 4 are repeated until the centroids con-

verge. The convergence is evaluated by comparing

the “movement” differences of the centroids between

iterations with a given threshold.

Once the centroids have been obtained, we pro-

ceed with the imputation stage of the data that have

lost values. We go through all the examples, detecting

those with MVs, determining which cluster it belongs

to, and therefore the centroid that represents it.

Once the centroid that represents the example with

lost values is obtained, we replace those missing val-

ues with the corresponding attributes belonging to the

centroid.

3.2 Big Data Fuzzy K-means

Imputation

Big Data Fuzzy K-means Imputation (BD-FKMI) is

based on the fuzzy version of K-means, which im-

plies that the examples will belong to all centroids but

with a given membership degree. If we consider the

differences among KMI and FKMI, we must point out

two of them before describing our proposal:

• Updating the centroids must consider all exam-

ples, not only those that are the closest to it. As a

result, from each point we get, instead of the near-

est centroid index, a vector of degrees of belong-

ing, where each element of the vector corresponds

to the membership degree that has that point with

each centroid.

• The data structure we have to calculate for each

centroid is no longer [no of points, cumulative

sum of points], but, following the formula of

the diffuse grouping algorithm, we calculate for

each centroid [sum of degrees, cumulative sum of

points × corresponding degree to the centroid].

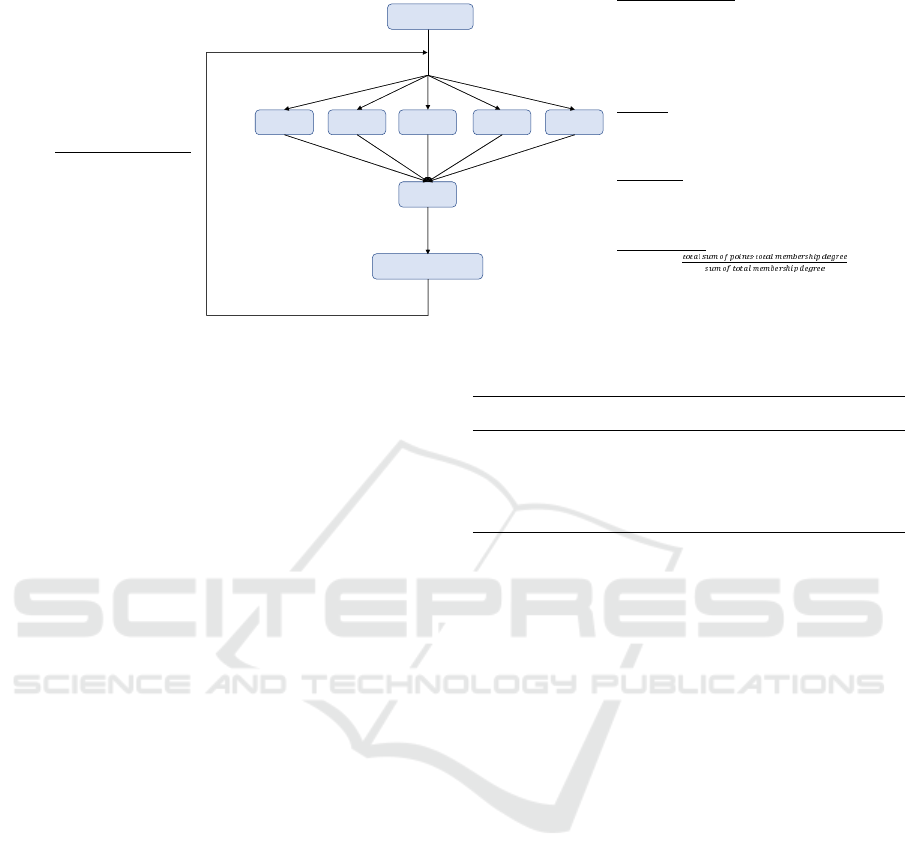
The algorithm follows the same structure and the

same series of processes than BD-KMI, but we need

to take into account the aforementioned differences

into the Map step. We describe the main algorith-

mic steps next, by following the schemata presented

in Figure 2. The membership calculation is the same

as the carried out in (Li et al., 2004) and for the sake

of brevity we will not reproduce entirely here.

1. Initialization of the Centroids: Just like KMI,

the initial centroids are randomly selected.

2. Map Phase: For each example in each partition

we compute a vector that represents the member-

ship degree to each of the centroids. In this case

the result of the execution of each partition will

result in a K × 2 matrix where the information of

each centroid is, (i) the sum of all membership de-

grees for each example and; (ii) the sum of each of

these data multiplied by its corresponding mem-

bership degree.

3. Reduce Phase: We group the results of each of

the partitions to obtain information on the total of

the data.

4. Centroid Update: We divide the sum of the data

by the sum of the degrees respect to each centroid.

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

318

DĂƉ DĂƉ DĂƉ DĂƉDĂƉ

ZĞĚƵĐĞ

ĞŶƚƌŽŝĚ ƵƉĚĂƚĞ

/ŶŝĐŝĂůŝǌĂƚŝŽŶ

ĞŶƚƌŽŝĚ ŝŶŝĐŝĂůŝǌĂƚŝŽŶ

ZĂŶĚŽŵ ƐĞůĞĐƚŝŽŶ ŽĨ ĐĞŶƚƌŽŝĚƐ

ĨƌŽŵ ĞǆĂŵƉůĞƐ ŝŶ ƚŚĞ ĚĂƚĂƐĞƚ

DĂƉ ƐƚĞƉ

ĂƚĂ ƉĂƌƚŝƚŝŽŶ

ŽŵƉƵƚĂƚŝŽŶ ƉĞƌ ĐĞƚƌŽŝĚ͗ ΀ƐƵŵ ŽĨ

ŵĞŵďĞƌƐŚŝƉ ĚĞŐƌĞĞƐ͕ ƐƵŵ ŽĨ

ƉŽŝŶƚƐΎŵĞŵďĞƌƐŝƉ ĚĞŐƌĞĞ΁

ZĞĚƵĐĞ ƐƚĞƉ

'ƌŽƵƉŝŶŐ ŽĨ ΀ƐƵŵ ŽĨ ƚŽƚĂů

ŵĞŵďĞƌƐŚŝƉ ĚĞŐƌĞĞ͕ ƚŽƚĂů ƐƵŵ ŽĨ

ƉŽŝŶƚƐΎƚŽƚĂů ŵĞŵďĞƌƐŚŝƉ ĚĞŐƌĞĞ΁

ĞŶƚƌŽŝĚ hƉĚĂƚĞ

EĞǁ ĐĞŶƚƌŽŝĚ с

ZĞƉĞĂƚ ƵŶƚŝů ĐŽŶǀĞƌŐĞŶĐĞ

ZĞƉĞĂƚ ƵŶƚŝů ƚŚĞƌĞ ŝƐ ůŝƚƚůĞ Žƌ ŶŽ

ĐŚĂŶŐĞ ƚŽĐĞŶƚƌŽŝĚƐ

Figure 2: Big Data Fuzzy K-means Impute outline

Steps 2 to 4 are repeated until the convergence of

the centroids is attained, in a similar fashion to BD-

KMI.

4 EXPERIMENTAL ANALYSIS

In this section we experimentally validate the pro-

posed algorithms with some well-known Big Data

benchmark datasets. Section 4.1 describes the exper-

imental framework used in our experiments. Section

4.2 is devoted to the analysis of the experiments’ re-

sults. Finally, Section 4.3 will present the computa-

tion times for the compared approaches.

4.1 Experimental Framework

In order to compare the different techniques, we have

considered three well-known Big Datasets, which fol-

lows:

• Susy: It has about 4 million instances with 19

attributes. The data have been obtained through

Monte Carlo simulations. The ﬁrst 8 attributes are

kinematic properties measured by the particle de-

tectors on the accelerator while the last ten char-

acters are functions of the ﬁrst 8 attributes.

• Higgs10: It has approximately 880 thousand in-

stances of 29 attributes each. As the previous

dataset was obtained through the Monte Carlo

method in the experimentation on subatomic par-

ticles.

• ECBDL14: The latest dataset is the largest one.

In the beginning it was devised for the prediction

of protein structure, and it was originally gener-

ated to train a predictor related to contact map pre-

diction in the CASP9 competition for ECBDL’14

Table 1: Parameters for the classiﬁers.

Classiﬁer Parameters

DT depth: 20, maxBins: 20

RF numTrees: 20, depth: 20, maxBins: 20

ANN epochs: 50, layers: 2

neuronsLayer1: 18, neuronsLayer2: 2

conference. It has 2 million instances and 631 at-

tributes.

Since the aforementioned datasets do not contain

MVs, we will artiﬁcially induce missing data in them

following a MCAR schema. The only restriction ap-

plied is to induce only one MV per example, which

would be more representative of MCAR (since hav-

ing more MVs in some instances would be related to

a MAR schema). The amount of MVs induce will

be 5, 10 and 30%, ranging from a low to highly MV

scenario.

As we have previously mentioned, there is no

other non-na

ıve imputation technique in Big Data.

Thus, we are limited to compare our two proposed

techniques either with:

• Deleting or ignoring the examples with MVs,

named as IC.

• Imputation by the mean value of each input at-

tribute, named as MC.

These two techniques are easily implemented in

Spark by using ﬁlter to detect the missing values and

the native functions to compute the cumulative sum-

mation of values in order to compute the mean value.

We want to evaluate how the imputation of the

compared techniques affects the performance of the

classiﬁers that would be used afterwards. To properly

evaluate such impact, we have selected some repre-

sentative classiﬁers from MLib, which follows: de-

A First Approach on Big Data Missing Values Imputation

319

Table 2: Accuracy results for Susy dataset.

5% of missing values 10% of missing values 30% of missing values

DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc)

BD-KMI(k=5) 0.782447 0.799291 0.783058 0.784201 0.799192 0.782340 0.787823 0.798408 0.780787

BD-KMI(k=15) 0.782540 0.799369 0.781930 0.784022 0.799221 0.781861 0.787458 0.798824 0.781265

BD-KMI(k=30) 0.781936 0.799334 0.781498 0.783486 0.799293 0.782304 0.786973 0.798929 0.781072

BD-FKMI(k=5) 0.781641 0.799301 0.782231 0.782242 0.799202 0.780907 0.782855 0.798951 0.782452

BD-FKMI(k=15) 0.781594 0.799348 0.781792 0.781486 0.799240 0.780951 0.782891 0.799054 0.782373

BD-FKMI(k=30) 0.781641 0.799245 0.781943 0.782154 0.799250 0.780796 0.783080 0.798977 0.782401

MC 0.781722 0.799384 0.782297 0.782090 0.799349 0.781459 0.782357 0.799070 0.782087

IC 0.780501 0.798985 0.781928 0.780040 0.799344 0.782029 0.777843 0.799021 0.782057

Table 3: Accuracy results for Higgs dataset.

5% of missing values 10% of missing values 30% of missing values

DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc)

BD-KMI(k=5) 0.683908 0.738168 0.628632 0.683232 0.737928 0.628159 0.682132 0.736913 0.628458

BD-KMI(k=15) 0.684011 0.738520 0.628272 0.683273 0.738078 0.627418 0.682167 0.736360 0.628511

BD-KMI(k=30) 0.684859 0.738268 0.627457 0.683835 0.737781 0.628733 0.682639 0.735936 0.628422

BD-FKMI(k=5) 0.684150 0.738195 0.627073 0.684333 0.737652 0.628078 0.682935 0.736784 0.628576

BD-FKMI(k=15) 0.684551 0.737827 0.627108 0.684171 0.737634 0.628078 0.683145 0.737112 0.628576

BD-FKMI(k=30) 0.683248 0.738243 0.627617 0.683639 0.738264 0.628078 0.683178 0.736725 0.628575

MC 0.684455 0.738275 0.627280 0.683708 0.737812 0.627210 0.681988 0.736915 0.628594

IC 0.682120 0.737390 0.627537 0.682118 0.736260 0.628446 0.675251 0.732435 0.628260

cision tree (DT), Random Forest (RF), and an artiﬁ-

cial neural network (ANN). The parameters used for

these classiﬁers have been experimentally adjusted

for the original datasets to obtain a good performance

by means of grid search, and then later applied to the

imputed version of the same datasets. The obtained

parameters can be found in Table 1. Both BD-KMI

and BD-FKMI only require to specify the number of

centroids k. For both imputation techniques we will

consider k = 5, 15, 30% We have used a 5-fcv valida-

tion to validate our proposals.

For all experiments we have used a cluster com-

posed of 20 computing nodes and one master node.

The computing nodes hold the following character-

istics: 2 processors x Intel Xeon(R) CPU E5-2620,

6 cores per processor, 2.00 GHz, 2 TB HDD, 64

GB RAM. Regarding software, we have used the fol-

lowing conﬁguration: Hadoop 2.6.0-cdh5.4.3 from

Cloudera’s open source Apache Hadoop distribu-

tion, Apache Spark and MLlib 1.6.0, 460 cores (23

cores/node), 960 RAM GB (48 GB/node).

4.2 Accuracy Analysis with the

Imputation Methods

In this section we will analyze the results obtained by

the classiﬁcation methods once the imputation meth-

ods have been applied for each dataset individually.

Table 2 presents the results for the Susy dataset.

From the results presented, the best imputation tech-

nique is BD-KMI, where in most cases it performs

best with few clusters. On the other hand, we must

stress that mean imputation (MC) is the best tech-

nique for RF. Due to the fact that MC maintains the

variance of the attribute, which RF can exploit better

thanks to its sampling. Thus, a multi-classiﬁer with

the capability of generating diverse base classiﬁers

could be more robust to na

ıve methos as MC. Nev-

ertheless, BD-KMI is the second best to RF, being the

most balanced option for Susy.

In Table 3 we show the results for Higgs dataset.

In this case, there is a clear domain of imputation

based in clustering. In general, the FKMI imputter

offers better results for datasets with high percentages

of missing values. However, for lower percentages of

missing values, BD-KMI obtains the best precision

scores. For this dataset, MC does not achieve the high

performance that was observed for RF in Susy.

Finally, Table 4 depicts the accuracy results in the

case of ECDBL’14 dataset. Observing the results,

BD-FKMI offers better results. As for the number of

centroids, it appears that BD-KMI gives better perfor-

mance with higher k, while in the case of BD-FKMI

this value varies to a greater extent. Comparing our

proposal with MC, the latter only out-stands (with a

narrow margin) when the number of MVs is medium

to high and only for DT. Thus, the option of using

imputation-based techniques is the safest option for

ECDBL’14 dataset.

As a general analysis, we can consider that the

proposed imputation methods outperform both MC

and IC. We must stress that deleting examples with

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

320

Table 4: Accuracy results for ECDBL’14 dataset.

5% of missing values 10% of missing values 30% of missing values

DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc) DT(Acc) RF(Acc) ANN(Acc)

BD-KMI(k=5) 0.980086 0.980233 0.980234 0.980083 0.980230 0.980233 0.980105 0.980234 0.980234

BD-KMI(k=15) 0.980067 0.980231 0.980232 0.980090 0.980235 0.980234 0.980100 0.980234 0.980234

BD-KMI(k=30) 0.980079 0.980234 0.980234 0.980078 0.980236 0.980235 0.980101 0.980233 0.980234

BD-FKMI(k=5) 0.980105 0.980233 0.980234 0.980101 0.980233 0.980235 0.980106 0.980236 0.980232

BD-FKMI(k=15) 0.980095 0.980232 0.980236 0.980090 0.980235 0.980235 0.980099 0.980227 0.980234

BD-FKMI(k=30) 0.980096 0.980231 0.980232 0.980109 0.980231 0.980233 0.980103 0.980237 0.980237

MC 0.980104 0.980233 0.980235 0.980126 0.980226 0.980235 0.980153 0.980229 0.980233

IC 0.980079 0.980231 0.980234 0.980037 0.980232 0.980234 0.980065 0.980234 0.980234

MVs (IC) is never the best option, and thus we are

being able to recover part of the information lost in

all scenarios, from low to high amount of MVs.

As for which version of the clustering based im-

putation we should choose, the choice depends on the

dataset. For instance, Susy dataset favors BD-KMI,

while for the two other datasets, we get better results

when using BD-FKMI. The number of centroids cho-

sen depends on the dataset as well. However, this is

a known feature of the original K-means clustering

technique and therefore, such behavior is inherited by

the imputation methods.

4.3 Running Times Analysis

In this section we present the running times for the

imputation methods and the impact that the number of

chosen centroids have in the performance. Figures 3a

to 3c depict the running times in minutes for each ap-

proach compared in the three benchmark datasets. As

we may appreciate, the fuzzy version BD-FKMI is

slower than its crisp version BD-KMI for the same

value of k. This overhead is a logical consequence of

the membership calculation for all the centroids that

BD-FMKI carries out and was also present in the non

Big Data version of both imputation methods.

We may also appreciate that IC has a running time

of almost zero in all cases. Since IC was implemented

with a native ﬁlter of Spark, its efﬁciency is very high.

However, we have shown in the previous section that

IC is never the best option to deal with MVs.

MC is also very efﬁcient and not depends on the

amount of MVs. Since the implementation of MC

implies the cumulative sum of all observed values in

the Map phase and the later division in the Reduce

step, the number of MVs will affect little to the sum

carried out. Again, MC is a very simple method that

will run fast, but we have also shown that it is rarely

the best option.

Both BD-KMI and BD-FKMI increase their run-

ning times as the number of MVs increase as the num-

ber of imputations carried out will increase with the

number of MVs. Increasing the number of centroids

k has a negative impact in the performance. However,

as occurs for Higgs dataset, the number of k can be too

high, causing a premature stagnation in the clustering

process and thus ending the process before reaching

the max number of iterations.

5 CONCLUSIONS

Two imputation techniques for MVs have been im-

plemented in Big Data that, although simple, consti-

tute a good starting point for futures developments of

the same type. Although Spark offers the machine

learning library (MLlib), it is in continuous growth

and lacks many algorithms important for the treat-

ment of MVs. The two implemented techniques of-

fer robust and efﬁcient results for Big Data datasets,

offering reasonable execution times. Both imputation

methods surpass in most cases other two classic tech-

niques of treatment of MVs, such as mean imputation

and elimination of the instances with lost values. It is

it is important to highlight the fact that both BD-KMI

and BD-FKMI outperform the method of eliminating

instances with MVs, since this will prevent a possible

loss of valuable information.

Regarding to the performance difference between

the two proposed imputation methods, experiments

show that BD-FKMI provides better results for high

percentages of MVs in the dataset, while the BD-

KMI performs better for dataset with lower amounts

of MVs. One of the aspects that we wanted to deeper

analyze is the inﬂuence of the number of centroids.

The results show that the inﬂuence of this parame-

ter is very dependent of the dataset. The increase in

the number of centroids in our experiments will not

always improve accuracy results. On the other hand,

this increase has impact on computational time, which

is why we have not reached higher k values in our ex-

periments.

As a future work, we intend to implement a

smarter way to select the initial centroids, which has

a great impact in the solution found by any K-means

variant. An additional improvement that we will con-

A First Approach on Big Data Missing Values Imputation

321

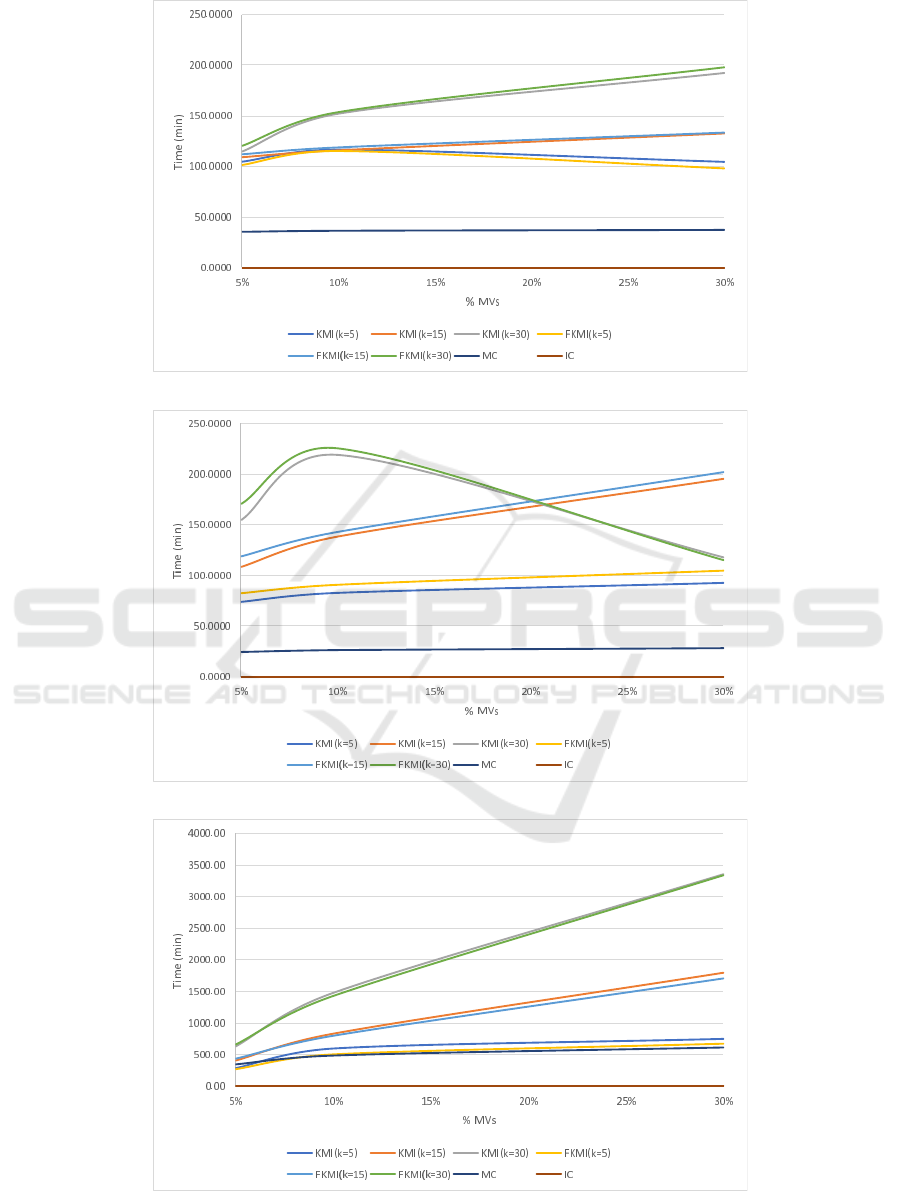
(a) Running times in minutes for Susy dataset

(b) Running times in minutes for Higgs dataset

Figure 3.

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

322

sider will be changing how the MVs are imputed. In-

stead of taking the reference attribute’s value from

the centroid, we will consider the use of a k-nearest

neighbor imputation among the closest examples in

the cluster, which may yield a closer imputed value

instead of always taking centroid’s attribute value.

ACKNOWLEDGEMENTS

This work has been supported by the project

TIN2017-89517-P granted by Ministerio de Ciencia,

Innovaci

on y Univesidades.

REFERENCES

enay, B. and Verleysen, M. (2014). Classiﬁcation in the

presence of label noise: A survey. IEEE Trans. Neural

Netw. Learning Syst., 25(5):845–869.

Garc

ıa, S., Luengo, J., and Herrera, F. (2015). Data prepro-

cessing in data mining. Springer.

Garc

ıa-Laencina, P. J., Sancho-G

omez, J.-L., and Figueiras-

Vidal, A. R. (2010). Pattern classiﬁcation with miss-

ing data: A review. Neural Computing and Applica-

tions, 19(2):263–282.

Gupta, P., Sharma, A., and Jindal, R. (2016). Scal-

able machine learning algorithms for big data analyt-

ics: a comprehensive review. Wiley Interdisciplinary

Reviews: Data Mining and Knowledge Discovery,

6(6):194–214.

Iafrate, F. (2014). A Journey from Big Data to Smart Data,

pages 25–33. Springer International Publishing.

John Walker, S. (2014). Big data: A revolution that will

transform how we live, work, and think.

Kaliamoorthy, S. and Bhanu, S. M. S. (2018). Multiple

imputation inference for missing values in distributed

datasets using apache spark. In International Confer-

ence on Advances in Computing and Data Sciences,

pages 24–33. Springer.

Kim, H., Golub, G. H., and Park, H. (2004). Missing

value estimation for DNA microarray gene expression

data: local least squares imputation. Bioinformatics,

21(2):187–198.

Laney, D. (2001). 3d data management: Controlling data

volume, velocity and variety. META group research

note, 6(70):1.

Li, D., Deogun, J., Spaulding, W., and Shuart, B. (2004).

Towards missing data imputation: a study of fuzzy k-

means clustering method. In International conference

on rough sets and current trends in computing, pages

573–579. Springer.

Little, R. J. A. (1988). A test of missing completely

at random for multivariate data with missing val-

ues. Journal of the American Statistical Association,

83(404):1198–1202.

Little, R. J. A. and Rubin, D. B. (2014). Statistical analysis

with missing data, volume 333. John Wiley & Sons.

Luengo, J., Garc

ıa, S., and Herrera, F. (2012). On the

choice of the best imputation methods for missing val-

ues considering three groups of classiﬁcation meth-

ods. Knowledge and Information Systems, 32(1):77–

108.

Petrozziello, A., Jordanov, I., and Sommeregger, C. (2018).

Distributed neural networks for missing big data im-

putation. In 2018 International Joint Conference on

Neural Networks (IJCNN), pages 1–8. IEEE.

Qu, Z., Yan, J., and Yin, S. (2016). Association-rules-based

data imputation with spark. In 2016 4th International

Conference on Cloud Computing and Intelligence Sys-

tems (CCIS), pages 145–149. IEEE.

Ram

ırez-Gallego, S., Fern

andez, A., Garc

ıa, S., Chen, M.,

and Herrera, F. (2018). Big data: Tutorial and guide-

lines on information and process fusion for analyt-

ics algorithms with mapreduce. Information Fusion,

42:51–61.

Royston, P. et al. (2004). Multiple imputation of missing

values. Stata journal, 4(3):227–41.

Schneider, T. (2001). Analysis of incomplete climate data:

Estimation of mean values and covariance matrices

and imputation of missing values. Journal of climate,

14(5):853–871.

Triguero, I., Garc

ıa-Gil, D., Maillo, J., Luengo, J., Garc

ıa,

S., and Herrera, F. (2018). Transforming big data into

smart data: An insight on the use of the k-nearest

neighbors algorithm to obtain quality data. Wiley In-

terdisciplinary Reviews: Data Mining and Knowledge

Discovery, page e1289.

Zaharia, M., Xin, R. S., Wendell, P., Das, T., Armbrust,

M., Dave, A., Meng, X., Rosen, J., Venkataraman, S.,

Franklin, M. J., et al. (2016). Apache spark: a uniﬁed

engine for big data processing. Communications of

the ACM, 59(11):56–65.

A First Approach on Big Data Missing Values Imputation

323