
Control of Uncertain Time Delay System with Astatism and
Parametric and Periodic Uncertainties using SSV and Factorization
for Two-Degree-of-Freedom-Controller
Marek Dlapa
a
Faculty of Applied Informatics, Tomas Bata University in Zlin, Nad Stranemi 4511, 760 05 Zlín, Czech Republic
Keywords: Parametric Uncertainty, Structured Singular Value, Matlab Toolbox, Global Optimization, Direct Search
Methods, Factorization.
Abstract: Application of the Robust Control Toolbox for Time Delay Systems with Parametric and Periodic
Uncertainties Using SSV (Structured Singular Value) for the Matlab system to uncertain time delay system
with astatism is performed. The D-K iteration and the algebraic approach implemented in the toolbox are
applied to 2
nd
order system with astatism and uncertain time delay and two other parameters in the numerator
and denominator of the plant transfer function. Multiplicative uncertainty is used for treating uncertain time
delay, the parametric uncertainty is modelled using general interconnection for the systems with parametric
uncertainty in numerator and denominator.
1 INTRODUCTION
Parametric uncertainties has been an issue of robust
control for several decades, the first tool was Map-
ping Theorem (Zadeh and Desoer, 1963) succeeded
by Kharitonov Theorem (Kharitonov, 1978; Bar-
mish, 1984 and Bialas, 1983), Edge Theorem (Bart-
lett et al., 1988; Barmish, 1989 and Sideris and de
Gaston, 1986) and Generalized Kharitonov Theorem
(Chapellat and Bhattacharyya, 1989) treating conser-
vatism in applications to feedback loop with SISO
(single-input single-out-put) controller. One of the
latest results is tree structured decomposition (Bar-
mish et al., 1989) yielding a general procedure
allowing the analysis of complex closed-loop cha-
racteristic polynomials in a polynomial time and the
results for specific multilinear structures (Barmish
and Shi, 1990; Chapellat et al., 1993 and Fu et al.,
1995) considering the closed-loop characteristic po-
lynomials corresponding to the series connections of
interval plants.
In this paper, toolbox treating parametric and
periodic uncertainties using structured singular value
(SSV or μ, see Packard and Doyle, 1993) imple-
mentting both the algebraic approach with subse-
quent optimization using evolutionary algorithm
a
https://orcid.org/ 0000-0003-2550-7062
(Dlapa, 2011; Dlapa, 2018) and D-K iteration as
reference method is applied to 2
nd
order system with
astatism and uncertain time delay and parameters.
The toolbox solves both parametric and dynamic
uncertainties including uncertain time delay. The
Robust Control Design Toolbox for Time Delay
Systems with Parametric and Periodic Uncertainties
Using SSV (http://dlapa.cz/homeeng.htm) deals with
uncertain time delay and parametric uncertainties in
the numerator and denominator of the plant transfer
function. The controller is derived for two-degree-of-
freedom and single feedback loop (2DOF and 1DOF
see Dlapa, 2014).
The controller is tuned using pole placement of
nominal closed loop poles solving Diophantine
equation in the ring of Hurwitz-stable and proper
rational functions (R
PS
). The poles of the nominal
closed loop are tuned via direct search methods –
Differential Migration (Dlapa, 2017) and Nelder-
Mead simplex method managing the issue of multi-
modality of the structured singular value in relation-
ship with nominal closed loop poles. This algorithm
tackles impossibility of usage of the weights with
poles on imaginary axis and convergence to a global
or even local minimum causing non-optimality of the
resulting controller in the D-K iteration (Stein and
Doyle, 1991).
Dlapa, M.
Control of Uncertain Time Delay System with Astatism and Parametric and Periodic Uncertainties using SSV and Factorization for Two-Degree-of-Freedom-Controller.
DOI: 10.5220/0007741205630570
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 563-570
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
563
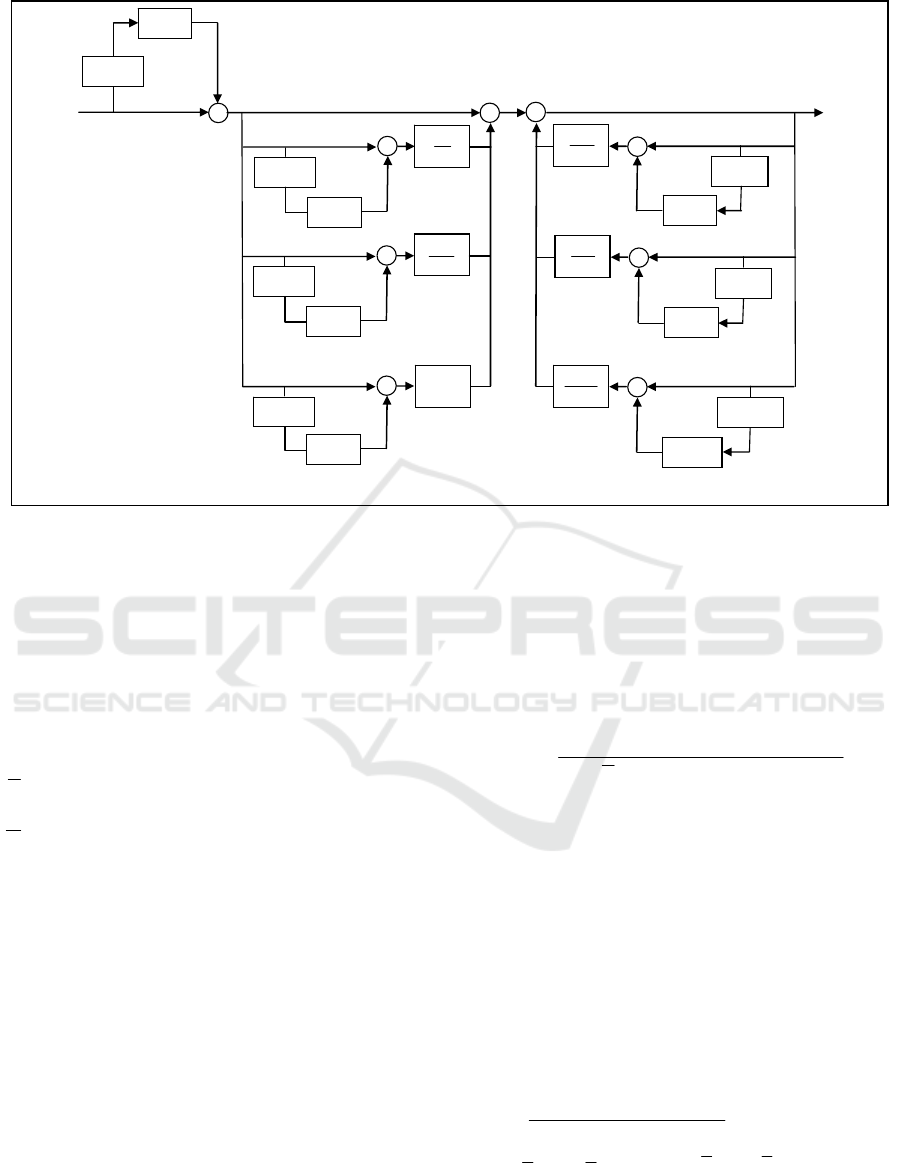
Figure 1: Modelling general parametric uncertainties system.
For reference, the controller derived using the D-
K iteration (see Doyle, 1985) is compared to the one
obtained from the algebraic approach showing the
pros and cons of both procedures. The resulting
controllers are compared in simulations of step res-
ponse for different values of time delays and perio-
dic changes of parameters with simple feedback loop
and two-degree-of-freedom structure (1DOF and 2DOF).
Notation used in the paper: || ||
is H
norm,
)(
denotes maximum singular value, R and C
nm
are real numbers and complex matrices, respec-tively,
R
are positive real numbers, I
n
is the unit matrix of
dimension n and R
PS
denotes the ring of Hurwitz-
stable and proper rational functions.
2 DEFINITIONS
Define as a set of block diagonal matrices
}1,,1,,1,,1,
:],,,,,,,,,,,[diag{
1111
11
KkFfTtSs
IIII
kk
ff
TS
nn
k
mm
fts
KFcTcrSr
RCRC
Δ
(1)
where S, T is the number of repeated scalar complex
and real blocks,
F, K is the number of full complex and real
blocks,
r
1
,, r
S
, r
1
,, r
T
, m
1
,, m
F
, n
1
,, n
K
are
positive integers defining dimensions of scalar
and full blocks.
For consistency among all the dimensions, the fol-
lowing condition must be held
nmrmr
K
k
k
F
f
f
T
t
t
S
s
s
1111
(2)
Definition 1: For M C
nn
is μ
(M) defined as
}0)det(,:)(min{
1
)(
MIΔ
M
Δ
(3)
If there is no making I – M singular, then
μ
(M) = 0.
3 MODELLING OF PARAMETRIC
UNCERTAINTIES FOR SSV
DESIGN
Consider general system with uncertain numerator
and denominator and uncertain time delay treating
parametric, periodic and time delay uncertainties:
1
110
10
)(
)(
n
n
n
sn
n
sasaas
esbsbb
sP
a
i
[
i
a – A
i
,
i
a + A
i
], b
i
[
i
b
– B
i
,
i
b
+ B
i
],
i = 0, 1, … , n–1,
[0, T
d
]
(4)
+
W
del
δ
del
+
W
b0
+
W
a0
n
s
a
0
+
δ
a0
1
1
n
s
a
+
δ
a1
s
a
n 1
+
δ
an-1
W
a1
W
an-1
+
W
b1
+
W
bn
+
δ
bn
δ
b1
δ
b0
n
s
b
0
1
1
n
s
b
n
b
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
564
Time delay and parametric uncertainties vary in the
predefined intervals.
1
ai
1
bi
1
del
(5)
And for weights W
ai
, W
ai
and W
del
the following
inequalities must be held for all
R:
1,,1,0 , niAW
iai
(6)
niBW
ibi
,,1,0 ,
(7)
d
Tj
del
ejW
1)(
(8)
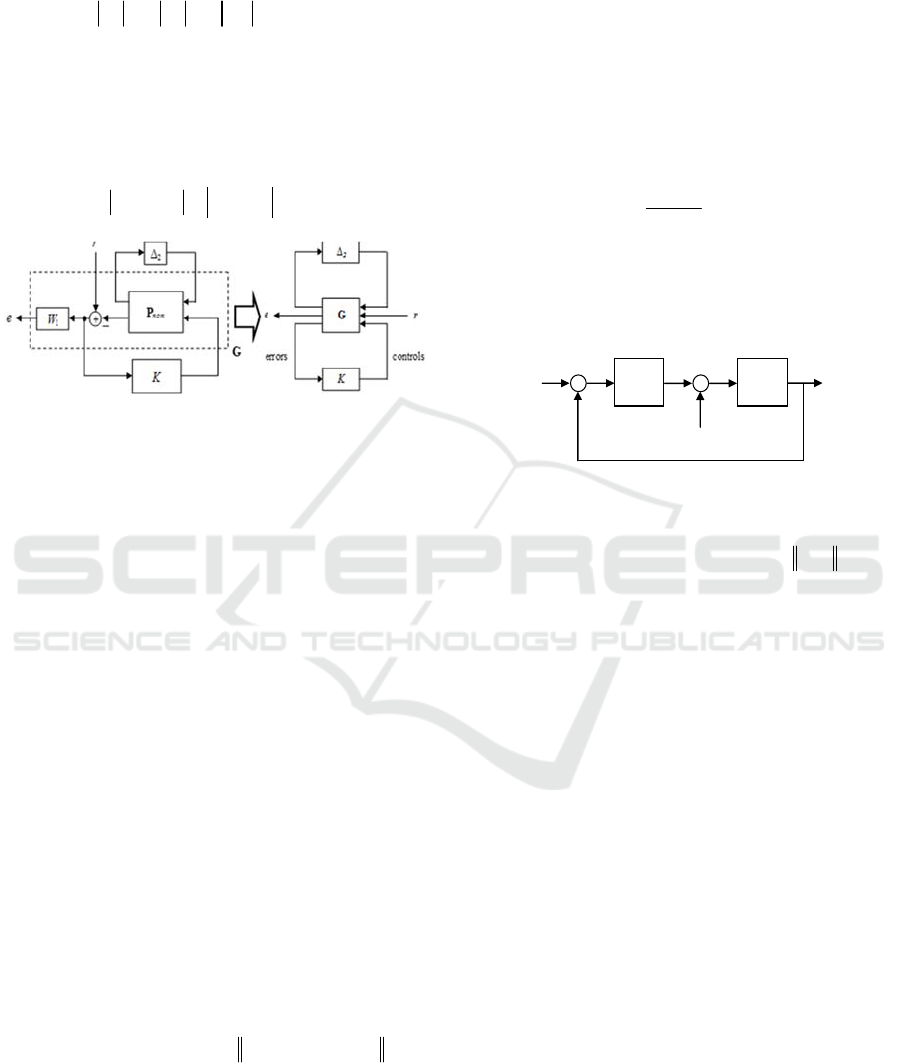
Figure 2: Closed-loop interconnection.
Plant (4) and Figure 1 can be transformed to the
interconnections in Figure 2 with the sensitivity
function as a performance indicator and
P
nom
being
open-loop interconnection from Figure 1.
Perturbation matrix has the form:
del
b
a
00
0Δ0
00
Δ
2
(9)
1
1
0
00
00
00
Δ
an
a
a
a
(10)
bn
b
b
b
00
00
00
Δ
1
0
(11)
For stability and performance Theorem 1 and the
following Corollary 1 hold:
Theorem 1:
For defined by (9) the loop in Figure 2 is well-
posed, internally stable and
1]),Δ,([
2
K
UL
GFF
if and only if
1)])(,([sup
gstabilizin
jK
L
K
R
GF
Δ
G
(12)
with
CΔ
P
,
Δ0
0
2
1
.
Proof: The proof is the same as in Doyle et al., 1982
and Packard and Doyle, 1993 except for the fact that
perturbations are complex matrices which simplifies
the proof and complies with the definition of μ (De-
finition 1).
Define sensitivity function as transfer function
from reference r to error e in Figure 3:
PK
S
1
1
(13)
Now, as a consequence of Theorem 1, a suffi-cient
condition for the robust stability and perfor-mance of
the feedback loop in Figure 3 can be formed for
sensitivity function S and family of plants (4).
Figure 3: Feedback loop.
Corollary 1: For the set of plants (4), the feedback
loop in Figure 3 is internally stable and
1
1
SW if
and only if (12), (5), (6), (7) and (8) hold.
Proof: The proof follows from Figure 1, inequalities
(12), (5), definitions (6), (7) and (8) and Theorem 1.
4 ALGEBRAIC -SYNTHESIS
The algebraic μ-synthesis can be applied to any
control problem that can be transformed to the loop
in Figure 2 where G denotes the generalized plant, K
is the controller,
del
is the perturbation matrix, r is
the reference and e is the output.
For the purposes of the algebraic μ-synthesis, the
MIMO system with l inputs and l outputs has to be
decoupled into l identical SISO plants. The nominal
model is defined in terms of transfer functions:
)()(
)()(
)(
1
111
sPsP
sPsP
s
lll
l
nom
P
(14)
For decoupling the nominal plant P
nom
(P
nom
invertible) it is satisfactory to have the controller in
the form
d
u
y
re
-
K
P
Control of Uncertain Time Delay System with Astatism and Parametric and Periodic Uncertainties using SSV and Factorization for
Two-Degree-of-Freedom-Controller
565
1
)]([
)(
1
)](det[)()(
s
sP
ssKs
nom
xy
noml
PPIK
(15)
where P
xy
is an element of adj[P
nom
(s)] = det[P
nom
(s)] ·
· [P
nom
(s)]
–1
with the highest degree of numerator
{adj[P
nom
(s)] denotes adjugate matrix of P
nom
}. The
choice of the decoupling matrix prevents the
controller from cancelling any poles or zeros from the
right half-plane so that internal stability of the
nominal feedback loop is held. The MIMO problem
is reduced to finding a controller K(s) which is tuned
via setting the poles of the nominal feedback loop
with the plant
lnom
xy
nomnomnom
xy
dec
s
sP
sss
sP
s
IP
PPPP
)](det[
)(
1
)()]()][(det[
)(
1
)(
1
(16)
Define
)](det[
)(
1
s
sP
P
nom
xy
dec
P
(17)
Transfer function P
dec
can be approximated by a
system
*
dec
P
with lower order than P
dec
)(
)(
)(
sa
sb
sP
dec
(18)
which can be rewritten in terms of its coefficients and
transformed to the elements of R
PS
A
B
sss
sasaas
sss
sbsbb
sP
n
n
n
n
n
n
n
dec
)())((
)())((
)(
21
1
110
21
10
*
, A,
B R
PS
(19)
The controller K = N
K
/D
K
is derived as solution of the
Diophantine equation
A
D
K
+ B
N
K
= 1 (20)
with A, B, D
K
, N
K
R
PS
. Equation (20) is the Bezout
identity. All feedback controllers N
K
/D
K
are given by
BTD
ATN
D
N
K
K
K
K
K
0
0
,
PS
00
, R
KK
DN
(21)
where
0
K
N
,
PS
0
R
K
D
are particular solutions of
(20) and T is an arbitrary element of R
PS
.
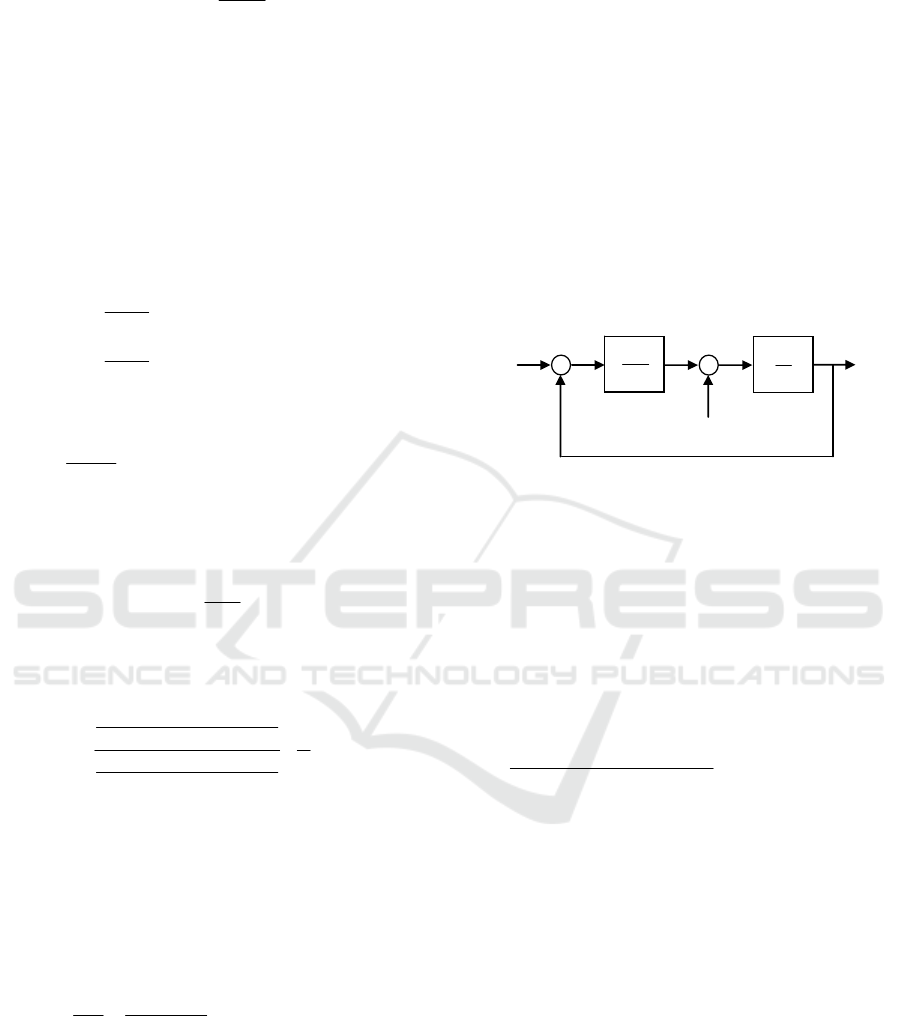
The controller K satisfying equation (20) guaran-
tees the BIBO (bounded-input bounded-output) sta-
bility of the feedback loop in Figure 4. This is a cru-
cial point for the theorems regarding the structured
singular value. If the BIBO stability is held, then the
nominal model is internally stable and theorems
related to robust stability and performance can be
used. The BIBO stability also guarantees stability of
F
L
(G, K) making possible usage of performance
weights with integration property implying non-exis-
tence of state space solutions using DGKF formulae
(see Doyle et al., 1989) due to zero eigenvalues of
appropriate Hamiltonian matrices. This procedure
results in zero steady-state error in the feedback loop
with the controller obtained as a solution to equation
(20) being neither possible in the scope of the
standard μ-synthesis using DGKF formulae, nor
using LMI approach (see Gahinet and Apkarian,
1994) leading to numerical problems in most of real-
world applications.
Figure 4: Nominal feedback loop.
The aim of global optimization in the algebraic
approach is to design a controller satisfying the
condition:
1)],,,,,,)(,([sup
221
11
gstabilizin
nnnnL
K
tt
KGF
Δ
G
, ω(–
∞,+∞
)
(22)
where n + n
1
+ n
2
is the order of the nominal feedback
system, n
1
is the order of particular solution, K
0
, t
i
are
arbitrary parameters in
)()(
211
2
2
1
10
ss
ststt
T
nnn
n
n
and µ
denotes the
structured singular value of LFT on generalized plant
G and controller K with Δ defined in (12).
Tuning parameters are positive and constrained to
the real axis since parameters of the transfer function
have to be real and due to the fact that com-plex poles
cause oscillations of the nominal feed-back loop.
A crucial problem of the cost function in (22) is
the fact that many local extremes are present. Hence,
local optimization does not yield a suitable or even
stabilizing solution. This can be overcome via
evolutionary computation solving the task very
efficiently.
5 EXAMPLE - PROBLEM
FORMULATION & SOLUTION
The problem to solve is 2
nd
order system with 1
st
order
d
u
y
re
-
k
k
D
N
A
B
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
566

astatism and uncertain time delay:
s
e
sasa
b
1
2
2
0
P
(23)
a
1
[1.8, 2.2], a
2
= 1,
b
0
[1.8, 2.2],
[0, 4]
The control objective is to find a controller for which
the robust stability and performance is held for every
plant from the set P. The weights follow from (6) and
(7):
2.0
1
a
W , 2.0
0
b
W
(24)
The time delay is treated by multiplicative uncertain-
ty (see Figure 1)
},1:)1({ C
deldeldeldel
WP
(25)
Figure 5: Bode plot of W
del
and
1
4
j
e
.
Let the nominal plant be
s
s
a
b
sP
2
2
)(
2
(26)
then for the weighting function W
del
the following
inequality must be held
P
being the set P omitting
the parametric uncertainties
)(1
)(
)(
jW
jP
jP
del
,
R
, P
P
(27)
which is equivalent with
)(1
jWe
del
j
,
R
, ];0[
d
T
(28)
The weight W
del
is defined as an envelope curve of
1
j
e
. For τ = 4, W
del
can have the Bode plot
depicted in Figure 5:
12
2
5.2)(
s
s
sW
del
(29)
The performance condition is of the form:
1
1
SW
(30)
where S is the sensitivity function and weight W
1
(see
Figure 2) is defined for the algebraic approach and D-
K iteration as follows:
50
1010010
004.0
)(
523
1
sss
sW
A
(31)
50
1010010
004.0
)(
523
1
sss
sW
KD
(32)
By the optimization of the poles α
i
via the Differen-
tial Migration and subsequent tuning by the Nelder-
Mead simplex method, resulting poles were obtained:
α
1
= 0.065, α
2
=0.063, α
3
= 2.021, α
4
= 62.338 (33)
yielding the controller
ss
ss
sK
A
62.49
0.25718.1824.618
)(
2
2
(34)
The controller obtained from the D-K iteration was
approximated by the 3
rd
order transfer function:
7-23
23
106.9980.06928.926
0.00030.04420.9680.332
)(
s
s
s
sss
sK
KD
(35)
The μ-plot in Figure 8 shows that both control-lers
have the supremum of μ below one and the ro-bust
stability and performance condition is satisfied.
a b
Figure 6: 2DOF feedback loop.
The controllers for 2DOF feedback loop (Figure
6a, 6b - algebraic approach and D-K iteration, respec-
tively) have the compensator (n
k2
, d
k2
, n
kdk2
, d
kdk2
)
defined as fraction of the factors corresponding with
most stable zero and least stable pole of K
A
and K
D-K
and feedback (n
k1
, d
k1
, n
kdk1
, d
kdk1
) and feed-forward
part (n
FW
, d
k1
, n
FW
, d
kdk1
) defined by the fraction of the
factors corresponding with remaining zeros and poles
of K
A
and K
D-K
with
0
1kFW
nn
and
FWdk
n
0
1kdk
n
(
0
1k
n
,
0
1kdk
n
being the coefficients of n
k1
and n
kdk1
of
zero exponent of s):
ss
s
d
n
k
k
62.49
0.1478 4.618
2
1
1
,
ss
d
n
k
FW
62.49
0.1478
2
1
,
s
s
d
n
k
k
1.74
2
2
(36)
0.06918.926
109.13 0.01540.3316
2
-52
1
1
ss
ss
d
n
kdk
kdk
,
0.06918.926
109.13
2
-5
1
ssd
n
kdk
FWdk
,
5-
2
2
101
2.87
s
s
d
n
kdk
kdk
(37)
10
-3
10
-2
10
-1
10
0
10
1
10
-3
10
-2
10
-1
10
0
10
1
1
4
j
e
del
W
1
srad
d
u
y
-
r
1
1
k
k
d
n
P
1k
FW
d
n
2
2
k
k
d
n
d
u
y
-
r
P
1kdk
FWdk
d
n
1
1
kdk
kdk
d
n
2
2
kdk
kdk
d
n
Control of Uncertain Time Delay System with Astatism and Parametric and Periodic Uncertainties using SSV and Factorization for
Two-Degree-of-Freedom-Controller
567

The periodicity is defined via sinusoids changing the
uncertain parameters in the intervals defined by (23):
)]sin(1[
00
00
tbb
bb
(38)
where
2
0
b
2.0
0
b
and
1.0
0
b
. The step res-
ponse for the periodic change (38) is in Figure 7.
Figure 7: Step response for periodic changes of parameters.
Figure 8: μ-plots for the controllers obtained by the D-K
iteration and algebraic approach
Figure 9: Simulations for simple feedback loop without
periodic changes – algebraic approach and D-K iteration.
Simulations in Figure 9 and 10 show that D-K
iteration yields non-zero steady-state error in contrast
to the algebraic approach having no steady state error
and faster set point tracking than the D-K iteration
controller. Simulations for periodic changes (38) in
Figure 11 and 12 prove that the 1DOF and 2DOF
feedback loops are stable for both the algebraic
approach and D-K iteration. In all simu-lations full
time delay is connected, i.e. τ = 4 s.
Figure 10: Simulations for 2DOF feedback loop without
periodic changes – algebraic approach and D-K iteration.
Figure 11: Simulations for simple feedback loop with
periodic changes – algebraic approach and D-K iteration.
Figure 12: Simulations for 2DOF feedback loop with
periodic changes – algebraic approach and D-K iteration.
y
t
0 20 40 60 80 100 120 140 160 180 200
0
50
100
150
200
250
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
-4
10
-3
10
-2
10
-1
10
0
mu Plot of Closed-loop System
Frequency
D-K iteration
Alg. approach
0 20 40 60 80 100 120 140 160 180 200
-
0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Time
Simulation
Reference
Output - D-K i teration 1DOF
Control sig nal - D- K iteration 1DOF
Output - alg. approach 1DOF
Control sig nal - alg . approach 1DOF
0 200 400 600 800 1000 1200 1400 1600
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
Time
Simulation
Reference
Output - D-K iteration 2DOF
Control signal - D-K iteration 2DOF
Output - alg. approach 2DOF
Control signal - alg. approach 2DOF
0 20 40 60 80 100 120 140 160 180 200
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Time
Simulation
Reference
Output - D-K iteration 1DOF periodic
Control signal - D-K iteration 1DOF periodic
Output - alg. approach 1DOF periodic
Control signal - alg. approach 1DOF periodic
0 200 400 600 800 1000 1200 1400 1600
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Time
Simulation
Ref erence
Output - D-K iteration 2DOF periodic
Control signal - D-K iteration 2DOF periodic
Output - alg. approach 2DOF periodic
Control signal - alg. approach 2DOF periodic
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
568

6 USER INTERFACE
The main window of the Matlab toolbox consists of
three sections (see Figure 13):
- System Definition
- Controller Design
- Simulation and Verification
Figure 13: The main window.
6.1 System Definition
System definition has the button for displaying the
dialog for entering parameters of the control plant
where the parameters of transfer function, the
maximum value of time delay and parameters for
periodic changes can be entered (Figure 14).
Figure 14: Dialog for entering parameters of the controlled
plant.
Figure 15: Dialog for entering the parameters of the weight
W
del
.
Another button displays the dialog for entering the
parameters of the weight W
del
treating uncertain time
delay (Figure 15) with button showing the Bode plot
of the weight W
del
compared to the left side of (28).
In the last part of system definition, buttons
showing dialogs for entering parameters of the
performance weight W
1
are placed. There are separate
weights for the D-K iteration and algebraic approach.
Each dialog has a button for showing the Bode plot of
the particular weight.
ACKNOWLEDGEMENTS
This work was supported by the Ministry of Educa-
tion, Youth and Sports of the Czech Republic within
the National Sustainability Programme project No.
LO1303 (MSM‐7778/2014).
REFERENCES
Barmish, B. R., 1984. Invariance of strict Hurwitz property
for polynomials with perturbed coefficients, IEEE
Transactions on Automatic Control, Vol. 29.
Barmish, B. R., 1989. A generalization of Kharitinov’s four
polynomial concept for robust stability with linearly
depen-dent coefficient perturbations, IEEE
Transactions on Automatic Control, Vol. 34, No. 2.
Barmish, B., Ackermann, J.E., Hu, H.Z., 1989. The tree
struc-tured decomposition: a new approach to robust
stability analysis, Proceedings Conference on
Information Sciences and Systems, John Hopkins
University, Baltimore.
Barmish, B., Shi, Z., 1990. Robust stability of class of
polyno-mials with coefficient depending multilinearly
on perturba-tions, IEEE Transactions on Automatic
Control, Vol. 35, No. 9.
Bartlett, A. C., Hollot, C., Lin, H., 1988. Root Locations of
an entire polytope of polynomials: it suffices to check
the edges, Mathematics of Control, Signals and
Systems, Vol. 1, No. 1, pp. 61-71.
Bialas, S., 1983. A necessary and sufficient conditions for
stability of interval matrices, International Journal of
Control, Vol. 37, pp. 717-722.
Chapellat, H., Bhattacharyya, S.P., 1989. An alternative
proof of Kharitonov’s theorem: robust stability of
interval plants, IEEE Transactions on Automatic
Control, Vol. 34, No. 3.
Chapellat, H., Dahleh, M., Bhattacharyya, S.P., 1993.
Robust stability manifolds for multilinear interval
systems, IEEE Transactions on Automatic Control,
Vol. 38, No. 2.
Dlapa, M., 2011. “Controller Design for a Two Tank
System Using Structured Singular Value and Direct
Search Methods,” 18th World Congress of the
International Federation of Automatic Control (IFAC),
August 28 - September 2, Milan, Italy, pp. 7511-7516,
ISSN: 1474-6670.
Control of Uncertain Time Delay System with Astatism and Parametric and Periodic Uncertainties using SSV and Factorization for
Two-Degree-of-Freedom-Controller
569

Dlapa, M., 2014. "Air-Heating Set Control via Direct
Search Method and Structured Singular Value," 13th
European Control Conference (ECC 2014), June 24-
27, Strasbourg, France, pp. 600-605, ISBN 978-3-
9524269-2-0.
Dlapa, M., 2017. „Cluster Restarted DM: New Algorithm
for Global Optimisation“. Intelligent Systems
Conference 2017 (IntelliSys 2017), September 7-8,
London, UK, pp. 1130-1135, ISBN 978-1-5090-6435-
9.
Dlapa, M., 2018. „General Parametric and Periodic
Uncertainties and Time Delay Robust Control Design
Toolbox,“ IEEE The 19th International Conference on
Industrial Technology (IEEE ICIT 2018), February 20-
22, Lyon, France, pp. 181-186, ISBN 978-1-5090-
5948-5.
Doyle, J. C., Wall, J., Stein, G., 1982. “Performance and
robust-ness analysis for structured uncertainty,” in
Proceedings of the 21st IEEE Conference on Decision
and Control, pp. 629-636.
Doyle, J. C., 1985. “Structure uncertainty in control system
design,” in Proceedings of 24th IEEE Conference on
decision and control, pp. 260-265.
Doyle, J. C., Khargonekar, P. P., Francis, B.A., 1989.
“State-space solutions to standard H2 and H∞ control
problems,” IEEE Transactions on Automatic Control,
vol. 34, no. 8, pp. 831-847.
Packard, A., Doyle, J. C., 1993. “The complex structured
singular value,” Automatica, vol. 29(1), pp. 71-109.
Fu, M., Dasgupta, S., Blondel, V., 1995. “Robust stability
under a class of nonlinear parametric perturbations,”
IEEE Transactions on Automation Control, Vol. 40,
No. 2.
Gahinet, P., Apkarian, P., 1994. “A linear matrix inequality
app-roach to H∞ control,” International Journal of
Robust and Nonlinear Control, 4, 421-449.
Kharitonov, V., 1978. Asymptotic stability of an
equilibrium position of a family of linear differential
equations, Differencialnye Uravneniya, Vol. 14.
Packard, A., Doyle, J. C., 1993. “The complex structured
singular value,” Automatica, vol. 29(1), pp. 71-109.
Sideris, A., de Gaston, R., 1986. Multivariable stability
margin calculation with uncertainty correlated
parameters, Proceedings Conference on Decision and
Control, Athens.
Stein, G., Doyle, J., 1991. “Beyond Singular Values and
Loop-shapes,” AIAA Journal of Guidance and Control,
Vol. 14, No. 1, pp. 5-16.
Zadeh, L., Desoer, C., 1963. Linear System Theory: The
State Space Approach, McGraw-Hill, New York.
Internet: http://dlapa.cz/homeeng.htm
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
570
