Incremental Principal Component Analysis:

Exact Implementation and Continuity Corrections

Vittorio Lippi

and Giacomo Ceccarelli

Fachgebiet Regelungssysteme Sekretariat EN11, Technische Universit

at Berlin, Einsteinufer 17, Berlin, Germany

Dipartimento di Fisica, Universit

a di Pisa, Largo Bruno Pontecorvo 2, I-56127 Pisa, Italy

Keywords: PCA, On-line, Incremental, Dimensionality Reduction.

Abstract:

This paper describes some applications of an incremental implementation of the principal component analysis

(PCA). The algorithm updates the transformation coefﬁcients matrix on-line for each new sample, without

the need to keep all the samples in memory. The algorithm is formally equivalent to the usual batch version,

in the sense that given a sample set the transformation coefﬁcients at the end of the process are the same.

The implications of applying the PCA in real time are discussed with the help of data analysis examples. In

particular we focus on the problem of the continuity of the PCs during an on-line analysis.

1 INTRODUCTION

1.1 Incremental PCA

Principal Component Analysis (PCA) is a widely

used technique and a well-studied subject in the lit-

erature. PCA is a technique to reduce data dimen-

sionality of a set of correlated variables. Several natu-

ral phenomena and industrial processes are described

by a large number of variables and hence their study

can beneﬁt from the dimensionality reduction PCA

has been invented for. As such PCA naturally ap-

plies to statistical data analysis. This means that such

technique is traditionally implemented as an ofﬂine

batch operation. Nevertheless, PCA can be useful

when applied to data that are available incrementally,

e.g. in the context of process monitoring (Dunia et al.,

1996) or gesture recognition (Lippi et al., 2009). The

PCA can be applied to a data-ﬂow after deﬁning the

transformation on a representative off-line training set

set using the batch algorithm (Lippi and Ceccarelli,

2011). This approach can be used in pattern recog-

nition problems for data pre-processing (Lippi et al.,

2009). Nevertheless one can imagine an on-line im-

plementation of the algorithm. An on-line implemen-

tation is more efﬁcient in terms of memory usage than

a batch one. This can be particularly relevant for

memory consuming data-sets such as image collec-

tions; in fact in the ﬁeld of visual processing some

techniques to implement incremental PCA have been

proposed, see for example (Arta

c et al., 2002). PCA

consists of a linear transformation to be applied to the

data-set. Dimensionality reduction is performed by

selecting a subset of the transformed variables that

are considered more relevant in the sense that they

exhibit a larger variance compared to the others. Usu-

ally the transformation is calculated and computed on

the Z-score, and hence the averages and the variances

of the dataset are taken into account. Depending on

the applications the algorithm has been extended in

different ways, adding samples on-line as presented

in (Arta

c et al., 2002) or incrementally increasing the

dimension of the reduced variable subset as seen in

(Neto and Nehmzow, 2005). A technique to dynam-

ically merge and split the variable subsets has been

presented in (Hall et al., 2000) Several approximate

incremental algorithms have been proposed for PCA,

e.g. see (Shamir, 2015) and (Boutsidis et al., 2015),

as well as for singular value decomposition (Sarwar

et al., 2002). An implementation for on-line PCA

has been proposed, for example, for the R language

(Degrasand and Cardot, 2015). In some cases the in-

cremental process is designed to preserve some spe-

ciﬁc information; for example in (Hall et al., 1998)

the average of the samples is updated with new obser-

vations.

Currently, to the best of our knowledge, there is

no available description of an exact incremental im-

plementation of PCA, where exact means that the

transformation obtained given n samples is exactly the

same as would have been produced by the batch algo-

Lippi, V. and Ceccarelli, G.

Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections.

DOI: 10.5220/0007743604730480

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 473-480

ISBN: 978-989-758-380-3

473

rithm, including the z-score normalization, a step that

is not included in previous works presenting a simi-

lar approach like(Arta

c et al., 2002). We decided in

light of this to describe the algorithm in detail in this

paper. The incremental techniques cited above (Hall

et al., 1998; Arta

c et al., 2002; Hall et al., 2000) are

designed to update the reduced set of variables and

change its dimensionality when it is convenient for

data representation. In the present work, no indica-

tion is provided for which subset of variables should

be used , i.e. how many principal components to con-

sider. All the components are used during the algo-

rithm to ensure the exact solution. After describing

the exact algorithm some implication of using this in-

cremental analysis are discussed. In particular, we

provide an intuitive deﬁnition of continuity for the ob-

tained transformation and then we propose a modiﬁed

version designed to avoid discontinuities.

The concept of continuity is strictly related to the

incremental nature of the proposed algorithm: in stan-

dard PCA the batch analysis implies that the notion of

time does not exist, e.g. the order of the elements in

the sample set is not relevant for the batch algorithm.

In our treatment we instead want to follow the time

evolution of variances and eigenvectors. We are thus

lead to consider a dynamical evolution.

The paper is organized as follows. In the remain-

ing part of the Introduction we recall the PCA algo-

rithm and we introduce the notation used. In Section

2.1 we give a detailed account of the incremental al-

gorithm for an on-line use of PCA. In Section 2.2 we

address the problems related to the data reconstruc-

tion, in particular those connected with the signal con-

tinuity. In Sections 3, 4 we then present the results of

some applications to an industrial data set and draw

our conclusions.

1.2 The Principal Component Analysis

The computation for the PCA starts considering a set

of observed data. We suppose we have m sensors

which sample some physical observables at constant

rate. After n observations we can construct the matrix













(1)

where x

is a row vector of length m representing the

measurements of the i

time step so that X

is a n × m

real matrix whose columns represent all the values of

a given observable.

The next step is to deﬁne the sample means ¯x

and

standard deviations σ

with respect to the columns

(i.e. for the observables) in the usual way as

¯x

n( j)

∑

i=1

n(i j)

(2)

n( j)

n − 1

∑

i=1



n(i j)

− ¯x

n( j)



(3)

where in parentheses we write the matrix and vector

indices explicitly. In this way we can deﬁne the stan-

dardized matrix for the data as







− ¯x







−1

(4)

where Σ

≡ diag(σ

) is a m × m matrix. The covari-

ance matrix Q

of the data matrix X

is then deﬁned

n − 1

. (5)

We see that Q

is for any n a symmetric m× m matrix

and it is positive deﬁnite.

Finally we make a standard diagonalization so that

we can write

= C

−1













(6)

where the (positive) eigenvalues λ

are in descending

order: λ

> λ

i+1

. The transformation matrix C

is the

eigenvectors matrix and it is orthogonal, C

−1

= C

Its rows are the principal components of the matrix Q

and the value of λ

represents the variance associated

to the i

principal component. Setting P

= Z

, we

have a time evolution for the values of the PCs until

time step n.

We recall that the diagonalization procedure is not

uniquely deﬁned: once the order of the eigenvalues is

chosen, one can still choose the “sign” of the eigen-

vector for one-dimensional eigenspaces and a suitable

orthonormal basis for degenerate ones (in Section 2.2

we will see some consequences of this fact). We stress

that, since only the eigenspace structure is an intrinsic

property of the data, the PCs are quantity useful for

their interpretation but they are not uniquely deﬁned.

2 ON-LINE ANALYSIS

2.1 Incremental Algorithm

The aim of the algorithm is to construct the covari-

ance matrix Q

n+1

starting from the old matrix Q

and

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

474

the new observed data x

n+1

. To do this, at the be-

ginning of step (n + 1), we consider the sums of the

observables and their squares after step n:

n( j)

∑

i=1

n(i j)

(7)

n( j)

∑

i=1

n(i j)

(8)

These sums are updated on-line at every step.

From these quantities we can recover the starting

means and standard deviations: ¯x

= a

/n and (n −

1)σ

= b

− na

. Similarly the current means and

standard deviations are also simply obtained.

The key observation to get an incremental algo-

rithm is the following identity:

n+1



+ ∆



−1

n+1

(9)

where y = x

n+1

− ¯x

n+1

is a row vector and ∆ is a

n × m matrix built repeating n times the row vector

δ = ¯x

− ¯x

n+1

. By deﬁnition nQ

n+1

= Z

n+1

and,

expanding the preceding identity, we get

n+1

=Σ

−1

n+1

−1

n+1

−1

n+1

∆)Σ

−1

n+1

−1

n+1

(∆

)Σ

−1

n+1

−1

n+1

∆

∆Σ

−1

n+1

z (10)

where z = yΣ

−1

n+1

and we used the fact that the Σs are

diagonal.

Recalling that by hypothesis all the columns of the

matrix Z

have zero mean and that the columns of the

matrix ∆ have the same number, we see that terms in

parentheses are zero. Thus

n+1

=Σ

−1

n+1

−1

n+1

nΣ

−1

n+1

δΣ

−1

n+1

+ z

z (11)

where δ

δ, z

z and Q

are three m × m matrices. We

now see that we can compute Q

n+1

by making opera-

tions only on m× m matrices and with the sole knowl-

edge of Q

and x

n+1

The computational advantage of this strategy is

that we do not need to save in the memory all the

sampled data X

n+1

and moreover we do not need to

perform the explicit matrix product in eq. (5), which

would require a great amount of memory and time

for n ≈ 10

5/6

. Consequently this algorithm can be

fruitfully applied in situations where the sensors num-

ber m is small (e.g. of the order of tens) but the data

stream is expected to grow quickly.

The meaning of the normalization procedure de-

pends on the process under analysis and the meaning

that is associated to the data within the current study:

both centering around the empirical mean and divid-

ing by the empirical variance can be avoided by re-

spectively setting ∆ = 0 or Σ = I.

In practice, one keeps n

start

observations and com-

pute Q as given by eq. (5) and the relative C (and

hence P

start

). Then the updated Qs are used, step by

step, to compute the n

values for the evolving PCs

in the standard way as p

= z

. In this way the last

sample is equal for any n to the one that would result

from a batch analysis until time step n. Instead the

whole sequence of the p

values with n

start

< n < n

ﬁnal

would not coincide with those from P

ﬁnal

, since the

Qs matrices change every time a sample is added, and

likewise for the Cs matrices. The most relevant im-

plications of this fact will be considered in the next

subsection.

The library for the present implementation of the

algorithm is available on the Mathworks website un-

der the name incremental PCA.

2.2 Continuity Issues

We now consider the problem of the continuity for the

PCs during the on-line analysis. In a batch analysis,

one computes the PCs using all the data at the end of

the sampling, obtaining the matrix C

ﬁnal

, and then, by

applying this transformation and its inverse, one can

pass from the original data set to the set PCs values.

Of course, since we are considering sampled data, we

cannot speak of continuity in a strict sense. As pre-

viously stated, the temporal evolution of the data is

not something relevant for the batch PCA. Regardless,

we may intuitively expect to use a sampling rate of at

least two times the signal bandwidth (for the sampling

theorem) usually even more, i.e. ten times. We hence

expect a limited difference between two samples in

proportion to the overall signal amplitude. For sam-

pled data we can then deﬁne continuity in a intuitive

sense as a condition where the difference between two

consecutive samples is smaller than a given thresh-

old. A discontinuity in the original samples may be

reﬂected in the principal components depending on

the transformation coefﬁcients, in detail

− p

n−1

= z

− z

n−1

(12)

that is equal to

− p

n−1

= (z

− z

n−1

+ z

n−1

− C

n−1

) (13)

The ﬁrst term would be the same for the batch pro-

cedure (in that case with constant C) and the second

term shows how p is changing due to the change in

Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections

475

Samples

50 100 150 200 250

Value

200

400

600

800

1000

1200

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

Var

100

PC var

Cumulative Var

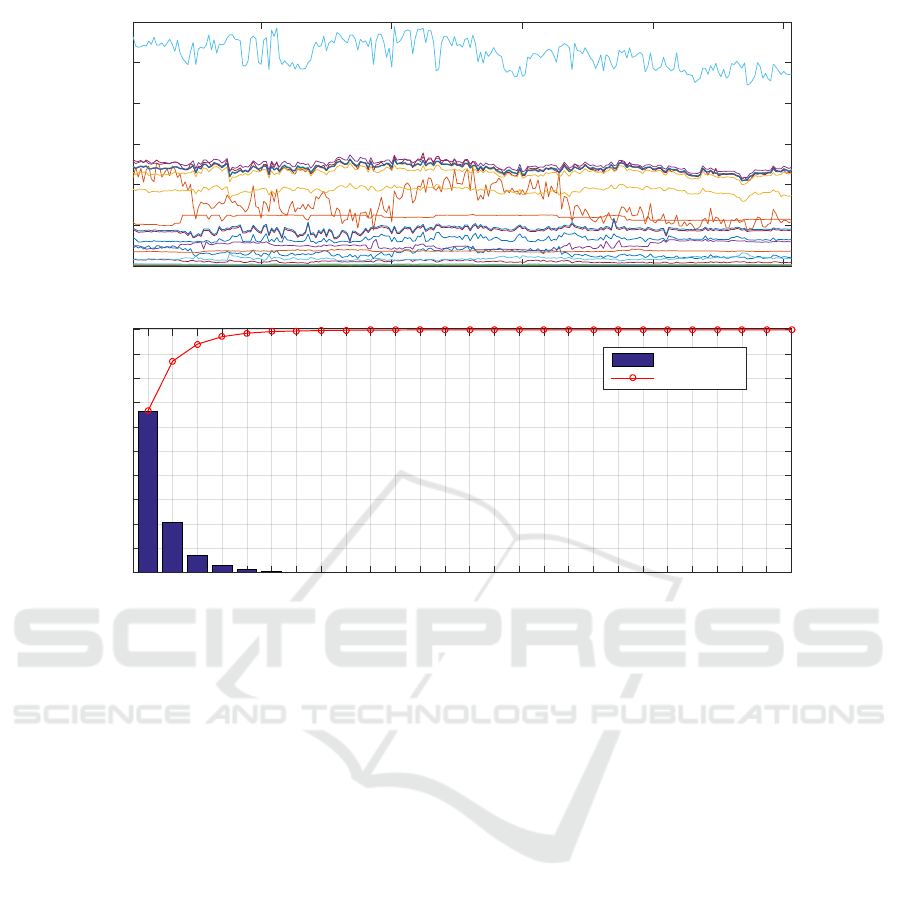
Figure 1: Top, data-set used in the example. Bottom, variances associated to the PCs of the system.

coefﬁcients C. We can regard this term as the source

of discontinuities due to the incremental algorithm.

To understand the problems that could arise, from

the point of view of the continuity of the PCs values,

let us consider the on-line procedure more closely.

We start with some the matrices Q

start

and C

start

At a numerical level the eigenvalues are all differ-

ent (since the machine precision is at least of or-

der 10

−15

), so that we have a set of formally one-

dimensional eigenspaces, from which the eigenvec-

tors are taken. Going on in the time sampling, we

naturally create m different time series of eigenvec-

tors.

We could expect that the difference of two subse-

quent eigenvectors of a given series be slowly varying

(in the sense of the standard euclidean norm), since

they come from different Cs that are obtained from

different Qs which differ only slightly (i.e. for the

last x

n+1

). But this is not fully justiﬁed, since the PCs

are not uniquely deﬁned and in some case two subse-

quent vectors of p

and p

n+1

can differ considerably,

as shown in the exaple in Figure 4. There are three

ways in which one or more eigenvector series could

exhibit a discontinuity (in the general sense discussed

above).

• Consider the case of a given eigenvalue associ-

ated with two eigenspaces at two subsequent time

steps, spanned by the vectors c

and c

n+1

. They

belong by hypothesis to two close “lines” but the

algorithm can choose c

n+1

in the “wrong” direc-

tion. In this case, to preserve the on-line continu-

ity as much as possible, we take the new PC to

be −c

n+1

, i.e. minus the eigenvector given by the

diagonalization process at step n + 1. The “right”

orientation can be identiﬁed with simple consid-

erations on the scalar product of c

with c

n+1

. Re-

calling the considerations at the end of Section

1.2, this substitution does not change the meaning

of our analysis.

• Consider the case where the differences of a group

of ν contiguous eigenvalues are much smaller than

the others: we can say that these eigenvalues cor-

respond in fact to a degenerate eigenspace. In this

case we can choose an inﬁnite number of ν or-

thonormal vectors that can be legitimately con-

sidered our PCs, but the incremental algorithm

can choose, at subsequent time steps, two basis

which considerably differ. To overcome this prob-

lem, we must apply to the new transformation a

change of basis in such a way not to modify the

eigenspaces structure and to “minimize” the dis-

tance with the old basis. Although the case of a

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

476

proper degenerated space on real data is virtually

impossible, as the difference between two or more

eigenvalues of Q is approaching zero, the numer-

ical values of the associated PCs can become dis-

continuous in a real time analysis. This by itself

does not represent an error in an absolute sense

in computing C

, as the speciﬁc C

is the same as

that which would be computed off-line.

• In the two previous cases the discontinuity was

due to an ambiguity of the diagonalization matrix.

A third source of discontinuity can consist into the

temporal evolution of the eigenvalues. Consider

two one-dimensional eigenspaces associated, one

with a variance that is increasing in time, the other

with a variance that is decreasing: there will be a

time step ¯n the two eigenspaces are degenerate.

This is called a “level crossing” and corresponds

in the algorithm to an effective swap in the “ cor-

rect” order of the eigenvectors. To restore conti-

nuity, the two components must me swapped.

3 EXAMPLES AND RESULTS

A publicly available data-set was used for this ex-

ample: it consists of snapshot measurements on 27

variables from a distillation column, with a sampling

rate of one every three days, measured over 2.5 years.

Sampling rate and time in general are not relevant per

se for PCA. Nevertheless, as we discussed the con-

tinuity issue it is interesting to see how the algorithm

behaves on physical variables representing the contin-

uous evolution of a physical system.

Variables represent temperatures, pressures, ﬂows

and other kind of measures (the database is of indus-

trial origin and the exact meaning of all the variables

is not speciﬁed). Details are available on-line (Dunn,

2011).

This kind of data set includes variables that are

strongly correlated amongst each other, variables with

a large variance and variables almost constant during

a time of several samples. In Figure 1 we display the

time evolution of the variables and the standard batch

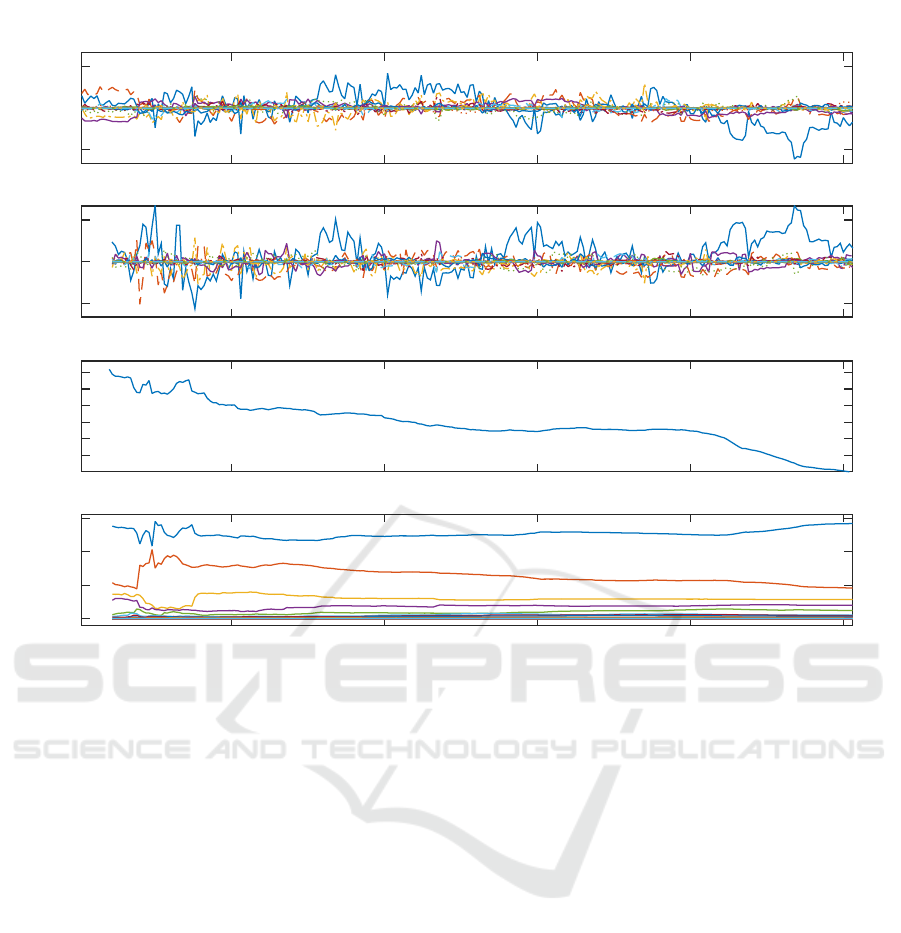
PCA. In Figure 3 the evolution of the covariance ma-

trix Q and the incremental PCs are shown. Notice that

the values p

are obviously not equal to the ones com-

puted with the batch method until the last sample. The

matrix Q almost constantly converges to the covari-

ance matrix computed with the batch method. Note

that at the beginning the Frobenius norm of the differ-

ence between the two matrices sometimes grows with

the addition of some samples, the number of samples

needed for Q to settle to the ﬁnal value depends on the

regularity of the data and the variations in Q may rep-

resent an interesting description of the analyzed pro-

cess. This is expected for the estimator of the covari-

ance matrix until m & n. While the sample covariance

matrix is an unbiased estimator for n → ∞, it is known

to converge inefﬁciently (Smith, 2005).

In order to quantify the efﬁciency of the algorithm

the computational of the proposed incremental solu-

tion has been compared with the batch implementa-

tion provided by the Matlab built-in function PCA on

a Intel Core i7-7700HQ CPU running at 2.81 GHz,

with windows 10 operative system. The results are

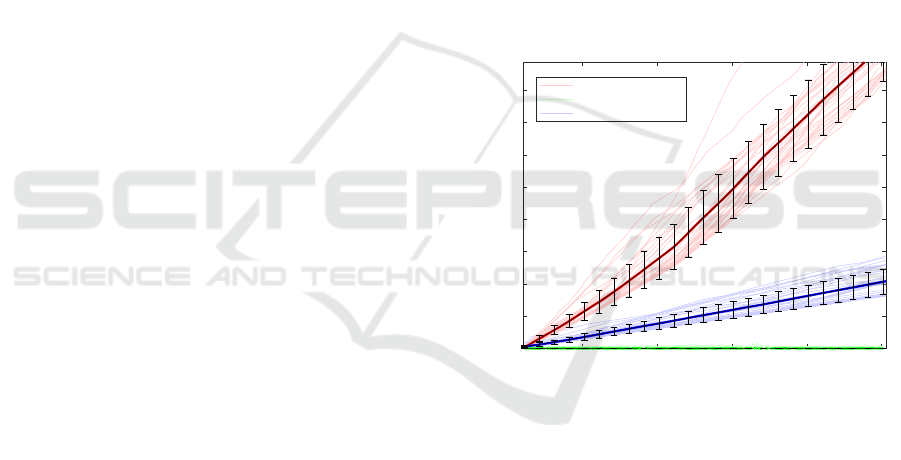
shown in Figure 2. The time required to execute the

incremental algorithm grows linearly with the number

of samples while the batch presents an increase of the

execution time associated with the size of the dataset.

As reasonably expected, the batch implementation is

more efﬁcient than the incremental one when the PCA

is computed on the whole dataset, while the incremen-

tal implementation is more efﬁcient when samples are

added incrementally.

50 100 150 200 250

Samples

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Time [s]

Batch (cumulative)

Batch(single case)

Incremental(cumulative)

Figure 2: Time required to execute the incremental PCA

and the batch implementation as function of the number of

samples. For the batch algorithm both the time required

to compute the PCA on the given number of samples (sin-

gle case) and the cumulative time required to perform the

PCA with each additional sample (cumulative) are shown.

The computational time is measured empirically and can

be affected by small ﬂuctuations due to the activity of the

operative system: in order to take this in account the aver-

age times (darker lines) and their standard deviations (error

bars) are computed on 33 trials. The batch implementation

is more efﬁcient than the incremental one when the PCA

is computed on the whole dataset, while the incremental

implementation is more efﬁcient when samples are added

incrementally.

In Figure 5 the variance of the whole incremental

PCA is shown. Comparing it with Figure 1 (bottom),

it is evident that the incremental PCs that are not lin-

early independent over the whole sampling time have

a slightly different distribution of the variance com-

Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections

477

50 100 150 200 250

Score

-10

50 100 150 200 250

Score

-10

50 100 150 200 250

||COV-wCOV||

samples

50 100 150 200 250

Figure 3: Application of the incremental algorithm to the sample data-set. The uppermost picture shows the 27 principal

components computed with the batch algorithm, the second from top the incremental PCA computed without continuity

check, the third picture from top represents the Frobenius norm of the difference between the covariance matrix computed

through the incremental algorithm and a given sample and the one computed on the whole sample-set. The lowermost picture

represents the variances associated to the PCs (eigenvalues of covariance matrix). The covariance matrix and the variable

values are the same for the batch algorithm and the on-line implementation when they are provided with the same samples.

The differences in the pictures are due to the fact that same transformation computed with the batch algorithm is applied to

the whole set, while the one computed online changes with every sample.

pared to the PCs computed with the batch algorithm.

Nevertheless they are a good approximation in that

they are still ordered by variance and most of the vari-

ance is in the ﬁrst components (i.e. more than 90% is

in the ﬁrst 5 PCs).

4 DISCUSSION AND

CONCLUSIONS

The continuity issues arise for principal components

with similar variances. When working with real data

this issue often affects the components with smaller

variance which are usually dropped and hence it can

be reasonable to execute the algorithm without taking

measures to preserve the continuity.

Nevertheless it should be noticed that, in some

process analysis, the components with a smaller vari-

ance identify the stable part of the analyzed data, and

hence the one identifying the process, e.g. the con-

trolled variables in a human movement (Lippi et al.,

2011) or the response of a dynamic system known

through the input-output samples (Huang, 2001).

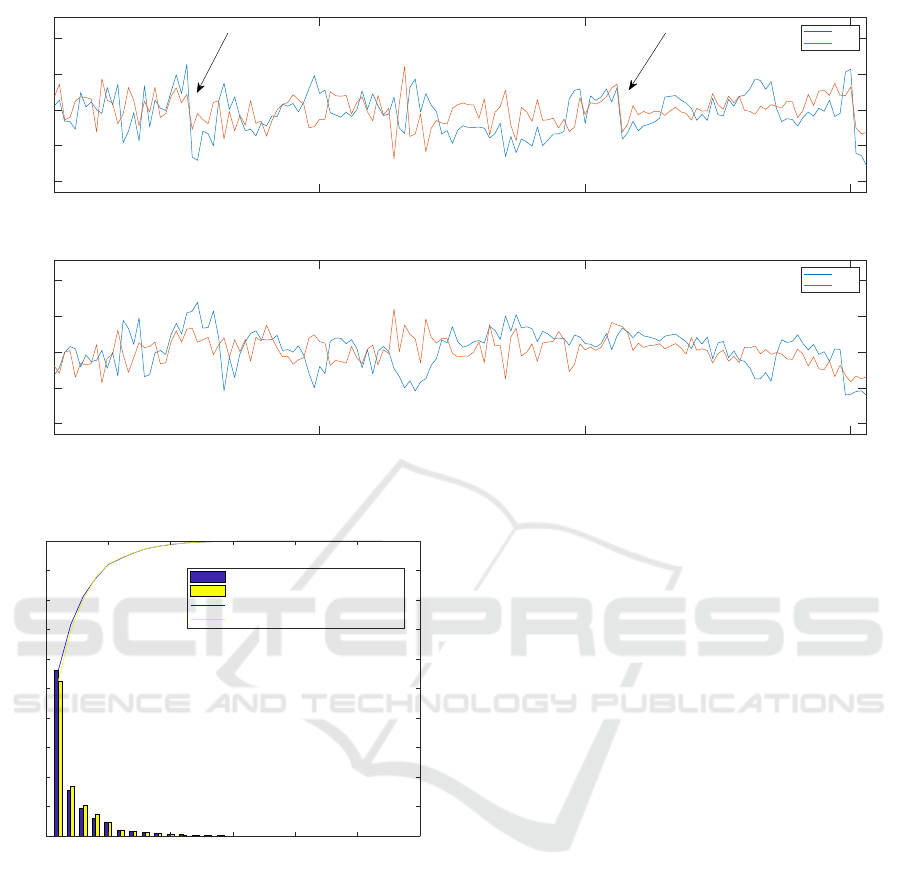
In Figure 4 the effects of discontinuities are

shown: two discontinuities present into the values of

one of the principal components are ﬁxed according

to Section 2.2. In case the continuity is imposed the

phenomenon is limited, but this comes at the price

of modifying the exact computation of the eigenvec-

tors for Q at a given step, in case of a degenerate

eigenspace. Anyway the error introduced on the Q

eigenvectors depends on the threshold used to estab-

lish that two slightly different eigenvalues are degen-

erate and so we can still consider the transformation

to be “exact”, but not at machine precision. In the

reported example, the two big discontinuities high-

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

478

100 150 200 250

-2

-1

Score

Without Continuity Constraint

PC 9

PC 10

100 150 200 250

Samples

-2

-1

Score

With Continuity Constraint

PC 9

PC 10

Figure 4: The ﬁgure shows the 9

and the 10

PCs computed without (top) and with (bottom) continuity constraints. Note

the discontinuity addressed by the arrows.

0 5 10 15 20 25 30

100

Var[%]

On-line PCA with continuity correction

Batch PCA

cumulative Var. On-line

cumulative Var. Batch

Figure 5: Variances and cumulative variance of the PCs

computed with the on-line algorithm including the continu-

ity correction (blue) and the ones computed with the batch

algorithm (yellow).The order of the on-line computed PCs

is the one produced by the transformation.. The difference

between the two set of PCs’ variances are due to the conti-

nuity correction and the fact that the variance of the on-line

series is computed on the whole set of data.

lighted by arrows disappear when the continuity is

imposed. Notice that the two PCs have different val-

ues in the corrected version also before the two big

discontinuities because of previous corrections on Q.

The choice as to whether or not the continuity is im-

posed depends on the application, on the data-set and

on the meaning associated with the analysis.

4.1 Software

The MATLAB software implementing

the function and the examples shown

in the ﬁgures is available at the URL:

https://it.mathworks.com/matlabcentral/ﬁleexchange/

69844-incremental-principal-component-analysis

ACKNOWLEDGMENTS

The authors thank Prof. Thomas Mergner for the

support to this work.

The ﬁnancial support from the European project H

(http://www.h2rproject.eu/) is appreciated.

We gratefully acknowledge ﬁnancial support for the

project MTI-engAge (16SV7109) by BMBF

G.C. has been supported by I.N.F.N.

REFERENCES

Arta

c, M., Jogan, M., and Leonardis, A. (2002). Incremen-

tal PCA for on-line visual learning and recognition.

In Pattern Recognition, 2002. Proceedings. 16th In-

ternational Conference on, volume 3, pages 781–784.

IEEE.

Boutsidis, C., Garber, D., Karnin, Z., and Liberty, E. (2015).

Online principal components analysis. In Proceedings

of the Twenty-Sixth Annual ACM-SIAM Symposium on

Discrete Algorithms, pages 887–901. SIAM.

Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections

479

Degrasand, D. and Cardot, H. (2015). onlinePCA: Online

Principal Component Analysis.

Dunia, R., Qin, S. J., Edgar, T. F., and McAvoy, T. J. (1996).

Identiﬁcation of faulty sensors using principal compo-

nent analysis. AIChE Journal, 42(10):2797–2812.

Dunn, K. (2011). http://openmv.net/info/distillation-tower.

Hall, P., Marshall, D., and Martin, R. (2000). Merging and

splitting eigenspace models. Pattern analysis and ma-

chine intelligence, IEEE transactions on, 22(9):1042–

1049.

Hall, P. M., Marshall, A. D., and Martin, R. R. (1998). In-

cremental eigenanalysis for classiﬁcation. In BMVC,

volume 98, pages 286–295.

Huang, B. (2001). Process identiﬁcation based on last prin-

cipal component analysis. Journal of Process Control,

11(1):19–33.

Lippi, V. and Ceccarelli, G. (2011). Can principal com-

ponent analysis be applied in real time to reduce the

dimension of human motion signals? In BIO Web of

Conferences, volume 1, page 00055. EDP Sciences.

Lippi, V., Ruffaldi., E., Avizzano, C. A., and Bergamasco,

M. (2009). Recognition of hand gestures tracked by a

dataglove: Exploiting hidden markov models discrim-

inative training and environment description to im-

prove recognition performance. In 5th International

Workshop on Artiﬁcial Neural Networks and Intelli-

gent Information Processing.

Lippi, V., Ruffaldi, E., Zelic, G., Lagarde, J., Tripicchio, P.,

and Avizzano, C. A. (2011). Uncontrolled manifold

and juggling: Retrieving a set of controlled variables

from data. In BIO Web of Conferences, volume 1, page

00056. EDP Sciences.

Neto, H. V. and Nehmzow, U. (2005). Incremental PCA: An

alternative approach for novelty detection. Towards

Autonomous Robotic Systems.

Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2002).

Incremental singular value decomposition algorithms

for highly scalable recommender systems. In Fifth In-

ternational Conference on Computer and Information

Science, pages 27–28.

Shamir, O. (2015). Convergence of stochastic gradient de-

scent for pca. arXiv preprint arXiv:1509.09002.

Smith, S. T. (2005). Covariance, subspace, and intrinsic

crame r-rao bounds. Signal Processing, IEEE Trans-

actions on, 53(5):1610–1630.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

480