An Approach of Extracting God Class Exploiting Both Structural and
Semantic Similarity
Pritom Saha Akash, Ali Zafar Sadiq and Ahmedul Kabir
Institute of Information Technology, University of Dhaka, Bangladesh
Keywords:
Code Smell, Refactoring, God Class, LDA, Cohesion, Coupling.
Abstract:
Code smell is a sign of design and development flaws in a software system which reduces the reusability and
maintainability of the system. Refactoring is a continuous practice of eliminating code smells from the source
code. A God Class is one of the most common code smells where too many responsibilities are defined in a
single class. God Classes reduce the quality of a system by increasing coupling and decreasing cohesion. In
this paper, we propose an approach for extracting a God Class into new classes by increasing class cohesion.
For this, both structural and semantic relationship between methods in a class are analyzed, and strongly
related methods are clustered and suggested to be in the same class. We assessed the proposed approach on
fifteen real God Classes from two well-known open source systems and it is shown that the cohesion among the
classes is increased after refactoring. A comparative result of our approach with a similar existing approach is
presented and it is found that our approach provides better results for almost all the experimented God Classes.
1 INTRODUCTION
Code smell being a programming practice, always de-
grades the quality, understandability and changeabil-
ity of source code (Fowler, 1999). It violates the
fundamental rules of Object Oriented Programming
(OOP) concept. One of the principle guidelines of
OOP is that, a class should focus on a specific respon-
sibility (high cohesion) and have limited dependency
with other classes (low coupling). However, through-
out the life cycle of a software development, it under-
goes many changes and manipulations, and for which
a class may become complex and large with addi-
tional responsibilities. It deteriorates the quality and
generates bad code smell which is generally known as
God Class (GC) or Blob (Brown et al., 1998).
A GC increases coupling and decreases cohesion
within classes which makes it difficult to meet change
requirements in the highly coupled and loosely cohe-
sive software applications. For this, eventually, it be-
comes very difficult for the developers and significant
design efforts are needed to maintain the application
with the course of time. Thus, for enhancing the mod-
ularization of a system, a GC needs to be restructured
by extracting it into smaller classes according to the
specific responsibility. The research area which ad-
dresses the problem of GC is known as refactoring,
specifically extract class refactoring (Fowler, 1999),
(Mens and Tourwe, 2004). There are two major chal-
lenges in refactoring a GC into several classes. First
one is to define which classes are to be identified as
GCs and second one is to extract the contextual simi-
larities among the methods in a class.
A large number of works have been carried out in
the area of GC refactoring. A two-step technique of
GC refactoring has been proposed in (Bavota et al.,
2010a) where the method chains are extracted by cal-
culating cohesion within the methods. Both structural
and semantic similarity between methods are con-
sidered while calculating the cohesion. A weighted
graph is then built from the calculated cohesion mea-
sures and a predefined threshold is used to cut the
edges of the graph. As an extension of this work, a
new research has been published where they empiri-
cally evaluated the effectiveness of their tool on real
GCs from existing open source systems (Bavota et al.,
2014). In another work, an approach based on graph
theory has been proposed in (Bavota et al., 2010b),
where the MaxFlow-MinCut algorithm is used to split
a class with low cohesion into two classes with higher
cohesion. One limitation of this approach is that, it
can only split a class into two classes. In (Gethers
and Poshyvanyk, 2010), an approach based on the
Relational Topic Models (RTM) has been proposed
to calculate a coupling metric for the object-oriented
software systems aiming at moving a class to a more
Akash, P., Sadiq, A. and Kabir, A.
An Approach of Extracting God Class Exploiting Both Structural and Semantic Similarity.
DOI: 10.5220/0007743804270433
In Proceedings of the 14th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2019), pages 427-433
ISBN: 978-989-758-375-9
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
427

suitable package.
In this paper, similar to the work in (Bavota et al.,
2014), we propose an approach for extracting a GC
into multiple classes exploiting both structural and
semantic similarity between methods. To calculate
semantic similarity between methods, textual infor-
mation from the methods is extracted to find impor-
tant topics using Latent Dirichlet Allocation (LDA)
algorithm (Blei et al., 2003). Then, the cosine simi-
larity between the topic distribution of two methods
is calculated. Structural similarity is calculated us-
ing the same procedure used in (Bavota et al., 2014).
Semantic and structural similarity matrices are then
combined using predefined weights to generate final
method by method similarity matrix. At last, a hier-
archical clustering (Tan et al., 2005; Jain and Dubes,
1988) algorithm is used to split the classes based on
this similarity matrix.
The remainder of this paper is structured as fol-
lows. Section 2 describes the related knowledge about
the LDA and the hierarchical clustering algorithm
used in this study. Section 3 presents the proposed ap-
proach. In Section 4, the empirical assessment of our
approach is presented. Finally, Section 5 concludes
the paper along with the direction for future work.
2 PRELIMINARIES
To understand our approach, the knowledge about the
LDA and Hierarchical clustering algorithm is impor-
tant. They are briefly discussed in this section.
2.1 Latent Dirichlet Allocation
LDA (Blei et al., 2003) is a generative probabilistic
model used for a collection of discrete datasets (e.g a
text corpus). It is also used as a topic model for dis-
covering abstract topics from a collection of text doc-
uments. LDA takes a number of documents as input
and provides a probabilistic model as output which
can describe how many words belong to a topic and
how a document is associated with the extracted top-
ics. The LDA model has the following fundamental
components:
• Word: A word is the unit element of data. In the
LDA model, a vocabulary of a set of words is built
such as, V = {w
1
, w
2
..., w
v
} .
• Document: A document is a sequence of N words
defined as d = (w
1
, w
2
, ..., w
N
). As an input of a
LDA model, a document is represented as a vector
of word occurrences.
• Corpus: A corpus is a collection of M documents
represented by, C = (d
1
, d
2
, ..., d
M
).
In a LDA model, a topic generates words. The prob-
ability that a word is generated by a specific topic
is determined by a symmetric Dirichlet distribution.
And, the probability that a document contains a word
from a specific topic comes from a different sym-
metric Dirichlet distribution. More technically, when
modeling a corpus, the following generative process
is assumed given a corpus with M documents and K
topics:
1. For each topic k ∈ {1, ..., K}, select φ
k
∼ Dirichlet
distribution(β).
2. For each document d ∈ {1, ..., M}, select θ
d
∼
Dirichlet distribution(α).
3. For each word i ∈ {1, ..., N
d
} in a document d
(a) Select a topic z
di
∼ Multinomial(θ
d
).
(b) Select a word w
di
∼ Multinomial(φ
d
).
LDA has been used in many software engineering
analysis tasks such as (Asuncion et al., 2010; Thomas
et al., 2010; Savage et al., 2010; Gethers et al., 2011).
It has been used as many preprocessing tasks like re-
ducing the feature size in software analytics. In this
study, we use the LDA model to extract topics from
all the methods in a GC which has been discussed in
Section 3.1.
2.2 Hierarchical Clustering
In our approach, we use the Hierarchical Agglom-
erative Clustering (HAC) algorithm. HAC is a gen-
eral family of clustering algorithms which builds
nested clusters by merging (bottom up) or splitting
(top-down) the observations successively. HAC is a
bottom-up approach of hierarchical clustering where
clustering starts from each observation in its own, and
the clusters are successively merged together. A tree
is used to represent the hierarchy of clusters which is
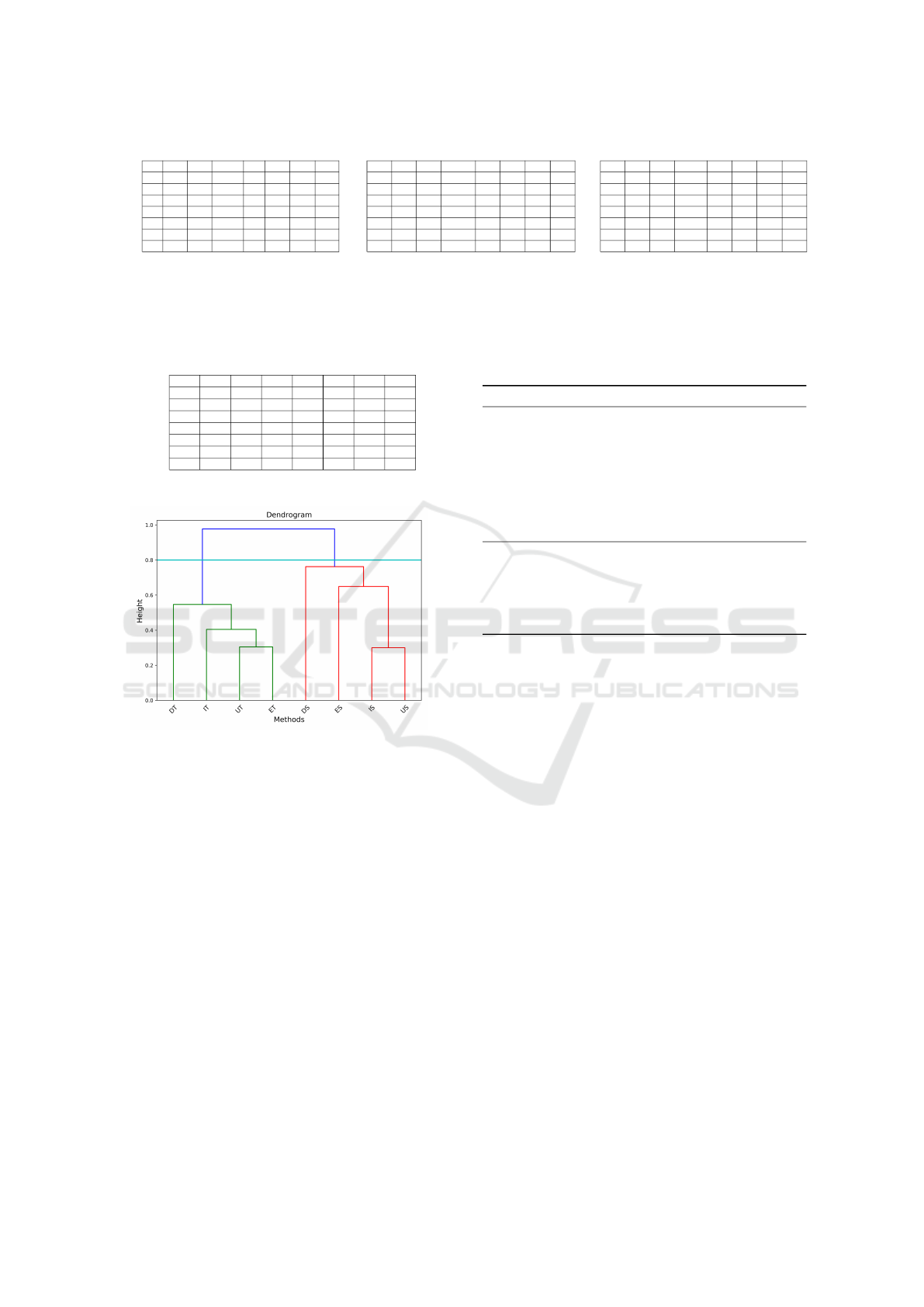
known as dendrogram. Fig. 4 shows an example of a
dendrogram. The root of the tree represents the final
cluster, the leaves are the entities and the actual clus-
ters are represented by the intermediate nodes. The
height of the tree represents the different levels of dis-
tance in which two clusters are merged.
In an HAC algorithm, there are two parameters
that control the clusters. The first one is the link-
age metric and the second one is a distance thresh-
old. The linkage metric determines which distance to
use between the sets of observations. The algorithm
merges two clusters that minimize this metric. There
are several types of linkage metrics such as complete
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
428

or maximum linkage, average linkage and single link-
age. The complete linkage uses the maximum dis-
tance between all the observations of two clusters, the
average linkage uses the average of the distances be-
tween all the observations of two clusters and the sin-
gle linkage uses the distance between the closest ob-
servations of two clusters. To determine the actual set
of clusters, a distance threshold is chosen as a cut-off
value. A distance threshold of 0.8 is used as a cut-off
value in the example dendrogram shown in Fig. 4.
The use of HAC in our study is discussed in Section
3.2.
3 PROPOSED APPROACH
In this section, we present a new approach of extract-
ing a GC. The proposed approach consists of two
steps. First, a method by method similarity matrix
is calculated considering both structural and seman-
tic similarity between methods. Then, the clusters of
methods are generated from this similarity matrix us-
ing an HAC algorithm.
3.1 Similarity Matrix Calculation
The first phase of the refactoring approach is calculat-
ing a method by method similarity matrix where each
entry represents how much proximate two methods
are to be included in the same class. For this, three
measures called Structural Similarity between Meth-
ods (SSM) (Gui and Scott, 2006), Call based Depen-
dence between Methods (CDM) (Bavota et al., 2011)
and Conceptual Similarity between Methods (CSM)
(Poshyvanyk et al., 2009) are calculated for every pair
of methods in a class.
3.1.1 Structural Similarity between Methods
SSM is a structural similarity between methods taking
account of the measures of both cohesion and transi-
tive (i.e indirect) cohesion between methods (Gui and
Scott, 2006). The SSM between two methods m
i
and
m
j
is calculated as follows:
SSM
i, j
=
(
|V
i
∩V
j
|
|V
i
∪V
j
|
if |V
i
∪V
j
| 6= 0
0 otherwise.
(1)
where V
i
and V
j
denote the instance variables accessed
by methods m
i
and m
j
respectively. The higher value
of SSM suggests that two methods are likely to be in
the same class.
3.1.2 Call based Dependence between Methods
CDM is also a structural similarity between meth-
ods which calculates how two methods are related by
method calls (Bavota et al., 2011). The CDM of meth-
ods m
i
to m
j
is calculated as follows:
CDM
i→ j
=
(
calls(m
i
,m
j
)
calls
in
(m
j
)
if calls
in
(m
j
) 6= 0
0 otherwise.
(2)
where calls(m
i
, m
j
) denotes the number of times
method m
j
is called from method m
i
and calls
in
(m
j
)
is the total number of incoming calls to method m
j
.
Finally, overall CDM between methods m
i
and m
j
is
CDM
i, j
= max{CDM
i→ j
, CDM
j→i
} (3)
3.1.3 Conceptual Similarity between Methods
CSM is a conceptual cohesion measure of each pair of
methods in a class (Poshyvanyk et al., 2009). It mea-
sures how semantically two methods are related. For
this, each method in the class is first represented as
a vector in the semantic space constructed by Latent
Semantic Indexing (LSI) (Deerwester et al., 1990).
CSM between two methods m
i
and m
j
is then calcu-
lated as the cosine of the angle of their vector repre-
sentations (v
i
and v
j
) as follows:
CSM
i, j
=
v
T
i
.v
j
||v
i
||.||v
j
||
(4)
where ||v
i
|| denotes the euclidean norm of vector v
i
.
In this study, instead of using LSI, we use LDA
topic modeling to represent every method in a vec-
tor space from topic distribution. For this, texts
from all methods are converted into a matrix of to-
ken counts (document-term matrix). The text of a
method includes identifiers, comments, and docs used
to describe the method. Before converting to the
document-term matrix following preprocessing on the
text is done:
• Texts are split into tokens based on space, camel
case, underscore, special character and numeric.
• Stop words are removed including programming
language keywords in the source code.
• Tokens are stemmed into original roots using
Porters stemmer (Porter, 1997) and converted into
lower case.
The LDA model takes the document-term matrix as
input and extracts pre-specified numbers of important
topics from the documents. It provides two matrices:
topic-word matrix and document-topic matrix as out-
put. Every row vector in the document-topic matrix
An Approach of Extracting God Class Exploiting Both Structural and Semantic Similarity
429

represents a method in terms of topic distribution. In
this study, the optimal number of topics for a class is
selected using cross-validation. Finally, the CSM of
the two methods is calculated by taking the cosine of
the angle of the corresponding topic distribution vec-
tors.
According to (Bavota et al., 2014), the three simi-
larity matrices are then combined by taking weighted
summation to generate the final method by method
similarity matrix, SM where each entry S M
i, j
repre-
sents the likelihood of two methods m
i
and m
j
to be
in the same class and calculated as:
SM
i, j
= w
ssm
.SSM
i, j
+ w
cdm
.CDM
i, j
+ w
csm
.CSM
i, j
(5)
where the summation of w
ssm
, w
cdm
and w
csm
is 1 and
each weight expresses the importance of correspond-
ing similarity measure.
3.2 Clustering
HAC is adapted to extract a set of clusters from
methods based on the similarity matrix calculated in
the previous step. The algorithm first assigns each
method to a cluster of its own. At every iteration,
it merges the two closest clusters based on similar-
ity and stops when all the methods are under the sin-
gle cluster. As mentioned in the previous section, an
HAC needs two parameters to specify which are link-
age metric and distance threshold. It is shown in (An-
quetil and Lethbridge, 1999) that complete linkage fa-
vors more cohesive clusters where the single linkage
provides less coupled clusters and the average linkage
stands in-between them. So, we choose average link-
age to maintain the trade-off between coupling and
cohesion. No fixed distance threshold has been cho-
sen to determine the number of clusters. Variable dis-
tance thresholds are applied with a range of 0.3 to 0.9
and the one giving the best result is selected.
An Illustrative Example
To better understand the application of the proposed
approach, we present an illustration on a simple ex-
ample partially shown in Figure 1. In this example,
there is a class named UserDB with two attributes and
eight methods. This class performs database opera-
tions for two different entities- student and teacher.
Figure 2 shows three similarity matrices, i.e., SSM,
CDM, and CSM calculated from this UserDB class.
Final method by method similarity matrix is calcu-
lated by combining these three matrices with a set of
arbitrary weights i.e., w
ssm
= 0.2, w
cdm
= 0.3, w
csm
=
0.5 (shown in Figure 3). This similarity matrix is used
public class UserDB {
private String TABLE STUDENT = ”student”;
private String TABLE TEACHER = ”teacher”;
/
*
Inserting student to database
*
/
public void InsertStudent (Student student){
boolean exist = ExistStudent(student);
String sql = ”INSERT INTO ”+ this.
TABLE STUDENT +”...”;
}
/
*
Update existing student
*
/
public void UpdateStudent (Student student){
boolean exist = ExistStudent(student);
String sql = ”UPDATE ”+ this.TABLE STUDENT+”
...”;
}
/
*
Delete existing student from database
*
/
public void DeleteStudent (Student student){
boolean exist = ExistStudent(student);
String sql = ”DELETE FROM ”+ this.
TABLE STUDENT+”...”;
//permanent delete
}
/
*
Check student exists or not
*
/
public boolean ExistStudent (Student student){
String sql = ”SELECT
*
FROM ”+ this.
TABLE STUDENT+”...”;
//check
}
/
*
Inserting student to database
*
/
public void InsertTeacher (Teacher student){
boolean exist = ExistTeacher(teacher);
String sql = ”INSERT INTO ”+ this.
TABLE TEACHER +”...”;
}
/
*
Update existing teacher
*
/
public void UpdateTeacher (Teacher teacher){
boolean exist = ExistTeacher(teacher);
String sql = ”UPDATE ”+ this.TABLE TEACHER+”
...”;
}
/
*
Delete existing teacher from database
*
/
public void DeleteTeacher (Student teacher){
boolean exist = ExistTeacher(teacher);
String sql = ”DELETE FROM ”+ this.
TABLE TEACHER+”...”;
//permanent delete
}
/
*
Check teacher exists or not
*
/
public boolean ExistTeacher (Teacher teacher){
String sql = ”SELECT
*
FROM ”+ this.
TABLE TEACHER+”...”;
//check
}
}
Figure 1: Example Java God Class.
in the HAC to construct the dendrogram shown in Fig-
ure 4. A cut-off value, 0.8 is used to generate the ac-
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
430

IS US DS ES IT UT DT ET
IS 1 1 1 1 0 0 0 0
US 1 1 1 1 0 0 0 0
DS 1 1 1 1 0 0 0 0
ES 1 1 1 1 0 0 0 0
IT 0 0 0 0 1 1 1 1
UT 0 0 0 0 1 1 1 1
DT 0 0 0 0 1 1 1 1
ET 0 0 0 0 1 1 1 1
SSM
IS US DS ES IT UT DT ET
IS 1 0 0 0 0 0 0 0
US 0 1 0 0.3 0 0 0 0
DS 0 0 1 0.3 0 0 0 0
ES 0.3 0.3 0.3 1 0 0 0 0
IT 0 0 0 0 1 0 0 0.3
UT 0 0 0 0 0 1 0 0.3
DT 0 0 0 0 0 0 1 0.3
ET 0 0 0 0 0.3 0.3 0.3 1
CDM
IS US DS ES IT UT DT ET
IS 1 1 0.1 0.1 0.1 0.1 0.1 0.1
US 1 1 0.1 0.1 0.1 0.1 0.1 0.1
DS 0.1 0.1 1 0.1 0 0 0.8 0.1
ES 0.1 0.1 0.1 1 0.1 0.1 0.1 0.6
IT 0.1 0.1 0 0.1 1 1 0.7 0.8
UT 0.1 0.1 0 0.1 1 1 0.7 0.8
DT 0.1 0.1 0.8 0.1 0.7 0.7 1 0.6
ET 0.1 0.1 0.1 0.6 0.8 0.8 0.6 1
CSM
IS = InsertStudent, US = UpdateStudent, DS = DeleteStudent, ES = ExistStudent
IT = InsertTeacher, UT = UpdateTeacher, DT = DeleteTeacher, ET = ExistTeacher
Figure 2: Three similarity matrices.
IS US DS ES IT UT DT ET
IS 1 0.70 0.24 0.35 0.04 0.04 0.04 0.05
US 0.70 1 0.25 0.36 0.04 0.04 0.05 0.06
DS 0.24 0.25 1 0.34 0.02 0.02 0.39 0.03
ES 0.35 0.36 0.34 1 0.04 0.03 0.04 0.32
IT 0.04 0.04 0.02 0.04 1 0.70 0.54 0.71
UT 0.04 0.04 0.02 0.03 0.70 1 0.54 0.71
DT 0.04 0.05 0.39 0.04 0.54 0.54 1 0.58
ET 0.05 0.06 0.03 0.32 0.71 0.71 0.58 1
Figure 3: Final method by method similarity matrix.
Figure 4: Cluster Dendrogram from example in Fig. 1.
tual clusters from the dendrogram. The class is split
into two new classes separated by corresponding re-
sponsibilities.
4 EXPERIMENTS AND RESULTS
In this section, the performance of the proposed ap-
proach is empirically evaluated. For this purpose, the
proposed approach is applied to refactor actual GCs
from two well known open source systems namely
Xerces and GanttProject. Table 1 summarizes the
properties of the classes of these two systems. We as-
sess the performance of our approach based on two
cohesion metrics, i.e., Lack of Cohesion of Meth-
ods (LCOM) (Chidamber and Kemerer, 1994) and
Conceptual Cohesion of Classes (C3) (Marcus et al.,
2008). The LCOM counts the difference between
the number of pairs of methods which do not share
Table 1: God Classes used in the experiment.
System God Class LOC Methods
Xerces
AbstractDOMParser 41775 45
AbstractSAXParser 1360 55
BaseMarkupSerializer 1275 61
CoreDocumentImpl 1497 119
DeferredDocumentImpl 1612 76
DOMNormalizer 1291 31
DOMParserImpl 820 17
NonValidatingConfiguration 403 18
XIncludeHandler 1331 111
GanttProject
GanttOptions 513 68
GanttProject 2269 90
GanttGraphicArea 2160 43
GanttTaskPropertiesBean 1685 27
ResourceLoadGraphicArea 1060 29
TaskImpl 329 46
any instance variables and the number of pairs where
two methods share at least one instance variable. The
higher the value of LCOM, the lower the class cohe-
sion. C3 metric measures the conceptual cohesion in
a class using textual similarity. The higher value of
C3 denotes the higher class cohesion.
The result of LCOM and C3 metrics of 15 God
classes before refactoring and after refactoring via our
approach are reported in Table 2. It is clearly observ-
able from Table 2 that, for all the classes, the cohesion
is improved after refactoring using our approach. For
instance, the C3 value of AbstractDOMParser class
was 0.23 before refactoring. Our approach refactors
the class into two classes and the C3 value of the two
new classes are 0.27 and 0.32. Reversely, the LCOM
value of the class has been reduced from 4 to 0 in the
two new classes. A Comparison over average C3 and
LCOM values after refactoring and before refactoring
for 15 God classes are shown in Figures 5 and 6 re-
spectively. In Figure 7, we also show a comparative
result with a similar existing approach (Bavota et al.,
2014) on the scale of average C3 measure. From the
Figure 7, we can say that for almost all the classes our
approach clearly outperforms the existing approach in
terms of average C3 cohesion metric.
An Approach of Extracting God Class Exploiting Both Structural and Semantic Similarity
431

Table 2: Cohesion results obtained refactoring the 15 God Classes.
System Class
Pre-refactoring Our Approach
LCOM C3
Split
classes
LCOM C3
Xerces
AbstractDOMParser 4 0.23 2 0, 0 0.27, 0.32
AbstractSAXParser 2308 0.13 3 673, 92, 60 0.18, 0.43, 0.24
BaseMarkupSerializer 1004 0.13 3 394, 0, 64 0.16, 0.45, 0.24
CoreDocumentImpl 6589 0.12 4 905, 381, 209, 178 0.13, 0.18, 0.24, 0.41
DeferredDocumentImpl 987 0.15 3 585, 10, 0 0.16, 0.59, 0.42
DOMNormalizer 1729 0.16 3 610 , 30, 106 0.20, 0.24, 0.22
DOMParserImpl 2250 0.22 3 901, 60, 66 0.27, 0.30, 0.41
NonValidatingConfiguration 157 0.12 2 77, 10 0.14, 0.18
XIncludeHandler 4790 0.15 4 259, 63, 49, 486 0.17, 0.47, 0.37, 0.29
Average 2202 0.16 192 0.28
GanttProject
GanttOptions 2626 0.18 3 1178, 19, 118 0.20, 0.54, 0.36
GanttProject 3632 0.12 3 1228, 74, 225 0.15, 0.16, 0.33
GanttGraphicArea 657 0.12 2 546, 3 0.14, 1.0
GanttTaskPropertiesBean 419 0.15 2 329, 2 0.15, 0.49
ResourceLoadGraphicArea 153 0.22 2 57, 19 0.23, 0.29
TaskImpl 7491 0.26 4 1745, 245 ,388, 24 0.33, 0.41, 0.6, 0.29
Average 2496 0.18 333 0.36
Figure 5: Average C3 before and after refactoring.
Figure 6: Average LCOM before and after refactoring.
5 CONCLUSION
In this paper, a new approach of extracting GC is pro-
posed. This approach suggests splitting a GC into
Figure 7: Comparison with an existing approach.
new classes with higher cohesion than the original
class. Both structural and semantic relationships be-
tween methods are extracted to calculate the similar-
ity between methods, and methods are clustered based
on the similarity measure. An empirical experiments
over 15 GCs from two open source systems has been
conducted to assess the performance of the proposed
approach. We also report a comparative result with a
similar existing approach and found that our approach
gives considerably better performance. The limitation
of this approach is that, it only gives suggestions of
extracting a predefined GC into several classes. As a
future research direction, we plan to propose an auto-
matic approach of detecting and extracting GCs, and
also intend to investigate the effect of different clus-
tering algorithms in GC refactoring.
ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering
432

ACKNOWLEDGMENT
This research is supported by the fellowship from
ICT Division, Ministry of Posts, Telecommunica-
tions and Information Technology, Bangladesh. No
- 56.00.0000.028.33.002.19.3; Dated 09.01.2019.
REFERENCES
Anquetil, N. and Lethbridge, T. C. (1999). Experi-
ments with clustering as a software remodularization
method. In Sixth Working Conference on Reverse En-
gineering (Cat. No.PR00303), pages 235–255.
Asuncion, H. U., Asuncion, A. U., and Taylor, R. N. (2010).
Software traceability with topic modeling. In Pro-
ceedings of the 32Nd ACM/IEEE International Con-
ference on Software Engineering - Volume 1, ICSE
’10, pages 95–104, New York, NY, USA. ACM.
Bavota, G., De Lucia, A., Marcus, A., and Oliveto, R.
(2010a). A two-step technique for extract class refac-
toring. In Proceedings of the IEEE/ACM International
Conference on Automated Software Engineering, ASE
’10, pages 151–154, New York, NY, USA. ACM.
Bavota, G., De Lucia, A., and Oliveto, R. (2011). Identify-
ing extract class refactoring opportunities using struc-
tural and semantic cohesion measures. J. Syst. Softw.,
84(3):397–414.
Bavota, G., Lucia, A., Marcus, A., and Oliveto, R. (2014).
Automating extract class refactoring: An improved
method and its evaluation. Empirical Softw. Engg.,
19(6):1617–1664.
Bavota, G., Oliveto, R., Lucia, A. D., Antoniol, G., and
Gu
´
eh
´
eneuc, Y. (2010b). Playing with refactoring:
Identifying extract class opportunities through game
theory. In 2010 IEEE International Conference on
Software Maintenance, pages 1–5.
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). La-
tent dirichlet allocation. J. Mach. Learn. Res., 3:993–
1022.
Brown, W. J., Malveau, R. C., McCormick, H. W. S., and
Mowbray, T. J. (1998). AntiPatterns: Refactoring
Software, Architectures, and Projects in Crisis: Refac-
toring Software, Architecture and Projects in Crisis.
John Wiley & Sons, 1. auflage edition.
Chidamber, S. R. and Kemerer, C. F. (1994). A metrics
suite for object oriented design. IEEE Transactions
on Software Engineering, 20(6):476–493.
Deerwester, S., Dumais, S., Furnas, G., Landauer, T., and
Harshman, R. (1990). Indexing by latent semantic
analysis. Journal of the American Society for Infor-
mation Science 41, pages 391–407.
Fowler, M. (1999). Refactoring: Improving the Design of
Existing Code. Addison-Wesley, Boston, MA, USA.
Gethers, M., Oliveto, R., Poshyvanyk, D., and Lucia, A. D.
(2011). On integrating orthogonal information re-
trieval methods to improve traceability recovery. In
2011 27th IEEE International Conference on Software
Maintenance (ICSM), pages 133–142.
Gethers, M. and Poshyvanyk, D. (2010). Using relational
topic models to capture coupling among classes in
object-oriented software systems. In 2010 IEEE Inter-
national Conference on Software Maintenance, pages
1–10.
Gui, G. and Scott, P. D. (2006). Coupling and cohesion
measures for evaluation of component reusability. In
Proceedings of the 2006 International Workshop on
Mining Software Repositories, MSR ’06, pages 18–
21, New York, NY, USA. ACM.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-
tering Data. Prentice-Hall, Inc., Upper Saddle River,
NJ, USA.
Marcus, A., Poshyvanyk, D., and Ferenc, R. (2008). Us-
ing the conceptual cohesion of classes for fault predic-
tion in object-oriented systems. IEEE Transactions on
Software Engineering, 34(2):287–300.
Mens, T. and Tourwe, T. (2004). A survey of software refac-
toring. IEEE Transactions on Software Engineering,
30(2):126–139.
Porter, M. F. (1997). Readings in information retrieval.
chapter An Algorithm for Suffix Stripping, pages
313–316. Morgan Kaufmann Publishers Inc., San
Francisco, CA, USA.
Poshyvanyk, D., Marcus, A., Ferenc, R., and Gyim
´
othy, T.
(2009). Using information retrieval based coupling
measures for impact analysis. Empirical Software En-
gineering, 14(1):5–32.
Savage, T., Dit, B., Gethers, M., and Poshyvanyk, D.
(2010). Topic lt;inf gt;xp lt;/inf gt;: Exploring top-
ics in source code using latent dirichlet allocation.
In 2010 IEEE International Conference on Software
Maintenance, pages 1–6.
Tan, P.-N., Steinbach, M., and Kumar, V. (2005). Introduc-
tion to Data Mining, (First Edition). Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA.
Thomas, S. W., Adams, B., Hassan, A. E., and Blostein, D.
(2010). Validating the use of topic models for software
evolution. In 2010 10th IEEE Working Conference on
Source Code Analysis and Manipulation, pages 55–
64.
An Approach of Extracting God Class Exploiting Both Structural and Semantic Similarity
433