
Improving the Attitude towards Mathematics via an ICT
Rearrangement of the 8
th
Grade Math Curriculum
Borislav Lazarov
Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Blok 8 Georgi Bonchev Str., Sofia, Bulgaria
Keywords: Attitude towards Mathematics, Dynamic Geometry Software, Synthetic Competence, Individual Educational
Trajectory.
Abstract: Under consideration is an experimental teaching in mathematics of an eight-grade high abilities student,
whose attitude towards mathematics initially was negative. The educational goal includes developing
student’s competence of synthetic type, i.e. a package of knowledge, skills and attitudes, which are
multifunctional and transferable. The European framework of key-competences is chosen to design an
individual educational trajectory (IET). An original didactic model is adopted as theoretical base for this IET.
The main issue in the IET was how to change the student’s attitude towards mathematics to positive. For
resolving this issue, a rearrangement of the syllabus is done by incorporating ICT. A large part of the routine
paper-and-pencil drills was replaced with dynamic-geometry-software exercises. Parallel to the compulsory
lessons in math, the IET included two project-oriented initiatives. The goal of these initiatives were to
reinforce the synthesis of the student’s analytical knowledge and skills, which were built separately in math,
ICT and arts. On this stage of the IET, the informal learning served as an accelerator in turning attitude in
positive direction. At the final stage of the experimental teaching, the student covers the general standard for
positive attitude towards mathematics.
1 INTRODUCTION
The concept of competence in European Commission
understanding consist of 3 components: knowledge,
skills and attitude (EU, 2006). The development of
knowledge and skills are parts of any math
curriculum in Bulgaria. There is a long tradition in
teaching any particular math topic in secondary
school and valid didactic methods are approved for
different age groups (Ganchev and Kuchinov, 1996).
The modern textbooks follow these methods and the
teachers are more or less prepared to apply them into
school practice. However, the recent international
assessments pointed on a general drop in performance
of the Bulgarian secondary school students in math
(PISA, 2016). It appears that Bulgarian eighth-
graders are not competent to cover some international
educational standards. Therefore, if the knowledge-
skills part of the education is still in a framework that
assures good results in the past, then maybe the
problem is in the students’ attitude.
We do not know examples of Bulgarian good
practice on improving the attitude toward
mathematics among eighth grade students. Outside
Bulgaria (where the European framework was
adopted) the attitude is related to high achievement,
or motivation, or engagement, which is not the case
we are interested in (Blackweir, 2016, p.16-17).
Therefore, we constituted a teaching experiment to
look for some possible stimuli for an eight-grader to
study math having in mind the Bulgarian educational
context.
The eighth grade mathematics curriculum in
Bulgarian secondary school is crucial in forming
students’ deductive abilities. The main didactical
instrument for this mission is the geometry part that
upgrades the axiomatic approach introduced in
seventh grade by 4 modules: vectors, rigid motions,
circle and geometrical constructions. Every module is
elaborated in a traditional mode lessons: introductory
example, definitions, theorems, drills. The students’
activities are supposed to be performed by hand
drawing and calculating, as well as deductive
reasoning based on a carcass of statements of
Euclidean geometry. We advocate the need of
renovation this traditional approach.
The experimental teaching described below
presents an attempt to reform the teaching method in
eighth grade math by introducing some computer
Lazarov, B.
Improving the Attitude towards Mathematics via an ICT Rearrangement of the 8th Grade Math Curriculum.
DOI: 10.5220/0007744203910397
In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 391-397
ISBN: 978-989-758-367-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
391

applications, mainly dynamic geometry software
(DGS), but also computer algebra system (CAS). As
we will show, this reform went far beyond the simply
technical issues and caused deep rethinking of the
bases.
2 THE INITIAL CONDITIONS
The student V started the eighth grade mathematics
classes declaring she hate math. V was studious and
she was doing regularly the obligatory math
assignments but without any enthusiasm. The most
unpleasant for her were the routine work:
calculations, algebraic transformations etc. During
the first term, the V’s test results were mediocre that
contrasts her high intellectual abilities in general.
Such status quo was unacceptable and the need for
change was obvious. In this connection, the following
questions were top of the agenda:
1) how the attitude towards mathematics of a student
of high potential abilities could be changed to
positive;
2) what part of the curriculum should by reorganized.
Therefor we designed a midterm individual
educational trajectory (IET). By IET we will
understand the organizational framework and plan
for realization of a medium term educational process
that are coherent with the individual specifics of the
learner and provides opportunities for the optimal
development of his/hers creative potential (Lazarov,
2012).
3 THE IET: A BIT OF THEORY
We summarized our previous experience in tutoring
advanced students in (Lazarov 2013A), where we
proposed a didactic model (called DMT) for
designing an IET. The movement along the IET
follows a kind of spiral. However, it is more
convenient to decompose this spiral into two
directions: vertical and horizontal. The vertical
direction is an iterative procedure that includes the
following components.
1) Formation of an individual informational
environment.
2) Individualization of the didactical resources,
including selection of the individual
(re)searching instruments.
3) Individualization of setting the educational goal,
including flexible approach to achieve it.
4) Individualization of the learning temps,
investigation activities, layout style.
5) Taking into account the individual reflexive
abilities and self-organization aptitude in
searching a synergetic effect. [ibid]
The DMT allows visualizing the iterations of an
IET as climbing floors. Here is the list of the steps to
be done in the k-th floor of the IET (the program
maximum).
…(k – 1) →
A proximal educational goal (of learning,
investigative or research type) is mapped out
with respect to the actual knowledge, skills and
attitude (KSA) of the student (actual
development).
A (very limited) informational resource is
determined which is focused on the goal.
All needed activities to extend the actual KSA
to a level required for reaching the stated goal
are performed.
Student proceeds to the goal in his own manner.
Analysis of the achievements (tutor
responsibility).
→ (k+1) …
The horizontal direction connects the iterations in
a specific way for which we will give details in the
next section.
4 IMPLEMENTATION OF THE
THEORY
The traditional style math teaching requires just a
white-board and some posters visualizing basic
geometry shapes and math formulae. The students’
classroom activities corresponding to such teaching
are related mainly to problem solving by paper-and-
pencil techniques. Therefore, the first step in our plan
was to expand the classroom equipment by computers
with DGS. We designed for V an IET, based on
implementation of DGS.
4.1 The Ground Floor of V’s IET
Initially the informational environment was limited to
the textbook (Paskaleva et al., 2013). Following the
syllabus, the linear simultaneous equations stood on
agenda. This was the right moment to start our plan
for overcoming V’s negative attitude to math. Among
the didactical tools we selected was learning by
syntax (Lazarov and Karakoleva, 2011). The correct
usage of the DGS requires from V a kind of
mathematics competence related to basic concepts of
CSEDU 2019 - 11th International Conference on Computer Supported Education
392
the analytical geometry: Cartesian coordinates, line-
equation correspondence, graphic interpretation of
simultaneous equations etc. Studying the DGS
interface V realized the need to learn the math
concepts deeply. The benefits came quickly: the
paper-and-pencil solution of simultaneous equations
is written on several rows; the DGS solution is limited
to entering the equations and interpretation of the
picture. Let us emphasize that we passed the
obligatory content in full scale to cover knowledge-
and-skills standards. V did just a part of the routine as
a DGS activity.
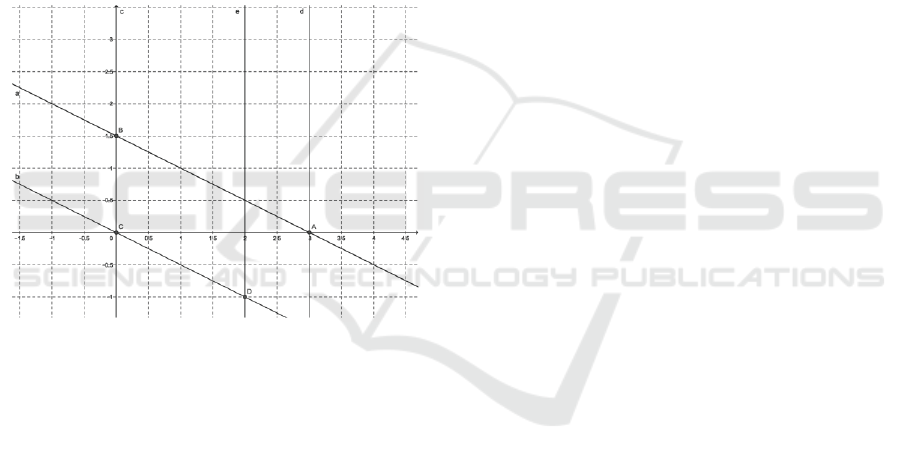
One can see the V’s uncertain first attempt in
using DGS in Figure 1. The genuine problem was to
solve graphically the simultaneous equations x+2y=3,
y+x/2=0. There are expendable elements as vertical
lines that appear in searching points of intersection
that actually do not exist.
Figure 1: V’s first attempts in applying DGS.
On this floor, V made successfully the first steps
in overcoming the routine calculations by application
of CAS.
About the attitude component of the competence,
our proximal educational goal was related with the
first two points of the Mathematical literacy key-
competence, as well as points ii. and iii. of the
Learning to learn key-competence (see the
Appendix). So, our program maximum at this stage
was fulfilled: V started dealing math with no bad
feelings.
4.2 The Second Floor of V’s IET
The next big step that V made was related to geometry
lessons: the rigid motions. The chapter in the textbook
started with a discussion about how to imagine a
plane that can move onto itself. Here the advantages
of the DGS versus paper-and-pencil style are
indisputable. No imagination was needed in general
but one can see the matter of a particular rigid motion
just dealing with DGS instruments to perform
translation, rotation, or symmetry.
V and a classmate of her started a project about
congruent shapes in real life environment. They
captured images of buildings, electric lighting poles,
street tessellation etc. and classified the repeating
shapes according to the type of the rigid motion that
could be recognized. For instance, the front view of
some buildings repeat the same form of the floors;
hence, they could be obtained by translation about a
vertical vector. Our educational goal in its attitude
part referred to points i., iv., and vi. of the key-
competence Learning to learn (see the Appendix).
We will skip more details of that stage of V’s IET
just mentioning that V’s attitude towards math ceased
being negative. Such change was probably caused by
the decontextualization of the math theory connecting
it with the everyday student’s experience.
4.3 The Third Floor of V’s IET
The project-oriented education was a part of the
school strategy at that time (Lazarov, 2018).
Moreover, students like working on educational
projects and we catch this opportunity to apply
integrated approach. V was no exception. The project
about the rigid motion in the city environment lifted
the V’s enthusiasm.
‘Rigid motion’ in Bulgarian translation is
‘ednakvost’ (pl. ednakvosti). Ednakvost has an
everyday meaning, which is slightly different from
the mathematical concept. It is close to ‘mapping a
figure onto congruent figure’ (figuratively, copy-
pasting). Here the ‘rigid’ part is not obligatory that
allows extending the math concept beyond the
geometry. In the following, we will use the word
ednakvost for expanding the meaning of the concept
of rigid motion beyond geometry.
So, we started another project on ednakvosti, this
time about figures in art. Our idea was to integrate
with math as much art as possible. After consulting
the music teacher, who suggested to consider the
music of Ravel’s bolero, we decided to go further and
to analyze the Maya Plisetskaya’s bolero dance
(YouTube, 2016). In our opinion, this movie is a pure
synthesis of music, dance, and filming. The project
idea was to observe how the show is composed of
figures in music and dance that are multiplied through
different ednakvosti.
The rhythmic part of Ravel’s bolero repeated 168
times the initial figure. V recognized here translation
(Figure 2). Another translation V observed in the two
Improving the Attitude towards Mathematics via an ICT Rearrangement of the 8th Grade Math Curriculum
393

Figure 2: Translation in the rhythmic section (a slide from
V’s presentation).
melodies, which are on top of this rhythm (Figure 3).
The second translation moves the musical figure from
flute to clarinet, then to bassoon, and so on. This was
the first coordinate of the translation vector. The
second coordinate is in the loudness, constantly rising
from pianissimo to fortissimo.
Figure 3: Translation in the melody (a slide from V’s
presentation).
Another ednakvoti V saw in the Maya
Plisetskaya’s dance. She recognized symmetry and
rotation. V managed to cut the YouTube clip into
short parts, which illustrated the corresponding
ednakvost. For this purpose, V found the free
software WEVIDEO in the www, learned by herself
how it works and applied it to a presentation. Let us
point that the filming of the dance emphasized the
dance figures in a very suitable manner for the project
goals. V caught this opportunity. E.g. she splitted one
of the movements into symmetrical origin and image,
which are shown together in the next movement that
completes the symmetry (ibid., 0:22-1:27); similarly,
V extracted rotation (ibid., 8:04-8:15).
V presented the project to her teachers and
schoolmates. At the end of the presentation, after the
final accords of bolero, she declared ‘ednakvosti are
everywhere’. This we accepted as the turning point
in change V’s attitude towards math to positive.
However, we consider the attitude in a synthesis with
some attitude components from other key-
competences, e.g. Cultural awareness and ICT ones
(Appendix).
4.4 The Top Floor of V’s IET
The time to harvest the fruits from the V’s
metamorphosis came with the curriculum unit about
Geometrical constructions. However, the application
of DGS in standard tasks requires deep revision of the
method. The ruler-and-compass axiomatic is not
coherent with DGS instruments. The conflict points
are discussed in details by Lazarov (2011).
Another issue relates the reasoning. Here two
points stand on agenda:
1) the traditional proof that the construction algorithm
produces the proper figure can be replaced by a check
for dynamical steadfastness of the DGS construction;
2) the conditions under which a figure exists can be
replaced by examination of the initial data.
4.4.1 The First Point
We illustrate the reasoning instead the proof by the
example in Figure 4. The theorem states that the
symmetric point of the orthocenter of a triangle about
any side lies on the circumcircle.
Figure 4: V’s applet illustrates the property of the
symmetric point of the orthocenter of a triangle.
The V’s applet allows checking different type of
triangles: acute, obtuse, right. The symmetric point
D’ of the orthocenter D of triangle ABC about the line
BC lies on the circumcircle, every time when any of
the vertices A, B, C changes its location. Let us point
that the rigor proof is not easy even for some math
teachers.
4.4.2 The Second Point
The analysis of existence of a figure we illustrate by
Figure 5 where V constructed isosceles triangle
having given base a and the circumradius r.
She introduces two sliders: one for the base a,
another for the radius r. The dynamic construction
allows examining the existence of a triangle with the
given properties.
Let us explain that the change of the method does
not change the educational goal of the topic Geomet-
CSEDU 2019 - 11th International Conference on Computer Supported Education
394

Figure 5: Construction of an isosceles triangle with given
base and circumradius.
rical constructions. The replacement of the axiomatic
of ruler-and-compass by the DGS operators develops
the same kind of algorithmic thinking. Moreover, the
computer-based application of the theory is a solid
ground to cultivate some designer abilities. E.g., V
made just for fun an applet for topological
transformation of a dog’s face into a cat’s face and
vice versa.
At this stage, we emphasize the last three points
of math key-competence, again in synthesis with key-
competence Learning to learn (Appendix).
5 DEVELOPING COMPETENCE
ALONG THE IET
The DMT describes in general a hypothetic
movement inside the floors of an IET (Lazarov,
2013). However, the details are rather specific for any
particular IET. Bulgarian educational legislation
operates with the category of key competences
(MON, 2015), while PISA framework takes
mathematical literacy as the basic construct (PISA,
2018). Our standing point differs from both cases:
building up a kind of synthetic competence is what
should be the educational goal in the secondary
school (Lazarov, 2013B).
The synthetic competence is a construct for the
methodology when designing IET, but it becomes a
personal attribute for any individual as an outcome of
the IET. Let us emphasize that the synthetic
competence is context sensitive. This is why the
educational context should be challenging and to
include stimuli of synthetic type. In our case, some of
the stimuli were the two project-oriented initiatives
on ednakvosti (remember 4.2. and 4.3.). Other stimuli
were set during the discussions on extracurricular
topics as the nine-point circle of a triangle, Euler’s
line, etc. Any time the DGS illustrations were done
by V. As result of her activity an archive of DGS
applets were created.
The knowledge and skills built on any floor of V’s
IET were tested by implementation in DGS activities
that assured a kind of transferability and
multifunktionality of knowledge and skills. Parallel
to this the V’s attitude towards mathematics lifted on
any floor (in our opinion). Therefore, we can speak
for a development of V’s knowledge-skills-attitude
package in a context that is different from the one, in
which the KSA package was elaborated. In other
words, the V’s synthetic competence was upgraded at
any floor of her IET.
Formation of the V’s individual informational
environment included web-based resources, e.g. the
paper about Ravel’s bolero (WikipediA, 2018). V was
not restricted in copy-pasting some paragraphs from
internet papers, but the citation ethics was strictly
under control. We agree with Petrovic (2018) about
the benefits of informal learning even in such
reproductive form. Moreover, we consider this type
of informal learning as an opportunity to
decontextualize the classroom knowledge. However,
the key-competence ICT attitude points (Appendix)
must be taken into account in any copy-paste
activities.
6 CONCLUDING WORDS
The Bulgarian secondary school theoretical
framework adopts explicitly the key-competences
from the European one (EU, 2006). However, the
responsibility for development of any key-
competence is spread all over the subjects and vice
versa: any subject covers several key-competences.
E.g. any of the themes Plane figures and solid bodies,
Probability and Functions covers 7 of 8 key-
competences (MON, 2015) (in fact there are 9 key-
competences in Bulgarian educational legislation).
Implicitly this means that a kind of synthetic
competence is in the scope of the compulsory
education, which is coherent with our standing point
about one competence of synthetic type.
Further, the attitude as a component of the
synthetic competence inherits the synthetic nature of
the competence. This was clearly seen during our
experimental teaching.
The concept of attitude is operationalized more
comprehensive in Bulgarian legislation (MON, 2015)
than the points we cite in the Appendix. However, the
existing instruments to measure the student’s attitude
in quantitative way, which we know, do not
correspond to the individual approach we applied.
E.g., take the attitude point 3.1.iii and think about
what it means to register 30% higher respect for truth.
The common instrument for this purpose is an inquiry
of the type given by Zakariya (2017, p. 82).
Improving the Attitude towards Mathematics via an ICT Rearrangement of the 8th Grade Math Curriculum
395

On the other hand, a qualitative evaluation is
possible and we observed (indirectly) rather positive
lift of V’s attitude towards math. Taking into account
that the V’s math test results are related mainly to the
knowledge and skills side of her learning process, we
would like to think that the higher score she achieved
at the end of the school year is also influenced by the
positive attitude she get during the experimental
teaching presented here.
ACKNOWLEDGEMENTS
The study is supported by the Educational and
Research Program Cherorizec Hrabar of the Institute
of Mathematica and Informatics, Bulgarian Academy
of Sciences. The author thanks the reviewers for the
comments.
REFERENCES
Blackweir, J. (2016). Attitudes towards mathematics:
Development and validation of an Attitudes towards
mathematics. Master thesis, Graduate School of
Education, Australia.
EU (2006). Recommendation of the European parliament
and of the council of 18 December 2006 on key
competences for lifelong learning. Official Journal of
the European Union 30.12.2006, L 394/15.
Ganchev, I. and Kuchinov, Y. (1996). Organizatsia i
metodika na uroka po matematika. Sofia. Modul.
(Organization and methodic of mathematics lesson) In
Bulgarian.
Lazarov, B. (2011). Paper and Pencil versus ICT –
Battlefield Geometry. In Е-learning, distance education
or ... The education of 21st century international
conference. Sofia, Bulgaria 6-8 April 2011. Conference
proceedings, p. 123-130.
Lazarov, B. (2012). Individualna obrazovatelna treaktoria –
izsledvane na chasten sluchay. Matematika i
informatika. No 3, 2012. p. 238-248. (Individual
educational trajectory – a case study) In Bulgarian.
Lazarov, B. (2013A). Application of some cybernetic
models in building individual educational trajectory.
Information Models and Analyses. Vol. 2, No1, 2013,
p. 90-99.
Lazarov, B. (2013B). Developing Synthetic Competence
along Individual Educational Trajectory. In
Proceedings of the International Conf. on Math. Edu.
on Creativity & Giftedness (August 9–10, 2013). The
Korean Society of Mathematical Education. p. 251-262.
Lazarov, B. (2018). Topic-oriented Upgrade of Subject-
oriented Educational System. In Tarasenkova, N. (Eds).
Current Status and Prospects of Mathematical
Education: Monograph. ISBN 978-615-00-2441-7 In L.
Kyba (A. Ed.). Budapest, Hungary: SCASPEE. p. 37-
53
Lazarov, B. and Karakoleva, S. (2011). Using CAS syntax
for education in mathematics. In Vissheto obrazovanie
v Bulgaria i strategia „Evropa 2020”. (Bulgarian
Higher Education and the Europe 2020 Strategy.)
MVBU Pblsh. ISBN 978-954-9432-43-5, p. 914-921.
MON (2015). NAREDBA № 5 ot 30.11.2015 g. za
obshtoobrazovatelnata podgotovka. DV, br. 95 ot
08.12.2015. (Bulgarian Ministry of Education.
Regulation No 5 of general education) In Bulgarian.
Paskaleva, Z., Paskalev, G., and Alashka, M. (2013).
Matematika 8. klas. Arhimed 2. (Mathematics for 8th
grade) In Bulgarian.
Petrovic O. (2018). Digital Media’s Alteration Mechanism
for Informal Learning. In Proceedings of the 10th
International Conference on Computer Supported
Education - Volume 2: CSEDU, ISBN 978-989-758-
291-2, p. 321-330. DOI: 10.5220/0006772303210330.
PISA (2016). https://www.businessinsider.com/pisa-
worldwide-ranking-of-math-science-reading-skills-
2016-12
PISA (2018). Directorate for Education and Skills
Programme for International Student Assessment.
Edu/Pisa/Gb(2018)4, 6 April 2018.
WikipediA (2018). https://en.wikipedia.org/wiki/Boléro.
YouTube (2016). Music by Maurice Ravel, choreography
by Maurice Béjart, dancing Maya Plisetskaya. Bolero.
https://www.youtube.com/watch?v=6vAvpUyFvrU.
Zakariya, Y.F. (2017). Development of Attitudes towards
Mathematics Scale (ATMS) using Nigerian Data –
Factor Analysis as a Determinant of Attitude
Subcategories. International Journal of Progressive
Education, Volume 13 Number 2. p. 74-84.
APPENDIX
The attitude component of Mathematics key-
competence in EUROPEAN COMMISSION, 2018.
ANNEX to the Proposal for a Council
Recommendation on Key Competences for Lifelong
Learning (page C 189/9) is defined as A positive
attitude in mathematics is based on the respect for
truth and a willingness to look for reasons and to
assess their validity. (https://eur-lex.europa.eu/legal-
content/EN/TXT/PDF/?uri=CELEX:32018H0604(0
1)&rid=7)
Below is an extraction from the communication Key
Competences in the Knowledge Based Society – A
framework of eight key competences. European
Commission (Sept. 2004). The quotations are taken
from the column ATTITUDES of the table on pages
5-13. Here the key-competence number corresponds
the source numbering.
3.1. Key-competence Mathematical literacy
i. overcoming ‘fear of numbers’;
CSEDU 2019 - 11th International Conference on Computer Supported Education
396

ii. willingness to use numerical computation in
order to solve problems in the course of
day-to-day work and domestic life;
iii. respect for truth;
iv. willingness to look for reasons to support one’s
assertions;
v. willingness to accept or reject the opinions of
others on the basis of valid (or invalid) reasons
or proofs.
4. Key-competence ICT (digital competence)
i. desire critically to assess information available;
ii. awareness that the lower threshold to access
information may need to be balanced by
higher standards of ethics and taste –
ability to distinguish what is ‘accessible’
from what is ‘acceptable’.
5. Key-competence Learning to learn
i. adaptability and flexibility;
ii. self-motivation and confidence in one’s
capability to succeed;
iii. a self-concept that upholds one’s willingness to
change and further develop competences;
iv. sense of initiative (to learn);
v. positive appreciation of learning as a life-
enriching activity.
8. Key-competence Cultural awareness
The term ‘cultural awareness’ comprises an
appreciation of popular culture and general social
mores, as well as the ability to appreciate
literature, art, music and other forms of creative
expression.
Improving the Attitude towards Mathematics via an ICT Rearrangement of the 8th Grade Math Curriculum
397
