
Improving the Performance of Road Network Analysis:
The Morandi Bridge Case Study
Vincenzo Petito, Maurizio Leotta
a
and Marina Ribaudo
b
Dipartimento di Informatica, Bioingegneria, Robotica e Ingegneria dei Sistemi (DIBRIS), Università di Genova, Italy
Keywords:
Centrality Measures, OpenStreetMap, Multi-core Computation.
Abstract:
Road network analysis is a fundamental tool for city planners and engineers for preventing, or finding possible
solutions to, gridlock congestion and immobility. In this work, we describe the computation of some classical
centrality measures for the road network of the region Liguria, in particular focusing on the effects of the
2018 Morandi bridge collapse. Given the size of the network graph derived from the OpenStreetMap publicly-
available data, we extended the JGraphT library to support multi-core computation. In this way, it is possible
to deal with large graphs (e.g., 53743 nodes and 125250 edges for the considered case study), representing
real networks, with relevant time savings (up to -87% on the adopted configuration). Results show that, on
the considered case study, even a classical measure like Betweenness centrality is able to provide interesting
insights on the road network under investigation.
1 INTRODUCTION
Urban population of the world has grown rapidly in the
last decades. According to the United Nations, in 2016
there were 7.4 billions inhabitants in the world (United-
Nations, 2016), and it is estimated that 68% of the
population will live in urban areas by 2050 (United-
Nations, 2018). Such ever-increasing urban population
requires city planners and engineers to look for ways
to analyze the road network in order to find possi-
ble solutions to gridlock congestion and immobility.
Moreover, network planning and traffic flow optimiza-
tion are also particularly important to try to mitigate
air pollutant emissions, which constitute an important
environmental issue in several countries.
Urban traffic analysis can be carried out by rely-
ing on different kinds of data, such as: (1) real traf-
fic data, recorded using for example pneumatic road
tubes counters, piezo-electric sensors, or video vehicle
detection (Windmill, 2018), (2) population data, typ-
ically generated from survey data or thanks to tools
for mobile crowdsensing such as Waze
1
, (3) networks
of roads such as maps equipped with other types of
data like the number of road lanes, or the max allowed
speed of the roads, etc.
a
https://orcid.org/0000-0001-5267-0602
b
https://orcid.org/0000-0003-0697-2225
1
https://www.waze.com
With traffic data it is possible to have a detailed
assessment of the road network status in terms of
hotspots, congestions, vehicle fleet composition, and
the like, while the analysis of the network topology
allows to perform traffic simulations or to answer to
questions such as “Which are the most important areas
of the road network?” or “What could happen to the
traffic if the topology of the road network changes?”.
Following the second approach, e.g. analysis of
the network topology, our work started with the in-
tention of computing centrality measures of the Open-
StreetMap
2
(OSM) road network of the region Liguria
and the city of Genoa. For the computation we se-
lected the Java library JGraphT finding that there was
room for performance improvements, since the library
was not exploiting all possible parallelism. Moreover,
during the course of this activity, a tragic event hap-
pened in the city since on August 14th an important
bridge on the highway that passes through the city, the
Morandi bridge, collapsed (Glanz et al., 2018). Thus
we decided to investigate how this event changed the
topology and graph metrics of the underlying network.
Therefore, the contributions of this paper are the
following: (1) a description of how it is possible to
take the open data extracted from OSM and to derive
interesting information about the road topology; (2) a
refinement of the JGraphT library in order to support
2
https://www.openstreetmap.org
Petito, V., Leotta, M. and Ribaudo, M.
Improving the Performance of Road Network Analysis: The Morandi Bridge Case Study.
DOI: 10.5220/0007745702590266
In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 259-266
ISBN: 978-989-758-371-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
259

multi-core computation; (3) an empirical evaluation
of the benefits obtained thanks to the JGraphT refine-
ment; (4) a preliminary evaluation of the effects of the
Morandi bridge collapse on the characteristics of the
region Liguria road network.
The rest of the paper is organized as follows: Sec-
tion 2 describes the model of the road network that
can be obtained starting from the data available in
OSM and briefly recalls some centrality metrics. In
Section 3 we present some related work and in Sec-
tion 4 we discuss the improvements applied to the
JGraphT library in order to fully exploit parallelism
and fix some problems. Section 5 reports the results of
the empirical study aimed at quantifying the improve-
ments due to the JGraphT modifications, and shows
a preliminary analysis of the effects of the Morandi
bridge collapse. Finally, Section 6 concludes the work
discussing possible future directions.
2 ROAD NETWORK AND
METRICS
In order to analyse a road network we need accurate
data representing the network itself. Our choice is to
rely on OpenStreetMap since nowadays it is one of
the major sources for roads information. OSM is a
crowd-sourced project collecting extensive geographic
data such as roads, buildings, or other elements like
points of interest, shops, traffic lights, etc. Indeed,
rather than the map itself, the data generated by the
project is considered its primary output: the entire
database of OSM can be freely accessed, and used
as the basis for third-parties map-based applications
or research studies that analyse roads characteristics
or use the map as a data source for traffic simulation
models (Zilske et al., 2011).
2.1 OSM Graph Description
OSM data can be downloaded in different ways start-
ing from the OSM website download area
3
. It is pos-
sible to download the full dataset (which is huge) or
to select smaller areas. Map data are XML formatted,
stored into .osm files, and can be serialized into other
formats to be used in third-party applications.
Elements are the basic components of the OSM
conceptual data model of the physical world. They
consist of (1) nodes, defining points in space, (2) ways,
defining linear features (e.g., roads, rivers, etc.) and
area boundaries (e.g., buildings, forests, etc.), and
3
https://wiki.openstreetmap.org/wiki/Downloading_
data
(3) relations, which are used to explain how differ-
ent elements work or are connected together.
A way is a sequence of nodes and two ways inter-
sect if they share a common node. Our first prototype
was developed by mapping intersections between ways
into graph nodes, and by connecting these nodes when
there was a way connecting them.
However, we realized that the JGraphT library sup-
ports centrality measures only for nodes and not for
edges and therefore we adopted a different graph struc-
ture, building a line graph
4
. Ways in OSM data be-
come nodes and there is an edge from node A to node
B if (1) the ways represented by A and B share an
intersection and (2) the orientation of the ways allows
a movement from A to B. Therefore, each node in the
graph represents a complete road or a segment, and
the resulting graph is directed.
Only public and accessible car roads have been
included into the graph. Any other type of way (pedes-
trian only, private, etc.) has been filtered out using the
tags in the OSM dataset describing roads properties.
To take into account physical constraints of the
road network and of the territory, graph edges must be
weighted. The weights have been computed taking into
account as main parameter the time in seconds needed
to traverse the source way, at full legal speed, w.r.t.
street characteristics. Each weight is in fact multiplied
by different (cumulative) coefficients which have been
defined considering several streets properties available
in the dataset.
Table 1 shows the model parameters that somehow
mimic the behaviours of the drivers. For instance, in
streets which are accessible to bicycles the average
speed decreases and therefore we used a coefficient
equal to 1.2 to mimic a crossing time increase. On the
other hand, in absence of pedestrians the temptation
to slightly overcome speed limits is high, at least in
countries where there is some tolerance with respect
to legal speed; hence we used a coefficient equal to
0.95 to mimic a crossing time decrease. The same
reasoning holds for all the model parameters in order to
take into account speed variations according to streets
properties.
Despite being arbitrarily chosen, the parameters,
and therefore the weights used in the computation,
allowed us to get results similar to those computed
by common navigation solutions like those in Google
Maps (in particular when searching for the fastest path
between two locations). Thus, even if they need to
be further refined, these values can be considered a
reasonable starting point for this preliminary study.
4
https://en.wikipedia.org/wiki/Line_graph
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
260

Table 1: Model parameters for different street properties.
Property of the street Coefficient
accessible to bicycles 1.2
accessible / not accessible to pedestrians 1.15 / 0.95
two-way / one-way 1.2 / 1
number of lanes 1 / 2 / >2 1.25 / 1.15 / 1
street type motorway / trunk / primary / secondary / tertiary / others 0.9 / 1.05 / 1.35 / 1.50 / 1.6 / 1.8
number of nodes on a way (approximating the windingness of a street) 1 + (way_nodes / 1000)
2.2 Graph Metrics
Classical centrality measures for network analy-
sis (Newman, 2018) can be used to identify the most
important segments and paths in a road network; the
measures we have selected are briefly recalled below.
Betweenness centrality (
BC
) of a node
n
within
a network quantifies the number of times the node
n
acts as a bridge along the shortest paths between two
other nodes. For every pair of nodes in a connected
graph, there exists at least one shortest path between
them such that either the number of edges that the path
passes through (for unweighted graphs) or the sum
of the weights of the edges (for weighted graphs) is
minimized. The
BC
for each node is the number of
such shortest paths traversing the node itself divided
by the total number of shortest paths in the graph.
Mathematically, let
σ
s,t
(n)
be the number of short-
est paths from nodes
s
to
t
that pass through node
n
and let
σ
s,t
be the total number of shortest paths from
s to t. Then the Betweenness centrality of node n is:
BC (n) =
∑
s,t
σ
s,t
(n)
σ
s,t
This metrics shows the ability of a node to observe
the communication flow in the network: being in a
position of high betweenness allows to “control” the
flow of information, of goods, of viruses, of ideas, etc.
passing through the node. Notice that in this work we
use a weighted graph and therefore the interactions
between nodes are no longer binary (e.g., presence or
absence of a link), but have different influence on the
network, depending on the weights of the links.
Closeness centrality (
CC
) of a node
n
is computed
as the reciprocal of the sum of the lengths of the short-
est paths between n and all other nodes in the graph.
Mathematically, let
L
s,n
the length of the shortest
paths from node
s
to
n
. Then, the Closeness centrality
of node n is:
CC(n) =
1
∑
s
L
s,n
Nodes with higher Closeness are more central in the
network but not necessarily they also have a higher
Betweenness, since they might be direct neighbours
of network bridges, without being bridges themselves.
CC is a very natural measure of centrality but its values
tend to span on a rather small range, being computed
by considering shortest paths lengths which generally
depend logarithmically on the size of the network. As
a consequence, often the differences among CC values
are visible only at the less significant trailing digits.
3 RELATED WORK
In the last years several papers investigated the prob-
lem of analysing traffic flows. For instance, classi-
cal centrality measures such as Degree, Betweenness,
Closeness, and Clustering are computed and correlated
in (Jayaweera et al., 2017) for three different networks
of a small area in the Sri Lanka city of Kiribathgoda,
in order to identify the most important points in the
network that directly affect traffic congestions. This
work is similar to ours, but the graphs which are anal-
ysed are of relatively small sizes, and therefore did not
pose computational issues like those we encountered
during our study.
The goal of (Puzis et al., 2013) is different since the
authors combine
BC
and traffic flow, obtained using
GPS traces produced by drivers’ smartphones, to find
optimal locations for traffic monitoring units. They
provide a deep network analysis showing that the orig-
inal definition of
BC
, in which shortest paths are com-
puted by counting hops, does not correctly capture the
actual evolution of traffic flow. More realistic results
can be obtained if transportation specific features such
as time to travel, link capacity, congestion in different
times of the day are taken into account too. Some
of these features are captured in our computation as
well, since we weighted the OSM graph as discussed
in Section 2.1.
The paper (Hadas et al., 2017) proposes the compu-
tation of novel centrality measures based on transfer-
able utility games and shows that more precise results
can be obtained. A drawback of this approach is the
complexity of the computation and the current solution
cannot be applied to large datasets like ours.
Improving the Performance of Road Network Analysis: The Morandi Bridge Case Study
261

The paper (Zilske et al., 2011) describes a work-
flow for generating multi-agent traffic simulation sce-
narios based on OSM maps and MATSim, a frame-
work to implement large-scale agent-based transport
simulations. Like in our case, roads characteristics
are extracted from OSM tags and the available infor-
mation (e.g., speed limits) are multiplied for specific
factors to define the model parameters which take into
account the usual drivers’ habits since, for instance,
“legal limits are seldom honored.” Again, for a de-
tailed simulation, OSM data need to be integrated with
other data sources, such as public transport informa-
tion, synthetic population models, commuters matrices
providing information of home-work-home paths.
(Castagnari et al., 2018) presents an agent-based
simulation framework built on top of MATSim. The
prototype is called Tangramob and it was developed
to provide to local public authorities and urban plan-
ners an easy-to-use tool to assess the impact of smart
mobility initiatives before their actual implementation.
Thanks to the simulation results, smart mobility so-
lutions combining different services can be studied
before their deployment. By observing the outcomes
of the simulation experiments, which consider aspects
such as travel time, CO2 emissions, cost of mobility,
and the like, it becomes possible to compare several
smart mobility initiatives before their implementation,
thus mitigating probable failures that can cause waste
of resources and trust. An example of use of the tool
applied to a small Italian city is discussed in the paper.
4 JGrapht IMPROVEMENTS
In this section we briefly introduce the software used
for the study, and then discuss the updates we made to
the JGraphT library to improve the execution time of
the computation.
To build the road network we selected the DBMS
PostgreSQL to manage and query OSM data because
of the availability of the PostGIS
5
extension which
provides additional features and functions that sim-
plify the interaction with GIS data. The open source
software Osmosis
6
has been used to transfer data from
OSM to PostgreSQL: to extract the road network of a
region of interest the bounding box of the region can
be selected by applying specific tag filters.
Graph visualization has been obtained thanks to
QGIS
7
, which has been chosen because of its support
to GIS data and PostgreSQL. Graph visualization is
5
https://postgis.net/
6
https://wiki.openstreetmap.org/wiki/Osmosis
7
https://www.qgis.org/
performed in several steps: each time a model parame-
ter (see Table 1) changes, the graph is loaded by our
custom software from PostgreSQL, elaborations are
performed, the new graph is stored back in GIS for-
mat to PostgreSQL, in a new table associated to the
current parameters set and, finally, visualized in QGIS.
Almost no manual operations are needed.
The Java programming language and the JGraphT
library were chosen for all the analyses but, after down-
loading JGraphT, we noticed that this library does not
support multi-core computation which is extremely
useful in case of large datasets, provided the problem
supports parallelization.
Our OSM dataset can exploit parallelism be-
cause the shortest paths between pairs of nodes can
be computed in parallel for different pairs, given
that these are independent tasks. Therefore we
decided to refine the implementation of JGraphT
to support parallelism, in particular by using the
Collection.parallelStream
8
method. When a
stream executes in parallel, the Java runtime parti-
tions the stream into multiple substreams; aggregate
operations iterate over and process these substreams
in parallel and then combine the results. In this way,
the computation becomes concurrent and it can use all
the cores available on the CPU. Such an optimization
allowed us to drastically reduce the execution times as
we will discuss in the next section.
In addition, some changes have been made to the
JGraphT library to allow the Betweenness module to
deal with large graphs. The first change is related
to the fact that in this module each node has a score
which is normalized as:
NormScore = Score/[(n − 1)(n − 2)]
We noticed that the result of the product
(n − 1)(n− 2)
was stored in an integer variable, thus limiting the
correct value of
NormScore
to graphs with less than
46343 nodes
9
. For larger graphs, wrong results are
computed because of integer overflow errors.
The second change is related to the Betweenness
centrality which was implemented using a priority
queue (implemented as a Fibonacci Tree) to run a
Dijkstra-like visit of the graph, and a HashMap to ef-
ficiently check whether a new priority for a node is
lower (thus better path) than the one of the best path
known at that moment. During the visit of the graph,
the priority of a node might change because a shorter
path is found. This update in the priority was reflected
8
https://docs.oracle.com/javase/8/docs/api/java/util/
Collection.html#parallelStream--
9
In Java, the MAX-value for integers is 2147483647.
This value is exceeded in the computation of
(n − 1)x(n − 2)
when n >= 46343.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
262

in the Fibonacci Tree but not in the HashMap used to
trigger an update of the Fibonacci tree. This inconsis-
tency leads to an unnecessary update of the Fibonacci
Tree (old priority was lower than the new one) and thus
to an exception in the Fibonacci Tree implementation
used by the library.
5 EMPIRICAL STUDY
The goal of the empirical study is twofold. In the
first part of this section we analyse the performance of
the JGraphT library obtained with the introduction of
parallelism; in the second part we discuss the changes
in the roads map after the Morandi bridge collapse.
5.1 The Road Map
Starting from the OSM data of the Northern-West
Italy
10
map, we reduced the graph to cover the Liguria
region bounding box. This can be obtained by using a
shapefile of the region and by filtering out those nodes
which are outside the area. After the filtering, the
resulting graph has 54852 nodes and 126847 edges.
Unfortunately, after this operation, the resulting
graph has some roads disconnected from the remain-
ing network (e.g., roads that enter for a small length
in the Ligurian territory but are not connected to the
rest of the network). We decided to remove them in
order to have a single, fully connected component. As
a consequence, the graph on which we made the exper-
iments has 53743 nodes and 125250 edges. A smaller
graph (Genoa Municipality) has been used for the per-
formance experiments, with 11811 nodes and 26590
edges. These final graphs are directed and weighted
according to the parameters of Table 1.
5.2 Single vs Multi-core: Evaluation
All the experiments on the OSM dataset were carried
out on a virtual machine running on a quite powerful
hardware. All the details on the systems (guest and
host) and settings are described in Table 2. With this
configuration we were able to easily create different
settings (i.e., changing the number of active CPUs).
The comparisons between the original single core
version of JGraphT and the new parallel version
were carried out using different numbers of cores and
threads, ranging from 1C 1T (e.g., 1 core and 1 thread
available for the virtual machine) to 8C 16T. In this
way, we were able to evaluate the scalability of the
10
https://download.geofabrik.de/europe/italy/nord-ovest.
html
Table 2: HW and SW characteristics of the system.
Host Windows Server 2016
Hypervisor Hyper-v
Guest Windows 10 Pro 1803
CPU AMD Ryzen 1700 8C16T
CPU Freq 3.0 GHz (3.7 GHz Turbo)
Host RAM DDR4 32GB 2133MHz
Guest RAM 12GB
Java version 1.8.0_152
Java SE RE build 1.8.0_152-b16
Java HotSpot 64-
Bit Server VM
build 25.152-b16, mixed
mode
Java Graph JGraphT 1.2.0
parallel implementation. The AMD Ryzen 1700 has 8
cores but it is able to execute up to 16 threads thanks
to the simultaneous multithreading technology
11
. For
both the
BC
and the
CC
computations (see Tables 3
and 4 respectively) we report the relevant statistics of
8 executions for each configuration. In this way we
can average any random fluctuation due to other con-
current computation or communication loads. Thus,
the Tables report the average, the std deviation, the
median and the min-max of the 8 computations for
each configuration (since the std dev is generally very
small, we will consider only the average values in the
discussion of the results).
For the computation of the
BC
with the original,
single core version of JGraphT, if we consider the
execution time, the major difference emerges when
using more than one core. Indeed, when a single core is
available, all threads running on the machine (e.g., the
SO threads) interfere with the execution of JGraphT
computations. This leads to higher execution times
(see column Single Core - 1C 1T in Table 3). Instead,
when the machine can access to 2 or more cores the
time required decreases (e.g., from 382s for 1C 1T to
286s for 2C 2T). It is interesting to note that the lowest
time is achieved when only 2 cores are available. This
is probably due to the presence of the “Turbo” effect.
More precisely, the AMD Ryzen 1700
12
CPU has a
base frequency of 3.0 GHz but thanks to the Precision
Boost technology it can reach up to 3.7 GHz when
only 1 or 2 cores are active and up to 3.2 GHz when
3 or more cores are active. The processor features
also the XFR (eXtended Frequency Range) technology
that increases the processor voltage and clock speed
beyond the maximum Precision Boost, when sufficient
11
https://en.wikipedia.org/wiki/Simultaneous_
multithreading
12
https://en.wikipedia.org/wiki/Ryzen#CPUs:
_Summit_Ridge_/_Whitehaven
Improving the Performance of Road Network Analysis: The Morandi Bridge Case Study
263
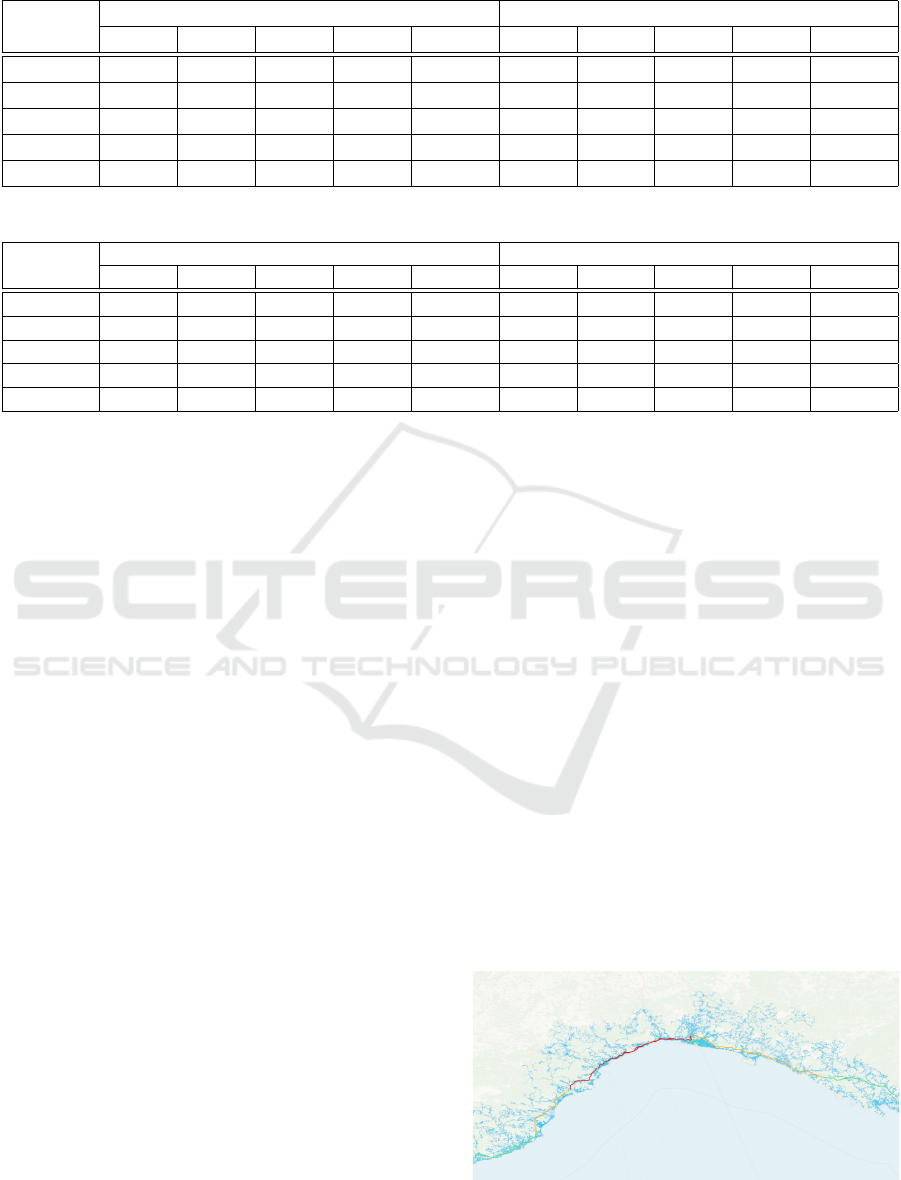
Table 3: Execution time for BC in different settings.
Time (s)
Single Core JGraphT Multi Core JGraphT
1C 1T 2C 2T 4C 4T 8C 8T 8C 16T 1C 1T 2C 2T 4C 4T 8C 8T 8C 16T
Average 382 286 300 320 337 382 176 103 62 60
Std Dev 2 2 2 4 21 13 1 3 3 1
Median 382 286 300 320 326 376 176 102 63 60
Max 387 289 303 330 398 408 179 109 68 62
Min 380 284 298 316 319 373 175 100 58 59
Table 4: Execution time for CC in different settings.
Time (s)
Single Core JGraphT Multi Core JGraphT
1C 1T 2C 2T 4C 4T 8C 8T 8C 16T 1C 1T 2C 2T 4C 4T 8C 8T 8C 16T
Average 212 171 181 192 206 214 100 55 31 27
Std Dev 1 1 2 1 15 9 2 2 2 1
Median 212 171 181 192 198 210 100 54 30 27
Max 215 174 184 193 247 229 104 58 35 28
Min 211 170 179 191 194 207 99 53 28 26
cooling is available. The combined effect of these
technologies explains the obtained results.
The results change with the multicore version of
the library since the computation scales well on the
additional cores. Indeed, when moving from 1 to 2 and
then to 4 cores the average execution time required
to compute
BC
is reduced of respectively about 2.1
(382/176) and 3.7 times (382/103). Similarly, from 1
to 8 cores the reduction is of about 6.1 times (382/62).
The more than linear improvement in the case of 2
cores can be explained with the effect of the back-
ground tasks running on the machine (recall that 1C
1T means that the virtual machine can access to only
1 core of the CPU). Interestingly, the support of addi-
tional threads, thanks to the simultaneous multithread-
ing technology, does not provide a relevant benefit
since, even when enabling 16 threads, the improve-
ment increases only up to 6.3 times w.r.t. the 1C 1T
configuration (i.e., only +3% in performances moving
from 8T to 16T).
The same considerations can be done for the
CC
computations which are reported in Table 4. The per-
formance trends among the various configurations are
very similar to those seen for Betweenness. It is in-
teresting to note that, in this case, the simultaneous
multithreading technology allows to reach better per-
formances: indeed when moving from 8C 8T to 8C
16T, the parallel implementation of JGraphT allows to
increase the performances of respectively about 7 and
7.8 times with respect to the 1C 1T configuration.
To summarize we can claim that:
•
Depending on the machine configuration, the orig-
inal version of JGraphT provides only slightly dif-
ferent performances, which are due to a different
behaviour of the hardware (e.g., combined effect
of the Precision Boost and XFR technologies).
•
The parallel implementation of JGraphT is able to
provide relevant performance improvements. In
our experiments, we observed an almost linear
improvement of the performances with respect to
the number of available physical cores. On the
other hand, the availability of additional virtual
cores beyond 8 physical cores does not provide
any significant benefit.
5.3 Effects of the Bridge Collapse
To provide a realistic simulation of the actual road net-
work configuration after the Morandi bridge collapse,
we removed the bridge itself from the graph, as well
as all the roads that have been closed after the event
(since damaged or considered dangerous).
As said in Section 2,
BC
allows to detect those
portions of a graph that shrink the distances between
nodes; in the case of a road network these are probably
the streets most used in practice by drivers. The results
Figure 1:
BC
of the Liguria road network before the Morandi
bridge collapse.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
264

Figure 2: BC: before (left) and after (right) Morandi bridge collapse (detailed vision).
show that the Morandi bridge has one of the highest
BC
in the map, a value of 0.2427, while the maximum
computed value is equal to 0.2556.
Sopra Elevata
13
, which is an important road that
serves a central area of Genoa Municipality, has a
medium
BC
, a value equal to 0.08. In fact these two
were the most used roads for drivers willing to reach
the centre of the city. Therefore,
BC
results success-
fully capture the fact that many shortest paths were
passing through those nodes. Indeed, the Morandi
bridge was actually one of the most important bridges
(also in graph terms) for the traffic in Liguria.
Figure 1 shows the
BC
of the whole region before
the bridge collapse, with higher values represented
with the red color and lower values represented in blue.
Figure 2 provides a detailed vision of the situation and
the effect of the Morandi bridge collapse is absolutely
relevant. A red important segment disappeared after
the collapse (since the highway was - and still is - inter-
rupted in that point) and alternative city streets (see the
black dots in the map) are now those with the highest
traffic, being the new bridges in the network. As a
consequence, these are also bottlenecks of the entire
network and, indeed, they are the site of traffic jams
during peak traffic hours. More in detail, as we can
see in Figure 2, after the event some central streets of
Genoa became the most important ones. For instance,
Via Cornigliano and Lungomare Canepa moved from
BC
values of 0.0221 and 0.0056 (quite low) to the
new values of 0.4990 and 0.4939, respectively, which
are now the highest values of the entire Liguria road
network.
The two curves in Figure 3 show the
BC
distribu-
tion before and after the collapse of Morandi bridge.
The y-axis represents the number of nodes in a bin (of
size 0.03) with a given value of
BC
; for readability all
nodes with BC equal to 0 are omitted from the plot.
13
https://it.wikipedia.org/wiki/Strada_sopraelevata_di_
Genova
Figure 3:
BC
distribution: before (solid, yellow) and after
(dashed, blue) Morandi bridge collapse.
Figure 4:
CC
distribution: before (solid, yellow) and after
(dashed, blue) Morandi bridge collapse.
The distribution is right skewed and it can be ob-
served that the tail becomes longer after the collapse,
since new nodes emerge with
BC
values which are out
of the scale before the collapse, as shown by the iso-
lated blue dashed line in the rightmost part of Figure 3.
Changes in the
CC
characteristics of the road net-
work can be observed as well, both at the map level or
by plotting curves. Nodes with high
CC
can be reached
over short distances and Figure 4 shows that, after the
crash, nodes are further away and the overall distances
increased, as daily witnessed by drivers. This is math-
ematically shown in the curves when observing the
Improving the Performance of Road Network Analysis: The Morandi Bridge Case Study
265

shift to left of the blue line w.r.t. the yellow line (e.g.,
nodes show a lower CC and therefore are further away
from each other).
The bin size in Figure 4 is 0.0003 and it can be
observed that, in accord to the theory, the CC results
span over a small range of values, much smaller with
respect to the BC results.
6 CONCLUSIONS AND FUTURE
WORKS
In this work we have presented the computation of
some classical centrality measures for the map of the
region Liguria, before and after the Morandi bridge
collapse, discussing the changes occurred to the street
network. In order to perform an efficient computation
we extended the implementation of the JGraphT library
to support multi-core computation.
The current implementation does not consider any
traffic data but we are planning to extend our work to
build a tool that takes into account also this data source,
possibly by accessing to real traffic data available at
the Municipality level. A second possible extension
will investigate whether a parallel solution could be of
help for the implementation of less classical centrality
measures like those introduced in (Hadas et al., 2017).
In this work we relied on the entire region Liguria
road network model. Thus, the analyses described
in this paper are focussed more on the impact of the
Morandi bridge collapse on “regional travellers” rather
than “city travellers”. As future work we plan to per-
form a multi-scale analysis in order to evaluate the
effects of the crash on different kind of travellers. This
could be very useful to understand the changes for
travellers moving between relevant portions of the city
(e.g., along the Valpolcevera valley
14
).
We think that an easy-to-use tool to assess the
inconveniences due to failures in the road network
caused by atmospheric events, temporary accidents,
lasting disasters, or target attacks could be extremely
helpful for local public authorities to simulate the im-
pact of failures before their occurrences.
An analysis of all the side-effects caused by the
collapse of the Morandi bridge is out of the scope of
this paper, but it is worth mentioning that a city like
Genoa, whose economy is heavily based on the ex-
change of goods through its port, in addition to the
paralysis of the private transport system, is nowadays
witnessing an important economic loss which will be
more clear in the next months. Therefore, we think
that a tool that can help to understand the impact of
14
https://en.wikipedia.org/wiki/Val_Polcevera
random or target failures, and possibly suggest how to
protect the network, for instance by adding some re-
dundancy, should be welcome by the public authorities
and decision makers.
REFERENCES
Castagnari, C., Corradini, F., Angelis, F. D., de Berardinis,
J., Forcina, G., and Polini, A. (2018). Tangramob: an
agent-based simulation framework for validating urban
smart mobility solutions. CoRR, abs/1805.10906.
Glanz, J., Pianigiani, G., White, J., and Patanjali, K. (2018).
Genoa bridge collapse: The road to tragedy. New York
Times. https://www.nytimes.com/interactive/2018/09/
06/world/europe/genoa-italy-bridge.html.
Hadas, Y., Gnecco, G., and Sanguineti, M. (2017). An
approach to transportation network analysis via trans-
ferable utility games. Transportation Research Part B:
Methodological, 105.
Jayaweera, N., Perera, R., and Munasinghe, J. (2017). Cen-
trality measures to identify traffic congestion on road
networks: A case study of Sri Lanka. IOSR Journal of
Mathematics, 13:13–19.
Newman, M. (2018). Networks. OUP Oxford.
Puzis, R., Altshuler, Y., Elovici, Y., Bekhor, S., Shiftan,
Y., and Pentland, A. (2013). Augmented betweenness
centrality for environmentally aware traffic monitor-
ing in transportation networks. Journal of Intelligent
Transportation Systems, 17:91–105.
United-Nations (2016). The world’s cities in 2016. https:
//www.un-ilibrary.org/population-and-demography/
the-world-s-cities-in-2016_8519891f-en.
United-Nations (2018). 68% of the world population
projected to live in urban areas by 2050. https:
//www.un.org/development/desa/en/news/population/
2018-revision-of-world-urbanization-prospects.html.
Windmill (2018). Vehicle sensing: Ten technolo-
gies to measure traffic. http://www.windmill.co.uk/
vehicle-sensing.html.
Zilske, M., Neumann, A., and Nagel, K. (2011). Open-
streetmap for traffic simulation. In Proceedings of 1st
European State of the Map Conference, pages 126–134.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
266
