Path Planning of a Mobile Robot in Grid Space using Boundary Node

Method

R. A. Saeed

and Diego Reforgiato Recupero

Department of Mathematics and Computer Science, University of Cagliari, Cagliari, Italy

Keywords:

Robot Path Planning, Boundary Node Method, Path Enhancement Method, Autonomous Mobile Robot.

Abstract:

This paper presents a new off-line path planning method for a mobile robot to generate an optimal or near-

optimal collision-free path between starting and goal points in a given working environment with obstacles.

In a new method called Boundary Node Method, the robot is simulated by nine-node quadrilateral element,

the centroid node represents the robot’s location and it moves with eight-boundary nodes in the working

environments. A robot is exploring an environment with the help of the node’s potential value at each location,

where the potential value is calculated based on the proposed potential function. The proposed method is

capable of generating the initial collision-free path for a mobile robot safely and quickly. Subsequently, an

additional new method called Path Enhancement Method is used to ﬁnd shortest path by reducing the overall

initial path length. The simulation results indicate that this method can successfully generate an optimal or

near-optimal collision-free path efﬁciently.

1 INTRODUCTION

Path planning has been widely applied in many

robotic applications (Atzeni and Recupero, 2018) to

perform various tasks that humans could not accom-

plish, such as nuclear facilities (Chao et al., 2018),

space exploration (Shum et al., 2015), rescue mission,

landmines and enemies in war ﬁeld (Zhang et al.,

2013), etc. Therefore, the problem of path plan-

ning has attracted many researchers’ attention (Zhang

et al., 2013; Kala et al., 2011). The objective of path

planning is to construct a collision-free path for mo-

bile robots to move from a starting point to destina-

tion point in a given working environment with ob-

stacles and optimizing it with respect to some cri-

teria, i.e. the walking distance, the walking time,

the energy consumption, etc (Leena and Saju, 2014;

Han and Seo, 2017; Victerpaul et al., 2017). The

existing methods are mainly categorized into classi-

cal and heuristic path planning (Zhang et al., 2013;

Han and Seo, 2017). The classical methods involve

ﬁnding a set of deﬁned steps to search for the solu-

tion from an initial position to a goal position, they

include cell decomposition, potential ﬁeld method,

subgoal network and road map (LaValle, 2006). It

https://orcid.org/0000-0002-7385-0167

https://orcid.org/0000-0001-8646-6183

has been found that the classical methods have some

disadvantages like high computational cost, trapping

into local minima and high time complexity in high

dimensions (Zhang et al., 2013; Brand et al., 2010;

Leena and Saju, 2014). Therefore, many heuris-

tic methods have been proposed, i.e. Genetic Al-

gorithm (GA) (Lamini et al., 2018), Particle Swarm

Optimization (PSO) (Zhang et al., 2013), Artiﬁcial

Neural Networks (ANNs), Ant Colony Optimization

(ACO) (Brand et al., 2010; Mac et al., 2016), and

Fuzzy Logic (FL) (Brand et al., 2010). Heuristic path

planning methods are computationally more efﬁcient

with better performances in term of path distance, ob-

stacle avoidance, and elapsed time (Brand et al., 2010;

Leena and Saju, 2014; Mac et al., 2016), but these

algorithms are not guaranteed to provide the optimal

solution (Rintanen, 2006; LaValle, 2006). The com-

binatorial path planning methods in continuous space

can solve many path planning problem and construct

optimal solution efﬁciently (Bi et al., 2008; LaValle,

2006; Huang and Tsai, 2011; Montiel et al., 2015;

Contreras-Cruz et al., 2015; Song et al., 2016).

Additionally, many researchers made some mod-

iﬁcations and extensions to improve the performance

and to overcome the limitations of the existing meth-

ods for solving the path planning problem. For in-

stance, authors in (Wang et al., 2018) proposed a

novel learning-based multi-RRT s (LM − RRT ) ap-

Saeed, R. and Recupero, D.

Path Planning of a Mobile Robot in Grid Space using Boundary Node Method.

DOI: 10.5220/0007747301590166

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 159-166

ISBN: 978-989-758-380-3

159

proach for robot path planning in complex environ-

ments with narrow passages. A new repulsive po-

tential function is proposed by (Ge and Cui, 2000)

to solve the problem of non-reachable goals with ob-

stacles nearby (GNRON) in potential ﬁeld method.

The shortest path with the minimum time required

for the global path planning is investigated in (Shilt-

agh and Jalal, 2013) by using Modiﬁed PSO. Authors

in (Fu et al., 2018; Guruji et al., 2016; Ducho

n et al.,

2014) proposed an improved version of A Star algo-

rithm to overcome inherent drawbacks of the origi-

nal A Star. A new ﬁtness function for GAs is pro-

posed by (Lamini et al., 2018) for optimizing en-

ergy consumption for a mobile robot. Some optimal

path planning algorithms are presented in (Jan et al.,

2008) for navigating mobile robot among obstacles

and weighted regions.

Many of the existing methods for robot path plan-

ning are able to ﬁnd a path from an initial position to

a given target, but they are either not accurate enough

or their efﬁciency is not sufﬁcient. Researchers have

always been seeking a better solution to improve the

performance of the existing path planning methods.

A list of goals that researchers of several previous

works have been pursuing is the following: improve

the accuracy (Liu et al., 2018; Shum et al., 2015;

Goyal and Nagla, 2014), improve the efﬁciency (Hu

and Yang, 2004), increase safety (Chao et al., 2018;

Shum et al., 2015; Fu et al., 2018), increase the capa-

bility (Shiltagh and Jalal, 2013), reduce the process-

ing time (Ducho

n et al., 2014; Guruji et al., 2016),

overcome the non-reachable goal problem (Ge and

Cui, 2000), pass through narrow passages (Jan et al.,

2008).

In the literature, the problem of path planning

for mobile robots has been widely discussed and re-

searchers explored a variety of solutions. However,

several important gaps and limitations remain to be

addressed. For example, in several works, the com-

putational time is still too high because of the pro-

cessing a lot of unnecessary points. Moreover, the

search for an optimal path might not succeed (Han

and Seo, 2017). And also, there are many methods

that use random operation to produce a set of solu-

tions for each independent run. Then, in order to ﬁnd

the optimized solution, all of these different solutions

are selected, combined and replaced. This process re-

quires a lot of computational time. Based on the limi-

tations and research gaps as previously explained, we

investigate a new efﬁcient method called Boundary

Node Method (BNM) to generate a feasible path for

the robot to move from starting point to ending point

in the workspace without colliding with any obsta-

cles. The BNM is capable of ﬁnding the path for mo-

bile robot effectively and efﬁciently in terms of path

length and computational time, even if the complexity

of the environment is increased. Moreover, a valuable

beneﬁt of this method is its simplicity and can be ap-

plied in a grid environment efﬁciently.

The remainder of this paper is structured as fol-

lows: Section 2 introduces the problem statement. In

Section 3, a brief description of the proposed method

for generating feasible path is introduced. In Sec-

tion 4, the application of the proposed method is pre-

sented, and then the evaluation results are reported

and discussed. Final conclusions and remarks for fu-

ture research improvements are provided in Section 5.

2 PROBLEM FORMULATION

The path planning problem is formulated as fol-

lows: for a given two-dimensional (2D) robot work-

ing space C ⊂ R

, the region of the working space oc-

cupied by obstacles is denoted by C

obs

and the region

of the working space free of obstacles is represented

by C

f ree

= C – C

obs

. Each position within C

f ree

reachable by the robot. The continuous workspace is

divided into square grid cells. Each grid cell of the

space has integer coordinates of the form C(x, y) ∈

C, 1 ≤ x ≤ n, 1 ≤ y ≤ m, which either corresponds to

a navigable area C(x, y) ∈ C

f ree

or a space occupied

by obstacles C(x, y) ∈ C

obs

. We assume that all infor-

mation related to the workspace is known in advance,

obstacles are also assumed to be ﬁxed in their position

in the workspace. Each grid cell C(x, y) in C

f ree

has a

potential value E(x, y) ∈ E, which is calculated based

on the potential function. The robot is requested to

move from starting point (C

) to goal point (C

) in the

workspace without colliding with any obstacles. It is

expected that the robot reaches the ﬁnal destination

point safely through the shortest walking route within

minimum computational time.

3 BOUNDARY NODE METHOD

In BNM, the robot is simulated by nine-node quadri-

lateral element, the centroid node represents the

robot’s location and it moves with eight-boundary

nodes in the workspace. The robot position in the

workspace is denoted by C

, y

) ∈ C

f ree

. The

robot moves forward and changes its motion direction

based on the potential values and features of bound-

ary nodes. All Way-points w visited by the robot se-

quentially represent the obtained initial feasible path

(IFP). For better clarity, these way-points are con-

nected into a continuous path, the line segment that

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

160

connects two way-points sequences is represented by

l,l+1

⊂ IFP. A complete path IFP is formed by con-

catenation of all inter-line segments P

l,l+1

, 1 ≤ l ≤

w − 1 as follows: IFP = [P

1,2

, P

2,3

. . . , P

w−1,w

]. The

robot’s working space used in this study is divided

into square grid cells, and the centre of all grid cells

in the given workspace meets the following equation:

C =

∑

x=1

∑

y=1

C(x, y) (1)

where n and m represent the width and height of the

workspace. C(x, y) represents the location of the grid

cells in the workspace, and the length of each grid cell

is equal to 1 unit.

After constructing a model for the workspace, the

potential value for each grid point E(k) (1 ≤ k ≤ N),

(N = n × m) is calculated based on the new proposed

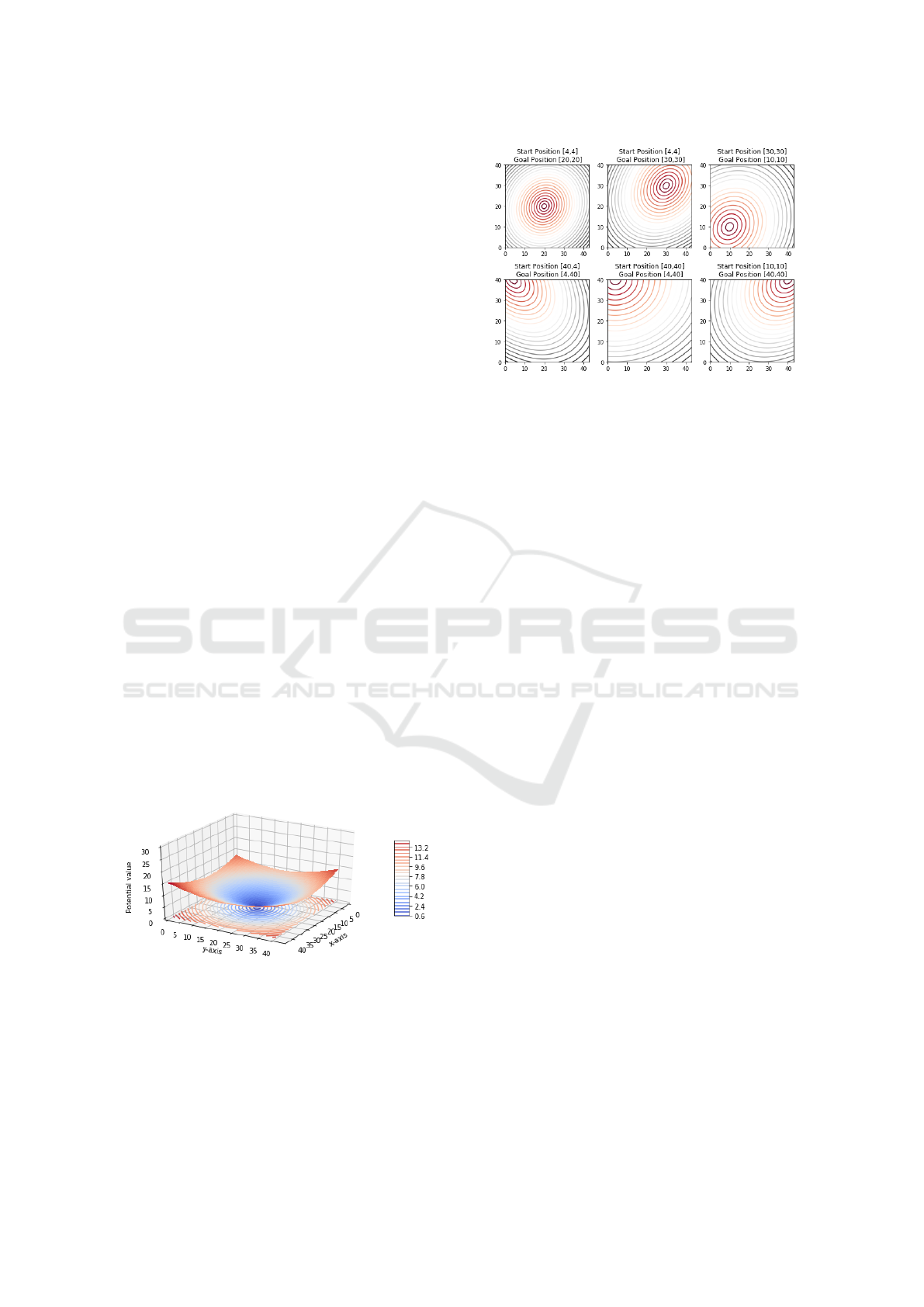
potential function as illustrated in Figure 1. The po-

tential function for several different starts and goal

positions are shown in Figure 2. The potential func-

tion is used to direct the robot toward the C

, and it

has the lowest potential value at a ﬁnal destination

point and the potential value increases as the robot

move further away. As shown in the Figure 2, the

line’s colour represents the potential value, i.e. the

blue line corresponds to the lowest potential value

and the red line corresponds to the highest potential

value. The shape of the potential function and obsta-

cles in a 2D model of the robot’s workspace is pre-

sented in Figure 3. As shown in the ﬁgure, a num-

ber of static obstacles (1 × 1 unit) are distributed at

different locations in the workspace. The centre of

obstacle’s cells is represent by Cartesian coordinates

obs

(h, l), (h = 1...2, l = 1...O), where h = 1 and h = 2

corresponding to x and y-coordinate, respectively, and

O representing the number of obstacles.

Figure 1: Potential value for each cell in the workspace in

3D view with contour plot. The size of the workspace is

44 × 44, and the C

is located (20, 20).

3.1 Simulate the Robot

In this method the robot is simulated by nine-node

quadrilateral element (see Figure 4a), the centroid

node represents the robot’s location (see Figure 4b)

Figure 2: Potential function with considering several dif-

ferent start and goal Locations.

and it moves with eight-boundary nodes exploring in

the workspace (see Figure 4c) to ﬁnd the IFP. The

nodes are denoted by p(q), (q = 1...9), and their lo-

cations can be formulated by using Equation 2. In

simulated model, the node p(5) represents the robot’s

location and the other nodes p(1 → 4) with p(6 → 9)

represent the boundary nodes which are distributed

uniformly around the robot location as shown in Fig-

ure 4a. The current location of all nodes in the

workspace at any iteration t is denoted by p

(t),

meanwhile the robot location in the simulated model

is denoted by p

(t) ∈ p

(t). The set of x and y-

coordinate of the robot and all boundary nodes are

represented by two vectors, x

(t) = (x

, x

, ..., x

)

and y

(t) = (y

, y

, ..., y

) respectively, p

(t) is

formed by vertically concatenating x

(t) and y

(t),

(t) = [x

(t); y

(t)].

p(q) =











x, y q=5

(x + v

, y), (x, y + v

(x − v

, y),

(x, y − v

) q = 2, 4, 6, and 8

(x + v

, y + v

), (x − v

, y + v

(x − v

, y − v

(x + v

, y − v

) q = 1, 3, 7, and 9

(2)

where x and y are the distance between the center of

the grid cell and x and y − axis, v

and v

are the hor-

izontal and vertical distance between the robot and

boundary nodes, we assume that v

= v

= 1 unit.

In each iteration t, the robot and boundary nodes

p(q), (q = 1...9) are moved in one particular direc-

tion in the workspace. The current robot’s location

with boundary nodes can be described as p

(t) =

(t); y

(t)], and the new updated location of all

nodes denoted by p

(t) = [x

(t); y

(t)]. The robot

Path Planning of a Mobile Robot in Grid Space using Boundary Node Method

161

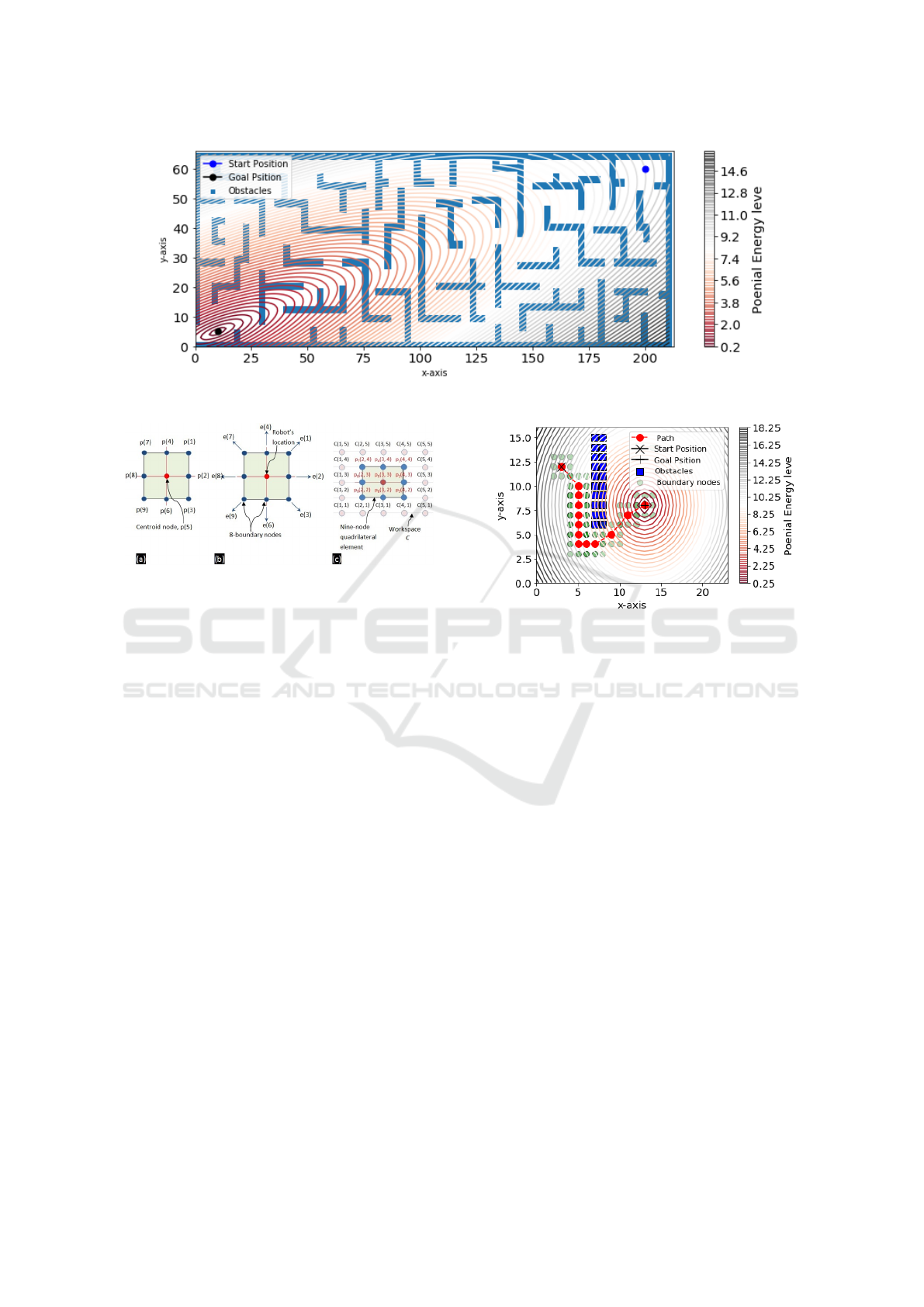
Figure 3: 2D model of the robot’s workspace.

Figure 4: A nine-node quadrilateral element (a) along with

its motion directions (b) and exploration location in the

workspace (c).

interference the obstacles when the distance between

the robot and the obstacles is less than 1 unit. There-

fore, the robot and boundary nodes require to avoid

obstacles and changing its moving direction by se-

lecting a new position in the C

f ree

. Characteristics

of boundary nodes, their position and potential val-

ues, guides the robot toward the goal location. On the

other hand, the characteristics of boundary nodes can

help the robot to avoid the obstacles. To explain how

the robot avoids the obstacles and changing its motion

direction with the help of boundary nodes, consider

a simple workspace example shown in Figure 5. As

shown in the ﬁgure, the robot position p(5) is repre-

sented by a red circle object and the boundary nodes

p(1 → 4) and p(6 → 9) are represented by green cir-

cle object.

Initially, the robot’s position p(5) is coincide with

(see Figure 5). In the ﬁrst iteration t = 1, the robot

with boundary nodes change their positions from cur-

rent position p

(1) to new position p

(1) toward the

goal. In the second iteration t = 2, as the robot move

toward the goal with boundary nodes, the nodes p(1),

p(2), and p(3) interference with the obstacles, as

demonstrated in the Figure 5. Then the robot investi-

gates the workspace to ﬁnd the next position without

colliding any obstacle. In this study, the direction of

the robot motion could be to the left, right, forward or

Figure 5: Demonstrates an example of path planning and

obstacle avoidance for mobile robot in a static environment

using BNM, where the sequence of the red circle objects is

represents the best solution of IFP.

backward. As shown in Figure 5, the robot can only

move in the y-direction, either upward or downward

direction. Changing the motion direction depends on

the potential value, E. Because E(4) is greater than

E(6), therefore the next position of the robot must be

in the downward direction. The same procedure is re-

peated by shifting the robot to the downward direction

until it passes the block of obstacles. The distance be-

tween the p

(t) and the C

is decrease step by step

until the robot reaches to the global minimum at the

goal position. The simulation result of the BNM is the

IFP, which is consist a set of way-points visited by

the robot starting from the initial point and ending at

the goal point. The BNM can generate the IFP safely

and efﬁciently, but the path is not optimal in term of

the total path length. Therefore, the PEM is intro-

duced to reduce the number of way-points as well as

the overall length of IFP.

3.2 Path Enhancement Method

This section introduces the PEM to obtain the short-

est path (see Figure 6) from IFP (see Figure 5). As

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

162

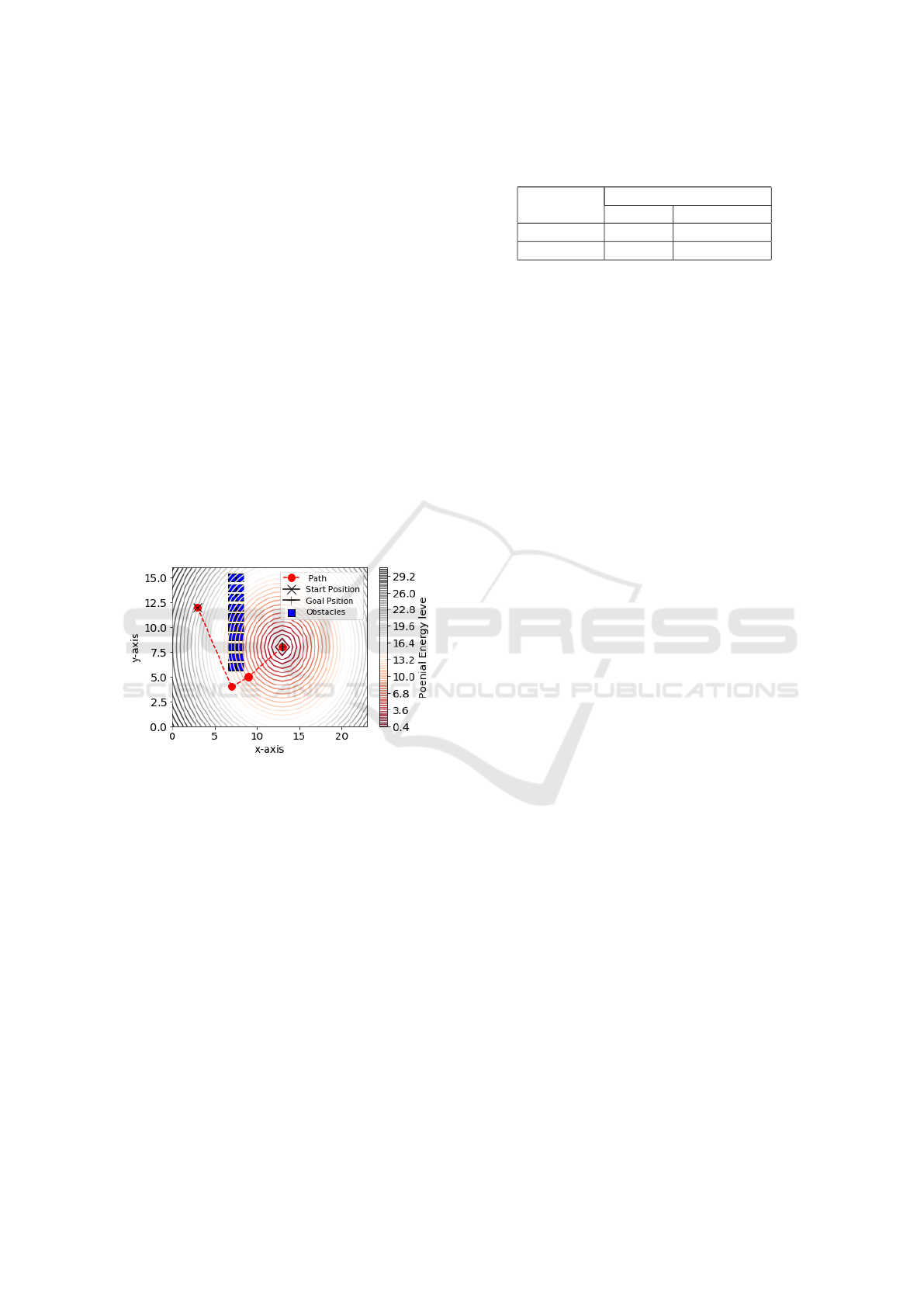
shown in the ﬁgure, the way-points in the IFP are rep-

resented by a set of red circles object between C

and

. The robot starts to move from the starting point

and tracked through all the intermediate waypoints

until it reaches the goal point. The PEM method is

applied to reduce the number of way-points as well as

the overall length of IFP. The applied results show

that the number of way-points between C

and C

has

been reduced from 13 (see Figure 6) to 4 way-points

(see Figure 6). The length of all line segments that

connects all way-points sequentially to each other is

representing the path length. The length of the short-

est path U is calculated by using the following equa-

tion:

U =

∑

i=1

(sqrt(u

(i) − u

(i))

+ (u

(i) − u

(i))

)

(3)

where U is the total path length, I is line segment

number and u

(i), u

(i) are represent

the x and y cartesian coordinates of the left-hand and

right-hand ends of the line segment U(i).

Figure 6: Constructing the shortest-path from way-points in

a 2D workspace. Way-points deﬁning the path are marked

with red circles object. The red dashed line represents a

shortest path found by using BNM and PEM.

4 SIMULATION

In this study, all simulations have been performed in

python. All simulations results presented in this paper

have been computed on a laptop Intel(T M) Core(T M)

i5-8300H CPU, 2.3GHz, and 8GB RAM. Two dif-

ferent workspace scenarios with different complexity

are designed. In the ﬁrst scenario, several different

start and goal Locations are considered. In all scenar-

ios the size of workspace and obstacles scattered in

the navigation space are same. Whereas, a complex

environment with a high number of obstacles in dif-

ferent sizes is considered in the second scenario. The

start and goal points are positioned in the free space

Table 1: The total path length of the initial and ﬁnal path

obtained by BNM and PEM.

Workspace Total Path Length [unit]

No. IFP Final Path

1 512.748 241.117

2 529.591 268.822

f ree

. The proposed method was examined to ﬁnd an

optimal or near the optimal path from C

to C

. The

simulation results of BNM and PEM are presented in

subsections 4.1 and 4.2, respectively.

4.1 Simulation Results of BNM

This section presents the application results of the

BNM for generating the IFP between C

and C

. The

simulation results for all tested scenarios are shown in

Figures 7 and 8. The achieved result of IFP is repre-

sented by a set of way-points w( j), ( j = 1 → J). Each

new point position w( j + 1) allocated after the current

point position w( j) on the path, where J represents the

time in which the robot is reaching to the ﬁnal desti-

nation point. In the ﬁrst scenario, the way-points of

the robot’s motion path are represented by red circles

object and for better clarity, these way-points are con-

nected into a continuous path (see Figure 7). In the

second scenario, the way-points of the robot’s motion

path are represented by the red solid line (see Fig-

ure 8).

From the ﬁgures, it is observed that the IFP allow

the robot to move from C

to C

, and avoid obstacles

successfully. As it can be seen from the results, BNM

was able to overcome the local minima problem. The

results show that BNM has been well applied to gen-

erate IFP for mobile robot and achieved important

achievements. However, the path is not optimal in

term of the total path length. In order to reduce the

overall length of IFP, a new method PEM is intro-

duced as explained in Section 3.2, and the application

results are presented in the following subsection.

4.2 Simulation Results of PEM

This section presents the obtained results of the PEM

to ﬁnd the optimal or near-optimal path. The best

obtained solutions are presented in Figures 9 and 10.

Whereas the red dashed lines in Figure 9 and red solid

lines in Figure 10 are represent the best-obtained so-

lution. As shown in the ﬁgures, the proposed method

can ﬁnd the collision-free path that covers the least

number of way-points to reach the ﬁnal destination

point. The computational results of the path length

from the proposed method for the second scenario is

provided in Table 1. As revealed in the table, the total

path length from [10, 5] to [200, 60] and from [200, 60]

Path Planning of a Mobile Robot in Grid Space using Boundary Node Method

163

Figure 7: The IFP obtained by using BNM for the ﬁrst scenario.

Figure 8: The IFP obtained by using BNM for the second scenario.

to [10, 5] is signiﬁcantly reduced, where the percent-

age of enhancement of the path length are 113% and

97% respectively.

5 CONCLUSIONS

In this paper we have introduced a new method called

Boundary Node Method BNM for solving the path

planning problem for a mobile robot. The proposed

method is applied to generate an initial collision-free

path for the mobile robot to move from starting point

to ﬁnal destination point without colliding with any

obstacles. Consequently, an additional method, Path

Enhancement Method PEM, is used to ﬁnd an opti-

mal or near optimal collision-free path from the ini-

tial path by minimizing the overall path length. Both

methods, BNM&PEM, are introduced to provide the

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

164

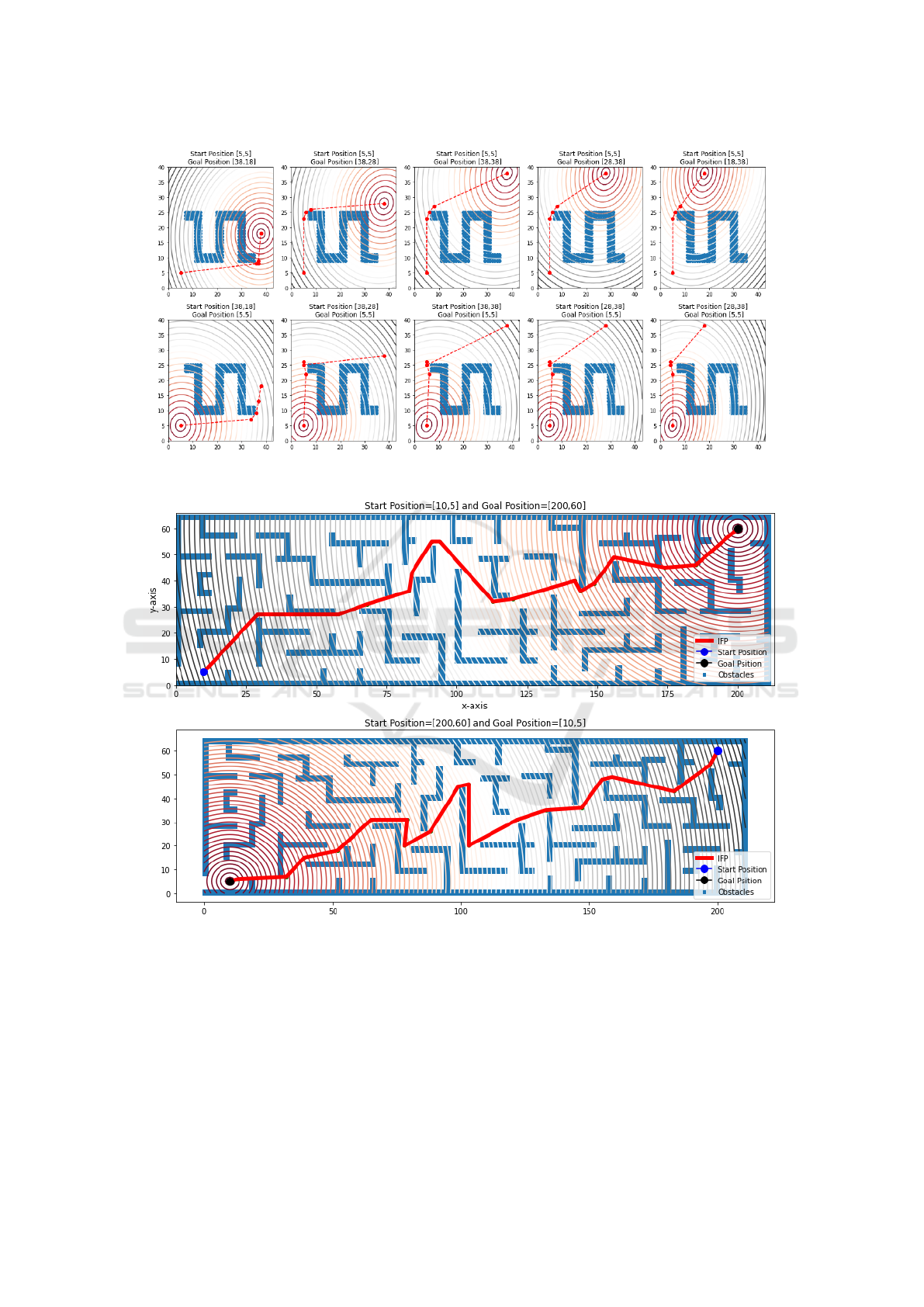
Figure 9: An optimal or near-optimal path obtained by applying BNM&PEM for the ﬁrst scenario.

Figure 10: An optimal or near-optimal path obtained by applying BNM&PEM for the second scenario.

optimal path between start and goal points. Simu-

lation results demonstrate that the BNM&PEM can

generate the optimal or near optimal collision-free

path for the mobile robot to navigate in a compli-

cated environment, efﬁciently. As future work, we

will deal with obstacles of different sizes and forms

(irregular or arbitrary shape) and static or dynamic.

Also, we will evaluate the performance of the other

proposed types of the elements such as nine-node cir-

cular, seventeen-node quadrilateral, and thirteen-node

octagonal. Finally, we are currently working on a val-

idation of the proposed method on real robots, NAO

from Aldebaran Robotics.

Path Planning of a Mobile Robot in Grid Space using Boundary Node Method

165

REFERENCES

Atzeni, M. and Recupero, D. R. (2018). Deep learning and

sentiment analysis for human-robot interaction. In The

Semantic Web: ESWC 2018 Satellite Events - ESWC

2018 Satellite Events, Heraklion, Crete, Greece, June

3-7, 2018, Revised Selected Papers, pages 14–18.

Bi, Z., Yimin, Y., and Wei, Y. (2008). Hierarchical planning

approach for mobile robot navigation under the dy-

namic environment. In Industrial Informatics, 2008.

INDIN 2008. 6th IEEE International Conference on,

pages 372–376. IEEE.

Brand, M., Masuda, M., Wehner, N., and Yu, X.-H. (2010).

Ant colony optimization algorithm for robot path

planning. In Computer Design and Applications (IC-

CDA), 2010 International Conference on, volume 3,

pages V3–436. IEEE.

Chao, N., Liu, Y.-k., Xia, H., Ayodeji, A., and Bai, L.

(2018). Grid-based rrt for minimum dose walking

path-planning in complex radioactive environments.

Annals of Nuclear Energy, 115:73–82.

Contreras-Cruz, M. A., Ayala-Ramirez, V., and Hernandez-

Belmonte, U. H. (2015). Mobile robot path planning

using artiﬁcial bee colony and evolutionary program-

ming. Applied Soft Computing, 30:319–328.

Ducho

n, F., Babinec, A., Kajan, M., Be

no, P., Florek, M.,

Fico, T., and Juri

sica, L. (2014). Path planning with

modiﬁed a star algorithm for a mobile robot. Procedia

Engineering, 96:59–69.

Fu, B., Chen, L., Zhou, Y., Zheng, D., Wei, Z., Dai, J., and

Pan, H. (2018). An improved a* algorithm for the

industrial robot path planning with high success rate

and short length. Robotics and Autonomous Systems.

Ge, S. S. and Cui, Y. J. (2000). New potential functions

for mobile robot path planning. IEEE Transactions on

robotics and automation, 16(5):615–620.

Goyal, J. K. and Nagla, K. (2014). A new approach of path

planning for mobile robots. In Advances in Comput-

ing, Communications and Informatics (ICACCI, 2014

International Conference on, pages 863–867. IEEE.

Guruji, A. K., Agarwal, H., and Parsediya, D. (2016). Time-

efﬁcient a* algorithm for robot path planning. Proce-

dia Technology, 23:144–149.

Han, J. and Seo, Y. (2017). Mobile robot path planning with

surrounding point set and path improvement. Applied

Soft Computing, 57:35–47.

Hu, Y. and Yang, S. X. (2004). A knowledge based

genetic algorithm for path planning of a mobile

robot. In Robotics and Automation, 2004. Proceed-

ings. ICRA’04. 2004 IEEE International Conference

on, volume 5, pages 4350–4355. IEEE.

Huang, H.-C. and Tsai, C.-C. (2011). Global path planning

for autonomous robot navigation using hybrid meta-

heuristic ga-pso algorithm. In SICE Annual Confer-

ence (SICE), 2011 Proceedings of, pages 1338–1343.

IEEE.

Jan, G. E., Chang, K. Y., and Parberry, I. (2008).

Optimal path planning for mobile robot naviga-

tion. IEEE/ASME Transactions on mechatronics,

13(4):451–460.

Kala, R., Shukla, A., and Tiwari, R. (2011). Robotic

path planning in static environment using hierarchical

multi-neuron heuristic search and probability based

ﬁtness. Neurocomputing, 74(14-15):2314–2335.

Lamini, C., Benhlima, S., and Elbekri, A. (2018). Ge-

netic algorithm based approach for autonomous mo-

bile robot path planning. Procedia Computer Science,

127:180–189.

LaValle, S. M. (2006). Planning algorithms. Cambridge

university press.

Leena, N. and Saju, K. (2014). A survey on path plan-

ning techniques for autonomous mobile robots. IOSR

Journal of Mechanical and Civil Engineering (IOSR-

JMCE), 8:76–79.

Liu, H., Xu, B., Lu, D., and Zhang, G. (2018). A path plan-

ning approach for crowd evacuation in buildings based

on improved artiﬁcial bee colony algorithm. Applied

Soft Computing.

Mac, T. T., Copot, C., Tran, D. T., and De Keyser, R. (2016).

Heuristic approaches in robot path planning: A sur-

vey. Robotics and Autonomous Systems, 86:13–28.

Montiel, O., Orozco-Rosas, U., and Sep

ulveda, R. (2015).

Path planning for mobile robots using bacterial po-

tential ﬁeld for avoiding static and dynamic obstacles.

Expert Systems with Applications, 42(12):5177–5191.

Rintanen, J. (2006). Introduction to automated plan-

ning. Lecture notes of the AI planning course, Albert-

Ludwigs-University Freiburg.

Shiltagh, N. A. and Jalal, L. D. (2013). Optimal path

planning for intelligent mobile robot navigation us-

ing modiﬁed particle swarm optimization. Interna-

tional Journal of Engineering and Advanced Technol-

ogy, 2(4):260–267.

Shum, A., Morris, K., and Khajepour, A. (2015). Direction-

dependent optimal path planning for autonomous ve-

hicles. Robotics and Autonomous Systems, 70:202–

214.

Song, W., LI, H.-x., and ZHANG, Y.-n. (2016). Path plan-

ning of mobile robot based on genetic bee colony al-

gorithm. DEStech Transactions on Computer Science

and Engineering, 1(cmee).

Victerpaul, P., Saravanan, D., Janakiraman, S., and Pradeep,

J. (2017). Path planning of autonomous mobile robots:

A survey and comparison. Journal of Advanced Re-

search in Dynamical and Control Systems, 9:1535–

1565.

Wang, W., Zuo, L., and Xu, X. (2018). A learning-based

multi-rrt approach for robot path planning in narrow

passages. Journal of Intelligent & Robotic Systems,

90(1-2):81–100.

Zhang, Y., Gong, D.-w., and Zhang, J.-h. (2013). Robot

path planning in uncertain environment using multi-

objective particle swarm optimization. Neurocomput-

ing, 103:172–185.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

166