
Energy-optimal Speed Trajectories between Stops and Their Parameter
Dependence
Eduardo F. Mello
a
and Peter H. Bauer
Department of Electrical Engineering, University of Notre Dame, 275 Fitzpatrick Hall, Notre Dame, U.S.A.
Keywords:
Energy, Efficiency, Optimal, Speed Profile, Electric Vehicle.
Abstract:
This paper addresses the problem of energy-optimal vehicle-speed trajectories between stops. The ideal
parameter-dependent trajectory is introduced, and it is shown that it reduces transportation energy drasti-
cally relative to “typical trajectories” seen in traffic. The resulting trajectories can easily be implemented in
self-driving cars and have the potential to significantly reduce transportation energy in networked vehicles
and cities. The usage of this energy-optimal speed trajectories between stops can save significant amounts of
energy, sometimes in excess of 30% when comparing to conventional traffic flow speed profiles. This paper
also addresses the impact that vehicle and segment parameters have on the savings. The role of parameters
such as the air drag coefficient, cross-sectional area, vehicle mass, efficiency, segment length, average speed,
as well as acceleration capability are investigated. It is shown that optimizing speed trajectories to minimize
transportation energy consistently results in energy savings. However, diminishing returns are observed for
certain scenarios, such as long, low-speed segments.
1 INTRODUCTION
The advent of self-driving cars, intelligent transporta-
tion, and connected vehicles opens new possibilities
for embedding a variety of algorithms into vehicles
that improve and optimize vehicle operations. This
is in contrast to the current situation where drivers
control vehicle routes and speeds, making the realiza-
tion of optimization algorithms difficult due to lim-
ited acceptance and poor execution by the driver. As
shown in (Stern et al., 2018), by adding a sufficient
portion of autonomous vehicles executing these em-
bedded algorithms, vehicles that do not use such algo-
rithms could be encouraged or even forced to follow
the lead of the self-driven car, at least in dense traf-
fic. This paper explores vehicle-embedded algorithms
that minimize energy usage in typical urban driving
situations, i.e. from stop to stop. While the approach
taken can generally be applied to any type of vehicle,
this paper is limited to electric drive systems. The
proposed concept minimizes the energy expended at
the battery, given the distance and the desired average
speed between two stops. Therefore, the algorithm
chooses the speed-versus-time trajectory that satisfies
the given constraints and minimizes transportation en-
a
https://orcid.org/0000-0002-2339-2305
ergy. In order to carry out this type of optimization,
one needs to know basic vehicle parameters such as
rolling resistance, air drag coefficient, frontal cross-
sectional area, vehicle mass, performance limits, and
efficiencies along the drivetrain, all parameters that,
for a given vehicle, are well known. The optimization
algorithm then takes these parameters and the con-
straints and generates the energy-optimal speed pro-
file. It will be shown that compared to “typical” speed
profiles, the optimization results in significant energy
savings.
Based on extensive on-road and dynamometer
testing, (Hooker, 1988) created guidelines for how a
driver should operate a vehicle between consecutive
stops; however, in some cases, these guidelines dif-
fered significantly, even for similar vehicles. Energy-
optimal speed trajectories were also considered for
large vehicles. However, the analysis was based on
vehicles equipped with internal combustion engines
(ICEs) where there is no regenerative braking and the
efficiency of the vehicles was not taken into account
(Henriksson et al., 2017).
In (Mandava et al., 2009), the authors propose an
algorithm that, by using traffic light controller infor-
mation provided to the vehicle by the roadside, speed
recommendations are presented to the driver. The
suggested speeds are generated so that the probabil-
Mello, E. and Bauer, P.
Energy-optimal Speed Trajectories between Stops and Their Parameter Dependence.
DOI: 10.5220/0007747605130520
In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 513-520
ISBN: 978-989-758-374-2
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
513

ity of green lights when approaching signalized inter-
sections in arterial roads is maximized, resulting in
energy savings and reduction of emissions due to the
reduction of speed variations and idling times. Ad-
dressing a similar problem, (Schuricht et al., 2011)
developed an algorithm capable of suggesting the
ideal speed profile the driver should adopt in order
to cross a traffic light without having to stop to mini-
mize the energy consumption. This research differs
from (Mandava et al., 2009) by using information
from traffic light controllers and data from a queue
length estimator. A slightly different solution was
proposed by (Nunzio et al., 2013). Instead of sim-
ply avoiding stops in a traffic corridor, the developed
algorithm evaluates multiple available no-stop speed
profiles and then chooses the most efficient scenario.
With a focus on plug-in hybrid electric vehicles,
(Qi et al., 2017) created a system capable of opti-
mizing the speed profile in a signalized arterial road
and co-optimizing the vehicle dynamics and hybrid
powertrain operations. In a similar approach, the au-
thors in (Barth et al., 2011) calculate the speed pro-
file which minimizes fuel consumption in a signal-
ized arterial road for a vehicle equipped with an inter-
nal combustion engine by reducing the total tractive
power demand and the idling time.
A separate line of research related to the work pro-
posed in this paper is presented by (Yi and Bauer,
2017b), where the impact of environmental factors
such as wind speed, rolling resistance, and temper-
ature on an electric vehicle’s energy consumption is
analyzed. In (Yi and Bauer, 2018), the authors pro-
pose a robust optimization model that exploits these
environmental factors to generate an optimal speed
profile. Finally, the result in (Yi and Bauer, 2017a)
estimates the energy consumption of an electric vehi-
cle based on three parameters (powertrain efficiency,
wind speed, and rolling resistance), with variable de-
gree of accuracy depending on energy reserves.
2 THE MODEL
In order to describe the expended energy of a vehi-
cle’s speed trajectory, one needs to consider all power-
absorbing components, i.e. air drag, rolling resis-
tance, acceleration/deceleration of the vehicle and hill
climbing. Therefore, based on the models presented
in (Yi and Bauer, 2017b), the power at the wheel,
denoted as P
wheel
can be written as shown in (1)
where m, v(t), ˙v(t), C
d
, and A are the vehicle’s mass
(which also models and includes the driveline iner-
tia), speed, acceleration, frontal drag coefficient, and
cross-sectional area, respectively. ρ is the air density,
f
r
is the coefficient of rolling resistance, and g is the
gravitational acceleration. In this analysis we assume
a flat surface, i.e. no hill climbing.
P
wheel
(t) = mv(t) ˙v(t) +
1
2
C
d
Aρv(t)
3
+ mg f
r
v(t) (1)
The power balance equation for forward motion
(2) and for regenerative breaking (3), i.e. reverse
power flow, are given by:
P
bat
(t) =
1
η
f rw
(P
wheel
(t)) for P
wheel
> 0 (2)
P
bat
(t) = η
reg
(P
wheel
(t)) for P
wheel
< 0 (3)
where P
bat
(t) is the power at the battery, η
f rw
is the
vehicle’s efficiency for forward power flow, and η
reg
is the vehicle’s efficiency in reverse power flow. The
battery energy, E
bat
, for the power flow is therefore
given by (4).
E
bat
=
Z
t
0
P
bat
(t)dt (4)
Discretizing the energy equation in (4), a constant
approximation can be used for all power absorbing
components. The acceleration term is approximated
by the difference in kinetic energy values at each dis-
tance segment. Each discretized energy segment, ∆E,
is described by (5), where v
n
denotes a constant-speed
segment and ∆t a sampling time.
∆E
n
=
m
2
v
2
n+1
−v
2
n
+
1
2
C
d
Aρv
3
n
∆t + mg f
r
v
n
∆t (5)
The optimization problem can then be formulated
in a piecewise discretized form, as shown in (6) and
(7). N represents the total number of segments and
∆E
0
denotes an energy segment where the forward
and reverse power flow efficiencies are accounted for.
∆E
0
n
=
(
1
η
f rw
∆E
n
f or ∆E > 0
η
reg
∆E
n
f or ∆E ≤ 0
(6)
E =
N
∑
n=1
∆E
0
n
(7)
Finally, the optimization problem can then be
written as shown in (8).
min
v
n
E
s.t.
N
∑
n=1
v
n
N
= v
avg
0 ≤ v
n
≤ v
max
d
max
≤
v
n+1
− v
n
∆t
≤ a
max
∀ n ∈ {1, ...,N − 1}
d
max
≤
−v
n
∆t
≤ a
max
i f n = N
(8)
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
514
where v
avg
is the desired average speed, v
max
is the
maximum allowed speed, d
max
is the maximum allow-
able deceleration, and a
max
is the maximum allowable
acceleration.
3 SIMULATION RESULTS AND
OPTIMIZATION
The optimization problem expressed in (8) was imple-
mented using the fmincon solver from MATLAB with
the Sequential Quadratic Programming (SQP) algo-
rithm. In order to verify if the optimization proposed
in this paper would be applicable to various vehicles
and scenarios, a number of simulations with different
parameter sets were performed. Initially, a short seg-
ment was tested with two vehicle models, one based
on a Nissan Leaf and the second based on a Tesla
Model S. Then, parameters such as average speed of
the vehicle, segment length, maximum tolerable acce-
lartions and decelerations, and the vehicle efficiency
were varied. Finally a larger sample of vehicles in a
number of different scenarios were tested.
3.1 Approximation of a Real Scenario
In order to define a baseline for typical traffic flow, the
Federal Test Procedure (FTP-75) drive cycle was an-
alyzed. To generate the typical traffic profile the drive
cycle was divided into segments (corresponding to the
periods for which the car is movement), normalized in
time and speed, and then all segments were averaged.
The curve generated was then approximated by
an exponential acceleration until it reached the max-
imum speed followed by a parabolic deceleration.
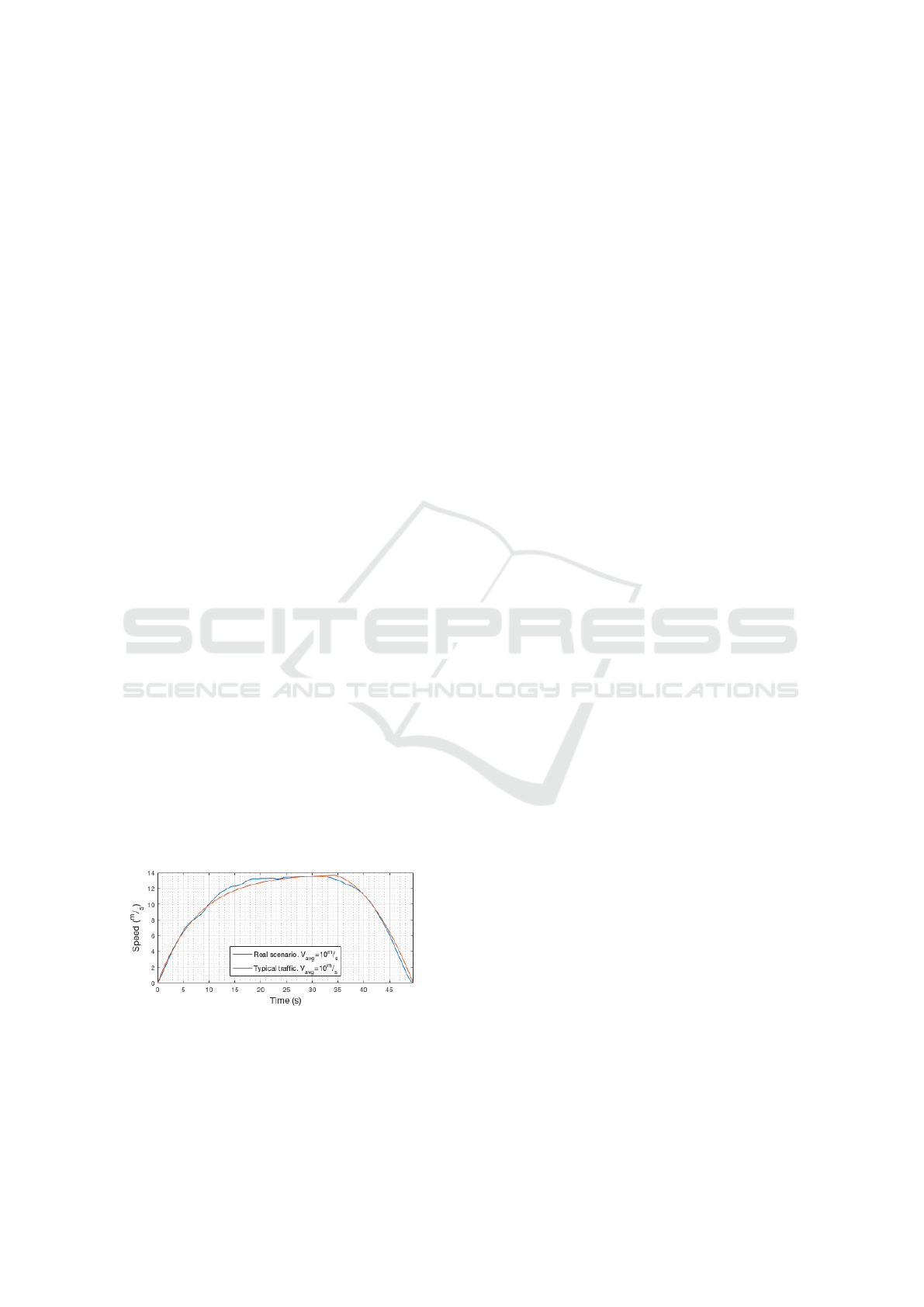
Both curves are shown in Figure 1 where the curve
“Real scenario” is extracted from the FTP-75 drive
cycle and the curve “Typical traffic” shows the ap-
proximated curve.
Figure 1: Speed vs. time of the “Real scenario” extracted
from FTP-75 and approximated “Typical traffic” flow.
3.2 Optimization Results for Urban
Traffic
The proposed optimization was used for a couple of
vehicles in order to verify the robustness of the results
relative to vehicle and infrastructure parameters. The
first tested case was for a vehicle with a parameter set
based on a Nissan Leaf in a 300-meter segment. The
second vehicle model utilized was based on a Tesla
Model S in a segment with the same 300-meter in
length.
3.2.1 Nissan Leaf
The baseline case is investigated for a midsize electric
vehicle (EV), which has its parameter set based on the
Nissan Leaf. The vehicle data set is given as follows:
m = 1525kg, f
r
= 0.01, C
d
= 0.29, and A = 2.27m
2
.
The average forward and reverse power flow efficien-
cies were approximated as η
f rd
= 0.7, and η
reg
= 0.2.
The speed trajectories for the approximation of the
typical traffic flow and the optimized trajectory are
shown in Figure 2. Figure 3 shows the acceleration
profile necessary to realize the aforementioned speed
profiles. And finally, the energy utilized by the vehi-
cle in each case is shown Figure 4.
In this simulation, the constraints imposed on the
optimizer were: the length between two consecu-
tive stops was chosen to be 300m, the average speed
throughout the profile had to be equal to 10m/s, the
maximum acceleration 4.6m/s
2
, the maximum decel-
eration -2m/s
2
, and finally, the initial and final speeds
equal to zero.
The results obtained show that the optimized
speed profile consumes 179.9kWs while the typical
traffic baseline uses 235.4kW s, a 23.59% reduction.
This demonstrates that the optimization proposed in
this paper has the potential of drastically minimiz-
ing the energy consumption in a route with necessary
stops.
3.2.2 Tesla Model S
The optimization was then repeated for a vehicle with
a parameter set based on the Tesla Model S. This vehi-
cle was chosen as it is another typical electric vehicle
and it has higher maximum acceleration and decelera-
tion than a Nissan Leaf. The parameter values utilized
are: m = 2018kg, f
r
= 0.01, C
d
= 0.24, and A = 2.8m
2
.
The average forward and reverse power flow efficien-
cies were approximated as η
f rd
= 0.7, and η
reg
= 0.2.
The distance between the two stops was kept at 300m.
The acceleration of the vehicle was limited to 8m/s
2
and the deceleration to -2.5m/s
2
.
Energy-optimal Speed Trajectories between Stops and Their Parameter Dependence
515
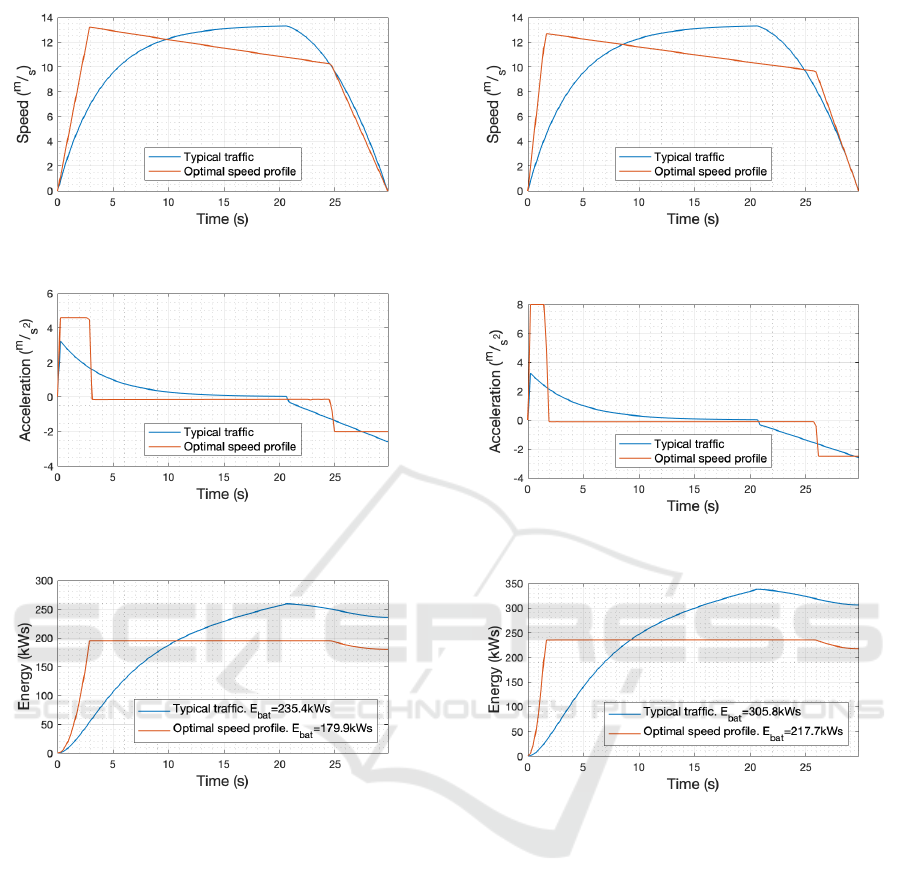
Figure 2: Speed for the “Typical traffic” and “Optimal
speed” profiles for a Nissan Leaf.
Figure 3: Acceleration for the “Typical traffic” and “Opti-
mal speed” profiles for a Nissan Leaf.
Figure 4: Energy for the “Typical traffic” and “Optimal
speed” profiles for a Nissan Leaf.
As already seen in Figure 2, the optimal speed
profile for this vehicle, Figure 5, is characterized by
three different stages (acceleration, coasting, and de-
celeration) until a complete stop is reached. With the
aforementioned parameters, the optimizer produced a
speed profile which uses 217.7kWs, as seen in Fig-
ure 7. This value is 28.81% less than the one obtained
for the typical traffic baseline, which used 305.8kWs,
saving 88.1kW s.
As expected, since the Tesla Model S is a heav-
ier vehicle with a larger cross-sectional area, it uses
more energy than the Nissan Leaf in each of the driv-
ing schedules, i.e. typical traffic baseline and optimal
speed profile. However, the Tesla Model S was able
to achieve greater percentage savings when compared
to the Nissan Leaf due to its greater acceleration and
deceleration.
Figure 5: Speed for the “Typical traffic” and “Optimal
speed” profiles for a Tesla Model S.
Figure 6: Acceleration for the “Typical traffic” and “Opti-
mal speed” profiles for a Tesla Model S.
Figure 7: Energy for the “Typical traffic” and “Optimal
speed” profiles for a Tesla Model S.
3.3 The Effects of Segment Length and
Average Speed
Two simulations were performed in order to verify
the effects of average speed and segment length in the
optimized speed profiles. Both simulations were per-
formed for the same vehicle with parameters based on
a Tesla Model S.
3.3.1 Midrange Segment Length and High
Speed
The initial scenario simulated was a segment of
1000m at an average speed of 20m/s. The stop-to-
stop length and average speed were chosen in order to
keep the accelerations and decelerations in our base-
lines within realistic margins. One important aspect
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
516
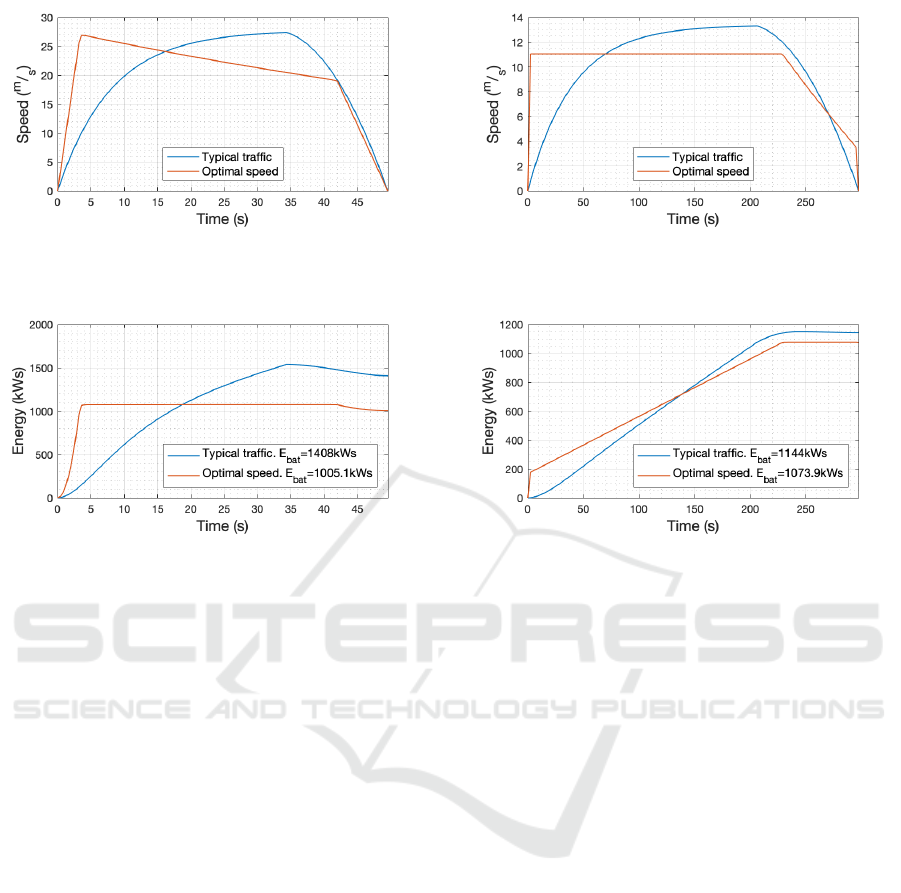
Figure 8: Speed for “Typical traffic” and “Optimal speed”
profiles for a stop-to-stop segment length of 1000m and av-
erage speed of 20m/s.
Figure 9: Energy for “Typical traffic” and “Optimal speed”
profiles for a stop-to-stop segment length of 1000m and av-
erage speed of 20m/s.
to be kept in mind is that the speed profile baselines
must have realizable accelerations in order to be com-
pared to the results of the optimizer, which has re-
alizable accelerations as constraints. In this case, as
shown in Figures 8 and 9, it was observed that the op-
timized speed profile saves 402.9kW s when compared
to the typical traffic baseline, which is equivalent to
28.61%. The total energy used in the simulation was
1408kW s for the baseline and 1005.1kW s for the op-
timal speed profile. Based on these results, it is clear
that the optimizer is capable of generating significant
savings even for higher speed scenarios.
3.3.2 Long Segment Length and Low Speed
Figures 10 and 11 show the simulation for a segment
length of 3000m at a speed of 10m/s, i.e. half of the
speed used in the previous case. The results obtained
from the optimizer show savings of 6.13% when com-
pared to the typical traffic baseline. This value corre-
sponds to 70.14kWs. With the information provided
by this simulation, it can be concluded that this op-
timization has diminished results when the length of
the stop-to-stop segment is drastically increased.
Figure 10: Speed for “Typical traffic” and “Optimal speed”
profiles for a stop-to-stop segment length of 3000m and av-
erage speed of 10m/s.
Figure 11: Energy for “Typical traffic” and “Optimal speed”
profiles for a stop-to-stop segment length of 3000m and av-
erage speed of 10m/s.
3.4 The Effects of Maximum Tolerable
Acceleration and Deceleration
As seen in Figure 8 and Figure 10, the optimal speed
profile is typically characterized by three to four
pronounced segments: acceleration, constant speed
(which in certain circumstances may not exist), coast-
ing, and deceleration. These well-defined segments
raise the question of what the effects of the acceler-
ation and deceleration limits (constraints of the opti-
mizer) are.
To verify the effects of the aforementioned lim-
its, the simulation in section 3.2.2 was repeated with
new limits for the acceleration and deceleration con-
straints. The segment length was kept at 300m with
an average speed of 10m/s. The acceleration of the
vehicle was limited to 4m/s
2
and the deceleration to
-1.25m/s
2
. These values correspond to half of the
ones used in section 3.2.2. With these parameters,
the optimizer produced a speed profile which uses
274.4kW s. This value is 10.44% smaller than the
one obtained for the typical traffic baseline, saving
31.98kW s. The optimal speed profile generated can
be seen in Figures 12 and 13.
In this simulation, the acceleration and decelera-
tion limits were set to half of the values utilized in sec-
tion 3.2.2. This change caused an increase in energy
Energy-optimal Speed Trajectories between Stops and Their Parameter Dependence
517
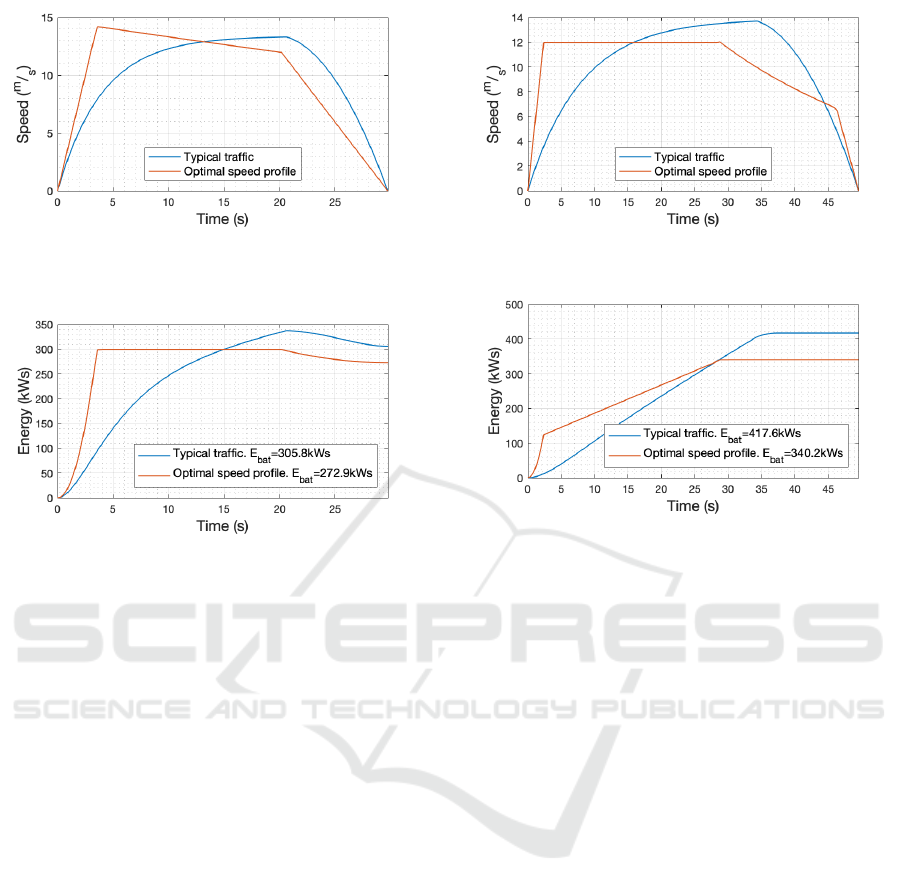
Figure 12: Speed for the “Typical traffic” and “Optimal
speed” profiles for a Tesla Model S with reduced maximum
acceleration and deceleration in a 300-meter segment.
Figure 13: Energy for the “Typical traffic” and “Optimal
speed” profiles for a Tesla Model S with reduced maximum
acceleration and deceleration in a 300-meter segment.
consumption of 55.2kW s. This energy increase corre-
sponds to 18.37% of the energy utilized by the vehi-
cle when higher acceleration and deceleration were
allowed. Thus, it can be stated that by increasing
the maximum tolerable acceleration and deceleration,
higher savings can be achieved.
3.5 The Effects of Vehicle Efficiency
3.5.1 Highly Inefficient Vehicle
In order to validate the robustness of the results with
respect to the vehicle model, another set of simula-
tions was run. The first simulation represents a highly
inefficient vehicle with the following parameters: m =
1000kg, f
r
= 0.015, C
d
= 1, and A = 3m
2
, η
f rd
= 0.6,
and η
reg
= 0. The acceleration was limited to 5m/s
2
and the deceleration to -2m/s
2
. The segment length
was set to 500m with an average speed of 10m/s.
The simulation output showed a significant im-
provement over the speed profile baselines for the in-
efficient vehicle, as seen in Figures 14 and 15. The
optimized speed profile was able to save 77.4kW s
over the typical traffic flow baseline, which corre-
sponds to 18.52% of improvement. Therefore, the
algorithm showed to be a very plausible option for
reducing the energy consumption of highly inefficient
electric vehicles.
Figure 14: Speed for the “Typical traffic” and “Optimal
speed” profiles for a highly inefficient vehicle.
Figure 15: Energy for the “Typical traffic” and “Optimal
speed” profiles for a highly inefficient vehicle.
3.5.2 Highly Efficient Vehicle
The second simulation assumes a model of a highly
efficient vehicle. Its parameters were defined as: m
= 2000kg, f
r
= 0.008, C
d
= 0.25, A = 2m
2
, η
f rd
=
0.9, and η
reg
= 0.5. The acceleration was once again
limited to 5m/s
2
and the deceleration to -2m/s
2
. The
segment length and average speed were also kept the
same—500m and 10m/s.
With the parameters described above, drops in en-
ergy consumption of 26.73% with respect to the typi-
cal traffic baseline were observed (Figures 16 and 17).
These savings correspond to 56.29kW s. Thus, it can
be assumed that the optimization is capable of signif-
icant energy savings for efficient and inefficient elec-
tric vehicles, where greater savings are observed for
an efficient vehicle.
3.6 Additional Vehicle Models and the
Impact of the Segment Length
A final set of simulations was performed in order
to compare a number of different scenarios where
the vehicle parameters, segment length, and average
speed were varied. Five vehicle parameter sets were
utilized and they are specified in Table 1. Vehicle type
1 has a parameter set similar to the parameters of a
Tesla Model S and vehicle type 2 has similar param-
eters to a Nissan Leaf. Parameters such as vehicle
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
518
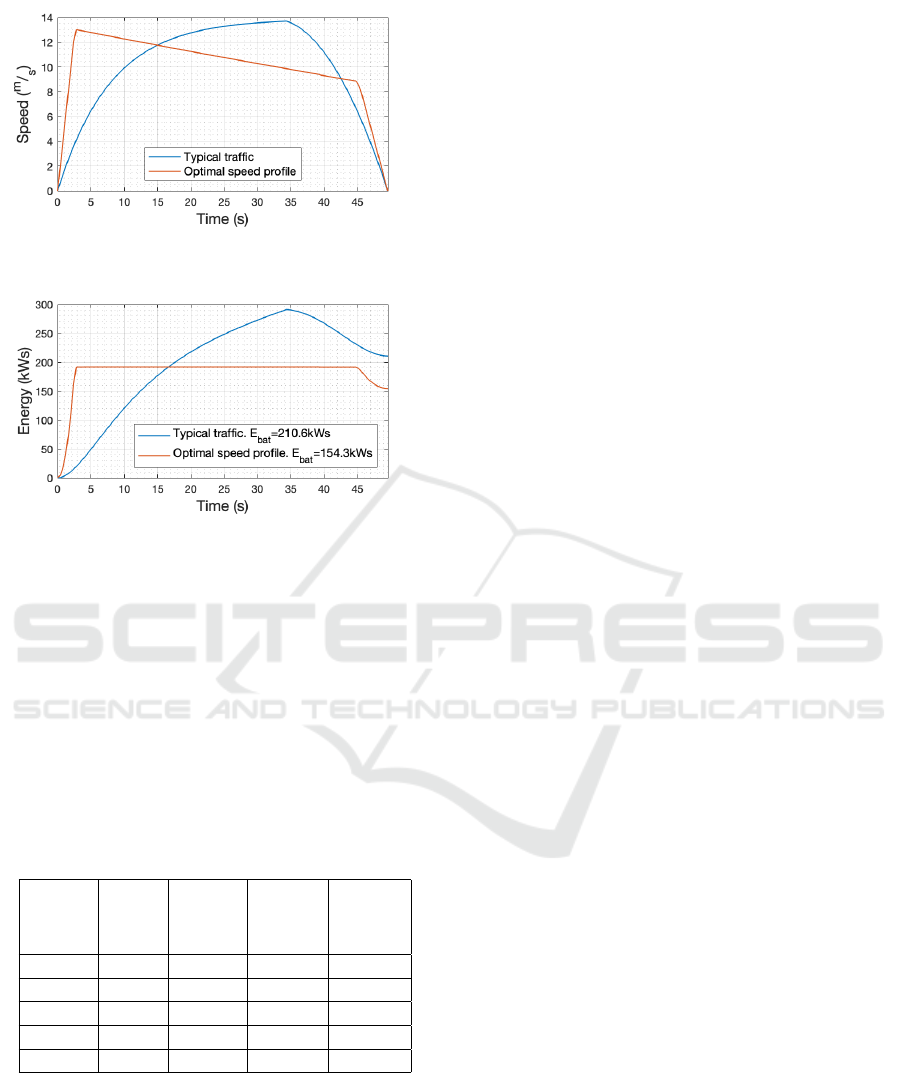
Figure 16: Speed for the “Typical traffic” and “Optimal
speed” profiles for a highly efficient vehicle.
Figure 17: Energy for the “Typical traffic” and “Optimal
speed” profiles for a highly efficient vehicle.
mass, cross-sectional area multiplied by air drag co-
efficient, efficiencies, and maximum acceleration and
deceleration were modified in order to analyze the
impact they have on transportation energy savings.
Vehicle type 3 is a variation of vehicle type 2 with
high maximum acceleration and deceleration. Vehi-
cle types 4 and 5 have extreme parameter sets with
high mass and low Cd
A
for the former and low mass
and high Cd
A
for the latter to illustrate the effects of
these vehicle parameters.
Table 1: Vehicle parameters utilized in simulations.
Vehicle
Mass
(kg)
C
d
A
(m
2
)
Max.
acceler.
(m/s
2
)
Max.
deceler.
(m/s
2
)
Type 1 2,018 0.6720 8 2.5
Type 2 1,525 0.6583 4.6 2
Type 3 1,525 0.6583 8 2.5
Type 4 2,500 0.5 4.6 2
Type 5 800 2.0 4.6 2
A segment length of 300 meters was used in most
simulations since it is a typical length for a suburban
block (Hooker, 1988).
Table 2 shows the results obtained. In all cases,
the optimal trajectory results in energy savings. These
savings demonstrate the robustness of the optimiza-
tion results with respect to the vehicle parameter set.
However, the segment length has a significant impact
on energy savings. Improvements ranging from 6%
to 41% were observed in this set of simulations.
These results show that energy savings are partic-
ularly high for short distance segments. Also, vehi-
cles capable of accelerating rapidly have greater sav-
ings in transportation energy, which is especially pro-
nounced in short segments. This can be seen by notic-
ing that Vehicle type 3 obtains higher savings than Ve-
hicle type 2 (mostly identical vehicles with exception
of the acceleration capabilities). Also, Vehicle type 1
obtained higher savings than Vehicle type 2 in almost
all scenarios. Finally, it can be observed that high sav-
ings are also obtained for vehicles traveling at higher
average speeds in long segments.
4 CONCLUSIONS
This paper shows that optimized speed trajectories
between stops can lead to significant transportation-
energy savings. Depending on the distance, average
speed, and vehicle parameters, energy savings can
reach approximately 40% relative to typically seen
speed profiles. It is important to note that savings are
dependent on the speed profile used as the baseline.
It was further shown that the optimal speed profile
usually has three to four distinct segments: acceler-
ation, constant speed (which is not present for short
distances), coasting, and deceleration. All speed tra-
jectories show the same trend regardless of the param-
eter set: the more energy that can be expended at the
beginning of the stop-to-stop segment, the higher the
savings.
In addition, this paper examined the effects of dif-
ferent vehicle parameters and operating conditions on
transportation energy savings relative to conventional
stop-to-stop speed trajectories. In all cases, the op-
timal trajectory results in energy savings, which in
the simulations presented in this paper range from 6%
to 41%, depending on the constraints and parameters
chosen. This is only possible due to the robust na-
ture of the optimization results obtained with respect
to vehicle and infrastructure parameters. Energy sav-
ings are particularly high for short distance segments.
Also, vehicles capable of accelerating rapidly have
greater savings in transportation energy, which is es-
pecially pronounced in short segments.
Therefore, the impact on self-driving electric ve-
hicles (EVs) and the associated transportation infras-
tructure is twofold: range improvement of EVs due to
lower energy expenditure in urban driving situations,
and less power demand from the grid to charge EVs.
It is important to note that the speed controller that
executes the optimal trajectory needs to communicate
Energy-optimal Speed Trajectories between Stops and Their Parameter Dependence
519
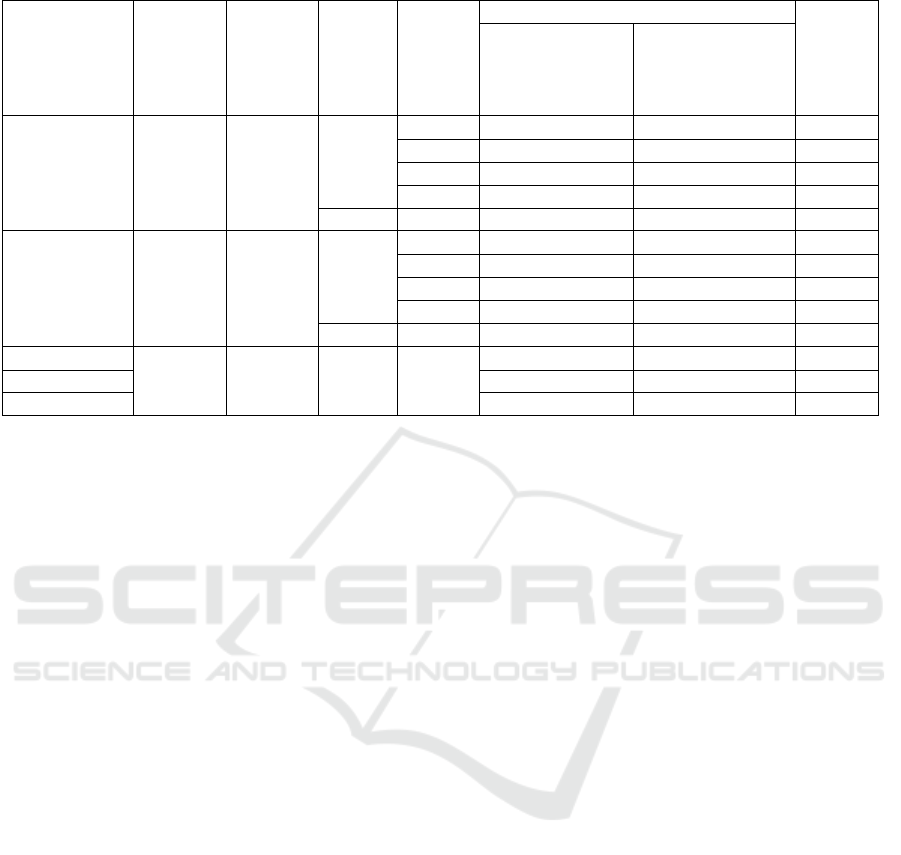
Table 2: Energy consumption for different vehicles and segment lengths.
Energy utilized
Vehicle
Forward
Power
Flow
Efficiency
Reverse
Power
Flow
Efficiency
Average
speed
(m/s)
Segment
length
(m)
Typical trajectory
(kW s)
Optimal trajectory
(kW s)
Energy
saved
Vehicle type 1 0.7 0.2
10
300 305.8 217.7 28.81 %
500 375.4 253.7 32.42 %
1,000 519.7 393.7 24.24 %
3,000 1,144.0 1,073.9 6.13 %
18 3,000 2,043.7 1,643.8 19.57 %
Vehicle type 2 0.7 0.2
10
300 235.4 179.9 23.59 %
500 290.9 203.9 29.91 %
1,000 407.7 314.4 22.88 %
3,000 915.1 853.8 6.7 %
18 3,000 1,695.7 1,392.7 17.87 %
Vehicle type 3
.7 .2 10 300
235.4 167.9 28.67 %
Vehicle type 4 449.2 291.9 35.02 %
Vehicle type 5 234.0 137.6 41.20 %
with the self-driving software in order to prevent ac-
cidents. Even though the proposed speed trajectories
have strong accelerations, the speeds in urban scenar-
ios are generally around 50km/h or less.
REFERENCES
Barth, M., Mandava, S., Boriboonsomsin, K., and Xia, H.
(2011). Dynamic eco-driving for arterial corridors.
In 2011 IEEE Forum on Integrated and Sustainable
Transportation Systems, pages 182–188.
Henriksson, M., Fl
¨
ardh, O., and M
˚
artensson, J. (2017). Op-
timal speed trajectories under variations in the driving
corridor. IFAC-PapersOnLine, 50(1):12551 – 12556.
20th IFAC World Congress.
Hooker, J. (1988). Optimal driving for single-vehicle fuel
economy. Transportation Research Part A: General,
22(3):183 – 201.
Mandava, S., Boriboonsomsin, K., and Barth, M. (2009).
Arterial velocity planning based on traffic signal in-
formation under light traffic conditions. In 2009 12th
International IEEE Conference on Intelligent Trans-
portation Systems, pages 1–6.
Nunzio, G. D., de Wit, C. C., Moulin, P., and Domenico,
D. D. (2013). Eco-driving in urban traffic networks
using traffic signal information. In 52nd IEEE Con-
ference on Decision and Control, pages 892–898.
Qi, X., Wu, G., Hao, P., Boriboonsomsin, K., and Barth,
M. J. (2017). Integrated-connected eco-driving sys-
tem for phevs with co-optimization of vehicle dynam-
ics and powertrain operations. IEEE Transactions on
Intelligent Vehicles, 2(1):2–13.
Schuricht, P., Michler, O., and B
¨
aker, B. (2011). Efficiency-
increasing driver assistance at signalized intersections
using predictive traffic state estimation. In 2011 14th
International IEEE Conference on Intelligent Trans-
portation Systems (ITSC), pages 347–352.
Stern, R. E., Cui, S., Monache, M. L. D., Bhadani, R.,
Bunting, M., Churchill, M., Hamilton, N., Haulcy,
R., Pohlmann, H., Wu, F., Piccoli, B., Seibold, B.,
Sprinkle, J., and Work, D. B. (2018). Dissipation
of stop-and-go waves via control of autonomous ve-
hicles: Field experiments. Transportation Research
Part C: Emerging Technologies, 89:205 – 221.
Yi, Z. and Bauer, P. H. (2017a). Adaptive multiresolu-
tion energy consumption prediction for electric ve-
hicles. IEEE Transactions on Vehicular Technology,
66(11):10515–10525.
Yi, Z. and Bauer, P. H. (2017b). Effects of environmen-
tal factors on electric vehicle energy consumption: a
sensitivity analysis. IET Electrical Systems in Trans-
portation, 7(1):3–13.
Yi, Z. and Bauer, P. H. (2018). Energy aware driving: Op-
timal electric vehicle speed profiles for sustainability
in transportation. IEEE Transactions on Intelligent
Transportation Systems, pages 1–12.
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
520
