A Novel 2.5D Shadow Calculation Algorithm for Urban Environment

Sukriti Bhattacharya, Christian Braun and Ulrich Leopold

Department for Environmental Research and Innovation (ERIN), Luxembourg

Luxembourg Institute of Science and Technology (LIST), Luxembourg

Keywords:

2.5D Shadow, Tensorﬂow, Bresenham’s Algorithm.

Abstract:

This paper proposes a novel efﬁcient algorithm to calculate a 2.5D shadow map based on a coherent math-

ematic formula concerning the sun’s position in a speciﬁc location, date and time. This work attempts to

improve the understanding of the underlying equations and data structures from an analytical, a geometric

and a dynamical systems perspective. By using scalable tensor data structure and inherent parallelism offered

by data-ﬂow based implementation the proof of concept is developed to test the technical feasibility of the

proposed algorithm. Results show noticeable and signiﬁcant improvements in overall performance keeping

accuracy at negligible differences.

1 INTRODUCTION

The Sun is the most signiﬁcant light source in the so-

lar system which beams light from a single intent in

space; there’s only one ray of light that can poten-

tially hit the surface point. So the associated intensity

level can therefore only be fully lit (100%) or fully

shadowed (0% ), depending on whether an obstacle

blocks the ray. This type of shadow is referred to as

hard shadow or umbra.

Solar Access has become a co-occurring issue for

urban planning. Access to sunlight is an indispens-

able part of a healthy human thermal comfort for in-

habitable buildings. Also, direct sunlight is of vi-

tal importance in architecture for reasons of mental

health as well as to reduce electric lighting and en-

ergy saving. Therefore, urban environmental spatial

analysis (Biljecki et al., 2015) often requires estimat-

ing whether a given point is in shadow or not, given

a representation of spatial obstructions such as build-

ings on a speciﬁc date and time precisely associated

with the solar position. Many planning authorities

now need light concerns to be addressed as part of

the outlining. Shadow Studies explain the inﬂuence

of development concerning sun and daylight access to

the neighboring context including surrounding build-

ings.

The combination of ray casting (Appel, 1968),

the process of determining the visibility between two

points and ray tracing (Whitted, 1980), the process of

following illumination paths by performing repeated

ray casts is the most frequently used method for

shadow calculation in off-line rendering. For decades,

the main drawback of this approach is the speed of the

algorithm. Precisely, it is incredibly time-consuming

to ﬁnd the intersection between rays and geometry.

In this paper, unlike any traditional ray tracing al-

gorithm, we propose a 2.5-D shadow construction al-

gorithm for buildings with effect to sun’s position for

real-time outdoor rendering. A trigonometric shadow

calculation algorithm is proposed on top of a quick

method of obtaining solar angular values. The en-

tire proof of the concept is developed in Python us-

ing Tensorﬂow (Abadi et al., 2015), an open source

software library developed by the Google Brain Team

using data ﬂow graphs and the tensor data structure.

The paper is organized as follow; Section 2 con-

tains the preliminary concepts required to understand

the algorithm proposed in Section 3. Section 4, de-

scribes the proof of concept by running it on a suit-

able use case, the performance of the prototype is also

discussed in the same section. Finally, the paper con-

cludes in Section 5 by describing the main features

and limitations of the present work.

2 BACKGROUND

This section provides a few necessary concepts and

describes the useful notations before we the actual

shadow calculation algorithm.

274

Bhattacharya, S., Braun, C. and Leopold, U.

A Novel 2.5D Shadow Calculation Algorithm for Urban Environment.

DOI: 10.5220/0007748602740281

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 274-281

ISBN: 978-989-758-371-1

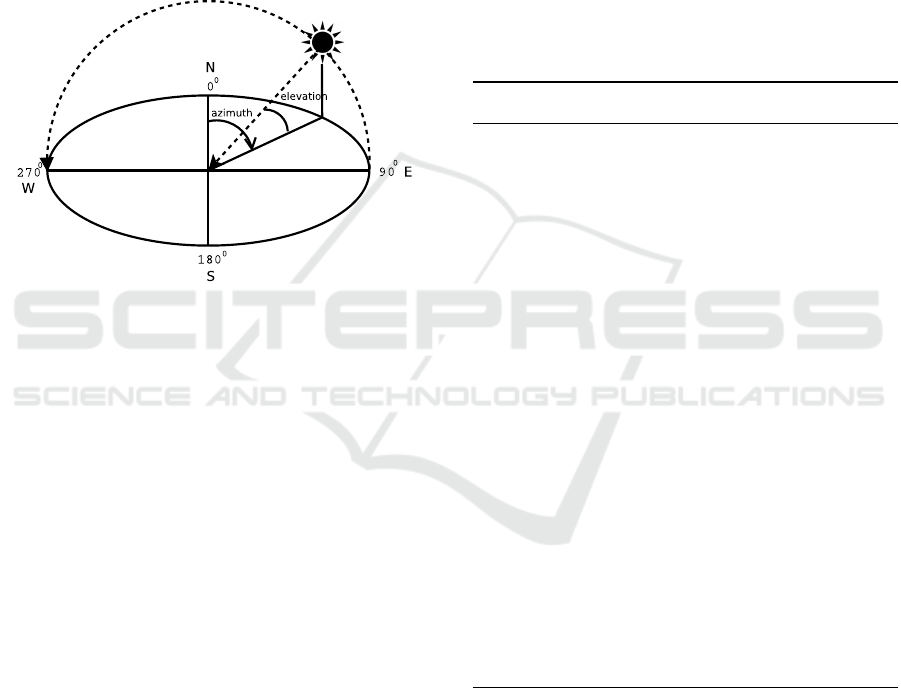
2.1 Sun Orientation

Solar orientation is the process of aiming something

at the Sun. Any solar technology like a solar panel

or a sun oven receives the highest amount of energy

when pointed or oriented at a right 90

◦

angle towards

the sun. Now we need to know how actually to mea-

sure the Sun’s position in the sky. Let’s assume we

are standing exact center of the Skydome, and the Sun

is somewhere at the inside surface of the dome. The

sun’s position on the Skydome is a combination of

two measurements as shown in Figure 1.

Figure 1: The Sun Position Diagram.

The ﬁrst measurement is the Sun’s direction on a com-

pass. A plumb line drawn from the sun to the hori-

zon intersects a speciﬁc degree on compass rows and

this angle is a measure of the Sun’s azimuth. We also

need to know Sun’s altitude or vertical angle, its an-

gular height above the horizon. The combination of

azimuth and elevation describes a speciﬁc spot on the

Skydome.

Algorithm 1 computes the sun position from sun-

rise to sunset of a speciﬁc latitude(φ) for a given

date(d) and a given interval of time in minute(τ). We

need to know two things before we calculate the Sun

position, the geographical location of the observer,

and the orientation of the Sun at that position. To de-

termine these two positions two sets of angles have to

be speciﬁed. The ﬁrst set, containing two angles, pin-

points the location on earth. They are a) latitude and

b) longitude(θ). The second set of angles is related to

the position of the Sun concerning a particular loca-

tion on the earth. These angles are 1) declination an-

gle, 2) elevation/altitude angle(α), 3) zenith angle(β),

4) azimuth angle(γ), and 5) hour angle(ω). The So-

lar declination angle is the angle between the equato-

rial plane of the Earth and the rotational plane of the

Earth around the Sun explained in line 4. ∆ in line 3

is the day angle and n is the day number which varies

from 1 on January 1st to 365 (366) December 31. The

hour angle is the angular displacement of the Sun east

or west of the local meridian due to the rotation of

the Earth around its axis 15

◦

per hour; morning neg-

ative, afternoon positive and during solar noon zero.

The hour angle for sunrise (ω

) and sunset (ω

) is

explained in line 5 and line 6, respectively. Line 7

converts the time interval τ to angle in radian τ

. The

loop at line 8 calculates the hour angles, I

from sun-

rise to sunset. Line 12 calculates the elevation angle

at hour angle ω

. The solar azimuth angle calculated

through line 13 to 17 is the angular distance of the

Sun’s projection on the horizontal plane at a place on

earth from a reference direction. Different authors use

different conventions for calculating solar azimuth an-

gle. In this paper, the azimuth angle is measured from

the north clockwise from zero to 360

◦

Algorithm 1: Sun Position Calculation from Sunrise to Sun-

set.

1: procedure SUNPOS(φ, τ, d )

2: n = dayofyear(d)

3: ∆ = (2.0 × π × n)/365.25

4: δ = sin

−1

(0.3978 × sin(∆ − 1.4 + 0.0355 ×

sin(∆ − 0.0489)))

5: ω

= cos

−1

(−tan(φ)× tan(δ))

6: ω

= −ω

7: τ

= τ × 0.261799

8: for (i = ω

; ω

≤ ω

; i = i + τ

) do

9: I

= i

10: end for

11: for each ω

∈ I

12: α[i] = sin

−1

(sinδ × sin φ + cos δ ×

cosω

× cos φ)

13: γ

= cos

−1



(sinδ × cos φ − cos δ ×

cosω

× cos φ)/cosα



14: if (i

≥ 0) then

15: γ

= 360

◦

− γ

16: end if

17: γ[i] = γ

18: i++

19: end for

20: Return α,γ

21: end procedure

2.2 Shadow Geometry

The foundation of all science and technology is math-

ematics, and one of the most important beaches of

mathematics is trigonometry. This section deﬁnes a

set of trigonometric equations for shadow length cal-

culation. These equations can be generalized to get

the shadow top co-ordinate.

In Figure 3, 4OPQ form a right angle triangle con-

sidering the fencepost OQ of height, h drove perpen-

A Novel 2.5D Shadow Calculation Algorithm for Urban Environment

275

Figure 2: Date: 22nd December Time: 08:30.

Figure 3: Shadow Calculation.

dicularly into the ground. Now the question is where

would the shadow fall? However, its very easy to ﬁg-

ure it out by drawing a line from sun across the top of

the fencepost all the way to the ground. In this case,

the length of the shadow |OP| can be calculated using

the acute angle between the horizon and the line to

the sun, alt(∠OPQ) in Equation 1. The angle alt is

commonly known as elevation angle or altitude angle.

tan(alt) =

| OP |

⇒ | OP | =

tan(alt)

meter.

(1)

The goal is to calculate the tip of the shadow lo-

cated at P(x, y), i.e. x meter East and y meter North

of the the base of the fencepost. Using right triangle

trigonometry on 4ORP, we get,

sin(azm − 180

◦

) =

| OP |

⇒

x = | OP | × sin(azm − 180

◦

) meter. (2)

azm is a horizontal angle measured clockwise from a

north base line, commonly known as solar azimuth

angle. Substituting |OP| from Equation 1 to Equation

2.2 yields x in Equation 3.

x =

tan(alt)

× sin(azm − 180

◦

)

= −

h sin(azm)

tan(alt)

meter (3)

The same way, y can be calculated by Equation 2.2

and Equation 5.

cos(azm − 180

◦

) =

| OP |

⇒

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

276

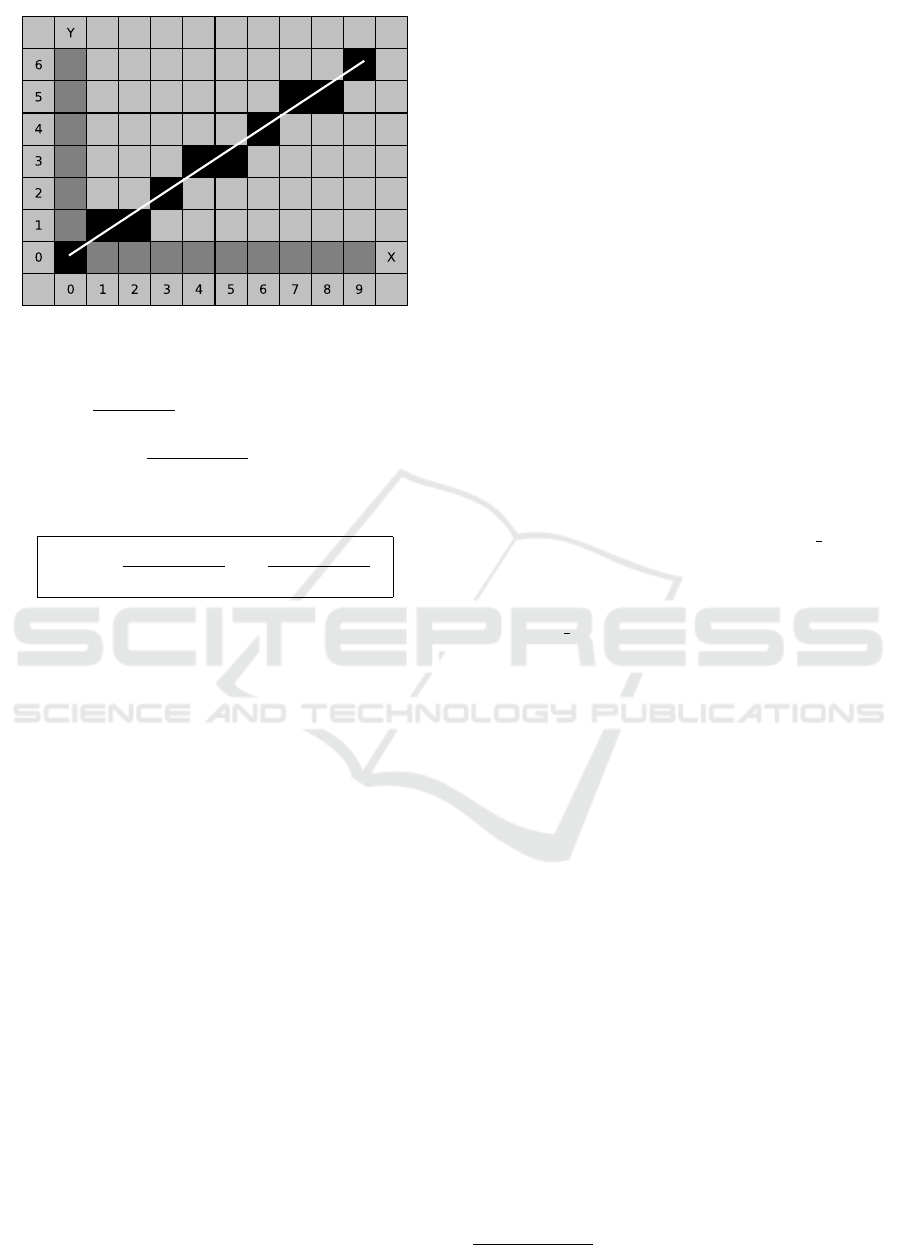
Figure 4: True line and its approximation.

y = | OP | × cos(azm − 180

◦

) meter (4)

y =

tan(alt)

× cos(azm − 180

◦

) =

−

h cos(azm)

tan(alt)

meter (5)

Therefore, from Equation 3 and Equation 5 the

shadow tip coordinate can be observed at

P =



−

h sin(azm)

tan(alt)

, −

h cos(azm)

tan(alt)



2.3 Bresenham’s Line Drawing

Algorithm

Bresenham’s line algorithm named after the inventor

Jack Elton Bresenham (Bresenham, 1965) is a funda-

mental line drawing algorithm in computer graphics.

Its primary use it to draw lines on raster graphics de-

vices. The line-drawing algorithm is based on draw-

ing an approximation of the real line, which is difﬁ-

cult to be drawn due to low precision caused by pixel

spacing on a PC monitor especially when dealing with

low resolutions.

In Figure 4, the true line is indicated in white

straight line starting from (0,0) to (9,6), and its ap-

proximation is indicated in black cells along the true

line. Bresenham’s line-drawing algorithm works in

the following ways; ﬁrst, it decides which axis is the

major axis and which is the minor axis based on the

length. X axis is the major axis in Figure 4. Starting

from the original position, in each iteration, the cur-

rent value of the major axis is incremented by exactly

one cell (pixel). Then it decides the most appropri-

ate pixel on the minor axis for the current pixel of the

major axis by checking which pixel’s center is closer

to the true line. Bresenham’s algorithm for approxi-

mate line drawing is all about this decision making. It

is not 100% precise but works effectively for higher

resolution.

3 METHODOLOGY

The 2.5D shadow of the buildings are generated by

executing SHADOW2D, explained in Algorithm 2 and

the entire process is illustrated using a block-diagram

in Figure 5. In line 2, the building heights are obtained

by subtracting the base height of the building from the

DSM. BLDHEIGHT performs this task as illustrated in

Algorithm 3. The DSM data is derived from a LiDAR

survey which gives directly the surface model in a de-

sired resolution. To obtain the building base heights

we used a tool called 3Dfier

(Biljecki, 2017) which

was developed by Delft University. It takes building

footprints and a LiDAR point cloud to extrude the

footprints to a LOD1 model in which buildings are

represented by block models (usually extruded foot-

prints). The base height of the resulting building cube

is based on descriptive statistics like the height values

of the 10% quantile of the points falling inside the

footprint. With available base heights linked to each

building footprint it is then easy to compute the differ-

ence between the top of the DSM and bottom of each

building to get the building height. sunpos t gets so-

lar orientation by means of azimuth and altitude angle

for a given date and time for each and every point in

the give building footprint.

sunpos t calls SUNPOS, described in Section 2.1

with two additional parameter time and building foot-

print in line 3. The coordinates function generate

the Cartesian co-ordinates for each and every point in

the given building footprint. From north (N), south

(S), east (E) and west (W) values ﬁrst, the four coor-

dinate corners, (W,S); (E,S); (E,N); (W,N) and

hence the coordinate of each and every point in the

building footprint is computed, respectively in line

4. From line 5 to 8 the algorithm is computing the

shadow tops (x

) for each point (x,y) in building

footprint ﬂowing the trigonometric formulation de-

rived in Section 2.2. Bresenham’s line drawing algo-

rithm explained in Section 2.3 is used to connect each

(x,y), (x

) pair in the grid to draw the shadow line.

4 CASE STUDY

A proof of concept is developed for the validation

of technical feasibility of the proposed algorithm at

a very high spatial resolution by using scalable ten-

sor data structure and inherent parallelism offered by

data-ﬂow based implementation in Tensorﬂow.

We run our proof-of-concept on Esch-sur-Alzette

(49

◦

44.988

N, 5

◦

50.016

E), located 5,505.41

https://github.com/tudelft3d/3dﬁer

A Novel 2.5D Shadow Calculation Algorithm for Urban Environment

277

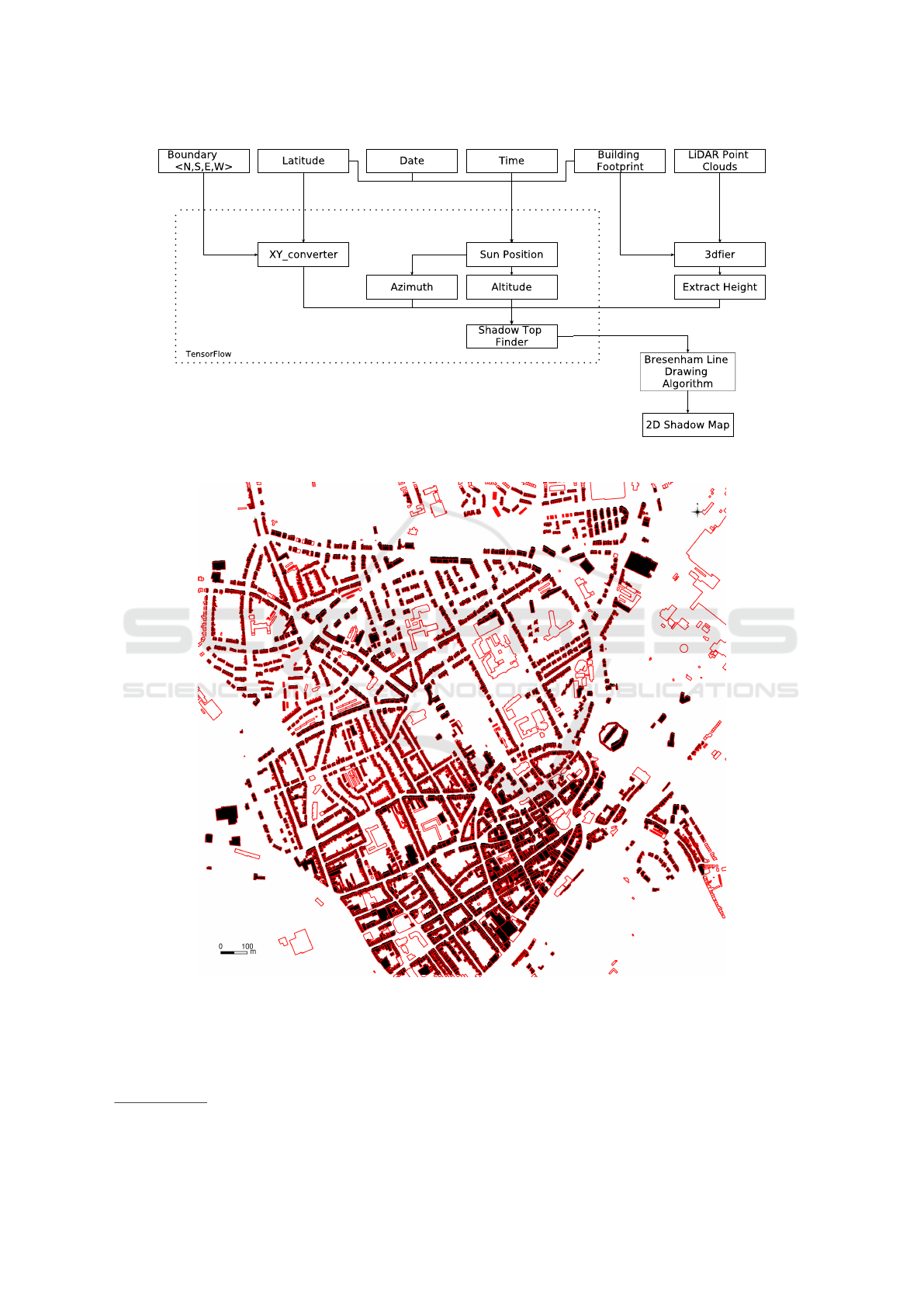
Figure 5: Block Diagram of Shadow Calculation Approach.

Figure 6: Date: 21st June December Time: 11:30.

km north of the equator, in the northern hemisphere

. It is situated in south-western Luxembourg on the

border with France, the second largest town after the

country’s capital Luxembourg city. The total area

https://fr.distance.to/Esch-sur-Alzette

of 14.35 km

with elevation above sea level ranging

from 279m to 426m. In this paper, we used a digital

elevation model of Esch-sur-Alzette. The grid is 1874

columns by 1828 rows, with a spatial resolution of 1

meter. The sun orientations from sunrise to sunset on

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

278

Figure 7: Date: 23rd September Time: 16:30.

Algorithm 2: 2.5D shadow calculation of buildings.

1: procedure SHADOW2.5D(hN,S,E,Wi, φ, d, t,

Bld

footpnt

, LiDAR

ptcld

)

2: H = BLDHEIGHT(Bld

footpnt

, LiDAR

ptcld

)

3: azm, alt = sunpos t(SUNPOS(φ, τ, d), t,

Bld

footpnt

)

4: XY = coordinates(hN,S,E,Wi, Bld

footpnt

)

5: for each hx,yi ∈ XY do

6: x

= −

H[x,y] * sin(azm)

tan(alt)

7: y

= −

H[x,y] * cos(azm)

tan(alt)

8: end for

9: for each hx,yi ∈ XY & each hx

i ∈ XY

10: print

pixel

(bresenham(x,y,x

))

11: end for

12: end procedure

June, 23

September, 22

March and 22

December are shown in Figure 9. SUNPOS (Algorithm

1) is used to generate the result. We plotted Figures of

cast shadow simulations for some exemplary sun po-

sitions over the year, namely, 23

September at 08:30

(Figure 2), 21

June (Figure 6) at 11:30, 22

Decem-

Algorithm 3: Building height calculation.

1: procedure BLDHEIGHT(Bld

footpnt

, LiDAR

ptcld

)

2: Bld

LOD1

= 3dfier(Bld

footpnt

, LiDAR

ptcld

)

3: Bld

= extract

(Bld

LOD1

)

4: Return Bld

5: end procedure

ber at 16:30 (Figure 7). The Figures showing building

footprints of Esch-sur-Alzette in red outlines and ar-

eas in black are covered by cast shadows of the build-

ings. The direction and length of the cast shadows are

determined by the position of the sun (Figure 2.1).

The town gets longer cast shadows when the sun po-

sition is low over the horizon in the morning (Fig-

ure 2) and evening (Figure 7) hours, and short and

more crisp shadows (Figure 6) when the sun reaches

zenith about mid day. One can clearly notice the

difference of sun position and resulting cast shadow

length and the inﬂuence to neighbouring buildings or

areas. Some unfavorable locations can end up receiv-

ing much less direct sunlight during the course over

the year due to their relative position to other objects.

A Novel 2.5D Shadow Calculation Algorithm for Urban Environment

279

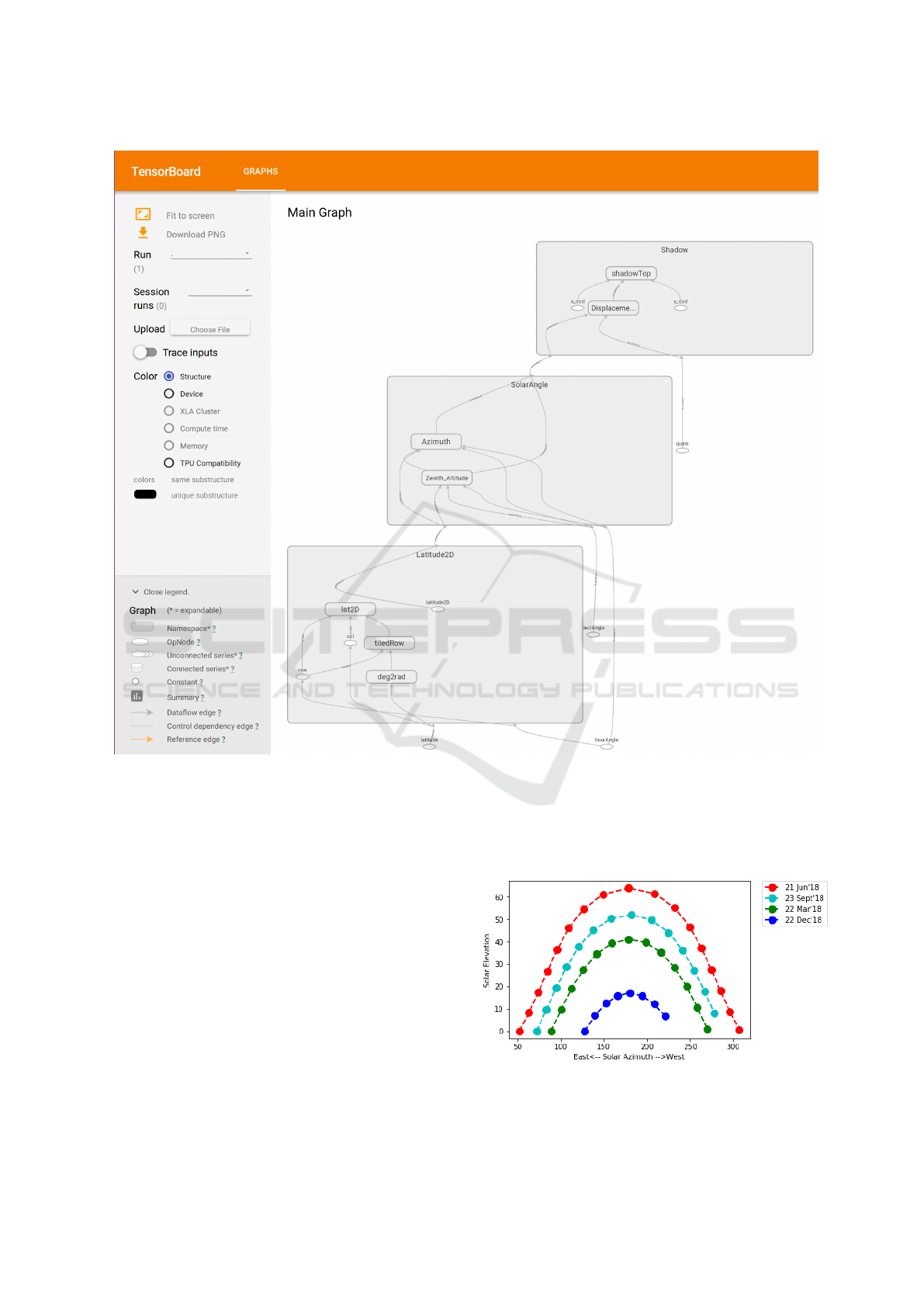
Figure 8: Dataﬂow graph generated by TensorBoard.

4.1 Performance

The proof of concept run on a 64 bit ma-

chine with Intel(R) Core(TM) i7-6800K CPU @

3.40GHz processor. The performance is quite sig-

niﬁcant. Figure 2, Figure 6 and Figure 7 took

42.26 secs, 29.63 secs and 113.20 secs, re-

spectively. The performance is remarkably faster

than r.sunmask module by Geographic Resources

Analysis Support System, commonly referred to

as GRASS (GRASS Development Team, 2017).

r.sunmask Calculates cast shadow areas from sun

position and DSM if the sun position is speciﬁed or

based on given date/time calculates the sun position

by itself.

The underlying data-ﬂow graph of the implemen-

tation of the algorithm is shown in Figure 8 using Ten-

sorboard. Tensorboard is the interface included with

any standard TensorFlow installation used to visual-

ize the data-ﬂow graph and other tools to understand,

debug, and optimize the model.

Figure 9: Sun path for Esch-sur-Alzette Calculated using

Algorithm 1.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

280

5 CONCLUSIONS

The main characteristics of the proposed 2.5D shadow

implementation can be described as follows,

• Deﬁning, optimizing, and efﬁciently calculat-

ing mathematical expressions involving multi-

dimensional arrays (tensors).

• Transparent use of GPU computing. One can

write the same code and run it either on CPUs or

GPUs.

• Implicit parallelism and distributed execution.

• High scalability of computation across machines

with huge data sets.

The building heights are valid for ﬂat roofs (L0D1

model). This ﬂatness of the terrain affects the accu-

racy of the cast shadows. In our future work, we are

considering digital elevation model to get the actual

hight of the object, towards a more accurate and ro-

bust shadow map.

ACKNOWLEDGEMENTS

This work has been funded and supported by the EN-

OVOS Foundation Luxembourg and the Luxembourg

Institute of Science and Technology (LIST) through

the SECURE project.

REFERENCES

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z.,

Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin,

M., Ghemawat, S., Goodfellow, I., Harp, A., Irving,

G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kud-

lur, M., Levenberg, J., Man

e, D., Monga, R., Moore,

S., Murray, D., Olah, C., Schuster, M., Shlens, J.,

Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Van-

houcke, V., Vasudevan, V., Vi

egas, F., Vinyals, O.,

Warden, P., Wattenberg, M., Wicke, M., Yu, Y., and

Zheng, X. (2015). TensorFlow: Large-scale machine

learning on heterogeneous systems. Software avail-

able from tensorﬂow.org.

Appel, A. (1968). Some techniques for shading machine

renderings of solids. In Proceedings of the April

30–May 2, 1968, Spring Joint Computer Conference,

AFIPS ’68 (Spring), pages 37–45, New York, NY,

USA. ACM.

Biljecki, F. (2017). Level of detail in 3D city models.

PhD thesis, Delft University of Technology, Delft, the

Netherlands.

Biljecki, F., Stoter, J. E., Ledoux, H., Zlatanova, S., and

C¸

oltekin, A. (2015). Applications of 3d city models:

State of the art review. ISPRS Int. J. Geo-Information,

4(4):2842–2889.

Bresenham, J. E. (1965). Algorithm for computer control

of a digital plotter. IBM Syst. J., 4(1):25–30.

GRASS Development Team (2017). Geographic Resources

Analysis Support System (GRASS GIS) Software, Ver-

sion 7.2. Open Source Geospatial Foundation.

Whitted, T. (1980). An improved illumination model for

shaded display. Commun. ACM, 23(6):343–349.

A Novel 2.5D Shadow Calculation Algorithm for Urban Environment

281