Impact of Social Welfare Methods on Multi-objective Resource

Allocation in Energy Systems

Aisha Umair

1 a

, Anders Clausen

1 b

, Yves Demazeau

2 c

and Bo Nørregaard Jørgensen

1 d

Center for Energy Informatics, University of Southern Denmark, Campusvej 55, Odense, Denmark

Laboratoire d’Informatique de Grenoble, Batiment IMAG, 700 avenue Centrale, Grenoble, France

Keywords:

Evolutionary Computation, Multi-objective Optimization, Social Welfare, Energy Systems.

Abstract:

Multi-agent resource allocation refers to the distribution of resources among agents. Resource allocation can

be particularly challenging if the agents have conﬂicting objectives over multiple interdependent issues. In

such cases, multi-objective optimization methods can be used to ﬁnd an optimal allocation of resources, that

maximizes social welfare. Social welfare refers to the welfare of the entire society of agents and therefore con-

sidered as a suitable metric for assessing the overall system performance in multi-agent resource allocation.

In this paper we study and discuss different notions of social welfare and investigate their impact on the opti-

mization outcome speciﬁcally for the problems comprising multiple conﬂicting objectives with interdependent

issues. To this end, we implement and apply different notions of social welfare to a real-world, complex prob-

lem, where a resource domain is responsible for making allocation of energy resources to multiple energy

intensive consumers (Commercial Greenhouse Growers). The problem is modeled as a multi-objective opti-

mization context. Our results show how different social welfare methods affect the optimization outcome and

result in different socially optimal resource allocations, depending on the behavior we expect from the system.

1 INTRODUCTION

Resource Allocation in a system involving multiple

agents is an important research issue, that has gained

a lot of attention in recent years. The agents may have

conﬂicting and incommensurable objectives with ra-

tional behavior. Such scenarios may demand multi-

objective optimization techniques based on the no-

tion of Pareto optimality, to ﬁnd an optimal alloca-

tion. In such cases, the optimization process ends up

with multiple Pareto-optimal allocations which repre-

sent trade-offs between conﬂicting objectives. This in

turn requires a selection of single outcome out of the

resulting Pareto-optimal set at the termination of opti-

mization process. In this regard, the concept of social

welfare as explained in Welfare Economics and So-

cial Choice Theory (Chevaleyre et al., 2006) is used

to rank all the Pareto-optimal outcomes (allocations)

depending on the behavior, desired from the system.

Several attempts have been made, which incor-

https://orcid.org/0000-0002-6949-9159

https://orcid.org/0000-0003-1333-7705

https://orcid.org/0000-0003-4059-9284

https://orcid.org/0000-0001-5678-6602

porate the notion of social welfare either within the

search process or to select the ﬁnal outcome in multi-

objective optimization problems. The authors in (Li

et al., 2009) proposed a mediated negotiation proce-

dure to obtain fair agreements by using fair compro-

mise direction while exploring the negotiation space.

A non-linear negotiation protocol is proposed in (Fu-

jita et al., 2012) to ﬁnd a secure and fair outcome

in a Pareto-optimal set. Similarly, the authors in

(Finkelstein et al., 2009) proposed a multi-objective

optimization approach to balance the requirements

fulﬁllment between customers of Motorola Com-

pany for hand held communication devices, such that

each customer is treated on fair basis. An exten-

sible component-based multi-objective evolutionary

approach has been proposed by authors in (Sørensen

and Jørgensen, 2017), which considers a climate con-

trol problem to optimize and ﬁnally applies utilitarian

social welfare to select one solution among Pareto-

optimal solutions. The authors in (Darmann and

Schauer, 2015) tries to maximize social welfare in

terms of Nash product while distributing indivisible

goods among agents.

To the best of our knowledge, the existing body of

literature considers derivable and quasi-concave util-

Umair, A., Clausen, A., Demazeau, Y. and Jørgensen, B.

Impact of Social Welfare Methods on Multi-objective Resource Allocation in Energy Systems.

DOI: 10.5220/0007761101790186

In Proceedings of the 8th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2019), pages 179-186

ISBN: 978-989-758-373-5

179

ity functions while applying social welfare criterion

within the search process. This indicates that the ap-

proach cannot be applied to nonlinear utility functions

scenarios. Work to investigate, compare and apply

different notions of social welfare to a multi-objective

problem for the selection of ﬁnal outcome is also lim-

ited in existing literature. Further, the notion of so-

cial welfare is based on unnormalized costs in most

studies. The consequence is that objectives may con-

tribute unevenly towards the selection of a ﬁnal out-

come. In such a context, social welfare methods can-

not be utilized to assess the overall performance in

the application domains, as utility cannot be directly

compared across objectives.

The main contributions of this paper are to 1)

compare and evaluate different notions of social wel-

fare on a common problem, 2) modify collective cost

functions (CCFs) of social welfare methods by uti-

lizing normalized costs for the selection of ﬁnal out-

come, 3) address the weaknesses of weighting mecha-

nism by introducing the notion of relative importance

graph, 4) evaluate modiﬁed social welfare methods on

a real-world problem to compare their properties with

respect to the selected optimization outcomes.

The paper is divided in six sections. Section 2

describes the methodology used to address multi-

objective multi-issue (MOMI) problems and a de-

tailed description of social welfare methods. The ex-

perimental setup is presented in section 3. Section 4

describes experiments and results. Section 5 presents

some ﬁndings deduced from the results, and ﬁnally

our conclusions are drawn in section 6.

2 METHODOLOGY

To perform resource allocation in MOMI problem,

Controleum, a generic MOMI negotiation frame-

work (Sørensen and Jørgensen, 2017), (Clausen et al.,

2014) is used. Controleum solves an optimization

problem with multiple objectives to generate a Pareto

front over the problem that is described in section 3.

2.1 Multi-objective Optimization

The problem deﬁnes a MOMI optimization context

consisting of N concerns, which negotiate over a set

of M issues, (s

...s

). The issue represents a de-

cision point over a resource, the value of which is ne-

gotiated by one- or several concerns. Each concern

, n ∈ N, deﬁnes a preference as a cost function,

for each issue s

, j ∈ M, over which the c

wishes

to negotiate. The optimization context has a Media-

tor, which is responsible for managing the optimiza-

tion process (Umair, 2018). The Mediator searches

for a contract, deﬁned as a vector of M issues val-

ues C = s

,. .. ,s

, that satisﬁes the preferences of the

concerns. The optimization process has three main

phases, i.e., initiation phase, optimization phase and

termination phase.

In the initiation phase, the Mediator initiates the

optimization by generating a population of random

contracts. Then the control goes to optimization

phase, where the Mediator presents the contracts to

each concern for evaluation. In response, each of the

concerns assigns cost values to all the contracts in the

population. The cost of the concern c

for a contract

C deﬁned as q

,C)

, describes the degree to which

the proposed contract adheres to the preferences of

the concern. Then, the Mediator selects the subset of

non dominated contracts using Pareto criterion. Af-

ter population selection, the Mediator generates the

next population of contracts by performing mutation

and crossover on randomly selected contracts from

the Pareto set. This process is repeated until a ter-

mination criterion is met.

At termination, the optimization process will end

up with multiple contracts on the Pareto front if the

concerns have conﬂicting preferences. The Mediator

is therefore responsible for selecting a ﬁnal contract

from the Pareto front adhering to the social welfare

criterion selected for the problem.

2.1.1 Relative Importance of Concerns

The concerns may have different signiﬁcance rela-

tive to each other. For example, achieving produc-

tion goal in a greenhouse domain seems to be rela-

tively more important than minimizing energy con-

sumption. In this kind of situation, it is necessary

to ensure the satisfaction of relatively more impor-

tant objectives before the satisfaction of relatively less

important objectives, to guarantee correct behavior of

the system. The concerns may also end up in a con-

ﬂict due to conﬂicting preferences. To handle such

scenarios, an approach based on weighting factor is

deﬁned in (Liu et al., 2014), to specify the relative im-

portance of users’ preferences. This approach poses

several weaknesses, 1) weights are problem depen-

dent and must be carefully set by the user because

the results are very much sensitive to weights ratio,

2) weights don’t map well to the problem domain.

To address the weaknesses of weights, we introduce

the notion of relative importance of concerns to de-

termine their order in the selection mechanism. The

relative importance between concerns c

and c

is de-

ﬁned in terms of three integer values -1, 1 and 0. -

1 means c

is relatively more important than c

, 1

means c

is relatively less important than c

and 0

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

180

means c

is equally important to c

. Once the relative

importance of each concern towards every other con-

cern is deﬁned, the relative importance graph (RIG)

is constructed, which is a directed graph deﬁned as,

RIG =< N,E >, where N = {N

,. .. ,N

} is a

set of nodes, and E = {E

,. .. ,E

} is a set of

edges. To construct a graph, a root node is created ﬁrst

and the ﬁrst concern c

in the sorted list of concerns

(which are sorted based on their relative importance)

is added to the top most node, i.e., root. Then another

concern c

is added by comparing it to the already

added concern c

. If the relative importance of c

and

towards each other is equal, then the concern c

placed in the same node N

, which already contains

concern c

. Otherwise, a new node N

is created and

concern c

is placed in node N

. Here, concern c

placed above concern c

. Finally, an edge is created

from node N

, containing c

to node N

, containing

. The RIG is used in the selection mechanism, to

select the ﬁnal contract at termination of optimization

process.

2.1.2 Selection of Final Contract

The selection of a ﬁnal contract is carried out hierar-

chically using RIG along with one of the SWOs de-

scribed in section 2.2. The SWO is applied ﬁrst to the

top level node in RIG. The selection mechanism will

select a subset of contracts from the current popula-

tion, which conforms to the preferences of the con-

cerns in the top level node according to the applied

SWO. A situation may arise where the subset from the

top level selection contains a single contract. In that

case, the next level nodes won’t be traversed. Other-

wise, the selection mechanism uses the subset in the

next level node to further ﬁlter the contracts. This pro-

cess continues until the subset contains only a single

contract or all nodes are traversed. In the end, if there

are multiple contracts in the subset of contracts, then

one contract is randomly selected from the subset as

a ﬁnal contract, as all the remaining contracts have

equal value to the concerns in the context.

2.2 Social Welfare Orderings

The concept of social welfare studied in Welfare Eco-

nomics and Social Choice Theory is used to model

the aggregation of concerns’ individual preferences.

Several means of quantifying the social welfare met-

ric among concerns exist, which are used in the exist-

ing resource allocation applications to ﬁnd an optimal

allocation (Chevaleyre et al., 2006).

Every contract C, C ∈ P

generates a cost vector,

as a result of concerns’ evaluation of the contract. The

concerns may have different nature of cost functions

with different cost distributions. Therefore, 0-1 scal-

ing is used to normalize concerns’ costs by extract-

ing minimum and maximum values from the non-

dominated population of contracts for each concern

(Umair, 2018). Suppose q

= {q

.. ., q

} ∈

, is a normalized cost vector, where q

is the nor-

malized cost of i

concern for contract C. The Collec-

tive Cost Function (CCF) represents a mapping from

such vectors to the reals f : R

→ R. The different

notions of social welfare can be modeled as a CCF.

Each CCF gives rise to a corresponding Social Wel-

fare Orderings (SWO), which deﬁnes a transitive and

complete binary preference relation  on cost vec-

tors. The SWOs are based on normalized costs. That

is to ensure that all concerns contribute equally in the

selection of ﬁnal contract. The SWOs can be roughly

classiﬁed in three categories, i.e, inequality, equality

and overall utility based SWOs.

2.2.1 Inequality based SWO

This category comprises elitist social welfare method,

which does not favour fairness among concerns.

Elitist Social Welfare. This SWO disregards fair-

ness and equality among concerns. The elitist SWO

ranks contracts based on the normalized cost of the

best-off concern, as deﬁned in equation 1.

(C ) = min{q

| t

∈ concerns} (1)

A contract C is preferred over contract C

(C ≺ C

)

if and only if (iff)

↑

, where

↑

repre-

sents the reordering of the normalized cost vector

= {q

,. .. ,q

} in an increasing order and

therefore deﬁned as,

↑

= {

↑

,. .. ,

↑

2.2.2 Equality based SWO

This category comprises six social welfare methods,

i.e., egalitarian, lexi-min, approximated fairness, fair-

ness analysis, quantitative fairness and entropy, which

are based on the notion of fairness.

Egalitarian Social Welfare. This SWO offers a

level of fairness and equality among concerns and de-

ﬁned as normalized cost of worst-off concern, shown

in equation 2.

(C ) = max{q

| t

∈ concerns} (2)

Hence (C ≺ C

) iff

↓

, where

↓

rep-

resents the reordering of the normalized cost vector

Impact of Social Welfare Methods on Multi-objective Resource Allocation in Energy Systems

181

= {q

,. .. ,q

} in decreasing order and

deﬁned as,

↓

= {

↓

,. .. ,

↓

}. This SWO

has a weakness that it only takes into account nor-

malized cost of worst-off concern while deﬁning the

ordering of contracts.

Lexi-min Ordering. This SWO is considered as a

reﬁnement of egalitarian SWO. In this SWO, (C ≺

) iff there exists an integer r ∈ {1, .. ., n}, such

that (

↓

)

= (

↓

)

for all i < r; and (

↓

)

(

↓

)

where

↓

= {

↓

,. .. ,

↓

} repre-

sents the reordering of the normalized cost vector

= {q

,. .. ,q

} in a decreasing order.

The idea of lexi-min SWO is appealing in a sense

that it overcomes the weakness with respect to egali-

tarian SWO. It starts by comparing the costs of worst-

off concerns and if the costs of worst-off concerns

coincide then it compares the costs of next worst-off

concerns and so on.

Approximated Fairness. This SWO (Fujita et al.,

2012) ranks contracts based on the squared sum of the

deviation of individual normalized costs of the con-

cerns from average of all concerns’ costs as deﬁned

in equation 3.

(C ) =

∑

i=1

− q

avg,C

)

(3)

where q

avg,C

∑

i=1

)

. Hence (C ≺ C

) iff

(C ) < SW

). A contract C is considered

ideal if its SW

(C ) = 0.

Fairness Analysis. The concept of fairness analysis

SWO (Finkelstein et al., 2009) ranks contracts based

on the standard deviation of the normalized cost of

each concern as deﬁned in equation 4.

(C ) =

∑

i=1

− q

avg,C

)

(4)

where q

avg,C

∑

i=1

)

. Hence (C ≺ C

) iff

(C ) < SW

Quantitative Fairness. This SWO is based on

Jain’s index (Huaizhou et al., 2014), which is de-

ﬁned as the fairness measure based on resource al-

location X, where n is the number of individuals.

is the amount of resource allocated to individuals

i = 1,2, .. ., n as shown in equation 5.

f (X) =

[

∑

i=1

]

∑

i=1

)

, 0 ≤ f (X ) ≤ 1 (5)

Fairness can be measured both in terms of resource

allocation and utility. Contrary to allocation fairness,

the fairness can be measured in terms of normalized

cost of concerns. In this case, the Jain’s index is

equal to 0 when all concerns have the same cost. The

quantitative fairness SWO with respect to concerns’

normalized cost vectors is modiﬁed and redeﬁned in

equation 6.

(C ) = 1 −

[

∑

i=1

((q

+ r)]

∑

i=1

((q

+ r)

(6)

where, [r ∈ Z

], 0 ≤ SW

(C ) ≤ 1. To avoid division

by zero, a positive integer r is added to the normalized

cost of each concern (equation 6). Hence (C ≺ C

) iff

(C ) < SW

Entropy. This SWO (Shannon, 2001) is deﬁned as

the fairness measure based on resource allocation X,

where n is the number of individuals and p

is the pro-

portion of resource X allocated to individual i. The

entropy of the distribution X, i.e., uncertainty of the

distribution X, is usually measured by H(X) as shown

in equation 7.

H(X) = −

∑

i=1

log

) (7)

where p

∑

i=1

)

and log

ln(p

)

ln(2.0)

. Assum-

ing that the costs returned by concerns in response to

the proportion of resource allocation, is a measure of

fairness. The entropy SWO with respect to concerns’

normalized cost vectors is modiﬁed and redeﬁned in

equation 8.

(C ) = σ − |

∑

i=1

log

)| (8)

where p

+ r

∑

i=1

+ r)

[r ∈ Z

]. A positive in-

teger r is added to the normalized cost of each con-

cern to avoid division by zero (equation 8). Here σ

is some arbitrarily large number  1. The entropy

SWO is smaller when contract is fair or vice versa.

Hence (C ≺ C

) iff SW

(C ) < SW

2.2.3 Overall Utility based SWO

This category comprises three social welfare meth-

ods, i.e., utilitarian, Nash product and median rank,

which take into account overall utility of concerns.

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

182

Utilitarian Social Welfare. This SWO ranks con-

tracts based on the sum of individual normalized costs

of concerns as deﬁned in equation 9.

(C ) =

∑

i=1

(9)

Hence (C ≺ C

) iff

∑

i=1

∑

i=1

Nash Product This SWO combines the features of

both utilitarian and egalitarian SWO to rank contracts

based on the product of individual normalized costs

of the concerns as deﬁned in equation 10.

(C ) =

∏

i=1

(10)

Hence (C ≺ C

) iff

∏

i=1

∏

i=1

. This no-

tion of social welfare favors both overall well-being

of concerns as well as reduced inequality among con-

cerns. The overall well-being is achieved by the fact

that, computing the product of concerns’ costs, en-

sures that the total normalized cost of concerns will

not increase too much as it will give rise to an increase

in the product of the costs. On the other hand, reduced

inequality is achieved by the fact that the contract with

equal low costs for all concerns is always the one with

lowest product of costs.

This SWO is applicable to non-negative and non-

zero cost vectors otherwise the result of Nash prod-

uct will ﬂuctuate between negative and positive val-

ues and a single zero cost in the normalized cost vec-

tor will make rest of the costs meaningless. There-

fore equation 10 is modiﬁed by adding a small pos-

itive value to the cost of each concern as shown in

equation 11. This is how; ranking of contracts based

on Nash CCF would still be meaningful for the cases

where concerns return zero cost.

(C ) =

∏

i=1

+ r) [r ∈ Z

] (11)

Median Rank Dictators. This SWO deﬁnes a so-

cial welfare based on the cost of middle-most con-

cern as deﬁned in equation 12. Let (

↓

)

represents

the r

largest normalized cost of any of the concerns

over contract C, and r = n/2, in case n is even and

r = (n + 1)/2, in case n is odd. Hence (C ≺ C

) iff

(

↓

)

< (

↓

)

(C ) = (

↓

)

(12)

3 EXPERIMENTAL SETUP

The experimental setup is based on a speciﬁc resource

allocation problem scenario, where a resource domain

(RD) is responsible for making energy allocations to

Commercial Greenhouse Growers (CGGs). CGGs

of today are advanced production facilities, which

require artiﬁcial supplementary lighting for plants

growth especially in winter seasons (Umair, 2018).

To better illustrate the impact of SWOs on an op-

timization outcome, we have chosen to focus on the

RD, which deﬁnes a MOMI context. In general, the

approach allows for inter-domain negotiations to bal-

ance interdependent issues distributed across several

problem domains. There are 7 concerns in RD in to-

tal. These concerns include one domain speciﬁc con-

cern (DC), and two representative concerns (RCs),

consumer RC (CRC) and consumer RC-sum (CRC-

sum) for each CGG. The RCs represent the prefer-

ences of CGGs in the RD. The RCs in the RD ne-

gotiate over issues reﬂecting energy allocation plans,

one for each CGG. An energy plan issue is a vector,

= {e

1,n

2,n

,. .. e

t,n

}, describing an hourly alloca-

tion of energy to the CGGs for an entire day. The

value of a time slot in the energy allocation plan issue

is 0 or 1 MWh. The conﬁguration of concerns in

RD is described in table 1. The RD uses the RIG, in

order to select the ﬁnal contract, where the DC in the

RD is assigned high relative importance compared to

the CRC and the CRC-sum to ensure an agreement

state between concerns in case of their conﬂicting

preferences. This conﬁguration is chosen to resolve

the conﬂict through graceful degradation of the pro-

duction requirements in CGGs without disrupting lo-

cal system operation. The number of CRCs in the RD

depends on the number of CGGs connected to RD.

There are three CGGs which are connected to RD, so

one set of CRC and CRC-sum is used for each CGG.

4 EXPERIMENTS

Considering the problem scenario described in sec-

tion 3, two sets of experiments have been conducted

to study the impact of different notions of social wel-

fare (described in section 2.2) on an optimization out-

come in terms of resource allocation. Each set of ex-

periments is run 20 times to show resilience towards

the potential random behavior sparked by the use of

genetic algorithm (GA).

The ﬁrst set of experiments simulates a scenario

with unconstrained resources. This means, sufﬁcient

amount of resources is available in the RD. In this

set of experiments, all the CGGs have the same pro-

Impact of Social Welfare Methods on Multi-objective Resource Allocation in Energy Systems

183

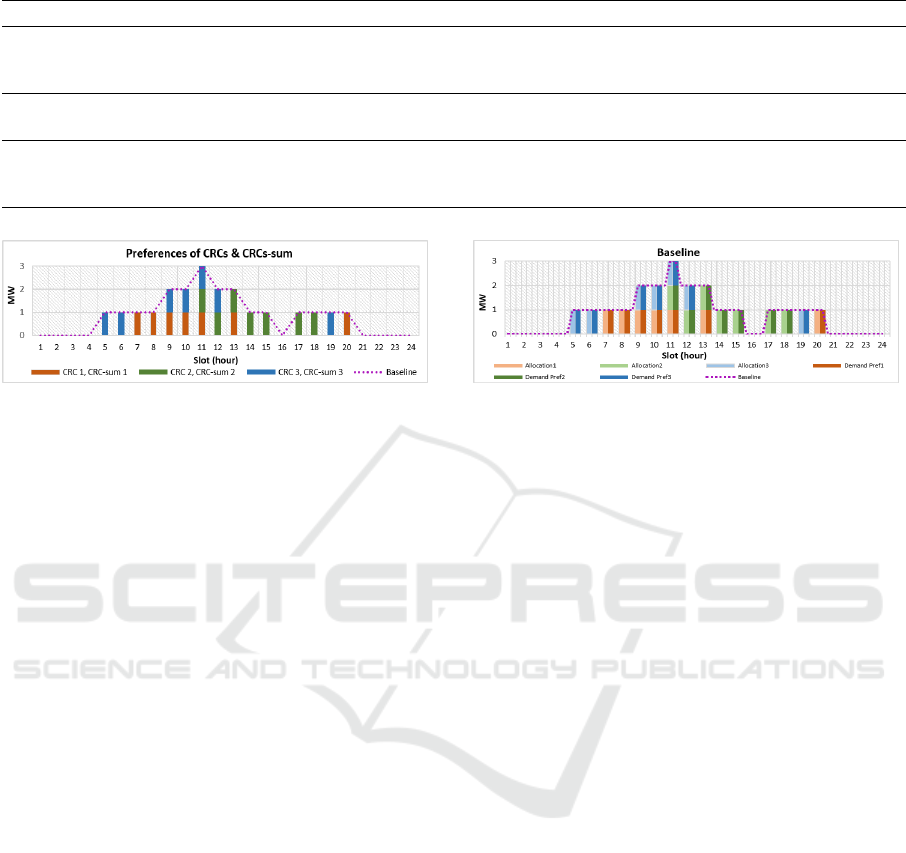
Table 1: Conﬁguration of concerns in RD.

Concern Preference Issue Cost Function Purpose

DC p

, represents an hourly resource e

, q

∑

i=1

− p

| To change planned aggregated consumption

capacity i.e., upper bound on amount e

, where, y =

∑

of CGGs to ensure that combined

of resources that can be allocated e

allocation complies with resource capacity

CRC

, represents the energy e

∑

i=1

i,n

− d

i,n

| To ensure that demand in each hour

efﬁcient demand proﬁle for CGG

matches with allocated amount of energy

CRC

sum(n)

represents the energy efﬁcient e

= |

∑

i=1

i,n

−

∑

i=1

i,n

| To ensure that correct amount of electricity

demand proﬁle for CGG

is allocated for CGG

it represents

regardless of the time it is allocated

Figure 1: Preferences of CRCs and CRCs-sum.

duction goals, i.e., each of the CRCs and CRCs-

sum is given the same demand preference in terms of

amount. However the time slots in which resources

are demanded, varies for each CRC and CRC-sum as

shown in ﬁgure 1. The experiment is repeated mul-

tiple times, i.e., the experiment is run once for each

notion of social welfare. These experiments serve to

show how different notions of social welfare lead to

the same optimization outcome, i.e., all the CRCs and

CRCs-sum will be allocated their requested demand,

in the scenarios where resources are unconstrained.

The second set of experiments simulates a sce-

nario where the resources are constrained. This

means, insufﬁcient amount of resources is available

in the RD. Likewise ﬁrst set of experiments, the de-

mand preferences for CRCs and CRCs-sum are equal

(ﬁgure 1) and the experiment is repeated for each no-

tion of social welfare. These experiments serve to

show how different notions of social welfare lead to

the different optimization outcomes in the scenarios

where resources are constrained, i.e.,when allocating

resources to CGGs in a resource-constrained setting,

1) overall utility based social welfare methods will

lead to an optimization outcome, that favors overall

well-being of CGGs, 2) inequality based social wel-

fare method will lead to an optimization outcome, that

disregards fairness and equality among CGGs, 3) fair-

ness based notions of social welfare will lead to an op-

timization outcome, that favors fairness and equality

among CGGs.

Figure 2: Results of baseline experiment.

4.1 Baseline Experiment Results

Figure 2 shows the results of this experiment. A base-

line proﬁle represents the optimal demand proﬁles for

the CGGs. The baseline proﬁle received from each

CGG will be regarded as a preference for their re-

spective CRCs and CRCs-sum in the RD. The CRC

and CRC-sum for each CGG in the RD play their role

and inﬂuence the optimization process by negotiating

over the issues, they are interested in. The CRCs and

CRCs-sum in the RD will try to minimize the distance

between their preference and the issue values, they

negotiate over. This is how, in case of unconstrained

resources, each CGG is provided with its preferred

energy plan i.e. no change is forced upon the CGGs

and therefore allocation matches with the demand in

each time slot and corresponds to the baseline proﬁle.

Table 2 shows the result of MOMI optimization

process in terms of allocations and demands. A

, A

and A

depict the electricity allocations (MWh) made

by RD for CGG

, CGG

, and CGG

respectively at

the termination of optimization process. Similarly

, D

, and D

show the electricity demands (MWh)

made by CGG

, CGG

, and CGG

respectively. As

can been seen in table 2, allocation matches with the

demand and each CGG is able to meet its demand

preference.

4.2 Constrained Experiment Results

Figure 3 shows the preference of DC in the RD, which

reﬂects the constrained resource scenario. The con-

ﬂict can be seen at slot 11, 12 and 13, where a DC

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

184

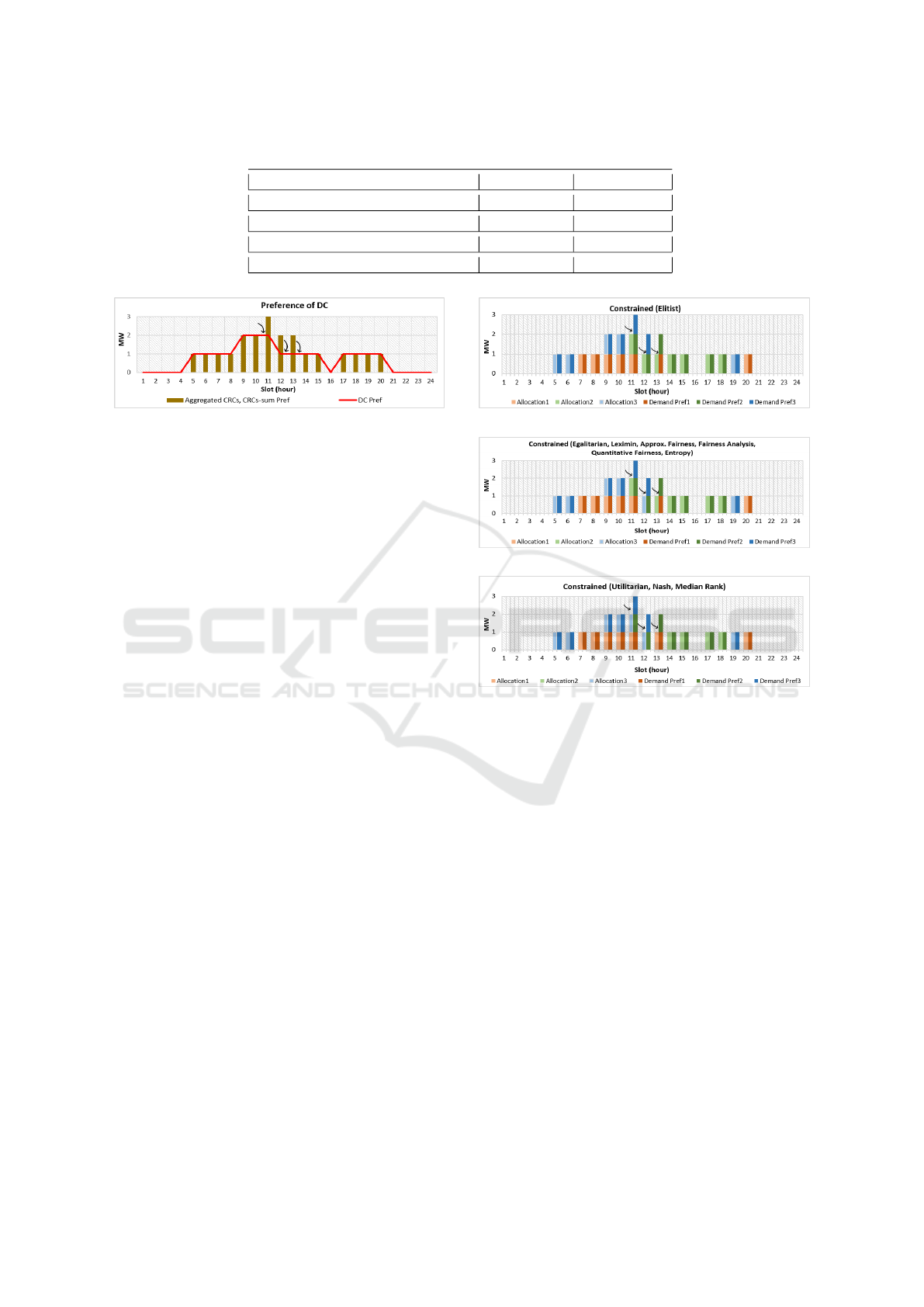
Table 2: Results of MOMI Optimization.

Experiments A

Baseline 7 7 7 7 7 7

Constrained (Inequality Based SWO) 6 7 5 7 7 7

Constrained (Equality Based SWOs) 6 6 6 7 7 7

Constrained (Overall Utility Based SWOs) 7 4 7 7 7 7

Figure 3: Preference of DC.

requires modiﬁcation to the baseline proﬁle, by pro-

viding 1 MW less energy in each of the conﬂicting

slots. This situation requires CGGs to shed their load

in the above mentioned slots. The results can be seen

in ﬁgures 4a to 4c.

Figure 4a shows the result of experiment with in-

equality based SWO. Here, the RIG based on elitist

SWO is used for the selection of ﬁnal contract in RD.

As explained earlier in section 2.2, elitist SWO tries

to minimize the cost of the best-off concern and en-

sures that at least one of the CGGs must achieve its

goal. As anticipated, allocations are made in a way,

where one of the CGGs, i.e., CGG

is provided with

its most preferred energy proﬁle, whereas the remain-

ing two CGGs are forced to reduce their demands. Ta-

ble 2 shows that CGG

and CGG

have made a com-

promise of 1 and 2 MW respectively, whereas CGG

meets its demand preference.

The same experiment is then repeated with SWOs,

which favor fairness among CGGs. The experiment

has been run once with each of the equality based

SWOs. In each experiment, one of these SWOs is

used for the selection of ﬁnal contract. The results

are shown in ﬁgure 4b. As can be seen that each of

these fairness based SWOs in the RD, ensures that all

the CGGs are treated equally and they will therefore

all concede as necessary to bridge the gap of the con-

ﬂict caused by the constrained resources. Here, CGG

sheds its load in slot 11, CGG

sheds its load in slot

12, whereas CGG

sheds its load in slot 13. Table 2

shows that all CGGs have made a compromise of 1

MW each and therefore deviated from their desired

demand preferences.

Next, the experiment is repeated with SWOs,

which favor the overall well-being of CGGs. The ex-

periment was conducted using overall utility based

SWOs, which all yielded similar results. The re-

sults are shown in ﬁgure 4c. As expected, each of

(a) Inequality based SWOs.

(b) Equality based SWOs.

Figure 4: Results of constrained experiment.

these SWOs favors overall well-being of the group

of CGGs. This explains that why the consequences

of constrained resources are unevenly divided among

CGGs, i.e., CGG

sheds its load in all the required

slots 11, 12 and 13, whereas C GG

and CGG

are

provided with the amount, they demanded. Similarly,

table 2 shows that CGG

has made a compromise of

3 MW and deviated from its demand preference.

5 DISCUSSION

Taking into consideration the production require-

ments and different types of plants in the greenhouse

domain, it is important to make a right choice about

which notion of social welfare should be applied to

select the optimization outcome. This may have a sig-

niﬁcant impact on plants with respect to their growth.

For instance, in unconstrained resource settings, the

results in ﬁgure 2 revealed that the selection of op-

Impact of Social Welfare Methods on Multi-objective Resource Allocation in Energy Systems

185

timization outcome can be done using any notion of

social welfare, as all the social welfare methods se-

lect the same outcome where all the CGGs are able to

meet their demand requirements without making any

compromise over production.

In constrained resource settings, we deduce some

facts about the selection of social welfare method with

respect to plant growth in CGGs. First, the inequality

based SWO can be applied to select the ﬁnal outcome

speciﬁcally for long-day photoperiodic plants which

are sensitive to the duration of day-night like rud-

beckia and california poppy. That is to ensure at least

one of the CGGs gets the required amount of light,

instead of making all the CGGs affected by the con-

strained resources, as seen in ﬁgure 4a. Second, over-

all utility based SWOs can be used to select the allo-

cation for day-neutral plants which do not require any

speciﬁc day length like rose and tomato growing. This

is because all these methods take into account overall

well-being of CGGs (see ﬁgure 4c). The CGG, which

takes the consequences of constrained resources will

not be affected too much due to their day-neutral sen-

sitivity. Third, for short-day plants like chrysanthe-

mum, christmas cactus, and poinsettia, it is recom-

mended to use equality based SWOs (ﬁgure 4b). This

is because they do not require long lighting hours. In

case of insufﬁcient resources, CGGs can easily make

a fair compromise with respect to their demand pref-

erence without affecting plant growth (Kumpf, 2019).

6 CONCLUSION

This paper discusses the properties and impact of dif-

ferent notions of social welfare on an optimization

outcome in MOMI optimization problems. In this

regard, a GA based MOMI optimization approach is

used to describe a complex, real world problem. To

study the impact of social welfare methods, two sets

of experiments are conducted in unconstrained and

constrained resource settings respectively. The results

show that different notions of social welfare lead to

different optimization outcomes and selection of the

social welfare method depends on the behavior we ex-

pect from the system.

In future works, we intend to investigate the im-

pact of social welfare methods on different real-

world problems which exhibit additional complexity

in terms of number of objectives. We aim to focus

on 1) combining different notions of social welfare

to select the ﬁnal optimization outcome, i.e., in cases

where multiple contracts yield same utilitarian score,

equality based SWOs can be applied to select the most

fair contract out of the resulting set of contracts yield-

ing high utilitarian score, 2) applying different notion

of social welfare at each level of RIG, i.e., in cases

where each level of RIG comprises more than one

concern.

REFERENCES

Chevaleyre, Y., Dunne, P. E., Endriss, U., Lang, J.,

Lemaitre, M., Maudet, N., Padget, J., Phelps, S.,

Rodriguez-Aguilar, J. A., and Sousa, P. (2006). Is-

sues in multiagent resource allocation. Informatica,

30(1).

Clausen, A., Demazeau, Y., and Jørgensen, B. N. (2014).

An agent-based framework for aggregation of man-

ageable distributed energy resources. In International

Conference on PAAMS, pages 214–225. Springer.

Darmann, A. and Schauer, J. (2015). Maximizing

nash product social welfare in allocating indivisible

goods. European Journal of Operational Research,

247(2):548–559.

Finkelstein, A., Harman, M., Mansouri, S. A., Ren, J., and

Zhang, Y. (2009). A search based approach to fair-

ness analysis in requirement assignments to aid nego-

tiation, mediation and decision making. Requirements

Engineering, 14(4):231–245.

Fujita, K., Ito, T., and Klein, M. (2012). A secure and fair

protocol that addresses weaknesses of the nash bar-

gaining solution in nonlinear negotiation. Group De-

cision and Negotiation, 21(1):29–47.

Huaizhou, S., Prasad, R. V., Onur, E., and Niemegeers, I.

(2014). Fairness in wireless networks: Issues, mea-

sures and challenges. IEEE Communications Surveys

& Tutorials, 16(1):5–24.

Kumpf, J. (2019). Lighting systems. [Online; accessed on

4-January-2019].

Li, M., Vo, Q. B., and Kowalczyk, R. (2009). Searching

for fair joint gains in agent-based negotiation. In Pro-

ceedings of The 8th International Conference on Au-

tonomous Agents and Multiagent Systems-Volume 2,

pages 1049–1056.

Liu, Y., Yuen, C., Huang, S., Hassan, N. U., Wang, X.,

and Xie, S. (2014). Peak-to-average ratio constrained

demand-side management with consumer’s prefer-

ence in residential smart grid. IEEE Journal of Se-

lected Topics in Signal Processing, 8(6):1084–1097.

Shannon, C. E. (2001). A mathematical theory of commu-

nication. ACM SIGMOBILE, 5(1):3–55.

Sørensen, J. C. and Jørgensen, B. N. (2017). An extensi-

ble component-based multi-objective evolutionary al-

gorithm framework. In Proceedings of the 6th ICSCA,

pages 191–197. ACM.

Umair, A. (2018). An Agent Based Approach to Co-

ordination of Resource Allocation and Process Per-

formance. PhD thesis, Syddansk Universitet. Det

Tekniske Fakultet.

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

186