
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic
Robot Coalition Formation: Approach and Use Case Description
Alexander Smirnov
1
, Leonid Sheremetov
2 a
and Nikolay Teslya
1 b
1
SPIIRAS, 14
th
line 39, St.Petersburg, Russia
2
Mexican Petroleum Institute, Eje Central Lázaro Cárdenas Norte, 152, Mexico City, Mexico
Keywords: Fuzzy Logic, Coalition, Coalition Game, Smart Contract, Robot, Dynamic.
Abstract: The paper describes an approach to dynamic formation of coalitions of independent robots based on the
integration of fuzzy cooperative games and smart contracts. Each member of the coalition is represented in
the form of an independent agent, negotiating at the stage of coalition formation for distribution of joint
winnings. A cooperative game with fuzzy core is used to form a coalition allowing coordinating the actions
of individual members to achieve a common goal, as well as to evaluate and distribute the overall benefit. To
implement the negotiation process and store the responsibilities of individual participants, it is proposed to
use the smart contract technology, which now become a part of the blockchain technology. Smart contracts
are used as entity where the requirements and expected winnings of each participant are stored. The final
agreement is also stored in form of smart contract that contains the distribution coefficients of the winnings
given all the conditions of participation in the coalition. The availability of smart contracts to all coalition
participants provides joint control over the fulfilment of the task assigned to the coalition. The paper describes
a use case based on precision farming to illustrate the main concepts of the proposed approach.
1 INTRODUCTION
The development of robots has reached a level where
it is highly important to organize their joint work.
There are a lot of existing models of robots joint work
such as swarms, flocks, and coalitions that differ by
the freedom of single participant. In contrast to robots
in swarms or flocks where they are limited in actions
by strong rules and actions of nearest neighbors,
robots in coalitions calculate their next steps based on
the common goal reaching according to the current
coalition state and set of alternatives provided by
norms of coalition (Klusch and Gerber, 2002).
Existing models of task solving in coalition claim that
a robot can receive a reward for the successful
problem solving according to its contribution. The
independency of robots makes it urgent to develop an
approach to coalition formation and interaction
organization between robots that allows making joint
decision during joint solution of the problem the
coalition is faced to.
There are many subject areas that require the use
a
https://orcid.org/0000-0001-9406-3712
b
https://orcid.org/0000-0003-0619-8620
of a coalition of robots to solve a complex problem,
including industrial cyberphysical systems, precision
farming, and remote or local explore of space objects.
Complex tasks in each area can be decomposed to
small simple tasks (for instance in precision farming
it is needed to scan the relief, check the soil
composition, select and put plant or seed in the soil,
water it) that are solved by single robots (Kardos et
al., 2017). To form a coalition robots provide their
competences and select tasks that they can perform.
Robots are equipped with different hardware and
software as well as expect different levels of reward.
Therefore, it is important to consider the
heterogeneity and provide common model to
consensus reaching during task decomposition and
resolution. Each robot is an independent agent with
own competencies and goals, which he aims to
achieve after the problem solving. In this case, the
coalition can be considered as a union of agents with
their own interests, which through the negotiation
make a decision on a joint solution of the problem and
the distribution of the reward.
Smirnov, A., Sheremetov, L. and Teslya, N.
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic Robot Coalition Formation: Approach and Use Case Description.
DOI: 10.5220/0007763003610370
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 361-370
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
361

The dynamic nature of the coalition implies a
changes in its composition, depending on changes in
the conditions of the problem being solved (Bayram
and Bozma, 2015). New robots should be quickly
familiarized with the current state of the problem
solution and provide description of own competences
to help to solve the problem. At the same time,
existing coalition members should operate without
any changes as defined in their plans. This problem is
usually solved by using external knowledge
repositories for storing the history of interaction
between coalition members. Such knowledge can be
stored in centralized or decentralized knowledge
bases. Centralized knowledge base usually provides
single access point for connecting robots to the data
network. Decentralized knowledge base allows to
organize a distributed network without any single
access point in which the knowledge base is
distributed among all participants with a share of the
backup, which makes the general information space
more resistant to the disconnection of one or more
nodes.
Most of the approaches to coalition formation are
characterized by the exponential nature of the
computations and communications complexity. To
transition from hyper-exponential and exponential
complexity to polynomial, the following parameters
are usually limited: the number of agents in one
coalition, the number of coalitions, and the rationality
of agents (Jennings et al., 2001). In this case, the
additional complexity is caused by the inability to
accurately estimate the size of the gain, which
introduces fuzziness into the formulation of the
problem.
In this paper, the use of cooperative games with
fuzzy core to form a coalition of robots is proposed to
solve the problems described above. This model
provides the following advantages when forming a
coalition: robots provide own competencies and the
expected individual benefit while actions of every
coalition are controlled by one of its member. The
existence of a coalition core allows coordinating the
actions of individual members to achieve a common
goal, as well as to evaluate and distribute the overall
benefit. When changing the conditions in which the
task was set, a dynamic change in the composition of
the coalition is envisaged, if necessary.
To store the rules of the game, competencies and
requirements of robots, as well as information about
the current state of coalitions and tasks, it is proposed
to use smart contracts over blockchain technology.
Smart contracts as a computerized protocol which
stores and carries out contractual clauses via
blockchain become a real tool used in industry (Cong
et al., 2017; Delmolino et al., 2016). In this work it is
proposed to use smart contracts to contain the rules
for forming a coalition and rules for changing the
composition of the coalition, defined using the theory
of fuzzy sets. The contract code, as well as the current
state of the solution of the problem, is stored in a
distributed log based on the blockchain technology.
This allows to provide a trusted information source
for robots to store and search coalition state. Since the
data in the block is linked to each other by calculating
the hash of the blocks in which they are stored, they
cannot be changed. It makes possible to provide
unchangeable process logs by which one can trace the
history of operations and, if necessary, find a weak
point, to enhance the effectiveness of future
coalitions.
The rest of the paper is organized as follows.
Related work is revised in the following section. A
fuzzy cooperative game (FCG) model with core is
described in Section 3. In Section 4, different criteria
of dynamic robot coalition formation are analyzed.
Section 5 provide information about smart contracts
and frameworks for robots negotiation during
coalition formation. Finally, the possible use case and
implementation scheme of a FCG over blockchain-
based smart contracts is proposed following by
conclusions.
2 RELATED WORK
The cooperative nature of modern robotic complexes
causes necessity of considering them within the
context of cooperative game theory in order to model
and understand their cooperative behaviour. The main
questions of coalition formation are: what coalitions
will be formed, how the common wealth will be
distributed among them and if the obtained coalition
structure is stable. Once coalitions are formed and
they have a feasible set of payoffs available to its
members, the question is the identification of final
payoffs awarded to each player. That is, given a
collection of feasible sets of payoffs, one for each
coalition, can one predict or recommend a payoff (or
set of payoffs) to be awarded to each player?
The payoff distribution should guarantee the
stability of the coalition structure when no one player
has an intention to leave a coalition because of the
expectation to increase its payoff. The benefit
distribution among the coalition members has proved
to be fuzzy, uncertain, and ambiguous (Hosam and
Khaldoun, 2006). Using the theory of fuzzy
cooperative games (FCGs), the uncertainty is
processed by means of the introduction of a fuzzy
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
362

benefit concept through the bargaining process to the
conclusion about the corresponding fuzzy
distribution of individual benefits among the coalition
members (Aubin, 1981).
The predictions or recommendations of payment
distribution are embodied in different solution
concepts. According to (Kahan and Rapoport, 1984),
cooperative games are divided into two classes based
on the way a solution of the game is obtained: games
with a solution set and games with a single solution.
Games with core considered in this paper, belong to
the former class and represent a mechanism for
analyzing the possible set of stable outcomes of
cooperative games with transferable utilities (Gillies,
1953). The concept of a core is attractive since it tends
to maximize the sum of coalition utilities in the
particular coalition structure. Such imputations are
called C-stable. The core of a game with respect to a
given coalition structure is defined as a set of such
imputations that prevent the players from forming
small coalitions by paying off all the subsets an
amount, which is at least as much they would get if
they form a coalition (we proceed with a formal
definition of a core in the following section). Thus the
core of a game is a set of imputations which are stable.
The drawbacks of the core is that, on the one
hand, the computational complexity of finding the
optimal structure is high since for the game with n
players at least
of the total
coalition
structures should be tested. On the other hand, for
particular classes of the game a core can be empty.
Because of these problems, using the C-stable
coalition structures was quite unpopular in practical
applications (Klusch and Gerber, 2002) and only
recently has attracted more attention of the
researchers, when the concept of fuzzy cooperative
games with core was introduced (Mareš, 2001; Shen
and Gao, 2010). For realistic applications like
collaborative work of groups of robots, additive
environments and the absence of the restrictions on
the type of membership functions should be
considered (Smirnov and Sheremetov, 2012).
For practical applications of FCGs, one of the key
problems is the management of the coalition
formation and payoff distribution tasks. In our
previous work, a negotiation algorithm has been
developed [18]. In this paper, we propose a novel
approach using blockchain technology.
With regard to the organization of robots
interaction, the blockchain is mostly used as
immutable storage for information exchange and
platform for smart contracts. Information stored in the
blockchain could contain records about task and
consumables distribution (Dorri et al., 2017; Verma
et al., 2017), smart contracts and reward transactions
(Zhang and Wen, 2017), as well as global knowledge
about coalition previous actions (Ferrer, 2016). In
combination with cooperative games blockchain
technology can provide more trust for communication
between robots, due to the storing information about
transactions in immutable log that are verified by
every coalition participant. In contrary to existing
approaches, blockchain does not require central
authority that provide trust for all nodes. All nodes
negotiate with each other coming to consensus with
one of possible mechanisms: Proof of Work, Proof of
Stake, or practical byzantine fault tolerance (Cachin
and Vukolić, 2017). The blockchain is used to
provide safe and trustiness logging of robots’ task
distribution and rewarding for task solving.
It is also noted that the combination of the peer-to-
peer network and the cryptographic algorithms used
in blockchain technology allow for a negotiation
process and consensus building without the presence
of any controlling authorities. The distributed nature
of the blockchain is proposed to be used in swarm
robotics to store global knowledge about swarm
actions (Ferrer, 2016). At the same time, due to
blockchain, the security of the transmitted data is
ensured (garbage data can affect the achievement of a
common goal), distributed decision making (creating
a distributed voting system for the solution),
separation of robots behaviour (switching between
behaviour patterns depending on the role in the
swarm), the emergence of new business models using
the swarm. In addition, the availability of a
distributed transaction ledger allows new robots to
join the swarm and gain all the knowledge they have
gained prior to the moment of inclusion by
downloading and analyzing the transaction history.
3 FUZZY COOPERATIVE GAME
MODEL WITH CORE
A generalized model of a fuzzy cooperative game
(FCG) with core was proposed in (Sheremetov, 2009;
Sheremetov and Smirnov, 2011; Smirnov and
Sheremetov, 2012). As shown in (Smirnov and
Sheremetov, 2012), the concept of a core is attractive
since it tends to maximize the sum of coalition
utilities in the particular coalition structure. The core
of a game is a set of imputations, which are stable.
The proposed model helped solving the problems of
the computational complexity of finding the optimal
structure and of the empty core, which enabled its use
in practical applications of selecting robots in coali-
tions.
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic Robot Coalition Formation: Approach and Use Case Description
363

A FCG is defined as a pair
, where
is nonempty and finite set of players, subsets
of joining together to fulfil some task
are
called coalitions K, and w is called a characteristic
function of the game, being
a mapping
connecting every coalition with a fuzzy
quantity
, with a membership function
. A modal value of
corresponds
to the characteristic function of the crisp game
:
. For an empty coalition
. A fuzzy core for the game
with the imputation
is a
fuzzy subset
of
:
(1)
where
is the fuzzy payment of a robot j
participating in a coalition ,
is the ordered
structure of effective coalitions; is a fuzzy partial
order relation with a membership function
, and
is a binary variable such that:
This variable can be considered as a result of
some robot’s strategy on joining a coalition.
A fuzzy partial order relation is defined as follows
(for more details see (Zadeh, 1971)). Let a, b be fuzzy
numbers with membership functions
and
respectively, then the possibility of partial order
is defined as
as follows:
(2)
The core
is the set of possible distributions of
the total payment achievable by the coalitions, and
none of coalitions can offer to its members more than
they can obtain accepting some imputation from the
core. The first argument of the core
indicates that
the payments for the grand coalition are less than the
characteristic function of the game. The second
argument reflects the property of group rationality of
the players, that there is no other payoff vector, which
yields more to each player. The membership function
, is defined as:
(3)
With the possibility that a non-empty core
of
the game
exists:
(4)
The solution of a cooperative game is a coalition
configuration
which consists of (i) a partition
of , the so-called coalition structure, and (ii) an
efficient payoff distribution x which assigns each
robot in Robot its payoff out of the utility of the
coalition it is member of in a given coalition structure
S. A coalition configuration (S, x) is called stable if
no robot has an incentive to leave its coalition in S due
to its assigned payoff x
i
.
It was proved that the fuzzy set of coalition
structures forming the game core represents a subset
of the fuzzy set formed by the structure of effective
coalitions. In turn, this inference allows us to specify
the upper possibility bound for the core, which is a
very important condition for the process of solution
searching, because in this case, the presence of a
solution that meets the efficiency condition may serve
as the signal to terminate the search algorithm
(Sheremetov, 2009).
The game purpose is to generate an effective
structure of robot coalitions for executing some task.
In turn, the generated structure of robot coalitions
represents the optimal configuration of the grand
coalition.
Individual robots use the technique of nonlinear
fuzzy regression to estimate the parameters of utility
functions for their payments (Haekwan and Tanaka,
1999). A “coalition robot” is enabled for constructing
membership functions (MF) of coalitions and
generating the game core (fuzzy-number generator).
The algorithm of fuzzy number summation for
obtaining coalition membership functions represents
an important element of the model. The sum
operation is based on Zadeh extension principle
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
364

(Zadeh, 1971) for fuzzy numbers а and b (which are
convex sets normalized in R):
(5)
where * can designate the sum or the product •
of fuzzy numbers. Each fuzzy set is decomposed into
two segments, a non-decreasing and non-increasing
one. The operation * is performed for every group of
n segments (one segment for each fuzzy set) that
belong to the same class (non-decreasing or non-
increasing one). Thus, a fuzzy set is generated for
every group of n segments. The summation result is
derived as superposition of these sets, which gives the
membership function as the sum of n fuzzy numbers.
4 CRITERIA FOR DYNAMIC
ROBOT COALITION
FORMATION
Group problem solving in many problem areas
requires a well-coordinated interaction of the
participants' actions during the coalition formation.
Regardless of the coalition model used, coalition
formation process can be considered as three types of
interrelated actions:
Generation of a coalition structure; a formation in
which agents within each coalition coordinate their
activities;
Solving the problem of optimization of each
coalition; union of agents' competencies for
effective problem solving;
Profit sharing between agents.
Once these actions are performed before problem
solving, a static coalition formation is considered.
The structure of static coalitions does not change over
time. At the time of optimization of the coalition, also
a plan for solving the problem is calculated as well as
all possible deviations from the plan. In case of a
deviation, for example, due to the failure of one of the
coalition members, the correction of the plan is
carried out by the forces of the last coalition members
taking into account the changed conditions in order to
return to the original plan with minimal losses.
A more complex, but flexible variant of a
coalition formation is the dynamic formation. In this
case, during the optimization, a plan of problem
solving is formed same as for the static coalition.
However, in case of deviation from the plan, a return
is made by changing the structure of the coalition, for
example, by adding a new participant. To do this, the
rules for the formation of the coalition should
describe actions for extraordinary situations, and the
overall benefit of the coalition, so the plan of action
is dynamically recalculated considering the context of
the task has changed.
The coalition efficiency can be evaluated by one
of the following parameters:
Minimizing the energy spent. The solution of each
task or sub-task can be estimated by the energy
(charge of the battery)
of the robot k that is
spent to solve it by using own competencies:
(6)
The exact amount of energy spent on solving the
problem is not possible to estimate precisely due to
the influence of a large number of external and
internal factors. However, based on average data on
similar problems, it is possible to obtain an
approximate estimation, which, however, introduces
fuzziness into the final decision to form a coalition.
In this case, the robots are interested in spending
minimum energy with the maximum efficiency. The
coalition efficiency can be estimated as relation of the
number of solved problems to the total energy
expended:
(7)
Robot uptime can serve as an analogue of the
estimated energy expended. Each of the robot units
has the probability of failure, which increases as
the operation proceeds. Solution of each task
requires a certain time of unit operation. Thus, the
estimation of failure probability is the ratio of the
time difference between the time of the node work
and the average time of uptime of this type of robot
units:
, where
– failure probability
of unit
by robot
,
– total work duration of
the unit
,
– last service time point. The
probability of entire robot failure will be evaluated
according to the maximum probability of nodes
failure
. An estimation of this
probability is also approximate. The efficiency
criterion in this case will be the maximum duration
of the coalition's overall work to the next
maintenance, which requires such a distribution of
tasks among the participants, so that the
probability of coalition member failure.
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic Robot Coalition Formation: Approach and Use Case Description
365
Maximizing the coalition benefit. For example, in
relation to precision farming, the coalition's benefit
is the cumulative crop of all cultures on the field.
This requires coordinated and timely interaction of
all robots in a dynamic coalition. The value of the
solution of the problem decreases with the passage
of time: the longer the task is postponed, the less
benefit it can provide. For example, untimely
watering due to the lack of robots in a coalition
with a sufficient supply of water can cause the
death of a crop, which will reduce the potential
benefit. Thus, the choice of coalition participants
and the distribution of tasks among them should be
carried out in such a way as to minimize downtime
and, accordingly, to maximize the overall benefit
of the coalition.
5 IMPLEMENTATION OF A
FUZZY COOPERATIVE GAME
OVER SMART CONTRACTS
In this section, the implementation of the rules of the
coalition game is proposed by means of smart
contracts, that describe the interaction of robots
during the coalition formation. This is enabled by the
ability of smart contracts within the scope of
blockchain technology to describe complex
algorithms by using the Turing-complete
programming language. Examples include Solidity
for the Ethereum platform (Buterin, 2014) or GoLang
and JavaScript for Hyperledger Fabric (Androulaki et
al., 2018).
5.1 Smart Contract Theory
The idea of smart contract was proposed in 1994 by
Nick Szabo. He had defined smart contract as “a set
of promises, specified in digital form, including
protocols within which the parties perform on these
promises.” (Szabo, 1996) The example of resource
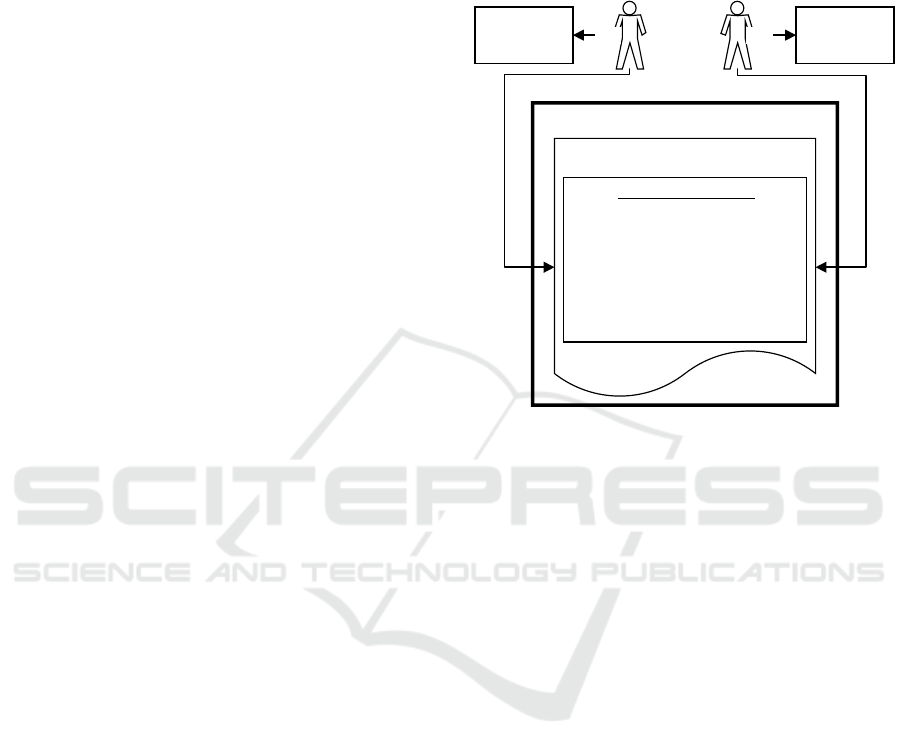
exchange is presented on Fig. 1.
In scope of the current level of information
systems, smart contracts are viewed as decentralized
applications that are available to all sides of the
contract through the cloud of in decentralized way,
for instance, blockchain. Due to the use of Turing-
complete language for contract description, it is
possible to implement rather complex algorithms. At
the same time, it is mandatory to have conditions
under which the contract must be executed as well as
the list of actions assigned to the submitted
conditions. All conditions of a smart contract must be
described in a strong mathematical way and provide
clear execution logic. In this regard, the first smart
contracts in the blockchain are created to formalize
the simplest relationships and consist of a small
number of conditions.
Figure 1: Smart contract usage example.
To be valid and trusted smart contracts have to be
signed by all sides with their private key (Goldreich,
2006) and sent as a transaction to be written to in the
cloud or decentralized storage. After signing by all
contract sides, the smart contract comes into force. To
ensure the automated performance of contract
obligations, an environment of existence is required
that allows fully automated execution of contracts.
This means that smart contracts can only exist within
an environment that has unrestricted access to
executable code of smart contract objects. Having
unimpeded access to the objects of the contract, the
smart contract monitors the specified conditions of
achievement or violation of the points and makes
independent decisions based on the programmed
conditions. Thus, the main principle of a smart
contract is the complete automation and reliability of
the performance of contractual relations between
participants.
5.2 Smart Contracts for Robot
Coalition Formation
Figure 1 shows the scheme of interaction of robots in
the coalition by means of a blockchain. It is proposed
to use two kinds of chains in the blockchain network
system for robot interaction: (i) for storing resources
and (ii) for storing contracts. All system resources
Trusted storage
Smart Contract
Resource A
Exchange of Resource A
Sides: Participant X, Participant Y
Resource: A
Statement:
If requirements_list is met
Then doExchange(X, A, Y B)
ChangeOwner(A, Y)
ChangeOwner(B, X)
Else CancelExchange()
Participant X Participant Y
Own Resource BOwn
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
366

including consumables, energy, reward, which are
represented by tokens, are stored in the resources
chains. In the chain with contracts, the rules of
cooperative game are stored, which are used by the
robots coordinators during the coalition forming and
the distribution of tasks. The first contracts in the
chain of contracts are rules for processing tasks and
assigning coalition core. New task is formed with a
program interface outside a coalition by problem
manager, or by the cores of another coalition in case
of obtaining a new context that cannot be processed
by the existing coalition. New tasks are stored in the
contract chain of the blockchain, from where they
become available for all coalition cores. Tasks
contain a formalized description of the goal, the initial
parameters and the amount of reward for the solution.
The robot coordinator selects robots guided by
contracts that describe their competencies and reward
expectations, as well as the rules of the cooperative
game, defined for the subject area to which the task
belongs. If the robot can participate in several
coalitions, each robot coordinator calculates the
cooperative game core and win for each of the
coalitions, as well as the availability of sufficient
resources for the robot successful work. If there are
enough resources for robot’s operations, it can
participate in several coalitions. Otherwise, the robot
is assigned to a coalition for which it can bring the
highest benefit. The reward for the successful
solution of the problem is distributed among the
coalition members based on the reward rules for the
cooperative game, described in the code of the
relevant contract.
Robot
i
Robot
j
Resource chain
Smart contract chain
Resource/
contract
Transactions
Resource/contract
Blockchain
Robot
CORE1
Task
1
Task
2
Task
3
Robot
k
Robot
l
Robot
CORE2
Task
4
Task
5
Task
6
Resource/contract
Resource/
contract
Transactions
Figure 2: Robot interaction in coalition through blockchain
and smart contracts.
6 PRECISION FARMING USE
CASE FOR FUZZY
COOPERATIVE GAMES WITH
SMART CONTRACTS
In this section, an example of solving the problems of
precision farming by coalition of robots is considered.
Robots are interact through the cyberphysical
framework presented in Figure 3. The framework is
based on the smart cyberphysical space created on the
top of smart space concept (based on the
“blackboard”) and blockchain. It provides the ability
to organize basic interaction of robots in the physical
and cyber (virtual) spaces. The interaction includes
solo and joint manipulations with physical objects,
information exchange about the current state of robots
Figure 3: Cyberphysical framework with blockchain support.
Smart space
Physical environment Cyber (virtual) environment
Robot Knowledge
processor
Robots sensors
& actuators
Information Service
Knowledge processor
Ontology
Ontology
BlockChain
Environmental
Sensors
Sensors Knowledge
processor
Physical
Objects
Ontology
Blockchain
Knowledge
processor
Ontology
Blockchain chain for smart contracts
Blockchain chains for resources
...
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic Robot Coalition Formation: Approach and Use Case Description
367

and objects for planning further joint actions during
the coalition formation.
The problem is stated as follows (Figure 4). There
is a field with various geological and ecological
characteristics of soils, suitable for growing several
crops that require different growth conditions. The
field is processed by a number of robots equipped
with devices for plowing, loosening, planting,
watering, fertilizing and harvesting crops. Each robot
is equipped with a set of sensors that allow to explore
the soil structure, light and humidity conditions in
each sector of the field. Based on the explored data a
map of the field is built, where the current conditions
are bound with the coordinates. Crops will be selected
for each sector based on the sector conditions that are
the most favorable in terms of yield, as well as
technologies will be selected for their care. The
technology of caring for each type of crop requires
the use of robots that are capable of carrying out
specific operations for the culture chosen, while some
robots are capable of performing operations on
several technologies, or the technologies can have
common steps being solved by the same type of
robots. Digital recording and storing of the history of
fieldwork and crops can help both in subsequent
decision-making and in drawing up special reporting
on the production cycle, which is increasingly
required by the laws of developed countries. This, as
well as the requirement of storing the history of
fieldwork requires the presence of a repository, in
which the history of actions and the results of field
processing will be recorded.
One of the typical coalitional tasks for precision
agriculture is the field exploration where different
types of robots are engaged. The overall task of the
study is divided between them into subtasks,
according to the available competences of the robots.
In this case, task division is performed using the
cooperative game model for the dynamic coalition
formation. Within the framework of this model,
individual robots interact with each other, putting
forward their competencies and requirements on the
basis of which the selection of coalition participants
is being carried out and their effectiveness in solving
the assigned task is estimated.
The blockchain network for the case study has
been implemented based on the Hyperledger Fabric
platform that is provided by community of software
and hardware companies leading by IBM
(Androulaki et al., 2018). The platform provides
possibilities of wide range configurations: changing
of a core database for transactions and block storing,
changing of consensus mechanisms, and changing
signature algorithms for peers’ interaction with
blockchain. For the case study presented in the paper,
the default configuration has been used that includes
Byzantine Fault Tolerate consensus mechanism
based on BFT-SMaRT core (Bessani et al., 2017),
Apache CouchDB as a database and an internal
solution for peer certification. This configuration
Figure 4: Coalition formation for precision farming task.
- «Blackboard»:
Distributed ledger (main storage)
Ledger KP
Sensors and services KPs
Combine harvester KP,
Ledger copy
Transportation robot KP,
Ledger Copy
Combine harvester KP,
Ledger copy
Tractor robot KP,
Ledger copy
Scout-robot KP,
Ledger copy
Coalition
Transportation robot KP,
Ledger Copy
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
368

provides processing of more than 3500 transactions
per second with latency of hundred ms. Also the
platform provides possibility to create smart-
contracts called chaincodes (program code that
describes interaction between resources) using Go or
Java programming languages. The chaincodes are
running in isolated containers of core peers of
Hyperledger based on the Docker technology stack.
Each chaincode contains rules for cooperative fuzzy
game that used for coalition participants negotiation.
The example of chaincode for core calculation is
presented at listing 1.
Listing 1: Example of a chaincode for coalition core
calculation.
var robots []Robot // Robot list
var tasks []Task // Tasks to be
solved
var core []FCG // Fuzzy coalition core
var coreMaxGain FGC // Core with max
gain
func coreCalc(stub
shim.ChaincodeStubInterface, args
[]string) (string, error) {
robots[i], tasks[j] = args[i],
args[j]
core = FCGCalculation(robots,
tasks) // according to
formula (2)
for c in core {
if c.gain > coreMaxGain.gain
coreMaxGain = c
}
for rob in robots{
// bind task for robot according
to formula (1)
stub.PutState(rob,
c.getTask(rob))
// Estimate and fix processing time
stub.PutState(c.getTask(rob),
CalcProcTime(rob))
}
}
}
7 CONCLUSIONS
Smart contracts as a computerized protocol which
stores and carries out contractual clauses via
blockchain between humans and machines, or
between multiple machines, are no longer just a
theoretical concept and are becoming a real tool used
in industry. Smart contracts have different future
applications in industry, ranging from robot
coalitions to the whole supply chain.
In this paper, the novel integrated model of
application of games with fuzzy coalitions and fuzzy
smart contracts, which can be applied to coalition
formation both for humans and robots, and between
multiple robots has been described. Fuzziness serves
as the fundamental component of realistic
cooperation models when there exist fuzzy
expectations of player and coalition benefits. When
an effective solution is found, individual benefits for
players (the agreement efficiency) increase, as well as
the capability of the coalition to find an effective and
stable agreement. In the definition of a fuzzy core, the
efficiency is taken into consideration by introducing
binary variables y
ij
into the fuzzy core. Fuzzy
payments {(w(I),x
ij
, w(K
i
))} may have any utility
function, linear or nonlinear, universal or not, which
enables the use of the model in real-world
applications. The blockchain model allows one to
avoid the synchronization problem, which is critical
for distributed negotiation algorithms with large robot
populations.
The use of the described FCG model for partners’
selection in supply chains has been already reported
by the authors. The integration of this model with
smart contracts can make coalition formation more
transparent and to smooth out the operations of the
tasks. The use of Internet of Things (IoT) sensors,
which track goods though the chain, from warehouses
to manufacturers and suppliers enables that the
finished product can be verified at each stage of the
task solving. If any stakeholder fails to meet the terms
of the contract, for instance if a robot did not perform
some operation on time, it would be clear for every
party to see and new coalitions can be arranged
dynamically.
The future work is aimed in two main directions.
The first one is to develop smart contracts for
participants changing in coalition. The changing
process will be based on the negotiation between
coalition core and robots outside the coalition that can
perform task instead of failed coalition members. The
other direction includes simulation based on the use
case scenario and comparison with other methods of
coalition formation.
ACKNOWLEDGEMENTS
The present research was supported by the projects
funded through grants # 17-29-07073, 17-07-00247
and 17-07-00327 of the Russian Foundation for Basic
Research.
Fuzzy Cooperative Games Usage in Smart Contracts for Dynamic Robot Coalition Formation: Approach and Use Case Description
369

REFERENCES
Androulaki, E., Barger, A., Bortnikov, V., Cachin, C.,
Christidis, K., De Caro, A., Enyeart, D., Ferris, C.,
Laventman, G., Manevich, Y., Muralidharan, S.,
Murthy, C., Nguyen, B., Sethi, M., Singh, G., Smith,
K., Sorniotti, A., Stathakopoulou, C., Vukolić, M.,
Cocco, S.W., Yellick, J., 2018. Hyperledger Fabric: A
Distributed Operating System for Permissioned
Blockchains 15.
Aubin, J.-P., 1981. Cooperative Fuzzy Games. Math. Oper.
Res. 6, 1–13. https://doi.org/10.1287/moor.6.1.1
Bayram, H., Bozma, H.I., 2015. Coalition formation games
for dynamic multirobot tasks. Int. J. Rob. Res. 35, 514–
527. https://doi.org/10.1177/0278364915595707
Bessani, A., Sousa, J., Vukolić, M., 2017. A byzantine
fault-tolerant ordering service for the hyperledger
fabric blockchain platform, in: Proceedings of the 1st
Workshop on Scalable and Resilient Infrastructures for
Distributed Ledgers - SERIAL ’17. ACM Press, New
York, New York, USA, pp. 1–10.
https://doi.org/10.1145/3152824.3152830
Buterin, V., 2014. A next-generation smart contract and
decentralized application platform. Etherum 1–36.
https://doi.org/10.5663/aps.v1i1.10138
Cachin, C., Vukolić, M., 2017. Blockchain Consensus
Protocols in the Wild 24.
https://doi.org/10.4230/LIPIcs.DISC.2017.1
Cong, L.W., He, Z., Zheng, J., 2017. Blockchain Disruption
and Smart Contracts. SSRN Electron. J. 48.
https://doi.org/10.2139/ssrn.2985764
Delmolino, K., Arnett, M., Kosba, A., Miller, A., Shi, E.,
2016. Step by Step Towards Creating a Safe Smart
Contract: Lessons and Insights from a Cryptocurrency
Lab, in: Grossklags, J., Preneel, B. (Eds.), Financial
Cryptography and Data Security. FC 2016., Lecture
Notes in Computer Science. Springer Berlin
Heidelberg, Berlin, Heidelberg, pp. 79–94.
https://doi.org/10.1007/978-3-662-53357-4_6
Dorri, A., Kanhere, S.S., Jurdak, R., 2017. Towards an
Optimized BlockChain for IoT. Proc. Second Int. Conf.
Internet-of-Things Des. Implement. - IoTDI ’17 173–
178. https://doi.org/10.1145/3054977.3055003
Ferrer, E.C., 2016. The blockchain: a new framework for
robotic swarm systems.
Gillies, D.B., 1953. Some theorems on n-person games.
Princeton University.
Goldreich, O., 2006. Foundations of cryptography, 1
edition. ed. Cambridge University Press.
Haekwan, L., Tanaka, H., 1999. Fuzzy approximations with
non-symmetric fuzzy parameters in fuzzy regression
analysis. J. Oper. Res. Soc. Japan 42, 98–112.
Hosam, H., Khaldoun, Z., 2006. Planning coalition
formation under uncertainty: Auction approach, in:
Proceedings - 2006 International Conference on
Information and Communication Technologies: From
Theory to Applications, ICTTA 2006. IEEE, pp. 3013–
3017. https://doi.org/10.1109/ICTTA.2006.1684896
Jennings, N.R., Faratin, P., Lomuscio, A.R., Parsons, S.,
Wooldridge, M., Sierra, C., 2001. Automated
Negotiation: Prospects, Methods and Challenges. Gr.
Decis. Negot. 10, 199–215.
https://doi.org/10.1023/A:1008746126376
Kahan, J.P., Rapoport, A., 1984. Theories of Coalition
Formation. Lawrence Erlbaum Associates, Inc.
https://doi.org/10.4324/9781315802657
Kardos, C., Kovács, A., Váncza, J., 2017. Decomposition
approach to optimal feature-based assembly planning.
CIRP Ann. 66, 417–420.
https://doi.org/10.1016/j.cirp.2017.04.002
Klusch, M., Gerber, A., 2002. Dynamic coalition formation
among rational agents. IEEE Intell. Syst. 17, 42–47.
https://doi.org/10.1109/MIS.2002.1005630
Mareš, M., 2001. Fuzzy Cooperative Games, Studies in
Fuzziness and Soft Computing. Physica-Verlag HD,
Heidelberg. https://doi.org/10.1007/978-3-7908-1820-
8
Shen, P., Gao, J., 2010. Coalitional game with fuzzy
payoffs and credibilistic core. Soft Comput. 15, 781–
786. https://doi.org/10.1007/s00500-010-0632-9
Sheremetov, L.B., 2009. A model of fuzzy coalition games
in problems of configuring open supply networks. J.
Comput. Syst. Sci. Int. 48, 765–778.
https://doi.org/10.1134/S1064230709050116
Sheremetov, L.B., Smirnov, A. V., 2011. A Fuzzy
Cooperative Game Model for Configuration
Management for Open Supply Networks. Contrib. to
Game Theory Manag. 4, 433–446.
Smirnov, A. V., Sheremetov, L.B., 2012. Models of
coalition formation among cooperative agents: The
current state and prospects of research. Sci. Tech. Inf.
Process. 39, 283–292.
https://doi.org/10.3103/S014768821205005X
Szabo, N., 1996. Smart Contracts: Building Blocks for
Digital Markets Copyright [WWW Document].
alamut.com. URL
http://www.fon.hum.uva.nl/rob/Courses/InformationIn
Speech/CDROM/Literature/LOTwinterschool2006/sza
bo.best.vwh.net/smart_contracts_2.html (accessed
9.16.17).
Verma, D., Desai, N., Preece, A., Taylor, I., 2017. A block
chain based architecture for asset management in
coalition operations, in: Pham, T., Kolodny, M.A.
(Eds.), Proc. SPIE 10190, Ground/Air Multisensor
Interoperability, Integration, and Networking for
Persistent ISR VIII. p. 101900Y.
https://doi.org/10.1117/12.2264911
Zadeh, L.A., 1971. Similarity relations and fuzzy orderings.
Inf. Sci. (Ny). 3, 177–200.
https://doi.org/10.1016/S0020-0255(71)80005-1
Zhang, Y., Wen, J., 2017. The IoT electric business model:
Using blockchain technology for the internet of things.
Peer-to-Peer Netw. Appl. 10, 983–994.
https://doi.org/10.1007/s12083-016-0456-1
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
370
