High-performance Pipelined FPGA Implementation of the Elliptic Curve
Cryptography over GF (2
n
)
Salah Harb
a
, M. Omair Ahmad
b
and M. N. S. Swamy
c
Electrical and Computer Engineering Department, Concordia University, 1440 De maisonnueve, Montreal, Canada
Keywords:
Cryptography, Elliptic Curve Cryptography, FPGA, Pipelining Architecture, Finite Field Operations, Field
Multiplications, Projective Coordination, Efficiency.
Abstract:
In this paper, a high-performance area-efficient hardware design for the Elliptic Curve Cryptography (ECC)
is presented, targeting the area-constrained high-bandwidth embedded applications. The high-speed design
is implemented using pipelining architecture. The applied architecture is performed using n-bit data path of
the finite field GF(2
n
). For the finite field operations, the implementation in the ECC uses the bit-parallel
recursive Karatsuba-Ofman algorithm for multiplication and Itoh-Tsuji for inversion. A modified efficient
montgomery ladder algorithm is utilized for the scalar multiplication of a point. The pipelined registers are
inserted in ideal locations, where balanced-execution paths among computing components are guaranteed. A
Memory-less finite state machine model is developed to control the instructions of computing the finite field
operations efficiently. The high-performance design has been implemented using Xilinx Virtex, Kintex and
Artix FPGA devices. It can perform a single scalar multiplication in 226 clock cycles within 0.63µs using
2780 slices and 360Mhz working frequency on Virtex-7 over GF (2
163
). In GF (2
233
) and GF (2
571
), a scalar
multiplication can be computed in 327 and 674 clock cycles within 1.05µs and 2.32µs, respectively. Comparing
with previous works, our design requires less number of clock cycles, and operates using less FPGA resources
with competitive high working frequencies. Therefore, the proposed design is well suited in the resources-
constrained real time cryptosystems like those in online banking services, wearable smart devices and network
attached storages.
1 INTRODUCTION
Elliptic curve cryptosystem (ECC) is a public-key
cryptography, which was first proposed by Neal
Koblitz and Victor Miller in the 1980s (Kocher et al.,
1999) , (Miller, 1985). Since then, many studies have
been conducted to explore its security levels against
other public-key cryptosystems such as El-Gamal,
RSA and Digital Signature Algorithm (DSA) (ElGa-
mal, 1985), (Rivest et al., 1978), which are based on
either the integer factorization or discrete logarithm
problems (McGrew et al., 2011). Equivalent secu-
rity levels with smaller sizes of keys, ease to imple-
ment, and resource savings, are reasons that give the
ECC to be very appealing and more dominant be-
tween the hardware reconfigurable implementations.
Moreover, ECC is well suited to be implemented in
such resource-constrained embedded systems, since it
a
https://orcid.org/0000-0002-5975-6537
b
https://orcid.org/0000-0002-2924-6659
c
https://orcid.org/0000-0002-3989-5476
provides same security levels as in RSA using small
keys. ECC has been standardized by IEEE and the
National Institute of Standard and Technology (NIST)
as a scheme in digital signature and key agreement
protocols (for Standardization (ISO), 2000).
Generally, most of cryptographic algorithms are
implemented in software platforms. Performing an
algorithm on a general purpose processor (e.g. CPU)
will require most of its resources to compute results
of intensive operations because of the large operands
used in these very accurate computations. More-
over, CPU is not suitable in performing such these
algorithms that having the parallel architecture in na-
ture. These issues prove that software implementa-
tion of encryption algorithms does not provide the
required performance. Due to the diversity in the
applications, the trade-off between area, speed and
power is required. Some applications, such as RFID
cards, nodes of wireless sensor networks and cell
phones, need a small area and power. Other applica-
tions, such as web servers, large bandwidth networks
Harb, S., Ahmad, M. and Swamy, M.
High-performance Pipelined FPGA Implementation of the Elliptic Curve Cryptography over GF (2n).
DOI: 10.5220/0007772800150024
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 15-24
ISBN: 978-989-758-378-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

and satellite broadcast require very high throughputs.
To cover the issues of software implementation and
meet trade-offs in numerous applications, the hard-
ware platforms have been utilized for implementing
the cryptographic algorithms, where high efficiency
to perform tasks is achieved in different applications.
Field Programmable Gate Array (FPGA) is one
of the preferable reconfigurable hardware platforms
(Xilinx, 2018a) which offers flexible and more cus-
tomizable methods for performing and evaluating dif-
ferent hardware implementations. Because of this
fact and since FPGAs have been employed by most
of the previous hardware implementations to evalu-
ate their performances; the presented ECC hardware
implementation in this paper have been performed
using Xilinx FPGA devices (Xilinx, 2018b). Scalar
point multiplication (SPM) is the main point opera-
tion in ECC cryptosystems or protocols such as Ellip-
tic Curve Diffie-Hellman (ECDH) (Diffie and Hell-
man, 1976) for key agreements and Elliptic Curve
Digital Signature (ECDS) for digital signatures.
SPM can be implemented over many finite fields
under either prime or polynomial fields. Finite fields
named also Galois Fields (GF), where GF (p) is a
prime field and GF (2
n
) is the polynomial field. SPM
has two point operations, doubling and adding points.
Each operation consists finite field operations such
as square, addition, multiplier. Figure 1 presents
the hierarchical implementation of the ECC proto-
col. Polynomial fields are more suited and efficient to
implement on a customizable platform such FPGAs
(Wenger and Hutter, 2011a).
ECC
Protocols
Scalar Point
Multiplier
Point Doubling Point Addition
Square Multiplication Inversion
Figure 1: ECC Cryptosystem Hierarchy.
To gain high performance in today’s high loaded
communication networks, utilization of hardware ac-
celerators for physical security has created a great de-
mand for efficient and high-speed implementations of
ECC. Based on this fact, many FPGA implementa-
tions of the ECC have been published in the litera-
ture, where various ranges of latencies and number of
clock cycles are achieved targeting applications that
require high/low throughputs. Providing high perfor-
mance as well as utilizing efficient area, is a challenge
to achieve it in FPGA’s ECC implementations.
In this paper, a high-speed area-efficient Xilinx
FPGA implementation of the ECC over GF (2
n
) using
the pipelining architecture is proposed. The main tar-
get of our work is to develop high performance design
that targets systems that have constrained resources
such as wearable smart devices, processing engines
in image steganographic systems (Dalal and Juneja,
2018), (Amirtharajan, 2014) and Internet of Things
(IoTs) network processors. This paper is organized as
follow: section 2 describes the arithmetic operations
of the ECC; section 3 describes our high-performance
hardware implementation core for ECC over GF (2
n
);
section 4 shows the results and comparisons; and fi-
nally, section 5 concludes this paper.
2 ELLIPTIC CURVE
CRYPTOGRAPHY (ECC)
Elliptic Curves (ECs) are formulated by the so called
Weiestrass equations, which can be performed over
by normal or polynomial basis. In this paper, we work
on the polynomial basis in GF (2
n
) for its efficiency on
the hardware platforms (Wenger and Hutter, 2011a).
Equation 1 represents the general form of the none-
singular curve over GF (2
n
) (Hankerson et al., 2006).
y
2
+ xy = x
3
+ ax
2
+ b (1)
where a, b ∈ GF (2
n
) and b 6= 0. A set of affine
points (x, y) satisfying the curve forms a group (Han-
kerson et al., 2006) with an identity point of that
group. There are two fundamental elliptic curve oper-
ations, doubling and adding points. Doubling point
is denoted as P
1
=2P
0
, where P
1
is (x
1
, y
1
) and P
0
is (x
0
, y
0
) while point addition is denoted as P
2
=
P
0
+P
1
, where P
2
is (x
2
, y
2
), and P
1
6= P
0
. All points
in the selected curve are represented in affine coor-
dinates. Finite fields operations are involved in the
ECC point operations such as addition, square, mul-
tiplication and inversion. Dealing with affine coor-
dinates requires an inversion field operation. Due to
the complexity in the inversion operation, a projective
coordinate is utilized to avoid it by mapping points
in affine (x, y) to be represented in (X, Y, Z) form.
Scalar Point Multiplication (SPM) is the main impor-
tant operation that dominants the ECC-based cryp-
tosystems. SPM is process of adding a point k times,
where k is a positive integer and P is a point on a
SECRYPT 2019 - 16th International Conference on Security and Cryptography
16

selected curve. SPM is based on the implementa-
tion of the underlying point operations, where a series
of doubling and adding points is performed by scan-
ning the binary sequence of the k scalar, where k =
k
n
k
n−1
. . . k
1
k
0
. There are several methods and tech-
niques to implement k.P efficiently. Binary Add-and-
Double Left-Right, Binary Add-and-Double Right-
Left as the work presented in (Harb and Jarrah, 2019),
Non-Adjacent-Form (NAF) (Moon, 2006) and mont-
gomery ladder method (Montgomery, 1987). Affine
coordinate system is the default representation that
some SPM methods use it to introduce the points on
the curves, while other SPMs utilize alternative pro-
jective coordinate systems for representing the points.
The reason of applying different projective systems is
to avoid the time-resource consuming inversion field
operation. However, it increases the number of field
multiplications. Generally, projective systems tend
to provide efficient ECC cryptosystem’s designs in
terms of area/latency.
Lopez-Dahab (LD) (L
´
opez and Dahab, 1998) is
one of the most efficient projective coordinate sys-
tems. Points in affine system are mapped to LD pro-
jective system, where P at (x, y) coordinate is equal to
P at (X = x, Y = y, Z = 1) coordinate. In any SPM,
the point multiplication algorithm must be selected
first for performing the k.P. The next step is to define
the projective coordinate system for representing the
points. The last step, the algorithm that is used in the
finite field operations, mainly, for the field multipli-
cation and inversion operations. Figure 2 illustrates
the main steps of constructing SPM at our ECC cryp-
tosystem. In the presented work, montgomery ladder
algorithm is selected as point multiplication algorithm
and LD coordinate system is defined to represents the
points. For the field multiplication and inversion oper-
ations, the Karatsuba-Ofman algorithm and Itoh-Tsuji
algorithm are implemented, respectively.
2.1 Finite Fields GF (2
n
)
ECC over GF (2
n
) is more suitable and efficient
in hardware implementations because the arithmetic
in the polynomial fields is carry-less. In GF (p),
finding points on an elliptic curve requires perform-
ing a square root algorithm (Harb and Jarrah, 2017)
(Wenger and Hutter, 2011b), while the process is
much easier over GF (2
n
), where the points can be
found using generators for polynomials. There are
2n-1 elements in GF (2
n
), which can be represented
as binary polynomials. For example, the element in
GF (2
n
) has a polynomial representation:
a
n−1
x
n−1
+ a
n−1
x
n−2
+ ... + ax + 1 (2)
Montgomery
Ladder Algorithm
Point Multiplication Algorithm
Projective Coordinate System
Lopez-Dahab
Finite Field Operations
Karatsuba-Ofman Itoh-Tsuji
Multiplication Inversion
Figure 2: Main Components of SPM.
where x
i
is the location of the ith term, and a
i
∈
[0,1] is the coefficient of the ith term. Arithmetic op-
erations are applied over these elements such as addi-
tion, multiplication, squaring and division (i.e. inver-
sion and multiplication). Adding two elements C = A
+ B is done using the logic XOR. Squaring an element
A
2
is computed by padding 0s between two adjacent
bits of the element. Multiplying two elements C = A
· B is much harder and slower operation than addition
and square.
Result of squaring an element or multiplying two
elements would be out of the field. To reduce it, an
irreducible polynomial of degree n (f(x)) is used by
applying the reduction (modular) step, such as C =
(A
2
) mod f(x) or C = (A · B) mod f(x). Inversion oper-
ation is the most complex operation in terms of time
and resources. Obtaining the inverse of an element A
is the process of finding another element B that sat-
isfies A · B ≡ 1 mod f(x). Note that, the f(x) has
a major role in the performance of these operations.
In this paper, all curves and irreducible polynomials
are chosen based on the recommendation of the NIST
(Gallagher, 2013).
3 HIGH-SPEED CORE FOR ECC
OVER GF (2
n
)
In this section, we introduce our proposed archi-
tecture of the high-speed ECC core over GF (2
n
).
Karatsuba-Ofman and Itoh-Tsuji algorithms are im-
plemented for performing both field multiplication
and inversion operations, respectively. The LD co-
ordinate system is used as projective coordinate sys-
tem to present the points. For the SPM, a modified-
pipelined montgomery ladder method is implemented
High-performance Pipelined FPGA Implementation of the Elliptic Curve Cryptography over GF (2n)
17

in such a way that an efficient number of pipelined
stages are inserted. Next subsections present more de-
tails about these algorithms.
3.1 Montgomery Ladder Scalar Point
Multilocation Algorithm
At present, montgomery ladder is one of the most
popular multiplication algorithms to perform k.P,
where k is an integer. It can be implemented in both
affine and projective coordinate systems. Doubling
and adding point operations are computed in an ef-
ficient way for every bit in the sequence of k = k
= k
t−1
k
t−2
. . . k
1
k
0
. Algorithm 1 shows the projec-
tive coordinate version of montgomery ladder method
(L
´
opez and Dahab, 1998). As it’s shown, the algo-
rithm is based on performing point operations recur-
sively using the x affine coordinate, which leads to
reduce the number of field multiplications. The y co-
ordinate is used at the post-process affine, which is
required to recover the affine coordinates from the
LD coordinates. This algorithm has been imple-
mented in many hardware implementations that pro-
vides high performance (Ansari and Hasan, 2008)
(Roy et al., 2013) (Mahdizadeh and Masoumi, 2013)
due to its speed, parallelism capability, resource-
constrained systems and power analysis resistance.
3.2 Area-constrained and
High-performance Tradeoff
High-performance ECC hardware implementations
are achieved by considering optimization techniques
such as short-critical path, required resources and
number of clock cycles to perform a single SPM. The
architectural pipelining optimization aims to optimize
the long-critical path of the design through break it
into stages. Number of clock cycles can be improved
by adopting the parallel field multiplication opera-
tions. All these optimization techniques impact on the
resources that are required for performing the SPM. In
pipelining, inserting registers to minimize the critical
path delay results in an increase on the number of the
clock cycles (latencies) and resources. Obtaining an
efficient pipelined design is done by determining the
number of the stages. More stages yield higher work-
ing frequencies but higher latencies. Balancing this
tradeoff can be achieved by considering an efficient
field multiplier, independency levels among point op-
erations, and finite-state machines that control these
operations effectively.
Algorithm 1: Montgomery Ladder Scalar Multiplier (k.P).
Input: k = k
t−1
k
t−2
...k
1
k
0
, Point P(x,y) on Elliptic Curve.
Output: A point Q = kP
X
1
← x; Z
1
← 1; X
2
← x
4
+ b; Z
2
← x
2
;
if k == 0 k x == 0 then
Q ← (0, 0);
end if
Stop;
for i = t −2 to 0 do
if k
i
== 1 then
Q (X
1
,Z
1
) ← add(X
1
, Z
1
, X
2
, Z
2
); ⇒ {
Z
1
← X
2
· Z
1
; X
1
← X
1
· Z
2
; T ← X
1
+ Z
1
;
X
1
← X
1
· Z
1
; Z
1
← T
2
; T ← x · Z
1
;
X
1
← X
1
+ T ; }
Q (X
2
,Z
2
) ← double(X
2
, Z
2
); ⇒ {
Z
2
← Z
2
2
; T ← Z
2
2
; T ← b · T ;
X
2
← X
2
2
; Z
2
← X
2
· Z
2
; X
2
← X
2
+ T ; }
else
Q (X
2
,Z
2
) ← add(X
2
, Z
2
, X
1
, Z
1
); ⇒ {
Z
2
← X
1
· Z
2
; X
2
← X
2
· Z
1
; T ← X
2
+ Z
2
;
X
2
← X
2
· Z
2
; Z
2
← T
2
; T ← x · Z
2
;
X
2
← X
2
+ T ; }
Q (X
1
,Z
1
) ← double(X
1
, Z
1
); ⇒ {
Z
2
← Z
2
1
; T ← Z
2
1
; T ← b · T ;
X
1
← X
2
1
; Z
1
← X
1
· Z
1
; X
1
← X
1
+ T ; }
end if
end for
Return Q (X
3
,Z
3
) = affine(X
1
, Z
1
, X
2
, Z
2
); ⇒ {
x
3
← X
1
/Z
1
;
y
3
← (x+X
1
/Z
1
)[(X
1
+x · Z
1
) (X
2
+x · Z
2
) + (x
2
+y)(Z
1
·Z
2
)]
(x · Z
1
· Z
−1
2
) + y; }
3.3 Proposed High-speed Area-efficient
ECC Core over GF (2
n
)
Algorithm 1 states that for performing single point
multiplication, three stages are covered; 1) map the
affine coordinates to LD coordinates, 2) perform dou-
bling and adding point operations recursively, and
3) recover the point from LD to affine coordinates.
Each iteration performs the same point operations
with swapping between input and output registers (X
and Z registers) depending on the current bit of the k
i
if it is 1 or 0. From this recursive manner, the authors
in (Mahdizadeh and Masoumi, 2013) noticed that the
initialization step of Algorithm 1 can be merged into
the main loop of the algorithm. the registers are be-
fore main loop: X
1
= 1, Z
1
= 0, X
2
= x, Z
2
=1. This
eliminates the need of precomputed values to be ob-
tained before starting the main loop.
However, it requires extra clock cycles for the
merged initialization step. The design in (Ansari
and Hasan, 2008) addressed the swapping feature
SECRYPT 2019 - 16th International Conference on Security and Cryptography
18

in Algorithm 1 and proposed a merged-improved
montgomery ladder point multiplication algorithm as
shown in Algorithm 2.
Algorithm 2 : Merged-Improved Montgomery Ladder
Scalar Multiplier (k.P).
Input: k = k
t−1
k
t−2
...k
1
k
0
, Point P(x,y) on Elliptic
Curve.
Output: A point Q = kP
X
1
← 1; Z
1
← 0; X
2
← x; Z
2
← 1;
if k == 0 k x == 0 then
Q ← (0, 0);
end if
Stop;
for i = t − 1 to 0 do
T ← Z
1
; Z
1
← (X
1
· Z
2
+ X
2
· Z
1
)
2
;
X
1
← x · Z
1
+ X
1
· X
2
· T · Z
2
;
T ← X
1
;
X
2
← X
4
2
+ b · Z
4
2
;
Z
2
← T
2
· Z
2
2
;
if (i 6= 1&k
i
6= k
i−1
) k (i == 0&k
i
== 0) then
swap(X
1
, X
2
, Z
1
, Z
2
); ⇒ {
T
1
← X
1
;X
1
← X
2
;
X
2
← T
1
;
T
2
← Z
1
;Z
1
← Z
2
;
Z
2
← T
2
; }
end if
end for
Return Q (X
3
,Z
3
) = affine(X
1
, Z
1
, X
2
, Z
2
); ⇒ {
x
3
← X
1
/Z
1
;
y
3
← (x +X
1
/Z
1
)[(X
1
+x · Z
1
) (X
2
+x · Z
2
) + (x
2
+
y)(Z
1
· Z
2
)] (x · Z
1
· Z
−1
2
) + y; }
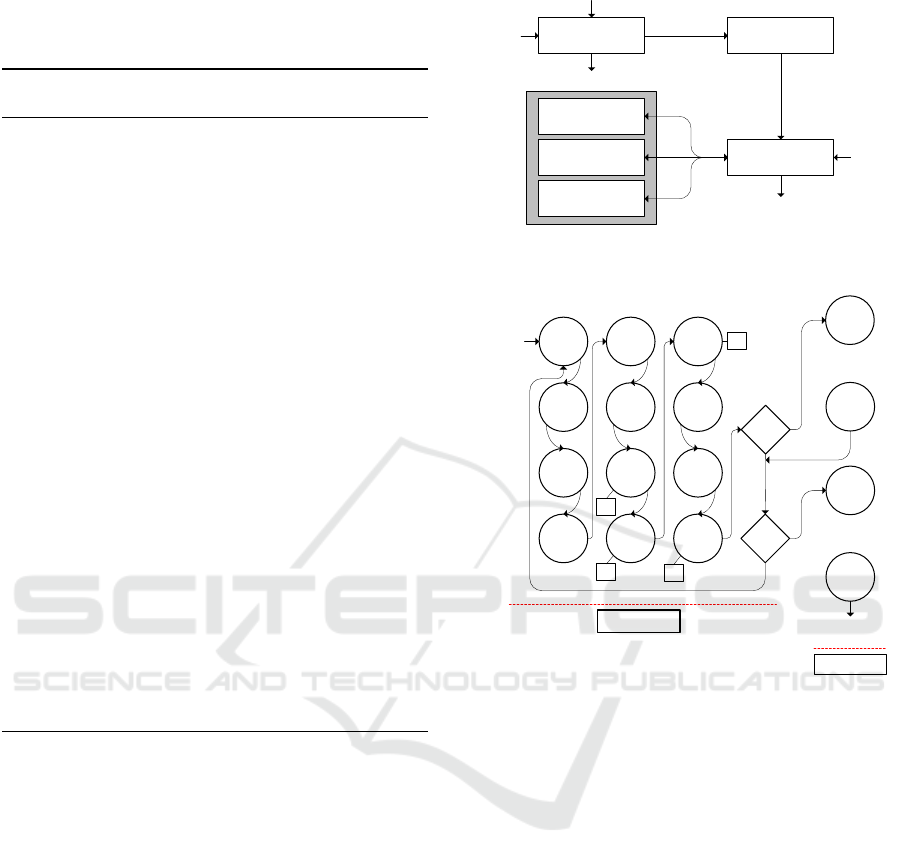
The proposed high-speed area-efficient hardware
design is shown in Figure 3. The general architecture
has three units, optimized finite-state machine con-
trol unit, GF (2
n
) arithmetic unit contains Karatsuba-
Ofman and square, and control signal unit. Next, fur-
ther details are given for these main unites in the high-
speed ECC core.
3.3.1 Finite-state Machine for the Proposed
ECC Core
Finite-State Machine (FSM) is a control model which
is developed to control any hardware design that has
many components such registers, addresses and flags.
Controlling design includes maintaining the proper
transitions between these components.
Each transition in FSM affects the state (i.e. cur-
rent values) of the registers and flags. FSM of the
proposed high-performance core is implemented in
an efficient way, where minimum number of states
have been utilized. Figure 4 represents the main FSM
Finite-State
Machine
Start
Reset
Control Signals
Address
Sel_Reg
Karatsuba-Ofman
Field Multiplier
Registers
GF (2
n
) Square
Done
Output
Input
Itoh-Tsuji
Inversion
Figure 3: The Proposed High-speed Area-Efficient Hard-
ware Design.
Yes
No
State
0
Start
State
1
State
2
State
3
State
7
State
6
State
5
State
4
State
8
State
9
State
10
State
11
x2
X
2
X
1
Z
1
Z
2
Main Loop
State
12
State
52
Itoh-Tsuji
...
Done
State
53
State
57
...
Swap
i = 0
Yes
No
Figure 4: State Machine of the Proposed SPM.
of the proposed high-speed core. As it’s shown, the
main loop of the merged-improved montgomery lad-
der SPM starts from state 0 and ends at state 11. At
state 11, the condition (the second if-statement in Al-
gorithm 2) of whether swapping registers must be
done or go back to state 0 for the next ki. The swap
process is done in a routine which starts from state
53 to state 57. Once the i is equal to zero, the results
are ready to be mapped back to the affine coordinates.
Itoh-Tsuji inversion algorithm is used to achieve that,
and it starts from state 12 to state 52. At state 52, a
done signal is asserted to indicate that mapping pro-
cess is done, and affine coordinates are obtained.
3.3.2 Computation Schedule for Montgomery
Ladder SPM
In this subsection, we introduce a new efficient
scheduling for performing a single scalar point based
on the merged-improved version as shown in Algo-
rithm 2. Free-idle cycles schedule is achieved by
performing the doubling and adding points in less-
High-performance Pipelined FPGA Implementation of the Elliptic Curve Cryptography over GF (2n)
19

1 x 0 1
X
2
Z
1
Z
2
1
X
1
Z
2
X
2
SQ
2
SQ
T T SQ
3
SQ
b T
4
ML SQ
5
// ML
6
ML // //
7
SQ ML T
8
AD x Z
1
9
ML
10
//
11
//
12
// ML
13
AD
14
AD
X
1
X
2
Z
1
Z
2
A B C
T
clk
AD = Add SQ = Square ML = Multplication
Adder Multiplier Square
Figure 5: State Machine of the Proposed SPM.
dependent way. This is done by parallelizing the field
operations of the point operations, such as squaring
and multiplying same or different operands, simulta-
neously. Figure 5 illustrates our new schedule, where
8 registers are utilized to perform a single loop in Al-
gorithm 2. A and B registers are operands that are
connected to the field multiplier, while register C is
operand of the square field operation. Register T is
a temporary register which is used to hold intermedi-
ate values. This zero-idle schedule can perform a sin-
gle SPM iteration in 14 clock cycles using the three
pipelined stages Karatsuba-Ofman multiplier, where
3 clock cycles are required to obtain field multipli-
cation results. One clock cycle for the square one
clock cycle for square. Four subsequent field mul-
tiplications and squares are performed independently
and simultaneously from clock number 1 to 4. Each
square result is stored at register T.
At 5, results of first multiplication (X
1
· Z
2
) is ob-
tained to multiply with the next multiplication result
(X
2
· Z
1
) at clock 6 and added at clock 7. Result of the
third multiplication (T
2
· Z
2
2
) is stored in Z
2
at clock 7.
The fourth multiplication (b · Z
4
2
) is obtained at clock
8 and added with register T which contains X
4
2
. Re-
sult of (X
1
· X
2
· T · Z
2
) is obtained at clock 10 which
is added to the result of (x · Z
1
) at clock 13. The total
number of clock cycles for performing a single SPM
consists of: initialization step, SPM process and LD
to affine routine. In our proposed ECC core, there are
9 clock cycles for initialization step, (blog
2
(k)+1c) x
14MUL for SPM process, and (9 k 10 k 13) x 3MUL
+ (162 k 232 k 570) for LD to affine routine.
For example, if the scalar k is 10 and GF (2
163
),
then the total number of clock cycles for perform-
ing a single SPM is equal to: 9 + (blog
2
(10) +
1c) x 14MUL + 9x3 + 162 = 254 clock cycles.
Note that, Itoh-Tsuji algorithm requires n-1 squares
and blog
2
(n − 1)c) + HW (n − 1) − 1 multiplications,
where the HW is the hamming weight of the integer
(n-1). For example: in GF (2
233
), 232 squares and
blog
2
(232) + 1c) + H W (232) − 1 = 7 + 4 − 1 = 10
multiplications.
3.3.3 Karatsuba-Ofman Field Multiplier
Field multiplication consists of two steps, first,
compute as C’ = A · B, the second is reducing the
C’ by using the mod operation as C = (C’) mod f(x).
This kind of multipliers is called as two-step classic
field multiplier. The interleaved field multiplier is one
of the classical field multipliers (Großsch
¨
adl, 2001)
that apply the two steps as shift and add operations
in iterations. Few resources are utilized to implement
the interleaved multipliers, which makes it a very
attractive one to the constrained-resources systems.
However, this type of multipliers has a very long
critical path due to the dependency between the
iterations. The Karatsuba-Ofman field multiplication
is a recursive algorithm that performs polynomial GF
(2
n
) multiplications in large finite fields efficiently
(Karatsuba and Ofman, 1962). Karatsuba-Ofman is
given and defined as follows: Let A and B be two
arbitrary elements in GF (2
n
). Result of C’ = A · B is
a product of a 2n-2 degree polynomial. Both A and B
can be represented as two split parts:
A = x
n/2
(x
n/2−1
· a
n−1
+ ·· · + a
n/2
)+
(x
n/2−1
· a
n/2−1
+ ·· · + a
0
) = x
n/2
· A
H
+ A
L
B = x
n/2
(x
n/2−1
· b
n−1
+ ·· · + b
n/2
)+
(x
n/2−1
· b
n/2−1
+ ·· · + b
0
) = x
n/2
· B
H
+ B
L
The polynomial of the product C’ is:
C
0
= x
n
· A
H
· B
H
+ x
n/2
(A
H
· B
L
+ A
L
· B
H
) + A
L
· B
L
The sub-products are defined as auxiliary polyno-
mials as follows:
C
0
0
= A
L
· B
L
C
0
1
= (A
L
+ A
H
)(B
L
+ B
H
)
C
0
2
= A
H
· B
H
Then the product C’ can be obtained by:
C
0
= x
n
·C
0
2
+ x
n/2
(C
0
0
+C
0
1
+C
0
2
) +C
0
0
This field multiplication can be recursive if we split
the auxiliary polynomials again with new auxiliaries
are generated. More recursions yield in an increased
SECRYPT 2019 - 16th International Conference on Security and Cryptography
20

GF (2
163
)
40
20
81
20
41
20 21
41
20
82
21
41
20 21
Recursive
Classic
GF (2
233
)
58
29
116
29
58
29 29
58
29 29
59
29
3
0
Recursive
Classic
117
GF (2
571
)
71
285
71
71 72 71 72
71 72
Recursive
Classic
286
142 143 143
143
Figure 6: Recursive Splits over Different Finite Fields.
delay for the Karatsuba-Ofman multiplier (Peter and
LangendOorfer, 2007). So, this recursion ends after
the threshold q splits, where it ends with a classical
field multiplier. Number of splits is optimum when
splitting reaches the balance between area utilized and
delay. The work in (Zhou et al., 2010) have discussed
this trade off in details. The best split for the GF
(2
163
), GF (2
233
) and GF (2
571
) fields, is shown in
Figure 6. The optimum split is coming from the used
FPGA technology in term of the lookup tables LUTs
(Zhou et al., 2010).
There are two technologies have been released: 4-
input LUT (i.e. old FPGA devices) and 6-input LUT
(i.e. new FPGA devices) (Percey, 2007), (Specifica-
tion, 2006). For GF (2
163
), at first recursive, we get
three auxiliaries: 2 of 82-bit multipliers and 1 of 81-
bit multiplier. Second recursive, 2 of 41-bit and 1 40-
bit multipliers for 81-bit multiplier, and 3 of 41-bit
multipliers for 82-bit multiplier. Third recursive, 2 of
21-bit and 1 20-bit multipliers for 41-bit multiplier,
and 3 of 20-bit multipliers for 40-bit multiplier. The
multiplier used after the recursive split is a single-step
(no mod operation) classic multiplier which is used
for all three fields. Figure 7 shows the logic gate im-
plementation for the classic multiplier. The critical
path of Karatsuba-Ofman multiplier is long due to the
recursive nature in its hierarchy. Applying an archi-
tectural improvement such as inserting pipelining reg-
isters between recursive splits improves the long crit-
ical path and provides a higher working frequency.
Efficient pipelined Karatsuba-Ofman multiplier
can be achieved when the critical path is the short-
est. In FPGA, the shortest critical path implies that
the delay-to-area ratio is the minimum in time and
utilized area. For achieving that, different pipelined
stages have been inserted in the Karatsuba-Ofman
multiplier. As shown in Figure 8, the efficient balance
in delay-to-area ratio over GF (2
163
) is achieved by
inserting exactly three pipelined stages, where 2121
B
0
A
1
A
0
A
n-1
B
n-1
C’
2n-2
A
n-2
B
n-1
A
n-1
B
n-2
C’
2n-3
A
n-1
B
0
C’
k
A
n-1
B
1
...
A
0
B
n-1
A
2
C’
2
A
1
B
1
...
A
0
B
2
B
0
A
0
B
1
C’
1
B
0
C’
0
...
...
Figure 7: Logic Gate Implementation for the Classic Multi-
plier.
0
2
4
6
2 3 4
1,800
2,000
2,200
2,400
2,600
Pipelined Stages
Delay-to-Area Combination
Slices
Delay (ns)
Figure 8: Delay-to-Area Ratio using Pipelined Stages.
slices are used and the maximum delay between two
registers is 3.4 ns. The first pipelined stage is inserted
after the classic multiplier, while the second stage is
located after combining all 40-bit, 41-bit, 81-bit, 82-
bit of recursive splits of the Karatsuba-Ofman multi-
plier. Note that, the FPGA technology that have been
used in Figure 8 is a 6-input LUT.
4 FPGA IMPLEMENTATION:
RESULTS AND COMPARISONS
The pipelining architectural approach is applied to the
proposed ECC core for higher speed with efficient uti-
lized area in terms of both working frequencies and
slices. Elliptic curve doubling and adding point oper-
ations are performed using a merged-improved mont-
gomery ladder scalar point multiplication algorithm.
The proposed ECC core doesn’t require any precom-
puted values or any memories for calculations, which
provides an efficient design with less slices and clock
cycles. An effective FSM is developed to control the
main ECC components, where a minimum number of
states are used for performing the merged-improved
montgomery ladder SPM. To verify performance of
the proposed SPM, our high-speed ECC core is imple-
mented over three finite fields, GF (2
163
), GF (2
233
)
and GF (2
571
) using many FPGA devices which are
High-performance Pipelined FPGA Implementation of the Elliptic Curve Cryptography over GF (2n)
21

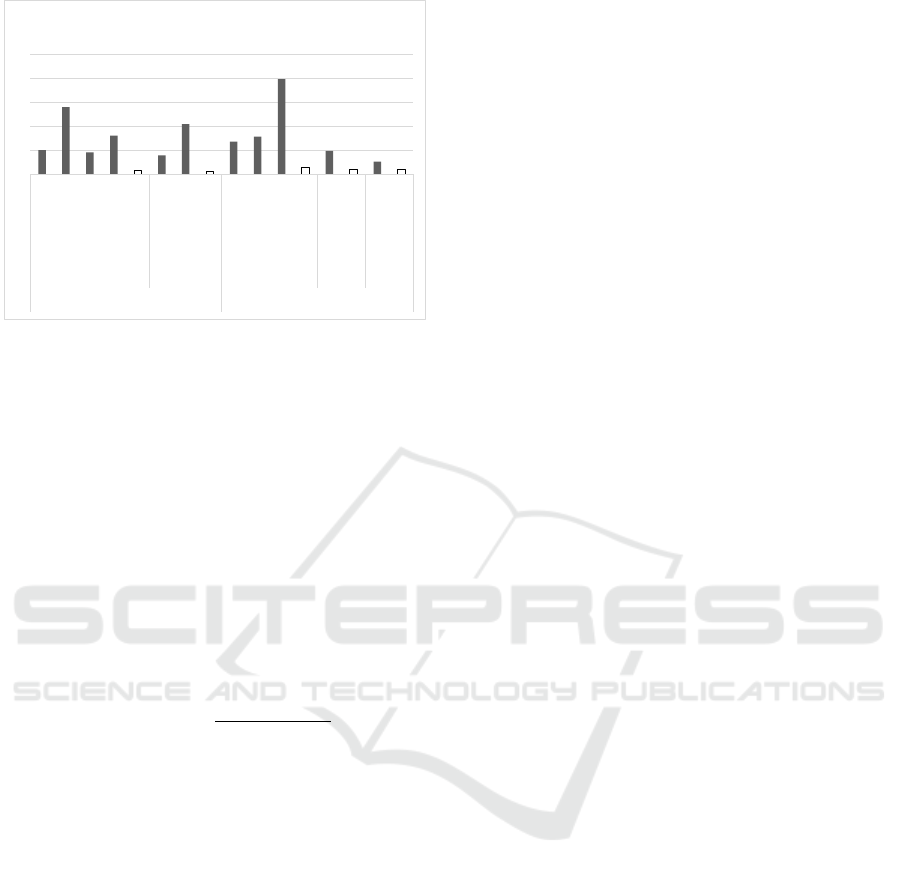
0
5
10
15
20
25
.
B. Rashidi
Z. Khan
Lijuan Li
D. Sutter
Proposed Core
.
B. Rashidi
Z. Khan
Proposed Core
B. Rashidi
Lijuan Li
D. Sutter
Proposed Core
B. Rashidi
Proposed Core
.
M Hossain
Proposed Core
Vertix-5
Virtex-7 Virtex-5 Virtex-7 Kintex-7
163
233
Time (µs)
Figure 9: Time Comparison between the Proposed High-
Speed Core and the Others.
provided by Xilinx (Przybus, 2010). Virtex-5, Virtex-
7, Kintex-7 and Artix-7 FPGA families are used to
implement the high-speed core.
The high-speed core has been synthesized, placed
and routed using Xilinx ISE 14.4 design suite (Xilinx,
2012). The optimization goal has been set to the bal-
ance strategy. A time constraint is applied for all re-
sults to achieve better area-speed ratio with zero tim-
ing error. Table 1 presents the place and route results
for the proposed high-speed ECC core. Table 2 in-
cludes our design compared with other previous ECC
hardware implementations. The efficiency is defined
as follows:
E f ficiency =
Numbero f bits
Time ·Slices
(3)
The proposed high-speed core provides higher
speed in both Virtex-7 and Kintex-7 FPGA devices,
since they are fabricated and optimized at 28nm tech-
nology (Przybus, 2010). Artix-7 device consumes
less resources which makes it well suited for the
battery-powered cell phones, automotive, commercial
digital cameras and IP cores of SoCs. The graphical
representation in Figure 9 represents the time compar-
ison between our proposed high-speed core and other
designs. As seen in Figure 9, our design has the low-
est execution time for performing a single success-
ful SPM. As shown in Table 2, the efficiency of our
proposed high-speed core outperforms the other ECC
hardware implementations. The design in (Rashidi
et al., 2016) provides higher frequencies but con-
sumes about twice the resources of the proposed core
over GF (2
163
) and using the same FPGA device.
The area-efficient hardware implementation in
(Khan and Benaissa, 2015) consumes less area than
the proposed core but requires 95% more clock cy-
cles. This large number of clock cycles comes from
writing/reading of the distributed RAM-based mem-
ory and register shift operations. In (Li and Li, 2016),
a pipelined architecture is applied to the SPM, which
achieves high performance in terms of the area and
working frequencies. However, it requires 84% ex-
tra clock cycles than our proposed clock cycles us-
ing the same device and field. Our high-speed core
achieves better efficiency than the design in (Sutter
et al., 2013). Our design has 88% less clock cycles,
33% higher frequency, 44% less slices than (Sutter
et al., 2013). Using Kintex-7 FPGA device, the de-
sign in (Hossain et al., 2015) performs on less slices
than the proposed core by 39% over GF (2
233
). Al-
though, large number of clock cycles is required for
performing single SPM. In (Hossain et al., 2015),
an iterative-based architecture is adopted by all main
SPM operations, where the binary (left-to-right) algo-
rithm is used for scalar multiplication, an interleaved
field multiplier is implemented for the multiplication
operations, and a modified Extended-Euclidian is ap-
plied for the inversion operation.
To sum up the comparisons, shifting registers, seg-
mented multipliers, or memory-based implementa-
tions results in large latency (clock cycle) as in (Khan
and Benaissa, 2015) and (Sutter et al., 2013). Itera-
tive architecture is not the efficient way for achieving
higher speeds as the work in (Hossain et al., 2015).
Pipelining architecture is more practical to apply for
achieving higher performance and maintaining the
balance between speed and area, as works (Rashidi
et al., 2016) and (Li and Li, 2016) do.
The balance in the speed-area ratio can be applied
when the optimal number of pipelined stages are in-
serted. Our high-performance ECC core uses few
slices with small latencies and high working frequen-
cies. This high-speed area-efficient ECC core makes
it very suitable to be used in different kinds of real-
time embedded systems such as cellphone banking
services, health-care monitoring using smart watches,
and accessing office networks and storage devices
while abroad.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, a high-speed area-efficient ECC core
over GF (2
n
) is proposed. Xilinx FPGA devices are
used to implement the core, where the pipelining ar-
chitecture is applied for achieving higher working
frequencies. A merged-improved montgomery lad-
der scalar point method is developed for performing
scalar multiplications (kP). Karatsuba-Ofman algo-
rithm is used for performing field multiplication op-
SECRYPT 2019 - 16th International Conference on Security and Cryptography
22

Table 1: FPGA Results of the Proposed High-Speed ECC Core: After Place and Route.
GF
Device LUTs F.Fs Slices
Clock Freq Time
Efficiency
(2
n
) Cycles (MHz) (µs)
163
Virtex-5
8,900 3,044 2,814 226 291 0.78 74584.42
233 15,672 4,333 4,585 327 217 1.51 33723.19
571 72,259 10,259 21,720 674 198 3.4 7722.93
163
Virtex-7
8,409 3,023 2,780 226 360 0.63 93397.85
233 16,003 4,323 4,762 327 310 1.05 46385.32
571 71,180 10,384 18,178 674 290 2.32 13515.38
163
Artix-7
8,417 3,016 2,693 226 191 1.18 51153.6
233 15,236 4,489 3,977 327 209 1.56 37445.44
163
Kintex-7
8,437 3,023 3,030 226 311 0.73 74028.16
233 15,221 4,483 4,915 327 309 1.06 44796.41
Table 2: Comparison between our High-Speed ECC Core and other Works over GF (2
n
).
GF
Device LUTs F.Fs Slices
Clock Freq Time
Efficiency
(2
n
) Cycles (MHz) (µs)
Rashidi
163
Vertix-5
- - 5,768 - 343 5.08 5562.87
233 - - 10,601 - 359 6.84 3213.32
163
Virtex-7
- - 5,575 - 437 3.97 7364.66
233 - - 10,528 - 496 4.913 4504.68
Khan
163
Virtex-5 3,958 1,522 1,089 4168 296 14.06 10645.71
Virtex-7 4,721 1,886 1,476 4168 397 10.51 64.47
Lijuan
163
Vertix-5
9,470 4,526 3,041 1,363 294 4.6 11652.35
233 15,296 6,559 4,762 1,926 244 7.9 6193.55
Sutter
163
Vertix-5
22,039 - 6,059 1,591 200 8.1 3321.26
233 28,683 - 8,134 2,889 145 19.9 1439.46
571 32,432 - 11,640 44,047 126 348 140.97
Hossain 233 Kintex-7 9,151 9,407 3,016 679776 255.66 2.66 29043.1
Proposed Core
163
Vertix-5
8,900 3,044 2,814 226 291 0.78 74584.42
233 15,672 4,333 4,585 327 217 1.51 33723.19
571 72,259 10,259 21,720 674 198 3.4 7722.93
163
Virtex-7
8,409 3,023 2,780 226 360 0.63 93397.85
233 16,003 4,323 4,762 327 310 1.05 46385.32
571 71,180 10,384 18,178 674 290 2.32 13515.38
163
Kintex-7
8,437 3,023 3,030 226 311 0.73 74028.16
233 15,221 4,483 4,915 327 309 1.06 44796.41
eration. Itoh-Tsuji method is applied for mapping
the LD coordinates back to the affine coordinates. In
GF (2
163
), A single scalar multiplication can be done
in 0.63µs at 360Mhz working frequency in Virtex-7
FPGA devices using 2780 slices, which is the fastest
area-efficient hardware implementation result. The
proposed ECC core was developed and evaluated us-
ing Xilinx ISE 14.4. Place and route results show our
implemented ECC core provide best performance in
terms of latency and utilized area compared to other
existing designs. The proposed ECC core would be
suitable for platforms that require efficiency in terms
of area/speed. Platforms deal with the public key
cryptosystems such as key exchange agreements in
ECDH and signing certificates in ECDS. On other
hand, our proposed ECC core can be integrated and
embedded with applications that have a security layer
in its implementations, such as image steganographic
engines. Design a separable secure image stegano-
graphic cryptosystem would be our next step in fu-
ture.
ACKNOWLEDGEMENTS
This work was supported in part by the Natural Sci-
ences and Engineering Research Council (NSERC) of
Canada and in part by the Regroupement Strategique
en Microelectronique du Quebec (ReSMiQ).
REFERENCES
Amirtharajan, R. (2014). Dual cellular automata on fpga:
An image encryptors chip. Research Journal of Infor-
mation Technology, 6(3):223–236.
High-performance Pipelined FPGA Implementation of the Elliptic Curve Cryptography over GF (2n)
23

Ansari, B. and Hasan, M. A. (2008). High-performance ar-
chitecture of elliptic curve scalar multiplication. IEEE
Transactions on Computers, 57(11):1443–1453.
Dalal, M. and Juneja, M. (2018). A robust and impercep-
tible steganography technique for sd and hd videos.
Multimedia Tools and Applications, pages 1–21.
Diffie, W. and Hellman, M. (1976). New directions in cryp-
tography. IEEE Transactions on Information Theory,
22(6):644–654.
ElGamal, T. (1985). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. IEEE
Transactions on Information Theory, 31(4):469–472.
for Standardization (ISO), I. O. (2000). Cryptographic tech-
niques based on elliptic curves.
Gallagher, P. (2013). Digital signature standard (dss). Fed-
eral Information Processing Standards Publications,
volume FIPS, pages 186–183.
Großsch
¨
adl, J. (2001). A bit-serial unified multiplier archi-
tecture for finite fields gf (p) and gf (2 m). In Inter-
national Workshop on Cryptographic Hardware and
Embedded Systems, pages 202–219. Springer.
Hankerson, D., Menezes, A. J., and Vanstone, S. (2006).
Guide to elliptic curve cryptography. Springer Sci-
ence and Business Media.
Harb, S. and Jarrah, M. (2017). Accelerating square root
computations over large gf (2m). In SECRYPT, pages
229–236.
Harb, S. and Jarrah, M. (2019). Fpga implementation of the
ecc over gf (2 m) for small embedded applications.
ACM Transactions on Embedded Computing Systems
(TECS), 18(2):17.
Hossain, M. S., Saeedi, E., and Kong, Y. (2015). High-
speed, area-efficient, fpga-based elliptic curve crypto-
graphic processor over nist binary fields. In Data Sci-
ence and Data Intensive Systems (DSDIS), 2015 IEEE
International Conference on, pages 175–181. IEEE.
Karatsuba, A. A. and Ofman, Y. P. (1962). Multiplication
of many-digital numbers by automatic computers. In
Doklady Akademii Nauk, volume 145, pages 293–294.
Russian Academy of Sciences.
Khan, Z. U. and Benaissa, M. (2015). Throughput/area-
efficient ecc processor using montgomery point mul-
tiplication on fpga. IEEE Transactions on Circuits and
Systems II: Express Briefs, 62(11):1078–1082.
Kocher, P., Jaffe, J., and Jun, B. (1999). Differential power
analysis. In Annual International Cryptology Confer-
ence, pages 388–397. Springer.
Li, L. and Li, S. (2016). High-performance pipelined archi-
tecture of elliptic curve scalar multiplication over gf
(2
m
). IEEE Transactions on Very Large Scale Integra-
tion (VLSI) Systems, 24(4):1223–1232.
L
´
opez, J. and Dahab, R. (1998). Improved algorithms for
elliptic curve arithmetic in gf (2 n). In International
Workshop on Selected Areas in Cryptography, pages
201–212. Springer.
Mahdizadeh, H. and Masoumi, M. (2013). Novel architec-
ture for efficient fpga implementation of elliptic curve
cryptographic processor over gf(2
163
). IEEE transac-
tions on very large scale integration (VLSI) systems,
21(12):2330–2333.
McGrew, D., Igoe, K., and Salter, M. (2011). Fundamen-
tal elliptic curve cryptography algorithms. Technical
Report 2018, Internet Engineering Task Force (IETF).
Miller, V. S. (1985). Use of elliptic curves in cryptogra-
phy. In Conference on the theory and application of
cryptographic techniques, pages 417–426. Springer.
Montgomery, P. L. (1987). Speeding the pollard and elliptic
curve methods of factorization. Mathematics of com-
putation, 48(177):243–264.
Moon, S. (2006). A binary redundant scalar point multipli-
cation in secure elliptic curve cryptosystems. IJ Net-
work Security, 3(2):132–137.
Percey, A. (2007). Advantages of the virtex-5 fpga 6-input
lut architecture.
Peter, S. and LangendOorfer, P. (2007). An efficient poly-
nomial multiplier in gf (2m) and its application to ecc
designs. In Design, Automation and Test in Europe
Conference and Exhibition, 2007. DATE’07, pages 1–
6. IEEE.
Przybus, B. (2010). Xilinx redefines power, performance,
and design productivity with three new 28 nm fpga
families: Virtex-7, kintex-7, and artix-7 devices. Xil-
inx White Paper.
Rashidi, B., Sayedi, S. M., and Farashahi, R. R. (2016).
High-speed hardware architecture of scalar multipli-
cation for binary elliptic curve cryptosystems. Micro-
electronics Journal, 52:49–65.
Rivest, R. L., Shamir, A., and Adleman, L. (1978). A
method for obtaining digital signatures and public-
key cryptosystems. Communications of the ACM,
21(2):120–126.
Roy, S. S., Rebeiro, C., and Mukhopadhyay, D. (2013).
Theoretical modeling of elliptic curve scalar multi-
plier on lut-based fpgas for area and speed. IEEE
Transactions on Very Large Scale Integration (VLSI)
Systems, 21(5):901–909.
Specification, P. (2006). Virtex-5 family overview.
Sutter, G. D., Deschamps, J.-P., and Ima
˜
na, J. L. (2013). Ef-
ficient elliptic curve point multiplication using digit-
serial binary field operations. IEEE Transactions on
Industrial Electronics, 60(1):217–225.
Wenger, E. and Hutter, M. (2011a). Exploring the design
space of prime field vs. binary field ecc-hardware im-
plementations. In Nordic Conference on Secure IT
Systems, pages 256–271. Springer.
Wenger, E. and Hutter, M. (2011b). Exploring the design
space of prime field vs. binary field ecc-hardware im-
plementations. In Nordic Conference on Secure IT
Systems, pages 256–271. Springer.
Xilinx, I. (2018a). Xilinx - adaptive and intelligent.
Xilinx, I. (2018b). Xilinx fpga devices, virtex, kintex, artix.
Xilinx, I. (April 24, 2012). Ise in-depth tutorial, complete
guide (ug695). Technical Report 14.1, Xilinx, Inc.
Zhou, G., Michalik, H., and Hinsenkamp, L. (2010). Com-
plexity analysis and efficient implementations of bit
parallel finite field multipliers based on karatsuba-
ofman algorithm on fpgas. IEEE Transactions on Very
Large Scale Integration (VLSI) Systems, 18(7):1057–
1066.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
24