ZKlaims: Privacy-preserving Attribute-based Credentials using
Non-interactive Zero-knowledge Techniques
Martin Schanzenbach
a
, Thomas Kilian, Julian Sch
¨
utte
b
and Christian Banse
c
Fraunhofer AISEC, Parkring 4, Garching near Munich, Germany
Keywords:
Zero-Knowledge, Attribute-based Credentials, Privacy, Identity and Access Management.
Abstract:
In this paper we present ZKlaims: a system that allows users to present attribute-based credentials in a privacy-
preserving way. We achieve a zero-knowledge property on the basis of Succinct Non-interactive Arguments of
Knowledge (SNARKs). ZKlaims allow users to prove statements on credentials issued by trusted third parties.
The credential contents are never revealed to the verifier as part of the proving process. Further, ZKlaims
can be presented non-interactively, mitigating the need for interactive proofs between the user and the verifier.
This allows ZKlaims to be exchanged via fully decentralized services and storages such as traditional peer-
to-peer networks based on distributed hash tables (DHTs) or even blockchains. To show this, we include
a performance evaluation of ZKlaims and show how it can be integrated in decentralized identity provider
services.
1 INTRODUCTION
Recent events surrounding the (ab)use of personal
identity information from social networks once again
rejuvenated the raison d’
ˆ
etre of privacy-preserving
identity management (Confessore, 2018). Classi-
cal attribute-based credential (ABC) systems such
as X.509 certificates raise privacy concerns as they
reveal potentially sensitive attribute values such as
name, age, or social relationships to the credential
verifier. In order to alleviate this issue, privacy-
preserving attribute-based credential (PP-ABC) sys-
tems have been proposed in the past (Paquin, 2011;
Camenisch and Van Herreweghen, 2002). PP-ABCs
rely on zero-knowledge protocols to prove statements
over attributes, rather than revealing the attribute val-
ues themselves. Some systems require that prover and
verifier must engage in an interactive proving proto-
col which implies that prover and verifier must be on-
line whenever a credential verification is performed.
Other approaches remedy this issue by requiring that
proofs of statements are predefined by the credential
issuer. This inevitably requires the prover to inter-
act with the issuer or verifier whenever a genuinely
new statement is required. Both properties are partic-
a
https://orcid.org/0000-0001-6153-504X
b
https://orcid.org/0000-0002-3007-6538
c
https://orcid.org/0000-0002-4874-0273
ularly problematic in decentralized identity manage-
ment systems where centralized identity services are
replaced by peer-to-peer attribute provisioning.
Recent advancements in the area of non-
interactive verifiable computation schemes and the
emergence of novel decentralized architectures such
as blockchains have paved the way for a new gen-
eration of decentralized, privacy-preserving identity
and access management (Kraft, 2017; Schanzenbach
and Banse, 2016; Schanzenbach et al., 2018; Friebe
et al., 2018). A common component in such systems
is a decentralized directory service used to provision
user attributes and credentials. Such services are re-
alized as a secure, shared storage medium such as a
blockchain or secure name system. In order to fully
leverage PP-ABCs, users must be able to present them
non-interactively over the shared medium. Hence, to
combine the privacy benefits of PP-ABCs with the
privacy advantages of decentralized identity manage-
ment, non-interactive PP-ABCs are necessary.
Our contribution is ZKlaims, a design and imple-
mentation for non-interactive, privacy-preserving cre-
dentials through the use of zero-knowledge proofs.
ZKlaims allows users to act as provers and create
proofs for any self-chosen statement over a creden-
tial issued to them without having to interact with an-
other party. This allows us to integrate ZKlaims into a
fully decentralized architecture where non-interactive
PP-ABCs are provisioned in a resilient, decentralized
Schanzenbach, M., Kilian, T., Schütte, J. and Banse, C.
ZKlaims: Privacy-preserving Attribute-based Credentials using Non-interactive Zero-knowledge Techniques.
DOI: 10.5220/0007772903250332
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 325-332
ISBN: 978-989-758-378-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
325

Figure 1: Actors and protocol primitives in a ZKlaims use case.
delivery mechanism. The core building blocks of our
design are zero-knowledge succinct non-interactive
arguments of knowledge (zkSNARKs). We present an
evaluation of our implementation discussing the space
and time tradeoffs of such a system. To illustrate the
use of ZKlaims, we show how it can be integrated into
a decentralized personal data sharing system.
2 BACKGROUND
zkSNARKs are a theoretical class of proofs which
satisfy a specific set of formal properties in order
to realize a non-interactive zero-knowledge (NIZK)
proof (Ben-Sasson et al., 2013). Its origin lies in the
area of verifiable computation (VC) schemes. There
are two actors in VC: The prover and the validator.
Respective schemes allow to prove the correct eval-
uation of a function given a set of inputs. This is
commonly advantageous in use cases where compu-
tation is offloaded onto a third party because the ac-
tual computation is resource-intensive. In this con-
text, verifiable computation schemes are usually engi-
neered to provide an efficient way to verify computa-
tion results and put less emphasis on the efficiency on
the evaluation and proving processes. In zkSNARKs,
the idea is that such schemes can easily be extended
to add a zero-knowledge aspect to the computation:
The verifier of the computation must be able to verify
the proof (i.e. the result of the computation) with-
out a private “witness” input. The “witness” is only
known to the prover, which is the entity that per-
forms the computation. Popular verifiable computa-
tion schemes which allow to build zkSNARK proofs
include Pinocchio and a scheme by Groth et al. (Parno
et al., 2013; Groth, 2016). The idea behind both ap-
proaches is that the verification of a result does not
require the function input. Hence, the verifier is able
to verify a computation result without knowledge of
what was actually the subject of the computation.
In the following, we define the functions and ob-
jects of a NIZK system, consisting of a setup, cre-
dentials definition, circuit construction, proof gener-
ation, verification, and a delivery mechanism. We
generalize the following high-level primitives of a zk-
SNARKs scheme:
Setup(ϕ) → (pk,vk) (1)
Prove(pk, ~a,~x) → π (2)
Veri f y(vk,π,~x) → {FALSE, T RUE} (3)
Initially, we must establish a “constraint system”
ϕ. A constraint system is a set of linear constraints
which are internally translated into circuits by the zk-
SNARK scheme. The constraint system is a blueprint
that allows us to define ground truths and derive the
proving key pk and verification key vk using a Setup()
procedure. The constraint system – and consequently
both pk and vk – are public information and are meant
to be known by prover and verifier, respectively. For
a constraint system to be useful in our design, it must
be constructed in a way that supports proofs on cre-
dentials. In order to achieve this, we define the setup
and constraint system construction in the design sec-
tion of this paper.
In order to generate a proof π, the prover must
supply the proof input vectors ~x and ~a as well as the
proving key pk. While ~x is a public parameter, ~a is
private and only known to the prover. To validate the
proof π, a verifier uses the verification key vk and the
public input vector~x as inputs to the validation proce-
dure. The verification result is either valid (TRUE) or
invalid (FALSE).
In the following, we use the above definitions of
a zkSNARK scheme in order to formalize the non-
interactive credential system ZKlaims.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
326

3 DESIGN
In the following, we present our design of ZKlaims
which satisfies the following three requirements:
Statements on Credentials: ZKlaims must al-
low users to generate proofs on third party issued cre-
dentials. The user must be allowed to freely choose
the statement. The verifier must be able to verify that
the statement is true with respect to the third party is-
sued credential without the knowledge of the actual
credential value.
Non-interactive Presentation: ZKlaims must al-
low verifiers to prove the correctness of a statement
non-interactively, e.g. without online interaction with
the user or the credential issuer.
Selective Disclosure: The user should have the
option to selectively disclose credential values if nec-
essary.
First, in addition to the prover and verifier we de-
fine a third actor: The credential issuer. The issuer
is a trusted third party that is issuing attribute-based
credentials (ABCs) to users which take the role of
provers. The credential contents are private and rep-
resent the private input vector ~a of the proving pro-
cedure. The prover is able to make any statement
regarding its issued credentials and create a proof π
which asserts that the statement is valid. The veri-
fier is an entity which requires the prover to prove the
validity of a certain statement. In our use case, this
statement is based on a specific attribute-based cre-
dential. The proof π is zero-knowledge in that the
verifier only learns whether or not the statement on
a credential is valid. The contents of the credential
are not disclosed to the verifier. Figure 1 illustrates
our scenario including the generation of the keys, a
proof and its verification. We use this illustration in
the following sections to explain the design and usage
of ZKlaims.
3.1 Attributes and Credentials
First, we define a ZKlaims credential C := (~a,~y, S).
We define the input vectors ~a and ~y as bit vectors:
~a :=~a
0
| .. . | ~a
n
where ~a
i
∈ {0,1}
∗
(4)
~y :=
~
h
0
| .. . |
~
h
n
where
~
h
i
= hash(a
i
) (5)
~y is the first and static part of the public input vector~x.
The other part of the input vector is variable and may
be chosen by the user as part of the proving process. It
is comprised of issuer-asserted user identity attributes
such as date of birth or email address. S is a signature
over ~y and is created by the issuer. The signature is
created through traditional public-key cryptography.
This allows a verifier to establish trust from their set
of trusted, third party credential issuers to the creden-
tial C and verify its authenticity.
We note that ~a contains n + 1 elements but there
are only n attributes while the last element is reserved.
This is a design choice for the following reason: We
define the last element ~a
n
to be a unique identifier of
the credential. It is a random nonce generated by the
credential issuer when the credential ~y is issued. The
nonce ensures that the credential is unique across sub-
jects even if their attributes ~a are the same.
We expect an issuer to provide a mechanism that
allows the user to retrieve credentials C through a
secure communication channel. This transfer is out
of scope of this work, but for web-based use cases
it can be realized through a traditional TLS channel
in combination with password-based user authentica-
tion. Then, the transfer of the credential from the is-
suer to the user can be performed through a simple
download procedure. The user then stores the creden-
tial in a wallet on a local storage under their control.
3.2 Constraint System and Keys
As discussed in the background section, we must de-
fine a “constraint system” ϕ. The entity responsible
for creating the constraint system is the credential is-
suer because it is the entity which is authoritative over
what kinds of attribute credentials it plans to issue to
its users. A ZKlaims constraint system ϕ
zklaim
must
be setup so that it enables a prover to prove statements
on credentials in the form C .
Figure 2 illustrates our circuit construction.
Constraint systems process input variables in an
algebraic circuit and output a boolean return value.
Hence, it is possible to combine multiple constraint
systems into one new constraint system. In our de-
sign, we define the linear constraint system ϕ
zklaim
as
a combination of n + 1 sub constraint systems:
ϕ
zklaim
:= ϕ
hashCompare
∧ (
n
^
i=0
ϕ
i
predCompare
) (6)
The hashCompare constraint allows the prover to
verify that the user provided private input vector ~a
matches the credential C contents. The second class
of constraint systems are used to model, prove and
verify comparative statements on the private input
~a. For this the issuer must pre-determine the num-
ber n of attributes that ~a may contain as it deter-
mines the upper bound of sub constraint systems of
type ϕ
predCompare
. As illustrated in Figure 2, each
ϕ
i
predCompare
constraint takes exactly one a ∈ ~a as in-
put whereas the ϕ
hashCompare
constraint system takes
the whole input vector ~a. As constraint systems are
ZKlaims: Privacy-preserving Attribute-based Credentials using Non-interactive Zero-knowledge Techniques
327

Figure 2: ZKlaims constraint system ϕ
zklaim
.
rigid in this regard, a change in the number of at-
tributes requires a regeneration of the constraint sys-
tem ϕ
zklaim
.
3.3 Proving
Using ϕ
zklaim
any entity is able to generate the pub-
lic proving key pk and verification key vk using
the respective Setup() procedure of the zkSNARKs
scheme. The key pk is used by the user in order to
prove the validity of statements on their attribute cre-
dentials. Each ϕ
i
predCompare
may be used by the prover
to impose a predicate ~p
i
with respect to a reference
value~r
i
. The hashed attribute references in~y are com-
bined with the above into the public proof input vector
~x:
~x :=~y | ~p |~r (7)
By default, each ~p
i
is initialized as a no-op dummy
operation which always evaluates to true. In order to
create a statement on an attribute ~a
i
, the user sets the
predicate ~p
i
to any combination of <, = and > or
their respective complements ≮, 6=, ≯. This predicate
is used in combination with a reference value~r
i
which
contains a value that the corresponding attribute ~a
i
is
to be checked against with the predicate ~p
i
. As an ex-
ample, to create a proof input which is supposed to
verify that a user is born before a certain data, the ref-
erence value ~r
i
for the “data of birth” attribute would
be set to a certain timestamp in the past which reflects
the age barrier. The position n of the reference value is
defined by issuer through the constraint system. The
predicate is set to ≮. Such a proof input ~p allows
users to prove that they are over a certain age.
In general, ~p can be chosen arbitrarily by a prover.
However, ϕ
hashCompare
is used to import the require-
ment that any prover must be able to provide a witness
in the form of a pre-image to ~y, namely ~a. As already
mentioned above, ~a – and in particular a ∈ ~a – serves
as a secret that the prover must present in the proving
process as part of a witness to the ϕ
hashCompare
con-
straint. Hence, only the subject which is in possession
of a credential C from the issuer is able to satisfy the
constraint system.
In order to validate a proof π, the prover must ap-
ply the public proof input ~x, the proving key pk as
well as the private input vector ~a to satisfy the con-
straint system ϕ
zklaim
and generate a proof π. The user
generates a proof as follows:
π ← Prove(pk,~a,~x) (8)
The user is able to provide the hashes in ~y and
the pre-image ~a from the credential C to satisfy the
ϕ
hashCompare
constraint system. The public input vec-
tor~x is built using~y, the predicate inputs vector ~p and
the reference value vector~r which represent the state-
ments made by the user on the attributes in ~a. We
expect that the predicates are defined a priori, for ex-
ample, through a negotiation between the verifier and
the user. The verifier can request from the user to pro-
vide a specific proof including certain predicates and
thus defines the respective predicate variables ~p and
~r .
SECRYPT 2019 - 16th International Conference on Security and Cryptography
328

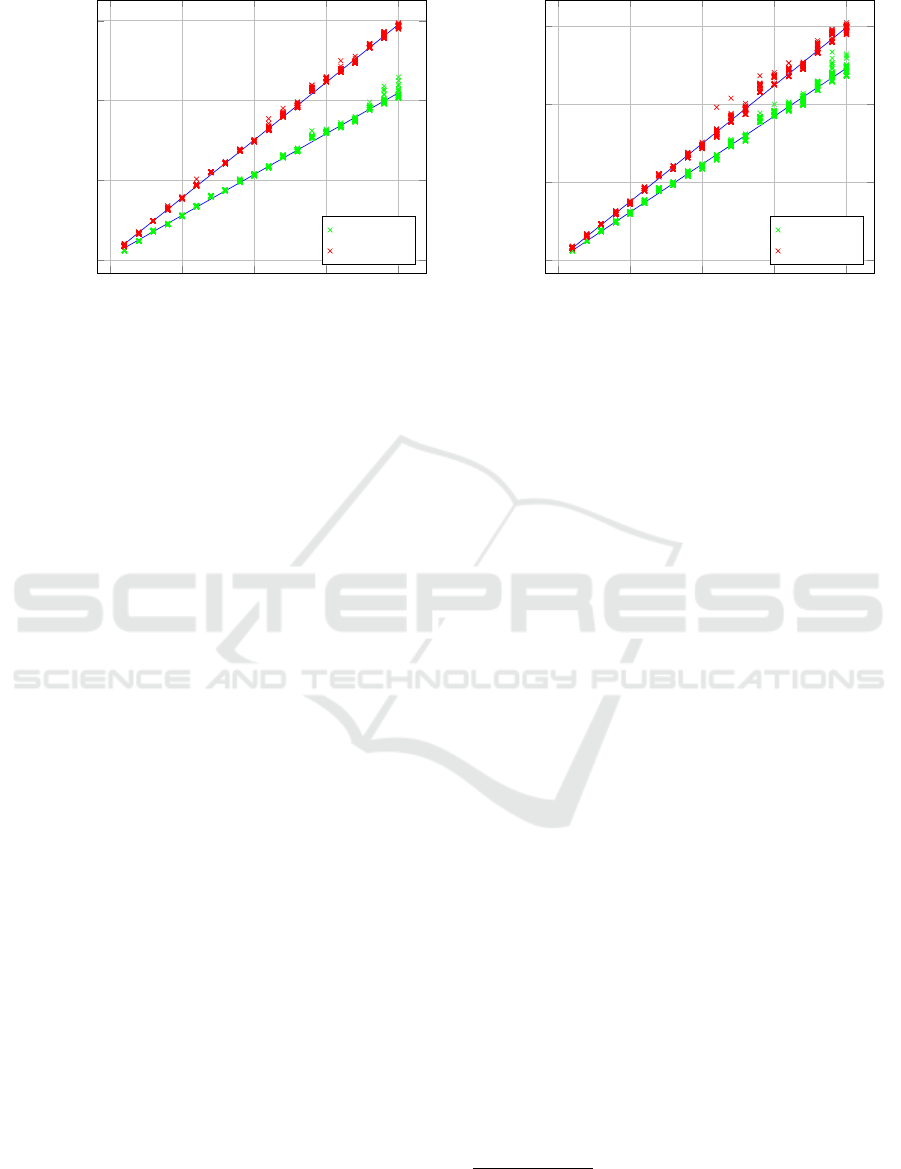
0 5 10 15 20
0
2
4
6
·10
4
Number of payloads
milliseconds
Groth
Pinocchio
0 5 10 15 20
0
2
4
6
·10
4
Number of payloads
milliseconds
Groth
Pinocchio
Figure 3: Left: time required to derive verification key vk & proving key pk from the constraint system ϕ
zklaim
. Right: time
required to create proof π depending on the number of attribute payloads.
After the user calculates the proof π, it can be pre-
sented to a verifier along with~x. We define a ZKlaims
context (π,~x, S) which – due to the non-interactive na-
ture of the proof – can be persisted by the user and
non-interactively retrieved and verified by a verifier.
3.4 Verification
It is not necessary for a verifier to directly interact
with the prover to verify a proof π. However, upon
retrieving the ZKlaims context (π,~x, S) and before the
verification of π, the verifier must verify the signature
S over ~y | y
i
∈ ~x. Using this information, the prover
proceeds to retrieve the correct proving key pk from
the trusted issuer and uses it to verify the proof π:
result ∈ {FALSE,T RU E} ← Veri f y(vk, π,~x) (9)
The verification function yields T RU E if the user
was able to provide inputs to ϕ
zklaim
that satisfy the
underlying constraint systems. It is essential that veri-
fiers check that the predicate inputs and reference vec-
tors ~p and ~r, which are provided by the user as part
of the ZKlaims context, are semantically what they
expect them to be. Especially if the verifier specif-
ically requested a predicate to be proven, such as
“age ≥ 18”, the respective predicate (greater or equal)
as well as input variable to check against must be cor-
rectly set.
4 IMPLEMENTATION AND
EVALUATION
Our reference implementation
1
is built on top of the
libsnark
2
library. zkSNARKs are based on verifiable
computation schemes. While libsnark supports a va-
riety of different schemes including Pinocchio (Parno
et al., 2013) we use the scheme of Groth (Groth, 2016)
which is also readily available. We settled on Groth
because it exhibits better performance than the other
schemes available in libsnark.
4.1 Performance and Evaluation
We evaluated the performance of ZKlaims for issuing,
proving and verification with respect to the number of
attributes in a single credential. Due to technical lim-
itations imposed by the underlying constraint system
we must use fixed size inputs to the constraint sys-
tem. We define a collection of attributes that fits into
a single input as a payload. In our implementation, a
single payload can hold up to five attributes. Our test
setup consisted of an Intel Core i7 7500U 3.2 GHz
with 16 GB of RAM. In Figure 3 we can see that the
time it takes to construct the issuer constrain system
increases linearly with the number of attribute pay-
loads in our credential. It takes roughly 2.5 seconds to
build a constraint system that supports five attributes
in a single payload and increases by the same amount
for every additional set. The time it takes a prover
to construct a proof depending on the amount of pay-
1
https://gitlab.com/kiliant/zklaim, accessed 2019/01/08
2
https://github.com/scipr-lab/libsnark, accessed
2019/01/08
ZKlaims: Privacy-preserving Attribute-based Credentials using Non-interactive Zero-knowledge Techniques
329

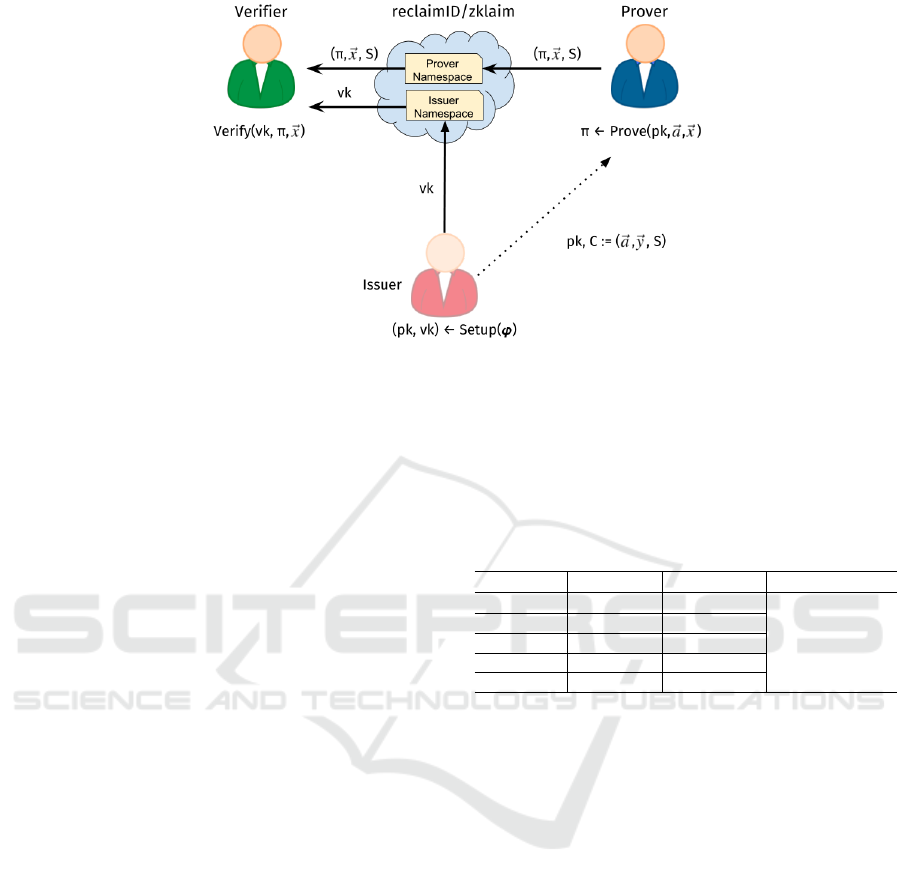
Figure 4: ZKlaims integration with the reclaimID identity provider.
loads defined by the issuer constraint system can be
found in Figure 3. We can see that just like the initial
construction of the constraint system, proof construc-
tion time also increases linearly with the number of
payloads. Creating a proof in the case of a single pay-
load takes roughly 2.4 seconds and increases by the
same amount for every additional set.
While we evaluated the time it takes the verifier to
validate proofs, the results suggest that the impact is
negligible: In ZKlaims, proof verification is simply a
matter of evaluating a polynomial function, measured
times range below 10 milliseconds. The issuer con-
straint system needs to be created only once at the
beginning. Proofs need to be constructed every time
a verifier has a new request regarding the predicates
it needs proven. Once a proof for a combination of
predicates exists, it can be stored and presented non-
interactively to any concerned verifier. In addition to
the evaluation of performance, we also assessed the
size of proving and verification keys as well as proof
size dependent on the number of payloads. The re-
sults can be found in Table 1, where we find that the
minimum size of a proving key is roughly 8.65 MB.
With every payload – i.e. every set of five attributes –
supported by the issuer constraint system, the proving
key increases in size by around 7 to 9 MB. At 20 pay-
loads, this results in a 174.51 MB proving key. Due
to this size constraint, issuers should either limit the
number of supported attributes or bootstrap dedicated
constraint systems so that a prover is only required to
handle proving keys for attributes actually relevant to
them. At the same time, the verification key takes a
minimum of 784 bytes and increases by 150 to 200
bytes per payload.
In summary, the bulk of the space and time re-
quired in ZKlaims must be provided by the prover.
Proofs itself are of constant size at 137 bytes which is
good news with respect to the required storage foot-
print. We can safely consider that most decentral-
ized storage systems are capable of accommodating
ZKlaims proofs.
Table 1: Key and proof sizes depending on the number of
payloads.
Payloads pk in MB vk in bytes Proof in bytes
1 8.65 784
5 43.15 1543
10 86.94 2493 137
15 133.37 3443
20 174.51 4436
4.2 Integration
We designed ZKlaims to specifically for decentral-
ized identity provider services that require or support
non-interactive presentation of identity attributes. To
publish and propagate ZKlaims objects such as the
issuer credential system, verification key and proofs,
we propose the use of secure, decentralized iden-
tity provider systems based on name systems such as
NameID (Kraft, 2017) and reclaimID (Schanzenbach
et al., 2018).
NameID (Kraft, 2017), is a blockchain-based
identity system that allows users to share identity at-
tributes over the namecoin blockchain. It features a
standards-compliant delivery mechanism – OpenID
Connect (Sakimura et al., 2014) – but relies on a
central rendezvous server. The nature of both the
OpenID Connect and blockchain architecture requires
that identity attributes can be presented without direct
interaction between users and relying parties. This is
partly due to the server-based architecture of OpenID
Connect but also a technical caveat of distributed
ledgers. In NameID, a central service in the form of
SECRYPT 2019 - 16th International Conference on Security and Cryptography
330

an OpenID Connect server enforces access control de-
cisions made by users.
An alternative to NameID is re-
claimID (Schanzenbach et al., 2018), which uses the
decentralized GNU Name System (GNS) (Wachs
et al., 2014a; Wachs et al., 2014b). reclaimID allows
users to be completely sovereign over their own
identities and selectively authorize access to identity
attributes using attribute-based encryption (ABE).
This approach mitigates the issue of public records
in the blockchain that we find in NameID. reclaimID
provides a fully decentralized storage and resolution
mechanism for identity attributes. It enables relying
parties, in our case represented by verifiers, to access
identity attributes without interacting with a trusted
third party or the user. Like NameID, reclaimID
also features an OpenID Connect layer to allow
standards-compliant integration into web services but
does so without the use of a central server. Instead,
client-side software is used to emulate the OpenID
Connect service on top the decentralized service
infrastructure.
We have decided to integrate ZKlaims into re-
claimID due its more decentralized nature and some
glaring shortcomings of NameID, such as public at-
tribute records. Given the strict size constraints of
proving and verification keys, due to technical con-
straints of name systems we assume that verification
keys must be exchanged out-of-band. However, since
the authority over the issuer constraint system – and
with it the keys – is the issuer itself and keys can be
presumed to rarely change, out-of-band distribution
using traditional means such as web servers is fea-
sible. On the other hand, distributing credentials and,
more importantly, proofs using any of the above name
system-based delivery systems is certainly possible.
Users create proofs and authorize verifiers to retrieve
and verify them from the name system in an efficient,
completely decentralized fashion.
In our implementation, the issuer publishes the
ZKlaims constraint system ϕ, the verification key vk
and the proving key pk in GNS. This record is pub-
lished in a namespace which is owned by the issuer.
This allows any prover to retrieve the issuer’s con-
straint system and proving key and to verify its in-
tegrity and use it as inputs in proving and verifica-
tion procedures. Figure 4 illustrates the integration
of ZKlaims with the reclaimID identity provider. The
prover shares the proving context including the proof
π, the proof input~x and the credential signature S with
the verifier over reclaimID. This is done by having the
prover store the proving context as an attribute record
in reclaimID. This attribute is shared with a verifier
through an out-of-band authorization protocol such as
OpenID Connect. Our reference implementation can
be found online as part of the GNUnet peer-to-peer
framework
3
.
5 RELATED WORK
U-Prove is a digital credential technology that allows
a prover to selectively disclose claims issued by an
issuer to a verifier (Paquin, 2011). The prover can
choose which claims to present to the verifier and
which to withhold. Our approach differs from U-
Prove in that it allows the prover to create a claim
using a predicate without interaction with the issuer.
For example, in U-Prove for provers to prove to an
issuer that they are “over 18 years old”, they must re-
quest this statement as part of a U-Prove token from
the issuer. In our design, the prover only requests the
attribute – e.g. “is 24 years old” – as claim from the
issuer. The prover can use this attribute to create arbi-
trary proofs using predicates based on this claim such
as “is not 20 years old”, “is 24 years old” or “is over
18 years old”.
Identity Mixer (Idemix) is another sophisticated
credential system that apart from PP-ABCs also pro-
vides anonymity (Camenisch and Van Herreweghen,
2002). It is already quite mature in that it already in-
cludes features such as attribute predicates, revocation
and selective disclose of attributes. Further, Idemix
allows a verifier to request disclosure of an attribute
from the issuer. What Idemix does not feature, is a
non-interactivity property. As such, “offline” presen-
tation of a credential to a verifier is not possible by de-
sign. What Idemix gains from this restriction, is that
a presented proof cannot be re-used by the verifier to,
e.g., impersonate the prover using the proof that was
presented to them. This feature is only really relevant
if the anonymity feature is also desired. Currently, our
system does not feature anonymity, so interactive ses-
sions between verifier and prover can be assumed to
be authenticated. The prover authentication can then
be bound to the credentials in question, for example
through an attribute holding their public key.
The authors of UnlimitID, propose the use
of algebraic MACs for privacy-preserving creden-
tials (Isaakidis et al., 2016). They propose a system
which allows users to create pseudonyms in order to
make it impossible for the IdP to track users across
relying parties. UnlimitID supports the selective dis-
closure of user attributes. However, it does not allow
the user to prove the correctness of statements on cre-
dentials without disclosing the credential value itself.
3
https://gnunet.org/git/gnunet.git/tree/src/zklaim?h=zkl
aim, accessed 2019/02/13
ZKlaims: Privacy-preserving Attribute-based Credentials using Non-interactive Zero-knowledge Techniques
331

6 SUMMARY AND FUTURE
WORK
In this paper we have presented ZKlaims, a design for
non-interactive privacy-preserving credentials based
on a non-interactive zero-knowledge protocol. We
have shown how zkSNARKs can be leveraged for de-
centralized identity provider services. We conducted
performance evaluations of ZKlaims to show that is
can be used in practice and where integrators must ac-
commodate for additional resources. Finally, we have
integrated our ZKlaims implementation into the de-
centralized identity provider reclaimID. This means
improved privacy for reclaimID users if they choose
to share ZKlaims proofs as attributes while at the
same time providing relying parties with strong as-
sertions by trusted third parties.
As a next step, we plan to address shortcomings
with current authorization protocols such as OpenID
Connect with respect to complex credentials such as
ZKlaims. OpenID Connect does not specify how re-
lying parties can request special credential types such
as certificates, ZKlaims or other third party asserted
attributes. This is due to the fact that the protocol
was not originally designed to be implemented on
top of decentralized infrastructures. However, in the
wake of self-sovereign identity systems (Kraft, 2017;
Schanzenbach et al., 2018; Sovrin, 2018), this is a
challenge in need of further research and develop-
ment.
In future work we also plan to investigate how
ZKlaims can be used in the Internet of Things. Specif-
ically, we plan on investigating how device can dis-
close metadata such as firmware versions to request-
ing parties in a minimal way. This could allow ser-
vices to query large fleets of devices for vulnerable
firmware versions without having all devices explic-
itly disclose the exact versions they run on.
ACKNOWLEDGMENTS
This work was partially funded by the Fraunhofer
Cluster Cognitive Internet Technologies.
REFERENCES
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., and
Virza, M. (2013). Snarks for c: Verifying program
executions succinctly and in zero knowledge. In Ad-
vances in Cryptology–CRYPTO 2013, pages 90–108.
Springer.
Camenisch, J. and Van Herreweghen, E. (2002). Design and
implementation of the idemix anonymous credential
system. In Proceedings of the 9th ACM conference on
Computer and communications security, pages 21–30.
ACM.
Confessore, N. (2018). Cambridge analytica and facebook:
The scandal and the fallout so far, the new york times.
Friebe, S., Sobik, I., and Zitterbart, M. (2018). Decentid:
Decentralized and privacy-preserving identity storage
system using smart contracts. In 2018 17th IEEE In-
ternational Conference On Trust, Security And Pri-
vacy In Computing And Communications (TrustCom),
pages 37–42.
Groth, J. (2016). On the size of pairing-based non-
interactive arguments. In Annual International Con-
ference on the Theory and Applications of Crypto-
graphic Techniques, pages 305–326. Springer.
Isaakidis, M., Halpin, H., and Danezis, G. (2016). Unlim-
itid: Privacy-preserving federated identity manage-
ment using algebraic macs. In Proceedings of the 2016
ACM on Workshop on Privacy in the Electronic Soci-
ety, pages 139–142. ACM.
Kraft, D. (2017). Nameid. https://nameid.org/.
Paquin, C. (2011). U-prove technology overview v1. 1. Mi-
crosoft Corporation Draft Revision, 1.
Parno, B., Howell, J., Gentry, C., and Raykova, M. (2013).
Pinocchio: Nearly practical verifiable computation. In
Security and Privacy (SP), 2013 IEEE Symposium on,
pages 238–252. IEEE.
Sakimura, N., Bradley, J., Jones, M., de Medeiros, B., and
Mortimore, C. (2014). Openid connect core 1.0 incor-
porating errata set 1. http://openid.net/specs/openid-
connect-core-1
0.html.
Schanzenbach, M. and Banse, C. (2016). Managing and
presenting user attributes over a decentralized secure
name system. In Data Privacy Management and Se-
curity Assurance - 11th International Workshop, DPM
2016, September 26-27, 2016, Proceedings, pages
213–220.
Schanzenbach, M., Bramm, G., and Sch
¨
utte, J. (2018). re-
claimid: Secure, self-sovereign identities using name
systems and attribute-based encryption. In Proceed-
ings of the International Conference on Trust, Secu-
rity and Privacy in Computing and Communications
(TrustCom).
Sovrin (2018). A protocol and token for self-sovereign
identity and decentralized trust. https://sovrin.org/wp-
content/uploads/2018/03/Sovrin-Protocol-and-Token-
White-Paper.pdf, 2019/02/02.
Wachs, M., Schanzenbach, M., and Grothoff, C. (2014a). A
censorship-resistant, privacy-enhancing and fully de-
centralized name system. In Cryptology and Network
Security, pages 127–142. Springer.
Wachs, M., Schanzenbach, M., and Grothoff, C. (2014b).
On the feasibility of a censorship resistant decentral-
ized name system. In Foundations and Practice of
Security, pages 19–30. Springer.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
332