Optimal Filtering Algorithm based on Covariance Information using a
Sequential Fusion Approach
R. Caballero-
´
Aguila
1 a
, A. Hermoso-Carazo
2 b
and J. Linares-P
´
erez
2 c
1
Departamento de Estad
´
ıstica e I.O., Universidad de Ja
´
en, Campus Las Lagunillas s/n, 23071 Ja
´
en, Spain
2
Departamento de Estad
´
ıstica e I.O., Universidad de Granada, Campus Fuentenueva s/n, 18071 Granada, Spain
Keywords:
Sequential Fusion Filtering, Random Parameter Matrices, Cross-correlated Noises, Covariance-based
Estimation, Sensor Networks.
Abstract:
The least-squares linear filtering problem is addressed for discrete-time stochastic signals, whose evolution
model is unknown and only the mean and covariance functions of the processes involved in the sensor mea-
surement equations are available instead. The sensor measured outputs are perturbed by additive noise and
different uncertainties, which are modelled in a unified way by random parameter matrices. Assuming that, at
each sampling time, the noises from the different sensors are cross-correlated with each other, the sequential
fusion architecture is adopted and the innovation technique is used to derive an easily implementable recursive
filtering algorithm. A simulation example is included to verify the effectiveness of the proposed sequential
fusion filter and analyze the influence of the sensor disturbances on the filter performance.
1 INTRODUCTION
Due to the progress of engineering, computer sci-
ence and technology, multisensor systems are exten-
sively used with different purposes in a large variety
of fields, such as target tracking, navigation guidance
or process monitoring and surveillance, among oth-
ers. These applications demand the necessity of effi-
ciently using all the information contained in the mul-
tiple sets of available data, coming from the differ-
ent sensors, which must be used to estimate the signal
of interest. In general, the application of suitable in-
formation fusion techniques in sensor networks pro-
vide more accurate estimations and more specific in-
ferences than traditional single-sensor systems. As
it is well known, the centralized fusion method pro-
vides optimal estimators, but suffers from heavy com-
putational burden and low sensitivity, while the dis-
tributed fusion architecture is more robust and flexi-
ble, but provides less accurate estimators in general.
The sequential fusion method, where the estimator is
updated by processing the sensor data one at a time
in a sequential way (instead of processing them as
a whole vector), overcomes these issues, achieving
a
https://orcid.org/0000-0001-7659-7649
b
https://orcid.org/0000-0001-8120-2162
c
https://orcid.org/0000-0002-6853-555X
the same estimation accuracy but a lower computa-
tional cost than the centralized one. For this reason,
the sequential fusion estimation problem in multisen-
sor systems is currently an active research topic (Feng
et al., 2018), (Lin and Sun, 2018), (Wen et al., 2013),
(Yan et al., 2013).
Assuming that, apart from the additive noises,
there are no uncertainties in the sensor measurements
and they are sent to the processing center over per-
fect transmissions, there exists a rich literature about
sequential estimation (see e.g., (Wen et al., 2013),
(Yan et al., 2013) and references therein). Neverthe-
less, the presence of random disturbances (stochastic
parameter perturbations, missing or fading measure-
ments, multiplicative noise, etc.) in the sensor output
measurements is usually unavoidable, due to network
bandwidth limitations or communication channel in-
accuracies (see (Hu et al., 2017), (Li et al., 2017),
(Caballero-
´
Aguila et al., 2017), (Liu et al., 2016) and
(Wang and Sun, 2017), among others). The use of
measurement models with random parameter matri-
ces provides a comprehensive framework to deal with
these uncertainties and the design of estimation algo-
rithms in this class of system models has aroused the
interest of the scientific community over the last few
years (see (Caballero-
´
Aguila et al., 2018), (Caballero-
´
Aguila et al., 2019), (Hu et al., 2013), (Sun et al.,
2017) and references therein).
Caballero-Águila, R., Hermoso-Carazo, A. and Linares-Pérez, J.
Optimal Filtering Algorithm based on Covariance Information using a Sequential Fusion Approach.
DOI: 10.5220/0007786405870594
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 587-594
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
587

Furthermore, practical applications usually in-
volve measurement noises that are correlated across
sensors ((Li et al., 2017), (Sun et al., 2017), (Wang
and Sun, 2017)) and, also, noise cross-correlation can
arise in the process of discretization of continuous-
time systems (Li, 2003), or after the transformation of
systems with random delays or packet-dropouts (Zhu
et al., 2013).
To the best of the authors’ knowledge, most se-
quential fusion estimation algorithms existing in the
literature require the knowledge of the signal evolu-
tion model. Hence, the use of covariance informa-
tion instead is a novelty and an interesting research
challenge. Motivated by the above considerations, our
aim in this paper is to design a covariance-based se-
quential fusion algorithm for the least-squares linear
estimator of a stochastic signal measured by a mul-
tisensor network, when the sensor outputs are per-
turbed by: 1) stochastic uncertainties modelled by
independent random parameter matrices and 2) addi-
tive noises modelled by cross-correlated random se-
quences.
The rest of the paper is organised as follows. In
Section 2, the observation model and the hypotheses
about the stochastic processes involved are described.
The innovation technique, which will be used to de-
rive the estimation algorithm, is detailed in Section 3.
The sequential fusion filtering algorithm is presented
in Section 4, together with the formulas of the esti-
mation error covariance matrices. In Section 5, the
feasibility and effectiveness of the proposed sequen-
tial filter is verified by a computer simulation exam-
ple. Finally, some concluding remarks are drawn in
Section 6.
Notation: R
n
denotes the n-dimensional Euclidean
space and R
n
1
×n
2
the set of all n
1
× n
2
real matrices.
For a vector ξ or a matrix Φ, we denote by ξ
T
and Φ
T
their transposes, and by Φ
−1
to the inverse of Φ. If
the dimensions of a vector or a matrix are not explic-
itly stated, they are assumed to be compatible with al-
gebraic operations. I and 0 denote the identity matrix
and the zero matrix, respectively. Finally, δ
k,h
denotes
the Kronecker delta function which is equal to one, if
k = h, and zero otherwise.
2 OBSERVATION MODEL
This paper is concerned with the optimal least-squares
(LS) linear estimation problem, using the sequential
fusion technique, for discrete-time random signals
from multisensor measurements with uncertainties
described by random parameter matrices and cross-
correlated sensor additive noises.
Let us consider a second-order signal process
whose evolution model is unknown and only infor-
mation about its second-order statistical properties is
available; namely, its mean and covariance functions
are assumed to be known.
More specifically, consider a networked system
with m sensor nodes which, at each sampling time,
k ≥ 1, and for each i = 1,... ,m, provide measured
outputs, z
(i)
k
∈ R
n
z
, of the signal vector, x
k
∈ R
n
x
, ac-
cording to the following observation model (see e.g.
(Caballero-
´
Aguila et al., 2016)):
z
(i)
k
= H
(i)
k
x
k
+ v
(i)
k
, k ≥ 1; i = 1, ...,m, (1)
on which the following hypotheses are imposed:
(a) The signal process,
{
x
k
}
k≥1
, has zero mean and
its autocovariance function is expressed in the fol-
lowing separable form:
E

x
k
x
T
h

= Λ
k
Ψ
T
h
, h ≤ k,
where, for k ≥ 1, Λ
k
,Ψ
k
∈ R
n
x
×n
are known ma-
trices.
(b)

H
(i)
k

k≥1
, i = 1,. ..,m, are independent se-
quences of independent random parameter ma-
trices, whose entries h
(i)
k,
rs
, for r = 1, . ..,n
z
and
s = 1,.. .,n
x
, have known means E[h
(i)
k,
rs
] and co-
variances Cov[h
(i)
k,
rs
,h
(i)
k,
pq
], for r, p = 1,... ,n
z
and
s,q = 1,. . .,n
x
.
(c) The additive noises

v
(i)
k

k≥1
, i = 1,. ..,m, are
white processes with zero mean and known
second-order moments:
E

v
(i)
k
v
( j)T
h

= R
(i, j)
k
δ
k,h
; i, j = 1, ...,m.
(d) For i = 1,... , m, the processes

x
k

k≥1
,

v
(i)
k

k≥1
and

H
(i)
k

k≥1
are mutually independent.
Remark 1. From hypotheses (a), (b) and (d), denoting
H
(i)
k
≡ E

H
(i)
k

and
e
H
(i)
k
≡ H
(i)
k
− H
(i)
k
, we have that
E[
e
H
(i)
k
x
k
x
T
k
e
H
(i)T
k
] = E[
e
H
(i)
k
Λ
k
Ψ
T
k
e
H
(i)T
k
], i = 1,... ,m,
where, for r,s = 1,. . ., n
z
, the (r,s)-th entries of these
matrices are given by:

E[
e
H
(i)
k
Λ
k
Ψ
T
k
e
H
(i)T
k
]

rs
=
n
x
∑
a=1
n
x
∑
b=1
Cov[h
(i)
k,
ra
,h
(i)
k,
sb
]

Λ
k
Ψ
T
k

ab
.
3 INNOVATION APPROACH TO
THE ESTIMATION PROBLEM
The innovation technique will be used to design a re-
cursive algorithm for the sequential filtering estima-
tors,
b
x
(S)
k/k
, of the signal x
k
based on the observations
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
588

provided by all the sensors up to time k. In this Sec-
tion, after introducing some basic notation, which will
be used hereafter, an expression for the innovation
process will be deduced.
3.1 Basic Notation
In the study of the sequential estimation problem we
will use the following notation:
− For i = 1,. .., m, Z
(i)
k
≡

z
(1)
k
,.. ., z
(i)
k

denotes
the set of measurements provided by the sensors
1,2,. .. , i, at time k.
− We will write Z
(0)
k
to mean that no measurements
are available.
− Since, for 1 ≤ h ≤ k, Z
(m)
h
is the set of measure-
ments provided by all the sensors at time h, then
Z
k
≡

Z
(m)
1
,.. ., Z
(m)
k

is clearly the set of all the
observations produced by all the sensors from the
initial time instant up to time k.
− The LS linear estimator of a random vector α
k
based on the observations

Z
k−1
,Z
(i)
k

will be de-
noted by
b
α
k/k,i
.
Without loss of generality, we will suppose that,
at each sampling time k, the measurements arrive in
the fusion center according to the sensor numbering
order; that is, for 1 ≤ i < j ≤ m, the observation from
the i-th sensor, z
(i)
k
, is received before the observation
from the j-th sensor, z
( j)
k
.
3.2 Innovation Process
For each fixed time instant k, the aim is to obtain,
b
x
k/k,i
, the LS linear estimator of x
k
based on the ob-
servations

Z
k−1
,Z
(i)
k

by a recursive algorithm in
i = 1,... ,m, and, for this purpose, an innovation ap-
proach will be used.
For a fixed k, we consider the observation z
(i)
k
and we denote
b
z
(i)
k/k,i−1
the estimator of z
(i)
k
based on

Z
k−1
,Z
(i−1)
k

. Clearly,
b
z
(i)
k/k,i−1
is the part of z
(i)
k
determined by the knowledge of the set of observa-
tions

Z
k−1
,Z
(i−1)
k

and, hence, the new informa-
tion or the innovation provided by z
(i)
k
is given by
the difference vector η
(i)
k/k,i−1
≡ z
(i)
k
−
b
z
(i)
k/k,i−1
. As it
is known (Kailath et al., 2000), the innovation pro-
cess is a white noise with zero mean and covariances
Ξ
(i)
k/k,i−1
≡ E[η
(i)
k/k,i−1
η
(i)T
k/k,i−1
], and the LS linear es-
timator based on the observations agrees with that
based on the innovations.
Hence, for i = 0,.. ., m, the LS linear estimator,
b
α
k/k,i
, of a random vector α
k
based on the observa-
tions

Z
k−1
,Z
(i)
k

can be expressed as a linear com-
bination of the innovations; specifically, we have the
following general expression:
b
α
k/k,i
=(1 − δ
k,1
)
k−1
∑
h=1
m
∑
j=1
E[α
k
η
( j)T
h/h, j−1
]Ξ
( j)−1
h/h, j−1
η
( j)
h/h, j−1
+(1 − δ
i,0
)
i
∑
j=1
E[α
k
η
( j)T
k/k, j−1
]Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
, k ≥1.
(2)
To obtain the innovation η
(i)
k/k,i−1
= z
(i)
k
−
b
z
(i)
k/k,i−1
,
we start from (1) and, applying the projection theory,
we have:
η
(i)
k/k,i−1
= z
(i)
k
− H
(i)
k
b
x
k/k,i−1
−
b
v
(i)
k/k,i−1
, i = 1,. .. ,m.
Due to the correlation of the sensor noises, the
noise estimator
b
v
(i)
k/k,i−1
is not negligible and it can
be derived from the general expression (2). Actu-
ally, taking into account that E[v
(i)
k
η
( j)T
h/h, j−1
] = 0, for
h ≤ k − 1 and j = 1,. . ., m, and denoting V
(i, j)
k
≡
E

v
(i)
k
η
( j)T
k/k, j−1
], from (2), we obtain that:
b
v
(i)
k/k,i−1
= (1 − δ
i,1
)
i−1
∑
j=1
V
(i, j)
k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
.
Hence, we have that
η
(i)
k/k,i−1
= z
(i)
k
− H
(i)
k
b
x
k/k,i−1
−(1 − δ
i,1
)
i−1
∑
j=1
V
(i, j)
k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
.
(3)
Next, using again (2) and denoting X
( j)
k,h
≡
E[x
k
η
( j)
h/h, j−1
], the LS linear estimator
b
x
k/k,i−1
is
expressed as a linear combination of the innovations
as follows:
b
x
k/k,i−1
= (1 − δ
k,1
)
k−1
∑
h=1
m
∑
j=1
X
( j)
k,h
Ξ
( j)−1
h/h, j−1
η
( j)
h/h, j−1
+(1 − δ
i,1
)
i−1
∑
j=1
X
( j)
k,k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
.
Hence, for each time k, the innovation η
(i)
k/k,i−1
, for
i = 1, .. ., m, satisfies:
η
(i)
k/k,i−1
= z
(i)
k
−(1 − δ
k,1
)H
(i)
k
k−1
∑
h=1
m
∑
j=1
X
( j)
k,h
Ξ
( j)−1
h/h, j−1
η
( j)
h/h, j−1
−(1 − δ
i,1
)
i−1
∑
j=1

H
(i)
k
X
( j)
k,k
+V
(i, j)
k

Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
.
(4)
Optimal Filtering Algorithm based on Covariance Information using a Sequential Fusion Approach
589

4 SEQUENTIAL FUSION
ESTIMATION PROBLEM
In this Section, using the sequential fusion method,
a recursive algorithm is derived for the LS linear fil-
tering estimators,
b
x
(S)
k/k
, k ≥ 1, of the signal x
k
based
on the observations Z
k
yielded by all the sensors up
to time k. The performance of these estimators is
measured by the filtering error covariance matrices,
Σ
(S)
k/k
≡ E[(x
k
−
b
x
(S)
k/k
)(x
k
−
b
x
(S)
k/k
)
T
], k ≥ 1, and, since
their computation is not included in the algorithm, an
expression for these matrices is also presented at the
end of this section.
4.1 Sequential Fusion Filtering
Algorithm
Under the hypotheses (a)-(d), for each k ≥ 1, the es-
timators,
b
x
k/k,i
are sequentially obtained by the follo-
wing recursive algorithm:
b
x
k/k,i
= Λ
k

O
k−1
+ o
k,i

, i = 1,. .. ,m,
(5)
where, starting from o
k,0
= 0 and O
0
= 0, the vectors
o
k,i
and O
k
are recursively obtained from
o
k,i
= o
k,i−1
+ M
(i)
k
Ξ
(i)−1
k/k,i−1
η
(i)
k/k,i−1
, i = 1,. .. ,m,
O
k
= O
k−1
+ o
k,m
, k ≥ 1.
(6)
The matrices M
(i)
k
≡ E

o
k,i
η
(i)T
k/k,i−1

are given by
M
(i)
k
= Ψ
T
k
H
(i)T
k
−

K
O
k−1
+ K
o
k,i−1

Λ
T
k
H
(i)T
k
−(1 − δ
i,1
)
i−1
∑
j=1
M
( j)
k
Ξ
( j)−1
k/k, j−1
V
(i, j)T
k
, i = 1,. .. ,m.
(7)
The matrices K
o
k,i
≡ E

o
k,i
o
T
k,i

and K
O
k
≡ E

O
k
O
T
k

are obtained from
K
o
k,i
= K
o
k,i−1
+M
(i)
k
Ξ
(i)−1
k/k,i−1
M
(i)T
k
, i = 1,. .. ,m,
K
O
k
= K
O
k−1
+ K
o
k,m
, k ≥ 1,
(8)
with initial conditions K
o
k,0
= 0 and K
O
0
= 0.
For i = 1,.. ., m, the innovation η
(i)
k/k,i−1
is calcu-
lated by
η
(i)
k/k,i−1
= z
(i)
k
− H
(i)
k
Λ
k

O
k−1
+ o
k,i−1

−(1 − δ
i,1
)
i−1
∑
j=1
V
(i, j)
k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
,
(9)
and the innovation covariance matrix, Ξ
(i)
k/k,i−1
, is
given by
Ξ
(i)
k/k,i−1
= H
(i)
k
Λ
k
M
(i)
k
+ V
(i,i)
k
, i = 1,. .. ,m. (10)
The matrices V
(i, j)
k
= E

v
(i)
k
η
( j)T
k/k, j−1
], for i = 1,. .. ,m
and j = 1, .. ., i, satisfy
V
(i, j)
k
= R
(i, j)
k
−(1−δ
j,1
)
j−1
∑
l=1
V
(i,l)
k
Ξ
(l)−1
k/k,l−1
×

H
( j)
k
Λ
k
M
(l)
k
+V
( j,l)
k

T
.
(11)
Finally, the sequential fusion filtering estimators
are given by
b
x
(S)
k/k
=
b
x
k/k,m
, k ≥ 1. (12)
4.1.1 Algorithm Derivation
From (2), to obtain the LS linear estimators
b
x
k/k,i
,
we start by calculating the coefficients X
( j)
k,h
=
E[x
k
η
( j)
h/h, j−1
], for h ≤ k and j = 1,. .. ,m.
From hypotheses (a), (b) and (d), we have that
E

x
k
z
( j)T
h

= Λ
k
Ψ
T
h
H
( j)T
h
, h ≤ k, j = 1, .. . ,m.
Using this property together with expression (4) for
η
( j)
h/h, j−1
, we have that, for h ≤ k and j = 1, . .. ,m:
X
( j)
k,h
= Λ
k
Ψ
T
h
H
( j)T
h
−(1−δ
h,1
)
h−1
∑
l=1
m
∑
s=1
X
(s)
k,l
Ξ
(s)−1
l/l,s−1
X
(s)T
h,l
H
( j)T
h
−(1−δ
j,1
)
j−1
∑
s=1
X
(s)
k,h
Ξ
(s)−1
h/h,s−1

H
( j)
h
X
(s)
h,h
+V
( j,s)
h

T
.
Hence, X
( j)
k,h
can be expressed as
X
( j)
k,h
= Λ
k
M
( j)
h
, h ≤ k; j = 1, .. . ,m, (13)
where M
( j)
h
is a function satisfying
M
( j)
h
= Ψ
T
h
H
( j)T
h
−(1−δ
h,1
)
h−1
∑
l=1
m
∑
s=1
M
(s)
l
Ξ
(s)−1
l/l,s−1
M
(s)T
l
Λ
T
h
H
( j)T
h
−(1−δ
j,1
)
j−1
∑
s=1
M
(s)
h
Ξ
(s)−1
h/h,s−1

H
( j)
h
Λ
h
M
(s)
h
+V
( j,s)
h

T
.
(14)
Now, taking into account that, from (2),
b
x
k/k,i
= (1 − δ
k,1
)
k−1
∑
h=1
m
∑
j=1
X
( j)
k,h
Ξ
( j)−1
h/h, j−1
η
( j)
h/h, j−1
+(1 − δ
i,0
)
i
∑
j=1
X
( j)
k,k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
,
using expression (13) and defining the vectors
o
k,i
≡
i
∑
j=1
M
( j)
k
Ξ
( j)−1
k/k, j−1
η
( j)
k/k, j−1
, i = 1,. .. ,m,
O
k
≡
k
∑
h=1
o
h,m
, k ≥ 1,
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
590

which, obviously, satisfy expression (6), we conclude
that the estimator
b
x
k/k,i
is given by (5).
Now, from (14) for h = k and j = i, defining the
matrices
K
o
k,i
≡ E

o
k,i
o
T
k,i

=
i
∑
j=1
M
( j)
k
Ξ
( j)−1
k/k, j−1
M
( j)T
k
,
K
O
k
≡ E

O
k
O
T
k

=
k
∑
h=1
K
o
h,m
,
(15)
expression (7) is obtained.
The recursive formula (8) for the matrices K
o
k,i
and
K
O
k
is obvious from (15).
Expression (9) for the innovation η
(i)
k/k,i−1
is easily
obtained by substituting (5) for
b
x
(i)
k/k,i−1
in (3).
To deduce expression (10) for the covariance
matrix Ξ
(i)
k/k,i−1
= E[η
(i)
k/k,i−1
η
(i)T
k/k,i−1
], we express
Ξ
(i)
k/k,i−1
= E[z
(i)
k
η
(i)T
k/k,i−1
], and use expression (1) for
z
(i)
k
. Then, since E[x
k
η
(i)T
k/k,i−1
] = X
(i)
k,k
= Λ
k
M
(i)
k
, and
E[v
(i)
k
)η
(i)T
k/k,i−1
] = V
(i,i)
k
, expression (10) is straightfor-
ward.
To obtain (11) for V
(i, j)
k
= E

v
(i)
k
η
( j)T
k/k, j−1

we
use (4) for η
( j)
k/k, j−1
; so, taking into account that
E[v
(i)
k
z
( j)T
k
] = R
(i, j)
k
, E

v
(i)
k
η
(l)T
h/h,l−1

= 0, for h ≤ k −1,
and E

v
(i)
k
η
(l)T
k/k,l−1

= V
(i,l)
k
, expression (11) is ob-
tained.
Finally, since Z
k
=

Z
k−1
,Z
(m)
k

, it is obvious that
the sequential fusion filter is given by (12), and the
algorithm is proven. 
4.2 Sequential Filtering Error
Covariance Matrices
Under the hypotheses (a)-(d), for each time instant
k ≥ 1, the estimation error covariance matrices,
Σ
k/k,i
≡ E[(x
k
−
b
x
k/k,i
)(x
k
−
b
x
k/k,i
)
T
], are sequentially
obtained by the following formula:
Σ
k/k,i
= Λ
k

Ψ
k
− Λ
k

K
O
k−1
+ K
o
k,i

T
, i = 1,. .. ,m,
where the matrices K
O
k
and K
o
k,i
are calculated by (8).
The sequential fusion filtering error covariance ma-
trix, Σ
(S)
k/k
= E[(x
k
−
b
x
(S)
k/k
)(x
k
−
b
x
(S)
k/k
)
T
], is given by
Σ
(S)
k/k
= Σ
k/k,m
, k ≥ 1.
Proof. From hypothesis (a), E[x
k
x
T
k
] = Λ
k
Ψ
T
k
; then,
expression for Σ
k/k,i
is clear taking into account that
Σ
k/k,i
= E[x
k
x
T
k
] − E[
b
x
k/k,i
b
x
T
k/k,i
],
and using (5) for the estimators
b
x
k/k,i
.
From (12) for
b
x
(S)
k/k
, is immediate that the sequen-
tial error covariance matrices are Σ
(S)
k/k
= Σ
k/k,m
. 
Note that the matrices Σ
k/k,i
only depend on the
matrices Λ
k
and Ψ
k
, which are known according to
hypothesis (a), and on the matrices K
O
k
and K
o
k,i
,
which are recursively calculated by (8). Thus, Σ
k/k,i
do not depend on the observations and, hence, these
matrices provide a measure of the performance of the
estimators
b
x
k/k,i
, i = 1,. . ., m,

and, in particular, of
b
x
(S)
k/k

even before we get any measurement data.
5 SIMULATION EXAMPLE
This section is devoted to analyze the effectiveness of
the proposed sequential fusion filtering algorithm by
a numerical simulation example. On the one hand,
this example illustrates how hypothesis (a) can cover
situations with state-dependent multiplicative noise
and, on the other, it shows how the proposed model
with random parameter matrices can describe differ-
ent kinds of sensor uncertainties.
Consider the same signal process as that in Exam-
ple 1 of (Feng et al., 2013); that is, a two-dimensional
signal x
k
generated by the following model with state-
dependent multiplicative noise:
x
k+1
=

F + ε
k
G

x
k
+ ρw
k
, k ≥ 1,
where
F =

0.95 0.01
0 0.95

, G =

0.01 0
0 0.01

, ρ =

0.8
0.6

.
The noise sequences

ε
k

k≥1
and

w
k

k≥1
are stan-
dard white gaussian scalar noises. The initial sig-
nal x
0
is a gaussian two-dimensional random vector
with zero mean and covariance matrix E[x
0
x
T
0
] = I.
These noise sequences and initial signal vector are
assumed to be mutually independent; then, it is easy
to see that the signal covariance function is given by
E[x
k
x
T
h
] = F
k−h
E[x
h
x
T
h
], h ≤ k, and hypothesis (a)
is satisfied taking Λ
k
= F
k
and Ψ
T
h
= F
−h
E
h
, where
E
h
≡ E[x
h
x
T
h
], h ≥ 1, is recursively obtained by:
E
h
= FE
h−1
F
T
+ GE
h−1
G
T
+ ρρ
T
, h ≥ 1; E
0
= I.
Consider scalar measurements of this signal, com-
ing from three sensors, according to model (1):
z
(i)
k
= H
(i)
k
x
k
+ v
(i)
k
, k ≥ 1, i = 1,2, 3,
where the random parameter matrices {H
(i)
k
}
k≥1
, i =
1,2,3 are defined by:
Optimal Filtering Algorithm based on Covariance Information using a Sequential Fusion Approach
591

• H
(1)
k
= µ
(1)
k
(0.74, 0.75), where {µ
(1)
k
}
k≥1
is a se-
quence of independent and identically distributed
(iid) random variables with uniform distribution
over [0.3,0.7]. Hence, continuous gain degrada-
tion in sensor 1 is modelled by {H
(1)
k
}
k≥1
.
• H
(2)
k
= µ
(2)
k
(0.75, 0.70), where {µ
(2)
k
}
k≥1
is a se-
quence of iid discrete random variables with
P[µ
(2)
k
= 0.9] = 0.8, P[µ
(2)
k
= 0.1] = 0.2.
Hence, the sequence {H
(2)
k
}
k≥1
models discrete
gain degradation in sensor 2.
• H
(3)
k
= µ
(3)
k
(0.80, 0.75), where {µ
(3)
k
}
k≥1
are iid
Bernoulli random variables with P[µ
(3)
k
= 1] = p,
∀k ≥ 1. The missing measurement phenomena
in sensor 3 is, hence, described by {H
(3)
k
}
k≥1
.
Note that 1 − p is the missing probability, which
means that the signal x
k
is missing from the k-
th measurement coming from the third sensor (or,
equivalently, that this measurement is only noise:
z
(3)
k
= v
(3)
k
) with probability 1 − p.
As in (Caballero-
´
Aguila et al., 2016), the noises
{v
(i)
k
}
k≥1
, i = 1, 2,3, are defined by v
(i)
k
= c
i
β
k
, i =
1,2,3, with c
1
= 0.25, c
2
= 0.5 and c
3
= 0.75, and
{β
k
}
k≥1
a standard Gaussian white process. Clearly,
according to hypothesis (b), these noises are corre-
lated only at the same time instant and R
(i, j)
k
= c
i
c
j
.
The proposed sequential fusion filtering algo-
rithm, as well as the formulas for the error covari-
ance matrices, have been implemented in a MATLAB
program and one hundred iterations have been run to
show the algorithm effectiveness. In order to illustrate
the influence of the missing probability on the filter
accuracy, the error variances have been calculated for
different probabilities p of the Bernoulli random vari-
ables modelling the missing measurement phenomena
of sensor 3.
First, considering p = 0.5, the sequential fusion
estimates have been calculated using simulated val-
ues of the signal and the observations coming from
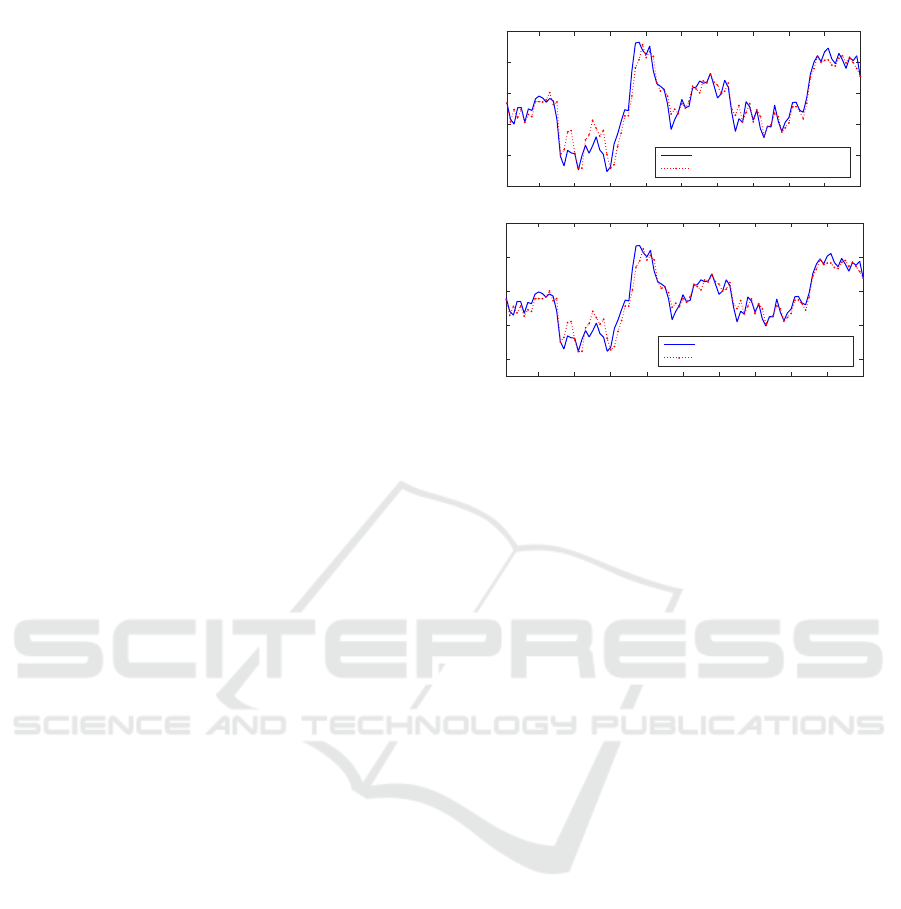
the three sensors. The results of a simulated signal to-
gether with the sequential filtering estimates are plot-
ted in Figure 1 which, for both the first and the second
signal components, shows a satisfactory tracking per-
formance of the proposed estimates.
As indicated above, the estimation error cova-
riance matrices, which do not depend on the simulated
data, measure the accuracy of the estimators. For
both signal components, in order to show the effect
of the missing measurement phenomenon on the per-
formance of the sequential filtering estimators, their
error variances have been calculated for values of p
Time k
10 20 30 40 50 60 70 80 90 100
-6
-4
-2
0
2
4
Simulated signal values
Sequential fusion filtering estimates
Time k
10 20 30 40 50 60 70 80 90 100
-4
-2
0
2
4
Simulated signal values
Sequential fusion filtering estimates
(I) First signal
component
(II) Second signal
component
Figure 1: Simulated signal values and sequential fusion fil-
tering estimates when p = 0.5.
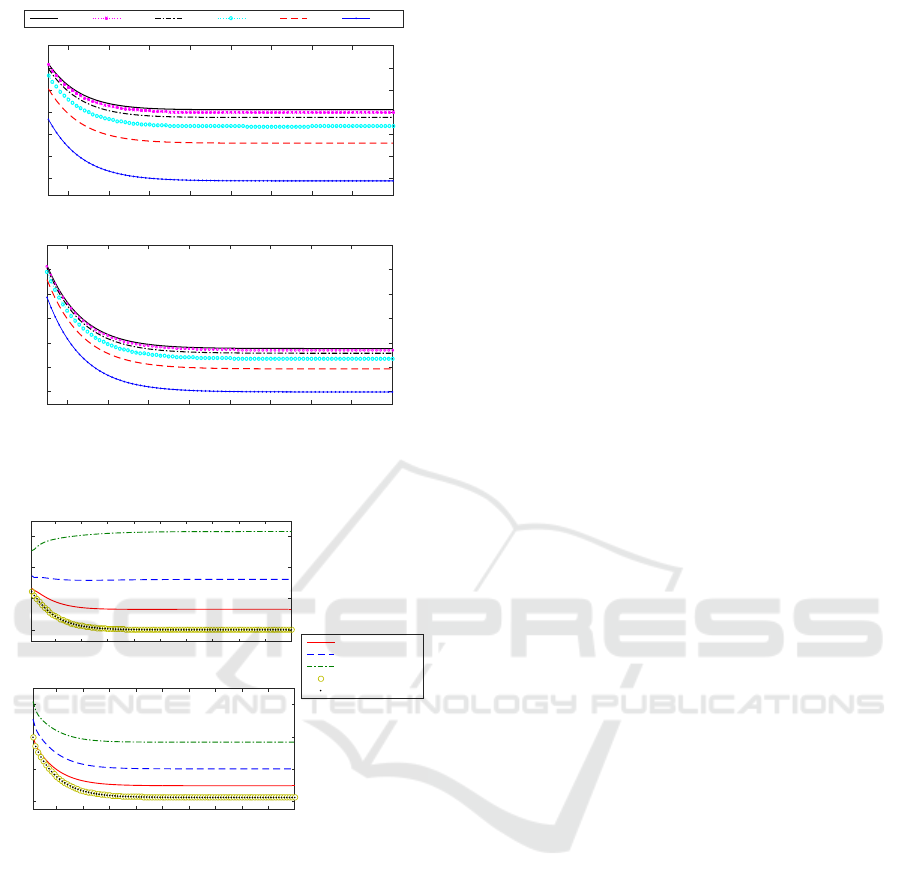
varying from 0.4 to 0.9; the results are displayed in
Figure 2. From this figure, it is observed that the
performance of the sequential filter is indeed influ-
enced by the probabilities p; actually, for both signal
components, the sequential filtering error variances
become smaller as 1 − p (the probability of missing
measurements) decreases, which, as expected, con-
firms that the performance of the sequential filters im-
proves as the probability p increases. For the values
p = 0.1, 0.2 and 0.3, no appreciable differences are
visually observed in comparison with the results ob-
tained for p = 0.4 and, therefore, these values have
been omitted in Figure 2.
Finally, we study the performance of the proposed
sequential fusion filtering estimators compared with
the local filters and the centralized fusion filter in
(Caballero-
´
Aguila et al., 2016), for which, consider-
ing p = 0.5, the error variances of the different fil-
ters have been calculated. These filtering error vari-
ances are displayed in Figure 3, which shows that the
sequential filtering error variances are smaller than
those of the every local filter and, hence, the sequen-
tial fusion filtering estimators outperform all the local
ones. Also, it can be observed that the error variances
of the sequential filter are identical to those of the cen-
tralized filter. This result was expected, since the cen-
tralized and sequential estimators are optimal based
on the same number of observations, and therefore,
they are actually equal to each other. Nevertheless,
the sequential fusion algorithm can significantly re-
duce the computational cost of the centralized fusion
algorithm; indeed, in this example the computational
complexity of the centralized algorithm has the order
of magnitude O(3
3
) and that of the sequential algo-
rithm has the order O(3).
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
592

!th
Iteration k
20 30 40 50 60 70 80 90 100
0.36
0.38
0.4
0.42
0.44
0.46
0.48
p = 0.4 p = 0.5 p = 0.6 p = 0.7 p = 0.8 p = 0.9
Iteration k
20 30 40 50 60 70 80 90 100
0.2
0.22
0.24
0.26
0.28
0.3
0.32
(II) Second signal component sequential filtering error variances
(I) First signal component sequential filtering error variances
Figure 2: Sequential filtering error variances for p from 0.4
to 0.9.
Time k
10 20 30 40 50 60 70 80 90 100
0.4
0.6
0.8
1
Local filter (sensor 1)
Local filter (sensor 2)
Local filter (sensor 3)
Centralized filter
Sequential filter
Time k
10 20 30 40 50 60 70 80 90 100
0.2
0.4
0.6
0.8
(II) Second signal
component
(I) First signal
component
Figure 3: Error variance comparison of the local filter and
the centralized and sequential fusion filtering estimators
when p = 0.5.
6 CONCLUSIONS
As it is known, centralized and distributed fusion esti-
mation algorithms present some handicaps, which can
be overcome by using the sequential fusion method,
whose estimation accuracy is identical to the central-
ized one, with the difference that the sensor data are
processed in a sequential way, thus having a consid-
erably lower computational cost. A review of the se-
quential fusion estimation algorithms in the literature
brings to light that they all require the knowledge of
the signal evolution model. However, in many practi-
cal applications, such information is not available and
only the first and second-order moments of the sig-
nal and the processes involved in the sensor measure-
ment equations can be obtained. For the first time,
this paper addresses the sequential fusion estimation
problem using covariance information when the sen-
sor measurement model includes random parameter
matrices and additive noises that are correlated across
sensors.
A simulation example shows how systems with
state-dependent multiplicative noise fit the proposed
covariance-based approach and how multiple uncer-
tainties in the measurement equations (namely, dis-
crete or continuous gain degradation and missing
measurements) are covered by the current measure-
ment model with random parameter matrices. The
simulation results illustrate the applicability of the
proposed sequential fusion filter and the effect of the
missing measurement phenomenon on the estimation
accuracy.
ACKNOWLEDGEMENTS
This research is supported by Ministerio de Eco-
nom
´
ıa, Industria y Competitividad, Agencia Estatal
de Investigaci
´
on and Fondo Europeo de Desarrollo
Regional FEDER (grant no. MTM2017-84199-P).
REFERENCES
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2016). Fusion estimation using measured
outputs with random parameter matrices subject to
random delays and packet dropouts. Signal Process-
ing, 127:12–23.
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2017). Fusion estimation from multisensor
observations with multiplicative noises and correlated
random delays in transmission. Mathematics, 5(3):45.
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2018). Centralized fusion approach to the
estimation problem with multi-packet processing un-
der uncertainty in outputs and transmissions. Sensors,
18(8):2697.
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2019). Networked distributed fusion esti-
mation under uncertain outputs with random transmis-
sion delays, packet losses and multi-packet process-
ing. Signal Processing, 156:71–83.
Feng, J., Wang, Z., and Zeng, M. (2013). Distributed
weighted robust Kalman filter fusion for uncer-
tain systems with autocorrelated and cross-correlated
noises. Information Fusion, 14:78–86.
Feng, X., Wu, L., and Wen, C. (2018). Sequential
fault-tolerant fusion estimation for multisensor time-
Optimal Filtering Algorithm based on Covariance Information using a Sequential Fusion Approach
593

varying systems. Discrete Dynamics in Nature and
Society, ID 4504206:9 pages.
Hu, J., Wang, Z., Alsaadi, F. E., and Hayat, T. (2017).
Event-based filtering for time-varying nonlinear sys-
tems subject to multiple missing measurements with
uncertain missing probabilities. Information Fusion,
38:74–83.
Hu, J., Wang, Z., and Gao, H. (2013). Recursive filter-
ing with random parameter matrices, multiple fad-
ing measurements and correlated noises. Automatica,
49:3440–3448.
Kailath, T., Sayed, A. H., and Hassibi, B. (2000). Linear
estimation. Prentice Hall, Upper Saddle River, New
Jersey.
Li, W., Jia, Y., and Du, J. (2017). Distributed filtering
for discrete-time linear systems with fading measure-
ments and time-correlated noise. Digital Signal Pro-
cessing, 60:211–219.
Li, X. (2003). Optimal linear estimation fusion, part vii:
Dynamic systems. In Proceedings of the 6th Interna-
tional Conference of Information Fusion. IEEE.
Lin, H. and Sun, S. (2018). Optimal sequential fusion es-
timation with stochastic parameter perturbations, fad-
ing measurements, and correlated noises. IEEE Trans-
actions on Signal Processing, 66(13):3571–3583.
Liu, Y., Wang, Z., He, X., and Zhou, D. H. (2016).
Minimum-variance recursive filtering over sensor net-
works with stochastic sensor gain degradation: Algo-
rithms and performance analysis. IEEE Transactions
on Control of Network Systems, 3(3):265–274.
Sun, S., Tian, T., and Lin, H. (2017). State estimators
for systems with random parameter matrices, stochas-
tic nonlinearities, fading measurements and correlated
noises. Information Sciences, 397–398:118–136.
Wang, X. and Sun, S. (2017). Optimal recursive esti-
mation for networked descriptor systems with packet
dropouts, multiplicative noises and correlated noises.
Aerospace Science and Technology, 63:41–53.
Wen, C., Cai, Y., Wen, C., and Xu, X. (2013). Optimal se-
quential Kalman filtering with cross-correlated mea-
surement noises. Aerospace Science and Technology,
26:153–159.
Yan, L., Li, X. R., Xia, Y., and Fu, M. (2013). Optimal
sequential and distributed fusion for state estimation
in cross-correlated noise. Automatica, 49:3607–3612.
Zhu, C., Xia, Y., Xie, L., and Yan, L. (2013). Optimal linear
estimation for systems with transmission delays and
packet dropouts. IET Signal Processing, 7(9):814–
823.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
594