
I Want to Break Square-free: The 4p −1 Factorization Method and Its
RSA Backdoor Viability
Vladimir Sedlacek
1,2
, Dusan Klinec
1
, Marek Sys
1
, Petr Svenda
1
and Vashek Matyas
1
1
Masaryk University, Czech Republic
2
Ca’ Foscari University of Venice, Italy
Keywords:
Backdoor, Complex Multiplication, Integer Factorization, RSA Security, Smartcard.
Abstract:
We analyze Cheng’s 4p −1 factorization method as the means of a potential backdoor for the RSA primes
generated inside black-box devices like cryptographic smartcards. We devise three detection methods for
such a backdoor and also audit 44 millions of RSA keypairs generated by 18 different types of cryptographic
devices. Finally, we present an improved, simplified and asymptotically deterministic version of the method,
together with a deeper analysis of its performance and we offer a public implementation written in Sage.
1 INTRODUCTION
Factorization of composite integers is an old and im-
portant problem and cryptographic schemes such as
RSA are based on its intractability. RSA is one of
the most frequently deployed public key cryptosys-
tems, and a possible factorization of RSA moduli
could have a serious impact on the security of real-
world applications, as was demonstrated in past in-
cidents such as finding weak RSA keys used for
TLS (Heninger et al., 2012), LogJam (Adrian et al.,
2015) or factorable RSA keys from cryptographic
smartcards known as the ROCA attack (Nemec et al.,
2017) with at least hundreds of millions affected de-
vices. The performance of already known factor-
ization methods, together with the required security
margin, determine the necessary security parameters
(e.g., the length of the prime factors p, q of the RSA
modulus n = p.q, conditions on the structure of the
primes). Relevant standards (e.g., NIST FIPS 140-
2 (National Institute of Standards and Technology,
2007), BSI TR-02102-1 (Bundesamt fur Sicherheit in
der Informationstechnik, 2018), keylength.com (Giry,
2019)) then define the minimal required parameters.
While the performance of the fastest general-
purpose factorization algorithms such as the Num-
ber Field Sieve (NFS) influences the minimal secure
length of the RSA moduli, the special purpose fac-
torization methods define the vulnerable format of
primes that should be avoided. The short list of fac-
torization algorithms is:
1. General-purpose – work for general integers
n. Pollard ρ (Pollard, 1975), Quadratic Sieve
(Pomerance, 1985) and asymptotically fastest
NFS (Pollard, 1993) belong to this group.
2. Special purpose – very efficient when a factor p|n
or n itself is of a special form:
(a) A certain number related to the prime factor p
is smooth (has only small prime divisors) – Pol-
lard’s p −1 (Pollard, 1974), Williams’s p + 1
(Williams, 1982), Bach-Shallit (Bach and Shal-
lit, 1985) and Lenstra’s Elliptic Curve (ECM)
(Lenstra, 1987) methods assume smoothness of
the integers p−1, p+1, φ
k
(p) (k-th cyclotomic
polynomial) and #E(p), respectively.
(b) Assumptions about p or n: there are fast
methods for n of the form n = p
r
q (Boneh
et al., 1999) or n = p
r
q
s
(Coron et al., 2016).
Cheng’s 4p −1 (Cheng, 2002a) method is ef-
fective whenever the square-free part of 4p −1
is small.
All of the mentioned methods look for a multiple kp
of some uknown prime divisor p|n. In the last step, the
methods compute gcd(n, k p) = d. If 1 < d < n, then
a factor is found and the factorization can continue
recursively. The methods are probabilistic since the
factorization fails when d = n.
If a special form of primes allows for an efficient
factorization of RSA moduli, an adversary is moti-
vated to subvert the prime generation to produce such
keys. This might serve as a backdoor, as the adversary
would then be able to perform the factorization much
Sedlacek, V., Klinec, D., Sys, M., Svenda, P. and Matyas, V.
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability.
DOI: 10.5220/0007786600250036
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 25-36
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
25

faster than anyone else. We focus on the relatively un-
known 4p −1 method in this paper, whose existence
might naturally introduce such a setting .
The contributions of the paper
1
are the following:
• we discuss the viability of the method as a poten-
tial backdoor from different perspectives;
• we perform an audit of a large RSA keypair
dataset generated by 18 different types of crypto-
devices with respect to a potential backdoor;
• we give a more detailed and more precise analysis
of the algorithm and show that the algorithm is
asymptotically deterministic;
• we present a simplification of the method and
show that the number of expected iterations is 2-4
times lower than stated in (Cheng, 2002b);
• we offer a compact public implementation of the
method in Sage, together with an extensive run-
time analysis;
• we discover and explain a discrepancy (that gov-
erns the possibility of modulus factorization) be-
tween random primes and primes generated by
certain smartcards.
The paper is organized as follows: In Section 2,
we give a brief overview of the method, together
with the related work. Description of the simplified
method can be found in Section 3. Section 4 is de-
voted to a deeper analysis of the method. Practical
limits of the method and time analysis of the Sage im-
plementation are discussed in Section 5. Section 6 is
concerned with the real-world impact of the algorithm
and covers both the backdoor discussion and our au-
dit. Finally, conclusions are given in Section 7.
2 PREVIOUS WORK
Chengs’s 4p −1 method is similar to Lenstra’s ECM
(Lenstra, 1987). Both methods work on an elliptic
curve (EC) E(Z
n
) (a set of points (x, y) ∈ Z
n
×Z
n
)
defined by a,b ∈ Z
n
and the Weierstrass equation:
E(Z
n
) : y
2
= x
3
+ ax + b,
where n is the number to be factored and 4a
3
+27b
2
6=
0 (mod n). Both methods work due to the natural
mapping (Z
n
(mod p)
7→ F
p
) that induces a homomor-
phism E(Z
n
) 7→ E(F
p
) by reducing the coordinates
modulo p.
The methods compute the mutiple mP for a point
P on E(Z
n
). If m ∈Z is a multiple of #E(F
p
) (order of
1
See the implementation and the additional materials at
https://crocs.fi.muni.cz/papers/Secrypt2019.
the EC over F
p
), then the computation of a certain in-
version modulo n fails (inversion of multiple of p for
p|n) during the scalar multiplication, which reveals p.
The methods perform the following steps:
1. choose an elliptic curve E(Z
n
),
2. choose a random point P ∈ E(Z
n
),
3. compute mP =
ϕ
m
(P)
ψ
m
(P)
2
,
ω
m
(P)
ψ
3
m
(P)
, for
ψ
m
(P),ω
m
(P),ϕ
m
(P) ∈ Z
n
,
4. compute gcd(ψ
m
(P),n).
The methods differ in two points: how the curve is
chosen and how mP is computed. In ECM, random
ECs are chosen with a hope that their order #E(F
p
) is
smooth, so m is taken here as product of small primes
(e.g., m = B! for some small B). It is hard to find a
point on the curve E(Z
n
) for the composite n in gen-
eral. In order to overcome this difficulty, the point P is
chosen first and the curve (respectively constants a, b)
is chosen accordingly in ECM.
In Cheng’s 4p −1 method, we hope that a given
D is a square-free part of 4p −1. The method con-
structs E(Z
n
) (computes a, b) so that the correspond-
ing E(F
p
) is anomalous (size of EC is equal to p
i.e. #E(F
p
) = p), so m = n is taken here as a mul-
tiple of p. Since the method constructs the EC first,
it is important that Cheng found a way how to avoid
working with points explicitly. Instead of a direct
computation of the scalar multiple nP, he used the
n-th division polynomial ψ
n
to compute the required
ψ
n
(P) = ψ
n
(x) for a randomly chosen x ∈ Z, which
he hopes to be an x-coordinate of some point on
E(F
p
). Cheng’s method uses the complex multipli-
cation (CM) method (Br
¨
oker and Stevenhagen, 2007)
to construct an anomalous EC. CM computes the j-
invariant of the curve as a root of the Hilbert poly-
nomial H
−D
(x) in F
p
corresponding to D. There are
two different yet related curves (twists) E and E
c
with the given j-invariant having exactly p −2 and p
points, respectively. The EC E is defined by the con-
stants a, b, which can be computed as rational func-
tions of the j-invariant, i.e., a = a( j),b = b( j) de-
fines E. The EC E
c
is defined by the j-invariant
and some quadratic non-residue c in F
p
, i.e., a =
a( j, c),b = b( j,c). Since the method cannot distin-
guish between a curve with p points and a curve with
p + 2 points over F
p
, Cheng’s method computes nP
(more precisely ψ
n
) for both curves. The method
iterates through various values of x (to guess the x-
coordinate of some point) and various values of c (to
guess the quadratic non-residue), hence two for-loops
are used in the method. Cheng stated that the proba-
bility of a successful guess of x or a correct twist is
1
2
.
Later research on ECs (Rubin and Silverberg, 2007)
SECRYPT 2019 - 16th International Conference on Security and Cryptography
26

showed that it is possible to choose the correct twist
(having p elements) with some small additional effort
(at least with the knowledge of p). However, we will
show later that Cheng’s method works for both twists
without influencing the probability of success.
Cheng introduced his method in 2002 in (Cheng,
2002a). The original method computes the j-invariant
as the root of the Hilbert polynomial (HP) H
−D
(X)
of degree one. Thus in this case we have a concrete
value of the j-invariant and are able to construct a
concrete EC E over Z
n
(up to a twist). There are
only six HPs of degree one that can occur (we are
not counting the cases −D ∈{−4,−7, −8} which are
excluded by a congruence condition on D) so the
method can be used for a prime divisor p of n of
six different forms. In the same year, Cheng gener-
alized his method in (Cheng, 2002b) for HPs of an
arbitrary degree. In the generalized version, a con-
crete j-invariant is not computed (as finding roots of
polynomials modulo n is very hard in general), but
the method works with j symbolically. In 2017, Shi-
rase published the paper (Shirase, 2017), where he
followed up on Cheng’s older publication (Cheng,
2002a) (he clearly missed the newer one). Although
Shirase “reinvented” Cheng’s method only for HPs
of degree at most two, the contribution of his work
is not negligible. Shirase improved Cheng’s unclear
description of his method (especially the equation
g(X) = P
n
(x) ∈Z/(n)[X] on page 6 of (Cheng, 2002b)
is not clear enough). On the other hand, his descrip-
tion is quite complex and can be simplified.
3 A SIMPLER VERSION OF
CHENG’S 4p −1 METHOD
In our simplified method, we assume that n, the num-
ber to be factored, has a prime divisor p satisfying
4p −1 = Ds
2
,
where D is square-free (note that this immediately im-
plies D ≡ 3 (mod 8). We will also assume D 6= 3 (the
case D = 3 is much easier and is handled separately
in (Shirase, 2017)). For simplicity of the presentation,
we will only deal with the case n = p ·q, where q is
also a prime, although this is not a necessary condi-
tion. The most important ideas involved in the algo-
rithm are the following:
1. the number of points on a curve E(F
p
) can be
controlled through the CM method – in our case,
finding a root j of the HP modulo p and construct-
ing an EC E with j as its j-invariant ensures that
E(F
p
) is either p or p +2;
2. instead of working with unknown roots j ∈ F
p
of
the HP H
−D
, we can make symbolic computations
in the ring Q := Z
n
[X]/(H
−D
(X));
3. division polynomials ψ
n
can be used to compute
desired zero denominators (ψ
n
(P) ≡ 0 (mod p))
in coordinates of the point at infinity O :
O = nP =
ϕ
n
(P)
ψ
n
(P)
2
,
ω
n
(P)
ψ
3
n
(P)
. (1)
Input : n (the integer to be factored); D (the
square-free part of
4p −1 for p|n)
Output: p (or failure)
compute H
−D,n
(X) (the −D-th HP modulo n);
Q ← Z
n
[X]/(H
−D,n
(X));
j ← [X ] ∈ Q;
k ← j ·(1728 − j)
−1
∈ Q (*);
a,b ← 3k,2k ∈ Q ;
choose bound B appropriately (for example
B = 10);
forall i ∈ {1, 2, ···,B} do
generate random x
i
∈ Z
n
⊆ Q;
z ← ψ
n
(a,b,x
i
) ∈ Q ;
d = gcd(¯z(X), H
−D,n
(X)) ∈ Z
n
[X] (*);
r ← gcd(d,n);
if 1 < r < n then
return r;
end
end
return failure ;
Algorithm 1: A simplified version of Cheng’s 4p −1 fac-
torization method.
In our simplified Algorithm 1 of Cheng’s algo-
rithm (Cheng, 2002a), two operations are marked
by (*) since these operations may fail. Both of
these operations (the computation of d or the inverse
(1728 − j)
−1
in Q) can be performed using the ex-
tended version of Euclid’s algorithm with polynomi-
als over Z
n
[X] as an input. The problematic step in
the Euclid’s algorithm is to compute q
k
,r
k−1
such that
r
k−2
= q
k
r
k−1
+ r
k
, when the leading coefficient lc of
r
k−1
polynomial is not coprime to n. However, this
means that we can directly return gcd(lc,n) > 1.
4 ANALYSIS OF THE METHOD
This section focuses on a clear description and ex-
planation of the method (Section 4.1) and its anal-
ysis (Subsections 4.2, 4.3). The original Cheng’s
method computes within two ECs – curve defined by
the a,b and its twist defined by same a, b and some
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability
27

quadratic non-residue c (mod p). Since p is un-
known, Cheng’s algorithm iterates through various c.
In Section 4.2 we show that Cheng’s algorithm works
for both twists, hence the c-loop can be omitted, and
the algorithm can be simplified to Algorithm 1. More-
over, in Subsection 4.3 we show that the average num-
ber of iterations (the x-loop) of the method depends
on the class number h(−D) (the degree of the HP
H
−D
(X)) and is close to 1 for a large D.
4.1 Correctness of the Algorithm
Many computations in the algorithm are performed
over the quotient ring Q = Z
n
[X]/(H
−D,n
(X)). With-
out proof, we claim that the substitution X 7→ j in-
duces a ring homomorphism h
j
: Q → F
p
. In other
words, any computation in Q corresponds to a sym-
bolic computation with a root j ∈ Z
n
of the HP (i.e.,
H
−D,n
( j) ≡ 0 (mod p)). Hence X 7→ j induces a ho-
momorphism Q 7→ Z
n
, which can be composed with
the natural projection Z
n
7→ F
p
to obtain the homo-
morphism h
j
. Figure 1 depicts the relation of compu-
tation in F
p
and Q through the h
j
. It should be noted
that, when working in Q, we are working symboli-
cally with all roots of the HP modulo p at once.
The key and most time consuming part of the al-
gorithm is the computation of the division polynomial
ψ
n
(P) related to the given EC E. In general, ψ
n
(P)
is a polynomial in a,b (that define E) and the coor-
dinates (x, y) of the point P. When n is odd, y only
occurs in even powers and thus can be removed us-
ing the defining Weierstrass equation, so that ψ
n
(P) =
ψ
n
(a,b,x) becomes a polynomial in a,b,x only. The
homomorphism h
j
maps ψ
n
(a,b,x) ∈ Q computed in
the method to 0 ∈ F
p
, as Figure 1 illustrates.
In Algorithm 1, we compute
gcd(¯z(X), H
−D,n
(X)) = d for the lift ¯z of z ∈ Q
to Z
n
[x]. Lemma 4 in (Cheng, 2002b) says that d
is a constant from Z
n
. Since h
j
(H
−D,n
(X)) = 0 and
h
j
(ψ
n
(a,b,x)) = 0, we must have d ≡ 0 (mod p).
For a further analysis, we will need to un-
derstand the structure of Q. First note that the
−D-th Hilbert polynomial splits completely mod-
ulo p (Br
¨
oker and Stevenhagen, 2007), so we have
H
−D
(X) ≡
∏
h(−D)
i=1
(X − j
i
) (mod p) for some pair-
wise distinct j
1
,..., j
h(−D)
∈Z (and therefore the ide-
als (X − j
i
) ⊆ F
p
[X] are pairwise comaximal). Now
let H
−D,p
(X), H
−D,q
(X) be the projections of H
−D
(X)
to F
p
and Z
q
, respectively. Applying the generalized
Chinese remainder theorem several times, we obtain
the isomorphisms:
Q = Z
n
[X]/(H
−D,n
(X))
∼
=
Z
q
[X]/(H
−D,q
(X)) ×F
p
[X]/(H
−D,p
(X))
∼
=
Z
q
[X]/(H
−D,q
(X)) ×
h(−D)
∏
i=1
F
p
[X]/(X − j
i
)
∼
=
Z
q
[X]/(H
−D,q
(X)) ×
h(−D)
∏
i=1
F
p
.
In particular, we have h(−D) different projections
from Q to F
p
, and these are essentially given by lift-
ing an element from Q to Z
n
[X], substituting some j
i
into the obtained polynomial and reducing the result
modulo p.
4.2 Both Twists Work
If the constructed curve E : y
2
= f (x) (where f (x) =
x
3
+ 3kx + 2k) has p points over F
p
, it is clear that
for x such that (
f (x)
p
) = 1, the value ψ
n
(x) will be
zero modulo p (since this x then represents a co-
ordinate of a point on E(F
p
)). However, if E has
p + 2 points over F
p
, it must be a quadratic twist
of some curve E
0
: y
2
= x
3
+ 3kc
2
x + 2kc
3
for some
c ∈ F
p
,
c
p
= −1, such that E
0
has p points over F
p
.
Then there is an isomorphism E → E
0
over F
p
(
√
c)
given by (x,y) 7→(cx,c
3/2
y). Since c is invertible, this
implies that the division polynomials of the curves
must also be related by an invertible transformation.
More specifically, if we let ψ
n,E
(x),ψ
0
n,E
0
(x) be the
division polynomials associated to E and E
0
, respec-
tively, then we have ψ
n,E
0
(x) = ψ
n,E
(cx). Thus if
f (c
−1
x)
p
= 1, the value ψ
n
(x) will be zero modulo
p as well. Since for fixed c the values c
−1
x have the
same distribution as x, we do not have to iterate over
the twists and can fix any of them instead.
Moreover, the probability that value ψ
n
(x) will
be zero modulo p for a fixed curve and a randomly
chosen x ∈ F
p
(more precisely, the projection of a
randomly chosen x ∈ Z
n
) is p
t
p
x
+ (1 − p
t
)(1 − p
x
),
where p
t
is the probability of choosing the right twist
and p
x
is the probability of the event
f (x)
p
= 1.
Thus under the classical heuristical assumption
that p
t
=
1
2
(or alternatively, after calculating that p
x
is very close to
1
2
), the above probability is
1
2
.
4.3 Expected Number of Iterations
Now we can estimate the probability that the core part
of the algorithm will work. First note that when we
are considering an EC over a product of rings, all the
SECRYPT 2019 - 16th International Conference on Security and Cryptography
28

F
p
: H
−D
( j) = 0 → (a,b) =
3 j
1728 − j
,
2 j
1728 − j
→ ψ
n
(a,b,x
i
) = 0
↑ h
j
: X 7→ j ↑ h
j
: X 7→ j ↑ h
j
: X 7→ j
Q : H
−D,n
(X) = 0 → (a,b) =
3X
1728 −X
,
2X
1728 −X
→ ψ
n
(a,b,x
i
).
Figure 1: A diagrammatic overview of arithmetic in F
p
and Q.
associated rational functions (such as the point multi-
plication expression (1)) can be computed coordinate-
wise, with the caveat that whenever the result in some
(but not all) coordinates would be the neutral element,
the whole result is undefined (as there are no “points
in semi-infinity”). This could be fixed by properly
defining the projective space over the product of rings,
but we do not need it here. This undefined behavior
is exactly what we want to achieve, as one of the de-
nominators will then reveal a factor of n.
Thus when we have an elliptic curve over
Q
∼
=
Z
q
[X]/(H
−D,q
(X)) ×
h(−D)
∏
i=1
F
p
,
the algorithm will succeed for a fixed x ∈ Z
n
when-
ever there is at least one copy of F
p
over which the
x corresponds to the right twist (unless this happens
over all of the copies at the same time and simultane-
ously over Z
q
[X]/(H
−D,q
(X)), which is extremely un-
likely, as q has no relation to H
−D
(X)). Heuristically,
these copies of F
p
behave independently, so by the ar-
gumentation in Section 4.2, the estimated probability
that one iteration of the loop over x
i
’s in Algorithm 1
reveal p is 1 −2
−h(−D)
. Therefore the expected num-
ber of the times the loop will have to be executed is
close to
1
1 −2
−h(−D)
=
2
h(−D)
2
h(−D)
−1
.
Thus when h(−D) = 1, one iteration of the loop
will work with probability around
1
2
, but for a large
h(−D), the probability is almost 1 and the algorithm
becomes almost deterministic. These claims are also
supported by an empirical evidence in Section 5.2.
Note that this is a better result than in both (Cheng,
2002a) and (Shirase, 2017), where both twists are
non-deterministically tested and the expected number
of execution times of the innermost loop is claimed to
be around 4.
5 TIME ANALYSIS AND
PRACTICAL LIMITS OF THE
METHOD
When we do not know D in advance, we could
try to loop through all possible values of D up to
some bound. This yields the complexity (Dlogn)
O(1)
(Cheng, 2002b), as the computation of the −D-th HP
is exponential in D, while all other parts of Algorithm
1 can be performed in a time polynomial in logN
and D. Compare this to Pollard’s p −1 method with
complexity (Blogn)
O(1)
, where B is the largest prime
factor of p −1). When D is small (or known), this
is polynomial in logn, which is asymptotically much
better than for any general classical non-quantum al-
gorithm.
This quickly becomes inefficient for larger val-
ues of D though, for several reasons. The degree
of the HPs grows quite fast, which complicates both
the computations in the ring Q and the computation
of the HPs themselves, and their coefficients grow
even more quickly, which might eventually become
a memory problem.
It is possible to compute the H
−D,n
(H
−D
modulo
n) directly (Sutherland, 2011) instead of the compu-
tation in Z, which significantly decreases the mem-
ory cost. For instance, H
−D
is about 93 GB for
D = 2 093 236 031 while H
−D,n
takes only 24 MB for
4096-bit n as the degree of the H
−D
is 100000.
The main practical limit is still the fact that the
method is only applicable to numbers of a special
form. For expected density results about these num-
bers, see Section 5.1.
5.1 The Expected Occurrence of
Factorable Numbers
We will limit ourselves to the RSA case here, because
it is probably the most important application of in-
teger factorization in the real-world. Let us take a
look at the expected frequency of factorable numbers.
First, let us assume that D is fixed and that p is a
random 2b-bit integer, so that 2
2b−1
< p < 2
2b
. The
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability
29
condition 4p −1 = Ds
2
is equivalent to
4p−1
D
being a
square of an odd integer. Since
2
2b+1
D
<
4p −1
D
<
2
2b+2
D
and the number of odd integer squares in the interval
2
2b+1
D
,
2
2b+2
D
is roughly
1
2
r
2
2b+2
D
−
r
2
2b+1
D
!
≈
2
b−2
√
D
, (2)
the number of possible 2b-bit primes such that the
square-free part of 4p −1 equals D can be roughly
estimated as
2
b−2
√
D
. Since the total number of 2b-bit
primes is around
2
2b
ln(2
2b
)
−
2
2b−1
ln(2
2b−1
)
≤
2
2b
b
(3)
by the Prime number theorem, we can roughly esti-
mate that the probability that a random 2b-bit prime
is vulnerable to factorization with respect to a given
D is around
b
√
D·2
b+2
(for D = 11 and 2b = 1024, this
is around 2
−507
).
If we instead consider all D’s up to some bound
B instead of one fixed D and use the well-known in-
equality
B
∑
k=1
1
√
k
< 2B −1,
it would follow from (2) that the number of possible
2b-bit primes such that the square-free part of 4p −1
equals D < B can be very roughly estimated as
B
∑
D=3
D≡3 (mod 8)
D is square-free
2
b−2
√
D
≤ 2
b−2
1
8
B
∑
D=1
1
√
D
< 2
b−4
·B,
which together with (3) gives an estimate that the
probability that a random 2b-bit prime is vulnerable
to factorization with respect to some D < B is around
Bb
2
b+4
(for B = 2
54
and 2b = 1024, this is 2
−453
).
5.2 Run-time Statistics
Implementation Details. We implemented the al-
gorithm in Sage, an open-source computer algebra
system. We note that to the best of our knowledge
there is no other implementation available for the vul-
nerable primes based on the same principle at the time
of writing this paper.
Since most of the mathematical utilities needed
are already implemented in Sage, the code is compact
and easy to use (although it could probably be opti-
mized even more). The only subtlety was the need
to set the internal recursion limit to 20 000 in order
to compute the n-th division polynomial (for n much
larger than 2
2048
, this should probably be increased
even more).
Experiment. The factorization algorithm complex-
ity is mainly determined by the class number h(−D)
– degree of the HP H
−D
. We sampled the func-
tion h(−D) over the square-free discriminants −D
(D ≡ 3 (mod 8)), so that we could measure the run-
ning time of the algorithm with the smallest discrim-
inant per given class number. To practically mea-
sure the running time of the factorization algorithm,
we performed the following experiment. For each
h(−D) ∈ [1,1000], we took the smallest absolute
value of the discriminant −D found, obtained by sam-
pling as described above. For each discriminant, we
randomly generated three composites with the vulner-
able prime p of bit-size b ∈ {256,512,1024,2048}.
The composite n = p ∗random prime(b) has thus bit-
size roughly 2b.
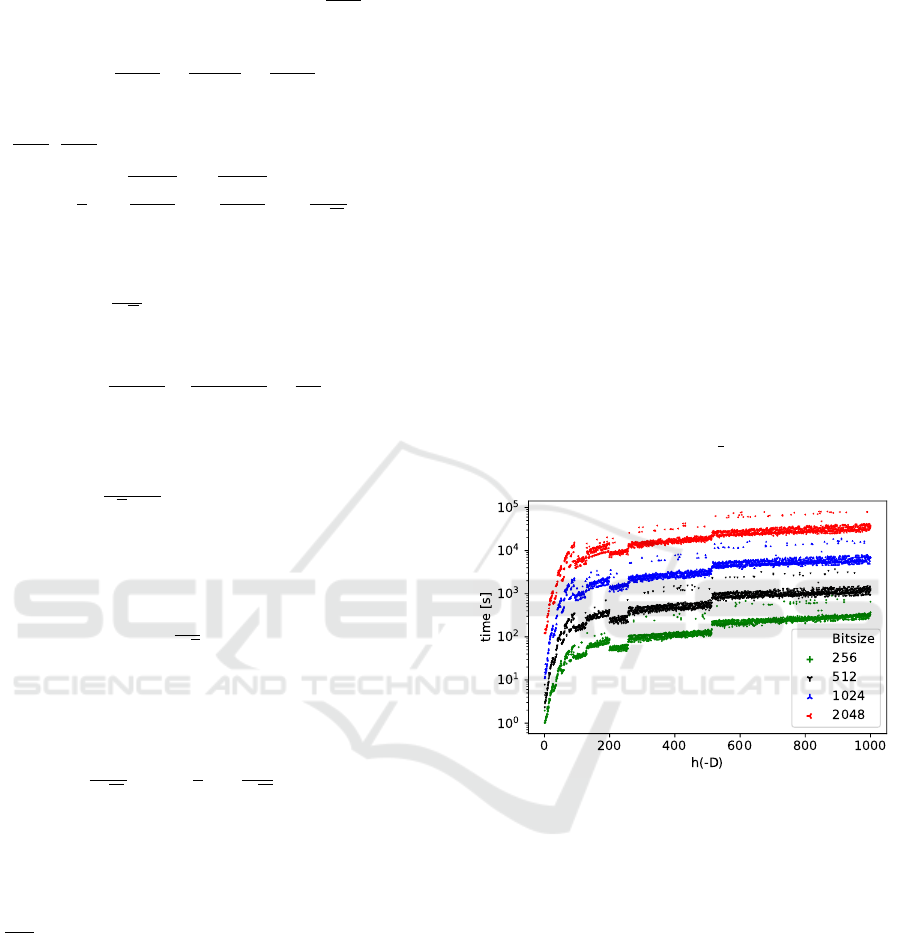
Figure 2: Observed running times of the factorization al-
gorithm for composite bit-sizes b ∈ {256, 512, 1024,2048}
bits for the smallest discriminant found per class number.
Three composites with the vulnerable prime of the given
bit-size were randomly generated per discriminant.
Figure 2 depicts the results of the experiment, i.e.,
the overall running time of the factorization algorithm
for composite n with respect to the given class num-
ber. Also, the relation between D’s and their corre-
sponding class numbers is depicted in Figure 3, where
we can see that the degree h(−D) of the HP oscillates
even for close values D.
For comparison, the current factorization record
using the number field sieve was achieved for an RSA
number with 768-bit modulus and it would take al-
most 2000 years if computed on a single core (in
2009) (Kleinjung et al., 2010).
SECRYPT 2019 - 16th International Conference on Security and Cryptography
30
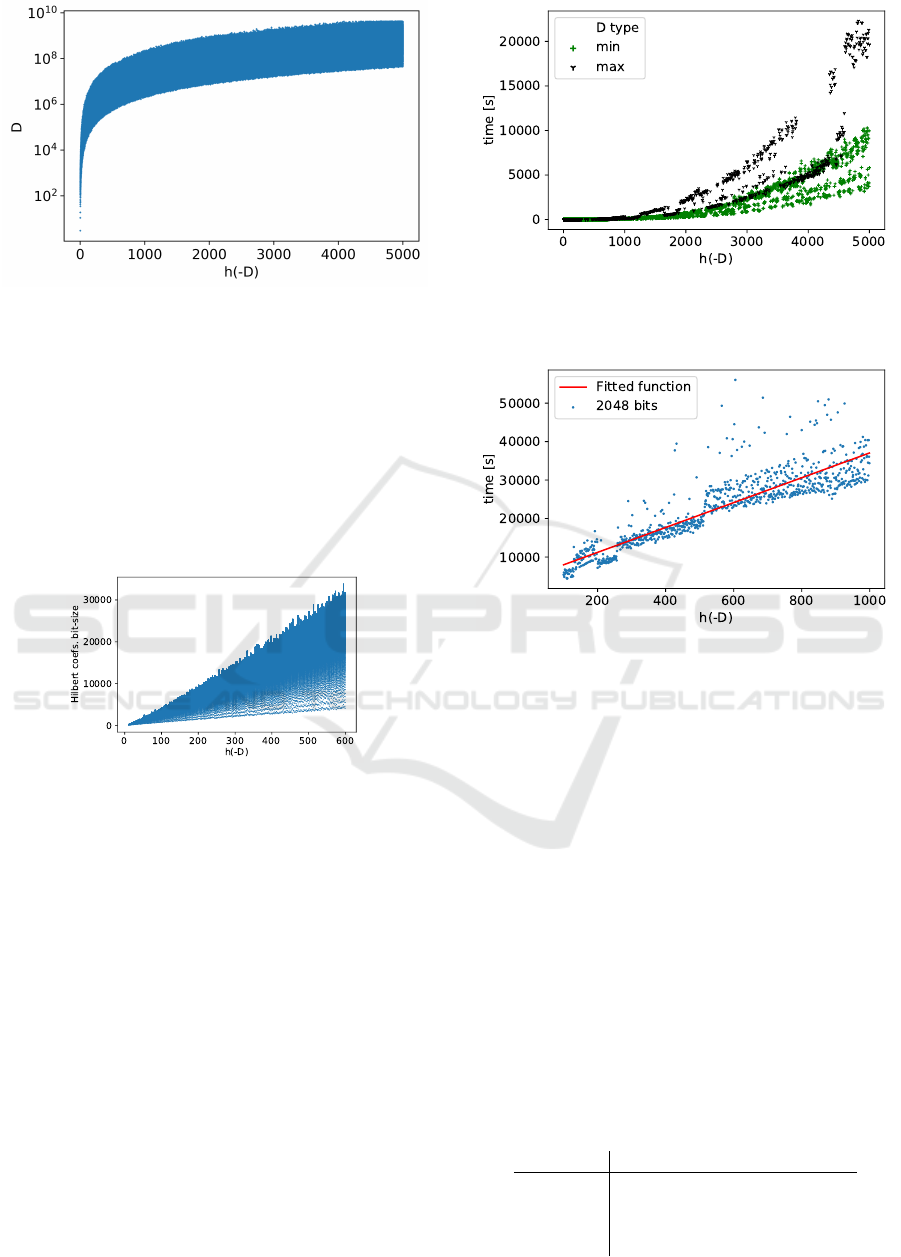
Figure 3: Log-scale of D sampled from the interval [0,2
32
+
3]) and corresponding h(−D).
Run-time Independence on D. The parameter D
affects the coefficient sizes and computation time of
the HP H
−D
. Besides that, the D does not affect the
rest of the algorithm. The computation of H
−D
is also
easily parallelizable. As we compute H
−D
modulo n,
from a certain class number, e.g., class number 110
for 4096-bit modulus, the coefficients of the H
−D
be-
come larger than n, thus the complexity depends only
on h(−D).
Figure 4: Bit-sizes of all Hilbert polynomial coefficients for
the smallest D corresponding to the given class number. The
figure illustrates run-time independence on D as coefficients
quickly grow over n.
Figure 4 demonstrates the growth of the coeffi-
cients of H
−D
(X). For comparison, Figure 5 shows
how the computation time is affected by D although
the class number is the same (in the case where reduc-
tion modulo n is only done afterwards).
Modulus Bit-size Complexity. As seen from the
experiment, the modulus bit-size contributes to the
overall complexity of the factorization algorithm by
a linear factor O(log(b)) with respect to the class
number as the modulus size mainly affects the divi-
sion polynomial. This enables us to empirically study
the factorization algorithm mainly with respect to the
class number with the lowest such D and with the low-
est bit-size to reduce computation time without af-
fecting the results validity. Figure 6 depicts the lin-
ear model curve fitting over 2048 prime based mod-
Figure 5: The time computation of the Hilbert polynomial
and values of maximal and minimal sampled D for class
numbers h(−D) in [1, 5000].
Figure 6: Running time for the factorization algorithm w.r.t.
h(−D) and fitted linear function for 2048 bit prime size.
uli and Table 1 shows the linear models fitted for all
tested bit-sizes.
Component Timing. The computation of the di-
vision polynomial is by far the most expensive op-
eration for class numbers under 1000 (and even for
higher ones if the HP is computed modulo n directly).
As class numbers grow over 1000, the H
−D
(X) com-
putation becomes more significant. Figure 7 illus-
trates the factorization algorithm timing by two com-
ponents, the evaluation of the division polynomial and
HP computation for b = 256. Around the class num-
ber 2000, the component timing becomes equal.
For higher class numbers, the H
−D
(X) computa-
tion asymptotically dominates the overall computa-
tion time.
Table 1: Runtime linear model fit with respect to the class
number.
p bit-size Fitted model
256 0.33887x − 1.17973
512 1.23834x + 81.44157
1024 6.57677x + 519.07422
2048 32.7223x + 4614.71032
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability
31

Figure 7: Algorithm log run-time breakdown to two major
components: the evaluation of the division polynomial and
the computation of H
−D
(X) for b = 256.
Inner Loop Iterations. Observe the number of in-
ner loop iterations in the depicted dataset. From the
total number of experiments 12 000 (1000·4 ·3), only
12 experiments needed more than one iteration. In
total, the average number of iterations is 1.001834.
The class number for all experiments requiring more
than one iteration was in the interval [1,4], which sup-
ports our claim that the number of expected iterations
quickly converges to 1 with higher class numbers.
Computation Resources. Due to the heteroge-
neous nature of the cluster and the job scheduling
system, the jobs were allocated different processors
types, namely Intel Xeon Gold 5120 2.20GHz, Gold
6130 2.10GHz, E5-2630 v3 2.40GHz, E5-2650 v2
2.60GHz. The worker nodes are shared among other
users, which affects caches of the processor and thus
the overall system performance. Due to the men-
tioned irregularities, the timing measurements are ap-
proximate. However, the jobs were allocated across
all CPU types randomly.
Running Time Step-changes. There are noticeable
changes in the running time of the factorization al-
gorithm for some class number ranges. Even though
the experiment jobs ran on a cluster with varying load
and processor types, we conclude these regions are
not a result of a systematic error as for each discrim-
inant there were three random composites generated,
this was performed for all four bit-sizes, thus it gives
12 different experiment jobs per single D. The effect
is observable in all bit-sizes in all experiments. The
regions are present even after the re-computation of
the region in further validation experiments. As the
division polynomial computation is the main running
time component, we conclude the regions are a result
of the particular Sage implementation, depending on
the class number. Currently, we have no detailed ex-
planation of the phenomena, and it remains an open
problem.
6 THE 4p −1 METHOD AS A
BACKDOOR
The analysis from the previous section shows that if
the RSA primes are sufficiently long and generated
randomly, it is almost impossible for the resulting
public key to be 4p −1 factorable in practice. Tak-
ing the contrapositive, if a public RSA key is 4p −1
factorable, there is an overwhelming probability that
at least one of the primes was generated in this way
on purpose, instead of being vulnerable by chance.
This could be interesting from the viewpoint of
kleptography (Young and Yung, 1997). It would be
possible to backdoor the prime number generation
methods in black-box devices (such as smartcards
or Hardware Security Modules (HSMs) to generate
prime(s) p such that the square-free part of 4p −1
is relatively small (as generating such primes is very
easy). We first describe the backdoor construction
process and later elaborate on the prospective detec-
tion methods, showing that the existence of the back-
door cannot be ruled out for the longer key lengths
like 2048 bits, if only keys (including private primes)
are available for the analysis.
In contrast, the RSA prime number generation in
a wide range of open-source cryptographic libraries
was already analyzed with no such backdoor found
(Svenda et al., 2016).
6.1 The Backdoor Construction
In this section, we investigate the properties of
Cheng’s 4p −1 method when used as a cryptographic
backdoor intentionally producing moduli that are fac-
torable. Namely, we analyze the possibility that the
backdoor with a particular choice of D will be both
reasonably efficient to exploit for an attacker with the
knowledge of chosen D (so he can compute the fac-
torization), yet very hard to detect by an Inquirer. We
define the Inquirer according to (Young and Yung,
1997) as a person examining the (large number of)
generated keys from a potentially backdoored imple-
mentation for the statistical presence of any charac-
teristics hinting at the existence of the backdoor. The
Inquirer wins if the backdoor is detected with non-
negligible probability. The attacker wins if the pres-
ence of the backdoor is not detected, yet the attacker
can still factorize the resulting keys in a reasonable
time frame.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
32

The use of the method as a backdoor has three
phases: 1) selection of suitable backdoor parameters,
2) generation of backdoored prime(s), and 3) factor-
ization of a given (backdoored) public key:
1. An attacker selects a value D with a suitably small
class number h(−D). An attacker can use either
a single fixed D (or a small number of them) for
all backdoored primes or generate a separate D for
every backdoored key.
2. During the RSA keypair generation, the first
prime is generated at random (non-backdoored),
while the second one is constructed as follows:
(a) Generate randomly an odd number s with the
length corresponding to the required length of
prime.
(b) Compute candidate prime p as p =
D·s
2
+1
4
.
(c) Check if candidate p is probable prime using,
e.g., the Miller-Rabin primality test.
(d) Output p if probable prime, or repeat the con-
struction with a different value of s if not.
3. The given public key is factorized using Algo-
rithm 1 as described in Section 3.
Method Advantages for Use as a Backdoor.
• All standard RSA key lengths now assumed se-
cure can be backdoored (including 2048, 4096
and 8192-bit lengths).
• No observable bias present in the public keys (if
the second prime is chosen at random and the
proper distribution of s is chosen).
• A favorable ratio between the factorization time
with the knowledge of D (an attacker) and the
time required by Inquirer to detect the existence
of such a D (see Figure 8).
• The adjustable factorization difficulty using value
D with suitable class number h(−D).
• The good parallelizability for the Hilbert polyno-
mial computation part of the factorization (Suther-
land, 2011) which dominates for the sufficiently
large class number – see Figure 7.
• The expected number of invocations of the Miller-
Rabin primality test during the keypair generation
is heuristically same as for the situation with truly
random (non-backdoored) primes.
Method Disadvantages (for use as a backdoor).
• Easy detection of the backdoor presence if private
keys are available for inspection and same D is
reused (two methods are discussed in Section 6.2).
• Need for quick establishment of the D used for
the key attempted for the factorization (as unique
D has to be used for every keypair).
• The backdooring of keys with short lengths (1280
bits and below) is detectable even when unique D
is used (Method 1).
• If the used value D is leaked, the backdoored keys
with this specific D become exploitable by anyone
(not “only us”).
6.2 Inquirer Detection Strategies
We propose three principally different methods to de-
tect the presence of backdoor for the different scenar-
ios concerning the availability of private keys for in-
spection and the length of the inspected keys.
Method 1: Inquirer with Access to the Public Keys
Only. An Inquirer picks a candidate D
i
value, as-
sumes the key being backdoored with this D
i
attempts
to perform the factorization using 4p −1 method. If
successful, both the presence as well as the actual pa-
rameter D
i
used is revealed. The na
¨
ıve method would
be to examine all possible values D
i
, starting from
11 until the allowed examination period is exhausted
(e.g., at least 1000 vCPU years worth of computa-
tion). Note that an attacker aims to use such a D that
has the corresponding class number h(−D) as small
as possible to achieve as fast factorization as possible.
Figure 3 shows the relation between the value D and
its h(−D).
Even if unsuccessful, this examination establishes
a lower limit on the computational time that an actual
attacker needs for the factorization of a key as seen
from Figure 3.
Figure 2 shows the running time to factor a com-
posite n with a particular choice of D, which is only
known to the attacker who generated n in this way,
i.e., using it as a potential backdoor. The experiment
illustrates the growth of the factorization complexity
for an attacker knowing the D. On the other hand, an
Inquirer trying to detect such a backdoor and without
the knowledge of particular D has to try all possible
D’s up to the D
max
. The detection complexity is thus
the sum of all factorization times up to the D
max
(or
surface under the curve up to the D
max
). For an illus-
tration of such case, see Figure 8.
Method 2: Inquirer with Access to the Private
Key(s) with Shorter Primes (up to ∼ 768 bits).
An Inquirer performs the direct factorization of 4p −
1 value by generic-purpose factorization method. The
resulting factors are then checked for the existence of
unexpectedly small D (or its multiplies), which would
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability
33

Figure 8: Estimated factorization times for an Inquirer
(without knowing D) and an attacker (knowing D) up to the
lowest D for class number 5000 and bit-size 1024. The in-
quirer tries all D’s up to the actual D.
implicate the possibility to use 4p −1 method for fac-
torization and thus a presence of the backdoor. The
remaining part must be also eligible for square root
computation. The expected size of D for a truly ran-
dom (non-backdoored) prime is large (around the bit-
length of the tested prime, see Figure 9 for the experi-
mental results from 10000 random primes), so a small
D is unexpected from non-backdoored keys.
Method 3: Inquirer with Access to a Large Num-
ber of Private Keys. An Inquirer collects large
number of private keys generated by inspected black-
box implementations and computes the batch-GCD
algorithm (Heninger et al., 2012) over all 4p − 1
values constructed from the corresponding primes.
Would the same D be used for any two primes, batch-
GCD will succeed in factorization, revealing the pres-
ence of the backdoor as well as D used. This method
is usable also for larger key lengths than would be
Method 2, efficiently analyzing 2048-bits keys and
longer.
Here we describe the batch-GCD method. Let
have g
i
= gcd
4p
i
−1,
∏
i6= j
4p
j
−1
for all primes
p
i
. Then for any two primes: 4p
i
−1 = D
i
s
2
i
and
4p
j
−1 = D
j
s
2
j
it holds that if D
i
= D
j
=⇒ D
i
|g
i
.
Thus, we factorize each g
i
=
∏
q
e
k
k
, compute a
candidate D
0
i
=
∏
q
h
k
k
, 0 ≤ h
k
≤ e
k
, i.e., a divisor of
g
i
, such that D
0
i
≡ 3 (mod 8)) and D
0
i
is square-free.
If
4p
i
−1
D
0
i
is a perfect square for some D
0
i
, we found D
i
,
a square-free part of the 4p
i
−1.
As an Inquirer can collect and investigate a large
number of private keys during batch-GCD, the prob-
ability of not investigating at least one pair of two
primes with the same D quickly decreases due to
the Birthday paradox. This motivates any sensible
backdooring attacker to use different D for every new
prime generated. Having a unique D generated in
turn creates the need for efficient reconstruction of the
D’s value on an attacker’s side, e.g., leaking it in ad-
ditional information like padding or maintaining the
large database of all the Ds used.
6.3 Audit of Real-world Keys
We collected a large dataset of 512, 1024 and 2048-bit
RSA keypairs generated by fifteen different crypto-
graphic smartcards and three HSMs with both public
and private keys stored (44.7 million keypairs in to-
tal). As we knew the keypair primes, we direcly use
Inquirer methods 2 and 3 to search for a D and at-
tempt to detect a potential backdoor.
Application of Method 2: Factorization of 4p-1.
We used a randomly selected subset from all keys
collected with 5 000 512-bit RSA keypairs and 100
public 1024-bit RSA keys for every inspected device.
Each prime is analyzed for vulnerability to the 4p −1
factorization method, using Algorithm 1 implemented
by the Sage computer algebra system for the actual
computation.
We factored 4p −1 (and 4q −1) and computed
their square-free parts. In the majority of cases, the
square-free parts were the numbers themselves, and
the smallest square-free part found having 490 bits
in the 1024-bit case and 229 bits in the 512-bit case.
Thus these public keys are far from being 4p −1 fac-
torable, and it would be impractical to use the 4p −1
factorization method on these keys. In fact, if these
keys could be factored with the method, then so would
be any randomly generated keys of the same bit-size.
The section 6.3.1 further discusses the observed re-
sults. Note, that we were not able to completely fac-
tor a small portion of these numbers in the given time
frame (2 hours for one number), but since the Sage
factorization algorithm contains a square test and re-
vealed prime factors as large as 110 bits in other cases,
we can be reasonably sure that the square-free parts of
these unfactored numbers are much larger than 2
54
as
well.
Application of Method 3: Batch-GCD. We used
all 44.7M collected private keys, including the 2048-
bit keys (these keys are not eligible for Method 2 due
to their length) to search for the shared value of D us-
ing the batch-GCD algorithm (Heninger et al., 2012).
Moreover, we added #D =
∏
D≤50868011
D, i.e., the
product of all square-free D’s congruent to 3 mod-
ulo 8 up to the minimal D with h(−D) = 5000 to a
batch-GCD dataset.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
34

We found that no two primes share a common
square-free part D in 4p −1 and due to #D all Ds
used have to be greater than 50868011. Therefore, we
can conclude that if the the backdoor is present, each
prime has to have its own unique D (as reusing any D
is very unlikely to be missed as it would have to be
drawn from a set of (44.7M)
2
possible Ds due to the
Birthday paradox to evade detection on our dataset).
Note that a unique D also means, that an attacker must
be able to 1) infer the D used for the given public key
and 2) compute the Hilbert polynomial for this spe-
cific D, slowing down the subsequent factorization.
Figure 9: Histogram of bit-lengths of square-free parts ob-
tained from the factorization of 4p −1 values constructed
from 10000 primes found in 512-bit RSA keys. All other
devices than explicitly listed produced a distribution undis-
tinguishable from the one of the random primes generated
by Sage (Sage RNG). The reason for the observed differ-
ences are explained in Section 6.3.1.
6.3.1 Distribution of Square-free Parts
We compared the distribution of the square-free parts
of 4p − 1 and 4q − 1 obtained by application of
Method 2 for every analyzed device and compared
these to the reference distribution for p and q gen-
erated randomly by Sage. No significant differences
were found, with two exceptions – G&D SmartCafe
6.0 and NXP J2E145G smartcards, as shown on Fig-
ure 9. Here, we explain the reason for the observed
differences.
The expected probability that the number 4p −1
is square-free for a large random prime p is
1 −
∑
r an odd prime
1
r(r −1)
≈ 0.748
(established experimentally from 10
6
random primes
generated by Sage), because for any (small) odd
prime r, 4 is invertible modulo r
2
and we have 4p ≡ 1
(mod r
2
) iff p ≡
1
4
(mod r
2
) and there are exactly
r(r −1) residue classes modulo r
2
that can contain
p. This is consistent with the experimental results ob-
tained from both Sage and most cards. However, we
observed from (Svenda et al., 2016) that G&D Smart-
Cafe 6.0 avoids primes p such that p −1 is divisible
by 3 or 5, while NXP J2E145G avoids primes p such
that p −1 is divisible by any number between 3 and
251 inclusive. If p 6≡1 (mod 3), then
4p −1 ≡ p −1 6≡0 (mod 3)
(so that 4p −1 cannot be divisible by 9, which would
otherwise happen with probability
1
2·3
). However, we
did not account for the effect of this condition on other
primes r, so the probability that 4p −1 is square-
free will not increase by
1
6
in this case, but only by
0.148 (for convenience again found experimentally).
Yet still, forbidding the case p ≡1 (mod 3) increases
the resistance to the factorization (even if only very
slightly). This case is special because
4p −1 −(p −1) = 3p ≡0 (mod 3).
On the contrary, forbidding the case p ≡ 1 (mod r)
for r 6= 3 decreases this resistance (although even
more marginally), because 1 is coprime to r and this
leads to forbidding r “good” possible residue classes
of 4p −1 modulo r
2
(note that 1 6≡
1
4
(mod r)
2
), so
that the probability that 4p −1 will be divisible by r
2
will be
1
r(r−1)−r
=
1
r(r−2)
instead of
1
r(r−1)
in the case
that the condition p 6≡ 1 (mod r) would not be im-
posed.
Experimentally (and for the sufficiently large
primes), we found that if p −1 has neither the fac-
tor 3 nor the factor 5, the probability that 4p −1 is
square-free is approximately 0.88. If a prime has no
factor between 3 and 251, the probability is approx-
imately 0.875, which closely matches the results ob-
tained from G&D SmartCafe 6.0 and NXP J2E145G
smartcards, respectively.
7 CONCLUSIONS
We proposed an improved version of Cheng’s 4p −1
method and performed a thorough analysis both theo-
retically and empirically. The conclusion is that even
though the 4p −1 factorization method is powerful in
theory, it does not seem to have any impact on real-
world applications due to a very limited set of num-
bers on which it can be applied, occurring extremely
rarely if the primes are randomly generated.
However, an attacker may intentionally generate
the primes to result in the factorable keys to form so-
called kleptographic attack, especially in the black-
box devices like cryptographic smartcards. We there-
fore analyzed more than 44 millions of keypairs gen-
erated by 15 smartcards and 3 HSMs and found no
indication of the backdoor presence in any of the ana-
lyzed devices. We were able to rule out the existence
of this backdoor for the key lengths of 512 and 1024
I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability
35

bits, where the detection method based on the full fac-
torization (Method 2) is applicable as no small D was
found.
Unfortunately, we cannot rule out the presence of
the backdoor in keys with longer lengths, like 2048
bits, despite of the availability and inspection of the
private keys. An attacker may use a unique D for
every prime generated, thus evading the detection by
batch-GCD based method (Method 3). The complete
backdoor detection (or its exclusion) is still an open
question.
As already mentioned in (Cheng, 2002b), there are
several other possibilities for future work on the topic
of 4p −1 factorization, including the exploration of
the possibility of using Weber polynomials instead of
Hilbert polynomials (whose coefficients do not grow
as quickly), using curves of a higher genus or study-
ing the discrete logarithm problem for primes of the
same structure. Moreover, the inherent asymmetry of
the factorization with and without the knowledge of D
could prove useful in the construction of some cryp-
tosystems.
ACKNOWLEDGEMENTS
We acknowledge the support of the Czech Science
Foundation, project GA16-08565S. The access to the
computing and storage resources of National Grid In-
frastructure MetaCentrum (CESNET LM2015042) is
greatly appreciated.
REFERENCES
Adrian, D., Bhargavan, K., et al. (2015). Imperfect for-
ward secrecy: How Diffie-Hellman Fails in Practice.
In 22nd ACM SIGSAC Conference on Computer and
Communications Security, 2015, pages 5–17.
Bach, E. and Shallit, J. (1985). Factoring with cyclotomic
polynomials. In Mathematics of Computation, vol-
ume 52, pages 443–450. IEEE.
Boneh, D., Durfee, G., and Howgrave-Graham, N. (1999).
Factoring n = p
r
q for large r. In CRYPTO ’99, pages
326–337. Springer-Verlag.
Br
¨
oker, R. and Stevenhagen, P. (2007). Efficient CM-
constructions of elliptic curves over finite fields.
In Mathematics of Computation, volume 76, pages
2161–2179. AMS.
Bundesamt fur Sicherheit in der Informationstechnik
(2018). Cryptographic Mechanisms: Recommenda-
tions and Key Lengths. Technical Guideline: TR-
02102-1, BSI.
Cheng, Q. (2002a). A New Class of Unsafe Primes. IACR
Cryptology ePrint Archive, 2002:109.
Cheng, Q. (2002b). A New Special-Purpose
Factorization Algorithm. Citeseer. http:
//citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.
1.8.9071&rep=rep1&type=pdf[Accessed 6.2.2019].
Coron, J.-S., Faug
`
ere, J.-C., Renault, G., and Zeitoun, R.
(2016). Factoring n = p
r
q
s
for large r and s. In RSA
Conference on Topics in Cryptology - CT-RSA 2016 -
Volume 9610, pages 448–464. Springer-Verlag.
Giry, D. (2019). Cryptography Key Length Recommenda-
tions. http:www.keylength.com.
Heninger, N., Durumeric, Z., Wustrow, E., and Halderman,
J. A. (2012). Mining your Ps and Qs: Detection of
Widespread Weak Keys in Network Devices. In 21st
USENIX Security Symposium (USENIX Security 12),
pages 205–220. USENIX.
Kleinjung, T., Aoki, K., et al. (2010). Factorization of a
768-bit RSA modulus. In Annual Cryptology Confer-
ence, pages 333–350. Springer-Verlag.
Lenstra, H. W. (1987). Factoring Integers with Elliptic
Curves. In Annals of Mathematics, volume 126, pages
649–673. Princeton University.
National Institute of Standards and Technology (2007).
Security Requirements for Cryptographic Modules.
FIPS 140-2, NIST.
Nemec, M., Sys, M., Svenda, P., Klinec, D., and Matyas,
V. (2017). The Return of Coppersmith’s Attack:
Practical Factorization of Widely Used RSA Mod-
uli. In ACM’2017 SIGSAC Conference on Computer
and Communications Security, CCS ’17, pages 1631–
1648. ACM.
Pollard, J. M. (1974). Theorems on factorization and pri-
mality testing. Mathematical Proceedings of the Cam-
bridge Philosophical Society, 76(3):521–528.
Pollard, J. M. (1975). A Monte Carlo method for factor-
ization. In BIT Numerical Mathematics, volume 15,
pages 331–334. Springer-Verlag.
Pollard, J. M. (1993). Factoring with cubic integers. In
The development of the number field sieve, pages 4–
10. Springer-Verlag.
Pomerance, C. (1985). The Quadratic Sieve Factoring Al-
gorithm. In Advances in Cryptology: EUROCRYPT
’84., pages 169–182. Springer-Verlag.
Rubin, K. and Silverberg, A. (2007). Choosing the correct
elliptic curve in the CM method. In Mathematics of
Computation, volume 79, pages 545–561. AMS.
Shirase, M. (2017). Condition on composite numbers easily
factored with elliptic curve method. IACR Cryptology
ePrint Archive, 2017:403.
Sutherland, A. V. (2011). Computing Hilbert class polyno-
mials with the Chinese remainder theorem. In Math-
ematics of Computation, volume 80, pages 501–538.
AMS.
Svenda, P., Nemec, M., Sekan, P., Kvasnovsky, R., For-
manek, D., Komarek, D., and Matyas, V. (2016). The
Million-Key Question – Investigating the Origins of
RSA Public Keys. In The 25th USENIX Security Sym-
posium (UsenixSec’2016), pages 893–910. USENIX.
Williams, H. C. (1982). A p + 1 Method of Factoring. In
Mathematics of Computation, volume 39, pages 225–
234. AMS.
Young, A. L. and Yung, M. (1997). Kleptography: Using
Cryptography Against Cryptography. In Advances in
Cryptology - EUROCRYPT ’97, International Confer-
ence on the Theory and Application of Cryptographic
Techniques, Konstanz, Germany, 1997, pages 62–74.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
36
