
Development and Validation of Active Roll Control based on
Actor-critic Neural Network Reinforcement Learning
Matthias Bahr, Sebastian Reicherts, Philipp Maximilian Sieberg, Luca Morss and Dieter Schramm
Chair of Mechatronics, University of Duisburg-Essen, Lotharstraße 1, 47057 Duisburg, Germany
Keywords: Artificial Neural Network, Active Roll Control, Neural Controller, Reinforcement Learning, Actor-critic,
Driving Maneuvers, Vehicle Dynamics, Machine Learning.
Abstract: This paper deals with the application of machine learning for active roll control of motor vehicles. For this
purpose, a special learning method based on reinforcement learning with an actor-critic model is used. It
discusses and elaborates the basic design of the neural controller and its optimization for a fast and stable
training. The methods mentioned are then validated. Both the training and the validation data are simulatively
generated with the software environments MATLAB / Simulink and IPG CarMaker, while the architecture
and training of the artificial neural network used is realized with the framework TensorFlow.
1 INTRODUCTION
Investigations in the field of vehicle dynamics and the
development of driver assistance systems have the
goal of increasing vehicle safety and ride comfort.
Active roll stabilization is an assistance system that
enhances both vehicle safety and driving comfort. By
means of actuators, components of the chassis can be
arbitrarily influenced within their physical limits.
These actuators are variably controlled via a control
unit. The development and optimization of such
regulations is one of the main tasks in the design of
driver assistance systems. In addition to conventional
PID controlling, other control algorithms such as a
fuzzy control are possible (Sieberg et al., 2018).
Due to the relevance of machine learning in
neuroinformatic, artificial neural networks are
increasingly being used in control engineering as
well. These can either completely replace the
conventional controllers or specify setpoint values for
the regulation, which are forecasted from the process
flow of the system to be controlled. This applicability
to active roll stabilization is presented in this article.
In comparison to supervised and unsupervised
learning the application of reinforcement learning to
control tasks of vehicle dynamics is rarely researched.
Also, the presented specific method of the actor-critic
is infrequently used for control tasks. Specially, the
transfer to the application of vehicle dynamics is a
comparative unexplored science. So, the developed
model and method has a highly scientific relevance.
The focus of this paper is not on the development
of an optimized controller for perfect stabilization,
but much more on the documentation that the
developed model proves useful for controlling the roll
angle of a motor vehicle and thus for other driving
dynamics. In this case, the roll angle is to be reduced
in comparison to a passive stabilization with common
spring and damper elements. This work is aimed to
investigate the utility of the actor-critic method for
control tasks and particularly controlling vehicle
dynamics. Nevertheless, the method can be applied to
a broad spectrum of control tasks.
This article will present the approach to develop a
controller based on the actor-critic Reinforcement
Learning method. The training and validation are
accomplished within a simulation environment
including MATLAB/Simulink, IPG CarMaker and
TensorFlow. The results are validated in comparison
to a passive roll stabilization.
2 RELEVANT RESEARCH
Boada et al., (2009) have made an approach on the
active control of roll-stabilizers based on machine
learning methods. Here, a simple ANN is trained on
the simulation of a single unit heavy vehicle model
with five degrees of freedom, using RL methods. The
ANN-architecture consists of a dynamic input layer
and an output layer. The few degrees of freedom of
the model used and the very ideal training and testing
36
Bahr, M., Reicherts, S., Sieberg, P., Morss, L. and Schramm, D.
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning.
DOI: 10.5220/0007787400360046
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 36-46
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
conditions leave room for the development of
machine learning control for more realistic scenarios.
In addition, the vast recent advances in the software
and hardware for developing artificial neural
networks, allow for more flexibility and potential in
implementing and validating RL methods.
Fu et al., (2017) apply RL for active suspension
control on a quarter-vehicle model with two degrees
of freedom. Due to the faster dynamics required for
vibration control, the controller uses a single critic-
ANN rather than the computationally more expensive
actor-critic dual ANN architecture, as it is sufficient
for the roll stabilization task presented in this paper.
In addition to the development in the automobile
sector, comparable neural network control
approaches in other fields are also considered since
certain tasks here can have close resemblance to the
intended approach in this proposal. Li et al., (2005),
for instance, develop a neural network controller for
a fin stabilizer for marine vessels utilizing an adaptive
neural network controller.
As part of the research presented in this article a
model based on actor-only reinforcement learning
was developed with less satisfactory results but with
purposeful findings.
3 MACHINE LEARNING
Machine learning is a highly discussed field in
modern science. Its goal is to generate numerical
solutions for certain problems using empirical
knowledge respectively data sets. The resulting
algorithm is represented by an artificial neural
network and worked out by various learning methods.
These learning methods can be divided into three
fundamental classifications, these being supervised,
unsupervised and reinforcement learning. The latter’s
use is investigated in this model and its vast majority
of approaches can be classified with the actor-only or
the critic-only methods (Konda and Tsitsiklis, 2003).
Both have advantages and disadvantages regarding
the way they operate. To bring these advantages
together and compensate the disadvantages, the
combined actor-critic model is used.
This chapter will show the usage of an artificial
neural network, the operation principle of
reinforcement learning and the actor-critic method
specifically.
3.1 Artificial Neural Network
The neural network is a term related to the
neurosciences and describes the composition of a
variety of neurons that resemble a function in a
nervous system. The engineering sciences try to
simulate the processes of a nervous system and
transfer it to technical problems. In contrast to a
biological construct, the term of an artificial neural
network is used in this context.
The origin and a simplification of artificial neural
networks is the perceptron (Rosenblatt, 1958). A
perceptron exclusively processes binary facts and can
thus represent Boolean functions. If a certain
threshold is exceeded by weighted inputs, the
perceptron is activated and outputs a one (true).
Otherwise it will respond with a zero (false). As a
result, different logic gates and classifications can be
performed, e. g. the XOR gate (Exclusive OR gate).
An artificial neural network is a generalization of a
perceptron and can also solve more complex
problems.
In general, artificial neural networks can be
defined by three elements: the single neuron, the
topology and the learning rule.
3.1.1 Neuron
A neuron can be mathematically described by its
activation, which represents the output. This
activation depends on the inputs of the neuron, the
weights of the inputs and the activation function.
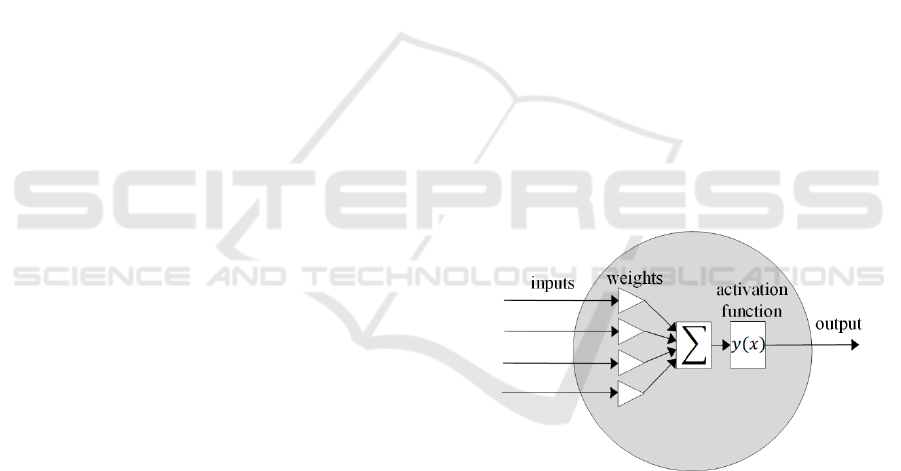
Figure 1: Structure of a neuron.
The inputs
are multiplied by their respective
weights
and then summed up, so that the argument
of the activation function is calculated by:
∙
(1)
The weights are the parameters that are gradually
adjusted and optimized during the training. They are
randomly initialized at the beginning.
Many different functions can be used for the
activation function. Karlik and Olgac (2011) compare
some common activation functions and analyse their
impact in the training performance. The activation
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning
37
function can be chosen separately for each layer or
even each single neuron in the artificial neural
network. The presented model in this article uses a
combination of three different functions: the
hyperbolic tangent shown in equation (2), a linear
function shown in equation (3) and the Rectified
Linear Unit shown in equation (4).
tanh
(2)
0,
(3)
(4)
The function value of the activation function
represents the output of the neuron and is used either
as input to the neurons of the next network layer or as
output of the network.
3.1.2 Topology
An artificial neural network consists of at least two
layers: the input and the output layer. For simple
learning problems, these two layers can be sufficient
to find an adequate solution. For more complex
systems, hidden layers are needed. If one or more
hidden layers are present, the term of deep learning is
applicable (Goodfellow et al., 2016).
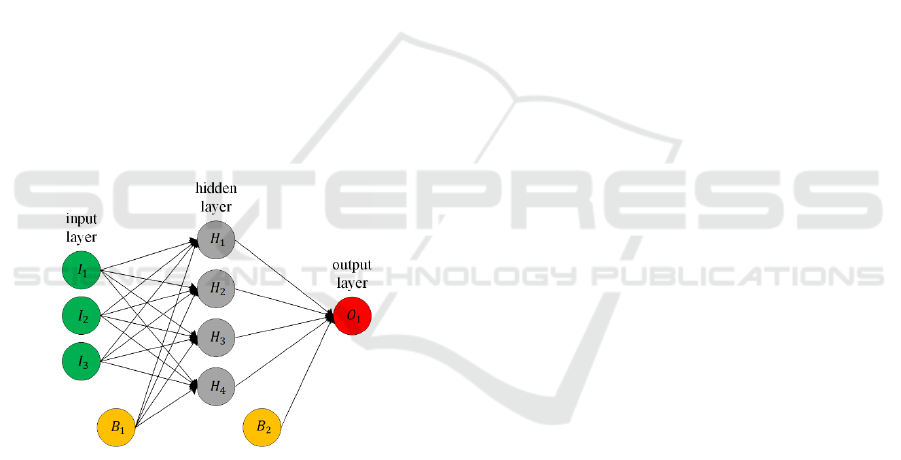
Figure 2: Exemplary architecture of an artificial neural
network.
The input layer with the neurons maintains the
values of the data sets used and thus the input of the
artificial neural network. The output layer with the
neurons maintains the output of the network. The
number of hidden layers with the neurons is not
limited but is recommended to be kept as small as
possible to reduce its complexity.
In addition to the outputs of the previous layer,
every hidden layer and the output layer has a bias .
The bias is a constant value and can be parameterized
during training, since it is also multiplied with its
weights. It is necessary to calculate a constant offset,
which is independent of any inputs e.g. for
compensating measuring noise.
The numerical relationship between the input and
output of the artificial neural network gives the
following:
∙
,
∙
,
(5)
∙
,
∙
,
(6)
With
being the number of input neurons and
being the number of neurons of the hidden layer.
If the inputs of a neuron consist only of the outputs
of the previous layer and the bias, it is referred to as a
feedforward network. If, on the other hand, the output
of the neuron is fed back as an input with a time delay,
a recurrent network is existent. This causes the output
of a neuron to become dependent on an output from
the previous time step. In this work, a fully connected
feedforward neural network is used.
3.1.3 Learning Rule
The learning rule is used to find suitable values for
the weights , with which the desired output is
achieved with a tolerable error. Equations (5) and (6)
show that the output is directly dependent on the
weights and the activation functions. An influence
during training only can be taken on the weights. The
basis of the most commonly used learning rules is the
Hebbian learning rule that says that a weight
,
is
adjusted when neuron and neuron are active at the
same time (Hebb, 1949). The weight change ∆
,
is
dependent on the outputs of the respective neurons
and
and a fixed hyperparameter . It forms the
product of these three components, so the
mathematical expression for weight adjustment
becomes:
∆
,
∙
∙
(7)
The parameter is the learning rate and an
elementary part of the training of an artificial neural
network. It decisively determines with which step
size the weights are adjusted. The learning rate can be
changed during training to ensure continuous learning
progress. However, an optimal learning rate cannot be
determined analytically due to the dependence on
randomness.
In this article a method with a gradient descent,
specifically backpropagation is presented. Therefore,
the squared error, also called loss , between the
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
38
desired output
and the observed output
, the
latter resulting from the random weight initialisation,
is calculated.
1
2
(8)
The bisecting factor is used for simpler
differentiation. The loss represents the deviation from
the optimum the controller can achieve. So, the goal
of the artificial neural network is to minimize it in a
proper way. To use this error for the weight
adjustment the partial derivatives and thus the
gradient is computed for every single weight. For
example, the modification of the weights between the
input and the first hidden layer is calculated as
follows:
,
,
∙
∙
,
(9)
With being the summed-up inputs and the output
of the respective neuron. Any connection between
layers can be computed analogously and thereby
every single weight can be adjusted separately. This
enables the possibility to propagate the summarized
error back to every single weight and to customize
it accordingly. This gradient now is multiplied with
the learning rate to get the weight change.
∆
,
∙
,
(10)
With advancing during the training, the loss
diminishes and thus the weight changes do. So, the
training always becomes more precise.
Because the gradient descent requires a given
output as a desired output
to calculate the loss, it
is often used for supervised learning. This article
however shows how to use it with reinforcement
learning.
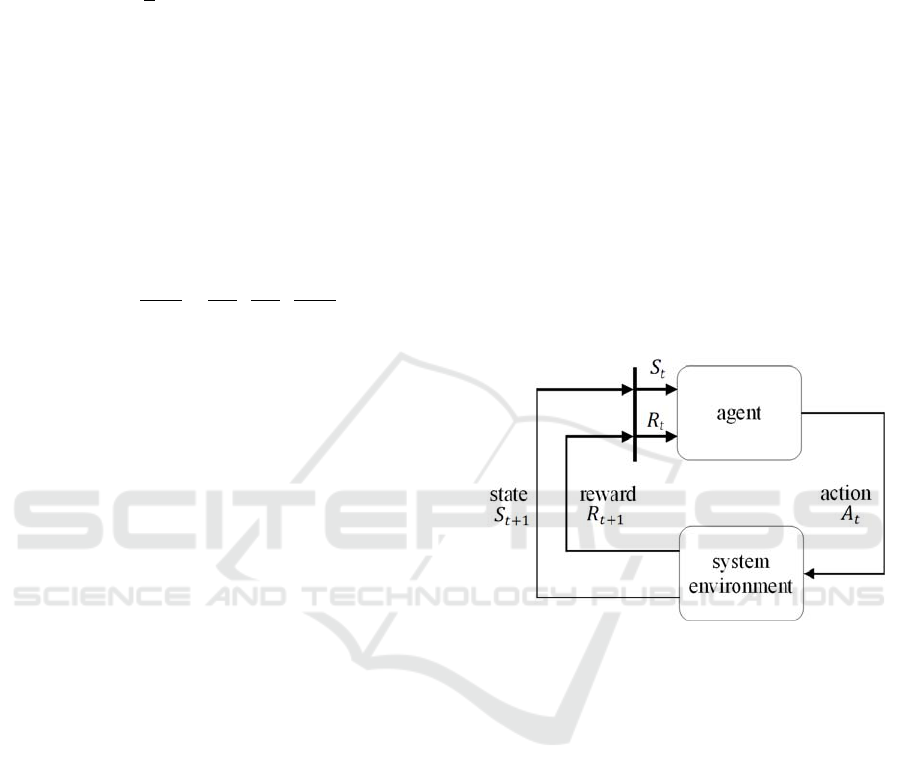
3.2 Reinforcement Learning
Reinforcement learning pursues the goal of assigning
inputs of the artificial neural network to certain
outputs in order to achieve a maximum reward
(Sutton and Barto, 2018). The artificial neural
network and the learning method, in the following
referred to as the agent, continuously interacts with
the system environment rather than with stored
training data sets as is the case in supervised or
unsupervised learning. The inputs of the artificial
neural network correspond to the states of the system
e.g. the roll angle and the outputs to the actions
carried out by the system e.g. the actuated torque. One
of the agent's responsibilities is determining the
desired nominal value
. It does this without
having any information about which action to take in
which state or whether the last performed action was
right or wrong. Instead, it must find out through
appropriate training, which action leads to the highest
reward. This is calculated by the system environment
by a given reward function for the current state
, the
associated executed action
and the resulting state
and is to be selected so that the agent in the case
of the maximum value, performs the desired action.
The reward function should therefore always be set
up as a function of a desired reference state or action
and is calculated by:
1
²
(11)
With R being the reward and the state or action to
be controlled with respect to the desired reference
state or action
.This results in a maximum reward
of one. Figure 3 shows the flow chart of
reinforcement learning.
Figure 3: Flow chart of reinforcement learning (Sutton and
Barto, 2018).
The agent receives the state and a reward from
the system environment in each time step and
calculates an action depending on the current level
of training. The assignment of the actions to the
respective states is summarized in the agent's
policy .
(12)
This policy will be adjusted during the training
through two simultaneous processes called
exploitation and exploration. In the case of
exploitation, the agent prefers already known and
executed actions that lead to a high reward. To be able
to get to know these actions and the underlying states
and thus incorporate them into its training data set, it
must react to states differently during exploration
than the previous training provides. This happens
through random variations of the already known
actions. The action selected by the agent may be
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning
39

numerically set with a randomly generated deviation
and thereby achieve a potentially higher reward. The
agent would therefore adapt its policy. Exploration
and time delayed reward are the two most important
characteristics that differentiate reinforcement
learning from other learning methods (Sutton and
Barto, 2018).
Due to this, it has the advantage that it can be
applied to interactive disciplines and to unknown,
dynamic environments and systems. While
supervised and unsupervised learning are limited to
learning data sets and extending to other data sets,
reinforcement learning can train follow-up states that
have been induced by the choice of the previous
action, thus involving a wide range of state-space.
3.2.1 Temporal Difference Learning
Temporal difference learning is a variant of value
approximation and is used by the Critic in the
developed model. Here, the agent adapts its policy not
only after a series of actions based on the return ,
which is simply the sum of successive rewards, but
continuously in each iteration step based on the
action-value function
,
. This determines,
comparable to the return, the sum of successive
rewards. However, in this case it does not wait for the
following iteration steps to be performed and instead
uses the expected rewards from the current strategy.
This means that
,
is always determined as a
function of the current policy and contains
approximated rather than real values. As a result, no
defined end of an episode is necessary, and the value
can be estimated continuously.
,
,
|
,
(13)
The agent sets up a new prediction of the action-value
in each step. The basic idea of temporal difference
learning is to minimize the deviation between
,
of
the current step and
,
of the next step (Tesauro,
1995). This is done by adjusting the weights of the
artificial neural network by means of
backpropagation. The loss to be minimized is then
defined as follows:
1
2
∙
,
,
.
(14)
In temporal difference learning, the policy is
therefore not optimized directly, but rather its
evaluation in the form of the action-value
.
3.2.2 Policy Gradient Method
An alternative to the value approximation or temporal
difference learning is the policy gradient method,
which is used by the Actor in the developed model.
The policy of the agent is parameterized with the
weights and a gradient method is used. Thus, a
policy is trained, which assigns the actions directly
to the states by equation (12). Through selective
weight adjustment, the desired relationship between
states and actions can be achieved.
The gradient
is approximated by the
current policy and the return
and is used by
equation (10).
,
,
,
,
(15)
For a detailed explanation and derivation of the
method, the literature of Sutton et. al. is
recommended (Sutton and Barto, 2018).
Compared to temporal difference learning, a
policy is generated directly which maximizes the
approximated return
depending on the gradient
instead of minimizing a deviation in the form of the
loss. Backpropagation can also be used for this
maximization of
.
3.3 Actor-critic
A large majority of reinforcement learning methods
can be categorized as actor-only and critic-only
(Konda and Tsitsiklis, 2003). While the
approximation of the action value function is used for
the critic-only, the actor-only uses a policy gradient
approximation (Sutton et al., 1999).
A disadvantage of the policy gradient method is
that the estimation of the gradient
has a high
variance and thus can lead to unwanted jumps in the
weight adjustment. In addition, each policy
adjustment creates a new gradient that is independent
of the previous one, which in turn prevents the
accumulation and consolidation of previous
information (Konda and Tsitsiklis, 2003). In the case
of a critic-only with a value approximation, on the
other hand, the policy is not optimized directly but via
,
. As a result, in principle good
approximations can be achieved, but there is no
guarantee that they will get close enough to their
optimum and achieve a sufficiently tolerable result.
The actor-critic model combines the advantages
and largely compensates the disadvantages of actor-
only and critic-only. Two separate artificial neural
networks are generated and trained, one each for the
actor and the critic. Together they form the agent.
The critic receives the state and the reward
from the system environment and the action from
the actor. From these quantities, the action value is
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
40
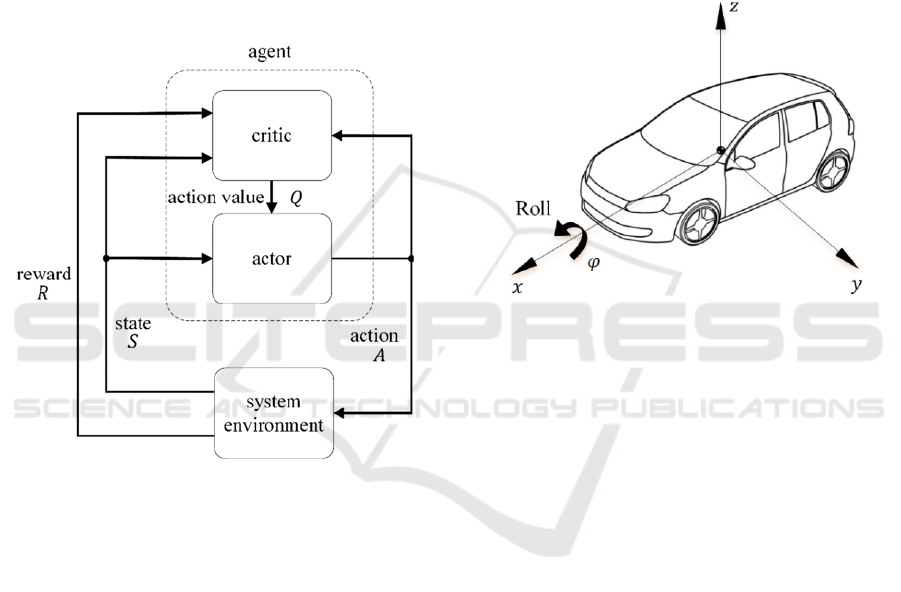
determined and the loss E optimized according to
equation (14). Then the critic transfers the
action-value to the actor, which maximizes it with the
policy gradient method. Since two successive actions
and states are required for temporal difference
learning, the states and actions are buffered and
transferred in the next step. This results in the model
shown in figure 4.
For the adjustment of the critic the tuple
,
,
,
,
is necessary. The actor
determines its policy using and after completing
the training, it is the part of the model that represents
the neural controller, as it sends an action back to the
system environment depending on the state.
Figure 4: Flow chart of the used actor-critic model
(Szepesvári, 2009).
4 VEHICLE DYNAMICS
For the development of a neural controller, an
understanding of the dynamical system to be mapped
is not of great importance, since the neural controller
is supposed to independently recognize and apply the
respective structure. Nevertheless, the concepts of
rolling and stabilizing are explained shortly.
The term "roll" describes the rotation around the
body-fixed longitudinal axis, which is quantified by
the angle . This movement largely depends on the
lateral and vertical dynamics of the vehicle and is
shown in figure 5.
The stabilizer, which is the actuator of the active
roll control, is rotatably mounted on the vehicle body
and connected at both ends with the respective wheel
suspensions. With different deflection of the two
wheels, the levers experience differently large
deflections, which result in a twisting of the torsion
bar and thus in a corresponding torsional torque
(Schramm et al., 2018).
For an active influence by the stabilizer this is
mechanically separated in the middle and the
resulting free ends coupled via an actuator. This
actuator is performed in this work by an electric
motor. Instead of the passive torque generated by
torsion, the electro-mechanical actuator imprints a
torque which ensures a controlled influence on the
roll angle.
Figure 5: Roll angle of a motor vehicle (Schramm et al.,
2018).
5 SIMULATION ENVIRONMENT
The training and validation of the controller is carried
out in simulation. The simulation environment
contains three software packages, each fulfilling
special requirements for the development process and
interacting in a master/slave communication shown in
figure 6. MATLAB is used as master. It guarantees
the communication and synchronization between the
different environments and can further be used for
any kind of signal processing. The training data is
generated by the software IPG CarMaker. It is used
for the task of a whole vehicle simulation in a virtual
environment. CarMaker offers an environment for
simulation and testing of whole vehicle systems under
realistic conditions. It provides driving conditions
dependent on different selection options such as the
used car or road. For the presented elaboration the
available Lexus RX400h, which is a Sport Utility
Vehicle (SUV) with one stabilizer per vehicle axle. A
detailed mathematical modeling is done within the
licensed software and is not directly visible to the
user.
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning
41
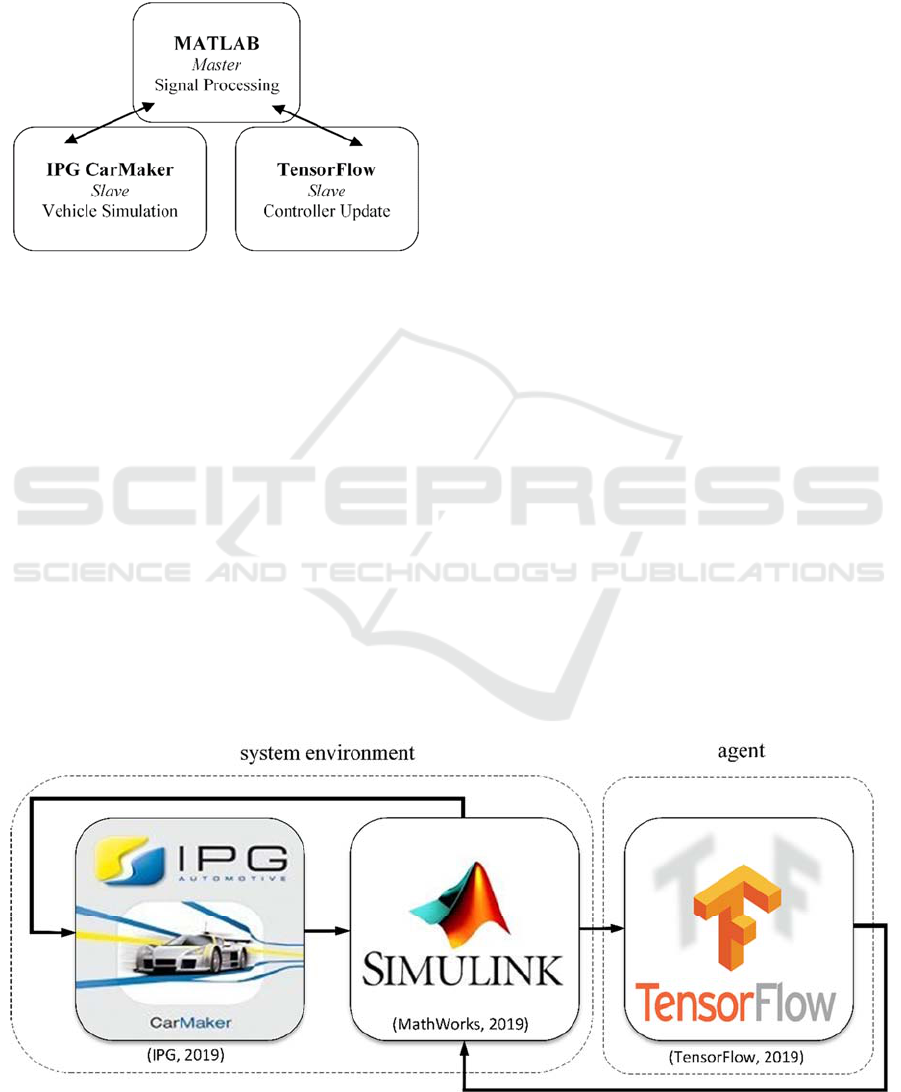
The track used is flat and has no slopes. The
vehicle can be controlled by providing physical
parameters via the interface in MATLAB/Simulink.
In this case the roll stabilization forces acting on the
car are manipulated.
Figure 6: Master/slave communication of the simulation
environment.
The driving conditions are transmitted to the
software MATLAB/Simulink in which the active roll
stabilization is realized. The results of this
stabilization are the mentioned stabilization forces in
dependence of the counter-torque
. The
counter-torque required for roll stabilization
corresponds to the output of the artificial neural
network, which is constructed and trained with the
frame work and the open source libraries from
TensorFlow. The counter-torque
is calculated
by the neural network with respect to the states . In
this work the states are the the roll angle , the roll
velocity , the roll acceleration and the lateral
acceleration
. TensorFlow is included in the loop
during training since it offers the developer high
agility in building and altering the structure of
artificial neural networks. The driving states are
therefore sent via MATLAB/Simulink to the agent
formed by TensorFlow before the active roll
stabilization. After the agent has determined an
output in the form of the counter-roll torque
as a function of the states, it sends this to
MATLAB/Simulink, where subsequently the
resulting roll stabilization forces acting on the vehicle
are transferred to IPG CarMaker. This feedback
message closes the simulation cycle. The data
exchange between MATLAB/Simulink and the
python based TensorFlow occurs through TCP/IP-
communication. The sample time of the simulation is
1 ms.
6 TRAINING
The training maneuvers represent the data available
during training and can be compared to the training
data set for supervised and unsupervised learning.
Depending on the learning problem, the methodology
of machine learning does not necessarily cover the
entire state space during training. Rather, the artificial
neural network is designed to develop and represent
an algorithm that provides satisfactory results in the
training data and is extra- and interpolatable over the
entire or most of the state space. The goal is to control
the roll angle . The desired reference angle in this
approach is
0 which results in the reward
function with respect to equation (11):
1²
(16)
When choosing the training maneuvers, however,
care must be taken to provide the agent with data that
can be used for extrapolation and interpolation. For
suitable roll stabilization, accelerations and roll an-
Figure 7: Flow chart of simulation environment.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
42
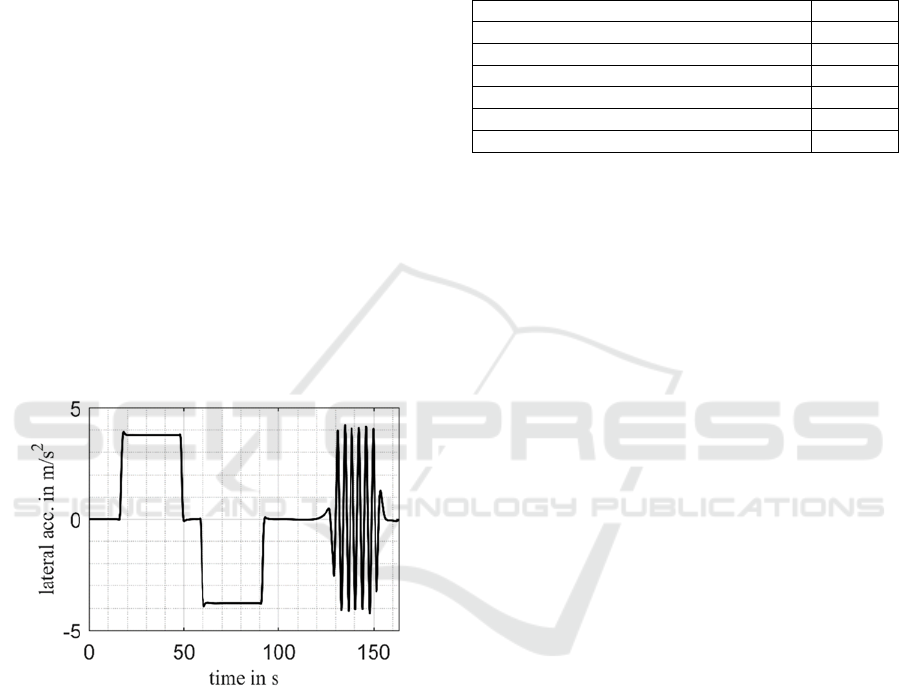
gles in both directions of the transverse axis must
therefore be available as input during training, so that
the neural controller can react differently to both
eventualities after completed training. For this reason,
the training maneuvers consist of stationary circular
drives according to ISO 4138 in both directions and a
slalom around pylons with a constant distance.
Stationary circular drives ensure that the agent
receives corresponding input variables over several
consecutive iteration steps, which require control and
contain lateral accelerations in one direction. This
allows the agent to train positive and negative
counter-torque separately in terms of time. Due to the
slalom ride, in which the lateral acceleration changes
periodically, the agent can train the steering angle
regarding variable driving dynamics. Straight
sections are inserted between the mentioned
maneuvers because the agent also has to learn to
deliver a torque of
0 Nm (or an absolute small
torque) facing no (or relatively small) lateral
acceleration despite its randomly distributed start
weights. All training maneuvers are carried out with
the vehicle speed 70 km/h. The radius of
curvature of the circle runs is 100 m and the
pylon distance of the slalom ride
36 m.
Figure 8: Lateral acceleration of the training maneuvers.
It should be noted here that the roll angle to be
controlled and the lateral acceleration have a dynamic
interaction, which causes the lateral acceleration to
change as a function of the set actuator torque during
the training. In addition, the three individual
maneuvers are repeated as often as desired and in
random order. The time-based arrangement of figure
8 thus only serves the compactness of the
representation and does not represent the training
course.
The preparation for training an artificial neural
network includes choosing several hyperparameters.
Calculation of optimal parameters is not readily
possible due to the highly interactive coupling and the
influence of the randomness that the agent requires
for its exploration in training. Training an artificial
neural network also means to adjust these parameters.
The finally used values for the most important
hyperparameters are shown in table 1.
Table 1: Most important used Hyperparameters.
Learnin
g
rate 0.0001
Number of neurons in first hidden la
y
e
r
100
Number of neurons in second hidden la
y
e
r
20
Variation standard deviation 2
Variation standard deviation decay 0.9999
Minimal variation 0.1
Reward deca
y
0.9
The importance of the learning rate is
mentioned in chapter 3.1.3. The architecture contains
of two hidden layers with different number of
neurons. The variation ensures the exploration of the
agent needed for Reinforcement Learning and is
carried out by a Gaussian distribution with the
standard deviation of 2. The resulting value is then
added to the calculated output of the network to get
different responses than expected. Moreover, the
standard deviation of the variation is decreased over
the subsequent iteration steps of the training by its
decay. By doing this the agent is guaranteed to follow
his policy getting better throughout training period.
The standard deviation is multiplied with the decay in
every iteration step until getting to its minimum. The
Reward decay
is used in equation (14) to lower the
influence of subsequent iteration steps compared to
the current iteration step.
The following presented results required 173
different training sessions while adjusting the
hyperparameters, the structure of the artificial neural
network and optimization algorithm. The session
leading to the final neural controller took about 20
million iteration steps and about 37 hours of
simulation time.
7 VALIDATION
Five different driving maneuvers are used to validate
the results. These consist of the training maneuvers
with varied radii, pylon distances and speeds and are
extended by the double lane change (ISO 3888-1). By
adding further driving maneuvers and varying the
traditional maneuvers, the interpolation and
extrapolability of the developed controller can be
evaluated. As a comparison, the passive roll stabilizer
is used. To assess the roll behaviour, the roll angle
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning
43
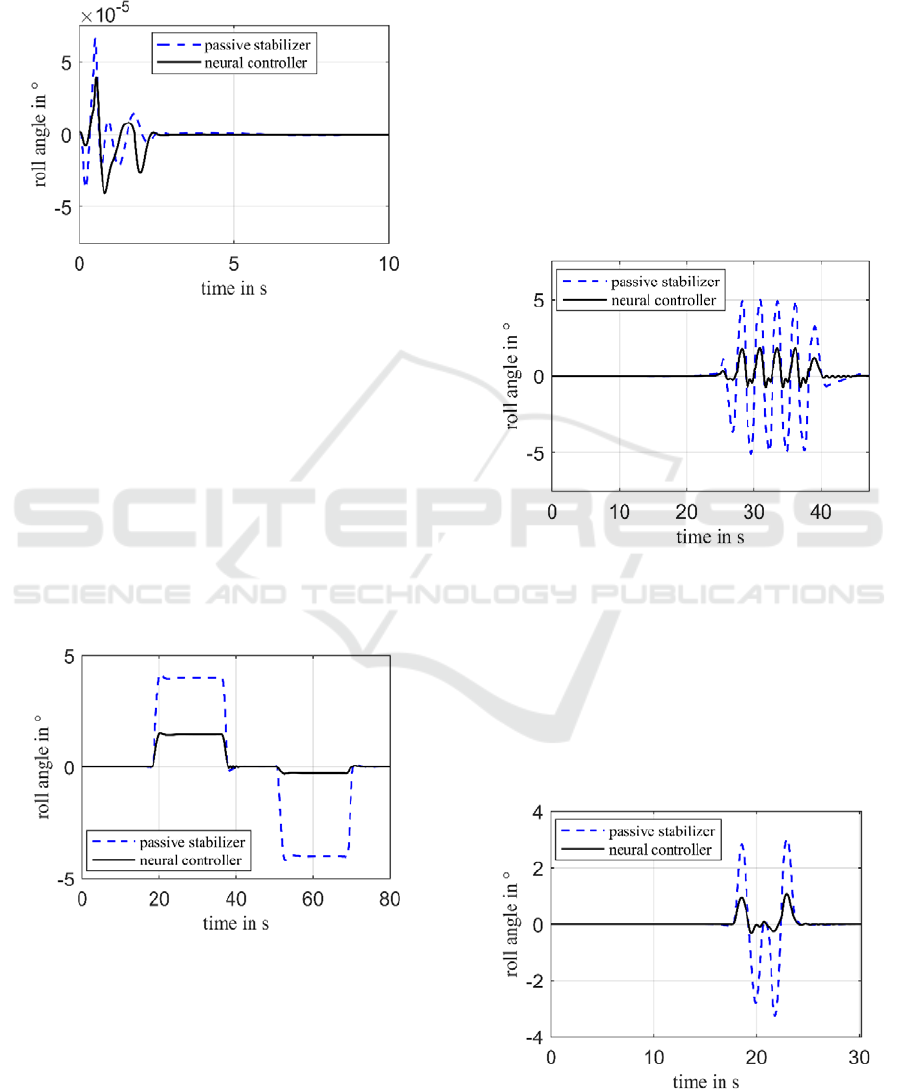
curve is compared in each case. For each maneuver
one case is selected to show its effect.
To validate the straight-ahead driving, this is
carried out at a speed of 50 km/h.
Figure 9: Straight-ahead driving at 50 km/h.
Figure 9 shows the roll angle for both the passive
stabilizer and the developed neural controller. Since
the vehicle has no lateral acceleration in a
straight-ahead drive without environmental
influences, the roll angle is constant 0 ° in the
case of a passive stabilizer. The deviance at the
beginning is neglectable and results from the
initialization of the vehicle with the simulation
environment. The developed neural controller shows
a similar behaviour.
For the stationary circuit (ISO 4138) the case with
50 km/h and 40 m is used.
Figure 10: Stationary circuit at 50 km/h and
40m.
The roll angle curve of the neural controller in
figure 10 works differently for negative and positive
lateral accelerations. Negative lateral accelerations
and roll angles are reduced more. A possible
explanation for this may be the random distribution
of the training maneuvers. In the test manager of IPG
CarMaker, driving maneuvers can be inserted,
duplicated as often as desired and then mixed. There
was a significantly higher number of the training
maneuvers for the training than was possible during
the training period. As a result, there is a possibility
that the mixture during training has significantly more
right-handed than left-handed curves, which can lead
to the observed differential behaviour. With the
neural controller, the roll angle in the left-handed
curve can be reduced from
4 ° to
1.47 °, resulting in a 63.25% reduction. In the
right-handed curve, a roll angle of
0.28 ° and
thus a 93% reduction is achieved.
The validation is shown exemplary at
50 km/h and a pylon distance of
18 m.
Figure 11: Slalom at 50 km/h and
18 m.
The result of the slalom ride reflects the previous
findings. The different control behaviour for negative
and positive lateral accelerations can be seen. Since
there are no irregularities in the six different slalom
runs with different speeds and pylon distances, it can
be concluded that the control behaviour of the neural
controller for slalom driving is extra- and
interpolatable.
Figure 12: Double lane change at 60 km/h.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
44

The double lane change (ISO 3888-1) is a pure
validation maneuver and thus evokes a driving
dynamic that was not explicitly trained by the agent.
However, this driving dynamic is comparable to that
of a slalom, so that similar results can be expected. It
is validated exemplary at 60 km/h.
As expected, the control behaviour of the neural
controller is very similar to that of slalom driving. It
shows that the control behaviour can also be
extrapolated to other maneuvers and driving
situations.
8 CONCLUSIONS
In the context of this work an active roll control with
an artificial neural network based on an actor-critic
reinforcement learning method has been successfully
realized. The neural controller was realized with the
TensorFlow libraries in a Python script and combined
with the simulation model of the entire vehicle and
the active roll stabilization contained therein via a
TCP/IP interface.
A guaranteed calculation of the torque to be set in
a fixed time interval and a time limit of the waiting
time of the TCP/IP interface created a real-time
control. If, in the defined waiting time, the actuator
does not receive any action from the neural network,
the torque is set from the previous time step. The
developed neural controller is able, at any time, to
stably reduce the roll angle caused by the centrifugal
force of the vehicle body by means of an actuator. The
functionality of the controller is thus given.
The results show that the developed controller
produces a rather uneven roll behaviour for both
directions of the steering angle in comparison to
established, conventional controllers. However, it has
been proven that roll stabilization by artificial neural
networks is possible and that the developed model is
able to replace conventional controllers. If the
knowledge gained in this work continues to be
applied to the model and extended with small and
precise optimizations, a neural controller with
symmetric behaviour can be trained for lateral
acceleration in both directions. Since the field of
machine learning works with very complex contexts
and is strongly randomized, this is a matter of time.
Basically, in 100 training runs with identical
hyperparameters, 100 different results can be
achieved, the extent of which is far from expedient.
Nonetheless, it has been shown that the neural
network used can provide a controller with tolerable
results. A fixed reproducibility of this result is not
given by the immense influence of randomness, but
due to the stochastics also better results are possible.
Due to its structure, the agent is able to adjust its
weights so that, for positive lateral accelerations, an
at least equal reduction of the roll angle is achieved,
as for negative transverse accelerations.
Further works will investigate the influence and
possible improvements by applying a regularization
on the weight adjustment to ensure the minimal
optimal weights and symmetric behaviour for
positive and negative lateral accelerations.
REFERENCES
Boada, M., Boada, B., Gauchia Babe, A. Calvo, J. and Diaz,
V., 2009. Active roll control using reinforcement
learning for a single unit heavy vehicle. In International
Journal of Heavy Vehicle Systems, 16(4), pp. 412-430.
Fu, Z.-J., Li, B., Ning, X.-B., Xie and W.-D., 2017. Online
Adaptive Optimal Control of Vehicle Active
Suspension Systems Using Single-Network
Approximate Dynamic Programming. In Mathematical
Problems in Engineering.
Goodfellow, I., Bengio, Y. and Courville, A., 2016. Deep
Learning, The MIT Press. London.
Hebb, D., 1949. The Organization of Behavior, John Wiley
& Sons, Inc. New York.
IPG, 2019. IPG Automotive’s Official Website. [online]
Available at https://ipg-automotive.com/ [Accessed
09 Feb. 2019].
Karlik, B. and Olgac, V., 2011. Performance Analysis of
Various Activation Functions in Generalized MLP
Architectures of Neural Networks. In International
Journal of Artificial Intelligence and Expert Systems
(IJAE), 1(4), pp. 111-122.
Konda, V. and Tsitsiklis, J., 2003. Actor-Critic Algorithms.
In SIAM Journal on Control and Optimization, 42(4),
pp. 1143-1166.
Li, H., Guo, C. and Jin, H., 2005. Design of Adaptive
Inverse Mode Wavelet Neural Network Controller of
Fin Stabilizer. In International Conference on Neural
Networks and Brain, 2005, 3, pp. 1745-1748.
MathWorks, 2019. MathWorks’ Official Website. [online]
Available at https://de.mathworks.com/ [Accessed 09
Feb. 2019].
Rosenblatt, F., 1958. The Perceptron: A probabilistic model
for information storage and organization in the brain. In
Psychological Review, 65(6), pp. 386-408.
Schramm, D., Hiller, M. and Bardini, R., 2018. Vehicle
Dynamics – Modeling and Simulation, Springer.
2
nd
Edition.
Sieberg, P., Reicherts, S. and Schramm, D., 2018.
Nichtlineare modellbasierte prädiktive Regelung zur
aktiven Wankstabilisierung von Personenkraftwagen.
In 4
th
IFToMM D-A-CH Konferenz 2018.
Sutton, R. and Barto, A., 2018. Reinforcement Learning: An
Introduction, The MIT Press. London, 2
nd
edition.
Development and Validation of Active Roll Control based on Actor-critic Neural Network Reinforcement Learning
45

Sutton, R., McAllester, D., Singh, S. and Mansour, Y.,
1999. Policy Gradient Methods for Reinforcement
Learning with Function Approximation. In NIPS'99 -
Proceedings of the 12th International Conference on
Neural Information Processing Systems, pp.
1057-1063.
Szepesvári, C., 2009. Algorithms for Reinforcement
Learning, Morgan & Claypool Publishers.
TensorFlow, 2019. TensorFlow’s Official Website. [online]
Available at https://www.tensorflow.org/ [Accessed
09 Feb. 2019].
Tesauro, G., 1995. Temporal Difference Learning and TD-
Gammon. In Communications of the ACM, 38(3), pp.
58-68.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
46
