
Stochastic Models of Non-stationary Time Series of the Average Daily
Heat Index
Nina Kargapolova
a
Laboratory of Stochastic Problems, Institute of Computational Mathematics and Mathematical Geophysics SB RAS,
Pr. Ak. Lavrent’eva 6, Novosibirsk, Russia
Department of Mathematics and Mechanics, Novosibirsk State University, Novosibirsk, Russia
Keywords: Stochastic Simulation, Non-stationary Random Process, Heat Index, Air Temperature, Relative Humidity,
Model Validation.
Abstract: In this paper two numerical stochastic models of time series of the average daily heat index are considered.
In the first model, time series of the heat index are constructed as a function of simulated joint nonstationary
time series of air temperature and relative humidity. The second model is constructed under the assumption
that time series of the heat index are non-stationary non-Gaussian random processes. Data from real
observations at weather stations were used for estimating models’ parameters. On the basis of the simulated
trajectories, some statistical properties of rare meteorological events, like long periods of time with high heat
index, are studied.
1 INTRODUCTION
It is known that of all the effects of the environment
on human beings, one of the most significant for the
human health and well-being are the factors
determining the thermal state of a person. With
adverse combinations of these factors, there is a threat
of hypothermia or overheating of a body (Kobisheva
et al., 2008; McGregor et al., 2015; Zare et al., 2018).
Different bioclimatic indices (heat / cold stress index,
heat index, weather severity index, etc.) are used to
assess the combined heat effects on the human body
of high temperature and relative humidity, cold
humid air and wind speed, as well as other
meteorological processes.
At present, to study the properties of the time
series of bioclimatic indices two approaches are
mainly used. In the framework of the statistical
approach, data from real observations are analyzed,
see, for example, (Kershaw and Millward, 2012;
Revich and Shaposhnikov, 2018; Shartova et al.,
2018). The second approach is a dynamical one – it is
based on the use of hydrodynamic models of
atmospheric processes (Gosling et al., 2009; Ohashi
et al., 2014).
a
https://orcid.org/0000-0002-1598-7675
In 2018, the author of the paper together with
colleagues at the Institute of Computational
Mathematics and Mathematical Geophysics SB RAS
(Novosibirsk, Russia) and the Voeikov Main
Geophysical Observatory (St. Petersburg, Russia)
began the development of a stochastic approach to
studying and simulation of the time series of
bioclimatic indices. For short time intervals (about
10–12 days), models of high-resolution time series of
the heat index and the enthalpy of humid air were
constructed and validated. These models take into
account the daily variations of the real weather
processes (Kargapolova et al., 2019).
The objective of this paper is to propose such a
stochastic model of time series of the average daily
heat index (ADHI) on a long intervals that would take
into account the influence of a seasonal variation of
air temperature and relative humidity on the time
series of the ADHI. In this paper two stochastic
models are considered. It is shown that the model
based on simulation of the joint time series of air
temperature and relative humidity does not reproduce
properties of the ADHI time series as good as it
reproduces properties of the high-resolution time
series of the heat index. In contrast, a model based on
simulation of the ADHI time series using the inverse
Kargapolova, N.
Stochastic Models of Non-stationary Time Series of the Average Daily Heat Index.
DOI: 10.5220/0007788502090215
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 209-215
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
209

distribution function method describes the real
process precise enough.
2 THE HEAT INDEX
To describe the influence of high air temperature and
relative humidity on a human being the so-called
“heat index” is frequently used (Steadman,1979;
Steadman, 1984). The overview and comparison of
existing approaches to the definition of this index is
provided in (Anderson et al., 2013). In this paper, the
average daily heat index
HI
is defined using the
approach, proposed in (Schoen, 2005):
0 0801 14
0 03755
1 0799 1
237 3 17 27
17 27 237 3
.D
.T
HI T . e e ,
. . T
D , lnH,
. . T
(1)
where
T
and
H
are the average daily air
temperature and relative humidity, respectively,
D
is dew point temperature. Here unit of measurement
of air temperature is a Celsius degree, and relative
humidity is measured in fractions of unity; the heat is
supposed to be dimensionless. It should be noted that
the heat index is not measured at weather stations, but
it could be calculated using the above-given formulas
based on the observed values of air temperature and
relative humidity.
Let
12 N
HI HI ,HI , ,HI
denote time series
of the average daily heat index (ADHI) on a
N
day
interval.
3 THE TH-MODEL
Since the heat index is a function of air temperature
and relative humidity, a natural approach to the
simulation of its time series is to simulate the joint
time series of air temperature and relative humidity
and then to calculate values of the heat index. Such an
approach was proposed and validated in
(Kargapolova et al., 2019) for the simulation of high-
resolution time series of the heat index at short time
intervals. The model proposed therein is based on the
model of periodically correlated joint time series of
air temperature and relative humidity detailed in
(Kargapolova et al., 2018).
Let us apply the approach described to the
simulation of time series of the ADHI at long time
intervals. Statistical analysis of real meteorological
data reveals that the joint time series
1 2 1 2NN
T,H T ,T , ,T ,H ,H , ,H
of the
average daily air temperature and relative humidity
long time intervals are non-stationary.
One-dimensional distributions and a correlation
structure of the joint time series of air temperature and
relative humidity are used as the model input
parameters.
In order to construct a stochastic model, the use of
sample one-dimensional distributions is not
reasonable, since the sample distributions do not have
any tails, and therefore do not allow one to estimate
the probability of occurrence of extreme values of the
heat index. In this connection, it is necessary to
approximate the sample distributions densities by
certain analytic densities, which, on the one hand, do
not greatly alter the form of a sample distribution and
its moments, and on the other – possess tails.
It should be noted that for approximation of the
empirical one-dimensional distribution
k
sx
of the
average daily temperature, the Gaussian distribution
is often used (Ogorodnikov, 2013; Richardson, 1981;
Richardson and Wright, 1984). However, the
numerical experiments have shown that if, despite an
increase in the complexity of simulation, one
approximates the temperature distribution with a
mixture
2
1
2
1
1
2
2
2
2
2
1
exp
2
2
1
1 exp ,
2
2
0 1, 1,N
k
kk
k
k
k
k
k
k
k
xa
gx
b
b
xa
b
b
k
(2)
of the two Gaussian distributions, the quality of the
model being significantly improved. In this paper, the
parameters
22
1 1 2 2
, , , , , 1,N
k k k k k
a b a b k
were
chosen using the algorithm, proposed in (Marchenko
and Minakova, 1980). This algorithm makes possible
to choose such parameters of the density (2) (and the
corresponding CDF
k
Gx
) that mathematical
expectation, variance and skewness of a random
variable with the density
k
gx
should be equal to
the corresponding sample characteristics, and the
function
k
gx
minimizes the Pearson functional
that describes the difference between
k
sx
and
k
gx
.
For approximation of one-dimensional
distributions of the average daily relative humidity
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
210

densities that are mixtures
k
bx
of the two Beta-
distributions (with the corresponding CDF
k
Bx
)
are used.
In this paper, to construct a model of the time
series
T,H
(and hence a model of time series
HI
) the
22NN
sample correlation matrix
T TH
HT H
RR
R
RR
(3)
is used. Here
,
TH
RR
are the sample autocorrelation
matrices of air temperature and relative humidity,
respectively, and
,
TH HT
RR
are the sample cross-
correlation matrices of these two weather elements.
For the simulation of
T,H
with given one-
dimensional distributions (1) and a given correlation
matrix (3), the method of inverse distribution function
was used (Ogorodnikov and Prigarin, 1996). In the
framework of this method, simulating the sequence
HI
comes down to an algorithm with four steps:
Step 1. Calculation of the matrix
R
that is a
correlation matrix of an auxiliary standard Gaussian
process
T',H'
. The element
i, jr
, 1,2i j N
of the matrix
R
is the solution to the equation
11
i, j
i, , ,,j
,,
,,
i
N
j
i
i
i
F x F y x y d
r
r
G x i N
B x i
xdy
N
F
where
i, jr
is an element of the matrix
R
corresponding to
i, jr
, the function
,, i, jxyr
is a distribution density of a bivariate Gaussian vector
with zero mean, variance equal to
1
and the
correlation coefficient
i, jr
between components
number
i
and
j
,
is a CDF of a standard
normal distribution.
Step 2. Simulation of the standard Gaussian
sequence
T',H'
with the correlation matrix
R
.
Step 3. Transformation of
T',H'
into
T,H
:
1
1
, 1, ,
, 1,
i i i
j j j
T G T i N
H B H j N
Step 4. Calculation of
HI
using its definition (1)
given in the previous section.
If the matrix
R
, obtained at the first step, is not
positive definite, it must be regularized. Several
methods of regularization are described in
(Ogorodnikov and Prigarin, 1996). In this paper, the
method of regularization based on substitution of
negative eigenvalues of the matrix
'R
with small
positive numbers was used. At the second step, the
simulation of the standard Gaussian sequence
T',H'
with the correlation matrix
'R
could be
done using the Cholesky or the spectral
decomposition of the matrix
'R
(Ogorodnikov and
Prigarin, 1996). The latter is used here. Steps 2-4 are
repeated as many times as many trajectories are
required.
Any stochastic model has to be verified before one
starts to use simulated trajectories to study properties
of a simulated process. For model verification, it is
necessary to compare simulated and real data based
estimations of such characteristics, which, on the one
hand, are reliably estimated by real data, and on the
other hand are not input parameters of the model.
In this paper, the long-term observations data
from weather stations located in different climatic
zones were used for verification. Although all
examples in this paper are given only for the stations
in the cities of Sochi (the Black Sea region, years of
observation: 1993-2015) and Astrakhan (the Caspian
Sea region, years of observation: 1966-2000), all the
conclusions are valid for all considered weather
stations.
The correlation coefficients
,
ik
corr HI HI
of
the ADHI time series are not input parameters of the
TH-model, so they could be used for the verification
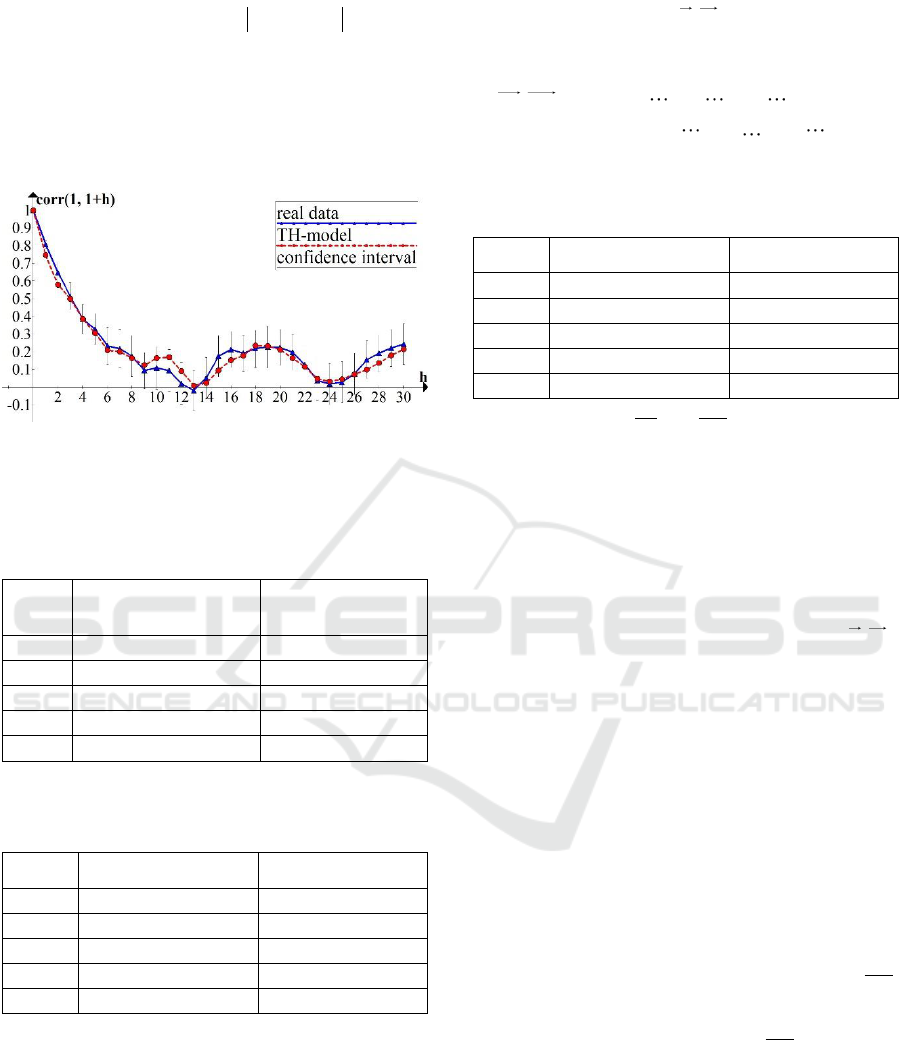
of this model. Figure 1 shows the correlation
coefficients
11
,
h
corr HI HI
, estimated with real
data (with
2
confidence interval) and with the
5
10
trajectories obtained with the TH-model. Numerical
experiments show that for all considered weather
stations and time intervals, the absolute difference of
correlation coefficients estimated with real and
simulated data does not exceed
2
. Hereinafter,
is a statistical estimate of the standard deviation of the
characteristic under consideration when estimating
with real data. Thus, the TH-model well reproduces
the correlation structure of time series of the ADHI.
As a matter of fact, other properties of real time
series of the ADHI are either not reproduced or poorly
reproduced by the TH-model. As an illustration,
Tables 1-3 show estimations of the average number
AN lev
of the days in a considered time-interval
with the ADHI above given level
lev
and estimations
Stochastic Models of Non-stationary Time Series of the Average Daily Heat Index
211
of the probability
1ii
p l P HI HI l
of a
rapid change in the heat index. Simulated data bases
estimations are given with significant digits only.
This means that the TH-model, despite its soundness
and applicability in cases of the high-resolution time
series, should not be used for the simulation of the
time series of the ADHI.
Figure 1: Correlation coefficients
11
,
h
corr HI HI
.
Astrakhan. July, 1-31.
Table 1: Estimations of
AN lev
. Astrakhan. August, 1-
31.
lev
Real data,
3AN lev
TH-model
20
28.206
1.630
27.193
24
21.088
2.819
14.463
28
10.441
0.887
1.032
32
2.853
1.586
0.007
36
0.500
0.640
0.000
Table 2: Estimations of the probability
pl
. Sochi. June,
1-30.
l
Real data,
3pl
TH-model
1
0.585
0.063
0.577
2
0.304
0.037
0.275
3
0.150
0.055
0.111
4
0.078
0.039
0.040
5
0.039
0.054
0.013
The most probable reason for the invalidity of the
TH-model is related to the fact that the heat index is
a nonlinear function of air temperature and relative
humidity. It leads to the significant difference
between the ADHI calculated with the average daily
temperature and relative humidity (as in the TH-
model) and the ADHI calculated as an average of the
values of the heat index calculated with real
meteorological high-resolution data. To avoid this
problem, instead of the
T,H
one should simulate
the high-resolution time series
1 2 1
1 1 1
11
11
nn
NN
nn
nn
NN
T ,T , ,T , ,T ,, ,T ,
T ,H ,
H , ,H , ,H , ,H
Table 3: Estimations of the probability
pl
. Astrakhan.
June, 1-30.
l
Real data,
3pl
TH-model
1
0.685
0.047
0.588
2
0.422
0.055
0.283
3
0.223
0.050
0.113
4
0.106
0.040
0.038
5
0.055
0.029
0.011
where
11
kk
ii
T ,H , k ,n, i ,N
are temperature and
relative humidity measured
n
times per day in a day
number
i
, respectively, then calculate the high-
resolution time series of the heat index and average
them to obtain the ADHI. It should be noted that this
approach to the simulation is time-consuming (for
instance, one has to solve
2
n
times more equations to
define the correlation matrix of an auxiliary Gaussian
process than in case of the simulation of the
T,H
time series).
4 THE HI-MODEL
In this section, another approach to the simulation of
the time series of the average daily heat index is
considered. In the framework of this approach
(denoted as the HI-model), at the first step, a sample
of real time series of the ADHI is formed using the
long-term observation data about the average daily
temperature and relative humidity. Then sample
histograms are approximated with some one-
dimensional distribution densities
, 1,
k
n x k N
and a sample
NN
correlation matrix
HI
R
is
estimated. In this paper,
, 1,
k
n x k N
is a mixture
of the two Gaussian distributions. Parameters of these
mixtures were chosen just as parameters of the
densities
k
gx
. To construct a completely
parametric stochastic model of the time series, it is
necessary to approximate the sample correlation
function with some analytic parametric function (like
was done with one-dimensional distributions). Such
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
212
an approximation is in the course of development.
The last step is the simulation of trajectories of the
ADHI with the given densities
, 1,
k
n x k N
and
the correlation matrix
HI
R
using the method of
inverse distribution function (in a similar way to steps
1-3 in the TH-model).
Results of verification of the HI-model are
provided below.
Tables 4 and 5 show the estimations of the
average number
AN lev
, defined in the previous
section. It is clearly seen that the HI-model well
reproduces this characteristic of the ADHI time series
both for harmless levels
lev
and for dangerous levels
(the heat index between 32 and 41 is the extreme
caution, between 41 and 54 is danger, above 54 is the
extreme danger).
Table 4: Estimations of
AN lev
. Astrakhan. August, 1-
31.
lev
Real data,
AN lev
HI-model
20
28.206
0.451
28.120
24
21.088
0.857
21.053
28
10.441
0.946
10.323
32
2.853
0.529
2.758
36
0.500
0.213
0.566
40
0.118
0.085
0.138
44
0.029
0.048
0.056
48
0.000
0.011
0.004
Table 5: Estimations of
AN lev
. Sochi. July, 1-31.
lev
Real data,
AN lev
HI-model
20
30.565
0.234
30.515
24
27.652
0.696
27.893
28
19.435
1.323
19.753
32
10.261
1.248
9.960
36
3.391
0.768
3.564
40
1.044
0.379
0.952
44
0.130
0.115
0.108
48
0.000
0.035
0.012
52
0.000
0.010
0.001
Another characteristic that was used both for the
verification of the HI-model and for the study of the
heat index time series properties was the probability
.pl
Tables 6 and 7 show the estimations of
pl
based on real data and simulated trajectories. For all
the considered weather stations and time intervals, the
absolute difference of
pl
estimated on real and
simulated data does not exceed
2
. This means that
this characteristic is well reproduced by the HI-
model.
The verification of the HI-model has shown that
this model with high accuracy reproduces many of the
statistical characteristics of real ADHI time series.
Accordingly, it is possible to use the HI-model to
study those properties of the time series that cannot
be studied using real data. Among other things, it is
possible to investigate an impact of an increase in the
average air temperature on the duration of periods
with the extremely high ADHI, on probability of the
occurrence of dangerous values of the ADHI and
other properties of adverse weather phenomena.
Below the results of one of the numerical experiments
conducted using the HI-model are given.
Table 6: Estimations of the probability
pl
. Sochi. June
1-30.
l
Real data,
pl
HI-model
1
0.585
0.021
0.638
2
0.304
0.022
0.360
3
0.150
0.018
0.183
4
0.078
0.013
0.084
5
0.039
0.008
0.035
6
0.021
0.005
0.014
7
0.011
0.003
0.005
8
0.006
0.002
0.002
9
0.000
0.001
0.001
10
0.000
0.001
0.000
The main idea of the experiment was to increase
the average daily temperature on condition that
relative humidity does not change, to estimate the
parameters of the distributions used in the HI-model
using the simulated temperature data, real relative
humidity data and real correlation coefficients, to
simulate the time series of the ADHI and to access an
average number
AN lev
of the days with the ADHI
above level
lev
. Simulation of air temperature non-
stationary time series was based on the model
proposed in (Kargapolova, 2018). Figure 2 shows the
results of this experiment for the four cases: when the
real average daily temperature was used and when the
average daily temperature was increased by
0.1 , 0.5 , 1.0
o o o
C C C
, respectively. The analysis
shows that for
32lev
(recall that it is the extreme
caution level) the number
AN lev
increases by
Stochastic Models of Non-stationary Time Series of the Average Daily Heat Index
213

40 50%
depending on a weather station
considered. For level
lev
above
41
values of the
AN lev
almost double. This means that
1.0
o
C
rise
in the average air temperature causes a hefty increase
of days when people must be careful being outside. In
this numerical experiment the simplest warming
scenario was used.
Table 7: Estimations of the probability
pl
. Astrakhan.
June 1-30.
l
Real data,
pl
HI-model
1
0.685
0.016
0.698
3
0.223
0.017
0.255
5
0.055
0.010
0.069
7
0.018
0.004
0.015
9
0.007
0.002
0.003
11
0.003
0.001
0.001
13
0.001
0.001
0.000
Figure 2: Average number
AN lev
of days with the
ADHI above level
lev
. Astrakhan. July, 1-31.
For a detailed study of the climate change
influence it is necessary to use more complex
scenarios. For example, dependence between
changing temperature and relative humidity is meant
to be taken into account. Study the possible
alternation of the ADHI using complex climate
change scenarios and stochastic models calls for
further investigations.
5 CONCLUSIONS
In this paper, it is shown that the TH-model used to
simulate high-resolution time series of the heat index
cannot be used to simulate the ADHI series. Another
approach (the HI-model) to the simulation of these
time series is proposed. The results of verification of
the HI-model and an example of its application for
studying the ADHI properties, which cannot be
studied from real data, are given.
In the future, it is intended to use the model
constructed for solving a number of bioclimatological
problems related to development of proper heat-/cold
waves prediction systems and long-range forecasting
of the climate regime alteration. To solve these
problems, it is necessary to turn the proposed model
into a fully parametric one and to add a capability to
simulate conditional time series.
ACKNOWLEDGEMENTS
This work was partly financially supported by the
Russian Foundation for Basic Research (grant No 18-
01-00149-a), Russian Foundation for Basic Research
and Government of Novosibirsk region (grant No 19-
41-543001-r_mol_a).
REFERENCES
Anderson, G.B., Bell, M.L., Peng, R.D., 2013. Methods to
calculate the heat index as an exposure metric in
environmental health research. In Env. Health
Perspect., Vol. 121, No 10. P. 1111-1119.
Gosling, S.N., McGregor, G.R., Lowe, J.A., 2009. Climate
change and heat-related mortality in six cities. Part 2:
climate model evaluation and projected impacts from
changes in the mean and variability of temperature with
climate change. In Int J Biometeorol., Vol.53, No 1. P.
31-51.
Kargapolova, N. A., 2018. Monte Carlo Simulation of Non-
stationary Air Temperature Time-Series. In Proc. of 8th
Int. Conf. on Simulation and Modeling Methodologies,
Technologies and Applications “SIMULTECH-2018”.
P. 323-329.
Kargapolova, N. A., Khlebnikova, E. I., Ogorodnikov, V.
A., 2018. Monte Carlo simulation of the joint non-
Gaussian periodically correlated time-series of air
temperature and relative humidity. In Statistical papers,
Vol. 59. P.1471-1481.
Kargapolova, N. A., Khlebnikova, E. I., Ogorodnikov, V.
A., 2019. Numerical study of properties of air heat
content indicators based on the stochastic model of the
meteorological processes. In Russ. J. Num. Anal. Math.
Modelling, Vol. 34, No 2. P. 95-104.
Kershaw, S.E., Millward, A.A., 2012. A spatio-temporal
index for heat vulnerability assessment. In Environ.
Monit. Assess., Vol. 184. P. 7329-7342.
Kobisheva, N.V., Stadnik, V.V., Klueva, M.V., Pigoltsina,
G.B., Akentieva, E.M., Galuk, L.P., Razova, E.N.,
Semenov, U.A., 2008. Guidance on specialized
climatological service of the economy. Asterion. St.
Petersburg. (in Russian)
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
214

Marchenko, A.S., Minakova, L.A., 1980. Probabilistic
model of air temperature time-series. In Meteorology
and Hydrology, No 9. P. 39-47. (in Russian)
McGregor, G.R., Bessemoulin, P., Ebi, K., Menne, B.,
2015. Heatwaves and Health: Guidance on Warning-
System Development. WMO &WHO.
Ogorodnikov, V.A., 2013. Stochastic models of
meteorological processes: Teaching aid. NSU.
Novosibirsk.
Ogorodnikov, V.A., Prigarin, S.M., 1996. Numerical
Modelling of Random Processes and Fields:
Algorithms and Applications, VSP. Utrecht.
Ohashi, Y., Kikegawa, Y., Ihara, T., Sugiyama. N., 2014.
Numerical Simulations of Outdoor Heat Stress Index
and Heat Disorder Risk in the 23 Wards of Tokyo. In J.
Appl. Meteor. Climatol., Vol. 53. P. 583-597.
Revich, B., Shaposhnikov, D.A., 2016. Cold waves in the
southern cities of the European part of Russia and
premature mortality of the population. In Problems of
forecasting, No 2. P. 125-131. (in Russian)
Richardson, C. W., 1981. Stochastic simulation of daily
precipitation, temperature and solar radiation. In Water
Resour. Res., Vol. 17. P. 182-190.
Richardson, C. W., Wright, D.A., 1984. WGEN: A Model
for Generating Daily Weather Variables. U. S.
Department of Agriculture, Agricultural Research
Service.
Schoen, C., 2005. A new empirical model of the
temperature– humidity index. In J Appl Meteorol., Vol
44. P. 1413-1420.
Shartova, N., Shaposhnikov, D., Konstantinov, P., Revich,
B., 2018. Cardiovascular mortality during heat waves
in temperate climate: an association with bioclimatic
indices. In Int. J. of Environmental Health Research,
Vol. 28, No. 5. P. 522-534.
Steadman, R.G., 1979. The Assessment of Sultriness, Part
I: A Temperature-Humidity Index Based on Human
Physiology and Clothing Science. In J. Appl. Meteor.,
Vol. 18. P.861-873.
Steadman, R.G., 1984. A universal scale of apparent
temperature. In J Climate Appl Meteorol., Vol. 23. P.
1674-1687.
Zare, S., Hasheminejad, N., Shirvan, H.E., Hemmatjo, R.,
Sarebanzadeh, K., Ahmadi, S., 2018. Comparing
Universal Thermal Climate Index (UTCI) with selected
thermal indices/environmental parameters during 12
months of the year. In Weather and Clim. Extremes,
Vol. 19. P. 49-57.
Stochastic Models of Non-stationary Time Series of the Average Daily Heat Index
215
