
An Efficient FHE Scheme to Secure Cloud Computing
Khalil Hariss
1,2 a
, Abed Ellatif Samhat
1 b
and Maroun Chamoun
2 c
1
Faculty of Engineering - CRSI, Lebanese University, Hadat, Beirut, Lebanon
2
Facult
´
e D’Ing
´
enierie - CIMTI, Universit
´
e Saint Joseph, Mar Roukoz, Beirut, Lebanon
Keywords:
Cloud Computing, Cloud Privacy, Fully Homomorphic Encryption, Domingo Ferrer, Learning with Error,
Key Switching, Circuit Evaluation, Storage Overhead, Known Plain-text Attack, Polynomial Resultant.
Abstract:
In this paper, we consider the privacy issue in cloud systems by using Homomorphic Encryption (HE) to pro-
vide secure computing at the cloud side. We use Domingo Ferrer (DF) homomorphic scheme to accomplish
this task. Before implementing DF in a cloud scenario, we resolve its main problems. The two concerned
problems are sensitivity to known plain-text attack and cipher-text dimension growth after homomorphic mul-
tiplication causing high storage overhead and reducing the scheme efficiency. DF is first made secure for cloud
systems by making the scheme much more resistant to the concerned attack due to the change of the encryp-
tion procedure. Second, DF is made efficient for cloud computing by introducing a new technique, called Key
Switching (KS). This technique reduces the high overhead by decreasing the extended cipher-text dimension
obtained after a homomorphic multiplication and preserving the homomorphic behavior. While users’ pri-
vacy at the Cloud side is preserved with HE, KS technique relies on publishing a matrix M. Different secret
keys are encrypted within M based on the hardness of Learning With Error (LWE). A deep crypt-analysis
and implementations under Python using SageMath Library are done in order to validate the efficiency of our
proposal.
1 INTRODUCTION
Cloud computing is formed of an embedded system
of different configurable computers that provide ser-
vices over the internet with a low cost of management.
Cloud systems rely on sharing different resources to
give better opportunities for outsourcing of storage
and computation. Users’ privacy at the Cloud side be-
comes critical when computation over the encrypted
stored data is required. In this case, they are obliged
to reveal some of their secret parameters in order to
perform arithmetic operations over their sensitive data
after decrypting it, then re-encrypting. An appropriate
solution for this problem is Homomorphic Encryption
(HE) since it allows non trusted parties to perform
computations over encrypted data. This new type of
encryption is suitable for Cloud computing (Chauhan
et al., 2015) and used in several real world applica-
tions such as medical application (Kocabas and Soy-
ata, 2014), etc. A cryptographic scheme having an
encryption function Enc is said to be homomorphic
a
https://orcid.org/0000-0001-9631-8467
b
https://orcid.org/0000-0002-1137-621X
c
https://orcid.org/0000-0002-1106-7409
if the evaluation of a circuit C satisfies the relation
Enc( f (X)) = f (Enc(X)), where f is the function that
performs the circuit C and X = [x
1
, x
2
, ....., x
l
] is a tu-
ple of l input plain-texts. C is an electrical circuit
that can be expressed in Boolean form. The function
f should therefore have a polynomial form contain-
ing addition and multiplication operations. As a con-
clusion, building a Fully Homomoprhic Encryption
(FHE) scheme is done by satisfying the two follow-
ing properties:
1. Addition
Enc
K
(x
1
+ x
2
) = Enc
K
(x
1
) + Enc
K
(x
2
) (1)
2. Multiplication
Enc
K
(x
1
× x
2
) = Enc
K
(x
1
) × Enc
K
(x
2
) (2)
where Enc
K
is the encryption function under a secret
key K and (x
1
, x
2
) are two plain-texts.
The notion of HE first appeared with the RSA
scheme in (Rivest et al., 1978). Several researchers
worked afterwards on the challenge of creating a HE
scheme that provides simultaneously efficiency and
robustness. Jospeh Domimgo Ferrer published in
Hariss, K., Samhat, A. and Chamoun, M.
An Efficient FHE Scheme to Secure Cloud Computing.
DOI: 10.5220/0007788803410349
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 341-349
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
341

(Domingo-Ferrer, 2002) a HE scheme based on poly-
nomial calculations. The most valued work was intro-
duced by the IBM researcher Craig Gentry in (Gen-
try, 2009) where he introduced the first theoretical
FHE scheme that supports unbounded number of cir-
cuit depth and his work consisted on lattice based
cryptography. Following Gentry works, several al-
gorithms were born such as the DGHV scheme (van
Dijk et al., 2010), (Hariss et al., 2017) that works over
the integers. DGHV suffers from high computational
complexity, public key size can attain 2.3 Gigabytes
and with an optimized implementation on a high-end
workstation, key generation takes 2.2 hours, encryp-
tion takes 3 minutes, and cipher-text refresh takes
30 minutes as given in (Coron et al., 2011). Crypt-
analysis has also shown that DGHV is sensitive to
Greatest Common Divisor (GACD) attack (Chen and
Nguyen, 2012). BGV (Brakerski et al., 2012), (Hariss
et al., 2017) is another FHE scheme that works over
lattices where its computational complexity is also
given by large poly-logarithmic factors. A wide state
of art regarding HE is given in (Martins et al., 2017),
(Aguilar-Melchor et al., 2013).
In this paper, we focus on Domingo Ferrer (DF)
encryption scheme introduced in (Domingo-Ferrer,
2002) that suffers from two main vulnerabilities:
1. Sensitivity to known plain-text attack: the scheme
is sensitive to this attack due to its algebraic struc-
ture as given in (Wagner, 2003).
2. Cipher Expansion: homomorphic multiplication
is a polynomial multiplication that increases the
cipher dimension exponentially after each opera-
tion. Thus causing a high storage overhead and
reducing the scheme efficiency.
We propose to make DF suitable for Cloud systems
first by enhancing its security level after modifying its
encryption procedure to make it much more resistant
against known plain-text attack. Second, we reduce
the high overhead, by using a new technique called
KS (Brakerski et al., 2012) based on publishing a new
matrix M. Using this public matrix M, a new cipher
c
f resh
under a new secret key K
f resh
can be obtained
such that c
f resh
= M × c where dimension(c
f resh
) <
dimension(c) and Dec
K
f resh
(c
f resh
) = Dec
K
(c) (c is a
cipher with high storage overhead with respect to a
secret key K with high storage overhead). Different
secret parameters are encrypted within the public ma-
trix M profiting from the hardness of Learning With
Error (LW E) (Regev, 2009).
The rest of this paper is organized as follow: in
section 2, the basic DF encryption scheme (Domingo-
Ferrer, 2002) is explained, then we introduce the LWE
problem given in (Regev, 2009). In section 3, the
two main problems of DF are solved as given above.
Crypt-analysis is given in section 4 where leverag-
ing the resistance of the scheme against known plain-
text attack is validated, and the security level of KS
is investigated. Implementations under Python us-
ing SAGEMath Library are given in section 5 in or-
der to validate the performance of our proposal for
Cloud systems. Finally conclusion and future works
are listed in section 6.
2 PRELIMINARIES
2.1 DF Encryption Scheme
2.1.1 Encryption Parameters
As stated in (Domingo-Ferrer, 2002), starting from
a security parameter λ, different parameters are de-
fined:
1. public modulus m ≥ 10
200
that have many small
divisors.
2. public integer d > 2 represents the cipher-texts di-
mension.
3. secret modulus m
0
should be a small divisor of the
public modulus m (m = (m
0
)
λ
).
4. secret key r ∈ Z
m
invertible by the multiplicative
law in the public ring Z
m
.
2.1.2 Encryption Procedure
Consider a plain-text a ∈ Z
m
0
, the encryption is given
by two steps:
1. Decompose Function: The plain-text
a is randomly decomposed into d ele-
ments (a
1
, a
2
, a
3
, ....., a
d
) ∈ [Z
m
]
d
such that
∑
d
i=1
a
i
mod(m
0
) = a.
2. Encryption: An invertible secret key r is ran-
domly picked from the public ring Z
m
. The
cipher-text π of the plain-text a is given by: π =
[a
1
r, a
2
r
2
, a
3
r
3
, ......, a
d
r
d
] (mod(m)). Cipher-
text can be written with a uni-variate polyno-
mial form: π(t) = (a
1
r)t + (a
2
r
2
)t
2
+ (a
3
r
3
)t
3
+
......(a
d
r
d
)t
d
(mod(m)).
2.1.3 Decryption Procedure
Decryption at the classified level, is simply done
by multiplying the i
th
coordinate π(i) of π by the
r
−i
mod(m) to retrieve a
i
mod(m) then we per-
form
∑
d
i=1
a
i
mod(m
0
) to retrieve a.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
342

2.1.4 Homomorphic Properties
1. Addition: Using the uni-variate polynomial form
π(t), adding two cipher-texts in Z
m
is simply
adding two polynomials in Z
m
[T ].
2. Multiplication: All terms are cross multiplied in
Z
m
, with d
1
th
degree by d
2
th
degree. The result is
a polynomial of degree d = d
1
+ d
2
, finally terms
of the same degree are added.
Starting from 2
l
cipher-texts of dimension d and af-
ter evaluating the multiplicative circuit of depth l
given in Fig. 1. The cipher-text dimension becomes
2
l
(d − 1) + 1. Thus dimension grows exponentially
with homomorphic multiplication. This problem will
be solved in section 3 after introducing the KS tech-
nique. The security of KS is based on the hardness of
LW E presented below.
2.2 Learning With Error (LWE)
2.2.1 LWE Problem
LW E is a machine learning problem introduced by
Oded Regev in (Regev, 2009). In LW E, we need to
learn the secret values of a vector s from a sample of
the form (a
i
, < s, a
i
> +e
i
), where a
i
are uniformly
chosen from Z
(1,n)
q
, e
i
is a noise distribution over Z
q
,
n is the dimension and q is the modulus.
In LW E, we define the Search Problem by:
Find s ∈ Z
(1,n)
q
given p noisy random inner prod-
ucts:
a
1
← Z
(1,n)
q
b
1
=< s, a
1
> +e
1
a
2
← Z
(1,n)
q
b
2
=< s, a
2
> +e
2
..... ....... ....... .................
..... ....... ....... .................
..... ....... ....... .................
a
p
← Z
(1,n)
q
b
p
=< s, a
p
> +e
p
(3)
Where e
i
← χ=Gaussian Distribution over Z
q
.
2.2.2 LWE Matrix Form
Suppose that we have the matrix A =
[a
1
, a
2
, a
3
, ....., a
p
] =
a
11
a
21
..... a
p1
a
12
a
22
..... a
p2
... ..... .....
a
1n
a
2n
..... a
pn
where
a
i
= [a
i1
, a
i2
, ...., a
in
]
1≤i≤p
∈ Z
(n,1)
q
.
Let s
t
= [s
1
, s
2
, ......, s
n
] ∈ Z
(1,n)
q
, e
t
=
[e
1
, e
2
, ....., e
p
] ∈ Z
(1,p)
q
.
The LW E problem given in Eq. 3 can be written
based on the following matrix form:
b
t
= s
t
A + e
t
∈ Z
(1,p)
q
(4)
Eq. 4 can be seen as a lattice equation, where s
t
A
forms the lattice points. As a lattice based cryp-
tography, e
t
can be considered as a plain-text en-
crypted under a secret key s
t
to obtain its correspond-
ing cipher-text b
t
. Decryption is a Closest Vector
Problem (CV P) that consists of finding the closest
lattice point to b
t
which can simply be resolved only
when having the secret key s
t
. Starting from a security
parameter λ, the security of LW E resides in taking the
dimension n ∼ poly(λ) and the modulus q ∼ poly(n)
and using poly(n) equations as given in (Brakerski
et al., 2012), (Regev, 2009).
3 ENHANCING DF ENCRYPTION
SCHEME
In this section, the two main problems of the DF
scheme (know plain-text attack and cipher-text expan-
sion) are investigated. First the security level of the
basic scheme given in (Domingo-Ferrer, 2002) is en-
hanced by changing the encryption procedure, then a
new technique called KS is introduced. KS reduces
the storage overhead of the cipher-text after each ho-
momoprhic multiplication without altering the homo-
morphic behavior of the scheme or changing the prim-
itive plain-text.
3.1 Enhancing The Security Level
3.1.1 New Encryption Procedure
Starting from a plain-text a ∈ Z
m
0
, the first step is kept
the same by randomly decomposing the plain-text a
into d elements in Z
m
such that
∑
d
i=1
a
i
mod(m
0
) = a.
The second step is modified by using a vector s
of d secret invertible keys as follow s = [r
1
, r
2
, ...., r
d
]
instead of using d powers of one invertible secret key
r (i.e. [r, r
2
, r
3
, ....., r
d
]). The cipher-text π will be
π = [a
1
r
1
, a
2
r
2
, a
3
r
3
, ....., a
d
r
d
] (mod(m)).
π can be written in a multi-variate polynomial form:
π(t
1
,t
2
,t
3
, ...., t
d
) = (a
1
r
1
)t
1
+ (a
2
r
2
)t
2
+ (a
3
r
3
)t
3
+
.... + (a
d
r
d
)t
d
(mod(m)).
We refer to Basic DF, the primitive scheme ex-
plained in (Domingo-Ferrer, 2002), while Modified
DF refers to the new encryption procedure.
An Efficient FHE Scheme to Secure Cloud Computing
343
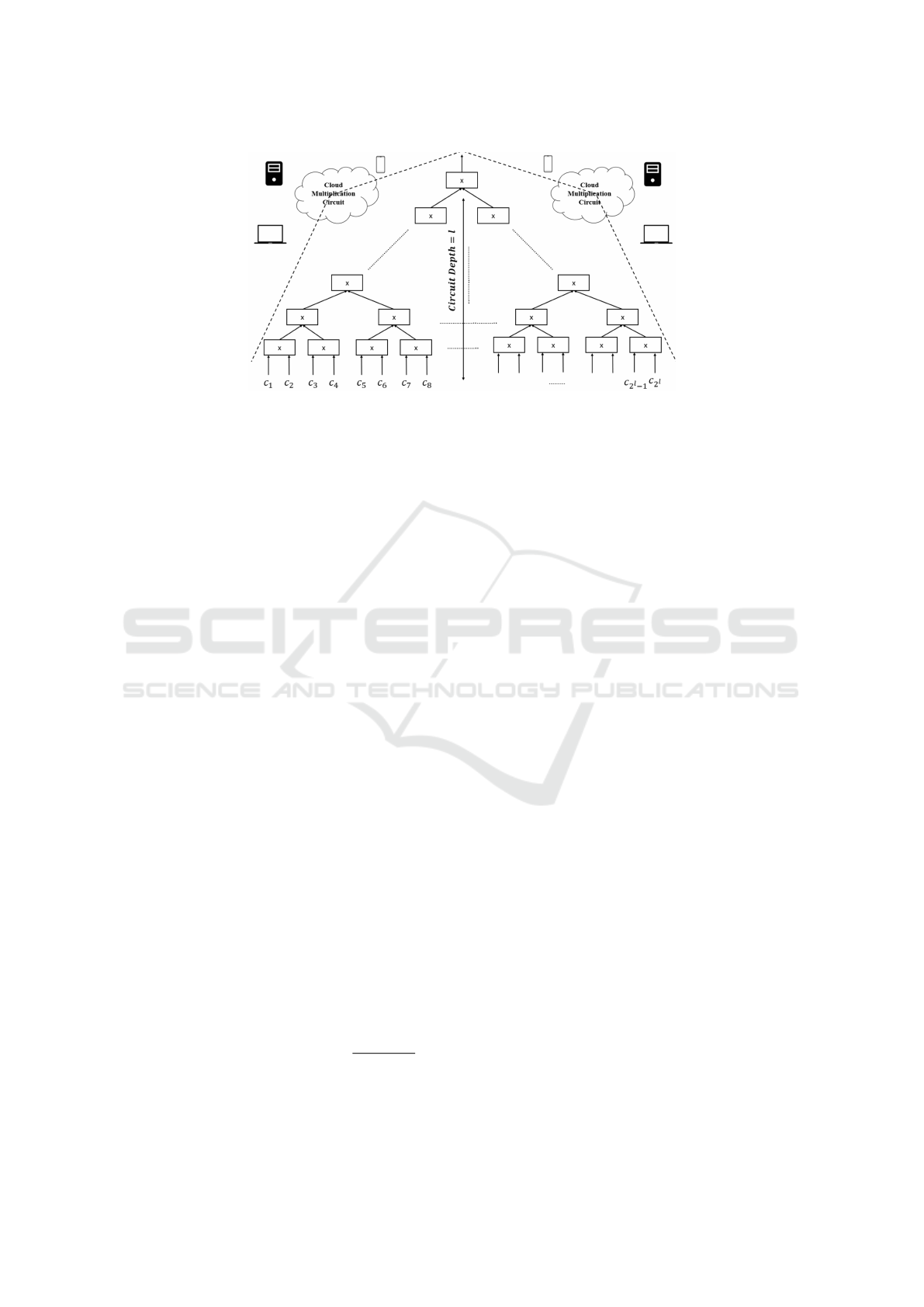
Figure 1: Cloud Multiplication Circuit.
3.1.2 Decryption Procedure
Having the secret parameters (m
0
, s =
[r
1
, r
2
, ..., r
d
]), decryption at the classified level
can be done by multiplying π(i) by r
i
−1
to obtain
a
i
mod(m). Then we perform
∑
i=d
i=1
a
i
mod(m
0
).
3.1.3 Homomorphic Properties
Starting from two plain-texts a
1
, a
2
, the two respec-
tive cipher-texts using Modified DF for a
1
and a
2
are:
π
1
= [a
(1)
1
r
1
, a
(2)
1
r
2
, ...., a
(d−1)
1
r
d−1
, a
(d)
1
r
d
] ((mod(m))
π
2
= [a
(1)
2
r
1
, a
(2)
2
r
2
, ....., a
(d−1)
2
r
d−1
, a
(d)
2
r
d
] ((mod(m))
1. Addition: Using multi-variate polynomial addi-
tion, π
1+2
= π
1
+ π
2
can be written as:
[(a
(1)
1
+ a
(1)
2
)r
1
, (a
(2)
1
+ a
(2)
2
)r
2
, ...., (a
(d−1)
1
+
a
(d−1)
2
)r
d−1
, (a
(d)
1
+ a
(d)
2
)r
d
] ((mod(m)).
Using s
−1
= [r
−1
1
, r
−1
2
, ......., r
−1
d
], we can demon-
strate that Dec
s
(π
1
+ π
2
) = Dec
s
(π
1
) + Dec
s
(π
2
)
and the modified scheme is additive homomor-
phic.
2. Multiplication: Using multi-variate polynomial
multiplication, π
1×2
= π
1
× π
2
can be written as:
[a
(1)
1
a
(1)
2
r
2
1
, a
(2)
1
a
(2)
2
r
2
2
, ..., a
(d−1)
1
a
(d−1)
2
r
2
d−1
, a
(d)
1
a
(d)
2
r
2
d
,
(a
(1)
1
a
(2)
2
+ a
(1)
2
a
(2)
1
)r
1
r
2
, (a
(1)
1
a
(3)
2
+
a
(1)
2
a
(3)
1
)r
1
r
3
, ..., (a
(1)
1
a
(d)
2
+ a
(1)
2
a
(d)
1
)r
1
r
d
,
(a
(2)
1
a
(3)
2
+ a
(2)
2
a
(3)
1
)r
2
r
3
, ..., (a
(2)
1
a
(d)
2
+
a
(2)
2
a
(d)
1
)r
2
r
d
, ...., (a
(d−1)
1
a
(d)
2
+
a
(d−1)
2
a
(d)
1
)r
d−1
r
d
] ((mod(m)).
We can demonstrate that the cipher-text di-
mension after homomorphic multiplication with
Modified DF will be N = C
2
d
+d =
d!
(d − 2)!2!
+d.
N will be reduced to d after introduc-
ing KS technique. To decrypt π
1×2
,
an extended version of the secret key
s
∗
= [r
2
1
, r
2
2
, ..., r
2
d−1
, r
2
d
, r
1
r
2
, r
1
r
3
, ...., r
1
r
d
,
r
2
r
3
, ....., r
2
r
d
, ......, r
d−1
r
d
] of dimension N is
used. The decryption of π
1×2
is done applying
the following inner product:
< s
∗
inverse
, π
1×2
> mod(m
0
) (5)
where s
∗
inverse
= [r
−1
mod(m), r ∈ s
∗
].
Based on Eq.5, we can validate that Dec
s
(π
1
×
π
2
) = Dec
s
(π
1
) × Dec
s
(π
2
) and the new encryp-
tion procedure is multiplicative homomorphic.
Remark 1. Eq.5 can be written in a matrix form:
plain-text = s
∗
inverse
π
1,2
mod(m
0
), where s
∗
inverse
∈
Z
(1,N)
m
and π
1,2
∈ Z
(N,1)
m
.
3.2 KS Technique
As it is mentioned previously, with homomorphic
multiplication the cipher-text dimension in both cases
(basic or modified) will expand into a bigger value
than the initial cipher-text dimension d. The main
concept of KS is that having an extended cipher-text
c
∗
with dimension N, with respect to an extended se-
cret key s
∗
also with dimension N, a new cipher-text
c
0
of dimension d with respect to a new secret key s
0
with dimension d should be calculated verifying this
equation:
Dec
s
∗
(c
∗
) = Dec
s
0
(c
0
) (6)
The main idea is to publish an encryption matrix M ∈
Z
(d,N)
m
defined by:
M(s
∗
→ s
0
) such that c
0
= Mc
∗
(Dimension : (d, 1) = (d, N)× (N, 1))
(7)
The new secret key is s
0
= [r
0
1
, r
0
2
, ....., r
0
d−1
, r
0
d
],
given that s
0
inverse
= [r
−1
mod(m), r ∈ s
0
] and t
0
=
SECRYPT 2019 - 16th International Conference on Security and Cryptography
344

[s
0
(i)
inverse
, 2 ≤ i ≤ d]. The public matrix M of di-
mension (d,N) is formed of two sub-matrices b and
A given by the following form
b
A
.
Matrix b forms the first row of the public matrix
M and is calculated by b = (−t
0
A +m
0
e +s
∗
inverse
)r
0
1
∈
Z
(1,N)
m
. The matrix A of dimension (d − 1, N) is built
based on a uniform distribution over Z
m
.
It is clear from matrix b, that the secret key
s
∗
is encrypted within the public matrix M based
on the hardness of LW E using the new secret
key s
0
, where m
0
is the secret modulus, and e =
[e
1
, e
2
, e
3
, ..., e
N−1
, e
N
] is random noise matrix.
Given that c
0
= Mc
∗
, we can demonstrate that:
s
0
inverse
c
0
mod(m
0
) = s
0
inverse
(Mc
∗
) mod(m
0
) =
(s
0
inverse
M)c
∗
− km
0
= (m
0
e + s
∗
inverse
)c
∗
− km
0
=
s
∗
inverse
c
∗
+ m
0
(ec
∗
− k) = s
∗
inverse
c
∗
mod(m
0
), where
k ∈ Z. Hence Eq.6 is verified.
4 CRYPT-ANALYSIS
In this section, crypt-analysis is firstly done by study-
ing the algebraic structure of the modified scheme to
show that it is more robust than the basic one. Sec-
ondly, by examining the security level of the public
matrix M used in KS technique. M should not leak
any useful information about secret keys (s, s
0
, m
0
) en-
crypted within it.
4.1 Known Plain-text Attack
4.1.1 Polynomial Resultant
Before analyzing the algebraic structure of the
scheme, a brief overview on uni-variate and multi-
variate polynomial’s resultants is given, as it is
mandatory in our crypt-analysis.
1. Uni-variate Polynomial:
Starting from two uni-variate polynomials f and
g:
(a) f (x) = a
0
+ a
1
x + a
2
x
2
+ ...... + a
n
x
n
=
a
n
π
n
i=1
(x − α
i
) = a
n
(x − α
1
)(x − α
2
)(x −
α
3
).....(x − α
n
)
(b) g(x) = b
0
+ b
1
x + b
2
x
2
+ ......b
m
x
m
=
b
m
π
m
j=1
(x − β
j
) = b
m
(x − β
1
)(x − β
2
)(x −
β
3
)......(x − β
m
).
As given in (Sylvester, 1851), the resultant of f
and g with respect to x is a function of the coeffi-
cients of f (x) and g(x) and defined by this equa-
tion:
Res( f , g, x) = a
m
n
b
n
m
π
i, j
(α
i
− β
j
) (8)
where f (α
i
) = 0 for 1 ≤ i ≤ n and g(β
j
) = 0 for
1 ≤ j ≤ m.
Lemma 1. The resultant of f (x) and g(x) is equal
to zero if and only if the two polynomials share a
common root.
As mentioned in (Sylvester, 1851), a practical
way to calculate the resultant of two uni-variate
polynomials is to calculate the determinant of the
(n + m) × (n + m) Sylvester matrix defined by:
Syl( f , g, x) =
a
n
a
n−1
a
n−2
......... a
0
a
n
a
n−1
......... a
1
a
0
................................................................
a
n
a
n−1
........ a
1
a
0
b
m
b
m−1
b
m−2
......... b
0
b
m
b
m−1
......... b
1
b
0
................................................................
b
m
b
m−1
........ b
1
b
0
Zeros fill the blank spaces, the first m rows of
Syl( f , g, x) are populated by the coefficients of
f (x), and the last n rows are filled with the co-
efficients of g(x).
2. Multi-variate Polynomial:
Resultant of multi-variate polynomials was inves-
tigated widely in the literature for both homoge-
neous and non homogeneous cases. In our case,
we will focus only on the homogeneous case. As
a practical way for calculating the resultant of
n multi-variate polynomials ( f
1
, f
2
, ...., f
n−1
, f
n
)
with n different variables (x
1
, x
2
, x
3
, ...., x
n
) was
given in (Allgower et al., 1992). Having the
Eq.9’s system formed of n linear homogeneous
polynomials with n different variables.
f
i
(x
1
, x
2
, ...., x
n
) = w
i,1
x
1
+ w
i,2
x
2
+ ..... + ...
+w
i,n−1
x
n−1
+ w
i,n
x
n
= 0
(9)
where 1 ≤ i ≤ n. The resultant of ( f
1
, f
2
, f
3
, ... f
n
)
with respect to (x
1
, x
2
, ....., x
n
) is equal to the de-
terminant of the matrix W = (w
i, j
) = Coe f f
j
( f
i
),
where (1 ≤ i ≤ n) and (1 ≤ j ≤ n).
If the determinant of the matrix W is equal to 0,
in this case the n linear polynomials f
1
, f
2
, .... f
n
share a common root (x
0
1
, x
0
2
, ......x
0
n
).
4.1.2 Equivalence Key
Given that the secret key for modified DF is
(m
0
, s = [r
1
, r
2
, r
3
, .....r
d−1
, r
d
]). Following (Wag-
ner, 2003) decryption will be possible with an equiva-
lent secret key (m
0
, [r
1
, r
2
, ......, r
d−1
, r
d
]), where r
i
=
r
i
mod(m
0
).
An Efficient FHE Scheme to Secure Cloud Computing
345

4.1.3 Oracle Model
Starting from M = 2 × poly(λ) × (d + 1) couples of
plain-text a
i
and its corresponding cipher-text C
i
.
1. Building the Matrix W :
From the M couples of plain-text/cipher-text, the
system of Eq.10 is built by picking (d + 1) cou-
ples.
C
1
i+k
r
−1
1
+C
2
i+k
r
−1
2
+ .... +C
d
i+k
r
−1
d
= a
i+k
mod(m
0
)
(10)
where 0 ≤ k ≤ d.
Adding to the system of Eq. 10 an extra parameter
r
d+1
= 1, gives birth to a new system formed of
(d + 1) equations with (d + 1) unknowns given in
Eq.11.
C
1
i+k
r
−1
1
+C
2
i+k
r
−1
2
+ .... +C
d
i+k
r
−1
d
−a
i+k
r
−1
d+1
= 0 mod(m
0
)
(11)
where 0 ≤ k ≤ d.
It is very sure that the (d + 1) multi-variate
homogeneous polynomials of Eq.11 share a
common root (r
−1
1
, r
−1
2
, r
−1
3
, ....., r
−1
d
, r
−1
d+1
= 1).
The resultant of these (d + 1) polynomials
should be a multiple of m
0
since all numbers
are in the ring Z
m
0
. The resultant matrix W
i
is
built as listed in section 4.1.1 for multi-variate
case. The k
th
row of matrix W
i
is given by
C
1
i+k
C
2
i+k
C
3
i+k
.......... C
d
i+k
− a
i+k
for
0 ≤ k ≤ d. Its determinant should be a multiple
of the secret modulus m
0
.
2. Recovering the Secret Modulus m
0
:
The procedure listed in the previous section is
repeated 2 × poly(λ) times to build 2 × poly(λ)
matrices W
i
.
Let T = [Det(W
i
), i ∈ {1, 2, 3, ..., 2 × poly(λ)}]
formed of 2 × poly(λ) multiples of m
0
.
Let Y = [gcd(T
i
, T
i+1
), i ∈ {1, 3, 5, ..., 2 ×
poly(λ) − 1}].
Depending on the well known fact given in (Vo-
gel, 2010) that having two large integers a and b,
gcd(a, b) = 1 is achieved with a probability close
to
6
π
2
. Based on this fact, the probability to pick
randomly {T
j
, T
k
} ⊂ T having gcd(T
j
, T
k
) = m
0
is close to
6
π
2
. Hence the probability to obtain
at least one m
0
among the values of Y is close
to (1 − (1 −
6
π
2
)
poly(λ)
). Finally m
0
is the most
common vote among the poly(λ) values of Y .
3. Recovering the Equivalent Secret Key:
After revealing the secret modulus m
0
, the equiva-
lent secret key to be recovered is [r
1
, r
2
, r
3
, ....., r
d
]
where r
i
= r
i
mod(m
0
). To do this, from the M
couples of plain-text/cipher-text, d couples are
picked to form the linear system of Eq.12.
C
1
i+k
r
−1
1
+C
2
i+k
r
−1
2
+ ...... +C
d
i+k
r
−1
d
= a
i+k
mod(m
0
)
(12)
where 0 ≤ k ≤ d − 1.
Finding the equivalent secret key can be achieved
by solving this linear system. This is only pos-
sible when its relative matrix is invertible in the
ring Z
m
0
. Based on (Brent and McKay, 1987),
given a prime number p, the probability f (p) to
find an invertible matrix in the ring Z
p
is at least
e
−2h
where h =
1
p − 1
. The secret modulus m
0
can be decomposed into its prime factors as fol-
low, m
0
= p
e
1
1
p
e
2
2
p
e
3
3
.......p
e
k
k
. In this case, the
probability of finding an invertible matrix in Z
m
0
is f (m
0
) = f (p
1
) × f (p
2
).... × f (p
k
) ≥ e
−2h(m
0
)
where h(m
0
) =
∑
{p
1
,p
2
,....,p
k
}
1
p
i
− 1
. After finding
the invertible matrix in ring Z
m
0
, the system of
Eq. 12 can be resolved using Gaussian elimina-
tion with O(d
3
(log(m
0
)
2
).
As a conclusion, Modified DF is secure against
this attack only when M, the number of couples
plain-text/cipher-text, is lower than d.
4.2 Comparison between Basic and
Modified DF in Terms of Security
Level
In this section, we will show that the Modified DF is
more robust that Basic DF.
1. Recovering m
0
:
Recovering m
0
for Basic DF is based on uni-
variate polynomials. Sylvester matrix given in
section 4.1.1 needs 2 polynomials instead of (d +
1). To recover the secret key m
0
with a proba-
bility close to (1 − (1 −
6
π
2
)
poly(λ)
), we need to
start the attack with 2 × poly(λ) × 2 couples of
plain-text/cipher-text in the basic version instead
of 2 × poly(λ) × (d + 1) in the modified one.
Hence recovering m
0
is made O(d) much more
harder than the basic one.
2. Recovering the Equivalent Secret Key:
In the case of Basic DF, the cipher-text of a
SECRYPT 2019 - 16th International Conference on Security and Cryptography
346

plain-text a with a secret key r is given by C =
[a
1
r, a
2
r
2
, a
3
r
3
, ......a
d
r
d
].
Supposing that z
h
= r
h
for 1 ≤ h ≤ d, a linear sys-
tem similar to the one given in Eq.12 is built, but
only one unknown z
1
= r should be calculated in-
stead of d unknowns [r
1
, r
2
, r
3
, ....r
d
] in Modified
DF.
4.3 KS Security
In this section the hardness of LW E is investigated be-
cause KS security depends on it.
Different secret keys s
∗
, s
0
= [r
0
1
|(t
0
)
−1
] and m
0
are en-
crypted within the public matrix M =
b
A
, where b =
(−t
0
A+m
0
e+s
∗
inverse
)r
0
1
∈ Z
(1,N)
m
and A = [A
i, j
, 1 ≤ i ≤
d − 1, 1 ≤ j ≤ N].
We recall that Z
m
is the public ring and N = C
2
d
+ d.
To reveal secret and random values in the public ma-
trix M, an attacker can build from the matrix b a linear
system of N equations having (2d +N +1) unknowns.
This system have infinite solutions which makes re-
covering the secret keys infeasible especially when
taking high values and respecting the security condi-
tions of LW E given in section 2.
In addition within the public matrix b, m
0
e + s
∗
inverse
is
considered as a plain-text encrypted under the secret
key s
0
. Decryption is a hard lattice problem (CV P)
where resolving it can be done only when knowing
the secret s
0
(Brakerski et al., 2012), (Regev, 2009).
5 EXPERIMENTATIONS
In this section, our proposal is validated by doing dif-
ferent implementations of DF.
All implementations are done under Python with
SAGEMath Library using a machine having the fol-
lowing specification: CPU-Intel Xeon, E5-2630, 2.40
GHZ, 8 CORES, 128 GB RAM.
Starting from a security parameter λ = 90, different
parameters are taken as follows: dimension d is var-
ied from 25 to 100 with step equal to 25, secret modu-
lus m
0
= 336, public modulus m = (m
0
)
λ
= (336)
90
>
10
200
.
5.1 First Experimentation
In this experimentation, two different plain-texts a
1
,
a
2
are taken from the plain-texts secret ring Z
336
, with
two respective cipher-texts C
1
, C
2
obtained by apply-
ing Modified DF. Dimension d is varied from 25 to
100 as given above. By this implementation, the mean
encryption time for 100 plain-texts , the mean decryp-
tion time for 100 cipher-texts, generation time of one
public matrix M are calculated. Finally, we calcu-
late C
mult
= C
1
× C
2
and using KS technique a new
fresh cipher-text C
0
= M × C
mult
is obtained, where
Dimension(C
0
) < Dimension(C
mult
) provided by the
mean execution time of KS for 100 iterations. In
Tab.1, we show dimension variation for different ma-
trices in function of the public parameter d.
Table 1: Matrix and Cipher-texts Dimensions.
X
X
X
X
X
X
X
X
d
Dimension
M C
mult
C
0
25 25x325 325 25
50 50x1275 1275 50
75 50x2850 2850 75
100 50x5050 5050 100
Different execution times in function of the pub-
lic parameter d are given in Tab. 2. Different re-
sults showed acceptable execution times for encryp-
tion, decryption and KS technique. Execution time
increase with dimension d growth is already expected
while providing a higher level of security. It is true
that for different values of d in Tab. 2, matrix M gen-
eration is taking the highest value, but it is generated
only once at the user side. User will execute encryp-
tion/decryption respectively for each couple of plain-
text/cipher-text and KS is performed by the Cloud af-
ter each homomorphic multiplication.
5.2 Second Experimentation
In the second experimentation, the evaluation proce-
dure of the Cloud circuit given in Fig. 1 is done using
three different implementations:
1. Implementation 1: Basic DF Without KS.
2. Implementation 2: Basic DF With KS.
3. Implementation 3: Modified DF With KS.
Figure 2: Execution Time In Function of Cloud Cicruit
Depth l.
An Efficient FHE Scheme to Secure Cloud Computing
347
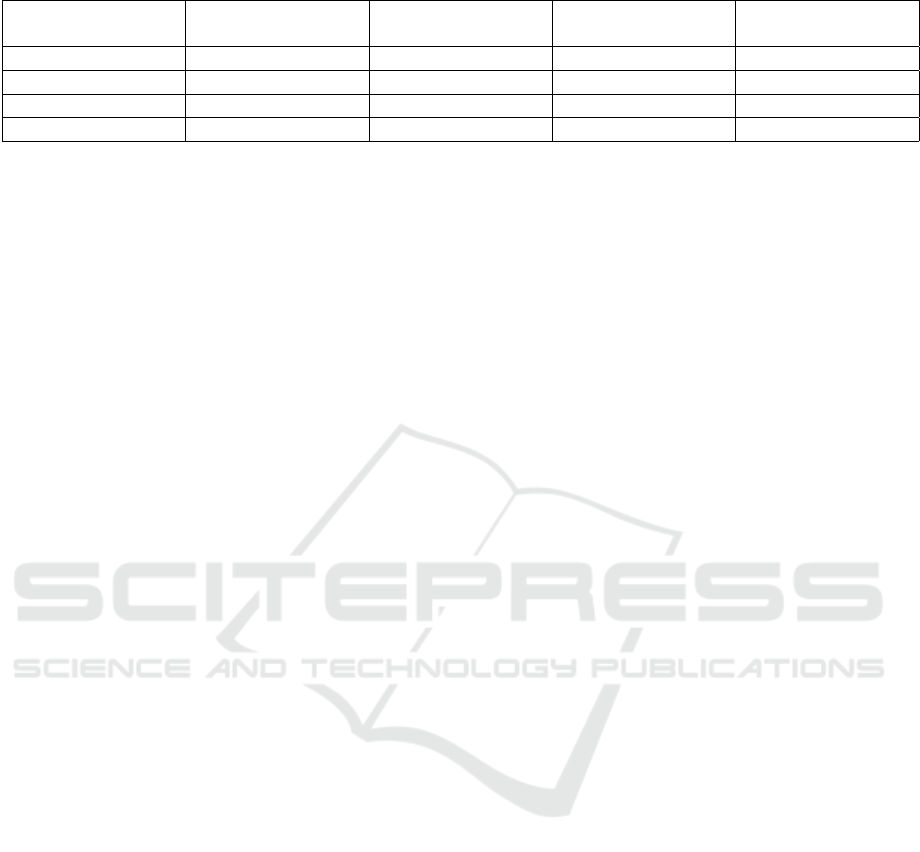
Table 2: Execution times in function of d.
X
X
X
X
X
X
X
X
X
X
d
Procedures
Mean Enc. Time Mean Dec. Time Matrix M Gen. Time Mean KS time
25 0.00046307 s 0.00018298 s 0.136013 s 0.01836656 s
50 0.0009448 s 0.00037313 s 0.740623 s 0.15121927 s
75 0.00128236 s 0.000484769 s 2.084263 s 0.56401619 s
100 0.00175928 s 0.000723319 s 5.392393 s 1.27906641 s
Choosing d = 50, a comparison between different
implementations is done in terms of execution time
and storage overhead in function of circuit depth l.
In Fig.2, different execution times for the three im-
plementations are drawn in function of circuit depth
l and given in log scale just for making results much
clearer. For circuit depth l higher than 6, which is the
complex circuits case faced in real world applications,
Basic DF Without KS is taking the highest execution
time, afterwards comes Modified DF With KS, and
the lower execution time is for Basic DF With KS (for
example in linear scale, with l = 10 and l = 7 respec-
tively, Basic DF Without KS took 6046.26 seconds
respectively 73.619958 seconds, while Modified DF
With KS took 261.21 seconds respectively 31.993578
seconds and Basic DF With KS took 14.57 seconds
respectively 1.733248 seconds). This result is inter-
preted by the fact that for a circuit with high depth,
Basic DF increases the storage overhead of cipher-
texts due to homomorphic multiplications.
Starting from d = 50, cipher dimension grows ex-
ponentially in function of circuit depth l in the case
of Basic DF Without KS (for example for l = 4 Ci-
pher Dimension becomes 785 and for l = 10 Cipher
Dimension becomes 50177), while it remains 50 for
the two others cases while using KS.
The new KS technique increases the efficiency of the
scheme by reducing the storage overhead of cipher-
texts. The difference in execution time between Ba-
sic DF with KS and Modified DF With KS is ex-
pected since the encryption is made more complicated
to leverage the security level.
6 CONCLUSION AND FUTURE
WORK
In this paper, we modified DF in order to be suit-
able for Cloud applications by resolving its two main
problems: sensitivity to known plain-text attack and
cipher expansion after homomorphic multiplication.
The first problem was resolved by changing the en-
cryption procedure. Crypt-analysis has shown that the
concerned attack becomes harder with the modified
version.
The second problem was treated by building a new
technique called KS that reduces the cipher-text di-
mension after each homomorphic multiplication. KS
is based on publishing a matrix M where different se-
cret parameters are encrypted within it based on the
hardness of LW E. Crypt-analysis has shown no se-
cret parameters leakage at the Cloud side.
Different implementations have validated our
work since KS improved the behavior of the scheme
in terms of execution time and storage overhead.
Crypt-analysis of DF has shown that the scheme
(Modified or Basic version) is secure against known
plain-text attack with high values of dimension d and
the public modulus m. Cloud systems can support
these security requirements since they are formed of
big data centers having intensive computation power
and storing capabilities.
Future work will consider applying the Modified
DF under LW E in a secure Cloud computing scenario
for a medical health care and a university applications.
ACKNOWLEDGEMENTS
This work has been partially funded with support
from the Lebanese University.
REFERENCES
Aguilar-Melchor, C., Fau, S., Fontaine, C., Gogniat, G., and
Sirdey, R. (2013). Recent advances in homomorphic
encryption: A possible future for signal processing in
the encrypted domain. IEEE Signal Processing Mag-
azine, 30(2):108–117.
Allgower, E. L., Georg, K., and Miranda, R. (1992).
The method of resultants for computing real solu-
tions of polynomial systems. SIAM J. Numer. Anal.,
29(3):831–844.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).
(leveled) fully homomorphic encryption without boot-
strapping. In Proceedings of the 3rd Innovations in
Theoretical Computer Science Conference, ITCS ’12,
pages 309–325, New York, NY, USA. ACM.
Brent, R. P. and McKay, B. D. (1987). Determinants and
ranks of random matrices over zm. Discrete Mathe-
matics, 66(1):35 – 49.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
348

Chauhan, K. K., Sanger, A. K. S., and Verma, A. (2015).
Homomorphic encryption for data security in cloud
computing. In 2015 International Conference on In-
formation Technology (ICIT), pages 206–209.
Chen, Y. and Nguyen, P. Q. (2012). Faster Algorithms
for Approximate Common Divisors: Breaking Fully-
Homomorphic-Encryption Challenges over the Inte-
gers. In Pointcheval, D. and Johansson, T., editors,
EUROCRYPT 2012, volume 7237 of Lecture Notes
in Computer Science, pages 502–519, Cambridge,
United Kingdom. IACR, Springer.
Coron, J.-S., Mandal, A., Naccache, D., and Tibouchi, M.
(2011). Fully homomorphic encryption over the inte-
gers with shorter public keys. In Rogaway, P., editor,
Advances in Cryptology – CRYPTO 2011, pages 487–
504, Berlin, Heidelberg. Springer Berlin Heidelberg.
Domingo-Ferrer, J. (2002). A provably secure additive and
multiplicative privacy homomorphism. In Proceed-
ings of the 5th International Conference on Informa-
tion Security, ISC ’02, pages 471–483, London, UK,
UK. Springer-Verlag.
Gentry, C. (2009). A Fully Homomorphic Encryp-
tion Scheme. PhD thesis, Stanford, CA, USA.
AAI3382729.
Hariss, K., Chamoun, M., and Samhat, A. E. (2017).
On dghv and bgv fully homomorphic encryption
schemes. In 2017 1st Cyber Security in Networking
Conference (CSNet), pages 1–9.
Kocabas, O. and Soyata, T. (2014). Medical Data Analytics
in the Cloud Using Homomorphic Encryption, pages
471–488.
Martins, P., Sousa, L., and Mariano, A. (2017). A survey on
fully homomorphic encryption: An engineering per-
spective. ACM Computing Surveys, 50:1–33.
Regev, O. (2009). On lattices, learning with errors, random
linear codes, and cryptography. J. ACM, 56(6):34:1–
34:40.
Rivest, R. L., Shamir, A., and Adleman, L. (1978). A
method for obtaining digital signatures and public-key
cryptosystems. Commun. ACM, 21(2):120–126.
Sylvester, J. (1851). On a Remarkable Discovery in the The-
ory of Canonical Forms and of Hyperdeterminants.
van Dijk, M., Gentry, C., Halevi, S., and Vaikuntanathan, V.
(2010). Fully homomorphic encryption over the inte-
gers. In Gilbert, H., editor, Advances in Cryptology –
EUROCRYPT 2010, pages 24–43, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Vogel, M. (2010). An introduction to the theory of numbers,
6th edition, by g.h. hardy and e.m. wright. Contempo-
rary Physics - CONTEMP PHYS, 51:283–283.
Wagner, D. (2003). Cryptanalysis of an algebraic privacy
homomorphism. In Boyd, C. and Mao, W., editors,
Information Security, pages 234–239, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
An Efficient FHE Scheme to Secure Cloud Computing
349
