Bus Regularity Evaluation using the Gini Index and the Lorenz

Curve: A Case Study of New Delhi Bus Network

Amine Melakhsou

and Neila Bhouri

University of Le Havre, 25 Rue Philippe Lebon, 76600 Le Havre, France

Université Paris-Est, IFSTTAR/COSYS/GRETTIA, F-77447 Marne la Vallée, Cedex 2, France

Keywords: Gini Index, Headway Regularity, Travel Time Regularity, Correlation Coefficient, Data Reconstitution.

Abstract: The ability of a public transport system to provide regular services is the main attraction for the system

users. Assessing the regularity of the provided services from the user’s perspective is thus crucial for

stakeholders in order to establish actions for maintaining or improving their system reliability level and

therefore increasing the number of the public transport users. The purpose of this paper is to reveal the

pertinence of the Gini Index based on the Lorenz curve as headway and travel time regularity indicator and

to carry out a case study of the reliability of a bus operator of the city of New Delhi. We began by

reconstituting the missed data in the provided automatic vehicle location data using an approximate

approach and then, using correlation coefficients, we studied the linear relationships, before and after data

reconstruction, between Gini Index and some of the most used regularity measures; headway regularity,

headway adherence, standard deviation and travel time variability. Results show that headway adherence

and standard deviation are the two indicators that have the higher correlations with the Gini index and that

Gini index is less influenced by missing data and errors.

1 INTRODUCTION

The literature is rich with indicators for public

transport reliability measurement but most of the

highly used ones are usually unsatisfactory for

service regularity measures of high-frequency buses

and are not immediately understandable for

inexperienced stakeholders (Bhouri, 2016) and do

not permit the comprehension of the entire issue.

Moreover, the existing indicators cannot be used to

compare between different routes, which is

important for the stakeholders in order to perceive

the ones in which more investments could be made.

This paper aims to study the relevance of the

Gini index (GI) as both headway regularity and

travel time regularity measures respecting both

user’s and operator’s perspectives. For the headway

regularity, we used GI based on the ratio between

actual and scheduled headways in order to evaluate

the adherence to the scheduled timetables. Unlike

the previously reported measures, GI can be used to

compare different routes in term of regularity and

the associated Lorenz curve, which is the graphical

representation of the distribution of the chosen

criterion of GI, is a handy tool for revealing more

information about the causes of irregularity that a

numerical value cannot provide.

For this purpose, a correlation study is

investigated between GI and previously reported

indicators including headway regularity (HR),

headway adherence (HA), standard deviation (STD)

and travel time variability (TTV). A bus system of

the city of New Delhi as a case study is selected to

evaluate correlations and to study related reliability

level of the operation. However, the provided

Automatic vehicle location (AVL) data presents

missing data which can lead to wrong conclusions.

To overcome this issue, an approximate data

reconstitution had been realized.

Finally, the correlation results are encouraging

for the use of GI as a versatile reliability measure

and helped to show that it is less affected by the

missing data and errors.

The paper is structured as follows; section 2

gives a literature review of the transport regularity

indicators with a spotlight on papers proposing new

ones, and a literature review of the use of the Gini

index in the transport domain. In section 3 we define

the used methods. In section 4 we analyze

correlation results and study the reliability of the bus

system of New Delhi and lastly, section 5 provides

conclusions and perspectives.

Melakhsou, A. and Bhouri, N.

Bus Regularity Evaluation using the Gini Index and the Lorenz Curve: A Case Study of New Delhi Bus Network.

DOI: 10.5220/0007795705690577

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 569-577

ISBN: 978-989-758-374-2

569

2 LITERATURE REVIEW

2.1 Literature Review on Transport

Indicators

There are a considerable number of researches

dealing with indicators that are used in the public

transport regularity. (Gittens, 2015) give definitions

and brief evaluations of 20 indicators sorted by their

function (Travel time indicators, schedule adherence

indicators, headway regularity indicators and wait

time indicators). The paper takes interest in whether

an indicator is “traveler-oriented” or not. According

to (Gittens, 2015) the preferred indicators to use by

bus operators are the percentage of buses running on

time and excess waiting time. The authors also

proposed a new composite indicator named Journey

Time Buffer Indicator “JTBI”. (Currie, 2012) review

nine reliability indicators and give a comparison

between them in terms of ease of understanding,

accuracy measure, agency comparability and cost-

efficiency, and give an overall rank for each one of

them. (Trompet, 2011) benchmark 12 international

bus benchmarking group (IBBG) bus operators with

four regularity indicators and list the advantages and

disadvantages of each one of the indicators

regarding the ease of communication, objectivity,

customer representation and the nature of inputs.

(Eboli, 2011) develop a methodology that

implements the objective (quantitative) and

subjective (results of surveys) aspects of an indicator

by implementing them to a single composite one.

The final indicator is obtained by solving an

optimization problem. The methodology has been

tested in a case study for several types of indicators,

among others, timetable adherence indicators. (De

Ona, 2016) suggest a remodeling of this

methodology by improving the optimization

formulation and by the use of cluster analyses (CA)

for the surveys.

(Jensen, 2014) review six types of timetable

reliability indicators used in railways and compare

them in terms of the information provided, the

applicability domain (lines, stations, aggregated) and

the necessary inputs for each one. In order to

evaluate indicators robustness, a comparison

between results of microscopic simulation and the

ones of the indicators has been carried out in this

study. (Fan, 2016) propose an indicator named The

Reported Waiting Time which predicts the waiting

time sensed by a traveler, this indicator allows bus

operators to better understand the concept of waiting

time from the customer’s point of view.

(Teng, 2015) propose a new formulation of bus

running indicator (BRI) based on bus planning travel

time (BPTT) which is also proposed by authors.

The existing indicators are however

unsatisfactory for high-frequency bus services

(Bhouri, 2016) and can’t answer the questions that a

transit manager would ask, such as: how regular a

bus route is? Among different routes, which one is

the most regular? What are the causes of

irregularity? The answers to these questions can be

given by the GI which gives an easy-understanding

and interpretable value even for inexperienced

stakeholders, and since it is a normalized measure it

can be used to compare different routes. In addition,

the associated Lorenz curve helps to extract more

information of the causes of irregularity.

2.2 Background on the Gini Index in

the Transport Field

The Gini index (also called the Gini ratio or the Gini

coefficient) is a measure of statistical distribution

introduced by the Italian statistician and sociologist

Gini Corridor; it is used to represent the income

distribution of a country’s residents.

Although it is used originally in economics, Gini

index had been used in other fields to measure

inequality; In the transport sector, we find a good

number of papers using GI; (Delbosc, 2011) adapted

the Gini index and Lorenz curve to assess public

transport horizontal equity (Horizontal equity means

that all population must have equal transit service

regardless to the variability of transit needs within

population groups.) for Australian city Melbourne.

Departing from this study (Delbosc, 2011) use

also the index to measure horizontal equity for

another Australian city and compares the results

with ones obtained from Melbourne, (Ricciardi,

2015) also compares the public transport vertical

equity, using Gini index, between 3 vulnerable

groups: elderly residents, no-income households,

and no-car households. (Delbosc, 2011) state that the

existing measures of transit equity may be complex

and not expressed by a single value; the use of GI in

this subject is thus interesting because it yields an

easy-understanding single value. GI has been largely

used in the evaluation of public transport equity, in

addition to these articles readers are referred to

(Jang, 2017) and (Pavkova, 2015).

To the best of our knowledge, there are only three

articles that use the GI for regularity evaluation:

(Lee, 2017) propose the use of GI as an evaluation

of travel time in order to assess its evenness among

road users. GI is calculated in a case study of roads

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

570

in Korea and is compared with standard deviation,

speed, buffer time and buffer index to evaluate the

significance of this measure; results show that the

Buffer index has the higher positive correlation with

the GI in this study.

(Henderson, 1991) assess headway regularity

using GI. Along with wait time indicator, headway

regularity based on GI was applied for several bus

routes of New York City and Manhattan before

being tested on a huge number of sets of random

headways in order to study their behaviors and rate

of change. (Bhouri, 2016) evaluate the adherence of

actual headways to the scheduled headways by

applying GI on the distribution of the ratio actual

headway to scheduled headway. Regularity is one of

the most important and relevant measures of public

transport reliability, regularity consists in that

successive vehicles depart, pass and arrive at a

predefined point with predefined time intervals and

with equal headways (Rudnicki, 1997). Regularity

accordingly means, in a perfect case, delivering a

service with equal waiting times and travel times for

all the riders.

3 METHOD

3.1 Formulation of the Gini Index as

Headway and Travel Time

Regularity Indicator

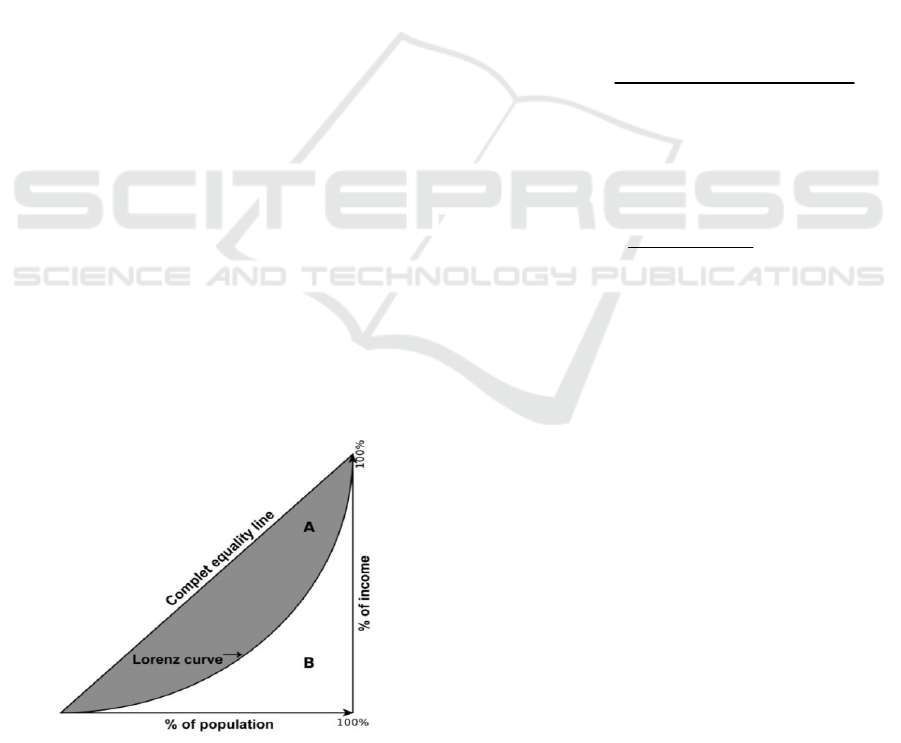
GI is based on the Lorenz curve (figure 1), it varies

from 0 to 1 with 0 indicating absolute equality and 1

indicating complete non-equality. The GI value

corresponds to the area of the shaded surface on the

Lorenz illustration.

Figure 1: The Lorenz curve.

In our study we calculate the Gini value using

trapezoids formula given by (1):

()()

kkk

YGXIXY

−

−=− −



(1)

Where n is the number of observations, X

is the

percentile of the cumulative proportion of the

population and Y

is the k

percentile of the

cumulative proportion of the income. The population

in our case is the number of the trips, and the

incomes are either the cumulative ratios actual to

scheduled headways when dealing with headway

regularity, or the cumulative travel times when

dealing with travel time regularity. The Gini index is

already a normalized measure but since we apply it

for a ratio between two variables (when dealing with

headway regularity), each ratio must be

renormalized in order to compare between different

bus routes as given by the formula:

()

actual headway scheduled headway

New Rat i o a

scheduled headway

(2)

With this modification, a same delay (say 5

minutes) has the same effect on the ratio (thus on the

Gini index) for lines with different frequencies.

Nmin Rline

Nline Rmin

(3)

Where Nline is the number of intervals for the

studied line, Rline is the timetable range of the

studied line Nmin and Rmin refer to the number of

intervals and the timetable range of the line “min”

such that Nmin /Rmin is the minimum of the

quantities Nline/Rline, whatever the line (this

implies α ≤1 ).

This leads to a new Gini index (related to α)

named N_GI

3.2 Correlation Coefficient

The correlation coefficient between two measures is

a dimensionless value which varies from -1 to 1; it

determines the degree and the direction of the linear

relationship between their movements. 1 indicates

total positive correlation while -1 indicates total

negative correlation, a correlation coefficient equal

to 0 means that the two measures are not linearly

related. The more it approaches 1 or -1 the stronger

the measures are related. We use the correlation

coefficient to compare the relations between the Gini

index and each of the presented indicators and see

Bus Regularity Evaluation using the Gini Index and the Lorenz Curve: A Case Study of New Delhi Bus Network

571

how they change in order to better understand the

behaviors of the Gini index.

3.3 Regularity Indicators

We present in what follows the highly used

indicators that will be adopted for our study.

3.3.1 Standard Deviation

The standard deviation is a statistical measure of the

dispersion of a dataset from its average.

3.3.2 Headways Adherence

HA is defined as the standard deviation of the

observed headways from the scheduled ones divided

by the average scheduled headways as given by the

formula:

()

AH M

−



(4)

Where AH is the actual headway, SH is the

scheduled headway and M is the mean actual

headways.

3.3.3 Headway Regularity

HR has been used by the New York transit authority

(Cramer, 2009), it provides the percentage of trips

having acceptable headways.

Since we will be using GI based on the ratio

R=(Actual Headway)/(Scheduled Headway), we

adapted HR to compute the number of trips with

acceptable ratios.

Moreover, we don’t know whether a ratio is

acceptable or not, we propose then another

formulation of HR using a confidence interval which

is given by:

Number of trips having a ratio CI

100

Number of all trips

HR ×=

∈

(5)

Where CI is the confidence interval with a length

of 6 sigmas:

];3[3

CI x x

σσ

−× ×=+

(6)

Where 



is the ideal case, i.e. when the actual

headway is equal to the scheduled one, which yields

to 



ideal

=1. When a ratio R

belongs to the CI, the

trip i is considered as having an acceptable ratio.  is

the standard deviation of the ratios of a given set and

n is the number of the trips.

3.3.4 Travel Time Variability

Also known as buffer index, it is defined as the extra

time a traveler should add to arrive on time 95% of

the time.

95TT MTT

TTV

−

(7)

Where TT

is the 95

percentile of the travel

time and MTT is the mean travel time.

3.4 AVL and Missed Data

Reconstitution Methodology

The main problem with the provided data is that we

do not have the time of a bus passage at all the stops;

these lost data cause discords between actual and

scheduled headways which lead to distorted

headways ratios. To overcome this issue and make

reliable conclusions, we added the missing data with

an approximate reconstitution method which utilizes

the distance between stops and the speed of the bus;

the approach consists, for a given missing, in adding

the amount of time T

=Distance

/Speed

to the

previous detected time, if it exists, if there is no

previous detected time we subtract the amount from

the posterior detected time and then from the added

time and so on until refilling all gaps. It is important

to mention that we might get some incoherencies

due to using the mean speed in the absence of

information on the real speed of a bus; in this case,

the reconstituted time is deleted to avoid

reproducing false data.

Our study is limited to 8 routes of the New Delhi

bus operator consisting of 4 high-frequency and 4

low-frequency routes, within the 30 days of

September 2016.

As mentioned, due to the number of missed data

that would distort the results, the reconstitution

model is applied to provide more accurate reliability

measurement.

We acquired 30 files of AVL data (each one

corresponding to a bus line for a day of September

2016) for all the routes stops that include actual and

scheduled times along with actual and scheduled

speed. We also got provided with a file that contains

data for only the departure stop and the terminus for

all the routes. These data are used to give a first

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

572

overview of correlations between GI and the other

indicators and also is used for the comparison

between the routes. Information on bus routes is

given in table 1.

Table 1: Information on the bus lines.

Length

(frequency)

Route N° Average

Scheduled

Headway

(minute)

Average

Observed

Headway

(minute)

Short

(Low)

403CLUP 23.3 31.05

403CLDOWN 24.46 33.28

Long

(Low)

185UP 32.75 51.67

185DOWN 32.94 44.34

Short

(High)

507CLUP 18.51 24.03

507CLDOWN 18.3 22.82

Long

(High)

165UP 11.67 15.44

165DOWN 11.75 16.91

4 RESULTS

In this section, we show the graphs of the different

indicators drawn for the route N° 403CLUP before

presenting and discussing the correlations results

between GI and the other measures.

At the end of the section, we study the reliability

of the bus services of the city.

4.1 A Visual Comparison between Gini

and the Regularity Indicators

To have a first look on the behaviors of the

indicators, we draw their charts for the bus route N°

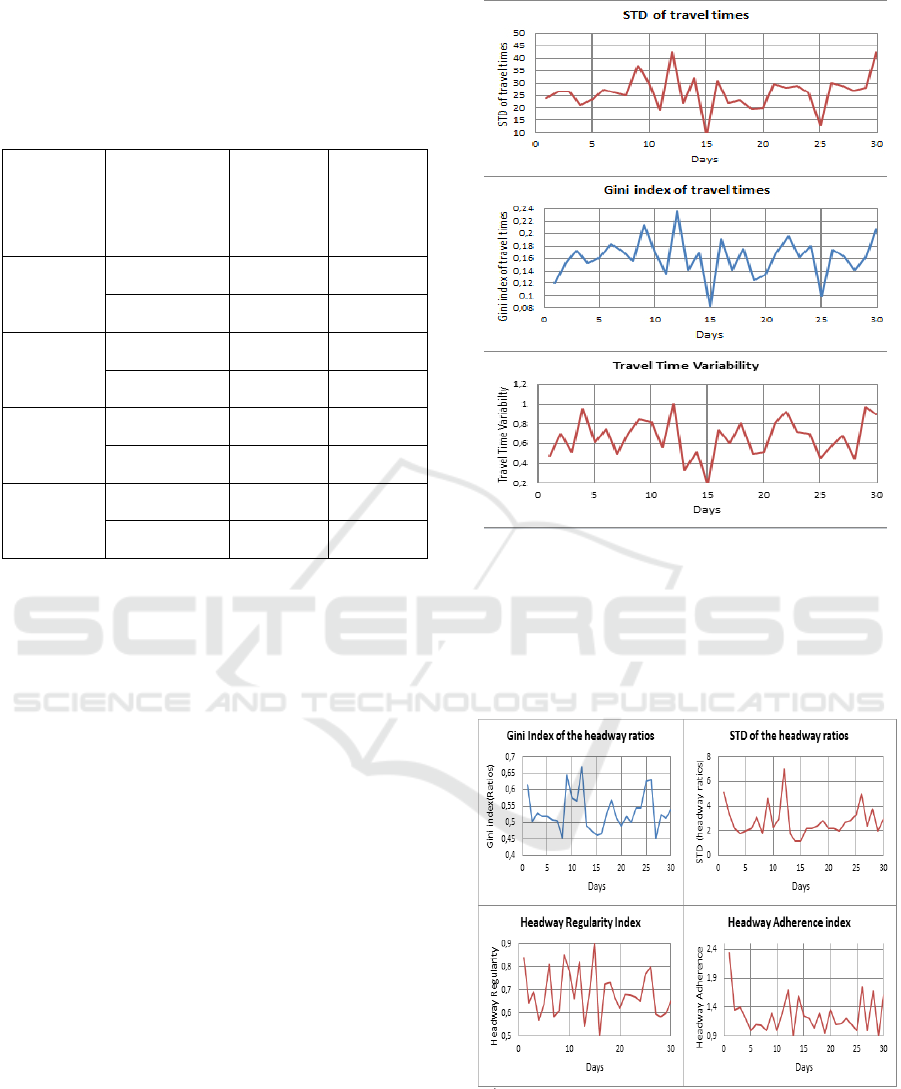
403CLUP within the 30 days, figure 2 shows the

graph of GI as a travel time indicator with the graphs

of STD of travel times and TTV while figure 3

shows the graph of GI for the headway ratios along

with the other headway regularity indicators.

We can notice from a first sight that GI concurs

more with the indicators of travel times and that it

has higher similarity with STD of travel times than

with the STD of headway ratios which demonstrates

already that resemblance between two given

indicators is not always the same.

Figure 2: Graphs of travel time regularity indicators for

the bus route 403CLUP within 30 days.

To better understand the relationships between

GI and the other measures; we use the correlation

coefficient because it is more efficient and faster

than the visual inspection of the charts.

Figure 3: Graphs of headway regularity indicators for the

bus route 403CLUP within the 30 days.

Bus Regularity Evaluation using the Gini Index and the Lorenz Curve: A Case Study of New Delhi Bus Network

573

4.2 Correlation Coefficients between

Gini and the Other Regularity

Indicators

Table 2 show the correlation coefficients obtained

for all the bus routes between GI and the used

indicators.

One can notice from table 2 that STD has the

higher correlation coefficients with GI; this is

expected since GI is based on STD, we also notice

that GI presents a good correlation with TTV and

HR which is encouraging for using the indicator for

both headway and travel time regularity but, it is

important to mention that these correlation results

would variate according to the nature of the data; in

fact, in a set of data which contains values that are

largely deviated from the mean, STD and TTV are

highly influenced by these values (LEE, 2017),

especially TTV because it takes into account only

the deviance of the 95

percentile from the mean ,

hence it shows larger deviations, while GI would

assess the reliability from the perspective of

evenness and may not show the same behavior as

STD and TTV, correlation would be less good in

this case while it would be excellent in the opposite

case.

In order to show the influence of data

characteristics on correlation, we compare the

correlation coefficient between GI and STD before

and after the data reconstitution for the bus route N°

165DOWN, figure 4 gives the correlation coefficient

values and the charts of GI and STD for day 1 before

and after.

We notice that correlations have increased from

0.84831 before reconstitution to 0.95621 after; this

is due to the fact that when adding the missing data

for this day we actually decreased the relative ‘huge

variations’ as figure 4 shows; before reconstitution

(the left side of the figure) there are a considerable

number of values that have large deflections from

the average which influenced the correlation

coefficient negatively, after the reconstitution the

data show fewer variations which clarify the

increment of correlation between GI and STD.

We also catch from figure 4 that GI is able to

detect huge variations but without amplifying them

unlike STD and TTV (TTV amplifies the variations

more since it computes the deviation between the

percentile and the mean, while STD computes

the average deviation from the mean.) which leads to

conclude that GI is less influenced by variations

caused by the errors and misses in data, in fact, the

correlation coefficient between STD before and after

is 0.3536 whilst the correlation coefficient between

GI before and after is 0.6379.

Table 2: correlation coefficients between GI and the other

indicators for all the bus lines.

Gini (Ratios) STD HR HA

Low-frequency routes

403CLUP 0.8076 0.6083

0.4251

403CLDOWN 0.7624 0.5368

0.6157

185UP 0.7240 0.5873

0.4049

185DOWN 0.7626 0.6448

0.5593

High-frequency routes

507CLUP 0.7730 0.6511

0.2909

507CLDOWN 0.7115 0.6860

0.3826

165UP 0.8188 0.6962

0.4617

165DOWN

0.7179 0.6454

0.5182

Gini

(Travel times)

STD

(Travel

times)

TTV

Low-frequency routes

403CLUP 0.9017 0.7322

403CLDOWN 0.9070 0.7825

185UP 0.9364 0.7617

185DOWN 0.9126 0.6221

High-frequency routes

507CLUP 0.9550 0.7445

507CLDOWN 0.9375 0.6179

165UP 0.9425 0.6259

165DOWN 0.9679 0.5932

If we draw the GINI index for all the buses at

once, before and after data reestablishment, we

would notice that GI values do not stir much, as

figure 5 shows.

Although for day 1, 526 missed data is

reconstituted (21.11% of the data) and 312 for day

26 (12.53 %), the curves before and after are not

very different and the Gini values are barely

changing, we noticed also that when drawing the

Lorenz curve for each stop separately the Gini

values still change slightly which enhances the

hypothesis of the ability of GI to provide a reliable

measurement, despite the data errors and misses.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

574

Figure 4: Correlation before (left) and after data

reconstitution.

After the data reconstitution, GI shows really

excellent correlations with HA, which means that

using GI based on the ratio actual to scheduled

headways is capable of assessing the adherence to

the planned timetable; table 3 shows the results for

data for several days.

Table 3: Correlation between GI and HA after data

reconstitution.

Day Correlation coefficient (GI, HA)

2 0.9514

5 0.9566

11 0.9767

26 0.8848

The poor correlations which were obtained

before reconstitution are surely caused by the

incoherence in the initial data. As to correlations

between GI and Headway Regularity, the observed

criterion that influences the correlation is the length

of the confidence interval, for some datasets; giving

a larger CI leads to better correlations. (The data is

not normally distributed thus, the characteristics of

CI are not the ones defined for the normal

distributions).

Finally, like any other indicator, GI has its

unique vision of regularity which is the evenness of

the distribution of the chosen criterion, it offers a

new point of view of the reliability of the public

transport. As the correlation study outcomes show,

GI agrees with the other indicators under some

Figure 5: Lorenz curve for all the stops before and after

data reconstitution.

conditions, outside these conditions it behaves

differently, this is not to be seen as a failure, on the

contrary, it shows another perspective from which a

bus operator can see the reliability.

In the next section, we discuss the results of the

case study of the reliability of the bus operator of

New Delhi and show the utility of the Lorenz

illustration.

4.3 Reliability of the Bus Services of

New Delhi

As a reminder, GI is a value between 0 and 1, the

value 0 indicates perfect equality while 1 indicates the

non-equality of the distribution. In what follows we

show and discuss results for the bus line 165DOWN

using the new data. Figure 6 shows the Lorenz curves

drawn for the ratio actual to scheduled headways for

the 1

and the 26

September. For the first day, GI

values show that the first 14 stops are more regular

than the rest, that’s why we see their curves approach-

ing more to the perfect equality line, in the rest of the

stops there are more bus bunches (the left side of the

curves are more parallel to the horizontal axe) and

more buses with headways that largely deviate from

the scheduled ones, shown by the higher discards of

the curves from the equality line at the right side.

Bus Regularity Evaluation using the Gini Index and the Lorenz Curve: A Case Study of New Delhi Bus Network

575

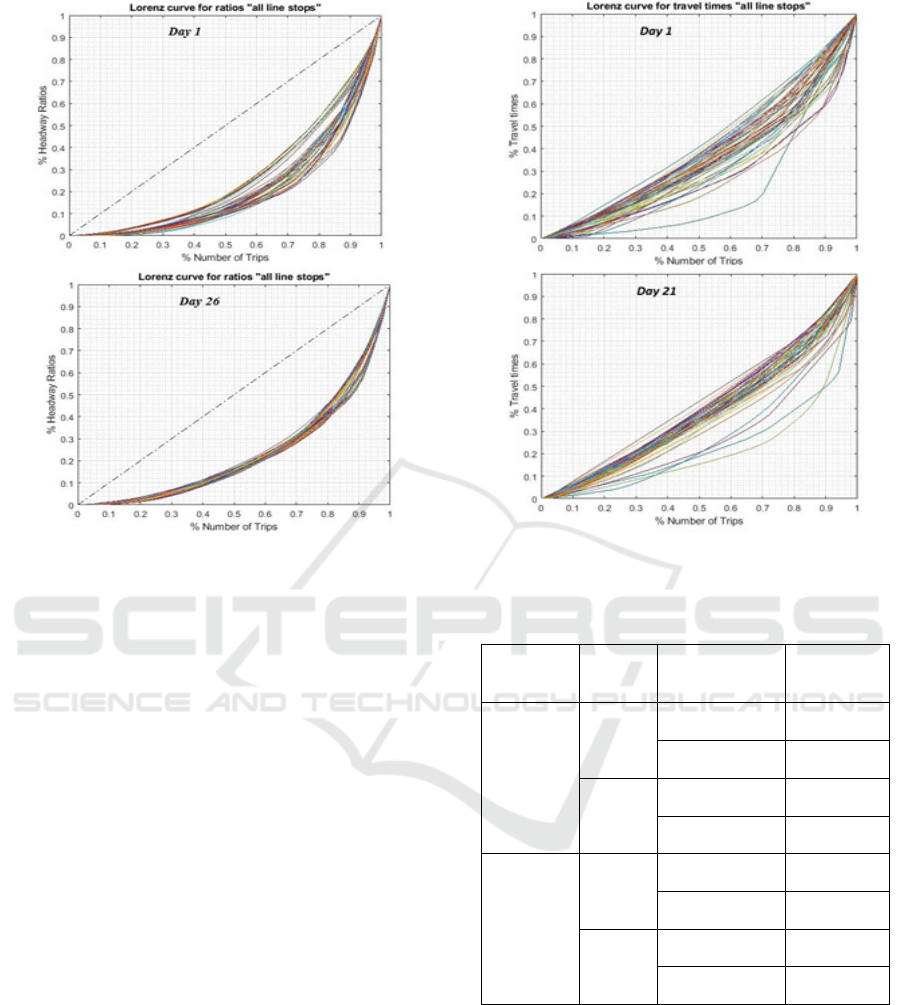
Figure 6: Lorenz curves for all 53 stops separately

(headway ratios).

For the day 26, the stops are showing

approximately the same behavior, the mean GI and

HA of this day are 0.5345 and 1.5175 which reveals

the irregularity of the service due to bus bunching

and disrespect to the scheduled timetable.

As an overall conclusion, the bus service for this

route within the month of September is not so decent

and suffers from bus bunching, which also leads to

the appearance of large intervals, and deviations

from the scheduled timetable, in addition, we

noticed that the number of performed trips varies

remarkably from a day to another which also is a

real cause of unreliability.

In terms of travel time regularity, the bus

operator seems to provide a correct service as can be

seen in figure 7, we can see that most of the curves

are near the equality line, but one particular curve

deviates highly for all the days, it is the road

between the stops “Libas pur GT ROAD “and

“Sanjay Ghandi Transport Nagar”, which is, in fact,

a highway highly influenced by traffic, otherwise for

the rest of the trips, most of the users are provided

with approximately equal travel times. In order to

compare the bus routes in term of headway

adherence, we apply the N_GI that was defined in

the methodology section by equation (2). Table 4

gives the mean N_GI values for all the studied bus

routes of the city of New Delhi.

Figure 7: Lorenz curves drawn for travel times for day 1

and day 21.

Table 4: Normalized Gini values for all bus routes.

Frequency Length Routes

Mean

N_GI

Low

Short 403CLUP 0.4752

403CLDOWN 0.4713

Long 185UP 0.4927

185DOWN 0.5103

High

Short 507CLUP 0.4841

507CLDOWN 0.5146

Long 165UP 0.5226

165DOWN 0.5215

The values of the N_GI on table 4 show that

most of the low-frequency routes are the more

regular, which is normal as the high-frequency

routes are harder to manage, also we notice that the

short length routes are more reliable comparing the

high length routes, in addition, the GI values are all

near 0.5 which indicates a mediocre service for all

the routes in terms of headway adherence.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

576

5 CONCLUSION

For the public transportation, regularity of the travel

times and the respect to the scheduled timetables are

the essential qualities that appeal the users,

nevertheless, deviating from the planned program

and from the expected travel time are inevitable.

Assessing the irregularities from the user’s

perspective is necessary for stakeholders in order to

establish actions for maintaining or improving their

system reliability level and to attract more users. In

this paper, we highlighted the relevance of the Gini

index based on the Lorenz curve as an indicator of

the adherence of actual headways to the pre-

established ones and as a travel time regularity

indicator, by showing its relationship with some of

the most used indicators: headways adherence,

headway regularity, standard deviation and travel

time variability.

Results show that headway adherence and

standard deviation are the two indicators that have

the higher correlations with the Gini index. We

noticed also that GI remains approximately stable

before and after data reconstitution and do not show

huge differences unlike the other used indicators,

which permitted to judge this indicator as less

affected by errors and misses in data. After revealing

the effectiveness of the presented measure, we

studied and discussed the reliability of the bus

services of the city using GI and the Lorenz curve.

The results of this study show that the services are

irregular in terms of headway adherence but on the

other hand, the users are provided by regular trips in

terms of travel time. An extension of our study

would be to develop a better data reconstitution

method, compare the Gini index with other

indicators and using other methods of comparison to

emphasize the relevance of the Gini index.

REFERENCES

Bhouri, Neila, Aron, Maurice, et Scemama, Gérard. Gini

Index for Evaluating Bus Reliability Performances for

Operators and Riders. In: Transportation Research

Board. 2016. p. 13p.

Gittens, Antonio et Shalaby, Amer. Evaluation of bus

reliability measures and development of a new

composite indicator. Transportation Research Record:

Journal of the Transportation Research Board, 2015,

no 2533, p. 91-99.

Currie, Graham, Douglas, N. J., et Kearns, Ian. An

assessment of alternative bus reliability indicators. In

Australasian Transport Research Forum. 2012.

Trompet, Mark, Liu, Xiang, et Graham, Daniel.

Development of key performance indicator to compare

regularity of service between urban bus operators.

Transportation Research Record: Journal of the

Transportation Research Board, 2011, no 2216, p. 33-

41.

Eboli, Laura et Mazzulla, Gabriella. A methodology for

evaluating transit service quality based on subjective

and objective measures from the passenger’s point of

view. Transport Policy, 2011, vol. 18, no 1, p.172-

181.

De Ona, Juan, De Oña, Rocio, Diez-Mesa, Francisco, et al.

A composite index for evaluating transit service

quality across different user profiles. Journal of Public

Transportation, 2016, vol. 19, no 2, p. 8.

Jensen, Lars Wittrup, Landex, Alex, et Nielsen, Otto

Anker. Evaluation of robustness indicators using

railway operation simulation. Computers in Railways

XIV: Railway Engineering Design and Optimization,

2014, vol. 135, p. 329.

Fan, Yingling, Guthrie, Andrew, et Levinson, David.

Waiting time perceptions at transit stops and stations:

Effects of basic amenities, gender, and security.

Transportation Research Part A: Policy and Practice,

2016, vol. 88, p. 251-264.

Teng, Jing et Lai, Xiong-Fei. A calculation method for bus

running index. In: Proceedings of the transportation

research board annual meeting, Washington, DC.

2015. p. 11-15.

Delbosc, Alexa et Currie, Graham. Using Lorenz curves to

assess public transport equity. Journal of Transport

Geography, 2011, vol. 19, no 6, p. 1252-1259.

Ricciardi, Anthony Michael, Xia, Jianhong Cecilia, et

Currie, Graham. Exploring public transport equity

between separate disadvantaged cohorts: a case study

in Perth, Australia. Journal of transport geography,

2015, vol. 43, p. 111-122.

Jang, Seongman, An, Youngsoo, Yi, Changhyo, et al.

Assessing the spatial equity of Seoul’s public

transportation using the Gini coefficient based on its

accessibility. International Journal of Urban Sciences,

2017, vol. 21, no 1, p. 91-107.

Pavkova, Katerina, Currie, Graham, Delbosc, Alexa, et al.

A New Approach to Exploring the Operational

Performance of Public Transport Links, the case of

Melbourne, Australia.

Lee, Soong-Bong, Lee, Seongkwan Mark, et Lee, Ki-

Young. A Gini coefficient based evaluation on the

reliability of travel time forecasting. Journal of King

Saud University-Engineering Sciences, 2017.

Henderson, Gary, Kwong, Philip, et Adkins, Heba.

Regularity indices for evaluating transit performance.

Transportation Research Record, 1991, vol.1297, p.3-9.

Rudnicki, Andrzej. Measures of regularity and punctuality

in public transport operation. IFAC Proceedings

Volumes, 1997, vol. 30, no 8, p. 661-666.

Cramer, A., Cucarese, J., Tran, M., Lu, A., Reddy, A.

(2009) Performance measurements on mass transit:

Case study of New York City Transit Authority.

Transportation Research Record: Journal of the

Transportation Research Board 2111, 125-138.

Bus Regularity Evaluation using the Gini Index and the Lorenz Curve: A Case Study of New Delhi Bus Network

577