
Variety-aware Routing Encoding for Efficient Design Space Exploration
of Automotive Communication Networks
Fedor Smirnov
1
, Behnaz Pourmohseni
1
, Michael Glaß
2
and J¨urgen Teich
1
1
Friedrich-Alexander-Universit¨at Erlangen-N¨urnberg (FAU), Erlangen, Germany
2
Ulm University, Ulm, Germany
Keywords:
DSE, Network Optimization, Automotive Networks.
Abstract:
The introduction of sophisticated ADAS has given rise to larger and more complex automotive communica-
tion networks whose efficient (in effort) and optimal (in quality) design necessarily depends on automated
network design techniques. Typically, these techniques either (a) optimize communication routes based on
topology-independent constraint systems that encode the inclusion of each network component in the route of
a message or (b) depend on a time- and memory-expensive enumeration of all possible transmission routes
to identify the optimal route. In this paper, we propose a novel approach which combines the advantages of
these two strategies to enable an efficient exploration of the routing search space: First, the given network is
preprocessed to identify so-called proxy areas in which each pair of nodes can be connected by exactly one
route. Contrary to network areas with a variety of different routing possibilities, proxy areas do not offer any
room for optimization. We propose two approaches—both integrable into existing constraint systems—which
exploit the knowledge gathered on proxy areas to improve the exploration efficiency during the routing opti-
mization process. Experimental results for two mainstream topologies of automotive networks give evidence
that, compared to state-of-the-art routing optimization approaches, the proposed approaches (a) offer an ex-
ploration speedup of up to ×185, (b) deliver network designs of equal or higher quality, and (c) enable an
automated design of significantly larger automotive systems.
1 INTRODUCTION
In recent years, a tremendous number of innovations
have been developed in automotive electronics. New
infotainment and driver assistance features introduce
a high demand of both computation and communica-
tion power and cause a rapid growth in the number of
electronic control units (ECUs) installed in a vehicle,
and, subsequently, an immense rise in the size and
complexity of automotive communication networks.
Indeed, modern automotive wiring harnesses feature
roughly 23kg in weight and 1.2 km in length (Interna-
tional Cablemakers Federation, 2015) which signifi-
cantly contributes to the overall weight and the mon-
etary cost of the vehicle. At the same time, the distri-
bution of safety-critical applications, e.g., airbag con-
trol or driver assistance, across multiple logically and
physically separated ECUs necessitates the underly-
ing communication network (interconnecting those
ECUs) to be regarded as safety-critical as well. As a
consequence, each design decision related to the com-
munication network must be evaluated with respect to
many, oftentimes conflicting, design objectives such
as monetary cost, weight, transmission timing, and
transmission reliability, which renders the manual de-
sign of these networks impractical, if at all feasible.
Compared to a manual design, approaches for de-
sign automationoffer an interesting opportunityto ad-
dress this challenge, as they reduce design errors and
offer design solutions of higher quality (Sangiovanni-
Vincentelli and Di Natale, 2007). Consequently, de-
sign automation has become an area receiving great
attention from the scientific community. As finding
the optimal network design is an NP-hard problem,
an enumeration of all possible combinations of de-
sign decisions is computationally infeasible, except
for very small problem sizes. Furthermore, especially
in case of complex communication networks, many
possible combinations of design decisions result in
infeasible solutions, e.g., a network design lacking
transmission routes between senders and receivers.
To cope with this problem, most design automation
approaches rely on constraint sets that describe con-
ditions that must be satisfied for a network design to
242
Smirnov, F., Pourmohseni, B., Glaß, M. and Teich, J.
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks.
DOI: 10.5220/0007797802420253
In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 242-253
ISBN: 978-989-758-374-2
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

be valid, e.g., constraints to enforce that a valid net-
work contains a transmission path between the sender
and the receiver(s) of each communication. The re-
solution of the constraint set, i.e., finding an assign-
ment of the design decision variables that satisfies
all constraints, is then either used as the main opti-
mization mechanism (Neubauer et al., 2018) or as a
repair mechanism (to repair infeasible designs into
valid ones) as part of a dedicated optimizer, e.g., an
evolutionary algorithm (Lukasiewycz et al., 2007).
In the embedded domain, the system design prob-
lem, i.e., the implementation of an application on a
given network architecture, is typically represented
by a set of constraints that encode a valid binding of
the application’s tasks onto the network’s resources, a
valid allocation of the required resources, and a valid
routing of messages that are transmitted between re-
sources executing data-dependenttasks (Blickle et al.,
1998). The computational effort for the generation
and the resolution of these constraints typically scales
exponentially with the number of encoded decision
variables and has an immense impact on the effi-
ciency and even the feasibility of the overall opti-
mization (Richthammer and Glaß, 2018). Except for
the most trivial network topologies, the routing con-
straints constitute the most complex part of the con-
straint set and introduce the largest share of encoded
decision variables.
The majority of state-of-the-art routing encoding
approaches fall into one of the following two classes:
(a) so-called route preprocessing (RP) approaches
which rely on a preprocessing phase to find all pos-
sible routes connecting each pair of nodes (Laursen
et al., 2016; Gavrilut et al., 2017). During the op-
timization, a message is then routed by selecting
one of the preprocessed routes that connect the mes-
sage’s source to its destination. Alternatively, (b) so-
called componential assembly (CA) approaches en-
code an activation variable that represents the in-
clusion of each network component—e.g., a link or
a node—into the route of each message and for-
mulate constraints to ensure the assembly of valid
routes (Al Sheikh et al., 2013; Nayak et al., 2016;
Schweissguth et al., 2017; Mahfouzi et al., 2018).
The resolution of these constraints provides an as-
signment of the activation variables based on which a
valid route is constructed by assembling the activated
components.
As shown in (Graf et al., 2014), the strengths and
weaknesses of RP and CA approaches are somewhat
complimentary. CA approaches encode the usage
of each network component per message, regardless
of the network topology. This not only introduces
a high number of encoding variables—especially in
case of complex routing behaviors like multicasts
(Lukasiewycz et al., 2014) or redundant transmissions
(Smirnov et al., 2018b)—but also results in an unne-
cessarily complex description of the routing optimiza-
tion search space. RP approaches, on the other hand,
use the preprocessing phase to acquire total knowled-
ge on the network topology and provide the optimizer
with a compact description of the actual search space.
However, their need for an enumeration of all routing
possibilities limits the applicability of RP approaches
to sparsely-connected network topologies where the
number of possible routes is small, even if the net-
work itself is not small. For densely-connected net-
work topologies, the encoding overhead of CA ap-
proaches is more than compensated by their superior
scalability. Furthermore, the fine-grained encoding of
routing decisions in CA approaches not only enables
the formulation of additional constraints, e.g., to re-
spect link capacity or the mutual exclusion of compo-
nents, but also results in a much better performance
when optimizing objectives which are strongly influ-
enced by individual components of the routes, for in-
stance, monetary cost or reliability (Smirnov et al.,
2018b).
Contribution: Real-life communication net-
works rarely completely fall into one of the two ex-
treme connectivity categories listed above (dense or
sparse), but rather constitute a connection of several
subnetworks, each being either sparse or dense. This
holds particularly true for automotive networks: On
the one hand, safety-critical ADAS applications make
a certain degree of transmission redundancy manda-
tory. On the other hand, the high cost pressure and the
necessity to reuse network designs from previous car
generations prohibit the free practice of redundancy at
every possible point. Rather than that, it seems more
likely that redundancy is considered only for the most
critical components, e.g., links which are especially
vulnerable or important. This redundancy scheme re-
sults in network topologies in which several sparsely-
connected subnetworks are connected with each other
via densely-connected network regions.
CA and RP approaches excel when processing ei-
ther densely- or sparsely-connected networks, respec-
tively. They, however, suffer in efficiency or practica-
bility when applied to the compound network topolo-
gies described above. In this paper, we introduce an
optimization approach that combines the strengths of
these two strategies and proves effective for such net-
works. In the proposed approach, the given network
is partitioned into network areas of one of the two fol-
lowing types: (a) proxy areas which offer exactly one
routing possibility between each pair of nodes con-
tained within them and (b) areas with a variety of dif-
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
243
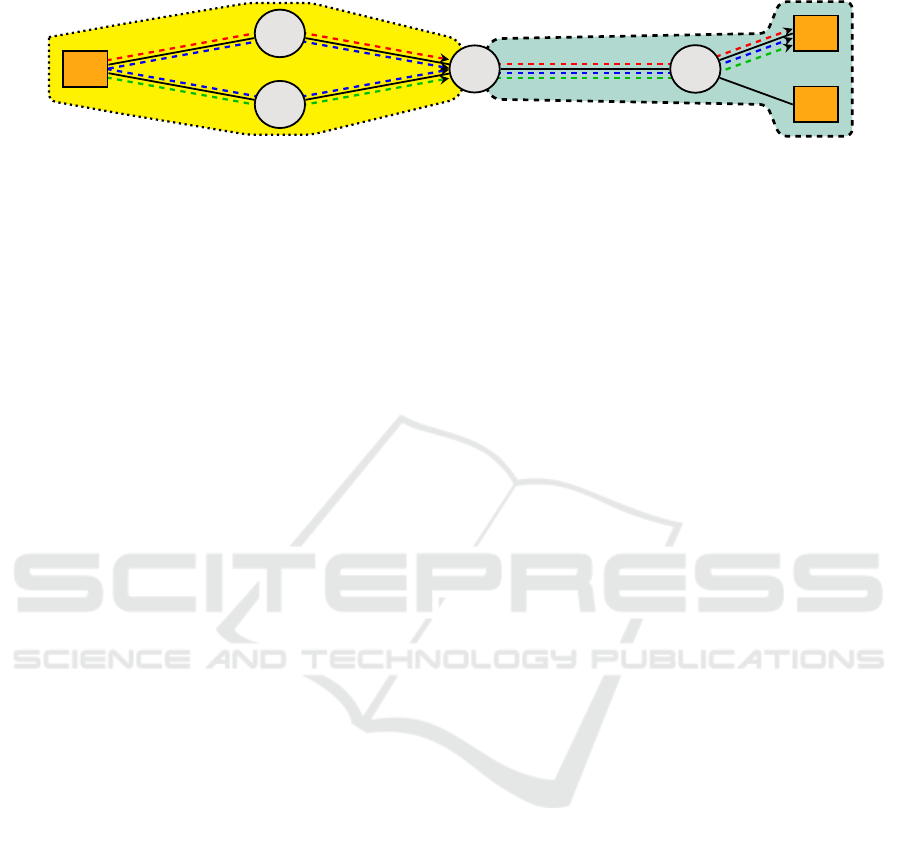
I
III
II
E
0
S
3
E
1
E
2
S
2
S
0
S
1
Variety Area
Proxy Area
Figure 1: Resource network consisting of a variety area (yellow/left) and a proxy area (green/right). All differences between
the routes connecting ECU E
0
to ECU E
1
(I, II, and III) occur within the variety area.
ferent routing possibilities between each node pair,
the so-called variety areas. The proposed approach
alleviates the optimization’s computational overhead
by exploiting the fact that—since any potential for
routing optimization is based on a variety of differ-
ent routing options—excluding proxy areas from the
optimization does not limit the search space, as any
valid route can be unambiguously described by speci-
fying its route segments within the variety areas.
We exemplify this for the simple network in Fig. 1
consisting of one variety area (yellow, left) and one
proxy area (green, right). For a communication be-
tween ECU E
0
and ECU E
1
, the architecture offers
three distinct routes (I, II, and III) which differ from
each other only in their respective segment in the vari-
ety area and are identical within the proxy area. Each
and every route between E
0
and E
1
can, therefore, be
uniquely specified by its route segment in the variety
area (the segment between E
0
and S
2
).
As part of our contribution, we (a) present a
lightweight algorithm that identifies proxy and vari-
ety areas of the given network, and (b) propose two
approaches to integrate the proxy concept into any
existing CA route optimization approach. The hereby
obtained encoding of the routing search space is tai-
lored to the given network topology, combines the ef-
ficiency of RP route optimization approaches with the
scalability and extensibility of CA approaches, and
can be applied to any application and any network.
Experimental results for two mainstream topologies
of automotive networks give evidence that an opti-
mization based on the proxy concept is faster by up to
two orders of magnitude, yields optimization results
of equal or higher quality compared to state-of-the-
art route optimization approaches, and, consequently,
enables an automated design optimization of systems
which are significantly larger than what existing ap-
proaches can practicably optimize.
The remainder of this paper is outlined as follows:
Section 2 provides an overview of the related work.
The system model is presented in Section 3. Section
4 details the proxy concept and shows how it is in-
tegrated into existing encoding approaches. Experi-
mental results are presented in Section 5, while Sec-
tion 6 concludes the paper.
2 RELATED WORK
A large body of research exists on the optimization
of routings during the design of embedded systems.
An introduction to the general problem and the dif-
ferent routing algorithms is given in (Wang and Hou,
2000). The authors of (Graf et al., 2014) provide a de-
tailed performance comparison between RP and CA
approaches and show that RP approaches can outper-
form CA approaches in sufficiently sparse networks.
Yet, in general, RP approaches are not considered to
be a good practice, as enumerating all routing pos-
sibilities is an NP-hard problem. To overcome the
scalability problem, RP approaches often limit the
search space. For instance, authors of (Laursen et al.,
2016) consider only the K shortest routes while the
RP heuristic presented in (Gavrilut et al., 2017) is tar-
geted at reusing the already allocated links.
The majority of existing routing optimization ap-
proaches can be viewed as CA approaches. A link-
based encoding for AFDX routings is presented in
(Al Sheikh et al., 2013). The authors of (Lukasiewycz
et al., 2009) go a step further and present a constraint
set where the routing is optimized together with the
mapping and the allocation of an embedded system.
Indeed, the easy modification to certain design goals
is an additional advantage of CA approaches. For
example, several works present constraint sets for a
joint optimization of routing and transmission sched-
ule (Nayak et al., 2016; Schweissguth et al., 2017;
Smirnov et al., 2017; Mahfouzi et al., 2018) or even
the optimization of the VLAN partitioning of an au-
tomotive network (Smirnov et al., 2018a). Yet, to the
best of our knowledge, existing CA approaches for-
mulate the constraints regardless of the topology. In
this paper, we show how each of these approaches can
be improved by restricting the exploration to the areas
which actually offer room for routing optimization.
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
244
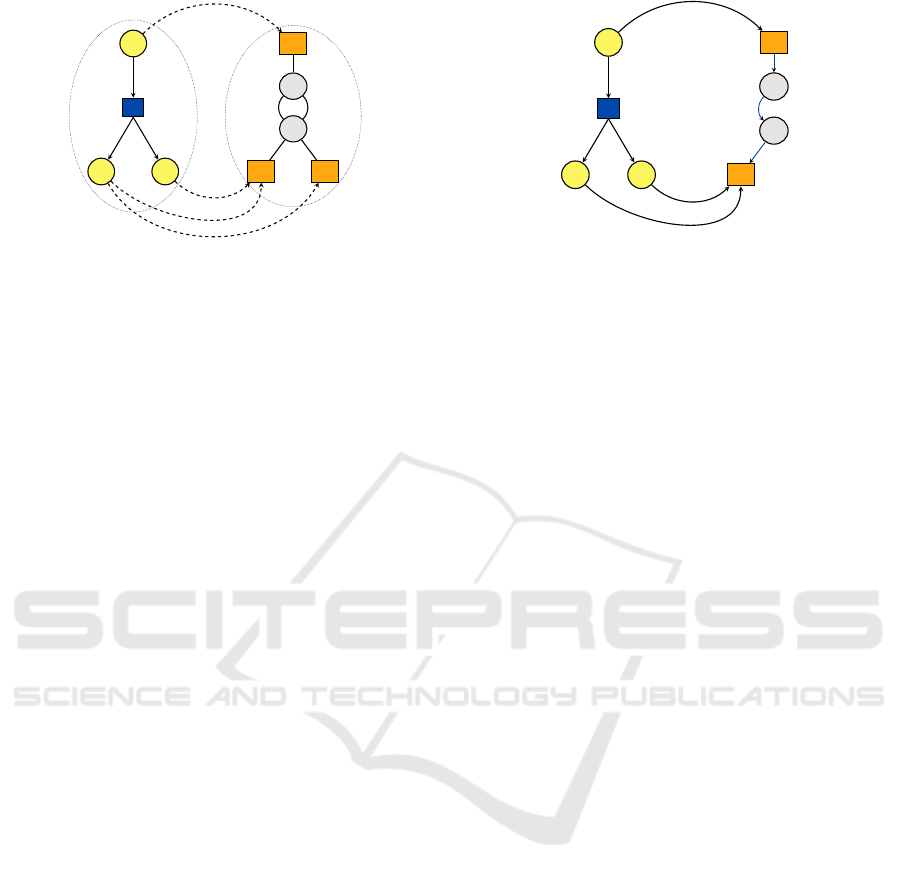
P
0
P
1
P
2
C
0
E
0
S
0
S
1
E
1
E
2
d
0
d
1
d
2
l
0
l
1
l
2
l
3
l
4
m
0
m
3
m
1
m
2
G
A
G
R
Figure 2: Illustrative example of a specification.
3 SYSTEM MODEL
The strategies presented in this paper can be applied
to any routing optimization approach relying on a
CA routing encoding. Without loss of generality,
we use the system model presented in (Lukasiewycz
et al., 2014) for the explanations throughoutthe paper.
There, the entire search space of the design problem at
hand is modeled by the so-called specification. Each
valid problem solution that is generated based on the
specification is referred to as an implementation.
3.1 Specification
The specification contains the architecture graph, the
application graph, and the mapping edges in-between.
Architecture Graph. The architecture graph
G
R
(N
R
, E
l
) consists of resource nodes N
R
= N
E
∪
N
S
, connected by bidirectional link edges l ∈ E
l
,
where each resource is either an ECU E ∈ N
E
or a
switch S ∈ N
S
.
Application Graph. The application graph
G
A
(N
T
, E
d
) contains task nodes N
T
= N
P
∪ N
C
and
data dependencies E
d
, where each task is either a pro-
cess P ∈ N
P
or a message C ∈ N
C
. Each data de-
pendency is a directed edge between a message and a
process. We refer to the predecessor and the succes-
sor tasks of a message as the source and destination
tasks of the message, respectively.
Mapping Edges. Each mapping edge
m = (P, E) ∈ E
m
indicates an ECU E ∈ N
E
on
which process P ∈ N
P
can be implemented.
Example. An example of a specification graph is
illustrated in Fig. 2. The application graph G
A
(left)
consists of three process tasks P
0
, P
1
, and P
2
which
have a data dependency, represented by their connec-
tion to the message task C
0
via dependency edges d
0
,
d
1
, and d
2
. The architecture graph G
R
on the right
side of the figure represents a switched ECU network
and consists of three ECUs E
0
, E
1
, and E
2
, connected
P
0
P
1
P
2
C
0
E
0
S
0
S
1
E
1
d
0
d
1
d
2
l
0
l
1
l
3
m
0
m
1
m
2
Figure 3: An example of an implementation that can be ge-
nerated from the specification in Fig. 2.
by switches S
0
and S
1
and links l
0
–l
4
. The four map-
ping edges m
0
–m
3
show that P
0
and P
2
can only be
implemented on E
0
and E
1
, respectively, while P
1
can
be implemented on both E
1
and E
2
.
3.2 Implementation
An implementation represents a valid solution of the
design problem and is derived from the specification
through a set of allocation, binding, and routing deci-
sions.
Allocation. During the allocation, a subset of the
architecture graph G
R
is chosen to form the allocated
architecture graph. In a valid design, only those re-
sources are allocated which are used to execute pro-
cesses or transmit messages.
Binding. The binding of processes to ECUs is
performed by choosing exactly one mapping edge
for each process. This edge then identifies the ECU
where the process is executed in the implementation,
the so-called binding target of the process.
Routing. In the implementation, the route of
each message C ∈ N
C
is represented by the routing
graph
−→
G
R
(C), a directed acyclic subgraph of G
R
with directed links. Each routing graph starts at the
binding target of the source task of its message and
has the binding target(s) of the destination task(s) as
leaf(/ves), hereby fulfilling the data dependencies.
Example. Figure 3 illustrates an example imple-
mentation that can be generated based on the specifi-
cation in Fig. 2. There, process P
0
is bound on ECU
E
0
, while processes P
1
and P
2
are bound on ECU E
1
.
The data dependencies between the sender process P
0
and its receivers P
1
and P
2
are satisfied by routing the
message C
0
from ECU E
0
to ECU E
1
over the route
consisting of links l
0
, l
1
, and l
3
and switches S
0
and
S
1
. In this case, ECU E
2
and links l
4
and l
2
are not
used to execute processes or route messages and are,
therefore, not allocated as part of the implementation.
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
245
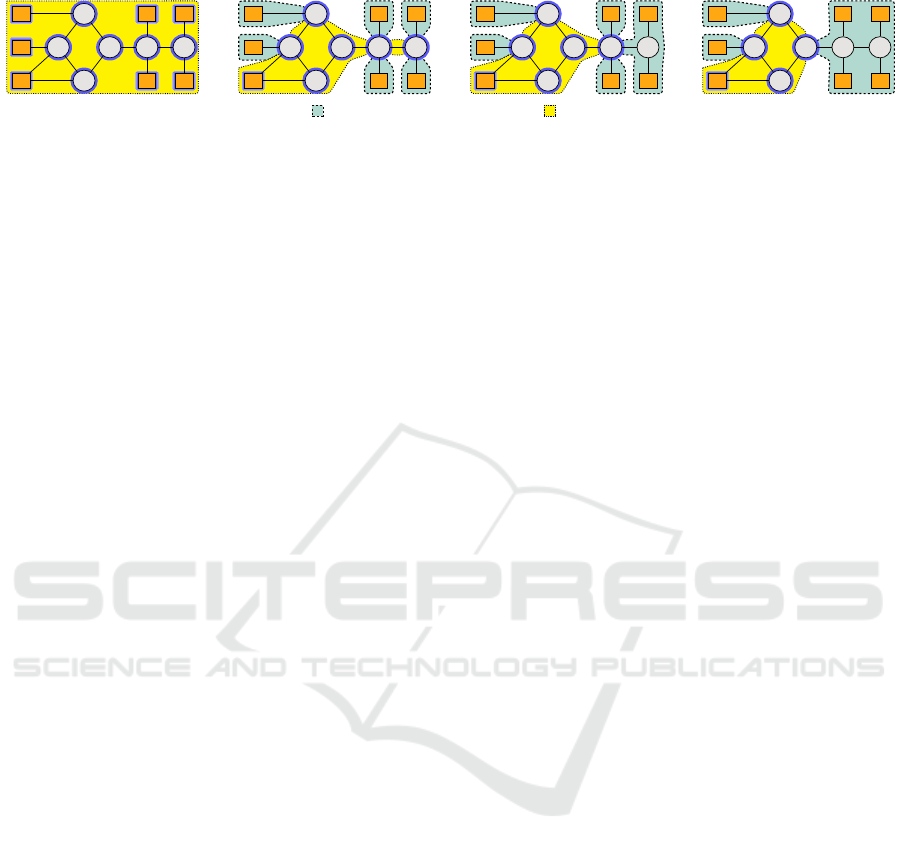
E
0
E
1
E
2
S
0
S
1
S
2
S
3
S
4
S
5
E
3
E
4
E
5
E
6
a) Initialization
l
0
E
0
E
1
E
2
S
0
S
1
S
2
S
3
S
4
S
5
E
3
E
4
E
5
E
6
b) Iteration 1
E
0
E
1
E
2
S
0
S
1
S
2
S
3
S
4
S
5
E
3
E
4
E
5
E
6
c) Iteration 2
E
0
E
1
E
2
S
0
S
1
S
2
S
3
S
4
S
5
E
3
E
4
E
5
E
6
d) Iteration 3
: Variance Area
: Proxy Areas
Figure 4: The proxy areas (dashed) are identified by iteratively establishing transitive proxy relations between resource pairs.
The variety area (dotted) encompasses all proxy masters (blue glow) and is reduced in each iteration.
4 VARIETY-AWARE ROUTING
ENCODING
4.1 Proxy Relations and Proxy Areas
CA routing optimization approaches encode, for each
link and each message, a decision variable to reflect
whether the link is used in the route of the message.
While this strategy ensures that no route is excluded
from the search space, it introduces unnecessary en-
coding variables for most networks. Consider, e.g.,
l
0
in Fig. 4a. This link connects ECU E
0
to the rest
of the network via switch S
1
. Since E
0
is accessible
solely through l
0
, one can conclude that l
0
is neces-
sarily used in each and every route to/from E
0
. Thus,
encoding a decision variable for the inclusion of l
0
in routes to/from E
0
provides no added optimization
value, as each route starting/ending at E
0
(referred to
as a proxy slave) can be uniquely specified using a
corresponding route starting/ending at S
1
(referred to
as the proxy master of E
0
).
Extending the concept of proxy (master/slave) re-
lations to larger network areas provides an even more
compact routing encoding. Consider, e.g., ECUs
E
3
–E
6
and switches S
3
, S
4
, and S
5
in Fig. 4d. In the
terminology used in this paper, we summarize these
resources and the links between them as a so-called
proxy area with S
3
as the proxy master of the entire
area. Between each pair of resources within a proxy
area, there exists exactly one possible route. In par-
ticular, there is exactly one possible route between
any of these resources and S
3
, the proxy master of
the area. Consequently, any connection between a re-
source outside the proxy area and a resource within
the area consists of an external route that connects the
outside resource to the proxy master and an internal
route connecting the proxy master to the proxy slave
inside the proxy area. Hereby, only the external route
can be established in multiple different ways (using
different sets of links) and is, therefore, relevant for
routing optimization. Contrary to that, there is only
one possible way to create the internal route. Links
within proxy areas, therefore, provide no benefit for
routing optimization and can be excluded from the
routing encoding.
4.2 Identification of Proxy Areas
We identify proxy areas within a given network us-
ing an iterative algorithm. This algorithm generates
a map of resources to their respective proxy masters
(where a proxy master is mapped to itself).
Initially, every resource is registered into a list of
potential masters. Over the course of several itera-
tions, the algorithm (I) examines every resource in the
list, (II) identifies proxy slaves (resources with only
one neighbor denoted as master), (III) updates their
map entry with their sole neighbor as their proxy mas-
ter, and (IV) eliminates them from the list of masters.
Proxy relations are transitive. Thus, if R is identified
as master of
e
R, R automatically becomes the master
of all slave resources of
e
R. The algorithm terminates
when no new proxy slaves are identified during an ite-
ration.
Figure 4 illustrates the functionality of the algo-
rithm. Each subsequent iteration identifies new proxy
slaves, expands the known proxy areas and shrinks the
variety area. The algorithm terminates when no new
proxy slaves are found in the fourth iteration. Except
from the proxy masters E
2
and S
0
–S
3
, which form the
variety area of the network, all resources are then lo-
cated inside proxy areas.
4.3 Adaptation of Existing Constraint
Systems
Exploiting the concept of proxy relations reduces the
number of encoding variables and improves the opti-
mization efficiency by excluding network areas with-
out routing variety. Following the steps presented in
this subsection, this concept can be integrated into
any routing optimization approach based on the en-
coding of individual network components. We first
detail how existing constraint sets can be adapted to
only encode route segments within variety areas. The
second part of this subsection then proposes two ap-
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
246

proaches to create the internal routes within proxy ar-
eas.
4.3.1 Routing Encoding in Variety Areas
CA encodings built on the assumption of fix source
and destination resources that are known prior to the
constraint formulation, e.g., (Al Sheikh et al., 2013)
or (Mahfouzi et al., 2018), do not require any adap-
tation of the constraints. The impact area of these
encodings can be limited by using the proxy mas-
ters over which the message enters/leaves the vari-
ety area—instead of the proxy slaves actually send-
ing/receiving the message—as the start/end points of
the encoded route.
Approaches where the source and the destination
of the message transmission are not known during the
constraint formulation—such as (Lukasiewycz et al.,
2014) or (Smirnov et al., 2018b), in which routing and
task mapping are optimized jointly—require an adap-
tation of the constraints. Such approaches implicitly
encode the transmission end points of a message as
the binding targets of the source/destination tasks of
that message. For these cases, we propose to encode
variables that indicate the start and the end points of
the encoded route within variety areas as follows.
We introduce variables
C
CC
C
S
R
and
C
CC
C
D
R
to encode the
end points of a route within the variety area. Vari-
able
C
CC
C
S
R
reflects that resource R is the route start point
of message C in the variety area. Similarly, variable
C
CC
C
D
R
reflects that resource R is the route end point of
message C in the variety area. We introduce new con-
straints to encode the activation of
C
CC
C
S
R
and
C
CC
C
D
R
accor-
ding to the binding of the source/destination tasks of
C and the proxy relations computed by the algorithm
presented in Section 4.2. The constraints state that
a proxy master R is the route start point for message
C (thus,
C
CC
C
S
R
= 1) if the source task of C is bound ei-
ther onto R or onto one of its proxy slaves and is not
the start point (thus,
C
CC
C
S
R
= 0) otherwise, encoded by
constraints (1) and (2), respectively. The constraints
that encode the activation of
C
CC
C
D
R
are generated anal-
ogously. Given these variables, existing routing en-
codings can be adapted by inserting these end-point
variables into any routing constraint that relates to the
start or the end point of the route of the respective
message.
∀C ∈ N
C
,
e
P ∈ N
−
(C),
e
R ∈ N
R
, em = (
e
P,
e
R) ∈
E
m
, R = M (
e
R) ∈ N
V
R
:
em
emem
em−
C
CC
C
S
R
≤ 0 (1)
C
CC
C
S
R
− (
∑
em
em
emem
em) ≤ 0 (2)
In the formulation above, N
−
(C) and N
+
(C) de-
note predecessor and successor tasks of message C,
respectively. N
V
R
designates all proxy masters. Func-
tion M : N
R
→N
V
R
returns the proxy master of a re-
source, as determined by the algorithm from Section
4.2. Throughout this paper, all encoding variables
are differentiated from the components of the system
model (detailed in Section 3) by a bold font. For ex-
ample,
m
mm
m denotes the encoding variable that is set to
1 iff mapping m is activated.
4.3.2 Route Creation in Proxy Areas
We propose two different approaches to create the
routes within proxy areas.
Exclusive Approach. In the first approach, referred
to as the exclusive approach, proxy areas are not
considered in the encoding of routing constraints.
Therefore, the resolution of the routing constraints—
adapted as detailed in Section 4.3.1—yields only the
route segments that connect the proxy masters of
the network (within variety areas). Then, in a post-
processing step, we extend the yielded route segments
with the unique internal routes (within the proxy ar-
eas) that connect proxy masters to the actual source
and destination resources to construct the complete
message route, which is used for the evaluation of de-
sign objectives such as cost, timing, or reliability.
Compact Approach. The exclusive approach of-
fers the biggest reduction of encoding variables and
the maximal optimization speedup. For certain prob-
lems, however, ignoring proxy areas may reduce the
optimization effectiveness, as it limits the ability to
formulate additional constraints regarding, e.g., the
capacity of the links within these parts of the network.
We address these cases with a second approach for
the creation of route segments within proxy areas. In
this so-called compact approach, the activation of in-
ternal links is encoded with a constraint set tailored
to the conditions found within proxy areas. By ex-
ploiting the fact that neither routing cycles nor redun-
dant route segments are possible within proxy areas,
the compact approach requires only a small number
of constraints that are formulated based on—already
existing—variables that describe task mapping and
component activation.
The compact approach is implemented by formu-
lating constraints (3)–(6) for each resource within a
proxy area. They ensure that the source process of a
message may only be mapped onto a resource inside
a proxy area if the resource is the binding target of a
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
247

destination process or has at least one activated out-
link (3). An in-link of a resource may only be active
if the resource is the binding target of a destination
process or has at least one activated out-link (5). Ana-
logous constraints apply to the binding of destination
processes (4) and the activation of out-links (6). Note
that these constraints are formulated with the assump-
tion of routing optimizations like (Lukasiewycz et al.,
2014) or (Smirnov et al., 2018b), where the end points
of the routes are not fixed
1
.
∀C ∈ N
C
, P ∈ N
+
(C),
e
P ∈ N
−
(C), m = (P, R) ∈
E
m
, em = (
e
P, R) ∈ E
m
, l = (R,
e
R) ∈ E
l
:
em
emem
em−
(
∑
m
m
mm
m) + (
∑
l
C
CC
C
l=(R,
e
R)
)
≤ 0 (3)
∀C ∈ N
C
, P ∈ N
+
(C),
e
P ∈ N
−
(C), m = (P, R) ∈
E
m
, em = (
e
P, R) ∈ E
m
,
e
l = (
e
R, R) ∈ E
l
:
m
mm
m−
(
∑
em
em
emem
em) + (
∑
e
l
C
CC
C
e
l=(
e
R,R)
)
≤ 0 (4)
∀C ∈ N
C
, P ∈ N
+
(C), m = (P, R) ∈ E
m
,
e
l = (
e
R, R) ∈
E
l
, l = (R,
e
R) ∈ E
l
:
C
CC
C
e
l=(
e
R,R)
−
(
∑
m
m
mm
m) + (
∑
l
C
CC
C
l=(R,
e
R)
)
≤ 0 (5)
∀C ∈ N
C
,
e
P ∈ N
−
(C), em = (
e
P, R) ∈ E
m
,
e
l = (
e
R, R) ∈
E
l
, l = (R,
e
R) ∈ E
l
:
C
CC
C
l=(R,
e
R)
−
(
∑
em
em
emem
em) + (
∑
e
l
C
CC
C
e
l=(
e
R,R)
)
≤ 0 (6)
5 EXPERIMENTS
We perform several experiments to evaluate the im-
pact of routing-variety awareness on the scalability
and the result quality of multi-objective routing opti-
mization approaches for two common classes of auto-
motivenetworks, namely, double-star and many-core.
In all experiments, we investigate how the scalability
and the result quality of a variety-unaware baseline
routing encoding approach is enhanced when it is ex-
tended with the exclusive or the compact implementa-
tions of the proxy concept presented in Section 4.3.2.
To evaluate the overall quality of the Pareto-
optimal system design solutions found during the op-
timization process under each investigated encoding
approach, we use the well-established ε-dominance
1
The constraint adaptation for the simpler case with
known route end points ((Al Sheikh et al., 2013), (Mahfouzi
et al., 2018)) is trivial and, therefore, not discussed here.
indicator (Laumanns et al., 2002) from the multi-
objective optimization domain. Broadly speaking,
this scalar measure reflects the distance in the multi-
dimensional objective space between a reference set
of high-quality solutions and the set of Pareto-optimal
solutions found by the evaluated approach. Thus,
for two solution sets, A and B, obtained using two
optimization approaches, the one with a lower ε-
dominance exhibits a smaller distance from the ref-
erence set, and thus, a higher quality of obtained so-
lutions. For all experiments presented in this sec-
tion, the reference set is a collection of the best solu-
tions found throughout the optimization processes of
all approaches. We plot the ε-dominance of each in-
vestigated approach versus the optimization run time.
This enables a compact representation and compari-
son of optimization speed, optimization convergence,
preprocessing time overhead, and the time required
for the constraint resolution throughout the optimiza-
tion process of each investigated approach.
We use the OPENDSE (Reimann et al., 2018)
system design optimization framework in all experi-
ments. It employs the SAT-Decoding system synthe-
sis approach (Lukasiewycz et al., 2007) which uses
the SAT4J (Le Berre and Parrain, 2010) constraint
solver and implements the broadly-used NSGA-II
(Deb et al., 2002) multi-objective genetic algorithm
to control the solution strategy used by SAT4J. Both
SAT4J and NSGA-II are integrated into the OPT4J
(Lukasiewycz et al., 2011) optimization framework
which is used by OPENDSE. Each optimization run
comprises 1, 000 generations. In each generation, 25
new solutions are generated using genetic operations
(crossover and mutation) on the previously found so-
lutions, and the population of solutions found so far
is updated accordingly. We consider a population size
of 100 solutions.
5.1 Double-star Architecture
In out first case study, we consider a safety-critical
application and double-star network topologies. The
message routing is optimized with respect to two de-
sign objectives, namely transmission reliability and
number of allocated links
2
. The application tasks
exchange a total number of 64 safety-critical mes-
sages, which are transmitted in both uni- and multi-
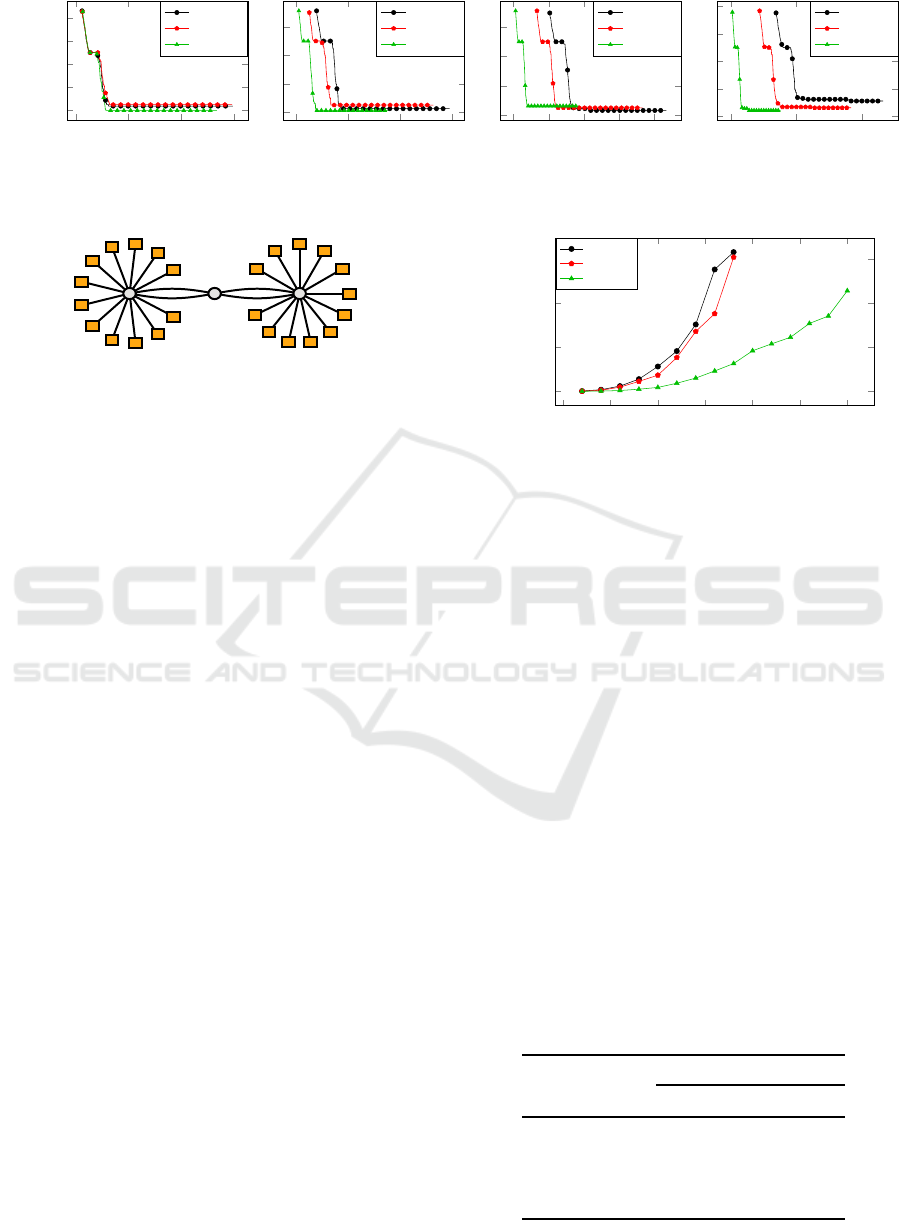
cast fashions. Figure 6 illustrates an exemplary 24-
ECU double-star network topology composed of two
12-ECU stars. The two stars are connected over two
communication hops, with the possibility for redun-
dant transmission between the two stars. Within each
2
This case study is inspired by a similar case study in-
vestigated in (Smirnov et al., 2018b).
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
248
0 100 200 300
0
0.2
0.4
0.6
0.8
Run time [s]
ε-dominance
8 ECUs
baseline
compact
exclusive
0 200 400
600
0
0.2
0.4
0.6
Run time [s]
24 ECUs
baseline
compact
exclusive
0 200 400
600
800
0
0.2
0.4
0.6
Run time [s]
40 ECUs
baseline
compact
exclusive
0
500
1,000
0
0.2
0.4
0.6
0.8
Run time [s]
56 ECUs
baseline
compact
exclusive
Figure 5: Average ε-dominance of 40 optimization runs for the double-star case study. Exploiting proxy areas results in an
optimization speedup that scales with the network size.
Figure 6: Exemplary double-star network topology with 24
ECUs connected by 3 switches.
star, the connection between each ECU and its imme-
diate switch offers no redundancy, so that each star
can be regarded as one proxy area.
For this experiment, we implemented the routing
encoding presented by the authors of (Smirnov et al.,
2018b). This encoding is used as the baseline routing
optimization approach. To implement the proposed
approaches, we refine the baseline encoding by iden-
tifying proxy areas of the network and implementing
the compact and the exclusive encoding approaches
detailed in Section 4. For each optimization approach,
we perform 40 optimization runs.
The experimental results presented in the follow-
ing are an average among the 40 optimization runs for
each approach. Figure 5 illustrates the ε-dominance
of the investigated routing optimization approaches
(baseline, compact, and exclusive) versus their opti-
mization run time for four double-star networks com-
posed of different numbers of ECUs (8, 24, 40, and
56), equally distributed between the two stars.
In terms of result quality, all approaches perform
similarly well, indicated by their ε-dominance indices
at the end of the optimization. Here, the exclusive ap-
proach offers an average final ε-dominance of 0.03,
and thereby, slightly outperforms the baseline and
compact approaches which offer an average final ε-
dominance value of 0.052 and 0.053, respectively.
In terms of optimization run time, however, the
variety-aware approaches, i.e., compact and exclu-
sive, offer a significant optimization speedup which
scales with the complexity of the problem. Recall
that the baseline approach encodes the activation of
every individual link in the network, even though a
big part of the network is contained within the two
proxy areas (stars) which do not offer any routing
0
50
100
150
200
250
300
0
10
20
30
Message Number
Generation time [min]
baseline
compact
exclusive
Figure 7: Excluding proxy areas from the optimization de-
cision space significantly reduces the constraint generation
time. For a fixed time budget (horizontal cut in the plot),
the exclusive approach enables the optimization of conside-
rably larger systems.
variety. The exclusion of proxy areas from the rou-
ting encoding significantly reduces the number of en-
coded decision variables, see Table 1. As a result,
the baseline approach requires more time (a) for con-
straint formulation and preprocessing which is visi-
ble as the initial run time offset in the plots in Fig. 5
and (b) for the constraint resolution which results in a
higher overall run time. A comparison among the four
plots in Fig. 5 also revealsthat these time overheads—
just like the number of the encoded variables—scale
with the problem complexity. Note that the time re-
quired for the identification of proxy areas for the
variety-aware approaches is negligible in comparison
to the time taken for constraint formulation, which is
reflected by the nearly identical run time of all ap-
proaches for the smallest network. All in all, the pro-
posed variety-aware approaches, compact and exclu-
Table 1: Number of the encoding variables for 64 messages
in different double-star topologies.
ECU Number
Variable Count
baseline exclusive
8 2, 988 2, 453
24 8, 088 3, 658
40 14, 831 4, 092
56 24, 199 4, 526
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
249

sive, significantly outperform the baseline approach,
as they offer results of similar quality at a smaller
optimization run time. Here, the compact approach
offers an optimization speedup of up to ×1.26 (and
requires 21% of the time needed by the baseline ap-
proach) with an average of ×1.14 (12%) over the four
networks, while the exclusive approach achieves an
speedup of up to ×3.06 (67 %) with an average of
×2.04 (43%).
To further investigate the scalability of the pro-
posed approaches, we measured the time required for
the generation of the routing constraints for the exem-
plary 24-ECU double-star topology depicted in Fig. 6
for different numbers of messages. The results are
illustrated in Fig. 7. Since routing constraints are ge-
nerated at design time, the time required for their ge-
neration is not subject to any hard restrictions. How-
ever, the constraint generation time scales exponen-
tially with the number of variables and may quickly
render an approach impractical. Indeed, with the
ongoing growth in the size of automotive networks
and the number of transmitted messages, the time re-
quired for the generation of routing constraints is pro-
gressively becoming the limiting factor for the appli-
cability of existing routing optimization approaches.
The baseline and the compact approaches are based
on the same set of variables and display similar ge-
neration times, which quickly grow with the num-
ber of messages in the system. While the exclusive
approach also displays an exponentially growing ge-
neration time, the required constraints are generated
within significantly shorter time intervals. With a time
budget of 20 minutes, the exclusive approach, e.g.,
is able to generate constraints for systems with twice
as many messages as the other two approaches. The
exclusive approach, therefore, enables the automatic
optimization of considerably larger systems.
5.2 Many-core Architecture
Many-core architectures represent an emerging class
of architectures in the embedded computing domain
which offer the scalable computation and communi-
cation power required by modern embedded applica-
tions. A many-core architecture integrates an exten-
sive number of, oftentimes heterogeneous, processors
onto a single chip where the processors are intercon-
nected by a communication network, referred to as a
Network-on-Chip (NoC).
Over the past decade, many-core architectures
have increasingly been viewed as promising candi-
dates for emerging automotive applications, as they
offer an order of magnitude higher processing power
cost-efficiently and enable the implementation of the
mixed-ASIL isolation, required for ISO 26262, see,
e.g., (Fuhrman et al., 2015). The authors of (Ober-
maisser et al., 2009) propose a many-core architec-
ture which is tailored to the specific requirements in
the automotive domain. This so-called integrated au-
tomotive architecture closely resembles a tiled many-
core architecture, which integrates processor tiles
(each composed of multiple resources, e.g., proces-
sors and memories) on a chip with a 2D grid NoC
interconnection scheme and offers superior perfor-
mance scalability. A part of such an architecture is
illustrated in Fig. 9.
While these distributed heterogeneous processor
networks offer great flexibility, finding the optimal
mapping of an application’s tasks onto the processors
of a tiled chip is a considerable challenge. Moreover,
recent research (Weichslgartner et al., 2014) shows
that a deterministic routing approach—such as XY-
routing, which is commonly used in the many-core
domain—may render numerous system design solu-
tions infeasible due to the violation of link capacities,
thus, limiting the number and the quality of feasible
solutions. Exploring the space of routing possibili-
ties may, therefore, significantly increase the quality
of found solutions.
In our next case study, we investigate the impact
of the proposed approaches on the efficiency and sca-
lability of routing optimization in many-core automo-
tive systems. In order to optimize the non-redundant
message routes, we have implemented the approach
presented in (Lukasiewycz et al., 2014) which we
consider as the baseline routing optimization ap-
proach. We extend the baseline with the proposed
compact and exclusive variety-aware strategies which
are then compared against the baseline approach.
The goal of our system synthesis optimization is
to find implementations of an automotive application
with 21 messages provided by the Embedded System
Synthesis Benchmarks Suite (E3S) (Dick, 2010) on
3×3- and 4×4-tiled many-core architectures, which
are optimal with respect to two design objectives,
namely energy consumption and makespan. For both
architecture sizes (3×3 and 4×4), the bandwidth of
each inter-tile link is quantized into 5 (hard) or 10
(relaxed) equal budgets, hereafter referred to as link
capacity, that can be utilized by the routed messages.
We use additional constraints to ensure that the band-
width capacity of each link is strictly respected. Since
the exclusive approach disregards links within proxy
areas, we use an additional evaluator—namely, link
capacity evaluator—to check the feasibility of found
design solutions in terms of respecting link capacities
inside proxy areas.
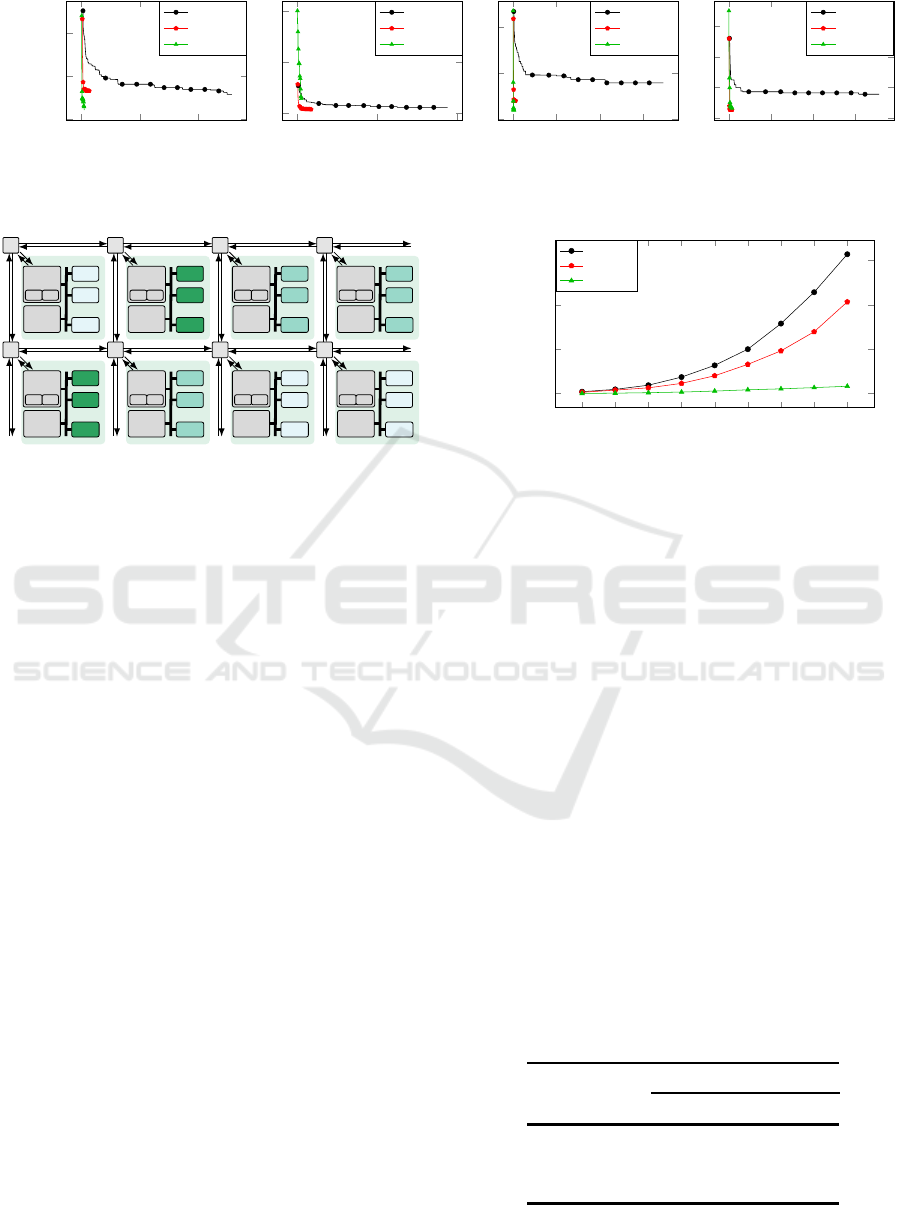
Figure 8 illustrates the ε-dominance of the in-
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
250
0 2,000 4,000
0
0.2
0.4
Run time [s]
ε-dominance
3×3 relaxed
baseline
compact
exclusive
0
0.5
1
·10
4
0
0.5
1
Run time [s]
3×3 hard
baseline
compact
exclusive
0 1 2 3
·10
4
0
0.2
0.4
Run time [s]
4×4 relaxed
baseline
compact
exclusive
0 1 2 3
·10
4
0
0.1
0.2
0.3
Run time [s]
4×4 hard
baseline
compact
exclusive
Figure 8: Average ε-dominance of 5 optimization runs for the many-core case study. Variety-aware approaches yield design
solutions of higher quality and offer an optimization speedup that scales with the complexity of the optimization problem.
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
Core
1
Core
2
Core
N
...
Tile
Memory
Network
Interface
RX TX
R
...
...
...
...
...
...
Figure 9: A heterogeneous tiled many-core architecture.
vestigated routing optimization approaches (baseline,
compact, and exclusive) versus their optimization run
time, averaged over 5 optimization runs. The pro-
posed variety-aware routing optimization approaches
(compact and exclusive) outperform the baseline ap-
proach in both (a) the quality of obtained solutions
(indicated by lower ε-dominance indices at the end of
the optimization) and (b) optimization run time.
Since each processor tile can be regarded as a
proxy area, a large portion of the networks is ex-
cluded from the routing constraints of the proposed
approaches. This significantly reduces the number of
encoding variables (see Table 2) and the time required
for constraint generation (see Fig. 10). Nonetheless,
due to the complex nature of tiled many-core architec-
tures, the complexity of the routing constraint systems
has a higher impact (compared to the sheer number of
variables) on the run time of routing optimization and
the quality of the final solutions. Here, both the exclu-
sive approach, which completely ignores the numer-
ous proxy areas, and the compact approach, which
uses a much simpler constraint set for the routing en-
coding within proxy areas (compared to baseline), re-
quire a considerably shorter time for the constraint
resolution. Consequently, since the constraint set has
to be resolved per network design generated through-
out the exploration, the rapid constraint resolution of
the variety-aware approaches results in a reduction
of up to two orders of magnitude in the total opti-
mization run time, compared to the baseline approach.
Moreover, their simpler constraint sets make it easier
2× 2
3× 3
4× 4
5× 5
6× 6
7× 7
8× 8
9× 9
10× 10
0
5
10
15
Architecture dimensions
Generation time [min]
baseline
compact
exclusive
Figure 10: Excluding proxy areas from the formulation of
routing constraints reduces the time required for constraint
generation and enables the automatic optimization of con-
siderably larger systems.
for the optimizer to learn correlations between indi-
vidual design decisions and the design objectives, so
that both the compact and the exclusive approaches
yield solutions of significantly higher quality com-
pared to the baseline, especially for the more complex
4×4 architecture.
On average, the baseline approach offers a final
ε-dominance of 0.102 and is evidently outperformed
by both the compact and the exclusive approaches,
which exhibit an average final ε-dominance of 0.067
and 0.065, respectively. Compared to the baseline,
the compact approach offers an average optimization
speedup of ×32.96. The exclusive approach offers an
even larger speedup of ×80.61 on average and a ma-
ximum speedup of ×186.4 in case of the 4×4 relaxed
architecture.
Table 2: Number of encoding variables for 21 messages in
different many-core architectures.
Architecture
Dimensions
Variable Count
baseline exclusive
2×2 4,629 984
6×6 42,397 9,888
10×10 119,135 28,040
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
251

A comparison between the exclusive and the com-
pact approach offers an other interesting insight. With
a link capacity of 10 (relaxed), finding routes without
link capacity violation is relatively easy, so that the
exclusive approach can create a sufficiently big popu-
lation of feasible solutions and outperform the other
two approaches in both run time and result quality.
However, with a link capacity of 5 (hard), creating
feasible solutions becomes more difficult. The con-
straints used in the exclusive approach cannot pre-
vent capacity violations within proxy areas, because
the links within these areas are not considered during
constraint formulation. Consequently, the exclusive
approach wastes a large share of the optimization time
creating solutions with capacity violations on links in
proxy areas, which are rejected by the capacity evalu-
ator. Contrary to that, the compact approach is aware
of every link in the architecture and offers the pos-
sibility to encode constraints that eliminate the pos-
sibility of link capacity violations in the first place.
The compact approach, thus, explores a search space
devoid of infeasible solutions and yields optimization
results of higher quality than the exclusive approach.
6 CONCLUSIONS
In this paper, we propose a novel strategy for an auto-
mated routing optimization of automotive networks.
The proposed approach exploits the knowledge about
so-called proxy areas in a given network, i.e., regions
that do not offer any routing variety. We have pre-
sented a lightweight algorithm that identifies proxy
areas in a given network, proposed two approaches to
exploit this knowledge during routing optimization,
and shown how the presented strategy can be inte-
grated into existing routing encodings. Experimen-
tal results for two types of automotive networks give
evidence that encoding approaches that are aware of
the proxy areas provide design solutions of equal or
higher quality, are up to 185 times faster, and enable
the automatic optimization of considerably larger sys-
tems than variety-unaware approaches.
REFERENCES
Al Sheikh, A., Brun, O., Ch´eramy, M., and Hladik, P.-E.
(2013). Optimal design of virtual links in afdx net-
works. Real-Time Systems, 49(3):308–336.
Blickle, T., Teich, J., and Thiele, L. (1998). System-level
synthesis using evolutionary algorithms. Design Au-
tomation for Embedded Systems, pages 23–58.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE transactions on evolutionary com-
putation, pages 182–197.
Dick, R. (2010). Embedded system
synthesis benchmarks suite (E3S).
http://ziyang.eecs.umich.edu/ dickrp/e3sdd/.
Fuhrman, T., Wang, S., Jersak, M., and Richter, K.
(2015). On designing software architectures for next-
generation multi-core ecus. SAE International Journal
of Passenger Cars-Electronic and Electrical Systems,
8(2015-01-0177):115–123.
Gavrilut, V., Zarrin, B., Pop, P., and Samii, S. (2017). Fault-
tolerant topology and routing synthesis for ieee time-
sensitive networking. In Proceedings of RTNS.
Graf, S., Reimann, F., Glaß, M., and Teich, J. (2014). To-
wards scalable symbolic routing for multi-objective
networked embedded system design and optimization.
In Proceedings of CODES+ ISSS.
International Cablemakers Federation (2015). ICF News.
International Cablemakers Federation.
Laumanns, M., Thiele, L., Deb, K., and Zitzler, E. (2002).
Combining Convergence and Diversity in Evolution-
ary Multiobjective Optimization. Evolutionary com-
putation.
Laursen, S. M., Pop, P., and Steiner, W. (2016). Routing
optimization of avb streams in tsn networks. ACM
Sigbed Review, 13(4):43–48.
Le Berre, D. and Parrain, A. (2010). The sat4j library, re-
lease 2.2, system description. Journal on Satisfiability,
Boolean Modeling and Computation, 7:59–64.
Lukasiewycz, M., Glaß, M., Haubelt, C., and Teich, J.
(2007). SAT-decoding in evolutionary algorithms for
discrete constrained optimization problems. In IEEE
Congress on Evolutionary Computation.
Lukasiewycz, M., Glaß, M., Reimann, F., and Teich, J.
(2011). Opt4J - A Modular Framework for Meta-
heuristic Optimization. In Proceedings of GECCO.
Lukasiewycz, M., Shreejith, S., and Fahmy, S. A. (2014).
System simulation and optimization using reconfig-
urable hardware. In Proceedings of ISIC.
Lukasiewycz, M., Streub¨uhr, M., Glaß, M., Haubelt, C.,
and Teich, J. (2009). Combined system synthesis and
communication architecture exploration for MPSoCs.
In Proceedings of DATE.
Mahfouzi, R., Aminifar, A., Samii, S., Rezine, A., Eles, P.,
and Peng, Z. (2018). Stability-aware integrated rou-
ting and scheduling for control applications in ether-
net networks. In Proceedings of DATE.
Nayak, N. G., D¨urr, F., and Rothermel, K. (2016).
Time-sensitive Software-defined Network (TSSDN)
for Real-time Applications. In Proceedings of RTNS.
Neubauer, K., Wanko, P., Schaub, T., and Haubelt, C.
(2018). Exact multi-objective design space explo-
ration using aspmt. In Proceedings of DATE.
Obermaisser, R., El Salloum, C., Huber, B., and Kopetz, H.
(2009). From a federated to an integrated automotive
architecture. IEEE Transactions on Computer-Aided
Design of Integrated Circuits and Systems, 28(7):956–
965.
Reimann, F., Lukasiewycz, M., Glaß, M., and Smirnov, F.
(2018). OpenDSE – open design space exploration
framework.
VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems
252

Richthammer, V. and Glaß, M. (2018). On search-space re-
striction for design space exploration of multi-/many-
core systems. In Proceedings of MBMV.
Sangiovanni-Vincentelli, A. and Di Natale, M. (2007). Em-
bedded system design for automotive applications.
Computer, 40(10).
Schweissguth, E., Danielis, P., Timmermann, D., Parzy-
jegla, H., and M¨uhl, G. (2017). Ilp-based joint rou-
ting and scheduling for time-triggered networks. In
Proceedings of RTNS.
Smirnov, F., Glaß, M., Reimann, F., and Teich, J. (2017).
Optimizing message routing and scheduling in auto-
motive mixed-criticality time-triggered networks. In
Proceedings of the 54th Annual Design Automation
Conference 2017, page 48. ACM.
Smirnov, F., Reimann, F., Teich, J., and Glaß, M. (2018a).
Automatic optimization of the vlan partitioning in
automotive communication networks. ACM Trans-
actions on Design Automation of Electronic Systems
(TODAES), 24(1):9.
Smirnov, F., Reimann, F., Teich, J., Han, Z., and Glaß, M.
(2018b). Automatic Optimization of Redundant Mes-
sage Routings in Automotive Networks. In Proceed-
ings of SCOPES.
Wang, B. and Hou, J. C. (2000). Multicast routing and its
qos extension: problems, algorithms, and protocols.
IEEE network, 14(1):22–36.
Weichslgartner, A., Gangadharan, D., Wildermann, S.,
Glaß, M., and Teich, J. (2014). Daarm: Design-time
application analysis and run-time mapping for pre-
dictable execution in many-core systems. In Proceed-
ings of CODES+ISSS.
Variety-aware Routing Encoding for Efficient Design Space Exploration of Automotive Communication Networks
253
