Optimal Path Planning with Clothoid Curves for Passenger Comfort

Edward Derek Lambert

, Richard Romano

and David Watling

Institute for Transport Studies, University of Leeds, 34-40 University Road, Leeds, U.K.

Keywords: Passenger Comfort, Clothoid, Path Planning, Automated Vehicle.

Abstract:

Highly automated vehicles operating at SAE automation level 4 and 5 will not require the occupants’ attention

to be on the road at all. They will be free to amuse themselves as passengers. This will have the side effect

of making them more vulnerable to motion sickness. Automated vehicles must plan paths which are feasible

for the vehicle and comfortable for its occupants. In railway and highway design, paths with clothoid based

transitions provide feasibility and comfort. This paper proposes a method for generating such a path using

constrained non-linear optimization and compares it to an existing method based on root ﬁnding.

1 INTRODUCTION

Smooth paths for Automated Vehicles are important

for ensuring dynamic feasibility(LaValle and Leidner,

2006a) and passenger comfort (Elsner, 2018). Nu-

merous representations have been developed to ac-

company different planning algorithms (LaValle and

Leidner, 2006b), (Katrakazas et al., 2015),(Paden

et al., 2016), (Schwarting et al., 2018). These include

cubic splines (Deits and Tedrake, 2015), combina-

tions of lines and arcs with minimum length (Dubins,

1957) and (Reeds and Shepp, 1990), parametric con-

tinuous curvature paths (Fraichard and Scheuer, 2004)

or clothoids (Wilde, 2009).

Considerable work has been done to develop em-

pirical measures which correlate well with passenger

comfort. Generally, acceleration and sometimes its

derivative jerk are taken to cause physical discom-

fort if they exceed some threshold. The effect of high

acceleration on the human body is well known from

studies undertaken on pilots and astronauts: g-forces

are certainly noticeable and at a high level will even-

tually lead to unconsciousness and death (McKen-

ney, 1970). At more modest levels acceleration is de-

tected by the inner ear and can lead to motion sickness

(Beard and Grifﬁn, 2014). The problems associated

with excessive jerk are more difﬁcult to quantify but

in certain circumstances, such as very short duration

motions they can be strongly associated with physical

https://orcid.org/0000-0002-2297-0441

https://orcid.org/0000-0002-2132-4077

https://orcid.org/0000-0002-6193-9121

discomfort (McKenney, 1970). There are also psy-

chological factors which may come into play when

riding in an automated vehicle such as perceived risk.

Some of these can be taken into account at the plan-

ning stage such as keeping a sufﬁcient distance from

obstacles to which a human driver would be able to

respond (Elsner, 2018).

Based on the assumption that keeping acceleration

and its rate of change tightly bounded, while main-

taining sufﬁcient distance from any obstruction, leads

to maximum passenger comfort, it is possible to eval-

uate some of the different path representations. All

path requirements can be met with any representation,

the difference is the efﬁciency with which the relevant

parameters can be evaluated. For the cubic spline the

position and derivatives can be evaluated cheaply to

check obstacle constraints are satisﬁed but the curva-

ture rate or sharpness must be derived from samples

along the curve once it is plotted.This is similar to the

way the curvature of existing roads can be measured

based on a series of samples along them (Zamﬁr et al.,

2016). For a clothoid the curvature rate (sharpness) is

the deﬁning parameter so it is cheap to evaluate for

each section, however the position must be computed

by evaluating Fresnel integrals (Wilde, 2009).

Clothoid curves have been in use for a long time in

the design of highway and railway easement curves to

transition between straight and curved sections com-

fortably and safely (Levien, 2008). For this reason we

propose that the use of clothoid curves (with an ap-

propriate upper bound on sharpness and curvature) is

sufﬁcient to ensure the physical comfort of the occu-

pants without further experimental results, and there-

Lambert, E., Romano, R. and Watling, D.

Optimal Path Planning with Clothoid Curves for Passenger Comfort.

DOI: 10.5220/0007801806090615

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 609-615

ISBN: 978-989-758-374-2

609

fore will proceed to address the problem of calculat-

ing the parameters for curves of this type which join

a given origin and destination as addressed by (Gim

et al., 2017) and (Wilde, 2009).

This paper goes on to describe a method for iden-

tifying the parameters of a clothoid spline joining two

points based on constrained non-linear optimization

in Section 4, and compares it to the bisection method

proposed by (Gim et al., 2017) detailed in Section 3.

1.1 Appropriate Limits

Correct choice of curvature and curvature rate limit is

essential for a smooth ride. The length of easement

curve required for a particular turn of curvature κ =

1/R is given by

s = κ/α

max

(1)

Certain parameters have been speciﬁed for Eu-

ropean Railway Design in ES13803 (Fischer, 2008).

These include a maximum cant rate of 50mm/s. Cant

is the height of one railway track above another and

is related to the path curvature by the requirement the

track remain ’balanced’ meaning that both rails are

loaded equally as a train passes over at design speed.

As a result, maximum sharpness α can be ex-

pressed in terms of the cant rate E assuming a bal-

anced track of gauge G and constant traversal speed

V .

α =

(2)

where g is the acceleration due to gravity, approxi-

mately 9.81m/s

. The appropriate sharpness to match

the cant rate limit is found to be α

max

= 4x10

−

If this rate can be sustained on existing roads without

requiring an unacceptable reduction in forward speed,

Level 5 autonomy could be as smooth and pleasant

environment for work or rest as a typical train jour-

ney, along with the additional privacy of car travel.

2 PROBLEM STATEMENT

Given a workspace W = IR

and an obstacle region

O ⊂ W and a robot deﬁned by a rigid body A ∈

W . Conﬁguration space C can be broken down into

obs

and C

f ree

. A single query must provide an ini-

tial conﬁguration q

∈ C

f ree

and a goal conﬁguration

∈ C

f ree

. The problem is to compute a continuous

path over τ : [0,L] → C

f ree

such that τ(0) = q

and

τ(L) = q

This is also known as the piano mover’s problem,

for more details see (Siciliano and Khatib, 2016). A

car can be treated as a rigid body that moves in a plane

with a state x = [x,y,ψ] where x and y indicate posi-

tion of the vehicle control point in the 2D plane and ψ

is the forward direction of the vehicle, measured an-

ticlockwise from the x-axis. Conﬁguration space has

dimension C = R

+ S

We place an additional restriction that the path

τ must have piecewise constant sharpness α =

ψ/ds

≤ α

max

so it takes the form of a clothoid

spline. The peak curvature must also be less than a

comfortable maximum κ = dψ/ds ≤ κ

max

3 METHOD 1: BISECTION

One approach to generating true clothoid curves be-

tween two positions is based on root ﬁnding. A gen-

eral approach for creating parametrized Continuous

Curvature Paths (pCCP) based on clothoids is detailed

in (Gim et al., 2017). The process begins with a dis-

crete set of samples, such as could be produced by

a lattice planner which did not take into account dif-

ferential constraints. Central to this approach is the

identiﬁcation of the parameters sharpness α

and de-

ﬂection δ

describing a matched clothoid pair which

terminates at a speciﬁed x

= [x

,ψ

], κ

=0. The

constraint on heading and curvature can be used to

calculate the sharpness and deﬂection of the second

clothoid segment from the ﬁrst. The terminating po-

sition can be found by evaluating the Fresnel inte-

grals to ﬁnd the 2D position error with respect to q

The error can be expressed relative to the end of the

clothoid pair to get the forward and lateral compo-

nents. There is then a two dimensional root ﬁnding

process based on bisection to arrive at the parameter

values which drive lateral error to zero.

A single clothoid segment parametrized in s is

deﬁned by the a constant sharpness α = d

ψ/ds

along its length. States on the path τ(s) =

[x(s),y(s),ψ(s),κ(s)] can be found by evaluating the

Fresnel integrals.

κ(s) = αs (3)

ψ(s) =

αs

(4)

x(s) =

∫

cosψ(u)du (5)

y(s) =

∫

sinψ(u)du (6)

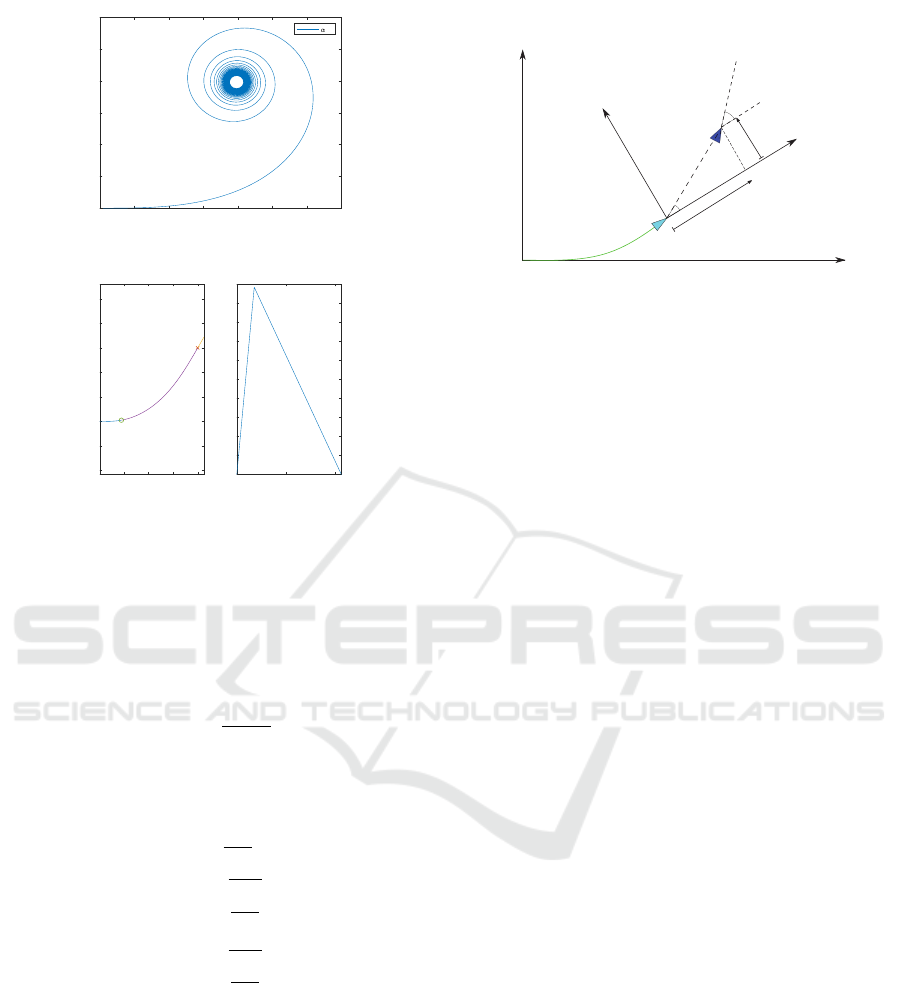
The result is a spiral shown in Figure 1. As an

easement curve, the most useful section is close to

the origin where the curvature is low and it is well

approximated by a cubic.

It is possible to construct a continuous curvature

path starting and ending with a straight line using two

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

610

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

x(m)

0.1

0.2

0.3

0.4

0.5

0.6

y(m)

Figure 1: A clothoid spiral with sharpness constant α = 5.

2 4 6 8

x [m]

-4

-2

y [m]

0 5 10

travel length [m]

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

curvature [1/m]

Figure 2: A matched pair of clothoids suitable for joining

two straight lines.

matched clothoid curves, one increasing the curva-

ture and the other decreasing it to maintain continuity.

This construction is shown in Figure 2. This gives

rise to some analytic relations between the ﬁrst and

second matched clothoid which are reproduced from

(Gim et al., 2017).



2δ

(7)

= κ

(8)

= θ

− δ

(9)

2δ

(10)



2δ

(11)



2δ

(12)

Using these relations and the bound-

ary condition of the starting conﬁguration

= [x,y, ψ, κ] = [0, 0, 0, 0] and ending conﬁgu-

ration q

= [x

,ψ

,0] the matched pair is fully

deﬁned by the sharpness α

and deﬂection δ

of the

ﬁrst segment. These parameters can be found as roots

of the (signed) lateral error.

The iterative procedure, based on the bisection

method for root ﬁnding is given below, using the sign

convention in Figure 3.

D[1]

D[2]

D[3]

τ(L)

Figure 3: The sign convention used for the forward and lat-

eral error to the goal at the end of the curve.

while sol==0 && iter<80

k1 = sqrt(2*deflection1*alpha1);

k2 = k1;

deflection2 = boundary(3) - deflection1;

alpha2 = k2*k2/(2*deflection2);

S1 = sqrt(2*deflection1/alpha1);

S2 = sqrt(2*deflection2/alpha2);

[x, y, psi, kappa] = clothoid_pair(alpha1,...

S1, -alpha2, S2);

n = length(x);

final_pose = [x(n), y(n), psi(n)];

D = decompose(boundary(1:3), final_pose);

DeT = D(1);

De = D(2);

iter = iter+1;

if abs(De)< tol

if DeT >= 0

sol=1;

end

if lambda*De<0

dAlpha = dAlpha/2;

end

if lambdaT*DeT<0

dDeflection = dDeflection/2;

end

lambda = De;

lambdaT = DeT;

dAlpha = abs(dAlpha)*sign(lambda);

dDeflection = -abs(dDeflection)*sign(lambdaT);

alpha1 = alpha1 + dAlpha;

deflection1 = deflection1 + dDeflection;

end

On careful examination there are a few important

differences from bisection as described in a textbook

Optimal Path Planning with Clothoid Curves for Passenger Comfort

611

and the presented method. Convergence is guaran-

teed of the textbook method for ﬁnding a root of a

scalar function of one dimension provided a single

zero crossing exists within the given interval (Atkin-

son, 1988). The number of iterations required to re-

duce the error below a given threshold has an upper

bound given by

|α − c

| ≤ [

]

(b − a) (13)

where b−a denotes the length of the original interval,

is the estimate after n iterations and α is the true

value of the root.

The method of (Gim et al., 2017) listed in Verba-

tim 3 does not require an interval containing the root,

only an initial guess smaller than the true value for

each parameter because there is an additional search

procedure. This relies on knowledge of the direction

of relative motion of the end of the path, in the for-

ward and lateral directions based on the two parame-

ters. The justiﬁcation is detailed in (Gim et al., 2017).

By inspection of the goal pose either two or four

clothoids are composed.



2 if ψ

> atan2(y

);

4 if ψ

< atan2(y

(14)

The four clothoid case proceeds by searching over the

heading of an intermediate point, at each iteration per-

forming the two clothoid estimation twice, once be-

fore the intermediate point and once after.

4 METHOD 2: NON-LINEAR

OPTIMIZATION

Numerical optimization based path planning is widely

used as it leads to ’better’ paths, having a lower

cost integral over their length with reduced sam-

pling artefacts compared to sampling based meth-

ods. The downside of numerical optimization is the

higher computational cost to ﬁnd a path. However,

the cost is dependant on the dimension of conﬁgura-

tion space, and road vehicles are well served by plan-

ning in C = R

+ S

, which is comparatively low. A

good review of planning techniques is given by (Si-

ciliano and Khatib, 2016).

The relations given in Equation 7- 12 are ﬁrst

used to reduce the number of parameters which need

to be searched to two, sharpness α

and deﬂection

.The cost is based on the squared distance along the

curve, made up of the ﬁrst clothoid length, the second

clothoid length and the straight line to the goal at the

end.

J(α

,δ

) = (s

+ s

+ ||x

− τ(L)||)

(15)

= arg min

,δ

J(α

,δ

) (16)

subject to

(

) = [

]

τ(1) = [x

,0]

≥ 0 ∀i ∈ [1,...,n

]

≥ 0 ∀i ∈ [1,...,n

]

κ(p) ≤ κ

max

∀p ∈ [0,L]

α(p) ≤ α

max

∀p ∈ [0,L]

(17)

5 PRELIMINARY RESULTS AND

DISCUSSION

The two methods were used to estimate the pa-

rameters of a transition curve starting at the ori-

gin with zero curvature and terminating at x

[8.000,6.000,1.047(60π/180)]. This boundary con-

dition requires two clothoids according to Equation

14.

2 4 6 8

x [m]

-4

-2

y [m]

0 5 10

travel length [m]

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

curvature [1/m]

Figure 4: Bisection method: Path output and curvature

[α

,δ

] = [0.0545,0.6554].

The results of the two approaches for a single

boundary condition representing a fairly tight left turn

of 60 degrees are shown in Table 1 and Figure 4 and

5. Interestingly the estimated parameters are differ-

ent, resulting in substantially different paths. Both

reach the target point with high accuracy and satisfy

the constraints to some degree.

Comparing in terms of optimality according to the

cost function chosen for the optimization method, the

terminal cost of the solution produced by bisection

is lower than that produced by fmincon the non-linear

constrained optimization tool in MATLAB with much

greater computational effort.

The investigation of the cost surface for this single

numerical example is seen in Figure 6 to be extremely

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

612

2 4 6 8

x [m]

-4

-2

y [m]

0 5 10

travel length [m]

-0.05

0.05

0.1

0.15

0.2

0.25

0.3

curvature [1/m]

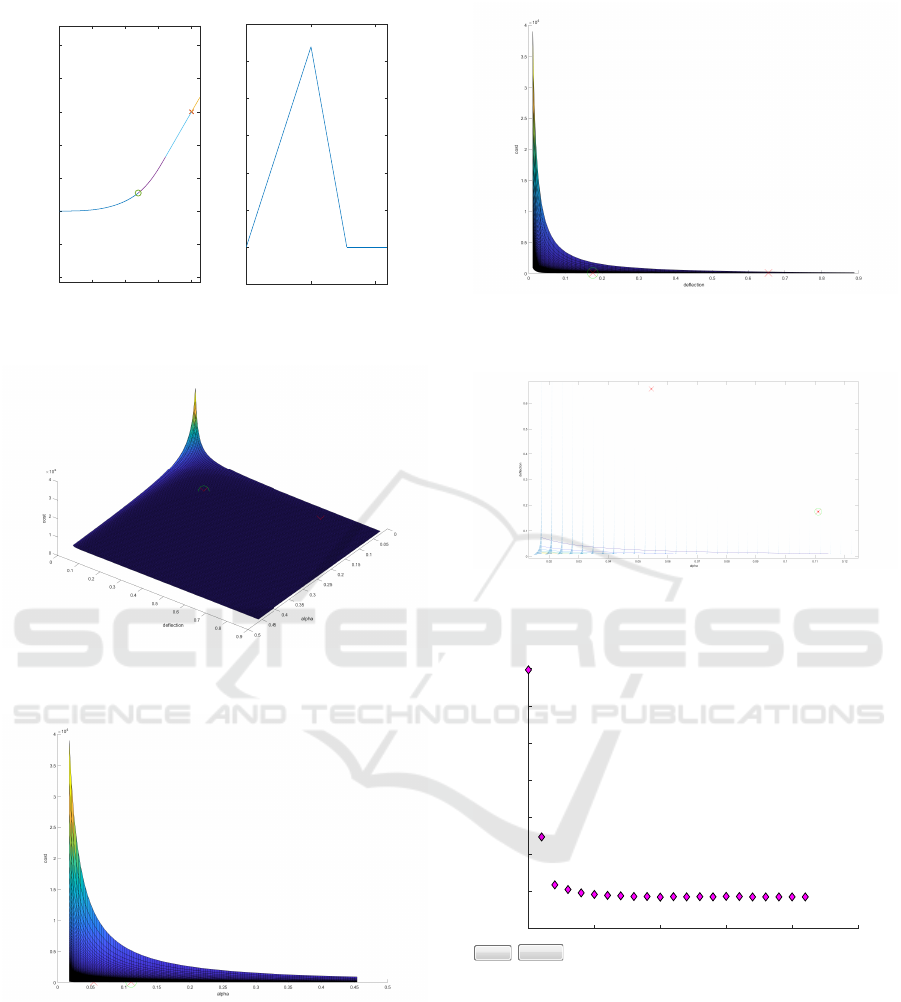
Figure 5: Optimization method: Path output and curvature

[α

,δ

] = [0.1111,0.1746].

Figure 6: The cost function surface for fmincon with pa-

rameter estimates from both methods shown as red crosses,

bisection with a green circle.

Figure 7: Cost against sharpness α, parameter estimates

from both methods shown as red crosses, bisection with a

green circle

ﬂat. This causes fmincon to terminate before reach-

ing the optimum based on a step size threshold. It ap-

pears that level sets of the cost have a shape close to

y=1/x as seen in Figure 9. The path produced by the

bisection method is shorter than the one identiﬁed by

a non-linear constrained optimization where the cost

was based on the path length. The different treatment

of the constraints permits slightly larger violation by

Figure 8: Cost against deﬂection δ, parameter estimates

from both methods shown as red crosses, bisection with a

green circle.

Figure 9: The cost function gradient for fmincon with pa-

rameter estimates from both methods shown as red crosses,

bisection with a green circle.

0 5 10 15 20 25

Iteration

110

120

130

140

150

160

170

180

Function value

Current Function Value: 118.495

Stop

Pause

Figure 10: Iterations of fmincon with α = 0.03 initial value.

bisection, but this does not adequately explain the sig-

niﬁcant difference in the resultant path.

To investigate the possibility both methods may

have converged to different local minima, both meth-

ods were initialized at the minimum reported by the

other. The result was that fmincon terminated very

close to the bisection minimum, with some constraint

violation, the step size threshold preventing further re-

duction in cost. The evolution for the two initial con-

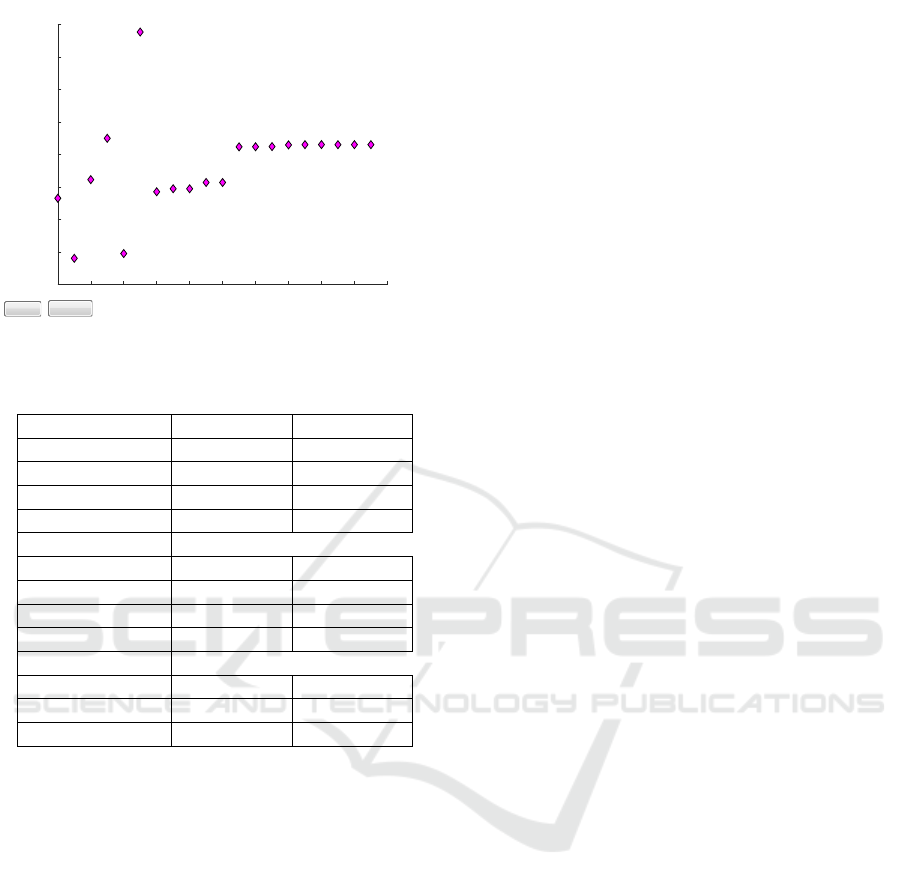
ditions is shown in Figure 10 and Figure 11. Both

terminate due to step size with an infeasible point.

Optimal Path Planning with Clothoid Curves for Passenger Comfort

613

0 2 4 6 8 10 12 14 16 18 20

Iteration

113.2

113.22

113.24

113.26

113.28

113.3

113.32

113.34

113.36

Function value

Current Function Value: 113.286

Stop

Pause

Figure 11: Iterations of fmincon with α =

bisection

initial

value.

Table 1: Comparison table for the two methods.

fmincon Bisection

0.0545 0.1111

0.6554 0.1746

Cost 118.4954 113.2531

Path Length 10.8856 10.642

Final Pose

x 6.477 7.996

y 3.361 5.992

ψ 1.0473 1.0452

κ -7.992e-05 -1.4731e-04

Constraint Error

Lateral 2.2751e-05 -4.4731e-06

Heading -1.4429e-04 2.000e-03

Curvature -7.992e-05 -1.4731e-04

Bisection, by contrast converged to almost the

same point as before when initialized from the fmin-

con minimum. The impressive stability may be due

to the search procedure exploiting the relationship be-

tween the input parameters and the error.

6 CONCLUSION

The results presented show the existing bisection

method from (Gim et al., 2017) is superior for ﬁnd-

ing a minimum length, continuous curvature path be-

tween an initial and ﬁnal pose in this case. Viola-

tion of heading and curvature constraints is slightly

higher, but the solution path length is shorter and the

results are more stable to changes in the starting esti-

mate. The potential advantages of restating the prob-

lem as a non-linear constrained optimization are not

realized because the solver is not able to improve the

cost while meeting the constraints. The given opti-

mization approach requires further development such

as a more robust solver which can ﬁnd a global mini-

mum.

We argue the non-linear constrained optimization

formulation is worth pursuing for many applications

because other constraints can be applied without hav-

ing to redesign the heuristic. For example, polygo-

nal obstacle constraints could be included with little

modiﬁcation. The cost function can also be modi-

ﬁed to prioritize different aspects such as minimiz-

ing curvature rather than path length. Another advan-

tage is the availability of robust general optimization

solvers such as ant colony optimization and genetic

algorithms which could be employed if necessary to

ﬁnd a global minimum.

7 FURTHER WORK

There is more work to be done tuning the cost func-

tion and solver so a stable minimum can be found on

this particular example. Beyond this, a range of other

simple two-clothoid examples could be generated to

show that convergence is consistent. Left and right

90 degree turns of different radius would be sufﬁcient

to produce a roadmap approximating a grid. There is

no reason to believe the cost surface for the reported

case is particularly difﬁcult to solve so investigation

of other boundary conditions is important. The next

step is to examine the four clothoid case, which allows

the creation of ‘lane change’ manoeuvres suitable for

overtaking, and then sequences of clothoids forming

splines.

One motivation for this work is the reduction of

motion sickness for passengers of autonomous vehi-

cles by smooth driving using clothoids. There are

numerous approximations to true clothoids which are

convenient in some cases, such as polynomial approx-

imation for x and y by Taylor expansion. The use of

approximate curves may increase numerical stability,

but will result in deviation from the exact clothoid

proﬁle. These small curvature discontinuities in the

path may or may not be noticeable by passengers. A

study where human participants rate their experience

when taken on an automated ride using true clothoid

curves and approximate ones would provide justiﬁca-

tion for further work on path generation with the exact

integrals.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

614

ACKNOWLEDGEMENTS

This research was made possible thanks to the ﬁnan-

cial support of a full-time EPSRC Doctoral Training

Partnership Studentship - Institute for Transport Stud-

ies, and also thanks to the ﬁnancial support of CASE

partner Guidance Automation Limited.

REFERENCES

Atkinson, K. E. (1988). An Introduction to numerical anal-

ysis, 2nd edition.

Beard, G. F. and Grifﬁn, M. J. (2014). Motion sickness

caused by roll-compensated lateral acceleration: Ef-

fects of centre-of-rotation and subject demographics.

Proceedings of the Institution of Mechanical Engi-

neers, Part F: Journal of Rail and Rapid Transit,

228(1):16–24.

Deits, R. and Tedrake, R. (2015). Efﬁcient mixed-

integer planning for UAVs in cluttered environments.

Robotics and Automation (ICRA), 2015 IEEE Interna-

tional Conference on, pages 42–49.

Dubins, L. E. (1957). On Curves of Minimal Length with a

Constraint on Average Curvature, and with Prescribed

Initial and Terminal Positions and Tangents. American

Journal of Mathematics,, 79(3):497–516.

Elsner, J. (2018). Optimizing Passenger Comfort in Cost

Functions for Trajectory Planning.

Fischer, S. (2008). Comparison of railway track transi-

tion curves in consideration of clothoid, cosine and

wiener bogen transition curves in the respect of the

env 13803-1, the

Obb standard and the hungarian rail-

way design regulations (tadr, nrr) in the interval of

v=120. . . 160 km/h for normal track gauge.

Fraichard, T. and Scheuer, A. (2004). From Reeds and

Shepp’s to Continuous-Curvature Paths. IEEE Trans-

actions on Robotics, 20(6):1025–1035.

Gim, S., Adouane, L., Lee, S., and D

erutin, J. P. (2017).

Clothoids Composition Method for Smooth Path Gen-

eration of Car-Like Vehicle Navigation. Journal of

Intelligent and Robotic Systems: Theory and Applica-

tions, 88(1):129–146.

Katrakazas, C., Quddus, M., Chen, W.-H., and Deka, L.

(2015). Real-time motion planning methods for au-

tonomous on-road driving: State-of-the-art and future

research directions. Transportation Research Part C:

Emerging Technologies, 60:416–442.

LaValle, S. M. and Leidner, D. (2006a). Chapter 13: Dif-

ferential Constraints. In Planning Algorithms, chap-

ter 13, pages 715–786. Cambridge University Press.

LaValle, S. M. and Leidner, D. (2006b). Chapter 3: Geo-

metric Representations and Transformations. In Plan-

ning Algorithms, chapter 3, pages 81–126. Cambridge

University Press.

Levien, R. (2008). The Elastica: A Mathematical History.

McKenney, W. R. (1970). HUMAN TOLERANCE TO

ABRUPT ACCELERATIONS: A SUMMARY OF

THE LITERATURE. Dynamic Science, 70(13).

Paden, B., Cap, M., Yong, S. Z., Yershov, D., and Frazzoli,

E. (2016). A Survey of Motion Planning and Control

Techniques for Self-driving Urban Vehicles. pages 1–

27.

Reeds, J. A. and Shepp, L. A. (1990). Optimal paths for

a car that goes forwards and backwards. 145(2):367–

393.

Schwarting, W., Alonso-Mora, J., and Rus, D. (2018). Plan-

ning and Decision-Making for Autonomous Vehicles.

Annual Review of Control, Robotics, and Autonomous

Systems, 1(1):annurev–control–060117–105157.

Siciliano, B. and Khatib, O. (2016). Robotics and the Hand-

book, pages 1–6. Springer International Publishing,

Cham.

Wilde, D. K. (2009). Computing clothoid segments for

trajectory generation. 2009 IEEE/RSJ International

Conference on Intelligent Robots and Systems, IROS

2009, pages 2440–2445.

Zamﬁr, S., Drosescu, R., and Gaiginschi, R. (2016). Prac-

tical method for estimating road curvatures using on-

board GPS and IMU equipment. IOP Conference Se-

ries: Materials Science and Engineering, 147(1).

Optimal Path Planning with Clothoid Curves for Passenger Comfort

615