
A Reconfigure Modelling of Double Stator PMSM
after Turn-to-Turn Short Circuit
Li Hao
1,2
, Emmanuel Schaeffer
2
and Tang Tianhao
1
1
The Institute of Electric Drives and Control Systems, Shanghai Maritime University, Shanghai 201306, China
2
Polytech Nantes, Université de Nantes, Saint Nasaire 44603, France
Keywords: Double Stator PMSM, Turn-to-Turn Short-circuit, Two-inputs Model, Tranditional Vector Control.
Abstract: This article presents an original modelling of a high speed double stator permanent magnet synchronous
machine (DSPMSM). When a turn-to-turn short-circuit fault occurs in the stator windings, the current flowing
in the short-circuited turns can be much higher than the phase current. And the unbalance between the phases
caused by the fault makes the phase voltage unmeasured. For overcoming this problem, a reconfiguration
modelling method is proposed. The reconfiguration is a model which input line voltage rather phase voltage
that can be measured correctly even if the machine is unbalanced. This advanced model is familiar with the
classical d-q model. Therefore the traditional vector control algorithm is still available, the machine can be
controlled by using the same signals (measured phase currents at the inverter level and DC bus voltage). A
simulation of a DSPMSM variable speed drive shows the relevance of the model.
1 INTRODUCTION
Multi-phases electrical machine have a raising
prospective in many applications, such as aerospace,
energy, precision manufacturing, electric vehicle and
so on. In these applications, the reliability of electrical
machine will be very important. Especially for multi-
phase machine, the possibility of malfunction is
higher because of the increasing of phases. There are
many type of internal faults in electrical machines,
most commons are open-circuit fault and short-circuit
fault. Of course, the Statistical data shows that open-
circuit fault in electrical machine is more frequent
than short-circuit fault, so the research on open-
circuit fault is more widespread. The fault tolerant
control algorithm for open-circuit is abundant, in the
contrast research on short-circuit fault is rare.
Because the fault situation for short-circuit is much
complex than open-circuit. The short-circuit fault
happened inside of machine can be divided into
phase-to-phase fault and turn-to-turn fault. The
former occurs between phases, or another is in one
single phase.
This article focus on turn-to-turn short-circuit fault
happening in the double stator PMSM machine
(double three phases machine). Figure 1 shows a kind
of 6 phases double stator PMSM of EMRAX
company. Figure 2 shows the electrical structure of
the machine found in the user’s manual of this kind
of machine.
Once the short-circuit fault occurs, the machine
will become asymmetry. The nutral point voltage of
electrical machine will drift. As the result, phase
voltage will be unmeasureable. So that the traditional
park model which is most common modelling method
for control algorithm will be uncorrect. The current
amplitude in the short-circuit winding is extremely
high. Especially in high speed condition, the short
circuit current may damage the machine. In order to
limit the current in the short-circuited windings. In
this article, a the line voltage inputs model for PMSM
has been proposed. Different from park model, this
modelling method is based on line voltage and loop
current instead of phase voltage and phase current. In
section II, the reconfigureation model for double
stator PMSM will be presented which can avoid the
influence of homopolar component. This modelling
method committee to overcome the unbalance caused
by short circuit fault that don’t have to predict the
zero-sequence current or voltage as people usually
does. The control system is based on flux oriented
control introduced in section III. In section IV, the
simulation results are presented in order to prove the
effectiveness the control strategy in this article.
Hao, L., Schaeffer, E. and Tianhao, T.
A Reconfigure Modelling of Double Stator PMSM after Turn-to-Turn Short Circuit.
DOI: 10.5220/0007802106090616
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 609-616
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
609

Figure 1: Exterior of a kind of double stator PMSM.
Figure 2: The electrical structure of EMRAX DSPMSM.
2 TWO-INPUTS MODEL
2.1 Turn to Turn Short Circuit Fault
What happens in windings after turn-to-turn short-
circuit fault is shown in figure 3. In figure 3, the fault
only occurs in phase A. In phase A, a parts of winding
has been short circuited, rest of them is still in series
of phase windings. As the result, the machine will
become asymmetry. The asymmetry between phases
cause many problem in machine operation. For
example, the synthetic field will no longer be a circle,
the decoupled between d axis and q axis will be
affected and homopolar component will make the
phase voltage unmeasurable. But it doesn’t mean that
the traditional vector control algorithm is ineffective.
In this chapter, an advanced modelling method is
proposed that such as make the line voltage as the
inputting of the machine rather than phase voltage.
The modelling method will be presented as follows.
Figure 4 is the schematic of short circuit faults on
phase A. For a PMSM, every phase in stator has N
turn coils in series. When turn-to-turn short circuit
occurs, Nc turn will be short circuited, only N - Nc
turns coils are connected in series with phase A. For
deriving the unbalanced model, set α=(N - N
c
)/N=1-
N
c
/N. The resistance of the short citcuited phase is αR,
self-inductance is α
2
L, mutual inductance is αM. In
this section, the two inputs model is derived by
supposing that the fault is happened in phase A of
stator 1.
Different from traditional park model, the inputs of
two-inputs model is line voltage U
1_ab
, U
1_bc
, U
2_ab
and U
2_bc
rather phase voltage. And the line current
will be replaced by loop currents J
1_1,
J
1_2
, J
2_1,
J
2_2
, as
figure 4 shows.
Figure 3: Turn-to-turn short circuit.
(a)
(b)
Figure 4: The equivalent circuit of line-voltage input model
(a) Stator 1. (b) Stator 2.
=(1-α)N
=αN
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
610

2.2 Two-inputs Model
In this part, it is assumed that the shrot-circuit fault
will happen in phase A of stator 1.The equivalent
circuit has been shown in figure 4. Phase voltage U
ab
and U
bc
are acted as the inputs of machine model, line
current is replaced by two loop current. e
a
, e
b
and e
c
is the back EMF. The original equation of voltage and
flux equation of PMSM is shown as follows:
(1)
(2)
For simplify the analysis, magnetic saturation,
eddy current, skin effect etc. will all be ignored. For
the sake of fault tolerant ability, the mutual
inductance between two stators are eliminated. V
1abc
and V
2abc
are the line voltage of the stator. Φ
1abc
and
Φ
2abc
are the flux linkage. R and L
s1
and L
s2
are line
resistance and inductance of both stator respectively.
and
are the magnetic flux of rotor which is
generate by Permanent magnetic material. The
relationship between phase voltage&loop current and
line voltage¤t is as follows:
(3)
(4)
Extracting the transition matrix C=
to
transfer the machine model from three-inputs model
(1) and (2) to the new two-inputs model:
(5)
(6)
Then the two equations above can be written as
follows:
(7)
(8)
Considering short-circuit fault, a fault matrix
should using the parameter α be introduced as follows:
(9)
The inductance matrix L
s1
, resistance matrix R and
magnetic flux of rotor which encompass permanent
magnetic material of unbalanced PMSM (stator 1)
embedding the fault matrix will become as follows:
(10)
(11)
(12)
Because the purpose of this model is that can use
the same control algorithm, so the machine model
should to be orthogonal and decoupled which is
similar with park model based on d-q frame. The
furthering transformation matrix has been found as
follows:
(13)
The transformation is shown as equation (14)-(15):
(14)
(15)
The V
1_αβ
, V
2_αβ
, Φ
1_αβ
and Φ
2_αβ
are voltage and
magnetic linkage at static orthogonal coordinate
frame just like αβ frame in Park model. Then the
model need to be transferred to a rotating coordinate
frame. This procession is similar with park rotation is
park transformation. Park matrix is required:
P=
:
A Reconfigure Modelling of Double Stator PMSM after Turn-to-Turn Short Circuit
611

(16)
(17)
In the above equations,
,
,
,
,
,
.
Besides, the torque equation and mechanical
equation are as equation (18) and (19):
(18)
(19)
3 CONTROL SYSTEM
There are several kinds of control strategy for PMSM,
including vector control, direct torque control (DTC),
model perspective control and so on. In this article the
line voltage input model is expected to work on
traditional control algorithm, so the flux oriented
control system is chosen. Field Oriented Control
(FOC) is a kind of vector control (Senjyu et al., 2001).
This control algorithm is dedicated to control the AC
machine just like the DC machine. Usually the park
transformation is used to achieve this idea that park
model is the equivalent DC machine model for AC
electrical machine. Chapter 2 have introduced a new
modelling method that similar with park model, so the
FOC control strategy is still available.
Figure 5: Control system of doubly stator PMSM.
The field oriented control divides the stator current
into two part: excitation component and torque
generation component. In d-q coordinate frame, d
axis current is acted as excitation current, and q axis
current is acted as torque generating current. In order
to get highest electrical torque, we want to the current
is engaged in generating the torque, so the reference
of d-axis current will be set to 0, the reference of q-
axis current is based on load torque as figure 5 shows.
Actually, the real control system should modulate
PWM capitalized on the output of controller that limit
the output voltage of converters. But in this article,
machine will be built in s-function as a math model,
so the voltage reference can effect on the machine
directly that don’t have to convert the signal to
energy.
As this article says before, FOC control system is
in order to control the AC motor resembles
controlling the DC machine that have good effect on
both Static and dynamic performance. It is better that
make the effect point of flux disturbance in the torque
loop (inner loop), so we can repress the disturbance
via torque feedback rather speed loop (outer loop)
which has some Hysteresis. The torque regulator will
be connected between the rotating speed regulator
and torque current (q-axis current) component
regulator. When flux fluctuates, we can regulate the
reference of torque current component through torque
regulator in time, as to remediate the influence of the
change of flux.
It is important to tune the parameter of control
system via some generic tuning method when
debugging a new control system. So we are going to
compute the parameters of controller by analytical
formulas. In the following, some tuning equations
will be presented.
The expression of PI controller is as follows:
(20)
The transfer function of PI controller is as follows:
(21)
The proportional parameter K
P
and integral
parameter K
I
is the function of damping factor ζ,
natural frequency ω
0
and time constant τ. The PMSM
is seems as a one order actuator:
(22)
The transfer function of the whole system can be
written in this form:
(23)
The parameter of PI controller can be determined
by damping factor ζ, natural frequency ω
0
and time
constant τ.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
612
The PI controller will be used in the d-q axis
current close loop control system. The speed loop
with PI controller will output the torque reference.
The current reference can be calculated through
torque regulator. Then the PI controller in current
loop will output the voltage setting of two stators.
4 SIMULATION RESULTS
Simulation results are conducted to investigate the
fault remediation effect of line voltage input model.
A motor which max power is 100kw is the prototype
of the simulation. The motor has 6 phases (two three
phases stators), Y-connection stator, and the
permanent magnetic material is on the rotor. The
parameter of the motor in this simulation is shown as
table 1 which is from UMAAFSMG, 2017.
Table 1: Parameter.
8
76μH
79μH
18μH
20μH
0.0350T
P ( pole pairs)
10
J (Rotor inertia)
421kg
f
v
(friction of rotor
and load )
1
Specific idle speed
(no load RPM)
14 RPM/1Vdc
Specific load speed
11 – 14 RPM/1Vdc
Firstly, it is necessary to compare the difference on
control effect between based on traditional park
model and line voltage input model that using the
same control strategy. This simulation is lasting 10s.
The rotating speed is set to 1800rpm at 1s, then a
125Nm load will be connected to machine at 5s.
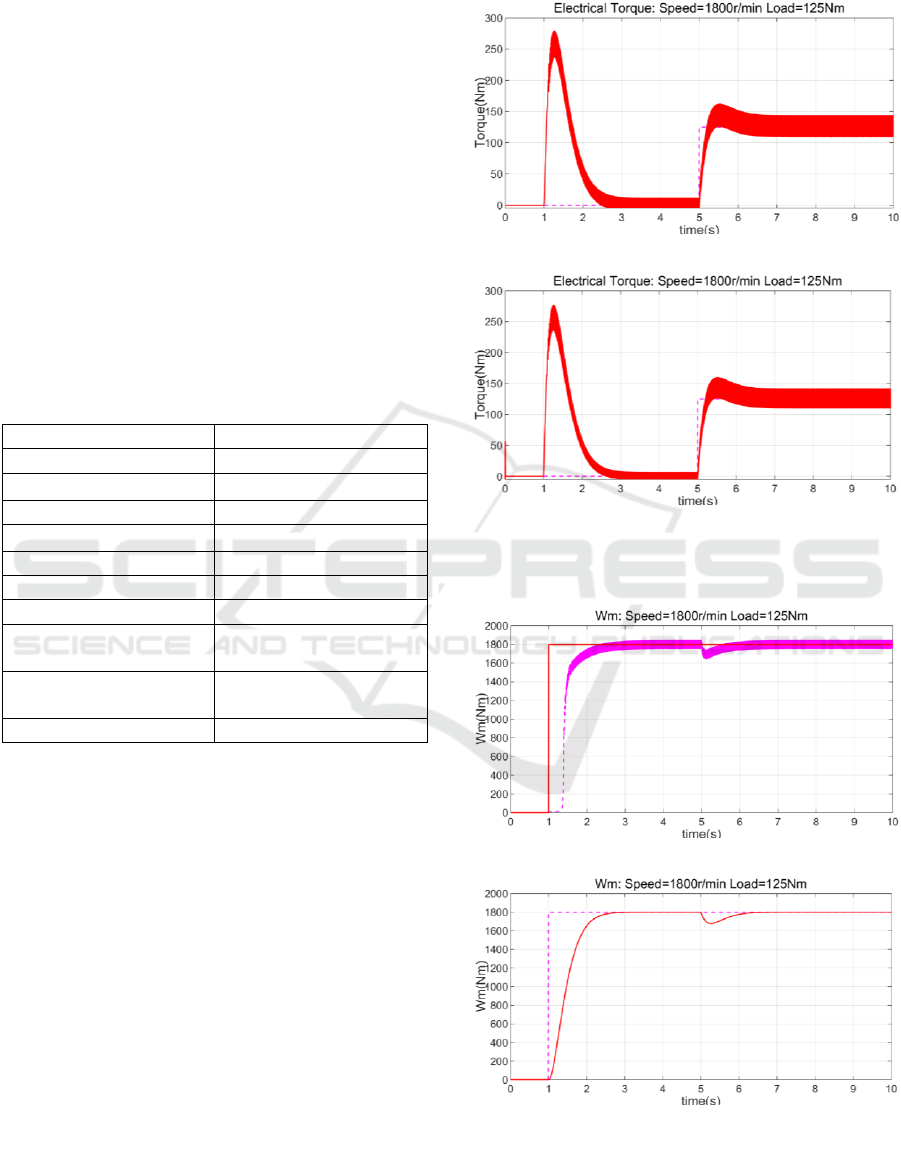
Figure 6-7 is the simulation result with α=0.8 that the
fault happens in phase A of stator 1. Figure 6 is the
result of electrical torque. Figure 7 is the comparison
of rotating speed between two kinds of model.
The peak to peak value of electrical torque
oscillation in steady state are 35.52Nm and 31.78Nm.
The reconfiguration model remediate the 10.52%
torque oscillation with the same double close loop
control system. As for rotating speed, it is obvious
that line voltage input model have manifest effect on
remediating the instability of mechanical speed as
figure 8 shows. Figure 8 are simulation results of
α=0.5. The oscillation are 87.54Nm and 71.34Nm, the
improved model remediate the 18.51% torque
oscillation.
(a)
(b)
Figure 6: Electrical torque. (a) Traditional park model (b)
Two-inputs model. α=0.8.
(a)
(b)
Figure 7: Rotating Speed. (a) Traditional park model
(b) two-inputs model. α=0.8.
A Reconfigure Modelling of Double Stator PMSM after Turn-to-Turn Short Circuit
613
(a)
(b)
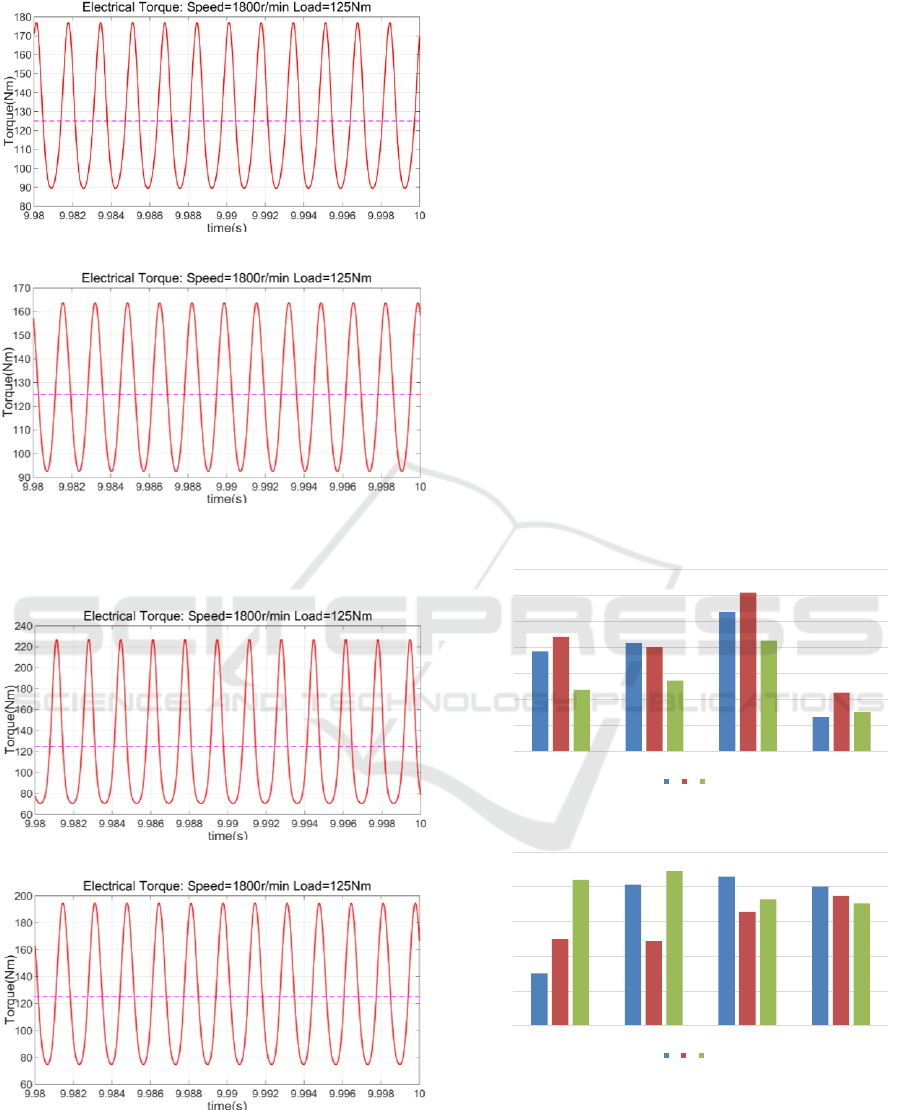
Figure 8: Electrical torque. (a) Traditional park model (b)
Two-inputs model. α=0.5.
(a)
(b)
Figure 9: Oscillation of electrical torque α=0. (a)
Traditional park model. (b) Two-inputs model.
In case of serious fault, such as α=0, which means
the all coils of faulty phase has been short circuited,
so that the torque ripple will be dramatic. Figure 9 is
the waveform of electrical torque when phase A of
stator 1 has been totally short circuited. We can see
that the oscillation of control system with traditional
model is quite high. As the figure 9 (a) shows, the
oscillation is 156.53Nm. This huge oscillation will
make the motor operated unstable even in large
inertia application. The electrical torque oscillation of
line voltage input model is 119.63Nm. The torque
ripple has been reduced 23.57% without any optimal
algorithm.
There are some other problems the turn-to-turn
short circuit may cause, such as high order odd
harmonics of phase current, especially the 3
rd
harmonic. These harmonics could increase the losses
of motor. Figure 10 is the comparison of 3
rd
harmonic
of current of phase A in stator 1 under the healthy
condition, α
1
=0.8, 0.5 and 0 fault respectively. We
can see that the line voltage input model can’t
remediate the harmonics of phase current. So that
other optimal method for harmonics is necessary.
(a) Traditional Park Model
(b) Line Voltage Input Model
Figure 10: Comparison of 3
rd
harmonic.
In addition, the more complicated fault condition
should be concentrated. For example, phase A of both
stators occur inter turn short circuit fault, and two
phases on one stator go wrong. Following simulation
present the fault occurs in two phases. In first one the
19.24%
20.82%
26.79%
6.58%
22.04%
20.07%
30.56%
11.27%
11.83%
13.61%
21.33%
7.54%
0.00%
5.00%
10.00%
15.00%
20.00%
25.00%
30.00%
35.00%
healthy 0.8 0.5 0
3
rd
harmonics of stator 1
ia ib ic
7.52%
20.29%
21.46%
20.02%
12.46%
12.17%
16.38%
18.70%
20.98%
22.23%
18.19%
17.60%
0.00%
5.00%
10.00%
15.00%
20.00%
25.00%
healthy 0.8 0.5 0
3
rd
harmonics of stator 1
ia ib ic
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
614

two phases is in one stator, α
1
=0.8 and α
2
=0.5. The
second is in both stators, α
1
=0.8 and α
5
=0.5. The
simulation result have been shown in figure 11 and
12. Load torque has been set to 125Nm, rotating
speed is 1800r/min.
(a) Electrical Torque
(b) Phase Current of Stator 1
(c) Phase Current of Stator 2
Figure 11: Simulation result of α=0.8 and 0.5 at phase A
and B of stator 1.
(a) Electrical Torque
(b) Phase Current of Stator 1
(c) Phase Current of Stator 2
Figure 12: Simulation result of α=0.8 and 0.5 at phase A
and B of stator 1.
In these simulation, the torque oscillation of two
kinds of fault are 58.99Nm and 106.10Nm. We can
see that if the fault occurs in both stator, the torque
ripple will be more serious than only occurs in one
stator.
5 CONCLUSION
This article has introduced an original modelling
method called line voltage input model for double
stator PMSM. This modelling method is dedicated to
overcome the unbalance caused by short-circuit fault.
The control system this article focused on is field
oriented control which is a classical vector control
algorithm. The simulation result validate that the
modified two-inputs model have positive effect on
remediate the oscillation of electrical torque and
rotating speed. But the side-effect of this modelling
method is that the high order harmonics will
increasing which may pollute the grid. So the
following work of this subject is that the high order
harmonic, extremely 3
rd
harmonic should be reduced.
Furthermore, this modelling method can be used in
some other kinds of control system, such as DTC,
model predictive control and sensorless control.
A Reconfigure Modelling of Double Stator PMSM after Turn-to-Turn Short Circuit
615

ACKNOWLEDGEMENTS
This paper is supported by National Natural Science
Foundation of China (Grant No: 61673260).
REFERENCES
Cao, W., Mecrow, B.C., Atkinson, G.J., Bennett, J.W. and
Atkinson, D.J., 2012. Overview of electric motor
technologies used for more electric aircraft
(MEA). IEEE transactions on industrial electronics,
59(9), pp.3523-3531.
Cavagnino, A., Lazzari, M., Profumo, F. and Tenconi, A.,
2002. A comparison between the axial flux and the
radial flux structures for PM synchronous motor. IEEE
transactions on industry applications, 38(6), pp.1517-
1524.
Wang, Y.C., Fu, W.N. and Li, X.J., 2017. A novel axial flux
stator and rotor dual permanent magnet machine. CES
Transactions on Electrical Machines and Systems, 1(2),
pp.140-145.
Senjyu, T., Kuwae, Y., Urasaki, N. and Uezato, K., 2001.
Accurate parameter measurement for high speed
permanent magnet synchronous motors. In 2001 IEEE
32nd Annual Power Electronics Specialists Conference
(IEEE Cat. No. 01CH37230) (Vol. 2, pp. 772-777).
IEEE.
Fernandez-Bernal, F., Garcia-Cerrada, A. and Faure, R.,
2001. Determination of parameters in interior
permanent-magnet synchronous motors with iron losses
without torque measurement. IEEE Transactions on
Industry Applications, 37(5), pp.1265-1272.
Kellner, S.L., Seilmeier, M. and Piepenbreier, B., 2011,
September. Impact of iron losses on parameter
identification of permanent magnet synchronous
machines. In 2011 1st International Electric Drives
Production Conference (pp. 11-16). IEEE.
Morimoto, S., Tong, Y., Takeda, Y. and Hirasa, T., 1994.
Loss minimization control of permanent magnet
synchronous motor drives. IEEE Transactions on
industrial electronics, 41(5), pp.511-517.
Huynh, C., Zheng, L. and Acharya, D., 2009. Losses in high
speed permanent magnet machines used in
microturbine applications. Journal of Engineering for
Gas Turbines and Power, 131(2), p.022301.
Wangguang, Zhonghua Wang, Dongxue Wang,Yueyang
Li, Meng Li, A Review on Fault-Tolerant Control of
PMSM, 2017 Chinese Automation Congress(CAC).
P3854~3859, 2017.
Lu, H., Li, J., Qu, R., Ye, D. and Xiao, L., 2017. Reduction
of unbalanced axial magnetic force in postfault
operation of a novel six-phase double-stator axial-flux
PM machine using model predictive control. IEEE
Transactions on Industry Applications, 53(6), pp.5461-
5469.
Aydin, M., Huang, S. and Lipo, T.A., 2010. Design,
analysis, and control of a hybrid field-controlled axial-
flux permanent-magnet motor. IEEE Transactions on
Industrial Electronics, 57(1), pp.78-87.
Locment, F., Semail, E. and Piriou, F., 2006. Design and
study of a multiphase axial-flux machine. IEEE
Transactions on Magnetics, 42(4), pp.1427-1430.
User’s Manual for Advanced Axial Flux Synchronous
Motors and Generators (UMAAFSMG), version 4.5,
January 2017.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
616
