Test Input Partitioning for Automated Testing

of Satellite On-board Image Processing Algorithms

Ulrike Witteck

, Denis Grießbach

and Paula Herber

Institute of Optical Sensor Systems, German Aerospace Center (DLR), Berlin-Adlershof, Germany

Embedded Systems Group, University of M

unster, Germany

Keywords:

Image Processing, Software Testing, Input Partitioning, Satellite Systems.

Abstract:

On-board image processing technologies in the satellite domain are subject to extremely strict requirements

with respect to reliability and accuracy in hard real-time. Due to their large input domain, it is infeasible to

execute all possible test cases. To overcome this problem, we deﬁne a novel test approach that efﬁciently and

systematically captures the input domain of satellite on-board image processing applications. To achieve this,

we ﬁrst present a dedicated partitioning into equivalence classes for each input parameter. Then, we deﬁne

multidimensional coverage criteria to assess a given test suite for its coverage on the complete input domain.

Finally, we present a test generation algorithm that automatically inserts missing test cases into a given test

suite based on our multidimensional coverage criteria. This results in a reasonably small test suite that covers

the whole input domain of satellite on-board image processing applications. We demonstrate the effectiveness

of our approach with experimental results from the ESA medium-class mission PLATO.

1 INTRODUCTION

Various on-board image processing applications are

subject to strict requirements with respect to reliabil-

ity and accuracy in hard real-time. Due to the large

input domain of such applications, testing the systems

manually is error-prone and time-consuming. Hence,

a test approach is needed that automatically and sys-

tematically generates test cases for testing such appli-

cations. However, the automated test generation for

on-board image processing applications poses a ma-

jor challenge: The large amount of input parameters

and their possible combinations leads to a high num-

ber of test cases. Hence, the systematic and efﬁcient

coverage of the whole input domain is expensive.

In existing work (Bringmann and Kr

amer, 2006;

Huang and Peleska, 2016), automated test approaches

for various domains, for example, for automotive

and railway applications, are presented. The authors

investigate huge input domains and complex func-

tional behavior. However, their focus is on event-

driven reactive real-time systems, and none of these

approaches is tailored to the domain of satellite on-

board image processing applications, where the com-

plexity is in the huge amount of possible input images.

In this paper, we present a novel test approach for

the domain of satellite on-board image processing ap-

plications. It is based on the (unpublished) master the-

sis of the ﬁrst author (Witteck, 2018). The objective

of our approach is to achieve a high coverage of the

input domain while at the same time using reason-

ably small test suites. For our proposed approach, we

adopt the equivalence class partition testing method.

In general, this method partitions a given input or out-

put domain into disjoint sub-domains called equiva-

lence classes (Varshney and Mehrotra, 2014). The use

of some test values as representatives of each class

reduces the number of required test cases (Bhat and

Quadri, 2015), while still systematically covering the

respective domains. In our test approach, we spec-

ify a dedicated partitioning for each input parameter

of satellite on-board image processing applications.

Moreover, we deﬁne multidimensional coverage cri-

teria for our application domain, which combines the

individual coverage criteria for each input parameter

and enables us to assess a given test suite for its cov-

erage on the complete input domain. Our test gener-

ation approach uses our multidimensional criteria to

automatically assess given test suites with respect to

their coverage of input combinations and automati-

cally generates missing combinations. Thus, our test

approach enables efﬁcient test case generation.

In order to investigate the efﬁciency of our pro-

posed test approach, we use the Fine Guidance Sys-

Witteck, U., Grießbach, D. and Herber, P.

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms.

DOI: 10.5220/0007807400150026

In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 15-26

ISBN: 978-989-758-379-7

tem (FGS) algorithm of the ESA (European Space

Agency) mission PLATO (PLAnetary Transits and

Oscillation of stars) as a case study. It is a satellite

on-board image processing algorithm to calculate the

high-precision attitude of the spacecraft by comparing

tracked star positions with known star positions from

a star catalog. The experimental results demonstrate

the effectiveness of our partitioning approach in terms

of an increased error detection capability.

This paper is structured as follows: In Section 2,

we give a brief overview of equivalence class parti-

tion testing and introduce the PLATO mission as well

as the FGS algorithm. In Section 3, we outline re-

lated work. In Section 4, we present our equivalence

class partitioning approach for on-board satellite im-

age processing applications. In Section 5, we present

experimental results, and we conclude in Section 6.

2 PRELIMINARIES

In this section, we introduce the necessary preliminar-

ies to understand the remainder of this paper.

2.1 Equivalence Class Partition Testing

To make testing more efﬁcient and less time consum-

ing, it is preferable to examine few test cases that

cover a large part of the system under test. Equiva-

lence class partition testing offers a possible solution

to this problem. It is a commonly used approach in

practice. The technique partitions a given input do-

main or output domain into disjoint sub-domains, the

equivalence classes. The method partitions the do-

main in such a way, that all elements in an equivalence

class are expected to provoke the same system behav-

ior according to a speciﬁcation. The partitioning is

based on one or multiple input parameters speciﬁed in

the requirements. Equivalence classes represent sub-

sets of parameter values that completely cover the in-

put or output domain. For the purpose of software

testing, it is therefore sufﬁcient to test some represen-

tative values of each equivalence class.

The selection of test cases from equivalence

classes can be made according to various criteria: us-

ing border values, testing special values or randomly

selecting test cases (Bhat and Quadri, 2015; Huang

and Peleska, 2016; Peter Liggesmeyer, 2009). The

approach removes redundant test cases but retains the

completeness of the tests. Hence, the approach re-

duces the test effort compared to exhaustive testing

(Bhat and Quadri, 2015).

2.2 Context: PLATO Mission

PLATO is an ESA mission in the long-term space sci-

entiﬁc program “Cosmic Vision” (ESA, 2012). The

German Aerospace Center (DLR) manages the inter-

national consortium for developing the payload and

scientiﬁc operation of the project (DLR, 2017).

The main goal of the PLATO mission is the de-

tection and characterization of Earth-like exoplanets

orbiting in the habitable zone of solar-type stars. It

achieves its scientiﬁc objectives by long uninterrupted

ultra-high precision photometric monitoring of large

samples of bright stars. This requires a very large

Field of View (FOV) as well as a low noise level.

To achieve a high pupil size and the required FOV

the instrument contains 26 telescopes for star obser-

vation. 24 normal cameras monitor stars fainter than

magnitude 8 at a cycle of 25 s. Two fast cameras

observe stars brighter than magnitude 8 at a cycle

of 2.5 s. The size of the FOV of a fast camera is

38.7

◦

×38.7

◦

. The cameras are equipped with four

Charge Coupled Devices (CCD) in the focal plane,

each with 4510 ×4510 pixels.

Each fast camera comes with a data processing

unit running the FGS algorithm. It calculates attitude

data with an accuracy of milliarcseconds from the im-

age data. This data is supplied to the attitude and or-

bit control system. The FGS is regarded as being a

mission-critical component which implies a extensive

test procedure.

Fine Guidance System Algorithm. Many space-

craft missions use a FGS to obtain accurate mea-

surements of the spacecraft orientation. We use the

PLATO FGS algorithm as a case study to investigate

the efﬁciency of our test approach.

The attitude calculation of a telescope is based on

measured star positions on the CCD compared to their

reference directions in a star catalog. Figure 1 gives

an overview of the FGS algorithm (Grießbach, 2018).

The autonomous attitude tracking is initialized

with an initial attitude given by the space craft. For

each pre-selected guide star an initial sub-window po-

sition is calculated by means of the camera model,

which transforms from sky coordinates to pixel coor-

dinates and vice versa (Grießbach, 2018). Guide stars

are predeﬁned stars in a star catalog that satisfy given

criteria. For example, the star magnitude is within

a certain range, the star has very low contamination,

etc. (Grießbach, 2018). The FGS algorithm calculates

centroids after reading 7 ×7 pixel sub-window every

2.5 s from the full CCD image.

A linear center of mass calculation estimates the

initial centroid position. To get a more precise solu-

ICSOFT 2019 - 14th International Conference on Software Technologies

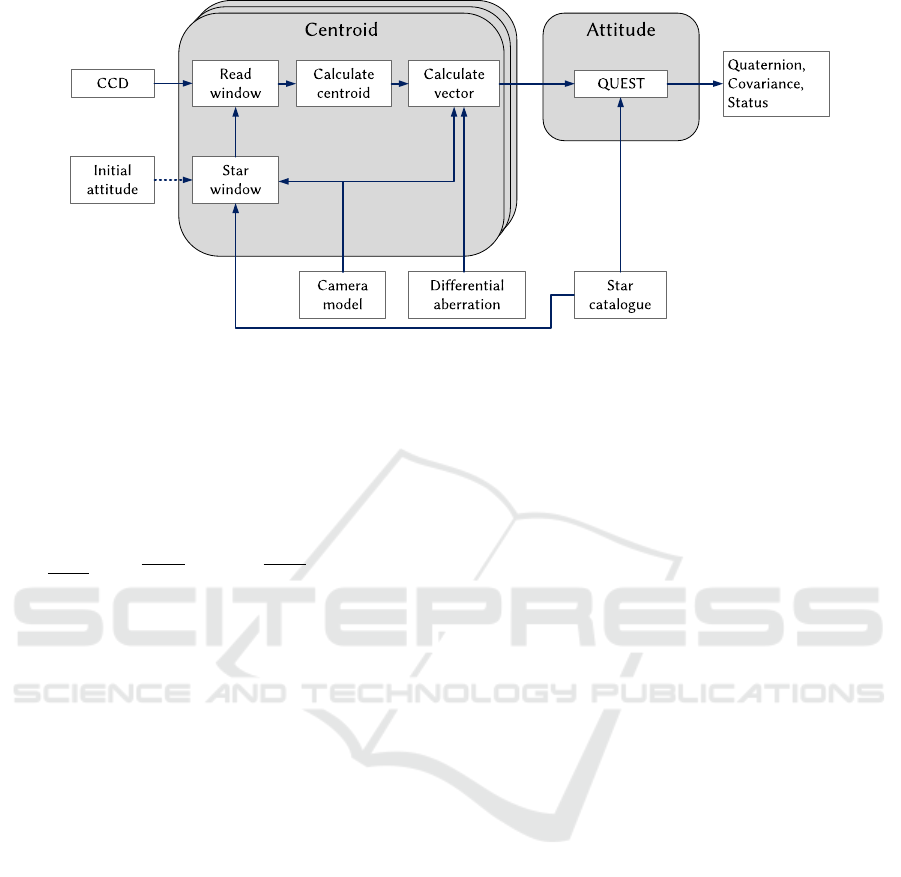
Figure 1: Overview of the FGS algorithm Grießbach (2018).

tion, the algorithm separately estimates each centroid

using a Gaussian point spread function (PSF) obser-

vation model. The PSF describes the distribution of

the star light over the CCD pixels. Equation (1) shows

the Gaussian PSF observation model h(i, j) of a single

pixel (Grießbach, 2018).

h =

2πσ

i+1

−

(u−u

)

2σ

j+1

−

(v−v

)

2σ

dv+D+ξ (1)

The FGS algorithm uses the measured pixel intensi-

ties to determine the centroid position (u

)

, in-

tensity I

, image background D and PSF width σ. A

non-linear least square ﬁtting method iteratively re-

ﬁnes the parameters of the PSF model. The FGS al-

gorithm calculates the correction by means of the QR-

decomposition (Grießbach, 2018). In the next step,

the pixel coordinates of the calculated centroid posi-

tion are transformed into star direction vectors in the

camera boresight reference frame. The x- and y-axis

of the detector and the optical axis of the camera de-

scribe the boresight reference frame.

In the last step, the FGS algorithm calculates an

attitude from at least two star directions in the bore-

sight reference frame and the corresponding reference

vectors from a star catalog. In addition, it delivers an

attitude covariance matrix.

3 RELATED WORK

Equivalence class partition testing “is probably the

most widely described, and one of the most widely

practiced, software testing techniques” (Kaner, 2004).

In this section, we present a selection of published

work on equivalence class partition testing.

3.1 Equivalence Class Partition Testing

Various studies investigated equivalence class parti-

tion testing strategies for different domains: railway,

automotive, avionics, etc. (Huang and Peleska, 2016).

In the automotive domain, DaimlerChrysler Re-

search developed a test approach, called Time Par-

tition Testing (TPT), to test the continuous behavior

of control systems. Bringmann and Kr

amer (2006)

explained the principle of the TPT approach using

an exterior headlight controller as an example. In

most cases, automotive embedded control systems are

based on complex functional behavior and a large in-

put domain. To increase the test efﬁciency the TPT

approach systematically selects test cases revealing

redundant or missing test scenarios. Using a graph-

ical state machine notation, the TPT approach parti-

tions a test scenario into stream-processing compo-

nents. Each component deﬁnes the behavior of output

variables depending on the behavior of input variables

up to a certain point in time, speciﬁed by a temporal

predicate. Test cases deﬁne variations in the state ma-

chine to test various functional aspects of the system

under test.

The study shows that state machines are suitable

to partition the temporal behavior of input and output

variables in order to model, compare and select test

cases. The modeled test cases test the complex func-

tional requirements of control systems. A huge in-

put domain and complex functional behavior are also

characteristics of the system class we investigate in

this paper. However, the behavior of systems from

this class is not dependent on the arrival time of the

input values. Hence, the TPT approach is not applica-

ble to the system class that we consider.

In (Huang and Peleska, 2016), the authors pre-

sented a model-based black-box equivalence class

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms

partition testing strategy used in the railway domain.

The approach automatically generates ﬁnite and com-

plete test suites for safety-critical reactive systems in

relation to fault models. Huang and Peleska investi-

gated the approach using the Ceiling Speed Monitor

of the European Train Control System as an exam-

ple for systems with potentially inﬁnite input domain

but ﬁnite output domain and internal variables. Their

approach models the reactive behavior of such sys-

tems by means of deterministic state transition sys-

tems. Moreover, it partitions the state space into a ﬁ-

nite number of equivalence classes such that all states

in a class provide the same output traces for the same

non-empty input trace. Based on these classes, they

generates a complete test suite in the following sense:

First, at least one test in this suite fails when testing

an application that violates a given speciﬁcation. Sec-

ond, each test in the suite passes for all applications

that satisfy the speciﬁcation. Huang and Peleska in-

vestigated models whose behavior can be represented

by state transition systems. However, we have no state

transition system description of our considered satel-

lite application. Hence, we present an approach that

does not need such a description.

4 MULTIDIMENSIONAL

COVERAGE CRITERIA FOR

AUTOMATED TESTING

Many image processing applications require various

input parameters such as position of an object in the

image, magnitude of an object, position of an object

in a pixel, a pattern to distinguish different objects,

etc. This leads to a huge input domain, which makes

testing expensive. Testing such applications manually

is error-prone and time-consuming. Therefore, auto-

mated test systems are needed. However, automated

test generation for satellite on-board image process-

ing applications poses a challenge: The number of

possible input parameter combinations in the test im-

age are very large. That means an enormous amount

of test cases is possible. This makes it hard to efﬁ-

ciently capture the huge input domain.

To overcome that problem, we deﬁne a partition-

ing approach that systematically selects test cases

from the huge input domain of satellite on-board im-

age processing applications. Our approach can be

used to assess and to enhance a given test suite. To

evaluate the efﬁciency of our test approach, we in-

vestigate a case study, namely the PLATO FGS al-

gorithm as described in Section 2.2. Satellite on-

board image processing algorithms especially require

extensive testing because such algorithms are subject

to strict requirements with respect to reliability and

mathematical accuracy.

Figure 2 depicts an overview of our proposed par-

titioning approach. The key idea is to deﬁne equiv-

alence classes on input parameters that are typically

used by satellite on-board image processing applica-

tions, namely position, magnitude, sub-pixel position,

and distribution model. Our main contributions are

threefold: First, we present novel concepts to partition

the individual input parameters of satellite image pro-

cessing algorithms into equivalence classes. Second,

we deﬁne multidimensional coverage criteria based

on a combination of the individual criteria for each

input parameter to efﬁciently cover the whole input

domain. Third, we deﬁne a test generation algorithm

that automatically selects test cases that completely

cover the whole input domain according to our multi-

dimensional coverage criteria.

The goal of the test is to automatically detect

errors in the on-board image processing application

code. To achieve this, our test generation algorithm

selects for each equivalence class combination a test

case from a given test suite as representatives. Thus,

our approach reduces the number of redundant test

cases. Furthermore, our algorithm generates new test

cases for missing combinations to reach complete

coverage of the input domain. The result is a rea-

sonably small test suite that covers the whole input

domain of the image processing application. The se-

lected test cases serve as input for our automated test-

ing framework. Moreover, we insert requirements for

the automated evaluation of the image processing ap-

plication results. If they do not meet the requirements,

the test detects an error.

The following sections describe the mentioned

steps of the partitioning approach in more detail us-

ing the PLATO FGS algorithm as a case study.

4.1 Assumptions and Limitations

In the following, we consider systems with objects in

an image as inputs. In the case study, the observed

objects are stars with magnitudes between 5.5 to 7.0,

uniformly distributed in the image (Grießbach, 2018).

We consider four parameters that affect the math-

ematical accuracy of the FGS algorithm: the guide

star position, magnitude, sub-pixel position, and PSF

shape. The test evaluation is based on the centroid po-

sition calculated by the centroid algorithm of the FGS.

The input of the centroid calculation is a single star.

We deﬁne a test star as a test case for the automated

test generation.

ICSOFT 2019 - 14th International Conference on Software Technologies

Figure 2: Overview of the partitioning approach.

4.2 Running Example: Input

Parameters

One of the main contributions of this paper is our def-

inition of multidimensional coverage criteria on the

input domain of satellite on-board image processing

applications. These criteria are based on the combi-

nation of equivalence classes of the FGS input star pa-

rameters given in Section 4.1. The mathematical ac-

curacy of the centroid estimation depends on the com-

bination of these input parameters. In this section, we

describe how the parameters affect the quality of the

centroid calculation.

The star signal is spread over all pixels in the sub-

image. Hence, each pixel includes information about

the star. However, 90 % of the energy is within 2 ×2

pixel around the centroid. Each pixel also contains

noise. We call the information usable if the star sig-

nal is little interfered by noise and the Signal-to-Noise

Ratio (SNR) is high. If the SNR in the pixel is suf-

ﬁcient, a linear independent equation exists for this

pixel. The centroid calculation needs at least 5 lin-

ear independent equations to estimate the 5 unknown

parameters of the pixel observation (cf. Equation (1)).

The distribution of the star signal depends on the

star position on the Focal Plane Assembly (FPA) and

the sub-pixel position. Due to optical aberrations of

the telescope, the PSF shape of the star is wider in

the FPA corner than close to the center. Assume the

other input parameters contain reasonably good, con-

stant values. Then a small PSF leads to a low number

of pixels with a high SNR and a low number of lin-

ear independent equations. In case of a wide PSF the

SNR is low but many linear independent equations

exist. Both cases can be sufﬁcient for an accurate pa-

rameter estimation (Grießbach, 2018).

The SNR in a pixel also depends on the centroid

sub-pixel position. Suppose the other parameters have

adequate, constant values. If the centroid is posi-

tioned in the pixel center, most star ﬂux is accumu-

lated in a few pixels. Then these pixels have a high

SNR compared to the neighboring pixel. In contrast,

more pixels have a sufﬁcient SNR if the centroid is on

the pixel border or corner. In this case, the star infor-

mation is distributed more evenly over several pixels.

The other pixels have a low SNR. Due to movement,

the centroid may move to neighbor pixels. This leads

to variations in the pixel illumination and the apparent

centroid position (Grießbach, 2018).

The star magnitude affects the measured ﬂux

(photoelectrons per second) of the star. The accumu-

lated number of photoelectrons per pixel denotes the

illumination of a pixel. Equation (2) shows the rela-

tion between the magnitude m and the corresponding

ﬂux F

in e

−

/s.

= F

T QA ∗10

−0.4∗m

(2)

with magnitude m, reference ﬂux F

of a star with

m = 0, transmission efﬁciency T of the optical sys-

tem, quantum efﬁciency Q of the detector, and effec-

tive light-collecting area A. As the equation shows,

the star ﬂux is non-linear to the magnitude of the star.

A low magnitude corresponds to a high number of

photoelectrons, corresponding to a higher SNR per

pixel. More information is usable than in case of a

high magnitude.

In addition, the accuracy of the centroid calcula-

tion depends on the PSF shape. In the best case sce-

nario, the shape is a symmetric Gaussian-PSF. Then,

the observation model perfectly ﬁts the star. There-

fore, the accuracy of the centroid calculation is high.

But in reality, the PSF shape is non-Gaussian. In that

case, the observation model is less accurate. Besides,

movements lead to stronger variations in the expected

centroid positions (Grießbach, 2018).

While individual parameter values might provide

a good centroid estimation, a combination of param-

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms

Figure 3: Examples of different low quality stars (Grießbach, 2018).

eters may change the quality of the results. For illus-

tration, Figure 3 shows some example stars with non-

Gaussian-PSF shape that are less suitable as guide

stars. They all lead to inaccurate estimation results.

What the three stars have in common is that their

intensity is concentrated on a pixel edge. For all stars,

the magnitude and FPA position are sufﬁciently good.

However, a small variation due to movement leads to

big changes of the illumination. Since the Gaussian-

PSF observation model does not ﬁt the star PSF shape

perfectly, the centroid estimation is less accurate and

the FGS assumes a big movement of the star.

4.3 Equivalence Class Deﬁnitions

The quality of the centroid calculation of the FGS al-

gorithm depends on various parameters. Thus, we de-

ﬁne the input domain as a set of input parameters I.

The set includes the position on the FPA P , the mag-

nitude M , the sub-pixel position E and the PSF shape

G. To keep the approach more ﬂexible the tester sets

the borders of equivalence classes. Thus parameters

can also be excluded from the analysis. In this sec-

tion, we present our concepts for partitioning the input

parameters P, M , E and G into equivalence classes.

Star Position on the FPA. Section 4.2 clariﬁes that

size and shape of the PSF depend on the star position

on the FPA. Since the PSF changes with the distance

to the FPA center, our idea is to partition the FPA into

equally sized, circular areas as seen in Figure 4. The

tester speciﬁes the initial radius r

. The rectangles

represent the image area of the fast camera CCDs.

We partition parameter P into equivalence classes

. Each class P

corresponds to a circular FPA area

with inner radius r

n−1

and outer radius r

P = P

∪P

∪...∪P

with 1 ≤n ≤I

(3)

Let S denote the set of available stars. A star s ∈ S

lies in an equivalence class P

if following condition

Figure 4: Example of cyclic borders of FPA equivalence

classes.

holds:

n−1

≤ p(s) < r

, with p(s) =

+ y

(4)

where (x

) is the position of star s on the FPA and

p(s) is the distance of the star s to the FPA center.

Star Magnitude. A useful partitioning of magni-

tude values into equivalence classes is not obvious.

Our idea is to partition the star ﬂux, which is non-

linear to the magnitude, range into I

∈N equidistant

parts that represent the equivalence classes. We deﬁne

Equation (5) to obtain the upper limit of a sub-range.

= F

7.0

+ j

5.5

−F

7.0

(5)

is the ﬂux of magnitude m

and j = 1...I

repre-

sents the j-th equivalence class of parameter M . F

5.5

and F

7.0

are the numbers of photons for magnitude 5.5

ICSOFT 2019 - 14th International Conference on Software Technologies

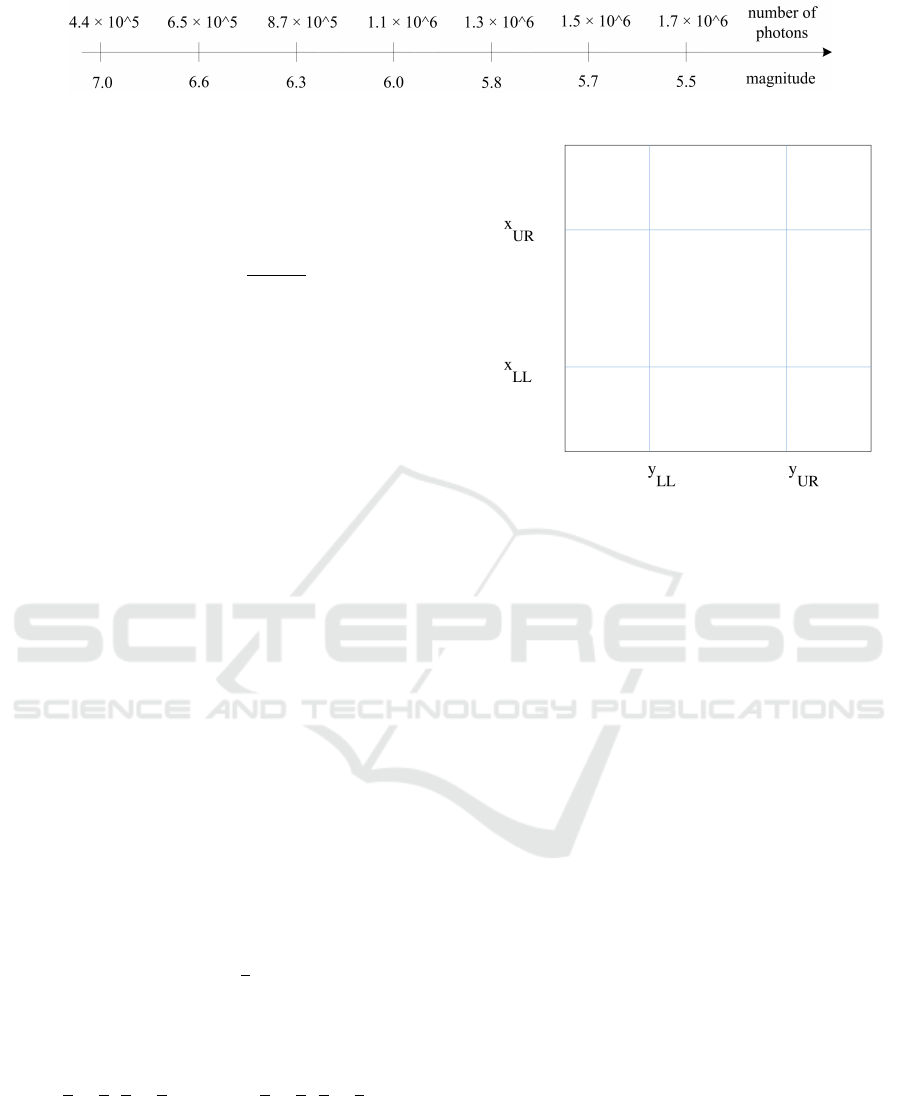
Figure 5: Example partitioning of magnitude range.

and 7.0. We calculate the ﬂux values F

5.5

and F

7.0

using Equation (2). Furthermore, we use Equation (6)

to recalculate the magnitude m

from the calculated

ﬂux limit F

of the ﬂux sub-range.

m = −2.5 ∗log



T QA



(6)

From a formal point of view, we partition the param-

eter M into equivalence classes M

M = M

7.0

∪... ∪M

5.5

(7)

with l

∈ R and 5.5 ≤ l

≤ 7.0. Each equivalence

class M

is a magnitude sub-range with upper limit

. Each available star s lies in equivalence M

if it

satisﬁes the condition in Equation (8).

j−1

≤ m(s) < l

(8)

where m(s) denotes the observed magnitude of star s

and l

with j = 1...I

is the upper limit of the j-th

magnitude sub-range. The tester speciﬁes the num-

ber of equivalence classes I

∈ N of the parameter

M . Figure 5 illustrates an example partitioning of the

magnitude range.

Star Sub-pixel Position. The quality of the cen-

troid estimation of stars close to a pixel border is as

sensitive to movements as the estimation of stars with

centroids on a pixel corner and vice versa. For this

reason, we divide the pixel area into different sub-

areas as shown in Figure 6.

The tester speciﬁes the ratio r of the central area

of the pixel to the pixel area, for example, 1/2, 3/5,

etc. If a is the pixel size, then the length of the edge

of the central area results from Equation (9).

b = a

√

r (9)

With that, we obtain the lower left corner l and the

upper right corner u of the central pixel area, with

l = (

−

) and u = (

) (10)

Based on these corners, we partition parameter E into

equivalence classes E

with i = 0...8. The equivalence

class E

is the i-th pixel sub-area. A star s lies in an

equivalence class if it satisﬁes the corresponding con-

dition.

E = E

∪E

∪... ∪E

(11)

Figure 6: Example borders of pixel equivalence classes.

: 0 ≤ e

(s) < x

∧ 0 ≤ e

(s) < y

: 0 ≤ e

(s) < x

∧ y

≤ e

(s) < y

: 0 ≤ e

(s) < x

∧ y

≤ e

(s) < a

: x

≤ e

(s) < x

∧ 0 ≤ e

(s) < y

: x

≤ e

(s) < x

∧ y

≤ e

(s) < y

: x

≤ e

(s) < x

∧ y

≤ e

(s) < a

: x

≤ e

(s) < a ∧ 0 ≤ e

(s) < y

: x

≤ e

(s) < a ∧ y

≤ e

(s) < y

: x

≤ e

(s) < a ∧ y

≤ e

(s) < a

(12)

(s) and e

(s) return the x-coordinate and y-

coordinate of s in the pixel respectively.

Star PSF Shape. We partition the parameters G in

two equivalence classes G

and G

since two PSF

shapes are distinctive (see Section 4.2). If a star has a

Gaussian-PSF shape it is in class G

otherwise it is in

class G

4.4 Multidimensional Coverage Criteria

We deﬁne multidimensional coverage criteria on the

input domain of satellite on-board image processing

applications to measure the coverage of a test suite

with respect to input parameter combinations. If the

measured coverage of a test suite is not complete, our

automated test generation algorithm automatically in-

serts test cases for missing combinations. This section

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms

presents our deﬁnitions of multidimensional coverage

criteria on the input domain I = {P ,M , E,G}.

The individual coverage of an input parameter de-

notes the ratio of equivalence classes that are covered

by at least one test case from a given test suite to the

number of equivalence classes of this input parame-

ter. Equations (13) to (16) show this deﬁnition for the

input parameters P , M , E and G.

# covered elements o f P

|P |

(13)

# covered elements o f M

|M |

(14)

# covered elements o f E

|E|

(15)

# covered elements o f G

|G|

(16)

The coverage domain for our multidimensional

coverage criteria is the Cartesian product of equiva-

lence classes of the input parameters P , M , E and G.

Therefore, an input combination is a tuple of equiv-

alence classes (P

), where P

∈ P , M

∈

M , E

∈ E and G

∈ G. Furthermore, a test case

is a star represented by a tuple of parameter values

(p,m,e,g) ∈ (P

). The following example

test cases clarify these deﬁnitions.

Example 1:

(930.4,6.5,(0.4,0.1),G) ∈ (P

2000

×M

6.6

×E

×G

)

The test star position is in the FPA area with radius

2000. The star belongs to equivalence class M

6.6

be-

cause its magnitude value is between 6.3 and 6.6.

The star center is located in the middle-left pixel sub-

area. That corresponds to equivalence class E

. The

star is part of equivalence class G

, because it has a

Gaussian-PSF shape.

Example 2:

(579.1,6.5,(0.9,0.2),G) ∈ (P

2000

×M

6.6

×E

×G

)

The test star is similar to the star in the ﬁrst example,

but it belongs to equivalence class E

, which means

that the center of the star is positioned nearby the up-

per left pixel border.

Our multidimensional coverage criterion is fully

satisﬁed if the test cases in a test suite cover all possi-

ble input combinations at least once. The number of

required covered input combinations for a complete

coverage is |P ×M ×E ×G|. In the remaining sec-

tions, we denote a test suite that completely covers

the input domain with respect to our multidimensional

coverage criteria as a complete test suite. The multi-

dimensional coverage C results from the ratio of the

amount of input combinations covered by at least one

test case to the total number of input combinations.

C =

# covered input combinations

|P ×M ×E ×G|

(17)

Our test approach calculates the individual and multi-

dimensional coverage of a given test suite using Algo-

rithm 1. The input parameters P , M , E, and G con-

tain I

, I

equivalence classes respectively.

Input: Test suite T S

Output: Multidimensional coverage Cov of

T S

1 C

= C

= C =

2 foreach tc with (p, m, e, g) ∈ TS do

3 i

= getPosECId(p);

4 C

←C

∪i

;

5 i

= getMagECId(m);

6 C

←C

∪i

;

7 i

= getPixECId(e);

8 C

←C

∪i

;

9 i

= getModECId(g);

10 C

←C

∪i

;

11 C ←C ∪(i

);

12 end

13 Cov

= |C

|/I

;

14 Cov

= |C

|/I

;

15 Cov

= |C

|/I

;

16 Cov

= |C

|/I

;

17 Cov = |C|/(I

·I

)

Algorithm 1: Coverage calculation.

For each test case in the given test suite, the al-

gorithm computes for each input parameter the index

of the corresponding equivalence class

from P , M , E and G. The algorithm adds the indices

to the sets C

, C

and C

respectively. More-

over, it inserts the tuple (i

) into the set C

that contains all covered input combinations. As the

algorithm uses the union operator to add the tuples to

the set, each tuple is included in the set only once.

The algorithm applies Equations (13) to (17) to com-

pute the individual and multidimensional coverage.

Our partitioning approach can be used to assess

the quality of test suites with respect to their cover-

age on the input space of a satellite on-board image

processing application with respect to individual and

multidimensional coverage criteria.

ICSOFT 2019 - 14th International Conference on Software Technologies

4.5 Automated Test Generation

In order to systematically generate a test suite that

completely covers the input domain according to our

multidimensional coverage criteria, we propose Algo-

rithm 2. The complete test generation algorithm uses

1 to assess a given test suite and then systematically

generates missing test cases.

Input: Input combination universe U , covered

input combination set C, test suite T S

Output: Complete test suite T S

1 Cov = computeMultidimCoverage(TS);

2 if Cov < 1 then

3 W ←U \C;

4 foreach w ∈W do

5 tc = generateTC(w);

6 T S ← T S ∪tc;

7 end

8 end

Algorithm 2: Generate complete test suite.

The algorithm generates set W that contains all

input combinations not covered by the given test

suite. For each input combination in W , the algorithm

uses procedure generateTC that generates a test case

by randomly selecting values from the equivalence

classes of the missing combinations. The algorithm

adds the newly generated test case to the test suite. In

this way, it efﬁciently inserts missing but relevant test

cases into the test suite. This increases the multidi-

mensional coverage and therefore the error detection

capability of the given test suite. The result of our

automated test generation is a complete test suite.

If the set of covered input combinations C is

empty, then the set of uncovered input combinations

W is equal to the universe of possible input combi-

nations U . Hence, Algorithm 2 can also be used to

generate a new test suite that completely satisﬁes the

multidimensional coverage criteria. Our automated

testing framework only selects one test case per input

combination. This efﬁciently reduces the number of

redundant test cases for the test execution.

5 EVALUATION

To evaluate our approach, we have implemented the

proposed partitioning and test generation algorithm.

We have evaluated its applicability and error detec-

tion capability for satellite on-board image processing

applications using the FGS algorithm of the PLATO

mission with various test suites.

5.1 Implementation

Figure 7 shows the block diagram of our test setup.

As the ﬁgure depicts, our test environment runs on a

Windows system. We have implemented the environ-

ment in C++ based on the model-view-controller pat-

tern. We allow the tester to specify input parameters

with or without graphical user interface (GUI).

Our automated test generation algorithm returns

a star catalog to simulate star data for missing in-

put combinations. The catalog is a text ﬁle that in-

cludes right ascension, declination, and magnitude of

stars that should be simulated. We manually insert the

catalog into the PLATO simulator PlatoSim (Marcos-

Arenal et al., 2014). PlatoSim writes the simulated

star data to a HDF5 ﬁle (The HDF Group, 2018).

Each ﬁle contains an image sequence of several time

steps of a star in a hierarchical ﬁle format. Since

PlatoSim is not developed for Windows systems, the

simulator runs in a Linux virtual machine.

As shown in Figure 7, we connect the Win-

dows system via a SpaceWire USB brick to a GR-

XC6S FPGA development board (PENDER ELEC-

TRONIC DESIGN GmbH, 2011) running at 50 MHz.

SpaceWire is a data-handling network for spacecraft

deﬁned in (ECSS Executive Secretariat, 2008). For

that, our test environment uses the C SpaceWire USB

API Library for the SpaceWire USB brick. A proto-

type of the FGS algorithm, written in C, runs on the

evaluation board. We load the software with the Leon

debug monitor GRMON onto this board. Via a UART

interface we receive debug information in a terminal.

For example, stack size, hardware information, etc.

Our objective is to evaluate our approach for the

development and test of the FGS algorithm imple-

mentation. Moreover, our goal is to test execution

time and mathematical accuracy of the FGS algorithm

under realistic conditions. For example, a calculation

on the development board is slower than the same cal-

culation on a Windows system. Therefore, we run the

application under test on the target hardware and keep

the test system in the software development cycle.

5.2 Experimental Results

In this section, we present the experimental results for

generating a test suite using our partitioning approach

for testing the PLATO FGS algorithm.

Since no investigations of the class boundaries

have yet been carried out, we have started by estimat-

ing the following parameters for the experiments:

- Initial radius r

of FPA partitioning: 1900 pixel

- Number of magnitude sub-ranges: 6

- Ratio r of central sub-area to pixel area: 0.2

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms

Figure 7: Block diagram of test setup.

Using the parameters leads to 8 equivalence

classes of input parameter P, 6 equivalence classes of

parameter M and 9 equivalence classes of E. Input

parameter G consists of two equivalence classes (G

and G

). Thus, our automated testing framework

needs 864 test cases to completely cover the whole

input domain of the FGS algorithm.

To evaluate the approach, we have investigated

the quality of two different test suites with respect to

their multidimensional coverage on the input domain.

One test suite contains 82 randomly generated stars.

Our automated test generation algorithm identiﬁes 10

stars in the suite as redundant. The test suite achieves

8.3 % coverage of the input domain with respect to

our multidimensional coverage criteria. Algorithm 2

from Section 4.5 enhances the suite to achieve com-

plete coverage on the input domain. In the following,

we call it complete test suite. The other test suite con-

tains 902 randomly generated but evenly distributed

stars. We call it random test suite and did not improve

it. Table 1 shows the coverage of the test suites for

each input parameter as well as the achieved multidi-

mensional coverage.

Table 1: Coverage values of the test suites.

random complete

Test stars 902 874

Covered input combinations 112 864

[%] 87.5 100.0

[%] 16.7 100.0

[%] 100.0 100.0

Multidim. coverage [%] 13.0 100.0

Table 1 shows that the utilization of the equiva-

lence class partitioning method reduces the random

test suite by hundreds of redundant test cases. Since

there are no unnecessary executions of redundant test

cases, this saves test time. Thus, the method increases

the efﬁciency of the test process. The random test

suite achieves a high individual coverage of three in-

put parameters. However, due to the low individual

coverage of input parameter M , the multidimensional

coverage of the test suite is low. Furthermore, Table 1

exhibits that the complete test suite covers the whole

input domain of the FGS algorithm.

To assess the partitioning approach, we have au-

tomatically inserted some faults into the code of the

centroid calculation of the PLATO FGS algorithm.

These injected faults belong to three classes: missing

assignment, wrong assignment and wrong condition.

For each test execution, we have injected a single er-

ror at a different position in the code. Our objective

is to check if the complete test suite achieves a higher

error detection capability than the random test suite.

In each experiment, our test application sent 1000

packets per selected test star, with one exposure each,

to the evaluation board running the FGS algorithm.

Our test application averages the resulting centroid

positions over all exposures and compares it with the

position in the star catalog. If the deviation of the po-

sitions is greater than a predeﬁned value, the test de-

tects the error. Table 2 shows the output for one test

case that detects a missing assignment error. The high

deviation of the calculated position from the given po-

sition reveals an error in the centroid calculation.

During the experiments, we have injected three

missing assignment errors, three wrong assignment

errors, and three wrong condition errors. Table 3 sum-

marizes the experimental results for both test suites.

The table shows long execution times for the tests.

The reason is that the evaluation board only receives

20 packets per second. Moreover, Table 3 shows that

both test suites do not reveal all injected errors with

respect to the given test criterion. The random test

suite, as well as the complete test suite, detects one

missing assignment error. In addition, 6 test cases

from the complete test suite reveal one wrong assign-

ICSOFT 2019 - 14th International Conference on Software Technologies

Table 2: Output for a sample test case.

Star-Id x [pixel] y [pixel] deviation [pixel] result

1 1 0 8 28 2.96 ×10

2.38 ×10

3.80 ×10

error detected

Table 3: Test suites evaluation results.

random complete

Test cases 112 864

Execution time [h] 1.5 11.8

Detected errors 1 3

Undetected errors 9 7

Error detection ability [%] 10.0 30.0

ment error and 1 test case detects one wrong condition

error. During the test development, we detected an er-

ror in the FGS algorithm code that we did not inject.

But using the speciﬁed test criterion, both test suites

do not detect the error. Moreover, the tests do not de-

tect three of the injected assignment errors because

the deviation only changes slightly in case of these

errors. In addition, for some test cases, the deviation

increases and in others decreases in such a way that

the speciﬁed deviation value is not reached. The tests

also do not detect the other injected errors and the

unintended error because these errors affect other pa-

rameters estimated by the centroid calculation. There-

fore, the deviation for all test cases is smaller than the

predeﬁned value in the test criterion. However, the

error detection capability of the complete test suite is

with respect to the speciﬁed test criterion three times

higher than the error detection capability of the ran-

dom test suite. Nevertheless, for both test suites, the

error detection capability is low because not all in-

jected errors affect the results in such a way that the

deviation increases. Therefore, our speciﬁed test cri-

terion is not suitable to detect all injected errors. This

shows, that the speciﬁed test criterion plays an impor-

tant role in the success of the tests.

We have speciﬁed another test criterion: the test

passes if the distance between the centroid position

calculated by an erroneous calculation and the cen-

troid position resulting from an assumed error-free

calculation exceeds a predeﬁned value. In this case,

not all test cases of the test suites detect the errors.

This means special input combinations are more ca-

pable to detect errors than others. In case of the wrong

condition errors and the unintended error, the percent-

age of error detecting test cases from the random test

suite is up to one third compared to the percentage of

error detecting test cases of the complete test suite.

Therefore, using the complete test suite increases the

conﬁdence to ﬁnd an error with the test. In the other

cases, the percentage of error detecting test cases is

approximately 99 % for both test suites. However, for

this test criterion, the complete test suite has a higher

error detection capability than the random test suite.

Our partitioning approach reduces the number of

relevant test cases. Therefore, applying the approach

increases the test efﬁciency. The results show that the

error detection capability of the test suite that com-

pletely satisﬁes our multidimensional coverage crite-

ria is signiﬁcantly higher than the capability of the

random test suite. The success of our approach de-

pends on the speciﬁed test criterion as well as on the

deﬁnition of the equivalence classes.

6 CONCLUSION

Due to the large input domain of on-board image

processing applications, an enormous amount of test

cases is possible. This makes it infeasible to capture

the whole input domain and execute the test cases ex-

haustively. In this paper, we have presented a test par-

titioning approach that systematically generates a rea-

sonably small test suite with complete coverage on the

input domain of satellite on-board image processing

applications. To achieve this, we have deﬁned a dedi-

cated partitioning for each input parameter of a satel-

lite on-board image processing application, and we

have deﬁned coverage criteria with respect to the pro-

posed equivalence classes. Based on these individual

coverage criteria, we have furthermore deﬁned mul-

tidimensional coverage criteria, which can be used

to assess a given test suite with respect to its cover-

age on the complete input domain. Finally, we have

presented an automated test generation algorithm that

systematically generates missing test cases according

to our multidimensional coverage criteria. As a result,

our approach is able to fully automatically generate

test suites that are complete with respect to our mul-

tidimensional coverage criteria. The tester speciﬁes

the size of our equivalence classes. This makes our

approach adjustable to available test times and also to

other image processing applications.

We have investigated the effectiveness of our pro-

posed test approach on the FGS algorithm as an ap-

plication with high criticality for the PLATO mission.

In the experiments, our automated test generation al-

gorithm generates a test suite that is complete with

respect to our multidimensional coverage criteria. To

demonstrate the effectiveness of our test approach, we

have compared the error detection capability of a ran-

Test Input Partitioning for Automated Testing of Satellite On-board Image Processing Algorithms

domly generated test suite and the generated complete

test suite. The use of our equivalence classes of the in-

put parameters reduces the number of redundant test

cases in the randomly generated test suite by 87.6 %.

During the experiments, we have successively in-

jected 9 errors in the FGS algorithm code to investi-

gate the error detection capability of both test suites.

We have used two different test criteria: First, a test

case detects an error if the distance between the cal-

culated centroid position and a given position is larger

than a predeﬁned value. Second, a test case detects an

error if the distance of the erroneous calculated po-

sition and an assumed error-free calculated position

exceeds a speciﬁed value. We have observed that dif-

ferent test criteria lead to different test results. For the

ﬁrst test criterion, the complete test suite detects 3 in-

jected errors while the randomly generated test suite

detects 1 injected error. The error detection capability

of the complete test suite is about 3 times higher than

the capability of the randomly generated test suite.

But both test suites do not detect all errors. In another

experiment, we have used the second test criterion.

In this case, not all test cases in the test suites detect

all errors. In the case of 3 injected errors and an un-

intended error, the percentage of error detecting test

cases in the complete test suite is again about 3 times

higher than for the randomly generated test suite. For

the other 6 injected errors, the percentage of error de-

tecting test cases is for both test suites about 99 %.

The experiments showed that a systematic test us-

ing our proposed partitioning approach increases the

error detection capability of a given test suite. This

makes the partitioning approach efﬁcient and effec-

tive. In addition, it facilitates the automated genera-

tion, the execution, and the evaluation of test cases.

So far, we have injected errors in the application

code. But in space, many missions suffer from cos-

mic radiation that ﬂips bits in binary code or cause

hot pixels in input images. We plan to investigate the

efﬁciency of our approach by injecting errors in input

data or in the binary code of the application in future

work. Finally, we have evaluated our approach with

a single application. Later on, we plan to investigate

the ﬂexibility of our approach for other applications,

for example, blob feature extraction in the robotics

domain (Bruce et al., 2000; Merino et al., 2006).

REFERENCES

Bhat, A. and Quadri, S. (2015). Equivalence class par-

titioning and boundary value analysis-a review. In

Intl. Conf. on Computing for Sustainable Global De-

velopment (INDIACom), pages 1557–1562. IEEE.

Bringmann, E. and Kr

amer, A. (2006). Systematic testing

of the continuous behavior of automotive systems. In

International Workshop on Software Engineering for

Automotive Systems, pages 13–20. ACM.

Bruce, J., Balch, T., and Veloso, M. (2000). Fast and

inexpensive color image segmentation for interactive

robots. In IEEE/RSJ Intl. Conf. on Intelligent Robots

and Systems, volume 3, pages 2061–2066. IEEE.

DLR (2017). Gr

unes Licht f

ur europ

aisches Weltraumte-

leskop PLATO. http://www.dlr.de/dlr/desktopdefault.

aspx/tabid-10081/151 read-22858/#/gallery/27241.

ECSS Executive Secretariat (2008). Space engineering.

SpaceWire – Links, nodes, routers and networks.

ESA (2012). ESA’s ’Cosmic Vision’. http://www.esa.int/

Our Activities/Space Science/ESA s Cosmic Vision.

Grießbach, D. (2018). Fine Guidance System Performance

Report. DLR, Berlin.

Huang, W.-l. and Peleska, J. (2016). Complete model-based

equivalence class testing. Intl. Journal on Software

Tools for Technology Transfer, 18(3):265–283.

Kaner, C. (2004). Teaching domain testing: A status re-

port. In Conference on Software Engineering Educa-

tion and Training, pages 112–117. IEEE.

Marcos-Arenal, P., Zima, W., De Ridder, J., Aerts, C., Huy-

gen, R., Samadi, R., Green, J., Piotto, G., Salmon,

S., Catala, C., et al. (2014). The PLATO Simula-

tor: modelling of high-precision high-cadence space-

based imaging. Astronomy & Astrophysics, 566:A92.

Merino, L., Wiklund, J., Caballero, F., Moe, A., De Dios,

J. R. M., Forssen, P.-E., Nordberg, K., and Ollero, A.

(2006). Vision-based multi-UAV position estimation.

IEEE robotics & automation magazine, 13(3):53–62.

PENDER ELECTRONIC DESIGN GmbH (2011). Gr-

xc6s-product sheet.

Peter Liggesmeyer (2009). Software-Qualit

at: Testen,

Analysieren und Veriﬁzieren von Software. Spektrum

Akademischer Verlag, 2 edition.

The HDF Group (April 05, 2018). Hdf5. https://portal.

hdfgroup.org/display/HDF5/HDF5.

Varshney, S. and Mehrotra, M. (2014). Automated software

test data generation for data ﬂow dependencies using

genetic algorithm. International Journal, 4(2).

Witteck, U. (2018). Automated test generation for satellite

on-board image processing. Master thesis, TU Berlin.

ICSOFT 2019 - 14th International Conference on Software Technologies