
Signal Estimation with Random Parameter Matrices and
Time-correlated Measurement Noises
R. Caballero-
´
Aguila
1 a
, A. Hermoso-Carazo
2 b
and J. Linares-P
´
erez
2 c
1
Departamento de Estad
´
ıstica e I.O., Universidad de Ja
´
en, Campus Las Lagunillas s/n, 23071 Ja
´
en, Spain
2
Departamento de Estad
´
ıstica e I.O., Universidad de Granada, Campus Fuentenueva s/n, 18071 Granada, Spain
Keywords:
Least-squares Estimation Algorithms, Filtering, Fixed-point Smoothing, Covariance Information, Random
Parameter Matrices, Time-correlated Noise.
Abstract:
This paper is concerned with the least-squares linear estimation problem for a class of discrete-time networked
systems whose measurements are perturbed by random parameter matrices and time-correlated additive noise,
without requiring a full knowledge of the state-space model generating the signal process, but only information
about its mean and covariance functions. Assuming that the measurement additive noise is the output of a
known linear system driven by white noise, the time-differencing method is used to remove this time-correlated
noise and recursive algorithms for the linear filtering and fixed-point smoothing estimators are obtained by an
innovation approach. These estimators are optimal in the least-squares sense and, consequently, their accuracy
is evaluated by the estimation error covariance matrices, for which recursive formulas are also deduced. The
proposed algorithms are easily implementable, as it is shown in the computer simulation example, where they
are applied to estimate a signal from measured outputs which, besides including time-correlated additive noise,
are affected by the missing measurement phenomenon and multiplicative noise (random uncertainties that can
be covered by the current model with random parameter matrices). The computer simulations also illustrate
the behaviour of the filtering estimators for different values of the missing measurement probability.
1 INTRODUCTION
The signal estimation problem in networked systems
is usually based on measurements that are perturbed
not only by additive noises, but also by other stochas-
tic disturbances from multiple sources, which might
be caused, for example, by the degradation of the
measuring devices or the presence of multiplicative
noises. Such random disturbances are usually inher-
ent to the network itself (network-induced uncertain-
ties) and they must be taken into account in the design
of both the observation models and the estimation al-
gorithms, so as to get proper estimations. For this rea-
son, the study of the estimation problem in this kind
of systems with one or several network-induced un-
certainties has become a hot research topic over the
last years (see e.g. (Gao and Chen, 2014), (Chen
et al., 2015), (Tian et al., 2016), (Caballero-
´
Aguila
et al., 2017), (Zhao et al., 2018), (Liu et al., 2018) and
a
https://orcid.org/0000-0001-7659-7649
b
https://orcid.org/0000-0001-8120-2162
c
https://orcid.org/0000-0002-6853-555X
(Yang et al., 2019)).
The introduction of random parameter matrices in
the mathematical model of the measured outputs pro-
vides a global frame to deal with some of the most
common network-induced uncertainties (multiplica-
tive noise, sensor gain degradation or missing mea-
surements, among others). This fact is boosting the
rise of several estimation algorithms in networked
systems with random parameter matrices under dif-
ferent assumptions about the noises and the processes
involved (see e.g. (Yang et al., 2016), (Sun et al.,
2017), (Wang and Zhou, 2017), (Caballero-
´
Aguila
et al., 2018), (Han et al., 2018) and (Caballero-
´
Aguila
et al., 2019)).
Another relevant issue when addressing the esti-
mation problem is the presence of non-white additive
noises perturbing the sensor measurements. Conven-
tional estimation algorithms usually provide accurate
estimations when the additive noise is either white or
correlated on a finite-time interval. However, we of-
ten come across more general situations involving se-
quentially time-correlated measurement noise, which
is usually the output of a linear system with white
Caballero-Águila, R., Hermoso-Carazo, A. and Linares-Pérez, J.
Signal Estimation with Random Parameter Matrices and Time-correlated Measurement Noises.
DOI: 10.5220/0007807804810487
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 481-487
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
481

noise. The design of recursive estimation algorithms
in this class of systems with time-correlated noise
is addressed, for instance, in (Liu, 2016), (Li et al.,
2017) or (Liu et al., 2017) and the time-differencing
approach is conventionally applied to deal with this
kind of noise correlation.
Bearing these considerations in mind, this paper
addresses the least-squares linear filtering and fixed-
point smoothing problems of discrete-time stochastic
signals under the following conditions:
Covariance Information. The state-space model gen-
erating the signal process is not necessarily known
and only information about its mean and covari-
ance functions are required in its stead.
Random Parameter Matrices. The measured outputs
can be corrupted by random uncertainties, which
are modelled in a comprehensive way by random
parameter matrices.
Time-correlated Measurement Noises. The additive
noise in the measurements is described by a
discrete-time linear model perturbed by white
noise.
The use of the time-differencing approach allows us
to transform the original measured data into an equiv-
alent set of transformed measurements, that are per-
turbed by white noise, and the problem is then re-
duced to find the optimal estimators based on this new
set of observations. For this purpose, the innovation
approach is used and recursive algorithms are derived
for the filtering and fixed-point smoothing problems.
The remainder of this paper is divided into four
sections. The measurement model and the problem
formulation are described in Section 2, where the
time-differencing approach is also detailed. Section
3 discusses the derivation of the filtering and fixed-
point smoothing algorithms, based on the innovation
technique. Section 4 illustrates the application of such
algorithms by a numerical simulation example, where
the performance of the estimators is assessed in terms
of their error variances. Finally, some concluding re-
marks are included in Section 5.
2 PROBLEM FORMULATION
The goal of this paper is to find a recursive algorithm
for the least-squares (LS) linear filtering and fixed-
point smoothing estimators of a discrete-time random
signal from noisy measurements which are perturbed
by random parameter matrices and time-correlated
additive noise vectors. The estimation problem will
be addressed using covariance information; that is, we
will assume that the evolution model of the signal to
be estimated is unknown and only information about
the mean and covariance functions of the signal and
the processes involved in the observation model are
available.
More precisely, consider the following observa-
tion model with random parameter matrices:
z
k
= H
k
x
k
+ v
k
, k ≥ 1, (1)
where, at each sampling time k, x
k
∈ R
n
x
is the signal
vector to be estimated, z
k
∈ R
n
z
is the measurement
vector at time k. The following assumptions on the
processes involved in (1) are required:
(i) {x
k
}
k≥1
, the signal process, has zero mean and
its covariance function is factorized as
E
x
k
x
T
s
= Λ
k
Ψ
T
s
, s ≤ k,
where, for k ≥ 1, Λ
k
,Ψ
k
∈ R
n
x
×n
are known ma-
trices.
(ii) {H
k
}
k≥1
is a sequence of independent random
parameter matrices, whose entries h
k,pq
, for
p = 1, ...,n
z
and q = 1, . . . , n
x
, have known
means, E[h
k,pq
], and second-order moments,
E[h
k,pq
h
k,p
0
q
0
], for p, p
0
= 1,...,n
z
and q,q
0
=
1,...,n
x
.
(iii) {v
k
}
k≥1
is a zero-mean time-correlated noise
process such that
v
k
= A
k−1
v
k−1
+ β
k−1
, k ≥ 1, (2)
where {A
k
}
k≥0
are known matrices, {β
k
}
k≥0
is a
zero-mean white noise with covariance matrices
E[β
k
β
T
k
] = B
k
, and v
0
is a random vector with
zero mean and covariance matrix V
0
.
(iv) The random vector v
0
and the processes
{x
k
}
k≥1
, {H
k
}
k≥1
and {β
k
}
k≥0
are mutually in-
dependent.
2.1 Time-differencing Approach
To address the LS estimation problem from the mea-
sured outputs (1) perturbed by time-correlated addi-
tive noise, such measurements are transformed with
the aim of removing the correlated noise. For that
purpose, the time-differencing approach (Liu, 2016)
is used to define a new set of measurements, whose
additive noise is not time-correlated, according to the
following model:
y
k
= z
k
− A
k−1
z
k−1
, k ≥ 2; y
1
= z
1
. (3)
Then, if we substitute (1) into the above equation and
we use (2) for v
k
, we obtain
y
k
= H
k
x
k
− A
k−1
H
k−1
x
k−1
+ β
k−1
, k ≥ 2;
y
1
= z
1
.
(4)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
482

Remark 1. Note that, since y
h
, for h = 2,. . . , L, is
obtained from z
h−1
and z
h
, the sets {y
1
,...,y
L
} and
{z
1
,...,z
L
} are equivalent in the sense that they can
be obtained one from the other by linear transforma-
tions. Consequently, LS linear estimator of x
k
based
on the original measurements {z
1
,...,z
L
} given in (1)
is just equal to that based on the new measurements
{y
1
,...,y
L
} given in (4). So, in order to address this
estimation problem, the first and second-order statis-
tical properties of the process {y
k
}
k≥1
are necessary.
Remark 2. The assumptions on the model guarantee
that the process {y
k
}
k≥1
given in (4) has zero mean
and its covariance matrices Σ
y
k
≡ E
y
k
y
T
k
, k ≥ 1, sat-
isfy
Σ
y
k
= Σ
Hx
k,k
− Σ
Hx
k,k−1
A
T
k−1
− A
k−1
Σ
Hx
k−1,k
+A
k−1
Σ
Hx
k−1,k−1
A
T
k−1
+ B
k
, k ≥ 2;
Σ
y
1
= Σ
Hx
1
+ A
0
V
0
A
T
0
+ B
0
,
(5)
where Σ
Hx
k,s
≡ E
H
k
x
k
x
T
s
H
T
s
is given by
Σ
Hx
k,s
= E[H
k
Λ
k
Ψ
T
s
H
T
s
] =
H
k
Λ
k
Ψ
T
s
H
T
s
, s < k,
E[H
k
Λ
k
Ψ
T
k
H
T
k
], s = k,
(6)
with H
k
≡ E[H
k
], k ≥ 1, and the (p, p
0
)-th entries of
the above matrices E[H
k
Λ
k
Ψ
T
k
H
T
k
] are calculated by
E
H
k
Λ
k
Ψ
T
k
H
T
k
pp
0
=
n
x
∑
q=1
n
x
∑
q
0
=1
E[h
k,pq
h
k,p
0
q
0
](Λ
k
Ψ
T
k
)
qq
0
, p, p
0
= 1,. . . , n
z
.
3 LS LINEAR ESTIMATION
ALGORITHMS
Given the set of measurements {y
1
,...,y
L
} in (4), the
aim in this Section is to design recursive algorithms
for the optimal estimators
b
x
k/L
within the class of lin-
ear estimators of the signal x
k
, based on these mea-
surements, using the LS optimality criterion. Specif-
ically, recursive algorithms for the filter,
b
x
k/k
, and
smoother,
b
x
k/k+N
, at the fixed point k for any N ≥ 1,
will be obtained.
3.1 Preliminary Results
Since the LS linear estimator of the signal,
b
x
k/L
, is
the orthogonal projection of the signal x
k
over the lin-
ear space spanned by the observations
{
y
1
,...,y
L
}
,
which generally are non-orthogonal vectors, to ob-
tain the estimation algorithms we will use a inno-
vation approach (Kailath et al., 2000). According
to such approach, the observation process {y
k
}
k≥1
is
transformed into an equivalent one, named innova-
tion process, of orthogonal vectors {µ
k
}
k≥1
, defined
by µ
k
= y
k
−
b
y
k/k−1
, where
b
y
k/k−1
is the orthogonal
projection of y
k
onto the linear space generated by
{
µ
1
,...,µ
k−1
}
, with
b
y
1/0
= E[y
1
] = 0.
Therefore, the LS linear estimator,
b
α
k/L
, of
any random vector α
k
based on the observations
{y
1
,...,y
L
}, can be calculated as a linear combina-
tion of the corresponding innovations, {µ
1
,...,µ
L
}.
Namely, denoting Π
h
= E[µ
h
µ
T
h
], the LS linear esti-
mator
b
α
k/L
is expressed as the following linear com-
bination of the innovations:
b
α
k/L
=
L
∑
h=1
E[α
k
µ
T
h
]Π
−1
h
µ
h
. (7)
3.1.1 Observation Predictor
Starting from expression (4) of the observations y
k
,
and taking into account that H
k−1
is correlated with
the innovation µ
k−1
, to obtain the predictor
b
y
k/k−1
the
observations y
k
are rewritten as follows:
y
k
= H
k
x
k
− A
k−1
H
k−1
x
k−1
+W
k−1
, k ≥ 2, (8)
where W
k
= β
k
− A
k
H
k
− H
k
x
k
, k ≥ 1.
Then, according to the projection theory, we have:
b
y
k/k−1
= H
k
b
x
k/k−1
− A
k−1
H
k−1
b
x
k−1/k−1
+
b
W
k−1/k−1
.
Now, to obtain the estimator
b
W
k/k
we use the gen-
eral expression (7). Since H
k
is independent of
µ
1
,...,µ
k−1
, it is easy to see that E[W
k
µ
T
h
] = 0, for
h < k, hence, denoting W
k
≡ E
W
k
µ
T
k
, from (7) we
have that
b
W
k/k
= W
k
Π
−1
k
µ
k
, k ≥ 1. So, the observa-
tion predictor
b
y
k/k−1
satisfy:
b
y
k/k−1
= H
k
b
x
k/k−1
− A
k−1
H
k−1
b
x
k−1/k−1
+W
k−1
Π
−1
k−1
µ
k−1
, k ≥ 2.
(9)
Now, we derive an expression for W
k
= E
W
k
µ
T
k
.
Since E[W
k
µ
T
h
] = 0, for h < k, it is clear that W
k
=
E
W
k
y
T
k
. Using (8) for y
k
, we have that E
W
k
y
T
k
=
E
W
k
x
T
k
H
T
k
, and, from the definition of W
k
, we ob-
tain that W
k
= E
W
k
µ
T
k
is calculated by
W
k
= −A
k
Σ
Hx
k,k
− H
k
Λ
k
Ψ
T
k
H
T
k
, k ≥ 1, (10)
where Σ
Hx
k,k
is given in (6).
3.2 LS Linear Filtering Algorithm
The starting points to derive the proposed LS linear
recursive algorithm for the filtering estimators,
b
x
k/k
,
are the general expression (7) for the estimators as
linear combination of the innovations, along with ex-
pression (9) for the one-stage observation predictor.
Also, a recursive formula for the filtering error co-
variance matrices, Σ
k/k
≡ E
(x
k
−
b
x
k/k
)(x
k
−
b
x
k/k
)
T
,
is obtained in this Section. These covariance matrices
are used to assess the accuracy of the filtering estima-
tors
b
x
k/k
when the LS criterion is used.
Signal Estimation with Random Parameter Matrices and Time-correlated Measurement Noises
483

3.2.1 Signal Filtering Estimators
From the general expression (7), obtaining the signal
filter,
b
x
k/k
=
k
∑
h=1
X
k,h
Π
−1
h
µ
h
, k ≥ 1, requires calcula-
ting the coefficients
X
k,h
≡ E
x
k
µ
T
h
= E
x
k
y
T
h
−E
x
k
b
y
T
h/h−1
, 1 ≤ h ≤ k.
Expression (4) for y
h
and the separable form of
the signal covariance, specified in assumption (i), lead
easily to
E[x
k
y
T
h
] = Λ
k
H
h
Ψ
h
− A
h−1
H
h−1
Ψ
h−1
T
, k ≥ 2;
E[x
k
y
T
1
] = Λ
k
H
1
Ψ
1
.
(11)
From now on, the following operator will be used
for notational simplicity:
H
ϒ
k
≡ H
k
ϒ
k
− A
k−1
H
k−1
ϒ
k−1
, k ≥ 2;
H
ϒ
1
≡ H
1
ϒ
1
,
(12)
and it will be applied to the matrices ϒ
k
= Λ
k
and
ϒ
k
= Ψ
k
that define the signal covariance function
(see assumption (i)).
Then, from (11) and (12), it is clear that
E
x
k
y
T
h
= Λ
k
H
T
Ψ
h
, 1 ≤ h ≤ k,
and, using (9) for
b
y
h/h−1
, together with (7) for
b
x
h/h−1
and
b
x
h−1/h−1
, the following expression for the filter
coefficients is obtained:
X
k,h
= Λ
k
H
T
Ψ
h
−
h−1
∑
j=1
X
k, j
Π
−1
j
H
h
X
h, j
+ A
k−1
H
h−1
X
h−1, j
T
−X
k,h−1
Π
−1
h−1
W
T
h−1
, 2 ≤ h ≤ k;
X
k,1
= Λ
k
H
T
B
1
.
Hence, if we define a function E
h
satisfying
E
h
= H
T
Ψ
h
−
h−1
∑
j=1
E
j
Π
−1
j
E
T
j
H
T
Λ
h
−E
h−1
Π
−1
h−1
W
T
h−1
, h ≥ 2;
E
1
= H
T
Ψ
1
,
we obtain that the coefficients X
k,h
can be expressed
as follows:
X
k,h
= Λ
k
E
h
, 1 ≤ h ≤ k.
So, by defining the vectors
e
k
≡
k
∑
h=1
E
h
Π
−1
h
µ
h
, k ≥ 1,
and using (7) for
b
x
k/k
, it is clear that the signal filtering
estimators are given by
b
x
k/k
= Λ
k
e
k
, k ≥ 1.
Now, using this expression and defining
K
e
k
≡ E
e
k
e
T
k
=
k
∑
h=1
E
h
Π
−1
h
E
T
h
, k ≥ 1,
a formula for the filtering error covariance matrix
Σ
k/k
is derived. Actually, from the Orthogonal Pro-
jection Lemma (OPL), we rewrite Σ
k/k
= E
x
k
x
T
k
−
E
b
x
k/k
b
x
T
k/k
; then, since E
b
x
k/k
b
x
T
k/k
= Λ
k
K
e
k
Λ
T
k
, using
assumption (i) for E
x
k
x
T
k
, we have
Σ
k/k
= Λ
k
(Ψ
k
− Λ
k
K
e
k
)
T
, k ≥ 1.
Bearing in mind the preceding results, using the
OPL to write the innovation covariance matrix as
Π
k
= E[y
k
y
T
k
] − E[
b
y
k/k−1
b
y
T
k/k−1
],
and taking into account that E[
b
y
k/k−1
e
T
k−1
] = H
T
Ψ
k
−
E
k
, the recursive filtering algorithm below can be de-
duced without trouble.
3.2.2 Recursive Filtering Algorithm
Under hypotheses (i)-(iv), the LS linear filter,
b
x
k/k
,
and the corresponding error covariance matrix, P
k/k
,
are given by
b
x
k/k
= Λ
k
e
k
, k ≥ 1
Σ
k/k
= Λ
k
Ψ
k
− Λ
k
K
e
k
T
, k ≥ 1,
where the vectors e
k
and the matrices K
e
k
= E[e
k
e
T
k
]
are recursively obtained from
e
k
= e
k−1
+ E
k
Π
−1
k
µ
k
, k ≥ 1; e
0
= 0,
K
e
k
= K
e
k−1
+ E
k
Π
−1
k
E
T
k
, k ≥ 1; K
e
0
= 0,
and the matrices E
k
= E[e
k
µ
T
k
] satisfy
E
k
= H
T
Ψ
k
− K
e
k−1
H
T
Λ
k
− E
k−1
Π
−1
k−1
W
T
k−1
, k ≥ 2;
E
1
= H
T
Ψ
1
.
The innovations, µ
k
, are given by
µ
k
= y
k
− H
Λ
k
e
k−1
− W
k−1
Π
−1
k−1
µ
k−1
, k ≥ 2;
µ
1
= y
1
,
and the innovation covariance matrices, Π
k
, are ob-
tained by
Π
k
= Σ
y
k
−
H
Λ
k
(H
T
Ψ
k
− E
k
)
−W
k−1
Π
−1
k−1
H
Λ
k
E
k−1
+ W
k−1
T
, k ≥ 2;
Π
1
= Σ
y
1
.
The vectors y
k
are given in (3), and the matrices Σ
y
k
and W
k
are calculated by expressions (5) and (15),
respectively. Finally, the notations H
Λ
k
and H
Ψ
k
are
defined in (12).
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
484

3.3 LS Linear Smoothing Algorithm
The goal in this Section is to derive a recursive algo-
rithm for the LS linear smoothing estimators,
b
x
k/k+N
,
at the fixed point k, for any N ≥ 1, as well as, a recur-
sive formula for the smoothing error covariance ma-
trices, Σ
k/k+N
≡ E
(x
k
−
b
x
k/k+N
)(x
k
−
b
x
k/k+N
)
T
.
3.3.1 Recursive Fixed-point Smoothing
Algorithm
Under hypotheses (i)-(iv), for each k ≥ 1, the LS li-
near fixed-point smoothers,
b
x
k/k+N
, N ≥ 1, are calcu-
lated by
b
x
k/k+N
=
b
x
k/k+N−1
+ X
k,k+N
Π
−1
k+N
µ
k+N
, N ≥ 1,
(13)
with initial condition given by the filter,
b
x
k/k
.
The matrices X
k,k+N
≡ E
x
k
µ
T
k+N
are recursively
obtained by
X
k,k+N
=
Ψ
k
− M
k,k+N−1
H
T
Λ
k+N
−X
k,k+N−1
Π
−1
k+N−1
W
T
k+N−1
, N ≥ 1;
X
k,k
= Λ
k
E
k
,
(14)
where M
k,k+N
≡ E[x
k
e
T
k+N
] satisfy the following re-
cursive formula
M
k,k+N
= M
k,k+N−1
+ X
k,k+N
Π
−1
k+N
E
T
k+N
, N ≥ 1;
M
k,k
= Λ
k
K
e
k
.
(15)
The fixed-point smoothing error covariance matrices,
Σ
k/k+N
, are obtained by
Σ
k/k+N
= Σ
k/k+N−1
− X
k,k+N
Π
−1
k+N
X
T
k,k+N
, N ≥ 1,
with initial condition given by the filtering error co-
variance matrix Σ
k/k
.
3.3.2 Smoothing Algorithm Derivation
Using the general expression (7), the smoothing esti-
mators are written as
b
x
k/k+N
=
k+N
∑
h=1
X
k,h
Π
−1
h
µ
h
, N ≥ 1;
hence, it is clear that, starting from the filter,
b
x
k/k
, the
fixed-point smoothing estimators are recursively ob-
tained by (13).
To obtain the recursive relation (14) for X
k,k+N
=
E
x
k
y
T
k+N
−E
x
k
b
y
T
k+N/k+N−1
, N ≥ 1, we proceed as
follows:
− On the one hand, the assumption (i) together with
(12), yield
E
x
k
y
T
k+N
= Ψ
k
H
T
Λ
k+N
.
− On the other, using that
b
y
k/k−1
= H
Λ
k
e
k−1
+ W
k−1
Π
−1
k−1
µ
k−1
,
it is clear that
E
x
k
b
y
T
k+N/k+N−1
= E
x
k
e
T
k+N−1
H
T
Λ
k+N
+X
k,k+N−1
Π
−1
k+N−1
W
T
k+N−1
, N ≥ 1.
Therefore, denoting M
k,k+N
= E
x
k
e
T
k+N
, expression
(14) holds and, using the recursive relation for the
vectors e
k
, given in the filtering algorithm, the recur-
sive expression (15) for the matrices M
k,k+N
is also
straightforward.
Finally, using (13) for the smoothers
b
x
k/k+N
, the
recursive formula for the fixed-point smoothing error
covariance matrices, Σ
k/k+N
, is immediately deduced,
and the smoothing algorithm is proven.
4 COMPUTER SIMULATION
RESULTS
This section analyzes a numerical simulation example
to illustrate the application of the recursive filtering
and fixed-point smoothing algorithms proposed in the
current paper.
Specifically, we consider that the signal to be es-
timated is a scalar signal {x
k
}
k≥1
which is generated
by the following first-order autoregressive model
x
k+1
= 0.95x
k
+ ω
k
, k ≥ 1,
where {ω
k
}
k≥1
is a zero-mean white Gaussian noise
with constant variance Var[ω
k
] = 0.1, for all k. The
autocovariance function of this signal is
E[x
k
x
s
] = 1.025641 × 0.95
k−s
, s ≤ k
which, in accordance with the assumption (i) on
the theoretical model, can be factorized in a semi-
degenerate kernel form, taking, for example,
Λ
k
= 1.025641 × 0.95
k
, Ψ
k
= 0.95
−k
.
The measured outputs of this signal are assumed
to be described by the following model with missing
measurements and multiplicative noise:
z
k
= θ
k
(1 + 0.9ε
k
)x
k
+ v
k
, k ≥ 1,
where
θ
k
k≥1
is a sequence of independent
Bernoulli random variables with constant probabili-
ties, P
θ
k
= 1
= θ. Hence 1 − θ is the probability
that the signal is absent in the measurements; that is,
the missing measurement probability. The multiplica-
tive noise,
ε
k
k≥1
, is a zero-mean Gaussian white
process with unit variance.
The additive noise, {v
k
}
k≥1
, is a zero-mean time-
correlated noise process such that
v
k
= 0.4v
k−1
+ β
k−1
, k ≥ 1,
Signal Estimation with Random Parameter Matrices and Time-correlated Measurement Noises
485
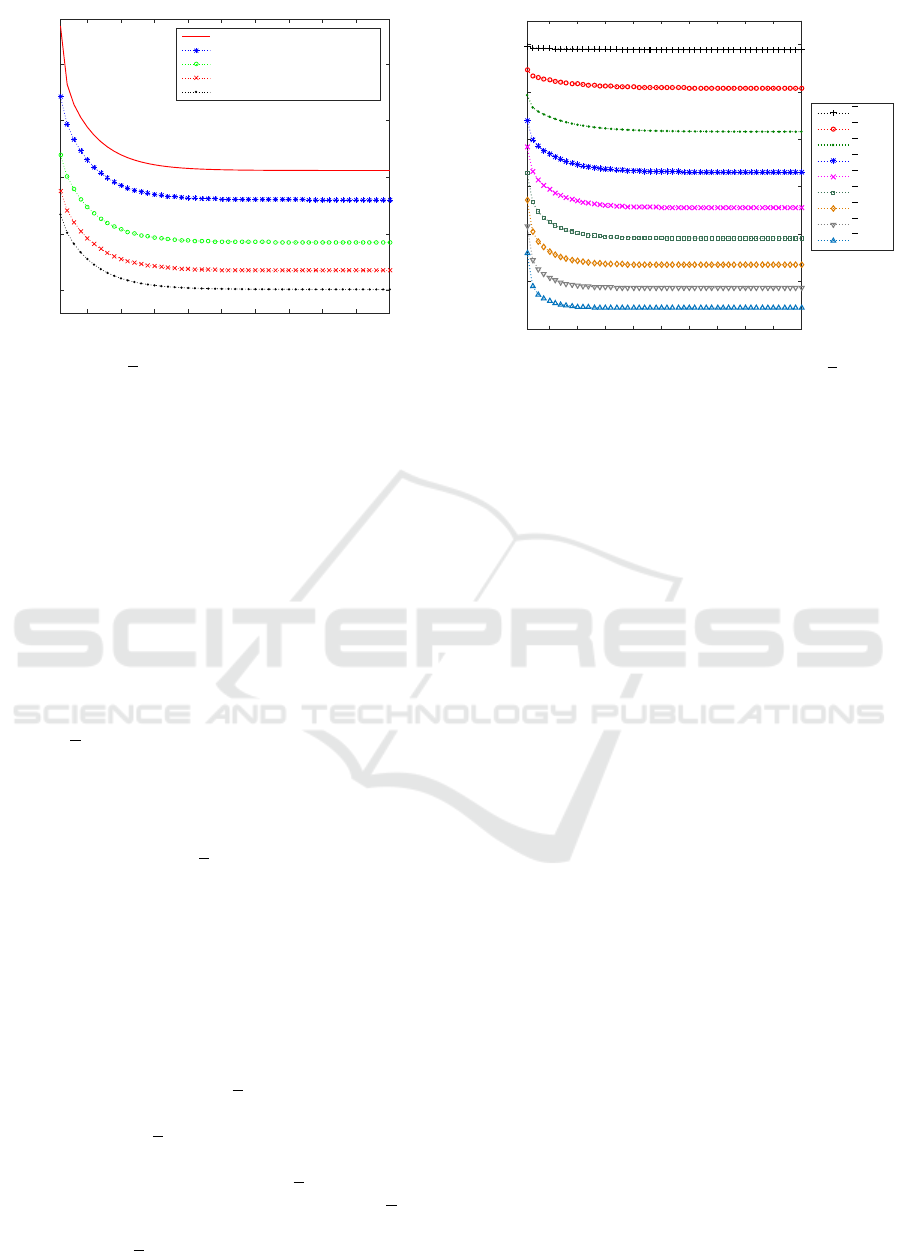
Time k
5 10 15 20 25 30 35 40 45 50
0.55
0.6
0.65
0.7
0.75
Filtering error variances, Σ
k/k
Smoothing error variances, Σ
k/k+1
Smoothing error variances, Σ
k/k+3
Smoothing error variances, Σ
k/k+5
Smoothing error variances, Σ
k/k+7
Figure 1: Error variance comparison of the filter and
smoothers, when θ = 0.5.
where {β
k
}
k≥0
is also a zero-mean Gaussian white
process with unit variance, and v
0
is a standard gaus-
sian random variable.
Finally, we assume that the processes involved in
the system model satisfy the independence hypothe-
ses assumptions imposed on the theoretical model.
The proposed algorithms have been implemented
in a MATLAB program to obtain the filtering and
fixed-point smoothing estimators, as well as the cor-
responding estimation error variances. Fifty iterations
of this program have been run to show the feasibil-
ity and effectiveness of the proposed estimation algo-
rithms. The estimation accuracy has been examined
by analyzing the error variances for different proba-
bilities, θ, of the Bernoulli variables modelling the
missing measurement phenomenon.
Performance of the Filtering and Smoothing Estima-
tors. The performance of the proposed LS linear es-
timators, measured by the estimation error variances,
has been assessed when θ = 0.5. The error variances
of both filtering and smoothing estimators are dis-
played in Figure 1 which shows that the error vari-
ances corresponding to the smoothers are less than
those of the filters (and, consequently, the perfor-
mance of the smoothing estimators is better), as it
could be expected. From this figure it is also gath-
ered that the estimation accuracy of the smoothers at
each fixed-point, k, becomes better as the number of
available observations increases.
Influence of the Probability θ. Analogous results to
those shown in Figure 1 are obtained for other values
of the probability θ that the signal is present in the
measurements. A global analysis of the filtering er-
ror variances versus the probability
θ is presented in
Figure 2. From this figure, it is inferred that as θ de-
creases (and, consequently, the missing measurement
probability, 1 − θ, increases) the filtering error vari-
Time k
5 10 15 20 25 30 35 40 45 50
Filtering error variances
0.4
0.5
0.6
0.7
0.8
0.9
1
θ = 0.1
θ = 0.2
θ = 0.3
θ = 0.4
θ = 0.5
θ = 0.6
θ = 0.7
θ = 0.8
θ = 0.9
Figure 2: Filtering error variances versus θ.
ance becomes greater and, hence, as expected, worse
estimations are obtained. Similar results are deduced
for the fixed-point smoothers.
5 CONCLUSIONS
Based on the LS optimality criterion, optimal algo-
rithms have been designed for the linear filtering and
fixed-point smoothing estimators of discrete-time ran-
dom signals using measured outputs with random pa-
rameter matrices and time-correlated additive noise.
The use of random parameter matrices yields a widely
applicable measurement model, which is suitable to
cope with different network-induced uncertainties in
the sensor measurements. The additive measurement
noise is assumed to obey a dynamic linear equation
corrupted by white noise. As it is usual in these
situations, the time-differencing approach has been
adopted to define, at each sampling time, an equiv-
alent measurement, which is a linear combination of
two consecutive measurements. After this transfor-
mation, we get an equivalent set of measurements,
where the time-correlation of the noise has been elim-
inated. Since the LS estimators of the signal based on
the original set of observations is equal to that based
on the new set of transformed observations, the orig-
inal estimation problem is simplified and reduced to
that of designing recursive algorithms for the filter-
ing and fixed-point smoothing estimators of the sig-
nal based on the transformed measurements. The al-
gorithm design has been carried out by an innova-
tion approach and without requiring the knowledge
of the signal evolution model, but only the first and
second-order moments of the processes involved in
the measurement model. To conclude, some com-
puter simulations have shown how the proposed al-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
486

gorithms are applicable to some common engineering
problems, involving missing measurements and mul-
tiplicative noise, which satisfy the system model un-
der consideration.
ACKNOWLEDGEMENTS
This research is supported by Ministerio de
Econom
´
ıa, Industria y Competitividad, Agencia
Estatal de Investigaci
´
on and Fondo Europeo de
Desarrollo Regional FEDER (grant no. MTM2017-
84199-P).
REFERENCES
Caballero-
´
Aguila, R., Garc
´
ıa-Garrido, I., and Linares-
P
´
erez, J. (2018). Distributed fusion filtering
for multi-sensor systems with correlated random
transition and measurement matrices. Interna-
tional Journal of Computer Mathematics, DOI:
10.1080/00207160.2018.1554213.
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2017). Covariance-based fusion filtering for
networked systems with random transmission delays
and non-consecutive losses. International Journal of
General Systems, 46(7):752–771.
Caballero-
´
Aguila, R., Hermoso-Carazo, A., and Linares-
P
´
erez, J. (2019). Centralized filtering and smoothing
algorithms from outputs with random parameter ma-
trices transmitted through uncertain communication
channels. Digital Signal Processing, 85:77–85.
Chen, B., Zhang, W., Hu, G., and Yu, L. (2015). Net-
worked fusion Kalman filtering with multiple uncer-
tainties. IEEE Transactions on Aerospace and Elec-
tronic Systems, 51(3):2332–2349.
Gao, S. and Chen, P. (2014). Suboptimal filtering of net-
worked discrete-time systems with random observa-
tion losses. Mathematical Problems in Engineering,
ID 151836.
Han, F., Dong, H., Wang, Z., Li, G., and Alsaadi, F. E.
(2018). Improved tobit Kalman filtering for systems
with random parameters via conditional expectation.
Signal Processing, 147:35–45.
Kailath, T., Sayed, A. H., and Hassibi, B. (2000). Linear
estimation. Prentice Hall, Upper Saddle River, New
Jersey.
Li, W., Jia, Y., and Du, J. (2017). Distributed filtering
for discrete-time linear systems with fading measure-
ments and time-correlated noise. Digital Signal Pro-
cessing, 60:211–219.
Liu, A. (2016). Recursive filtering for discrete-time linear
systems with fading measurement and time-correlated
channel noise. Journal of Computational and Applied
Mathematics, 298:123–137.
Liu, W., Shi, P., and Pan, J. S. (2017). State estimation for
discrete-time Markov jump linear systems with time-
correlated and mode-dependent measurement noise.
Automatica, 85:9–21.
Liu, W., Wang, X., and Deng, Z. (2018). Robust centralized
and weighted measurement fusion Kalman predictors
with multiplicative noises, uncertain noise variances,
and missing measurements. Circuits, Systems and Sig-
nal Processing, 37:770–809.
Sun, S., Tian, T., and Lin, H. (2017). State estimators
for systems with random parameter matrices, stochas-
tic nonlinearities, fading measurements and correlated
noises. Information Sciences, 397–398:118–136.
Tian, T., Sun, S., and Li, N. (2016). Multi-sensor informa-
tion fusion estimators for stochastic uncertain systems
with correlated noises. Information Fusion, 27:126–
137.
Wang, W. and Zhou, J. (2017). Optimal linear filtering de-
sign for discrete time systems with cross-correlated
stochastic parameter matrices and noises. IET Con-
trol Theory & Applications, 11(18):3353–3362.
Yang, C., Yang, Z., and Deng, Z. (2019). Robust weighted
state fusion Kalman estimators for networked sys-
tems with mixed uncertainties. Information Fusion,
45:246–265.
Yang, Y., Liang, Y., Pan, Q., Qin, Y., and Yang, F. (2016).
Distributed fusion estimation with square-root array
implementation for Markovian jump linear systems
with random parameter matrices and cross-correlated
noises. Information Sciences, pages 446–462.
Zhao, Y., He, X., and Zhou, D. (2018). Distributed filter-
ing for time-varying networked systems with sensor
gain degradation and energy constraint: a centralized
finite-time communication protocol scheme. Science
China Information Sciences, 61: 092208:1–15.
Signal Estimation with Random Parameter Matrices and Time-correlated Measurement Noises
487
