Camera and Lidar Cooperation for 3D Feature Extraction

Burtin Gabriel

, Bonnin Patrick

and Malartre Florent

4D-Virtualiz, 10 Allee Evariste Galois, Clermont-Ferrand, France

LISV, Universite de Versailles St Quentin, 10-12 Avenue de l’Europe Velizy, France

Keywords:

Line Segment Detection, Algorithm Optimization, Camera-lidar Sensor Fusion, Localization, Extended

Kalman Filter.

Abstract:

The objective of this work is to use efﬁciently various sensors to create a SLAM system. This algorithm

has to be fast (real-time), computationally light and efﬁcient enough to allow the robot to navigate in the

environment. Because other processes embedded require large amount of cpu-time, our objective was to use

efﬁciently complementary sensors to obtain a fairly accurate localization with minimal computation. To reach

this, we used a combination of two sensors: a 2D lidar and a camera, mounted above each other on the robot

and oriented toward the same direction. The objective is to pinpoint and cross features in the camera and

lidar FOV. Our optimized algorithms are based on segments detection. We decided to observe intersections

between vertical lines seen with the camera and locate them in 3D with the ranges provided by the 2D lidar.

First we implemented a RGB vertical line detector using RGB gradient and linking process, then a lidar data

segmentation with accelerated computation and ﬁnally we used this feature detector in a Kalman ﬁlter. The

ﬁnal code is evaluated and validated using an advanced real-time robotic simulator and later conﬁrmed with a

real experiment.

1 INTRODUCTION

The robot of the future is built to work in the new

hi-tech ”factory”. It is given tasks to complete in

a cluttered, yet structured and human environment.

To complete these tasks, the robot must move be-

tween locations, with a possibility of encountering

humans. We need a navigation system to able to

work fast, be reliable and take advantage of the struc-

tured characteristic of the environment. This problem

can be divided in sub-tasks: localization, mapping,

path-planning, control and safety management. All

these tasks must be performed within an embedded

computation unit on the robot. This means that each

task must consume computational resources as little

as possible. On the other hand, the robot is moving

and needs a regular update on its status. The goal is

to reduce computation cost induced by each element

of the navigation system. The concept of localiza-

tion is to give the robot an idea of ”where” it is on

a map. This map can be either known previously or

built during the robot evolution in the environment,

also known as SLAM (simultaneous localization and

mapping (Durrant-Whyte and Bailey, 2006)).

In our case, the environment is human made, com-

posed of a ﬂat ﬂoor, rooms with various sizes, shapes

and furniture, all of them connected though hallways.

This environment is likely to be an hospital, a factory

or ofﬁces, thus it is populated and traveled by humans

at all times. The place is neither collaborative (we

don’t use man-made landmarks) nor hostile (nothing

is going to make an attempt at putting the robot out of

action). Humans are considered as ”passive” distur-

bance and are not likely actively trying to break the

robot. Human detection and handling have yet to be

done but are not part of this work; however, they have

direct effects on the degrees of freedom. These two

steps are indeed achieved through the analysis of sen-

sor data provided by a camera. As we can see, one

sensor is already decided. This human detection pro-

cess is particularly CPU-consuming and have priority

(safety is the most important task), therefore, the CPU

time allowed to our algorithm is reduced. This low-

ered CPU time availability is a major constraint to be

taken into account in the design of our localization

method.

First we will have a look at previous and related

work, then we will detail the vision and lidar process

followed by an implementation of this feature extrac-

tor in a SLAM algorithm using an Extended Kalman

Gabriel, B., Patrick, B. and Florent, M.

Camera and Lidar Cooperation for 3D Feature Extraction.

DOI: 10.5220/0007808900230033

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 23-33

ISBN: 978-989-758-380-3

Filter. At last, the performances are ﬁrst evaluated us-

ing an advanced real-time robotic simulator (Burtin

et al., 2016), then with a real robot/sensor set-up.

2 RELATED WORK

Using segments to perform SLAM processing have

been explored either with a lone lidar (Roumelio-

tis and Bekey, 2000), (Choi et al., 2008) or camera

alone (Huang, 2008), (Lemaire and Lacroix, 2007),

(Micusik and Wildenauer, 2015), (Zuo et al., 2017).

SLAMs are generally split between sparse and dense

vision algorithms. Sparse SLAMs are using only a

few salient features in the image to compute the lo-

calization, for example the ORB-SLAM (Mur-Artal

et al., 2015). Each feature is represented and stored

speciﬁcally in the map to be used later as reference

in the localization algorithm. These types of process

only need a small percentage of the pixels from the

entire image to be tracked, while dense methods use

almost all the pixels. Because dense methods such

as DTAM (Newcombe et al., 2011) uses every pixels

from the image, users need a powerful hardware to

perform all the operations in real-time. Most of the

time, GPU processing is used to improve the compu-

tation speed. RGB-D (Kinect, Xtion) and depth cam-

era sensors brought new SLAMs systems (Engelhard

et al., 2011), (Schramm et al., 2018), with new ap-

proaches. They avoid the issue of initialization from

unknown range for the features. Monocular cameras

have the weakness to be unable, using only one frame,

to obtain the distance between an object and the cam-

era for its given pixel in the image (scale effect). LSD

(Von Gioi et al., 2012) is massively used by monoc-

ular and stereo-vision SLAMs systems (Engel et al.,

2014) or (Pumarola et al., 2017) but this line segment

detector is too generic and extracts all segments avail-

able while processing only B&W images: the pro-

cess is not optimized enough. Moreover, the RGB to

B&W conversion is a potential danger of missing gra-

dients because of the gray level conversion method.

The idea to use both lidar and monocular camera has

been more usually applied to mobile objects detec-

tion and tracking (Premebida et al., 2007), (Asvadi

et al., 2016), (De Silva et al., 2018) but more rarely

to localization itself. In our case, we will focus on

the detection of vertical lines in the camera because

they are commonly found and invariants regarding our

environment. The common slam, using these types

of features are commonly referred as ”bearing” only

slam (Bekris et al., 2006), they are proven effective in

minimalist set-ups with simple environments (Huang,

2008), (Choi et al., 2008), (Zuo et al., 2017).

In order to extract these vertical segments in the

image (which are supposed to be the projection of 3D

vertical structures of the scene: doors, angles of corri-

dors), we are looking for classical edge segmentation

composed of well known steps (Nachar et al., 2014):

1. gradient computation ;

2. thinning ;

3. closing ;

4. linking ;

5. and polygonal approximation.

The gradient computation being the most time

consuming step, we will detail the choice of the

appropriate algorithm in this section, its adaptation

and its time optimized implementation (Cabrol et al.,

2005) in the next section.

The gradient computation algorithms could be

classiﬁed into three categories, according to their

complexity, and the size of the neighborhood:

• 2 × 2: Roberts (Roberts, 1965) proposed in the

60’s;

• 3 × 3: Prewitt (Prewitt, 1970), Sobel (Sobel,

1978) and Kirsh (Kirsch, 1971) in the 70’s;

• JF Canny ((Canny, 1983)) (in OpenCV),

R.Deriche ((Deriche, 1987)) in the 80’s.

Although better quality results are obtained by algo-

rithms of the last category, the best compromise be-

tween the quality of results and the sum of computa-

tions, for our real-time and embedded robotic appli-

cation, is given by the second one.

The principle of Prewitt and Sobel algorithms is to

compute the projection of the gradient

−→

G on the axis

of the image:

−→

and

−→

ﬁrst and, then, to perform a

rectangular to polar transformation to obtain:

• the gradient magnitude, which is the reﬂect of the

transition between two regions;

• the gradient argument, which is orthogonal to the

local edge direction. This information is reduced

to the knowledge of direction of the neighbor

pixel in the orthogonal direction of the edge for

the thinning step, ie. four directions.

−→

G || =

(

−→

G .

−→

)

+ (

−→

G .

−→

)

Arg(

−→

G ) = arctan

−→

G .

−→

G .

−→

In order to obtain quite same results, and avoid

the computations (in double ﬂoats if done without ap-

proximation) of the rectangular to polar transform,

Kirh introduced two diagonal direction of projection:

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

−→

and

−−→

−45

. Thus the gradient magnitude was ap-

proximated by the longer projection, and the argu-

ment by the Freeman code corresponding to the best

projection.

−→

G || = Max{|

−→

G .

−→

|,|

−→

G .

−→

|,|

−→

G .

−→

|,|

−→

G .

−−→

−45

Arg(

G) =











0, if ||

−→

G || = |

−→

G .

−→

6, if ||

−→

G || = |

−→

G .

−→

1, if ||

−→

G || = |

−→

G .

−→

7, if ||

−→

G || = |

−→

G .

−−→

−45

Another way, which seems to be promising, is to

use Edgels or Line Segment Detectors: small edge

segments are gathered into bigger ones using region

growing algorithms.

3 APPROACH

The most important statement considering our hy-

pothesis is the fact that the robot is evolving in a

man-made environment, comparable to an industry

(factory) or ofﬁce/hospital type. We state that the

robot will encounter numerous structured elements

with strong vertical and horizontal lines. Consider-

ing a ﬂat ﬂoor, we also assume that the movement

is only 2D. With this new assumption and the previ-

ous one, we can narrow features to propose a sparse

localization method using speciﬁc landmarks. The

most invariant observable elements in the image, as

explained before, are going to be the vertical lines. 3D

horizontal and other more random lines would have

an incidence angle due to the point of view of the

camera and wouldn’t be invariant in the image, thus

inducing more computation to detect and track them.

The localization process is an optimized parallel

pipeline able to cross data from the lidar and camera

sensors (Figure: 1). Each data process is split, but

synchronous to use both extracted data at the same

moment during the feature extraction stage. The ob-

jective is to detect a feature and determine its 3D po-

sition in the camera frame. The camera process ex-

tracts vertical lines in the image while the lidar pro-

cess does a segmentation and a time-forward predic-

tion to match the camera’s data time-stamp.

The lidar, placed horizontally on the robot, pro-

duces an horizontal plane with the successive dis-

tances measurements. Our lidar process produces,

through the lidar segmentation algorithm, a set of

lines representing the environment around our robot.

The camera, located above the lidar, through the lines

detection algorithm, extracts a set of vertical lines in

the focal plane of the image. The fusion of both of

these data gives us a set of 3D points in the camera

frame (Figure: 2).

Figure 1: System overview.

Figure 2: Feature (P) detected in the focal and lidar plane.

First we will see the optimized vertical lines de-

tection algorithm for images processing.

Then we will develop the 3D points extraction

process using the camera vertical features and the hor-

izontal lines from the lidar process.

In the end, we will propose a SLAM implemen-

tation using the extracted features from the previous

processes.

3.1 Vision Process

Our goal is to extract vertical segments for a real time

vision system on a small robot. Although general pur-

pose edge detectors exist, and we implement several

kinds by ourselves (Cabrol et al., 2005), they are not

optimal in our particular case.

If we refer to the quicker general purpose method

proposed by Kirsh, the use of the horizontal mask

which detects horizontal gradient ie. local vertical

edge, is sufﬁcient. This simple remark allows to di-

vide by more than four (one mask compared to four

masks computation and the selection) the required

computing time.

In the same manner all the following steps: thin-

Camera and Lidar Cooperation for 3D Feature Extraction

ning, closing, linking, and polygonal approximation

are simpliﬁed (Nachar et al., 2014), and could be run

faster:

• for the thinning step: only the horizontal left

neighbor pixel is considered;

• for the closing step: only the one vertical neigh-

bor, depending on the direction of the edge is re-

cursively followed;

• for the polygonal approximation: this step is

wholly simpliﬁed, because only vertical segments

are taken into account. There is only one vertical

segment by edge, so there is no need to compute

a distance between the edge and the segment in

order to cut the edge into several segments consti-

tuting the polygonal line.

The adaptation from B&W to RGB edge segmen-

tation which is not available on OpenCV is trivial.

However, there are in images a lot of chrominance

edges, that is to say edges between regions from dif-

ferent colors with the same luminance, which are im-

possible to extract using B&W edge segmentations.

Starting from the following observation, a chromi-

nance edge is marked in at least one of the three com-

ponent (Red, Green or Blue) and on each pixel three

gradient’s magnitudes are computed: one for each

component: ||

−→

||, ||

−→

||, and ||

−→

||. Then, the mag-

nitude of the color gradient is obtained:

−→

|| = max||

−→

||,||

−→

||,||

−→

The color gradient replaces the B&W (or luminance)

gradient for the following steps.

The proposed optimization for detecting vertical

edges (only) is algorithmic and can be implemented

either in CPU or GPU. We implemented the op-

timized version of gradient computation and edges

thinning steps on CPU under the SPMD (Simple Pro-

gram Multiple Data) programming model. The image

is divided in several adjacent strips and each is given

to a CPU core. We are going to implement this on

OpenCL using a RaspberryPi’s GPU.

3.2 Lidar Process and Fusion

In this section, we will detail the lines extraction from

lidar’s data and their fusion with features previously

extracted from the image.

3.2.1 Previous Work

In a former work, we applied Wall-Danielsson to the

lidar pointcloud (Burtin et al., 2018). This method,

originally used in the vision ﬁeld, was found to be

(a) Indoor environment

(b) Polygonal approximation

Figure 3: Results of indoor polygonal approximation using

a UTM-30LX Hokuyo lidar.

efﬁcient at segmenting lidar data very fast and ac-

curately because lidar data are represented as linked

edge points, result from the edge linking step. The re-

sult of this segmentation is a polygonal approximation

of the environment around the lidar sensor (Figure 3).

This provides us an approximation of a solid shape

representing the environment around. The solid shape

can be transformed with translation and rotation to

perform prediction of the would-be measured dis-

tance in a certain amount of time with a given evo-

lution of the robot.

3.2.2 Follow Up

Those lines computed previously in the polygonal ap-

proximation exist in the 2D plane deﬁned by the li-

dar’s lasers. Therefore, we can compute the coordi-

nates of these lines in the camera frame with the ex-

trinsic parameters (homogeneous transformation ma-

trix between lidar and camera frames).

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

The image process provides us vertical lines in the

focal plane of the camera (3.1). We can compute from

each line a 3D plane (CDE) (cf. Figure: 2) com-

posed of the line segment (DE) and the focal point of

the camera (C). These three points describe a unique

plane (CDE) and we can compute its cartesian coor-

dinates:

(CDE) : a · x + b · y + c · z + d = 0 (1)

The objective is to compute the intersection be-

tween a 3D plane and a 3D line extracted from the

camera and lidar data. This is basic geometry, we

solve the following system:











= x

+ k · (x

− x

)

= y

+ k · (y

− y

)

= z

+ k · (z

− z

)

· a + y

· b + z

· c = −d

(2)

We have the points A = (x

) and B =

), end of each sides of the lidar segment and

describing the line (L).

We solve the system to ﬁnd the point P =

The solution is assured to be unique and exist-

ing because (AB) is not coplanar nor collinear with

(CDE) plane.

It’s important to note that points A and B are pro-

jected in the camera frame at the exact moment the

image is taken. Because the lidar and camera have

different frame rates, data aren’t synchronized and are

generated at different moments.

To tackle this issue, we apply the method previ-

ously explained, composed of two transformations:

1. The prediction of the would-be lidar’s measure,

considering the current velocities and the time

step between the lidar and the camera data;

2. The rigid transformation between lidar and cam-

era frame;

3.3 Localization using a SLAM Method

The extracted features are 3D points, but with our hy-

pothesis of planar environment we can make a 2D as-

sumption. 3D features become 2D and we can deﬁne

them in the camera frame with cartesian (x

) or po-

lar coordinates.

We decided to implement a SLAM system using

an extended Kalman ﬁlter (Kalman, 1960) with the

observations from both the camera and lidar using the

cartesian coordinates.

The estimation of the state vector, including the

2D pose ( ˆx

, ˆy

) and the ”n” features is 3 + 2 × n

long:

= [ ˆx

, ˆy

, ˆx

, ˆy

,· · ·, ˆx

, ˆy

] (3)

and the measurement vector, issued by the fea-

tures in polar coordinates:







− x

)

+ (y

− y

)

= arctan(

− y

− x

) − α

(4)

Our evolution model estimates the pose of the

robot at the next step with the evolution function f

taking

, the state vector, and

, the command ap-

plied to the robot, as parameters:

k+1

= f(X

) + q

(5)

is a Gaussian, white noise with zero-mean, repre-

sentative of the evolution noise.

The four steps of the Kalman algorithm are: Predic-

tion, Observation, Innovation and Update.

Prediction.

We predict the state vector (

k+1,k

) at step k + 1 with

the evolution function. The covariance matrix associ-

ated to the prediction (P

k+1,k

) is also computed:

k+1,k

= F

k,k

+ F

k,k

+ Q

(6)

while F

and F

are jacobians such as:











∂f

∂

k,k

∂f

∂u

(7)

k,k

is the noise of the command (Gaussian, white and

with zero-mean).

With the predicted state, we compute the observation

estimates:

estimate

= h(X

k+1,k

) (8)

Observation.

In this step, we apply the previous method explained

and obtain the observation vector: z

observed

We match the observed values with the estimated

ones using the Mahalanobis distance (chi-square)

and RGB horizontal gradient. It’s a two steps

validation: ﬁrst we reduce the area of research

using the uncertainty of the feature and, in case of

indeterminate corresponding to multiple features in

the area, we distinguish between themselves using

the horizontal RGB. This feature has been extracted

from a vertical line, which is why the horizontal

gradient is representative, salient and most likely

unique in this restricted area.

Innovation.

The innovation vector is as follows:

= z

observed

− z

estimate

(9)

Camera and Lidar Cooperation for 3D Feature Extraction

The Jacobian H

of the i

observation is:







−(x

− x

)

−(y

− y

)

0 .. .

− x

)

− y

)

...

− y

)

−(x

− x

)

1 .. .

−(y

− y

)

− x

)

...







(10)

And: r

− x

)

+ (y

− y

)

Update.

The update step uses the innovation and the Kalman

gain (K

) to update the predicted state and the new

covariance matrix:











= P

k+1,k

· H

· (H

· P

k+1,k

· H

)

−1

k+1,k+1

k+1,k

+ K

· I

k+1,k+1

= P

k+1,k

− K

· H

· P

k+1,k

(11)

4 RESULTS

The previous approach have been tested with both vir-

tual and real setups. We will detail both experiments

in the following section.

4.1 Virtual Testing

One of the sides objectives in developing this local-

ization method was the development, use and valida-

tion of an advanced robotic simulator. The concerned

simulator is 4DV-Sim (http://www.4d-virtualiz.com/),

developed by the company 4D-Virtualiz. Its develop-

ment was initiated by two robotic PhD students (per-

ception and command ﬁelds), that needed a power-

ful and capable simulator to speed up their work. It

has become a professional tool dedicated to real-time

robots simulation in an HIL (Hardware In the Loop)

manner. The aim of this simulator is to replicate very

accurately real environments, sensors and robots into

the virtual world, including shadows, textures, geo-

referencing, communication protocols, disturbances,

etc (Figure: 4).

This simulator offers sensors with diverse degrees

of realism: it was possible during early prototyping

to use a ”perfect” LIDAR, providing perfects mea-

sured ranges, without any measurement noise. Later,

when our algorithm obtained appropriate results, we

increased the complexity by adding random Gaussian

measurement noise. Finally, before ﬁeld testing, we

experimented the algorithm with the virtual replica of

the real sensor. This virtual sensor has exactly the

same characteristics than the real one: FOV, resolu-

tion, noise measurement, maximum range, frequency

and even the communication protocol. The simula-

tor is able to work in an hardware in the loop fashion

(a) Real sensors

(b) Virtual sensors

Figure 4: Comparison of Camera, GPS ans LIDAR sensors

between real data and data produced with the 4DV-Sim sim-

ulator.

which means that once the source code is validated

with the virtual platform, it can be instantaneously

carried to the real platform to be executed.

The use of a simulator also gives the opportunity

to have exact repeatability to compare the results, ac-

cess to ground truth and produce various datasets with

different environments and robot set-ups, advantages

we do not posses with experiments in real environ-

ment.

The simulated robot is a Dr. Robot Jaguar, virtu-

ally equipped with a URG-4LX Hokuyo lidar and a

640x480 global-shutter camera (pinhole model) (Fig-

ure: 5). The simulated lidar has the same parameters

than the real URG-04LX (min angle, max angle, res-

olution, frequency, etc.) and the noise added to the

measures is Gaussian distributed with parameters pro-

vided by the factory data-sheet.

Figure 5: Dr Robot Jaguar equipped with a URG-30LX li-

dar and RBG camera.

Figure 6: Simulated indoor environment containing the

robot (red circle) and command trajectory (yellow).

The environment we used is a replica of a real

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

(a) Simple

(b) Complex

Figure 7: Same environment, different complexity.

American hospital (Figure: 6). All doors, doorways,

beds, hallways have the right scale and materials ef-

fects. In preliminary work, we used two different sets

of textures and lighting effects to improve gradually

the performance of the vision algorithm (Figure: 7).

4.1.1 Vision

In this section, two kinds of optimization for the Real

Time Vision step will be presented, combined, and

then discussed:

• of the algorithm: in order to detect vertical edges,

only the horizontal gradient computation is re-

quired;

• of the implementation: the data ﬂow program-

ming model (Cabrol et al., 2005) is used, that is

to say the computation of the pixel address is re-

alized sequentially, pixel by pixel, by pointer in-

crementation.

A reference is proposed: it is a classical imple-

mentation of the Kirsh ﬁlter (Kirsch, 1971) in B&W

and color RGB imagery. In this implementation, the

computation of the pixel address is directly realized

using one multiplication and one addition. The use of

functions to access to the pixel value: get pixel()

and put pixel() increases the computing time by

30%.

For each combination (algorithm / implementa-

tion) two computing time are presented:

• the low level processing, that is to say the gradient

computation;

• the global time, where vertical segments are ob-

tained.

One can notice that the low level processing is the

most time consuming step, because the computations

are performed on each pixel of the image. Conse-

quently, the optimization of this step is the most im-

portant to realize, but it is also the most effective and

easy to realize because of the regularity of the com-

putations.

Time results are a mean using one hundred test

RGB images (in .ppm format) given by our simula-

tor on the hospital environment. As the content of the

images is roughly similar, the computing time is quite

constant. For more precision, the temporal measure-

ment is realized on a loop of one hundred iterations.

Time results are measured on a PC HP Pro-book

equipped of a processor Intel Core i5-630, at 2.4 GHz,

with 16 Go of Memory. Images are in VGA format:

640 columns × 480 lines.

In B&W imagery, the Kirsh Algorithm takes 36

ms, and the global processing leading to the detection

of the vertical segments 42,2 ms. The results for RGB

color imagery are the following, in milliseconds:

Table 1: Average computation time in milliseconds.

Algo - Impl No Opt Optimized

Kirsh: 4 Masks 111 (93 %) - 119 20 (87 %) - 22,9

Horizontal Mask 30,2 (92 %) - 32,6 10,5 (77 %) - 13,6

In term of Speed Up, the results are the following:

Table 2: Acceleration depending on the method and the op-

timization.

Algo - Impl No Opt Optimized

Kirsh: 4 Masks 1 5,19

Horizontal Mask 3,65 8,75

As a conclusion, the increase of nearly factor 9 in

computation time must be pointed out. It allows our

vertical segment detection to run at video rate (ie. in-

ferior to 40 ms) on one core. The use of less than

15 ms leaves the possibility to hook this segmenta-

tion part to other high level processing, and guaranty

a latency time of less than a video frame. Using the

SPMD programming model for the implementation of

the gradient computation and edge thinning steps, a

speed up of 3.8 is achieved using manual attribution

on the 4 cores of the RaspberryPi against 2.7 using

the Raspian load balancing.

4.1.2 Localization

We implemented the vertical detector presented pre-

viously and added the lidar data to obtain our 3D fea-

tures. In order to reduce the computation time we

limited the number of detected vertical lines and nar-

rowed this to the lines around the horizon, we can ob-

serve the projection of the 3D extracted features from

the previous image in cooperation with the lidar us-

ing camera intrinsic and extrinsic parameters (Figure:

8b).

In addition of the previous optimizations, we used

regions of interest (ROI) to reduce the number of pix-

els processed during each steps. To deﬁne these ROI,

we use the estimated position of the known feature

in the image and deﬁned the width of the bound-

ing box using the uncertainty related to this feature

with a minimal width of 10 pixels. The height of

Camera and Lidar Cooperation for 3D Feature Extraction

(a) Original image

(b) Features

Figure 8: Use of ROI and the 2D features results in the

SLAM map.

ROI’s bounding box is ﬁxed to 1/4 of the image.

This is linked to the lidar’s position: every ”hit” from

the lidar will be contained within the bounding box,

whether the range is 0.5 or 30m (lidar’s minimum and

maximum range). The use of the ROI (Figure: 8b) is

extended to the full width of the image when the algo-

rithm looks for new features to add to the SLAM sys-

tem. This allows a complete scan but has to be done

at a lower frequency to save CPU-usage The average

time needed to extract verticals in a ROI is 1.6623ms.

Using a sparse SLAM system (even without multi-

threading), we can reasonably track enough features

in real time to feed a localization process.

We performed our experiment in the simulated en-

vironment using the described robot and setup; The

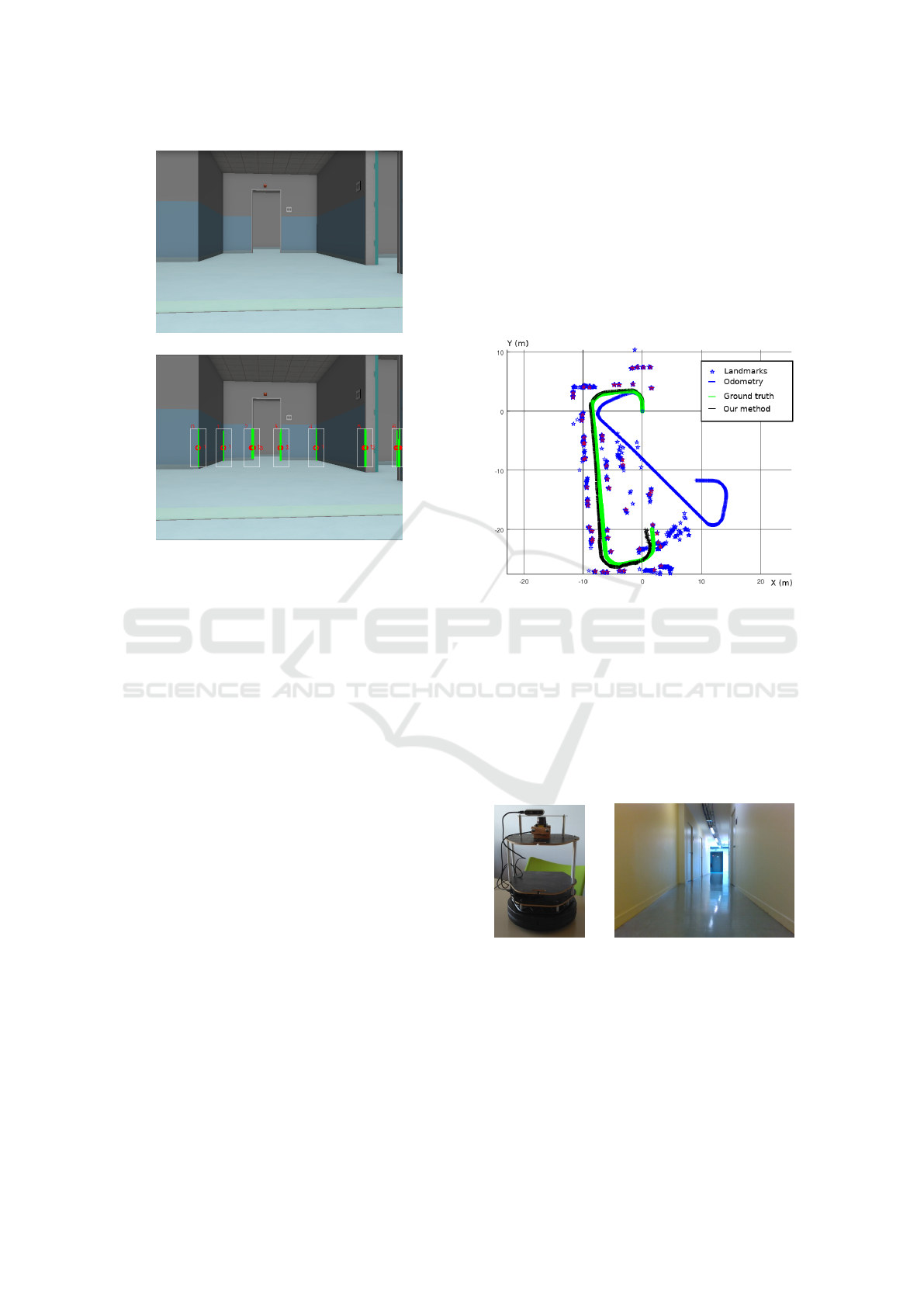
result is displayed in the Figure: 9. The blue stars

are the extracted and tracked features. One can rec-

ognize the shape of the building shown in top-view

from Figure: 6. The green track is the ground truth

from the simulator. The blue track is the estimated

localization using only the odometry. We can observe

the rapid drift of the odometry during turns and it’s

relative precision during forward motion. The black

track is the estimated position of the robot using the

kalman ﬁlter. The track is split in two parts, the ﬁrst

part has a very precise localization (an average 2cm

error relatively to the ground truth), then a diverging

part. The second part has an increasing error is due to

a small error in heading at the moment of initialization

of new landmarks when the robot faced the hallway.

This is due to the lack of visual landmarks available

in this part of the virtual map. This slight shift added

a small angle that had repercussion on the next 25m

of evolution to a ﬁnal 0.3m error over a 40m trajec-

tory. Blue stars are our observed landmarks and red

one are registered in the map created. This conclude

our virtual tests, considering that further tests should

be on a real robot to conﬁrm the results.

Figure 9: Localization results.

4.2 Real Experiments

Real experiment were conducted in the hallway of a

public building. We used a Kobuki TurtleBot2 plat-

form with an Hokuyo 04LX and an Intel Realsense

D435 placed on the top of the robot. The environment

we experienced in is about 40m long, having several

patio doors with large panes, solid doors and shiny

ﬂoor (Figure: 10).

(a) Real robot

(b) Hallway

Figure 10: Set-up and environment used for the experiment.

The RealSense sensor is used only to provide

a global shutter 640x480 image, we didn’t use the

RGB-D feature because it did not provide depth in-

formation with sufﬁcient range and precision. The

corner seen on the left of the hallway is not seen at

3m (Figure: 11).

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

(a) Environment

(b) Intel D435

Figure 11: Comparison of depth detection.

4.2.1 Localization

The real environment brought additional complex-

ity to the sensors due to two facts: the large win-

dows panes and the ﬂoor that reﬂects the environment.

The ﬁrst issue comes from the sun light that blinds

the LIDAR sensor depending on the intensity of the

rays. The second is brought by the clean plastic ﬂoor

that create ”false” verticals in the image by reﬂecting

lights on the ceiling and doors. The ﬁrst issue was

solved by ﬁltering the LIDAR data while the second

one was only a matter of ROI focusing to exclude mis-

leading verticals.

Our strong initial hypothesis, 2D movement and

camera-lidar rig coplanar to the ﬂoor, is reasonable

: even with small angular errors, we still manage to

detect vertical lines in our image.

Figure 12: Detections with the real set-up.

As explained before, we do not have a proper

ground-truth available for real experiment, thus we

can’t know the exact position of the robot during the

experiment but we do have the 2D model of the build-

ing provided by the architects. This model have been

produced using precise (< 1cm) measurement by pro-

fessional surveyors, therefore, we can estimate the ef-

ﬁciency of the robot localization using the compari-

son between the landmarks registered by our system

and the solid shape given by exact model (black shape

in ﬁgure 13).

We compared the localization efﬁciency with an-

other method: the canonical scan matcher (CSM)

(Censi, 2008). We tried the ORB-Slam (Monocular)

but the complex light rendered the initialization im-

possible. Since there is no loop closing in this hall-

way, the CSM should not have particular disadvan-

tage.

On the Figure 13, we can observe the results of

the different methods. The black trajectory is the lone

odometry. The red one is the CSM result. The Blue

stars are the landmarks registered by our method, and

the trajectory is green. The odometry is outside the

building frame but not that much, contrary to the vir-

tual odometry, this one is more precise. This can be

explained by the motion method of the robot: the vir-

tual is a 4 wheeled robot and the TurtleBot is a 2

wheeled. The later present a reduced slippery dur-

ing the turns, thus reducing the error on the odometry

that made the assumption of slip-free rolling condi-

tion. The low range of the LIDAR and narrow FOV

of the camera limits the number of landmarks avail-

able but the algorithm manages to detect several of

them and successfully tracked, even with a complex

lighting.

Camera and Lidar Cooperation for 3D Feature Extraction

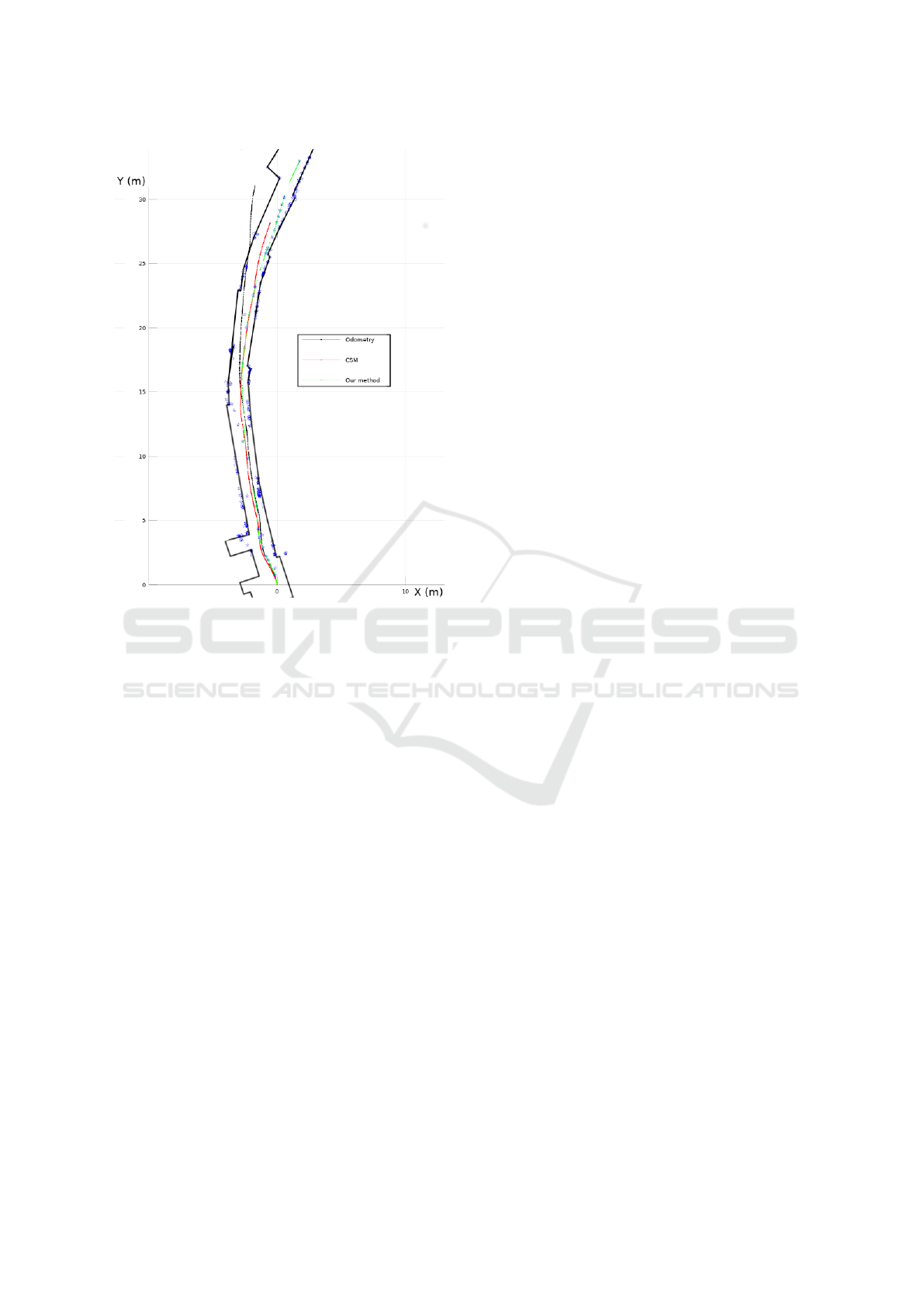
Figure 13: Localization results.

5 CONCLUSIONS

In this paper, we proposed an approach to extract fea-

tures from both camera and lidar sensors while saving

CPU-time. Upon this feature extractor, we built an

extended Kalman ﬁlter to provide fast robot localiza-

tion, re-using sensors data from others purposes. We

evaluated the interest in focused images processing to

reduce the computation time and observed a signiﬁ-

cant improvement, enough to process all features in

real-time on a low grade computer. First, the local-

ization method has been evaluated with an advanced

robotic simulator and shown interesting results. Then

the very same algorithm was used as-is later on a real

platform, using the same sensor than the simulated

ones. The landmarks localization in the experiment

in the real hallway are conclusive regarding the 2D

model of the building. We can reasonably state that

the simulation was accurate enough to provide signiﬁ-

cant preliminary results. It allowed a real-time testing

during the early development of the algorithm, having

incremental complexity and access to ground truth.

This helped signiﬁcantly during the design of the sys-

tem before using the real robot for ﬁnal and real tests.

In future work, we will focus on improvement of

the SLAM system to avoid heading shifts and include

a loop-closing method to rectify the map. The use

of RGB-D sensors to combine the image and depth

with less calibration and more accurate results is an

interesting perspective with more depth range.

ACKNOWLEDGEMENTS

This research was performed within the framework

of a CIFRE grant (ANRT) for the doctoral work of

G.Burtin at 4D-Virtualiz and LISV.

REFERENCES

Asvadi, A., Girao, P., Peixoto, P., and Nunes, U. (2016). 3d

object tracking using rgb and lidar data. In Intelligent

Transportation Systems (ITSC), 2016 IEEE 19th In-

ternational Conference on, pages 1255–1260. IEEE.

Bekris, K. E., Glick, M., and Kavraki, L. E. (2006). Evalu-

ation of algorithms for bearing-only slam. In Robotics

and Automation, 2006. ICRA 2006. Proceedings 2006

IEEE International Conference on, pages 1937–1943.

IEEE.

Burtin, G., Bonnin, P., and Malartre, F. (2018). Vision based

lidar segmentation for accelerated scan matching. In

Journal of Communications, volume 13, pages 139–

144.

Burtin, G., Malartre, F., and Chapuis, R. (2016). Reduc-

ing the implementation uncertainty using an advanced

robotic simulator.

Cabrol, A., P.Bonnin, V.Hugel, K.Boucheffra, and

P.Blazevic (2005). Temporal optimized edge segmen-

tation for mobile robotics. SPIE Optics Photonics,

Application of Digital Image Processing XXVIII, July

31st- August 4th 2005, San Diego, California, USA.

Canny, J. (1983). Finding edges and lines in images. MIT

AI Lab Tech Report TR-720.

Censi, A. (2008). An ICP variant using a point-to-line met-

ric. In Proceedings of the IEEE International Confer-

ence on Robotics and Automation (ICRA), Pasadena,

CA.

Choi, Y.-H., Lee, T.-K., and Oh, S.-Y. (2008). A line fea-

ture based slam with low grade range sensors using

geometric constraints and active exploration for mo-

bile robot. Autonomous Robots, 24(1):13–27.

De Silva, V., Roche, J., and Kondoz, A. (2018). Robust

fusion of lidar and wide-angle camera data for au-

tonomous mobile robots. Sensors, 18(8):2730.

Deriche, R. (1987). Using canny’s criteria to derive a re-

cursively implemented optimal edge detector. Inter-

national Journal of Computer Vision, 167-187.

Durrant-Whyte, H. and Bailey, T. (2006). Simultaneous lo-

calization and mapping: part i. IEEE robotics & au-

tomation magazine, 13(2):99–110.

Engel, J., Sch

ops, T., and Cremers, D. (2014). Lsd-slam:

Large-scale direct monocular slam. In European Con-

ference on Computer Vision, pages 834–849. Springer.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

Engelhard, N., Endres, F., Hess, J., Sturm, J., and Burgard,

W. (2011). Real-time 3d visual slam with a hand-held

rgb-d camera. In Proc. of the RGB-D Workshop on

3D Perception in Robotics at the European Robotics

Forum, Vasteras, Sweden, volume 180, pages 1–15.

Huang, H. (2008). Bearing-only SLAM : a vision-based

navigation system for autonomous robots. PhD thesis,

Queensland University of Technology.

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Transactions of the ASME–

Journal of Basic Engineering, 82(Series D):35–45.

Kirsch, R. (1971). Computer determination of the con-

stituent structure of bio1ogical images. Computers

and Biomedical Research 4, 315-328.

Lemaire, T. and Lacroix, S. (2007). Monocular-vision based

slam using line segments. In Robotics and Automa-

tion, 2007 IEEE International Conference on, pages

2791–2796. IEEE.

Micusik, B. and Wildenauer, H. (2015). Descriptor free vi-

sual indoor localization with line segments. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 3165–3173.

Mur-Artal, R., Montiel, J. M. M., and Tardos, J. D. (2015).

Orb-slam: a versatile and accurate monocular slam

system. IEEE Transactions on Robotics, 31(5):1147–

1163.

Nachar, R., Inaty, E., Bonnin, P., and Alayli, Y. (2014).

Polygonal approximation of an object contour by de-

tecting edge dominant corners using iterative corner

suppression. VISAPP International Conference on

Computer Vision Theory and Applications, pp 247-

256, Jan 2014, Lisbon, Portugal.

Newcombe, R. A., Lovegrove, S. J., and Davison, A. J.

(2011). Dtam: Dense tracking and mapping in real-

time. In Computer Vision (ICCV), 2011 IEEE Inter-

national Conference on, pages 2320–2327. IEEE.

Premebida, C., Monteiro, G., Nunes, U., and Peixoto, P.

(2007). A lidar and vision-based approach for pedes-

trian and vehicle detection and tracking. rn, 10:2.

Prewitt, J. (1970). Object enhacement and extraction. Pic-

ture processing and Psychopictorics, BS. Lipking and

A.Rosenﬁeld ed, Academic Press.

Pumarola, A., Vakhitov, A., Agudo, A., Sanfeliu, A.,

and Moreno-Noguer, F. (2017). Pl-slam: Real-time

monocular visual slam with points and lines. In

Robotics and Automation (ICRA), 2017 IEEE Inter-

national Conference on, pages 4503–4508. IEEE.

Roberts, L. (1965). Machine perception of 3d solids. Opti-

cal & electro optical information processing, JP.Tipett

and al., Cambridge, MIT Press.

Roumeliotis, S. I. and Bekey, G. A. (2000). Segments: A

layered, dual-kalman ﬁlter algorithm for indoor fea-

ture extraction. In Intelligent Robots and Systems,

2000.(IROS 2000). Proceedings. 2000 IEEE/RSJ In-

ternational Conference on, volume 1, pages 454–461.

IEEE.

Schramm, S., Rangel, J., and Kroll, A. (2018). Data fusion

for 3d thermal imaging using depth and stereo camera

for robust self-localization. In Sensors Applications

Symposium (SAS), 2018 IEEE, pages 1–6. IEEE.

Sobel, I. (1978). Neighborhood coding of binary images for

fast contour following and general binary array pro-

cessing. Computer Graphics and Image Processing

vol 8,.

Von Gioi, R. G., Jakubowicz, J., Morel, J.-M., and Randall,

G. (2012). Lsd: a line segment detector. Image Pro-

cessing On Line, 2:35–55.

Zuo, X., Xie, X., Liu, Y., and Huang, G. (2017). Robust vi-

sual slam with point and line features. arXiv preprint

arXiv:1711.08654.

Camera and Lidar Cooperation for 3D Feature Extraction