
Genetic Programming based Synthesis of Clustering Algorithm for
Identifying Batches of Electronic Components
Evgenii Sopov
a
and Ilia Panfilov
b
Reshetnev Siberian State University of Science and Technology, Krasnoyarsk, Russia
Keywords: Hyperheuristics, Genetic Programming, Genetic Algorithm, Clustering, Electronic Component Analysis.
Abstract: A manufacture of electronic components involves the quality management, but still characteristics of
components from different batches may vary. For many highly precise and reliable applications, such as
aerospace or military systems, it is necessary to identify and use components from the same batch. This
problem is usually stated as a clustering problem or as a k-centroids allocation problem. The k-centroids
problem is a generalization of the Fermat–Weber location problem, which is known to be NP-hard. Genetic
algorithms have proved their efficiency in solving many hard optimization problems. Genetic algorithms are
also used in clustering algorithms for defining initial points of centroids for location-allocation clustering
algorithms. At the same time, standard genetic algorithms demonstrates low performance in solving real-
world clustering problems, and, as a result, different heuristic-based modifications have been proposed. In
this study, we will synthesize a new selection heuristic for a genetic algorithm, which is used for solving the
clustering problem of identifying batches of electronic components. We will use a genetic programming based
hyperheuristic for creating a selection operator represented by a probability distribution. The results of solving
two real-world batch identification problems of microchip manufactures for aerospace applications are
presented and are compared with base-line approaches and some previously obtained results.
1 INTRODUCTION
Modern aerospace on-board equipment and control
systems contain electronic components (ECs) of high
accuracy and reliability requirements. A manufacture
of such ECs involves the quality management. At the
same time, an EC base may combine units from
different suppliers or units produced in different
periods of time. Such ECs from different production
batches can be inhomogeneous because of different
raw source materials or deviations in manufacturing
processes. As result, some characteristics of ECs from
different batches may vary, even the characteristics
are in a feasible domain. Many manufactures perform
incoming quality control, additional rejection tests
and destructive physical analysis of ECs, and, finally,
identify and use ECs from the same batch.
The problem of identifying batches of ECs is an
unsupervised learning problem and it can be stated as
a clustering problem. For continues clustering
problems, Minimum Sum of Squares Clustering
a
https://orcid.org/0000-0003-4410-7996
b
https://orcid.org/0000-0002-6465-1748
(MSSC) or k-means method is usually applied. The
main feature of the problem of identifying batches of
ECs is that variations in measured characteristics are
too small and are limited by accuracy of
measurements. Thus, we have to deal with discrete
values, for which the discretization step is defined by
the measuring device. For discrete clustering
problems, k-median (k-medoids) method can be
applied. K-means and k-medians are very similar
methods and have the same advantages and
disadvantages. Both methods are sensitive to initial
positions of cluster centers. Random choosing of
initial centers can converge to an incorrect grouping
of objects, even for easy clustering problems. Many
different techniques for initializing initial centers
have been proposed. One of the most popular and
efficient approaches is evolutionary (EAs) and
genetic (GAs) algorithms for continuous and discrete
problems respectively.
The k-centroid problem is a generalization of the
Fermat-Weber location problem, which is known to
202
Sopov, E. and Panfilov, I.
Genetic Programming based Synthesis of Clustering Algorithm for Identifying Batches of Electronic Components.
DOI: 10.5220/0007810702020209
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 202-209
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

be NP-hard. GAs have proved their efficiency in
solving many hard optimization problems. They also
can be applied in solving clustering problems. At the
same time, standard GAs demonstrate low
performance in solving real-world clustering
problems. There have been proposed many heuristics
for modifying GAs. In (Bandyopadhyay and Maulik,
2002) a new general-purpose heuristic and in
(Kazakovtsev and Antamoshkin, 2014) a greedy
heuristic for improving the GA performance in
solving EC batches identification problem have been
proposed.
The most recent studies in the field of EAs
propose new approaches for automated designing and
fine-tuning of search metaheuristics, which are called
hyperheuristics (HHs). Genetic programming (GP)
has been proposed as a method for automatically
generating computer programs. Today GP is used in
the field of machine learning for a wide range of
applications. GP can be also applied as a
hyperheuristic for generating search heuristics and
metaheuristics (so-called GPHH) (Burke et al., 2013).
A selection operator is an important component of
any evolutionary or genetic algorithm. The selection
operator is intended to improve the average fitness of
a population by giving individuals with better fitness
a higher probability to be copied into the next
generation. The traditional selection operators are
inspired by nature and use straightforward and simple
ways for calculating the probability of being selected.
In this study will use GPHH to synthesize a new
problem-specific selection operation for the GA
applied in solving the problem of identifying batches
of ECs.
The rest of the paper is organized as follows.
Section 2 describes related work. Section 3 describes
the proposed approach. In Section 4, the results of
numerical experiments are discussed. In the
Conclusion the results and further research are
discussed.
2 RELATED WORK
Cluster analysis (or clustering) is a main task of
exploratory statistical data analysis and unsupervised
machine learning applied for many real-world
problems (Xu and Tian, 2015).
Many applied clustering problems can be reduced
to the problem stated in the location theory. In the
location theory, an analyzed object is assigned to a
cluster by assigning it to the closest center of clusters
(centroid). If the distance is calculated using
Euclidean or another metric, the problem is called the
k-median problem. If the squared Euclidean distance
is used, it is called the k-means problem. Finally, if
centers of clusters are selected from the given objects,
this is called the k-medoid problem (Mladenovic,
2007; Brimberg, 2008).
In the formal way, the k-centroid problem is a
generalization of the Fermat-Weber location problem
(Wesolowsky, 1993; Farahani, 2009), which is an
NP-hard optimization problem stated as in (1)
(Megiddo and Supowit, 1984). There have been
proposed many search heuristics for solving the
problem. Many recent approaches are based on GAs
(Hruschka et al., 2009).
(1)
where is a set of points, is a set of centroids,
is weight coefficients and is a distance measure.
The problem of identifying batches of ECs is the
particular problem that arises in not general-purpose
manufactures, such as manufacture of aerospace on-
board and control systems. Data collected for
analyzing ECs are usually unique and they need a
specific clustering algorithm that can deal with
features of the data. At the same time, the data are
complex for comprehensive analysis, thus applying
GAs that can optimize “black-box” models is more
preferable.
EAs and GAs are metaheuristics based on a
combination of simple basic heuristics, including
selection, recombination, mutation, cloning and
others. The performance of a EA depends on the
correct choice of heuristics and on fine-tuning
corresponding parameters (Eiben et al., 2007). In
(Kazakovtsev et al., 2016) new GAs have been
proposed for solving the given problem of identifying
batches of ECs, which apply greedy heuristics for
better convergence in the multimodal search space.
Hyperheuristic approaches perform a search over
the space of heuristics or metaheuristics when solving
optimization problems. In a HH approach, different
heuristics or heuristic components can be selected,
generated or combined to solve a given problem in an
efficient way. There exist many HHs for optimization
problems, and the best results for today are achieved
with HHs based on GP (Burke et al., 2009). The
application of GP as a HH is a rather new direction in
the field of automated algorithm design. GP builds
candidate solutions to the problem from a set of
primitives, which are represented by single operators,
functions or whole heuristics and metaheuristics. One
of the main advantages of GP is that it simultaneously
Genetic Programming based Synthesis of Clustering Algorithm for Identifying Batches of Electronic Components
203

provides the structural synthesis of a solution and the
tuning of its parameters. The solution can be a
human-readable symbolic expression (a formula) or a
computational algorithm (an executable computer
program).
A selection operator is an important component of
any EA or GA (Blickle and Thiele, 1996). From the
point of view of search optimization, selection
focuses the search process on promising regions in
the search space, while recombination performs a
random search within previously explored regions,
and mutation discovers new points in the search
space. Any selection operator can be viewed as a
probability distribution that assigns the chance of
being chosen for further operations to every
individual in a population. Thus, selection can be
defined as a mapping (of a function) to the [0, 1]
interval. The domain of the mapping function
comprises ranks for the ranking, tournament and
truncation selection schemes, and comprises fitness
values for the proportional selection. In this study, we
will focus on the automated design of a selection
operator using a GP-based HH.
3 PROPOSED APPROACH
Any clustering problem can be solved using a
Location-Allocation algorithm. One of the most
popular and well-studied approaches is Alternating
Location-Allocation (ALA) algorithm. The general
ALA scheme is presented below.
is a training set, where
is an object to be classified.
is a set of initial positions for
centers of clusters
and
is the number of clusters.
ALA-algorithm:
1. For
find the closest center
2. Find new centers
for all clusters
.
For the squared Euclidian metric (
), new
centers are calculated using the following
formula (2):
(2)
where
, if there is no preferences for
classified objects.
3. If
, then
set t=t+1 and go to step 1, else go to step 4.
4.
are centres of
clusters.
We will use the standard binary GA for searching
initial positions for applying the ALA algorithm. We
have chosen the binary GA because of predefined
domains and discrete values of objective variables in
the given clustering problem.
The following general scheme for our GA is used:
1.
crossover type and probability, mutation
probability. Selection operator is defined by
the current solution from GPHH.
is the binary
representation of a candidate-solution that
contains initial positions of centers for applying
the ALA algorithm.
2. Randomly initialize a population.
3. Evaluate fitness using formula (3):
(3)
where
is the result of applying the ALA
algorithm. The fitness value is minimized.
4. Apply selection, crossover and mutation and
create new population.
5. If a stop condition is satisfied, then STOP, else
go to step 3.
In this study, we will use the following conception
of applying GP for designing selection operators,
proposed in (Sopov, 2017). We will use the GP
algorithm as a meta-procedure for solving a symbolic
regression problem, in which tree solutions represent
probability distributions. A raw solution is
normalized, and after that is executed as a selection
operator in the GA.
Each tree solution in the GP is a function with
arbitrary codomain (denoted as
, where
is a rank of the -th individual after ranking).
We need to provide some transformation of the
function for applying it as a selection operator
(4)-(5). We will bound the domain
with rank values and will apply normalization.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
204
,
(4)
,
,
(5)
A GA is a stochastic search procedure, thus it is
necessary to evaluate the average results of solving an
optimization problem for estimating the performance
of the GA. The GA performance is used for assigning
the fitness value to the GP solution that represents a
selection operator applied in the GA. We will use the
following formula (6):
(6)
where is the number of independent runs of the GA
that uses the selection operator represented by
,
is the best found solution in the -th
run.
4 EXPERIMENTAL SETUPS AND
RESULTS
4.1 EC Batches Identification Problem
We will apply the proposed approach for solving two
real-world problems of batch identification for
140UD25AS1V and 1526IE10 integrated circuits
(ICs) applied in Russian aerospace manufactures.
In the general case, for weakly investigated data,
there is no information about the number of clusters.
In our study, the problems are stated as clustering
problems with the known number of clusters.
The 140UD25AS1V dataset contains 56 EC units
from 3 batches. Each unit is described by 42
measured parameters.
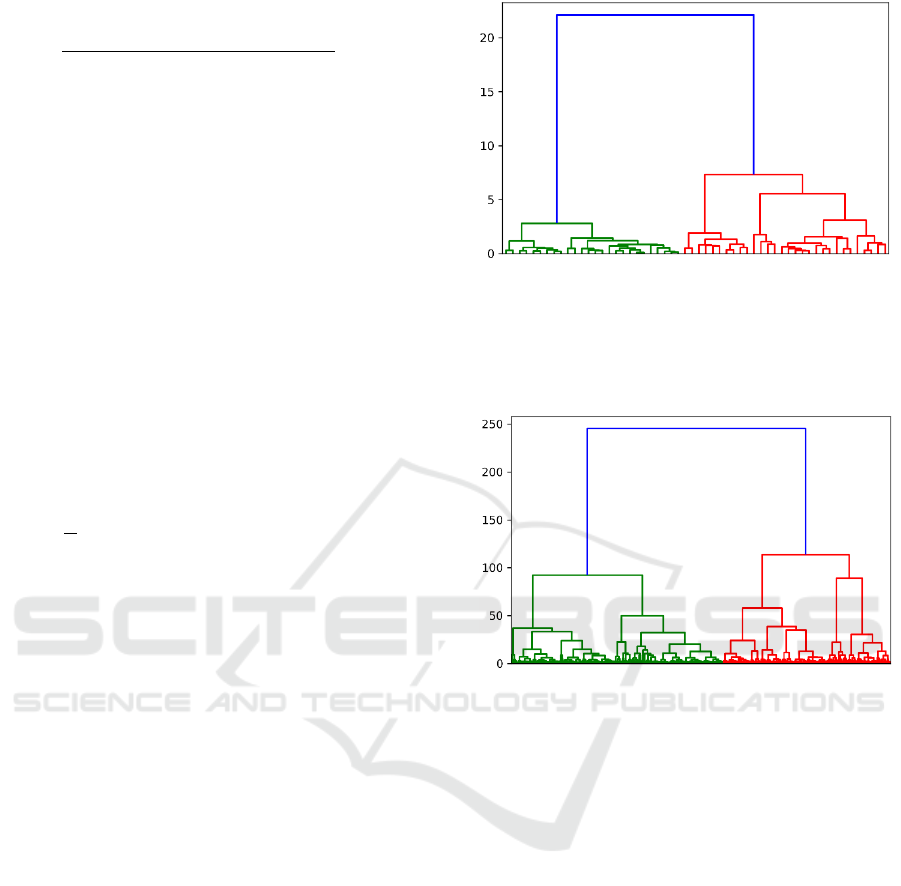
The dendrogram using the centroid metric for the
140UD25AS1V dataset is presented in Figure 1,
where the bottom axis contains objects from the
dataset and the vertical axis corresponds to the
linkage distance. As we can see, the data have a
structure and can be divided into several groups.
Figure 1: Hierarchical clustering for 140UD25AS1V.
The 1526IE10 dataset contains 3987 EC units
from 7 batches. Each unit is described by 202
parameters. The dendrogram for the data is presented
in Figure 2.
Figure 2: Hierarchical clustering for 1526IE10.
The given datasets also contain information on
batches, and we can solve the problem of identifying
batches of ECs using a classification approach.
Unfortunately, such information on batches is not
always presented, thus the problem becomes
unsupervised. In the study, we will remove any
information on batches when solving the clustering
problem, but we will use this information for
calculating error of grouping ECs.
4.2 Experimental Setups
All algorithms have been implemented using Python
language in the Spyder IDE. GP and GA realizations
are based on DEAP framework (Fortin et al., 2012).
The ALA algorithm is realized using Sklearn.cluster
framework (Pedregosa et al., 2011.).
The numerical experiments have been performed
on Intel i7-4790 3.60GHz CPU using parallel
computations.
Settings for algorithms used in the experiments
are presented in Table 1 and 2.
Genetic Programming based Synthesis of Clustering Algorithm for Identifying Batches of Electronic Components
205

4.3 Experimental Results
The experimental results of 40 independent runs of
the GP are presented in Table 3. Figures 3 and 4
demonstrate variations of the best-found fitness in the
runs.
We have also compared the GP-based results with
the results of applying the standard GA with the linear
rank selection and with the k-median ALA algorithm
with random initialization.
Table 1: The GP algorithm settings.
Parameter
Value
Population size
50
The grow method
Full
Max depth of trees
6
The functional set and
probabilities for
initializing functional
nodes
The terminal set
;
Constants initialization
random uniform
distribution in
the linear ranking
the exponential ranking
with
Crossover
one-point with probability
equal to 0.95;
Mutation
one-point with probability
equal to 0.01;
Maximum number of
generations
1000
Number of independent
runs
40
We have also applied the Wilcoxon-Mann-
Whitney test with the significance level equal to 0.05
for checking if there statistically significant
difference in the results. The test have proved that the
GP-based approach outperform the standard GA and
the ALA with random initialization.
Table 2: The GA algorithm settings.
Parameter
Value
Population size
100
Encoding accuracy
for each objective
variable is defined by
values of the variable
Initialization
random in the binary
search space
Crossover
two-parent random
uniform with probability
equal to 1.00
Mutation
bits inversion with
probability equal to
Selection.
based on GP solutions
Maximum number of
generations
50
Number of independent
runs
40
Table 3: The results for the clustering problem.
GP-based
140UD25AS1V
1526IE10
best
6758.66
3050.7
median
8088.69
4872.59
worst
9852.17
7211.01
mean
8064.35
4937.55
sd
588.57
920.53
Classification
error
7.14%
11.21%
Standard GA
140UD25AS1V
1526IE10
best
7968.78
3872.28
median
9467.09
5826.83
worst
13947.65
9051.11
mean
9624.56
5935.89
sd
1171.29
1221.75
Classification
error
16.30%
22.73%
ALA with random initialization
140UD25AS1V
1526IE10
best
13534.32
7349.74
median
21587.31
11980.54
worst
14891.72
10522.45
mean
15048.25
10488.22
sd
1318.86
766.26
best
13534.32
7349.74
Classification
error
25.19%
43.97%
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
206
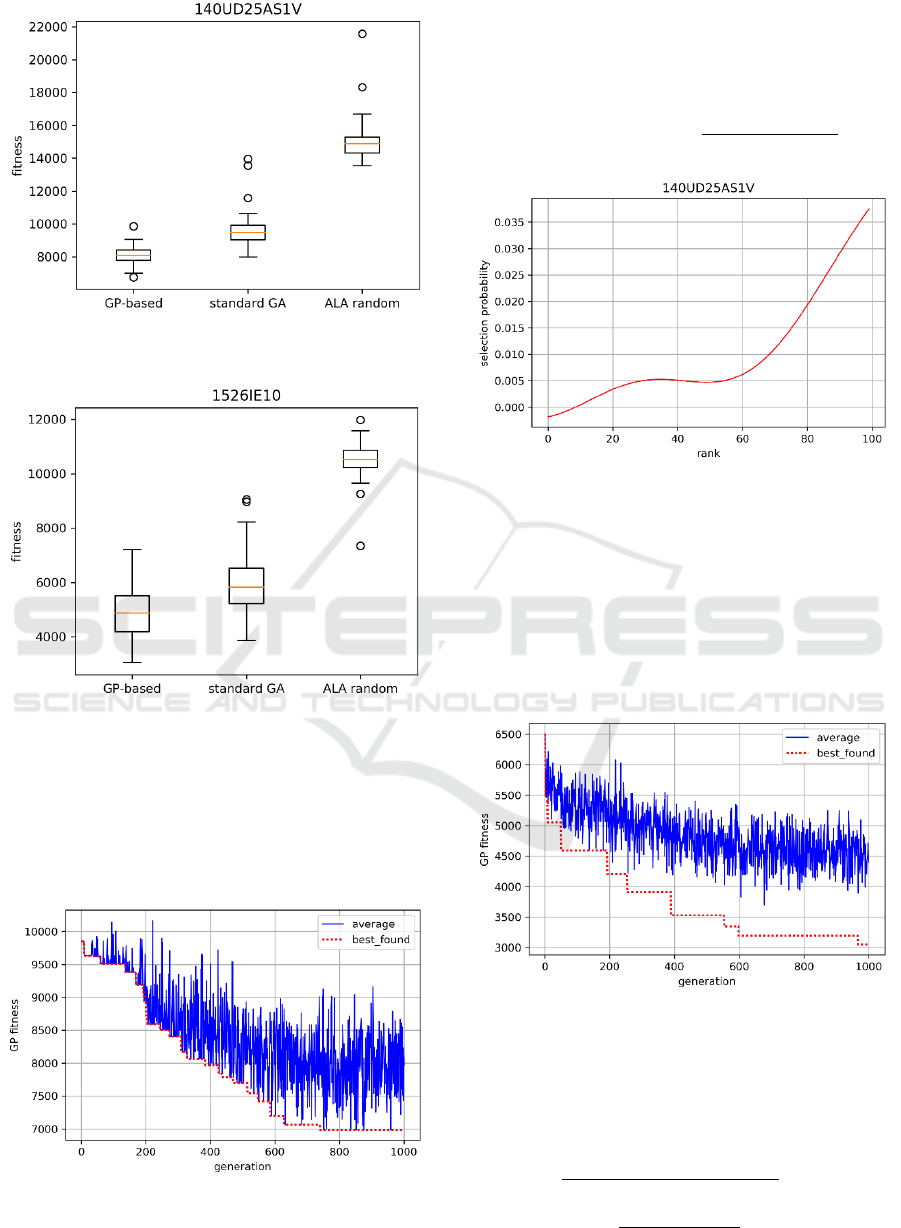
Figure 3: Variation diagram for the 140UD25AS1V
problem.
Figure 4: Variation diagram for the 1526IE10 problem.
The fitness convergence diagram for the best run
of the GP algorithm solving the 140UD25AS1V
problem is presented in Figure 5. The dashed (red)
line corresponds to the best-found solution and the
solid (blue) line corresponds to the average of
population.
Figure 5: GP fitness convergence for 140UD25AS1V.
The expression of the best-found solution in the
best run for the 140UD25AS1V problem and its
graph are presented in (7) and Figure 6 respectively.
(7)
Figure 6: The graph of the best-found selection operator for
140UD25AS1V.
The fitness of the best-found solution for
140UD25AS1V problem is 6758.66. It improves the
previously found solution (7291.67) in (Kazakovtsev
et al, 2016a) by 7.3%.
The fitness convergence diagram for the best run
of the GP algorithm solving the 1526IE10 problem is
presented in Figure 7.
Figure 7: GP fitness convergence for 1526IE10.
The expression of the best-found solution in the
best run for the 1526IE10 problem and its graph are
presented in (8) and Figure 8 respectively.
(8)
Genetic Programming based Synthesis of Clustering Algorithm for Identifying Batches of Electronic Components
207
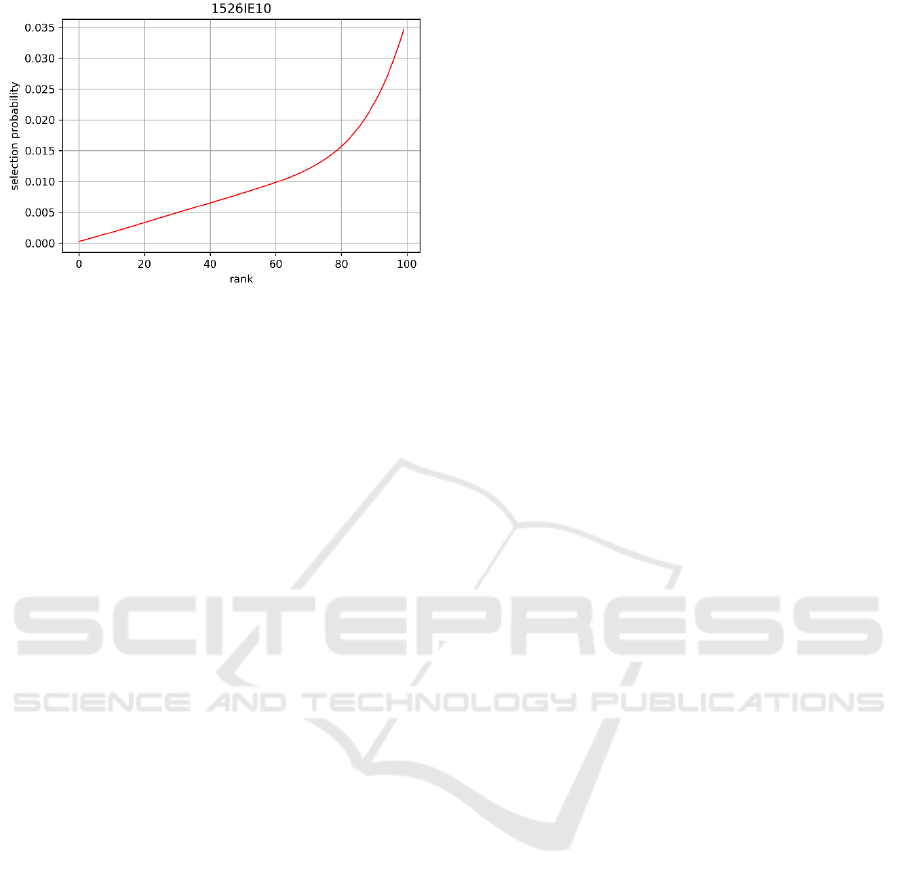
Figure 8: The graph of the best-found selection operator for
1526IE10.
The fitness of the best-found solution for
1526IE10 problem is 3050.70. It also improves the
previously found solution (3440.1) in (Kazakovtsev
et al., 2018) by 11.3%.
As we can see from the results, the proposed
approach is able to synthesize new selection
heuristics for solving problems. The proposed
solutions outperform some base-line and previously
obtained results.
5 CONCLUSIONS
In this study, we have proposed a genetic
programming based approach, which is used for the
automated synthesis of clustering algorithm for a real-
world problem of identifying batches of electronic
components. The clustering problem is reduced to the
Fermat-Weber location problem, which is NP-hard
optimization problem. The proposed clustering
algorithm combines a GA for searching global-
optimal initial positions of centroids and an ALA
algorithm for performing local search of positions and
final clustering. The GP algorithm is used as a
hyperheuristic for creating a problem-specific
(dataset-specific) selection heuristic, which provides
the optimal (or suboptimal) performance of the GA
algorithm for the given clustering problem.
Our numerical experiments have shown that the
proposed approach is able to deal with real-world
problems of identifying batches of 140UD25AS1V
and 1526IE10 ICs and provides high accuracy of
assigning ECs to correct clusters. Moreover, the
synthesized algorithms provide statistically
significant better performance than some general-
purpose algorithms do. The results obtained in the
paper also outperform the results previously obtained
by other authors.
In our further works, we will try to apply the
approach to the problem of the automated synthesis
of other genetic operators such as crossover and
mutation. In addition, we will use a selective
hyperheuristic for automated choosing of the best-fit
to the problem ALA algorithm.
ACKNOWLEDGEMENTS
This research is supported by the Ministry of
Education and Science of Russian Federation within
State Assignment № 2.1676.2017/ПЧ.
REFERENCES
Bandyopadhyay, S., Maulik, U., 2002. An evolutionary
technique based on K-Means algorithm for optimal
clustering, Information Science, Vol. 146, pp. 221-237.
Blickle, T., Thiele, L., 1996. A comparison of selection
schemes used in evolutionary algorithms. In: Evol.
Comput. 4(4). pp. 361-394.
Brimberg, J., Hansen, P., Mladenovic, N., Salhi, S., 2008.
A Survey of Solution Methods for the Continuous
Location-Allocation Problem, International Journal of
Operations Research, 5, pp. 1-12.
Burke, E., Gendreau, M., Hyde, M., Kendall, G., Ochoa, G.,
Ozcan, E., Qu, R., 2013. Hyper-heuristics: A survey of
the state of the art, Journal of the Operational Research
Society, 64 (12), pp. 1695-1724.
Burke, E., Hyde, M., Kendall, G., Ochoa, G., Ozcan, E.,
Woodward, J., 2009. Exploring hyper-heuristic
methodologies with genetic programming, In:
Computational Intelligence: Collaboration Fusion and
Emergence, New York, Springer. pp. 177-201.
Eiben, A. E., Michalewicz, Z, Schoenauer, M., Smith, J. E.,
2007. Parameter Control in Evolutionary Algorithms,
In: Parameter Setting in Evolutionary Algorithms,
Volume 54 of the series Studies in Computational
Intelligence. pp. 19-46.
Farahani, R., 2009. Facility location: Concepts, models,
algorithms and case studies, Berlin Heidelberg:
Springer-Verlag, p. 549.
Fortin, F. -A., De Rainville, Fr. -M., Gardner, M. -A.,
Parizeau, M., Gagné, C., 2012. DEAP: Evolutionary
Algorithms Made Easy, Journal of Machine Learning
Research, No. 13, pp. 2171-2175.
Hruschka, E., Campello, R., Freitas, A., De Carvalho, A.,
2009. A survey of evolutionary algorithms for
clustering, IEEE Transactions on Systems, Man, and
Cybernetics, Part C: Applications and Reviews, v.39
n.2, p.133-155.
Kazakovtsev, A., Stupina, A., Orlov, V, Stashkov, V.,
2016a. Fuzzy clustering of EEE components for space
industry, IOP Conference Series: Materials Science
and Engineering, Vol. 155. pp. 012026.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
208

Kazakovtsev, L., Antamoshkin, A., 2014. Genetic
algorithm with fast greedy heuristic for clustering and
location problems, Informatica (Slovenia), Volume 38,
Issue 3, pp. 229-240.
Kazakovtsev, L., Orlov, V., Kazakovtsev, V., 2016b. New
genetic algorithm with greedy heuristic for clustering
problems with unknown number of groups, FACTA
UNIVERSITATIS (NIS), Ser. Math. Inform., Vol. 31,
No 4, pp. 907–917.
Kazakovtsev, L., Rozhnov, I., Orlov, V., 2018. Increase in
Accuracy of the Solution of the Problem of
Identification of Production Batches of Semiconductor
Devices, in proc. 4th International Conference on
Actual Problems of Electronic Instrument Engineering,
APEIE 2018, pp. 363-367.
Megiddo, N., Supowit, K. J., 1984. On the complexity of
some common geometric location problems, SIAM
Journal on Computing 13, pp. 182–196.
Mladenovic, N., Brimberg, J.,Hansen, P.,Moreno-Pérez, J.,
2007. The p-Median Problem: A Survey of
Metaheuristic Approaches, European Journal of
Operational Research, 179, pp. 927-939.
Pedregosa, F. et al., 2011. Scikit-learn: Machine Learning
in Python, Journal of Machine Learning Research, vol.
12, pp. 2825-2830.
Sopov, E., 2017. Genetic Programming Hyper-heuristic for
the Automated Synthesis of Selection Operators in
Genetic Algorithms, in Proc. of 9th International Joint
Conference on Computational Intelligence, IJCCI’17
pp. 231-238.
Wesolowsky, G., 1993. The Weber problem: History and
perspectives, Location science, No. 1, pp.5-23.
Xu, D., Tian, Y., 2015. A Comprehensive Survey of
Clustering Algorithms, Annals of Data Science, Volume
2, Issue 2, pp 165–193.
Genetic Programming based Synthesis of Clustering Algorithm for Identifying Batches of Electronic Components
209
