Adaptive Controller for Uncertain Multi-agent System Under
Disturbances
Sergey Vlasov
a
, Alexey Margun, Aleksandra Kirsanova and Polina Vakhvianova
Faculty of Control Systems and Robotics, ITMO University, Kronversky Pr. 49, St. Petersburg, 197101, Russia
Keywords:
Adaptive Control, Robotics, Robust Control, Parametric Uncertain.
Abstract:
This research is devoted to solving the problem of adaptive control algorithm synthesis for a mobile robots that
is part of a multi-agent system. Proposed approach consists of trajectory planner and inner agent controller.
The case of the passway intersection by the group of mobile robots is considered. Trajectory planner is based
on intersection management approach. Adaptive consecutive compensator used for agent controller synthesis.
Proposed approach provides control scheme which doesn’t depend on plant parameters. A group of mobile
robots is built for experimental evaluation of proposed approach. Obtained results confirm effectiveness of the
developed algorithms.
1 INTRODUCTION
Robotic systems are widespread in different spheres
of human activity. They are widely used in indus-
try, daily life, entertainment. Autonomous systems
that simplify people’s lives are becoming increasingly
popular. Among them there are multi-agent systems,
which consist of many robots, connected in a com-
mon network. Today, mobile multi-agent systems are
widely used by various major corporations, such as
Aliexpress, Amazon, etc. Robots perform various
functions, such as transportation of goods, cleaning of
premises, delivery of correspondence. Different algo-
rithms of automatic control are used for solving com-
plex tasks for the movement of robots and goods. Be-
sides, robots with different inner controllers are con-
trolled by one system to solve different tasks. Agents
have different parameters, for example, various en-
gines, which will give a various moment of force on
the motor shaft, can also have special wheels or al-
ternative wheel bases. Moreover some parameters
are nonstationary during functioning. All these pa-
rameters affect the synthesis of automatic control al-
gorithms, thereby complicate the development of the
whole system. If on the manufacture or warehouse
moving a lot of robots the crossroad become bottle
neck.
Scientific community conducts research in this
field. The article(Li et al., 2011) is about the
a
https://orcid.org/0000-0002-8345-7553
finite-time consensus problem for leaderless and
leader–follower multi-agent systems with external
disturbances. The paper (Olfati-Saber, 2006) de-
scribes theoretical framework for design and analysis
of distributed flocking algorithms, two cases of flock-
ing in free-space and presence of multiple obstacles
are considered. The article (Lauer and Riedmiller,
2000) focuses on distributed reinforcement learning
in cooperative multi-agent-decision-processes, where
an ensemble of simultaneously and independently
acting agents tries to maximize a discounted sum of
rewards. Our team also have achievement in this area.
The article(Bazylev et al., 2014) proposes a new con-
trol design of quadrotor with attached 2-DOF robotic
arm. In this research we make new control system for
new robotic agents.
The paper propose use of adaptive controller
which doesn’t depend on agents parameters for con-
trol of mobile robots group. Formal problem state-
ment is in the Section 2. Planing controller design for
system is in Section 3. Inner controller synthesis and
its stability analysis is in Section 4. Robots setup de-
scribed in Section 5. The results of experiments of
obtained control laws are shown in Section 6. Finally,
the research is summarized in Conclusions.
198
Vlasov, S., Margun, A., Kirsanova, A. and Vakhvianova, P.
Adaptive Controller for Uncertain Multi-agent System Under Disturbances.
DOI: 10.5220/0007827701980205
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 198-205
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 PROBLEM STATEMENT
We have multi-agent system consists of different
agents described by linear differential equations. All
agents are under disturbances. Parameters of agents
and disturbances are unknown but their upper and
lower bounds are known. Let us consider case, when
agents are moving through crossroad.
Main task is to develop control system which al-
low robots ride through crossroad without incident
and under disturbances, minimize difference between
acceleration of all agents in system. In this case, we
allocate two separate tasks
• Develop main control system, witch will keep all
information about all agent and say to each who
were will ride;
• Synthesis of controller which will have the same
structure for all different robots neglecting agents
parameters deviations. All necessary controller
parameters should be tune automatically.
Goal of main control is to transfer agents from
certain initial state to specified final state in a way
that some functional Y raise to extreme value with
excepted restriction. Specified Y is a bandwidth of
a simple road element size like little agent in the sys-
tem. Planning controller give to agent speed of mov-
ing y
mi
(t).
Every agent is described by equations
Q
i
(p)y
i
(t) = R
i
(p)u
i
(t) + f
i
(t)+
+
N
∑
i=1,i6= j
c
i j
(p)y
j
(t) +
M
∑
j=1,i6= j
γ
i j
(p)u
j
(t),
i = 1,N, j = 1,M,
(1)
where Q
i
(p) and R
i
(p) are linear differential opera-
tors with unknown parameters and degrees n
i
and m
i
respectively, y
i
(t) ∈ R are output signals, u
i
∈ R are
inputs, f
i
(t) are external bounded disturbances, c
i j
(p)
and γ
i j
(p) are linear differential operators with un-
known coefficients which describe input and ouptput
cross couplings respectively, N and M are numbers
of input and output signals, p = d/dt is a differential
operator, ρ
i
= n
i
− m
i
≥ 1 is a relative degree of i−th
subplant.
It is necessary to build inner controller which sat-
isfies following condition
|y
i
(t) − y
m
i
(t)| ≤ δ
i
,∀t ≥ T, (2)
where δ is a required accuracy, T is a time of tran-
sients.
Introduce following assumptions:
Assumption 1. All subplants of (1) are minimum
phase, i.e. R
i
(λ) are Hurwitz polynomials, where λ
is a complex variable.
Assumption 2. Unknown coefficients of operators
Q
i
(p) and R
i
(p) belong to the known compact set Ξ.
Assumption 3. Only the output variable is available
for measurements. Its derivatives are unmeasurable.
Assumption 4. The relative degree of the plant model
is assumed to be known.
Assumption 5. Maximum amplitude of disturbance
are known all disturbances are piecewise smooth.
3 PLANNING CONTROLLER
DESIGN
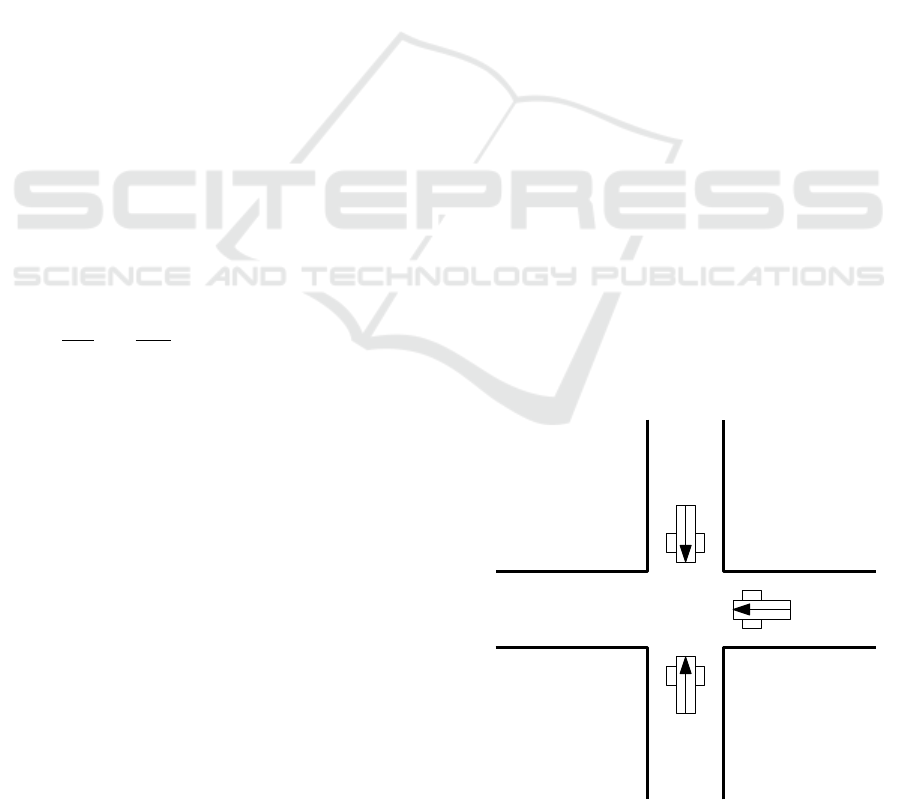
For a complete understanding of the intersection man-
agement, we should describe crossroad. It shows on
Fig1. It contains an intersection of four roads, each
may move in one direction only.
We have some agents stay on different parts
of crossroad. During the distributed intersection
management robots collaborate at some time point.
Let’s the road consist of the set of elementary areas
p
0
,..., p
n
. The crossroad is located on the area P
i
,
0 < i < n. In this context c represents a maximum
speed on the one road. It is necessary to provide
the intersection with other robots from the moment
when the agent has enough distance for safe braking.
Therefore, we need c + 1 steps to stop. Hence, the
full path of the braking is (c(c+ 1))/2+1 elementary
areas. In an example that present on the Fig.1, the
robot must start the process of interaction with other
vehicles at the moment when they located on position
p
i
((c(c + 1))/2 + 1).
Robot routing is based on the following basic prin-
ciples:
Figure 1: Schematic view of crossroad.
Adaptive Controller for Uncertain Multi-agent System Under Disturbances
199

1. Turning is performed according to scheme on
Fig.2;
2. Speed on the turning areas equals 1;
3. Speed of moving robot on the previous or next
time point may differ from the actual speed by
more than 1;
4. The robot tries moving with the maximum speed.
At low speeds, it seeks the opportunity to restore
it to maximum value;
5. Speed more than maximum is unacceptable.
In addition, when choosing variant of priority pas-
sage need to ensure maximum bandwidth of cross-
road for robots. In practice increasing bandwidth lead
to decrease interval between agents. And the endow-
ment as, in the some time interval T crossroad must
pass as possible robots, provided that in any random
moment of time (t
0
+ k) ∈ T would not be applying
for one simple area more then two agents. Then band-
width of road area will be higher the greater next treat-
ment
Y =
∑
L
l=1
∑
N
j=1
∑
M
i=1
n
l ji
M
, (3)
where N is count of robots on crossroad, L is count of
simple areas on crossroad, M is count of time interval,
for which N robots pass crossroad,
n
l ji
=



1, if j is robot in time i on the l element,
and n
l ji−1
6= n
l ji
0, in other case.
Conflict is the point in time when two or more
robots locate in the same elementary area. Rerout-
ing proceed according to order of conflict situations
occurrence. Each car involved in the conflict must
change route using speed reduction. It allows to solve
all other conflicts. In a general case, each conflict has
two possible crossroad intersection plans. We use a
variety of criteria to determine the best possible op-
tions.
According to Fig.2, when the agents driving up
to the crossroad elementary area after which it will
have to change the motion direction, the agent must
reduce speed to the minimum possible value. Speed
reduction is carried out according to the general prin-
ciples of smooth braking. After the robot passed the
intersection, it accelerates smoothly to the maximum
desired speed.
This approach computing by table meth-
ods(Viksnin et al., 2016).
1
1
1
2
2
3
3
Figure 2: Schematic view of crossroad.
4 INNER CONTROLLER DESIGN
4.1 Controller Design
For controller synthesis we use consecutive compen-
sator approach (Margun and Furtat, 2015), (Mar-
gun et al., 2017a). Compensator applied in decen-
tralized manner (independent controller for all sub-
plants). Choose control law as follows
u
i
(t) = −(α
i
+ β
i
)K
i
(p) ˆe
i
(t), (4)
where α
i
, β
i
> 0, K
i
(λ) are such Hurwitz polyno-
mails of degrees ρ
i
− 1 that (Q
i
(λ) + αR
i
(λ)K
i
(λ))
are Hurwitz polynomials, ˆe
i
(t) are estimates of errors
e
i
(t) = y
i
(t) − y
m
i
(t).
Taking into account (1) and (4) obtain errors dy-
namics in the form
(Q
i
+ αR
i
K
i
)e
i
= R
i
K
i
(−(α
i
+ β
i
)(e
i
− ˆe
i
) − β
i
e
i
)+
+ ϕ
i
(t) +
N
∑
i=1,i6= j
c
i j
e
j
+
+
M
∑
j=1,i6= j
γ
i j
(α
i
+ β
i
)K
i
(e
i
− ˆe
i
)−
−
M
∑
j=1,i6= j
γ
i j
(α
i
+ β
i
)K
i
e
i
,
ϕ
i
(t) = −Q
i
y
m
i
+
N
∑
i=1,i6= j
c
i j
y
m
j
+ f
i
,
(5)
where ϕ
i
(t) is a bounded function.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
200

Rewrite (5) in state space representation





















˙
ε
i
= A
i
ε
i
+ B
i
(−β
i
e + (α
i
+ β
i
)(e
i
− ˆe
i
))+
B
1
i
ϕ
i
+
N
∑
i=1,i6= j
W
i j
ε
i
+ (α
i
+ β
i
)
M
∑
j=1,i6= j
U
i j
(e
i
− ˆe
i
)+
+
N
∑
i=1,i6= j
D
i j
ε
j
,
e
i
=
¯
L
i
ε,
(6)
where ε
i
is an error state vector of i - th subplant,
A
i
,B,B
1
i
,W
i j
,U
i j
,D
i j
are matrices obtained from (5)
to (6) transition,
¯
L
i
= [1 0 ... 0].
Rewrite Closed loop system (6) in matrix form





˙
ε = Aε + B(−βe + (α + β)(e − ˆe)) + B
1
ϕ+
+W ε +U (e − ˆe) + Dε,
e =
¯
Lε,
(7)
where ε
T
= [ε
1
... ε
N
], A = diag{A
i
}, B
1
=
diag{B
1
i
}, α = diag{α
i
}, β
i
= diag{β
i
}, ϕ
T
=
[ϕ
1
... ϕ
N
] is a vector of bounded functions,
W,U,D are matrices obtained form (6) to (7) transi-
tion.
For implementation of control law (4) it is neces-
sary to know ρ − 1 derivatives of output signal. For
their estimation introduce observer (Margun et al.,
2017b)
(
˙
ξ
i
(t) = σ
i
Γ
i
ξ
i
(t) + σ
i
G
i
e
i
(t),
ˆe
i
(t) = L
i
ξ
i
(t),
(8)
where ξ
i
(t) ∈ R
ρ
i
−1
is an observer state vector, Γ
i
=

0 I
ρ
i
−2
−k
1
i
... −k
ρ
i
−1i

are Hurwitz matrices, G
i
=
[0 0 k
1
i
]
T
, I
ρ
i
−2
is a identity matrix of order ρ
i
−2,
L
i
= [1 0 ... 0], σ
i
> α
i
+ β
i
.
Rewrite (8) in matrix form
(
˙
ξ(t) = σΓξ(t) + σGe(t),
ˆe(t) = Lξ(t),
(9)
where ξ(t) = diag{ξ
i
(t)}, σ = diag{σ
i
}, L =
diag{L
i
}.
Introduce error of observer estimates
(
η
i
(t) = L
T
i
e
i
(t) − ξ
i
(t),
˙
η
i
(t) = σ
i
Γ
i
η
i
(t) + L
T
i
˙e
i
(t).
(10)
and rewrite it in matrix form
(
η(t) = L
T
e(t) − ξ(t),
˙
η(t) = σΓη(t) + L
T
˙e(t),
(11)
where η(t) = diag{η
i
(t)}.
Finally closed loop system with observer takes the
form





˙
ε = Aε + B(−βe + (α + β)(e − ˆe)) + B
1
ϕ+
+W ε +U (e − ˆe) + Dε,
˙
η = σΓη + L
T
˙e,
(12)
Let us analyse stability of (12).
Introduce Lyapunov function candidate
V = ε
T
(t)Pε(t) + η
T
(t)Hη(t), (13)
where P and H are solutions of Lyapunov equations
A
T
p+PA = −Φ
1
,Γ
T
H +HΓ = −Φ
2
respectively, Φ
1
and Φ
2
are positive defined symmetric matrices.
Differentiating (13) along trajectories (12) gives
us
˙
V = ε
T
(A
T
P + PA)ε− 2βε
T
PB
¯
Lη+
+ 2ε
T
P(U + (α + β)B)Lη + 2ε
T
PB
1
ϕ+
+ 2ε
T
P(W + D)ε + ση
T
(Γ
T
H + HΓ)η+
+ 2η
T
HL
T
¯
L(A + D +W )ε − 2βη
T
HL
T
¯
LB
¯
Lη+
+ 2(α + β)η
T
HL
T
¯
LBLη+
+ 2η
T
HL
T
¯
LB
1
ϕ + 2η
T
HL
T
¯
LU Lη.
(14)
where υ is a small positive number.
Right terms of (14) are bounded by inequalities
− 2βε
T
PB
¯
Lη ≤ βυε
T
ε + βυ
−1
η
T
¯
L
T
B
T
PPB
¯
Lη,
2ε
T
PU Lη ≤ υε
T
PU LL
T
U
T
Pε + υ
−1
η
T
η,
2ε
T
PBLη ≤ υε
T
PBLL
T
B
T
Pε + υ
−1
η
T
η,
2ε
T
PB
3
ϕ ≤ βε
T
PB
3
B
T
3
Pε + β
−1
ϕ
T
ϕ,
2η
T
HL
T
¯
L(A + D +W)ε ≤
υε
T
(A + D +W)
¯
L
T
LHHL
T
¯
L(A + D +W)ε+
+ υ
−1
η
T
η,
2η
T
HL
T
¯
LB
1
ϕ ≤ βη
T
HL
T
¯
LB
1
B
T
1
¯
L
T
LHη + β
−1
ϕ
T
ϕ
(15)
Taking into account (15) bound derivative of Lya-
punov function
˙
V ≤ −ε
T
R
1
ε − η
T
R
2
η + θ, (16)
where R
1
= Φ
1
− 2P(W + D) − βυ − υPULL
T
U
T
P −
υ(α + β)PBLL
T
B
T
P − βPB
1
B
T
1
P − υ(A + D +
W )
¯
L
T
LHHL
T
¯
L(A + D +W ),
Adaptive Controller for Uncertain Multi-agent System Under Disturbances
201

R
2
= σΦ
2
− 2βHL
T
¯
LB
¯
L − 2(α + β)HL
T
¯
LBL −
2HL
T
¯
LU L − βυ
−1
¯
L
T
B
T
PPB
¯
L − 2υ
−1
− (α + β)υ
−1
,
θ = 2
ϕ
T
ϕ
β
.
It should be noted that we always can provide pos-
itivity of R
1
,R
2
by choose of big enough α and σ.
Combining (13) and (16) we obtain
˙
V ≤ −ςV + θ, (17)
where ς =
λ
min
(R
1
)
λ
max
(P)
, λ
min
(·)(λ
max
(·)) are minimum
(maximum) eigenvalues of corresponding matrices.
Solving inequality (17) with respect to V yields
V ≤ (V (0) −
θ
ς
)e
−ςt
−
θ
ς
. (18)
Because of λ
min
(P)ε
T
ε ≤ V , we can calculate
bounds on tracking error
|e| ≤
s
1
λ
min
(P)

V (0) −
θ
ς

e
−ςt
+
θ
ς

(19)
Therefore proposed controller provides tracking
of outputs for the reference trajectory in steady state
with accuracy
δ =
s
1
λ
min
(P)
θ
ς
(20)
4.2 Controller Tuning
To increase the plant stability and reduce the tracking
error we need to increase controller coefficients. But,
when coefficient reach some value, further increasing
leads to insignificant reducing of the tracking error.
Moreover, increasing of controller coefficients leads
to increasing of overshoot and required control signal
magnitude. For adaptive tuning of the controller in
(Bobtsov, 2008) following algorithm is proposed
˜
k =
Z
t
0
χ(s)ds,
χ(t) =

0,|e| < δ,
χ
0
,|e| > δ,
σ = σ
0
˜
k
2
,
(21)
where
˜
k = α + β, χ
0
is an arbitrary chosen positive
number which control velocity of coefficient increas-
ing.
But there is no any recommendation for controller
coefficients initial values choosing. Note, that algo-
rithm (21) does not guarantees stability of closed loop
system during transient time. The choice of the coef-
ficients close to the their desired values will provide
stability, significantly reduce the control tuning time
and therefore the transient time.
Let us propose an algorithm to solve this problem.
Step 1. On the base of known bounded set Ξ define
set of Kharitonov polynomials (Kharitonov, 1978) for
open-loop systems
P
1
= q
0
+ q
1
s + q
2
s
2
+ q
3
s
3
+ ...,
P
2
= q
0
+ q
1
s + q
2
s
2
+ q
3
s
3
+ ...,
P
3
= q
0
+ q
1
s + q
2
s
2
+ q
3
s
3
+ ...,
P
4
= q
0
+ q
1
s + q
2
s
2
+ q
3
s
3
+ ....
(22)
Step 2. Use consecutive compensator method and
tuning algorithm (21) with zero initial conditions of
controller coefficients for stabilization of each poly-
nomial.
˜
k
i
=
Z
t
0
χ
i
(s)ds,
χ
i
(t) =

0,|e| < δ,
χ
0i
,|e| > δ,
χ
0i
= α
i
+ β
i
,
σ
i
= σ
0i
˜
k
2
i
,
i =
1,4.
(23)
Step 3. Choose the maximum values of the
Kharitonov polynomials coefficients of the regulators
as the initial values of the plant controller. In this case
adaptive tuning algorithm takes the form
˜
k = max(
˜
k
i
) +
Z
t
0
χ
i
(s)ds,
χ(t) =

0,e < δ,
χ
0
,e > δ,
χ
0
= α + β,
σ = σ
0
˜
k
2
.
(24)
The characteristic polynomial of the closed-loop
system has the form Q(λ) + (α + β)R(λ)D(λ), where
first term is non Hurwitz polynomial and second term
is Hurwitz polynomial. Thus, the increasing of the
controller coefficient suppresses an unstable compo-
nent of a closed-loop system. Therefore, sufficiently
large choice of coefficients provides stability of the
Kharitonov polynomials, and hence the stability of
control plant too.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
202

5 AGENT MODEL SETUP
Let us describe the mathematical model of agent,
which was created for multi-agent systems experi-
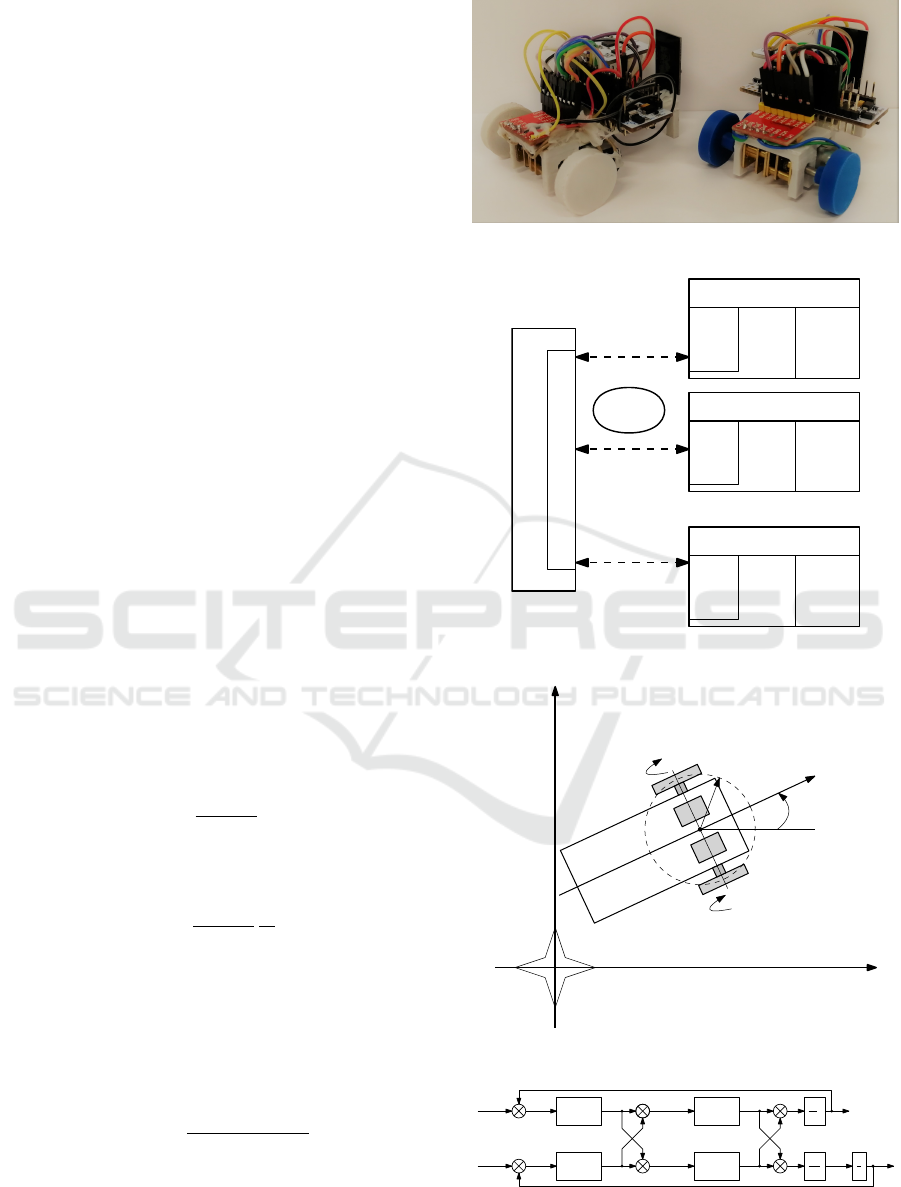
ments. There is the photo of agent on the Fig.3.
The agent is a hand made robot with two
wheels, computing boards and battery. It dimensions
are (0.070×0.055×0.050)m. Hardware are consists
of microcontroller board, DC-motors driver board,
IMU-module board and Wi-Fi module board. Main
controller of agent is STM32F031K6. Wi-Fi board is
ESP-01 module with own firmware.
On the outdoor robots coordination is defined by
satellite navigation systems, but when experiments
are made in laboratory which in the building, it is
impossible to use navigation systems. It this case
we use IMU-module consist of accelerometer on chip
LIS331DLH, electronic compass on chip LIS3MDL,
gyroscope on chip L3G4200D and barometer. On
measuring from this module we calculate coordinates
of robots.
For control all agents in system has been imple-
mented next structure - on PC make up Wi-Fi ac-
cess point and start TCP server application. This
application interacts with control system on Matlab.
Each agent by ESP-01 application connect to Wi-Fi
network, connect to TCP server and make a bridge
between STM controller with own control system
and between Matlab control system of all multi-agent
stand. This schematic can be seen in Fig.4
Describe robot motion as change coordinates of
central point of robot in time. Robot schematically
imaged on Fig.5. Value of longitudinal speed is de-
fined as average between linear speed of each wheel
V =
ω
l
+ ω
r
2
r
k
(25)
where ω
l
,ω
r
angular speed of wheels, r
k
radius of
wheel. If angular speed of wheels is different, raised
rotation moment
ω =
ω
l
+ ω
r
2
r
k
R
(26)
where R long wheel base.
We can consider angular speed of each wheel
ω
r
(s) = W
D
r
(s)U
r
(s)
ω
l
(s) = W
D
l
(s)U
l
(s)
(27)
where U
r
(s),U
l
(s) are Laplace image of control volt-
age, W
D
r
,W
D
l
transfer function of motors in from
W (s) =
1/k
t
e
t
m
s
2
+t
m
s + 1
(28)
Adding control low(4) designed in Section 4 writ-
ten in transfer function form to robot model we get
agent with controller. Structure of agent demonstrated
by Fig.6.
Figure 3: Photo of robots.
TCP-server
Wi-Fi
TCP
ESP
STM
Agent
client
TCP
ESP
STM
Agent
client
...
TCP
ESP
STM
Agent
client
Multi-agent control system
Figure 4: Multi-agent system connection.
D
r
D
l
V
ϕ
R
ω
l
ω
r
N
E
S
W
Y
X
Figure 5: Schematically images of agent.
W
D
r
(s)
r
k
2
W
D
l
(s)
r
k
2R
+
+
+
−
ω
r
(s)
ω
l
(s)
V (s)
ω(s)
U
r
(s)
U
l
(s)
W
V
(s)
W
ω
(s)
+
−
+
+
U
1
(s)
U
2
(s)
V
∗
(s)
ω
∗
(s)ω
∗
(s)
+
+
−
−
1
s
ϕ(s)
ε
v
(s)
ε
ϕ
(s)
Figure 6: Structure of agent with controller.
Adaptive Controller for Uncertain Multi-agent System Under Disturbances
203

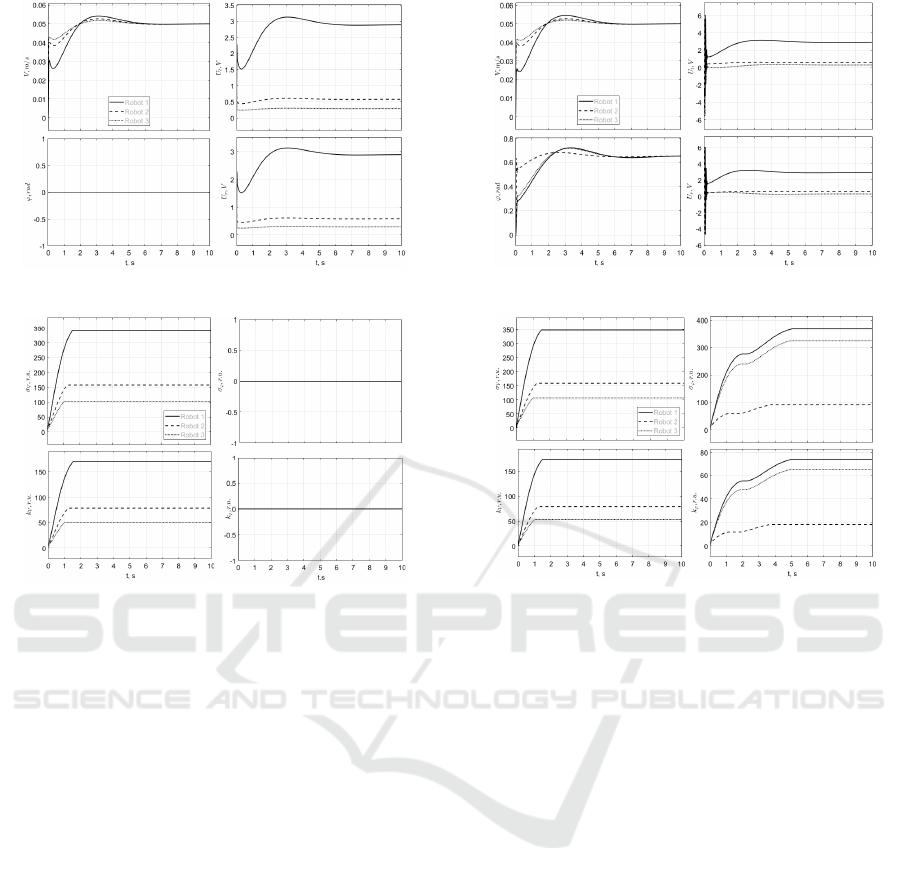
Figure 7: Experiment 1. Speed and angle of 3 robots.
Figure 8: Experiment 1. Regulators coefficients of 3 robots.
6 EXPERIMENTS
We take 3 different models of robots with same mo-
tors and different wheels and wheels base. Parameters
of the systems
1. Robot 1. r
k
= 0.01m., robot base 0.02m.
2. Robot 2. r
k
= 0.05m., robot base 0.02m.
3. Robot 3. r
k
= 0.1m., robot base 0.2m.
There are two experiments, the first is set speed
of motion of robot V = 0.05m/s and angle ϕ = 0,
the next is set the same speed, but with angle ϕ =
0.65rad. Result of experiments are on Fig.7 - 10.
According to the graphs in first experiment, take
required speed it time about 2 seconds, but first robot
with some over-regulation(Fig. 7). Control signals are
higher on robot with small wheels, and in this case,
coefficients of regulator high on this robot(Fig. 8).
In the next experiment, when robots ride and turns,
transition processes of speed are same as in first ex-
periment. But in control signals we can see emer-
gence at start of motion, after that, processes be-
comes simple(Fig. 9). Coefficients of regulator in-
crease too(Fig. 10).
Figure 9: Experiment 2. Speed and angle of 3 robots.
Figure 10: Experiment 2. Regulators coefficients of 3
robots.
7 CONCLUSIONS
During this research, was designed control system for
group of robots moving through crossroad. The pur-
posed approach consist of external controller which
define desired speed of robots and inner adaptive con-
trol system. Designed adaptive control law provide
desired moving speed with necessary accuracy inde-
pendently of parameters of agents. For analysis con-
trol multi-agent system own robots were made. Ex-
periments on this robots show effectiveness of the de-
veloped system.
ACKNOWLEDGEMENTS
This work was supported by Goverment of Russian
Federation (Grant 08-08).
REFERENCES
Bazylev, D., Zimenko, K., Margun, A., Bobtsov, A., and
Kremlev, A. (2014). Adaptive control system for
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
204

quadrotor equiped with robotic arm. 2014 19th Inter-
national Conference on Methods and Models in Au-
tomation and Robotics, MMAR 2014, pages 705–710.
Bobtsov, A. (2008). Output control algorithm with the com-
pensation of biased harmonic disturbances. Automa-
tion and Remote Control, 69(8):1289–1296.
Kharitonov, V. L. (1978). The asymptotic stability of the
equilibrium state of a family of systems of linear
differential equations. Differentsial’nye Uravneniya,
14(11):2086–2088.
Lauer, M. and Riedmiller, M. (2000). An algorithm for dis-
tributed reinforcement learning in cooperative multi-
agent systems. pages 535–542.
Li, S., Du, H., and Lin, X. (2011). Finite-time consen-
sus algorithm for multi-agent systems with double-
integrator dynamics. Automatica, 47(8):1706–1712.
Margun, A., Bobtsov, A., and Furtat, I. (2017a). Algorithm
to control linear plants with measurable quantized out-
put. Automation and Remote Control, 78(5):826–835.
Margun, A. and Furtat, I. (2015). Robust control of lin-
ear mimo systems in conditions of parametric uncer-
tainties, external disturbances and signal quantization.
2015 20th International Conference on Methods and
Models in Automation and Robotics, MMAR 2015,
pages 341–346.
Margun, A., Furtat, I., and Kremlev, A. (2017b). Robust
control of twin rotor mimo system with quantized out-
put. IFAC-PapersOnLine, 50(1):4849–4854.
Olfati-Saber, R. (2006). Flocking for multi-agent dynamic
systems: Algorithms and theory. IEEE Transactions
on automatic control, 51(3):401–420.
Viksnin, I. I., Zikratov, I. A., Shlykov, A. A., Belykh, D. L.,
Komarov, I. I., and Botvin, G. A. (2016). Planning of
autonomous multi-agent intersection. 8:01007.
Adaptive Controller for Uncertain Multi-agent System Under Disturbances
205