Semi-supervised Audio Source Separation based on the Iterative

Estimation and Extraction of Note Events

Alejandro Delgado Castro

and John E. Szymanski

Department of Electronic Engineering, University of York, North Yorkshire, U.K.

Keywords:

Audio Source Separation, Note Event Detection, Fundamental Frequency Estimation, Note Event Tracking,

Separation of Overlapping Harmonics, Time-domain Subtraction, Semi-supervised Estimation.

Abstract:

In this paper, we present an iterative semi-automatic audio source separation process for single-channel poly-

phonic recordings, where the underlying sources are isolated by clustering a set of note events, which are

considered to be single notes or groups of consecutive notes coming from the same source. In every iteration,

an automatic process detects the pitch trajectory of the predominant note event in the mixture, and separates

its spectral content from the mixed spectrogram. The predominant note event is then transformed back to

the time-domain and subtracted from the input mixture. The process repeats using the residual as the new

input mixture, until a predeﬁned number of iterations is reached. When the iterative stage is complete, note

events are clustered by the end-user to form individual sources. Evaluation is conducted on mixtures of real

instruments and compared with a similar approach, revealing an improvement in separation quality.

1 INTRODUCTION

Separating pitched instruments from within poly-

phonic single-channel mixtures represents a challeng-

ing task which has been intensively studied during the

last few decades, with direct applications in music

information retrieval (MIR), audio coding and com-

pression, content-based analysis, among many oth-

ers (Zivanovic, 2015). Most of the complexities in-

volved in this process are due to the very rich and

non-stationary nature of music, whose evolution over

time and frequency creates many regions where the

sources overlap (Raﬁi et al., 2018).

Audio source separation algorithms are based on

established signal processing techniques, such as in-

dependent subspace analysis (Taghia and Doostari,

2009), non-negative matrix factorization (Bryan and

Mysore, 2013), or computational auditory scene anal-

ysis (Jang et al., 2003). Estimated sources are ex-

tracted using additive synthesis or time-frequency

masking, where overlapping content is resolved by

sinusoidal modelling (Parsons, 1976), spectral ﬁlter-

ing (Every and Szymanski, 2006), common ampli-

tude similarity (Li et al., 2009), amplitude and phase

reconstruction (Ponce de Le

on V

azquez and Beltr

https://orcid.org/0000-0002-5475-7813

https://orcid.org/0000-0003-2525-654X

azquez, 2012), or harmonic bandwidth companding

(Zivanovic, 2015). In recent years, deep neural net-

works have also been explored as a way to introduce

machine learning into the separation process (Grais

et al., 2017; Chandna et al., 2017).

A common practice followed by various separa-

tion approaches is to estimate and extract all under-

lying sources jointly, relying on a good characteriza-

tion of their components. One way to characterize au-

dio sources is by tracking their fundamental frequen-

cies across time. However, when pitch trajectories

for multiple sources are automatically estimated from

the input mixture, their accuracy deteriorates and the

complexity of the joint separation approach increases.

On the other hand, an iterative framework in

which sources are separated in sections should have

several advantages. First, the system only needs to

concentrate on separating a small section of audio in

every iteration, and second, the number of interact-

ing components should decrease after each section is

extracted, reducing the complexity of detecting other

sections still present in the mixture.

In this paper, we propose an audio source separa-

tion strategy in which the underlying sources are ob-

tained by clustering a set of note events, which can be

seen as harmonic sounds representing either a single

musical note or a group of consecutive notes coming

from the same source. These note events are automat-

Delgado Castro, A. and Szymanski, J.

Semi-supervised Audio Source Separation based on the Iterative Estimation and Extraction of Note Events.

DOI: 10.5220/0007828002730279

In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 273-279

ISBN: 978-989-758-378-0

273

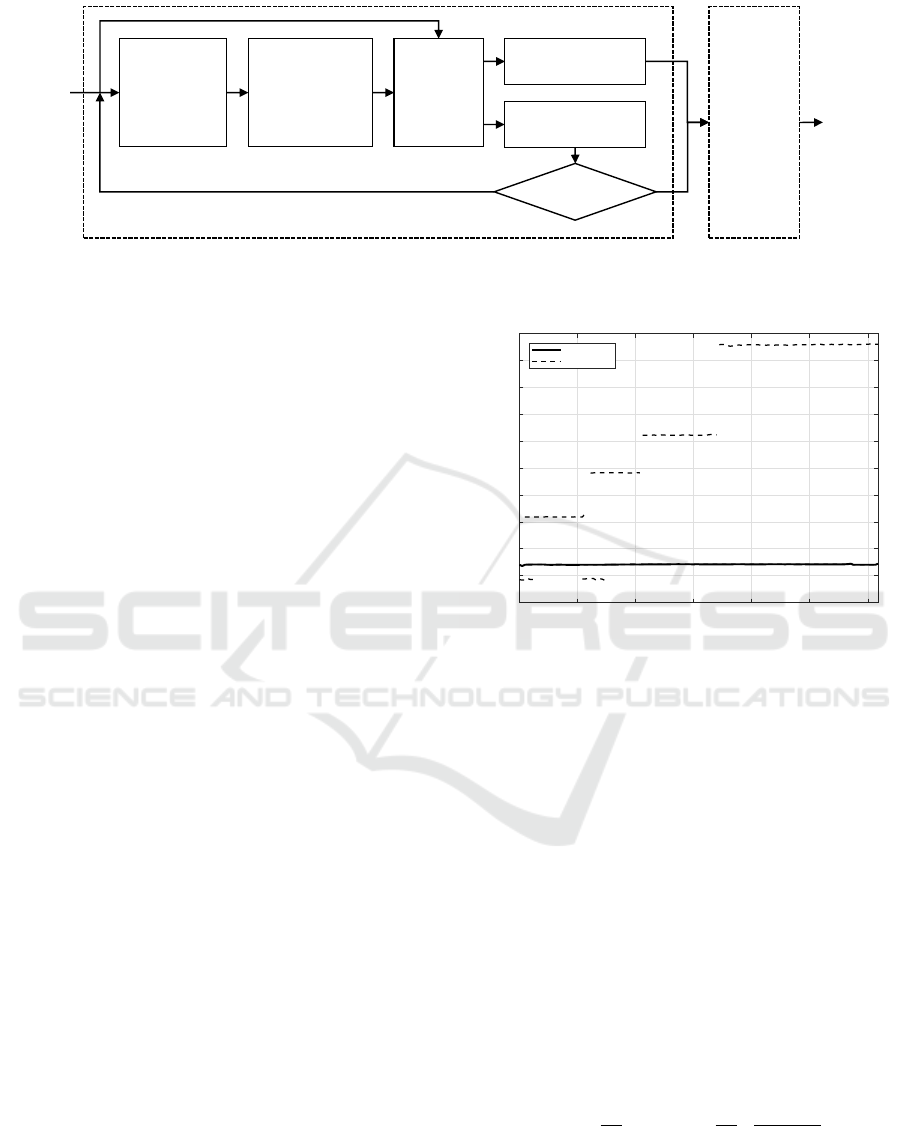
Input

Audio

Mixture

Initial

Multipitch

Estimation

Using

(Duan et al.,

2010)

Selection of the

Predominant

Note Event and

its Pitch

Trajectory

Note Event

Separation

Extracted

Note Events

Residual

Last

Iteration?

Clustering

of Note

Events into

Sources by

means of

User

Interaction

Yes

Separated

Sources

Automatic Supervised

Figure 1: Block diagram of the proposed system showing its two main stages: the automatic detection and separation of note

events, and their clustering into individual sources.

ically detected and separated from the input mixture

using an iterative approach. Every iteration consists

of detecting the pitch trajectory of the predominant

note event, separating its spectral content, and extract-

ing its energy from the mixture using subtraction in

the time domain. A simpliﬁed block diagram of the

proposed system is shown in Figure 1.

The rest of the paper is organised as follows. Sec-

tions 2 describes the processing stages involved in a

single iteration of the system, in which a note event is

detected and separated from the input mixture. Sec-

tion 3 deals with the clustering of note events into

sources once the iterative stage is complete. Evalu-

ation is conducted in Section 4 where separation re-

sults are compared against the ISSE software pack-

age, which is based on a user-informed version of

non-negative matrix factorization (NMF) and proba-

bilistic methods. Finally, Section 5 summarizes our

conclusions from this work.

2 ITERATIVE STAGE

2.1 Pitch Trajectory of the Predominant

Note Event

In every iteration, the input signal is decomposed us-

ing the Short-Time Fourier Transform (STFT), with-

out using zero-padding, and the multipitch detector

in (Duan et al., 2010) is used to generate the array P

of fundamental frequency estimates, with dimensions

J × M, where J is the number of pitch estimates in

every frame and M is the number of frames in the de-

composition. A salience measure is then assigned to

each of these estimates, based on the spectral mag-

nitude summation of their ﬁrst H partial amplitudes.

Considering the m-th frame, the salience of its j-th

pitch candidate can be written as:

0 0.5 1 1.5 2 2.5 3

Time (s)

300

400

500

600

700

800

900

1000

1100

1200

1300

F0 (Hz)

Predominant

Note Events

Figure 2: Note events detected in a mixture of viola and

clarinet during the ﬁrst iteration of the system. The viola

note has been selected as the predominant event.

∑

h=1

X(m,h f

) (1)

where S

is the salience of the j-th pitch candidate in

frame m, with fundamental frequency f

= P( j, m),

and X(m, f ) is the magnitude spectrogram of the cur-

rent input signal. Note events are detected by ﬁnding

continuous segments of estimates, across all levels of

P, for which the change in fundamental frequency be-

tween adjacent frames is not higher than one semi-

tone. All detected note events are arranged in a table

and their predominances are computed. Considering

the k-th note event in the table, existing in level j = j

starting at frame m

and ending at frame m

, its pre-

dominance is deﬁned as follows.

∑

m=m



− m



(2)

where N

and N

are normalization constants that map

the total salience and duration of note events into the

range 0 to 1. The note event with the highest predom-

inance is selected as the predominant one. Its pitch

SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications

274

820 840 860 880 900 920 940 960 980 1000

Frequency (Hz)

100

150

Magnitude

Observation

Dominant

Subtraction

820 840 860 880 900 920 940 960 980 1000

Frequency (Hz)

100

150

Magnitude

Dominant

Secondary

(a)

(b)

Figure 3: Separation of an overlapping harmonic. (a) Mag-

nitude spectra of the original mixture, dominant component

and subtraction. (b) Magnitude spectra of principal and sec-

ondary components. A diamond marks the ideal centre fre-

quency of the current harmonic partial.

trajectory, formed by the fundamental frequency esti-

mates assigned to it, is expanded to encompass poten-

tial misallocated estimates in adjacent frames. If an

adjacent frame has an estimate within a semi-tone of

the average pitch of the note event, it is added on to

the pitch trajectory of the note event, providing that

its salience does not indicate a transition to a differ-

ent note event. The expanded pitch contour is used to

estimate the magnitude spectrogram of the separated

predominant note event.

An example is presented in Figure 2 for a mix-

ture of viola and clarinet, where the ﬁrst plays the

note A4, while the second plays the notes D]5, G5,

A]5, and D]6. During the ﬁrst iteration, seven note

events are detected in the mixture and the long viola

note (event 1) is selected as the predominant one. No-

tice that note events 6 and 7 do not correspond to real

musical notes, they originate from spurious estimates

misleadingly generated by the multipitch estimator at

this stage, and which are later removed by the system.

2.2 Separated Magnitude Spectrogram

of the Predominant Note Event

The pitch trajectory of the predominant note event

contains its fundamental frequency estimates and the

indexes of the frames in which they are active. It is

now possible to ﬁnd a set of harmonically related par-

tials in every frame, associated with these fundamen-

tal frequencies by analysing each magnitude spectrum

and ﬁnding spectral peaks closest to the ideal har-

monic frequencies.

Parameters for each selected spectral peak (cen-

tre frequency, absolute magnitude and phase angle)

0 0.5 1 1.5 2 2.5 3

Time (s)

1000

2000

3000

Frequency (Hz)

0 0.5 1 1.5 2 2.5 3

Time (s)

1000

2000

3000

Frequency (Hz)

(a)

(b)

Figure 4: Estimation of the ﬁrst predominant event in a mix-

ture of viola and clarinet. (a) Spectrogram of the input mix-

ture. (b) Spectrogram of the separated predominant note

event (viola A4). In both cases, the frame size is 2048 sam-

ples and the hop size is 256 samples.

are computed and used to generate a synthetic single-

component sinusoidal partial, hereafter referred as the

dominant component of the spectral peak. If there is

no overlap with other sources, the dominant compo-

nent can be used to construct the separated magnitude

spectrum of the predominant note event in the current

frame. However, if the spectral peak also contains

contributions from other sources, it is considered as

a shared peak, and further processing is required to

achieve the separation of its components.

Following the method presented in (Parsons,

1976), the dominant component is subtracted from

the shared peak in order to ﬁnd potential overlapping

components. If a signiﬁcant peak appears in the sub-

traction, it is treated as energy coming from a different

source and its parameters are used to generate a sec-

ondary component. Assuming a dual-peak model for

the shared peak, in which the observation is a combi-

nation of the target harmonic partial plus some other

interfering partial, the synthetic component closer to

the ideal harmonic frequency, associated with the pre-

dominant note event, is selected and used to construct

the separated magnitude spectrum.

Figure 3 shows an example of an overlapping par-

tial in the mixture of viola and clarinet previously

mentioned, taken from a time frame centred at t =

1.3 s. It can be noticed that the dominant component

(centred at 925 Hz) is the fundamental harmonic of

the clarinet ( f

= 922 Hz), whilst the secondary com-

ponent (centred at 882 Hz) is the second harmonic

of the viola ( f

= 442 Hz). Given that the secondary

component is much closer to the ideal position of the

second harmonic of the viola, it is selected and used to

construct the magnitude spectrum of the separated vi-

ola. The magnitude spectrograms of the input mixture

Semi-supervised Audio Source Separation based on the Iterative Estimation and Extraction of Note Events

275

0 0.5 1 1.5 2 2.5 3

Time (s)

300

400

500

600

700

800

900

1000

1100

1200

1300

F0 (Hz)

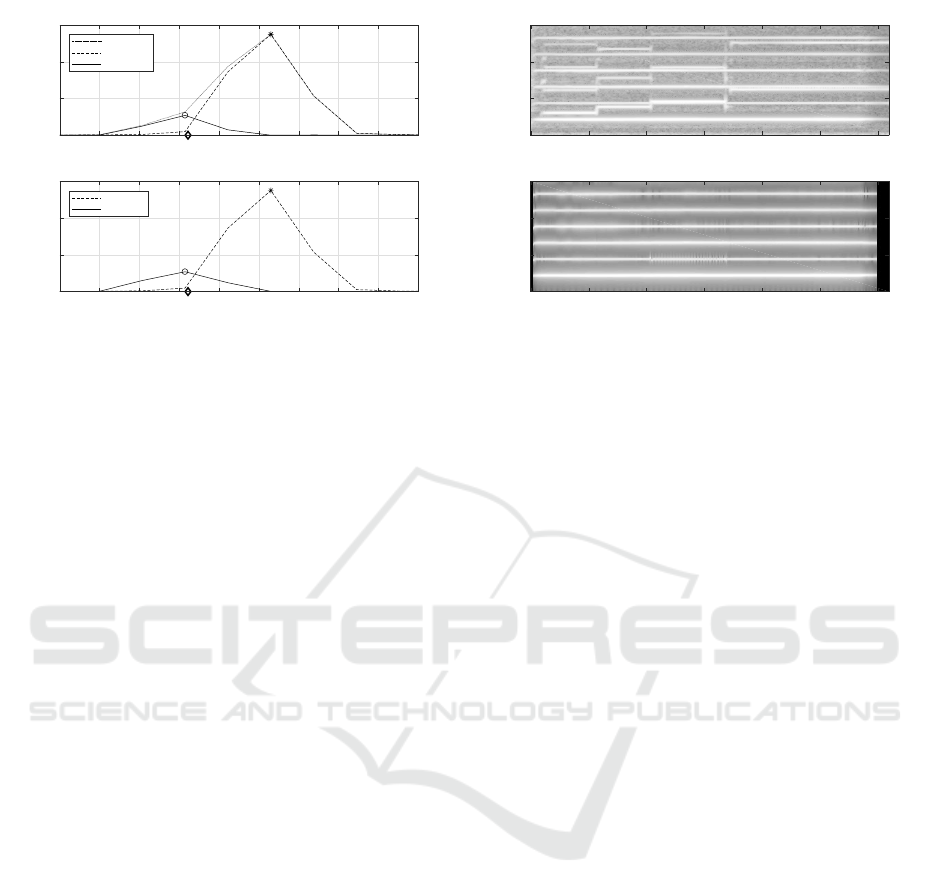
Figure 5: Estimated pitch trajectories of ﬁve note events, it-

eratively extracted from a mixture of viola and clarinet. The

numbering of the trajectories follows the extraction order.

and the estimated predominant note event are shown

in Figure 4. Notice the separation of the overlapping

region between t = 1.1 s and t = 1.7 s.

2.3 Reconstruction and Subtraction

Time-frequency masking was considered for the ex-

traction of the separated predominant note event from

the input mixture, but ﬁtting an appropriate mask

proved difﬁcult for note events having low fundamen-

tal frequencies. Hence, the extraction of the predomi-

nant note event is carried out by reconstructing its sep-

arated spectrogram, retaining the original phase infor-

mation of the mixture, and subtracting it from the in-

put mixture in the time domain. The main advantage

of this strategy is that the estimated harmonics of the

predominant note event are not signiﬁcantly distorted

by other harmonic partials in the nearby, or by other

frequency components associated with other sources.

A residual is also obtain after the subtraction, and

it is used as the new input signal for the next itera-

tion. The iterative process continues until a prede-

ﬁned maximum number of iterations is reached.

3 CLUSTERING

At the end of this iterative stage, most of the energy

contained in the original mixture should have been al-

located within a set of note events, which can be clus-

tered to form individual sources by the end-user, who

may use the pitch trajectories of the separated note

events as a hint to ﬁnd an appropriate clustering of the

events. The end-user can also listen to each individual

note event in order to obtain further guidance. Group-

ing or instrument identiﬁcation algorithms could be

used at this stage to remove the need for user input,

0 0.5 1 1.5 2 2.5 3

-1

Amp

(a)

0 0.5 1 1.5 2 2.5 3

-1

Amp

(b)

0 0.5 1 1.5 2 2.5 3

-1

Amp

(c)

0 0.5 1 1.5 2 2.5 3

-1

Amp

(d)

0 0.5 1 1.5 2 2.5 3

Time (s)

-1

Amp

(e)

Figure 6: Extracted note events from a mixture of viola and

clarinet. (a) Viola A4, (b) Clarinet D]6, (c) Clarinet A]5,

(d) Clarinet D]5, and (e) Clarinet G5.

0 0.5 1 1.5 2 2.5 3

-1

Amp

0 0.5 1 1.5 2 2.5 3

-1

Amp

0 0.5 1 1.5 2 2.5 3

-1

Amp

0 0.5 1 1.5 2 2.5 3

Time (s)

-1

Amp

(a)

(b)

(c)

(d)

Figure 7: Original and estimated sources from a mixture of

viola and clarinet. (a) Original viola, (b) Estimated viola,

but are not the emphasis of this research. Continuing

with the example mixture of viola and clarinet, after

ﬁve iterations of the system, the ﬁnal set of estimated

pitch trajectories is presented in Figure 5, and their

corresponding extracted note events are shown in Fig-

ure 6. The end-user is now able to cluster note events

2, 3, 4 and 5 in order to form the separated clarinet,

while note event 1 is used to form the separated viola.

A comparison between the original and the estimated

sources, for the example mixture of viola and clarinet,

is presented in Figure 7.

4 EVALUATION

Separation performance is evaluated in three different

experiments, where the proposed algorithm is applied

to a number of audio mixtures. The ﬁrst two exper-

iments consider audio mixtures consisting solely of

SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications

276

pitched sources, while the third one introduces one

percussive source. Four pitched instruments are stud-

ied (violin, clarinet, tenor saxophone and bassoon),

taken from excerpts of the Bach10 database (Duan

et al., 2010). The percussive source consists of a syn-

thesized sequence of snare drums and cymbals. These

test recordings are available online

The quality of the separation is assessed by mea-

suring the source to distortion ratio (SDR), source to

interference ratio (SIR), and source to artifacts ratio

(SAR), as deﬁned in (Vincent et al., 2006), where

each estimated source ˆx

is decomposed as follows.

ˆx

= x

target

+ e

interference

+ e

noise

+ e

artifacts

(3)

where x

target

= f (x

) is a version of the true source x

modiﬁed by some allowed distortion f (·), and where

interference

, e

noise

, and e

artifacts

are the interferences,

noise and artifacts error terms, respectively. These

terms should represent the part of ˆx

perceived as com-

ing from x

, from other unwanted sources, from sensor

noise, and from other causes.

The aforementioned objective measures assign

equal weights to all error terms, which means that all

types of distortions contribute equally to the overall

quality of the extracted source (Cano et al., 2016). A

set of MATLAB



functions, created by F

evotte et. al.

and referred as BSS Eval Toolbox

, is available online

and can be used to calculate these objective measures

evotte et al., 2005).

Separation results are averaged out in every ex-

periment and compared with another semi-supervised

approach, known as the Interactive Source Separation

Editor (ISSE) (Bryan and Mysore, 2013), where the

end-user provides annotations in order to constrain,

regularize, or otherwise inform the algorithm. These

annotations are introduced at the beginning of the pro-

cess by highlighting relevant sections on the input

spectrogram, while the separation of the sources is

obtained by an implementation of the NMF approach.

Within the existing user-assisted audio source separa-

tion methods, ISSE constitutes a representative exam-

ple that has the additional advantage of being open-

source and freely available

Oracle estimates are also calculated in every mix-

ture, according to Vincent et. al. (Vincent et al.,

2007), and their averages are presented in every ex-

periment as a reference. In theory, they represent

the highest achievable results that a time-frequency

masking-based separation method can obtain. A set

of MATLAB



functions is also available online

and

http://www-users.york.ac.uk/ adc533/download

http://bass-db.gforge.inria.fr/bss eval/

http://isse.sourceforge.net/

http://bass-db.gforge.inria.fr/bss oracle/

can be used to calculate these estimates, in particular,

the function bss nearopt monomask, which generates

near-optimal time-frequency masks using the STFT

with a sine window (Vincent and Plumbley, 2007).

The proposed iterative estimation/separation sys-

tem (IES) is applied with a frame size of 2048 sam-

ples, 87.5% overlap, a Hanning window, and H = 5

partials for the salience measurement. In every frame,

the maximum number of extracted harmonic partials

is set to 30 in order to capture most of the energy as-

sociated with the selected note event. The maximum

number of note events to be extracted from within ev-

ery mixture is set to 45. The ISSE, on the other hand,

is applied to every mixture using the recommended

settings (frame size of 4096 samples and 50 basis vec-

tors per source), while the annotations are introduced

to extract one source at a time.

4.1 Two Harmonic Sources

In this experiment, a set of 18 audio mixtures with

polyphony 2 are considered. Overall, the number of

notes being played is 279, with fundamental frequen-

cies spanning from F2 (86 Hz) to F]5 (750 Hz). Sep-

aration results are presented in Table 1, where the

IES system shows an average improvement of 25%

in SDR over the ISSE algorithm.

Table 1: Separation Performance in Audio Mixtures with

Polyphony 2 (Harmonic Instruments).

Method

Separation Performance (dB)

SDR SIR SAR

IES 12.87 19.93 14.66

ISSE 9.35 12.76 15.05

Oracle 18.16 26.96 19.01

Although the ISSE seems to generate slightly less

artifacts, the separated sources also exhibit higher lev-

els of interference, suggesting that the annotations

are not providing enough information to completely

characterize each individual source. This problem is

partially solved in IES by assuming that the under-

lying sources are harmonic, which provides a simple

but effective way to identify their frequency compo-

nents based on the knowledge of their fundamental

frequencies. The proposed dual-peak model provides

a sharper separation of shared harmonics, which also

reduces interference among the separated sources.

4.2 Three Harmonic Sources

A different set of 12 audio mixtures with polyphony 3

are now considered, where the number of notes being

Semi-supervised Audio Source Separation based on the Iterative Estimation and Extraction of Note Events

277

Table 2: Separation Performance in Audio Mixtures with

Polyphony 3 (Harmonic Instruments).

Method

Separation Performance (dB)

SDR SIR SAR

IES 8.81 15.69 10.63

ISSE 7.31 9.34 13.17

Oracle 14.04 23.20 14.79

played is 386, and their fundamental frequencies are

in the range F3 (175 Hz) to F]5 (750 Hz). Results for

this experiment are presented in Table 2.

The incorporation of a third source represents a re-

duction of the separation quality, as can be observed

for both algorithms. A higher number of simultane-

ous sources means additional difﬁculties in provid-

ing good annotations for the sources, reducing the

overall performance of ISSE, but it also means addi-

tional problems during the separation of overlapping

harmonics, which affects IES quality. However, the

higher number of note events in the mixture and the

proximity of their frequency components are causing

a higher reduction in the separation performance of

IES, in comparison with the previous experiment.

Octave-related notes, which are present in some

of the mixtures analysed in this experiment, introduce

an additional challenge for both algorithms and affect

the separation performance. The IES system is able

to detect the pitch trajectories of many octave-related

notes, however, an accurate separation of the original

note events is not possible, since the amplitudes of

their harmonic partials cannot be correctly estimated

from the mixed spectrogram. Similarly, the ISSE sys-

tem also has problems interpreting overlaps between

annotations of different sources and tends to allocate

most of the shared energy into only one of the sources.

4.3 Two Harmonic and One Percussive

Sources

The third experiment considers the same set of mix-

tures used in Section 4.2, but the third pitched instru-

ment (tenor saxophone) is replaced with a percussive

source. A total of 239 harmonic notes are still present,

with fundamental frequencies in the range A3 (220

Hz) to F]5 (750 Hz), and several hundred new percus-

sive events are introduced. Results for this experiment

are presented in Table 3.

The IES method presented here is designed to de-

tect harmonic content, consequently the percussive

output is contained in a residual signal together with

other non-harmonic content. In the case of ISSE, the

percussion is instead extracted ﬁrst by exploiting ad-

ditional user-provided annotations of solo percussive

Table 3: Separation Performance in Audio Mixtures with

Polyphony 3 (Harmonic and Percussive Instruments).

Method

Separation Performance (dB)

SDR SIR SAR

IES 11.98 18.36 13.49

ISSE 11.32 16.14 14.26

Oracle 14.86 24.60 15.65

regions of the spectrogram.

In this experiment, both algorithms show similar

separation quality, with the IES approach still show-

ing slightly less interference in the separated sources,

while the ISSE approach introduces slightly less arti-

facts. In this speciﬁc example, the percussive source

does not affect the detection of note events within the

IES system but, more generally, low energy percus-

sive effects might impact on the detection of musical

notes with a fundamental frequency below 200 Hz.

An important advantage of IES over ISSE is that

it allows end-user interaction during the ﬁnal stage of

the process (clustering of note events), which seems

to be more effective than using it at the beginning

of the separation, as in the case of the ISSE pro-

cess. From the user perspective, listening to separated

events and grouping them into individual sources is

far easier than recognising harmonic structures and

estimating frequencies from within the spectrogram

of a complex audio mixture.

5 CONCLUSIONS

In this paper, a novel semi-supervised approach for

single-channel audio source separation was intro-

duced, based on the iterative estimation and extrac-

tion of note events, and their subsequent clustering

into separated sources by end-user interaction during

the ﬁnal stage of the process. Direct subtraction in

the time domain is used here during the separation

of each note event, which provides a softer way of

extracting its estimated spectral energy from within

the mixture and reduces the levels of interference be-

tween the separated sources.

After evaluation on a set of test mixtures with

polyphonies 2 and 3, the proposed system outper-

formed the ISSE NMF-based approach, in which end-

user interaction is used at the beginning of the sepa-

ration process. Positive separation results were also

obtained by the IES system for audio mixtures with

polyphony three including percussive effects, despite

the complexities of performing pitch tracking in the

presence of percussive sounds. Finally, grouping sep-

arated note events into sources was found to be more

SIGMAP 2019 - 16th International Conference on Signal Processing and Multimedia Applications

278

effective than recognising structures from within the

spectrogram of a complex audio mixture.

Further work will be conducted with the aim of al-

lowing the separation of notes in octave relation, and

improving the separation of low-pitched notes. Dif-

ferent approaches to automate the clustering of note

events into sources will also be explored, as a way

to deliver a fully-automated source separation system

that could be compared with other unsupervised algo-

rithms based on machine learning.

ACKNOWLEDGEMENTS

The authors would like to thank the University of

Costa Rica and the Costa Rican Ministry of Science,

Technology and Telecommunications for their sup-

port in founding this research.

REFERENCES

Bryan, N. J. and Mysore, G. J. (2013). Interactive reﬁne-

ment of supervised and semi-supervised sound source

separation estimates. In Proceedings of the 38th IEEE

International Conference on Acoustics, Speech and

Signal Processing, pages 883–887.

Cano, E., Fitzgerald, D., and Brandenburg, K. (2016). Eval-

uation of quality of sound source separation algo-

rithms: human perception vs quantitative metrics. In

Proceedings of the 24th IEEE European Signal Pro-

cessing Conference, number 1, pages 1758–1762.

Chandna, P., Miron, M., Janer, J., and G

omez, E. (2017).

Monoaural audio source separation using deep convo-

lutional neural networks. In Proceedings of the 13th

International Conference on Latent Variable Analysis

and Signal Separation, pages 258–266.

Duan, Z., Pardo, B., and Zhang, C. (2010). Multiple fun-

damental frequency estimation by modeling spectral

peaks and non-peak regions. IEEE Transactions on

Audio, Speech and Language Processing, 18(8):2121–

2133.

Every, M. R. and Szymanski, J. E. (2006). Separation of

synchronous pitched notes by spectral ﬁltering of har-

monics. IEEE Transactions on Audio, Speech and

Language Processing, 14(5):1845–1856.

evotte, C., Gribonval, R., and Vincent, E. (2005). BSS

EVAL toolbox user guide. Technical Report 1706,

Institut de Recherche en Informatique et Syst

emes

eatoires.

Grais, E. M., Roma, G., Simpson, A., and Plumbley, M. D.

(2017). Two-stage single-channel audio source sepa-

ration using deep neural networks. IEEE/ACM Trans-

actions on Audio, Speech and Language Processing,

25(9):1469–1479.

Jang, G. J., Lee, T. W., and Oh, Y. H. (2003). Single-channel

signal separation using time-domain basis functions.

IEEE Signal Processing Letters, 10(6):168–171.

Li, Y., Woodruff, J., and Wang, D. (2009). Monaural mu-

sical sound separation based on pitch and common

amplitude modulation. IEEE Transactions on Audio,

Speech and Language Processing, 17(7):1361–1371.

Parsons, T. W. (1976). Separation of speech from in-

terfering speech by means of harmonic selection.

The Journal of the Acoustical Society of America,

60(1976):911.

Ponce de Le

on V

azquez, J. and Beltr

an Bl

azquez, J. R.

(2012). Blind separation of overlapping partials in

harmonic musical notes using amplitude and phase re-

construction. EURASIP Journal on Advances in Sig-

nal Processing, (223):1–16.

Raﬁi, Z., Liutkus, A., Stoter, F. R., Mimilakis, S. I., Fitzger-

ald, D., and Pardo, B. (2018). An overview of lead

and accompaniment separation in music. IEEE/ACM

Transactions on Audio, Speech and Language Pro-

cessing, 26(8):1307–1335.

Taghia, J. and Doostari, M. A. (2009). Subband-based

single-channel source separation of instantaneous au-

dio mixtures. World Applied Sciences Journal,

6(6):784–792.

Vincent, E., Gribonval, R., and F

evotte, C. (2006). Perfor-

mance measurement in blind audio source separation.

IEEE Transactions on Audio, Speech and Language

Processing, 14(4):1462–1469.

Vincent, E., Gribonval, R., and Plumbley, M. D. (2007). Or-

acle estimators for the benchmarking of source separa-

tion algorithms. Signal Processing, 87(8):1933–1950.

Vincent, E. and Plumbley, M. D. (2007). BSS ORACLE

toolbox version 2.1 user guide. Technical report.

Zivanovic, M. (2015). Harmonic bandwidth companding

for separation of overlapping harmonics in pitched

signals. IEEE/ACM Transactions on Audio, Speech

and Language Processing, 23(5):898–908.

Semi-supervised Audio Source Separation based on the Iterative Estimation and Extraction of Note Events

279