
Simulation of Racing Greyhound Kinematics
Md Imam Hossain
a
, David Eager
b
and Paul Walker
c
Faculty of Engineering and Information Technology, University of Technology Sydney, Sydney,
PO Box 123, Broadway 2007, Australia
Keywords: Greyhound Racing, Greyhound Kinematics, Dynamic Simulation, Numerical Simulation, Rigid Body
Dynamics, Injury Prevention, Animal Welfare.
Abstract: This paper outlines greyhound dynamics results for yaw rate, speed, and the congestion pattern during a race
derived through numerical modelling. The simulation results presented are also correlated to actual race data
to validate modelling performance and reliability. The tasks carried out include the development of a
numerical model for greyhound veering and race related supporting models, creating track 3D models
replicated from actual survey data of the track, establishing a simulation environment that emulates an actual
greyhound race, and the processing of both simulation and actual race data. The results show that greyhounds
are susceptible to experience varying high acceleration in first five seconds into the race, during which a
minimum average forward acceleration of 3.9 m/s
2
was calculated, a peak yaw rate magnitude of 0.4 rad/s
before the bend while transitioning into the track, and congestion during a race is affected by lure driving
performance.
1 INTRODUCTION
Greyhound racing is a popular sport in many
countries where the industry is thriving. Gradually,
focus is changing to best-racing performance
outcomes while minimising race injuries on the
tracks. As a result, simulation of greyhound racing
becoming an increasingly important technique for
evaluating races as it would directly and indirectly
benefit many parties including track designers, race
operations managers to name few.
When it comes to the greyhound, they are able to
travel by a maximum speed averaging above 70 km/h
on the land. This astonishing speed is achieved
through galloping gait of a greyhound which is also
preferred gait for most quadrupedal mammals
(Krasny, and Orin, 2004). However, musculoskeletal
injuries are a common happening in racing
quadrupeds such as greyhounds when compared to
non-racing quadrupeds (Sicard et al., 1999). A study
showed that various track dynamic conditions, as well
as greyhound running speed, have a significant
influence on race performance and injuries (Iddon et
a
https://orcid.org/0000-0002-1246-3454
b
https://orcid.org/0000-0003-1926-7867
c
https://orcid.org/0000-0003-3988-3966
al., 2014, Mahadavi et al., 2018, Hasti et al., 2017a).
Likewise, investigation of five tracks showed that
factors such as track surface grades, achievable speed,
and race distance resulted significant effect on
greyhound injury rates (Iddon et al., 2014). Moreover,
various observations of racing greyhound injuries
indicated that congestion at the start of the race as
well as at the immediate bend in the track is a
precursor to major race injuries (Hayati et al., 2017b).
For greyhound racing, a traditional approach for
analysing race dynamics can be cumbersome and
difficult to achieve. This is because traditional
techniques such as graphical and analytical methods
sometimes lack accuracy and the complexity can
increase exponentially for a relatively simple
practical problem (Garcia et al., 2012). An alternative
solution is numerical analysis and methods through
fast processing of alphanumeric data, data
formulation and computational methods (Garcia et
al., 2012). In the numerical approach, mathematical
models are developed from observation of physical
and technical processes where derived equations are
computed at discrete points in the time (Griebel et al.,
2010). Furthermore, the availability of corresponding
Hossain, M., Eager, D. and Walker, P.
Simulation of Racing Greyhound Kinematics.
DOI: 10.5220/0007829000470056
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 47-56
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
47

physical or technical processes results would allow
verification of numerical results or improvements to
developed numerical model methods (Griebel et al.,
2010).
This paper describes the design and mechanism of
dynamic numerical models for conducting greyhound
racing simulation which is processing efficient and
yet robust enough to extract various greyhound
kinematics and racing dynamics, which include
greyhound yaw rate, speed, congestion pattern,
greyhound path following as well as factors which
affect racing performance. Furthermore, the design
and mechanism described can be expanded and
utilised in other prospective areas such as vehicle and
quadruped running simulations with multiple
interacting factors having proper constraints in place.
The realistic constraints are such that any dynamic
system models developed exhibit controllability of
the numerical algorithms output convergence
(Respondek, 2010). This is because controllability of
dynamical systems allows extension of dynamic
systems conditions for given problems (Respondek,
2005).
Moreover, this paper analyses simulation and
actual race data for deriving trends in racing
greyhounds. The simulation carried out were matched
to available field data configuration such as eight
greyhounds running over a defined distance in a track
which has two bends track paths as well as two
straights track paths.
2 MATHEMATICAL MODEL
DEVELOPMENT OVERVIEW
To create a viable model for greyhound racing, there
are various variables which first need to be identified
and addressed. These variables may come from
within the racing track or from the greyhound. By
considering racing track and greyhound as different
systems their inherent system behaviour defining
variables can be identified. Furthermore, race
operational configuration and running conditions
define a system which by emulating it creates
necessary inputs for a simulation model of greyhound
racing.
2.1 Model Scope
When a greyhound is racing, its motion can be
defined and traced in term of displacement, velocity,
and acceleration in Euclidean space. While the
nominal acceleration of greyhound can be directly
related to forces acting on it, deriving of the
instantaneous displacement and velocity of
greyhound can be a complex task. This is because the
instantaneous displacement and velocity of a
greyhound in racing not only depend on the racing
track design and racing operational running
conditions but also rely on the adjacent greyhounds’
dynamic profiles. This creates a greater
unpredictability in the controllability of a
greyhound’s instantaneous displacement and velocity
during a race. Furthermore, observation has
confirmed that a racing greyhound can bump into
another adjacent greyhound as well as follow a
particular path, which is not defined by its motion
limiting force factors but are an inherent part of race
dynamics. Consequently, the interactions between
greyhounds in a race have a significant impact on the
greyhound race dynamics. A greyhound veering
model is developed which outputs greyhound
locations during a race from the start of the race till
the end. The model predicts the path taken by
individual greyhounds during a race while having
each greyhound its own character in terms of
velocities. Finally, the model calculates adjacent
greyhounds’ locational, track design and race
operational influences and optimises potential
locations of greyhound during a race. In the simplest
form, the model can be described by a finite
dimensional system state equation. This model is said
to be controllable if and only if the control variable
would allow the system to reach any final state in the
control space in the finite time from any given initial
state (Respondek, 2005).
2.2 Understanding of Greyhound
Racing Elements
There are a number of distinct elements which take
part in a greyhound racing. While some of these
racing elements are dynamic in nature, there are also
elements which are static and have a great impact on
a racing greyhound. The main dynamic bodies in
racing are the lure during a race, adjacent racing
greyhounds, and individual greyhound limbs which
are required for greyhound locomotion. The
fundamental static bodies relating to racing are race
starting boxes locations and orientations relative to
track, track surface properties including surface
traction, impact attenuation qualities, track camber,
and track racing line. During a race, lure, starting
boxes, and track are regulated to certain degrees that
their behaviours are controlled and follow a specific
predefined pattern.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
48

2.3 Model Composition and
Mechanism
By considering a greyhound as a point object its
overall motion in a race can be formulated by
knowing the factors which induce the motion as well
as the factors which alter the motion characteristics as
a result of combined racing environmental and
greyhound limits. The main driving factor for
greyhound motion is greyhound stride while the
motion altering factors are greyhound natural steering
limits, collision in a race, track geometry and surface
condition, lure velocity profile and track boundaries.
These discrete factors are modelled using kinematics
and vectors equations where kinetics equations and
input to output unit tests are used for finding initial
and final values for the model equations.
Superposition principle is applied to the model
equations to solve for aggregated results of discrete
race dynamics factors and calculate greyhound
location during a race using Euler's method. The
summation of discreet factors can be expressed as
V(v
1
+ v
2
+ v
3
+ v
4
+ v
5
+ v
6
+ v
7
+ v
8
+ v
9
)
= V(v
1
) + V(v
2
) + V(v
3
) + V(v
4
) + V(v
5
) +
V(v
6
) + V(v
7
) + V(v
8
) + V(v
9
)
(1)
In which V is the final velocity vector function for
v
1
... v
9
discrete factors of race dynamics. The v
1
factor represents greyhound stride acceleration
velocity due to the sum of all the forces exerted by a
greyhound’s stride which can be modelled using
Newton’s second law (2). This is also the forward
acceleration of greyhound. It was assumed that a
greyhound’s exerted stride force remains constant for
the entire race duration although, in reality, data show
greyhound acceleration is highly variable during the
first three strides. However, as the time fraction of the
first three strides is relatively small compared to
entire race duration, a linear acceleration model and
an averaged value of greyhound maximum
accelerations are appropriate for getting stable final
velocity output. For constant acceleration, greyhound
maximum forward acceleration is calculated using
Eq. 3 where greyhound final velocity (v) is 19.4 m/s,
greyhound displacement (s) for reaching final
velocity is 15 m and initial velocity (v
0
) is 0 m/s. This
maximum forward acceleration is plugged into Eq. 4
to calculate the greyhound stride acceleration velocity
factor v
1
. In Eq. 4, v
0
is greyhound velocity in
previous time instant and dt is the time elapsed
between v and v
0
.
∑ F = ma
s
(2)
v2 = v
0
2
+ 2 * a
s
* s
(3)
v = v
0
+ a
s
* dt
(4)
The purpose of the v
2
factor is to provide
greyhound the motivation to race as well as steer
greyhound heading as it moves in the track.
Therefore, this factor is a function of greyhound’s
lure line of sight, frictional force, and centrifugal
force vectors. However, observation of greyhound
race and race data have confirmed that lure line of
sight is a significant guiding influence for greyhound
path following around the track in absence of other
influences such as congestions due to adjacent racing
greyhounds. As a result, the lure line of sight vector
was considered also a function of frictional force, and
centrifugal force vectors (Eq. 5). The lure line of sight
vector is constructed from lure and greyhound
instantaneous locations in the track. The frictional
force has two components where one is due to track
camber (θ) and another one is the nominal friction due
to greyhound instantaneous velocity as denoted by m
* g * sin θ and C * v respectively.
Lure line of sight vector = lure line of sight
vector + centrifugal force vector + paw and
track surface frictional force vector
(5)
Centrifugal force = m * v
2
/ R
(6)
Greyhound paw and track surface frictional
force = (m * g * sin θ) + (C * v)
(7)
In Eq. 6, R is instantaneous radius of curvature of
greyhound path following and m is greyhound mass.
In Eq. 7, m is greyhound mass and C is a constant.
The v
3
factor is a tweaking vector to v
2
factor to
achieve precise greyhound heading movement
without which results in unnatural greyhound heading
movement behaviour. The reason for this, in real-
world greyhound heading direction change does not
go through step change to meet the lure following
path instead it goes through many mini-movements to
catch up lure following path. This creates a lag
between greyhound spotting lure location and
greyhound merging with the lure following path.
Moreover, greyhound has physical turning limits at
an instant. All of these phenomena are modelled using
a steering vector which is a function of greyhound
current heading direction vector and lure line of sight
vector.
Steering vector = lure line of sight vector –
current heading direction vector
(8)
Simulation of Racing Greyhound Kinematics
49

The v
4
final velocity factor determines the
outcome of greyhound checking and bumping as well
as greyhound collision avoidance tendency to
adjacent greyhound during a race which results in
greyhound surrounding aware variable velocities.
These situations in a race are modelled by using a
collision avoidance vector which successively finds
greyhounds in proximity and through a number of
iterations construct a clearance vector. The exact
number of iterations was chosen based on simulation
time stamps and convergence of the clearance vector.
Furthermore, by assuming there is no collision
between two greyhounds vertically, circle to circle
collision detection is used for checking overlapping
greyhounds.
Collision avoidance vector = location vector of
greyhound in proximity – location vector of
greyhound
(9)
Clearance vector = current heading direction
vector – collision avoidance vector
(10)
The v
5
factor finds the effect of track cross falls
on greyhound veering. As the effect of cross fall can
be proportional to track banking angle (θ) at spot
location, a linear calibrated force is used along with
normal force vector for calculation. To find banking
angle at a given location in track, the track surface is
discretised using small triangles where the vertices of
each triangle are used for finding normal force vector
(N) and corresponding bangle angle (θ).
N
x
= U
y
* V
z
– U
z
* V
y
(11)
N
y
= U
z
* V
x
– U
x
* V
z
(12)
N
z
= U
x
* V
y
– U
y
* V
x
(13)
Normal force vector (N) magnitude =
m * g * cos θ + (C * v)
(14)
Where, U = p
2
- p
1
and V = p
3
– p
1
for p
1
, p
2
, p
3
triangle vertices and m is greyhound mass and C is a
constant.
While racing greyhound avoids colliding with
track boundaries like inside lure rail. The v
6
factor is
used for applying a track boundary collision
avoidance vector to final velocity vector. For this
purpose, track boundaries are sampled with a number
of evenly spaced points and by using nearest points to
greyhound location boundary collision avoidance
vector is found.
Boundary collision avoidance vector =
location vectors of adjacent points on track
boundaries – location vector of greyhound
(15)
The v
7
factor models variable track surface
conditions at different track locations as well as
variable greyhound stride acceleration from greyhound
to greyhound for the race period. Modelling of variable
track surface conditions is essential, as, despite
identical stride from a greyhound over the race period,
non-uniform track surface conditions such as hardness,
softness, and coefficient of friction determine
greyhound stride acceleration. This factor is a function
of stride duration, race time, and a random number
generator.
The v
8
factor adds a specific greyhound behaviour
to final velocity vector which occurs when a greyhound
is lagging behind the lure significantly as observed
from various races. It was noticeable that greyhound
maintains an additional offset distance from track
inside boundary to get a better sight of the lure
depending on the distance between greyhound and
lure. However, various races also indicate that this
specific behaviour varies from greyhound to
greyhound. This situation is modelled by constructing
a boundary offset vector which is a function of
greyhound distance to lure, minimum offset from the
boundary and a constant as given below:
Boundary offset vector = minimum offset
from boundary * (distance to lure / C)
(16)
Where minimum offset from boundary and C are
calibrated to be 0.5 m and 5 m respectively.
The v
9
factor defines lure motion in terms of track
path and leading greyhound location in the race. For
this factor, a model function is created which takes into
account of track predefined lure travel path and lure
and leading greyhound separation distance to provide
lure instantaneous velocity which would maintain lure
driving for the duration of a race while maintaining a
separation distance. The model function first calculates
heading direction of the lure by copying track
curvature profile and then set lure instantaneous speed
based on the lure and leading greyhound separation
distance. The setting of lure instantaneous speed (S) is
based on the following rules where the constants were
tweaked to meet the lure driving performance:
((A > B → (C > 30 → X = 1.9489)) ∧ (A > B
→ (C > 20 → X = 3.3378)) ∧ (A > B → (C >
15 → X = 6.1156)) ∧ (A > B → (C > 10 → X
= 8.893)) ∧ (A > B → (C > 5 → X =
16.9489)) ∧ (A > B → (C > 1 → X = 17.504))
∧ (A > B → (C > 0.2 → X = 17.782))) ∧ ((A
< B → (C > 14 → X = 14)) ∧ (A < B → (C >
10 → X = 18.62)) ∧ (A < B → (C > 5 → X =
17.504)) ∧ (A < B → (C > 1 → X = 16.9489))
∧ (A < B → (C > 0.2 → X = 20))
(17)
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
50

In which A is distance between leading greyhound
and lure, B is maintaining separation distance, C is
the difference between A and B, and finally X is lure
instantaneous speed.
Finally, in the greyhound motion model
composition, vertical acceleration velocity factor was
neglected since instantaneous vertical velocity is
negligible compared to other greyhound velocity
influencing factors because of low track surface
penetration by greyhound paw during galloping in a
race.
3 SIMULATION PLATFORM
The Blender software package was used as the
simulation platform for creating contents for
simulation visualisation as well as implementation,
setup and data extraction of the simulation models
using Python programming language. First, race track
3D model was imported into Blender virtual
Euclidean space from track survey data where it is
constructed and formatted to meet the needs of
mathematical models. Then, racing elements 3D
models such as starting boxes, greyhounds, lure and
shape defining objects such as track boundary curves
were created in Blender virtual Euclidean space
meeting mathematical model requirements. Finally,
the Blender Python application programming
interface was used for writing simulation code inside
Blender software package. The primary components
of simulation code are: greyhound object which
defines a greyhound’s dynamic model as well as it’s
state in a particular time stamp, a lure object which
defines lure dynamic model and its state in a
particular time stamp, a method for calculating
collision between greyhounds, and a method
containing code for simulation numerical solver and
updating 3D models in Blender virtual Euclidean
space. For both lure and greyhounds’ motions, the
numerical solver calculates time-varying behaviour
of each dynamic system by solving models functions
and numerical integration using Euler method where
the results from each model function are compounded
using superposition principle. For example, the final
location of each dynamic object is determined by
integrating the velocity over time as follows:
S = ∫v * dt
(18)
S
new
= S
old
+ v * dt
(19)
Where S
new
is the new location, S
old
is the old
location, v is instantaneous velocity and dt is the
smallest unit of time in simulation.
The global variables in the simulation setup are
lure initial speed, lure maintaining acceleration, lure
starting acceleration, greyhound maximum average
acceleration, greyhound maximum speed, greyhound
minimum speed, lure greyhound separation distance,
starting boxes locations and orientations, and lure
offset from the starting boxes before racing. These
variables were adjusted to match greyhound races.
4 SIMULATION RESULTS AND
PERFORMANCE EVALUATION
To validate greyhound racing model simulation
results greyhound race data were retrieved from
IsoLynx system. The IsoLynx system captures real-
time greyhound coordinates data during a race where
it can trace a greyhound’s location in the track in
terms of X and Y coordinates relative signal towers.
Different races greyhound coordinate data from both
simulation results and actual race were used for
validating simulation models performances. The
races which were selected from both simulation and
actual race have identical setups in terms racing time
of the day, racing distance to rule out unknown
factors affecting the comparisons as well as to find
different racing factors general trends. Moreover,
simulation and race data were resampled to match
greyhound stride duration since greyhound dynamics
state is reflected with every stride. Finally,
simulations were run with slightly varying lure
driving, greyhound maximum acceleration behaviour
configurations from nominal values to exaggerate the
effects of different racing factors outcomes. The
following sections analyses model simulation
performance to race data.
4.1 Greyhound Performance Indicators
The following major greyhound kinematics variables
were analysed.
4.1.1 Path Following
As greyhound races, they follow a specific path in the
track. The following graphs show X and Y
coordinates of a single greyhound during a race. The
graphs show that greyhound path coordinates shape
from simulation model results closely match with
race data. By looking into rate change of coordinates
subtle differences were also analysed. The maximum
and minimum percentage differences between
simulation and race for X coordinates are 6% and 7%
respectively. The maximum and minimum
Simulation of Racing Greyhound Kinematics
51
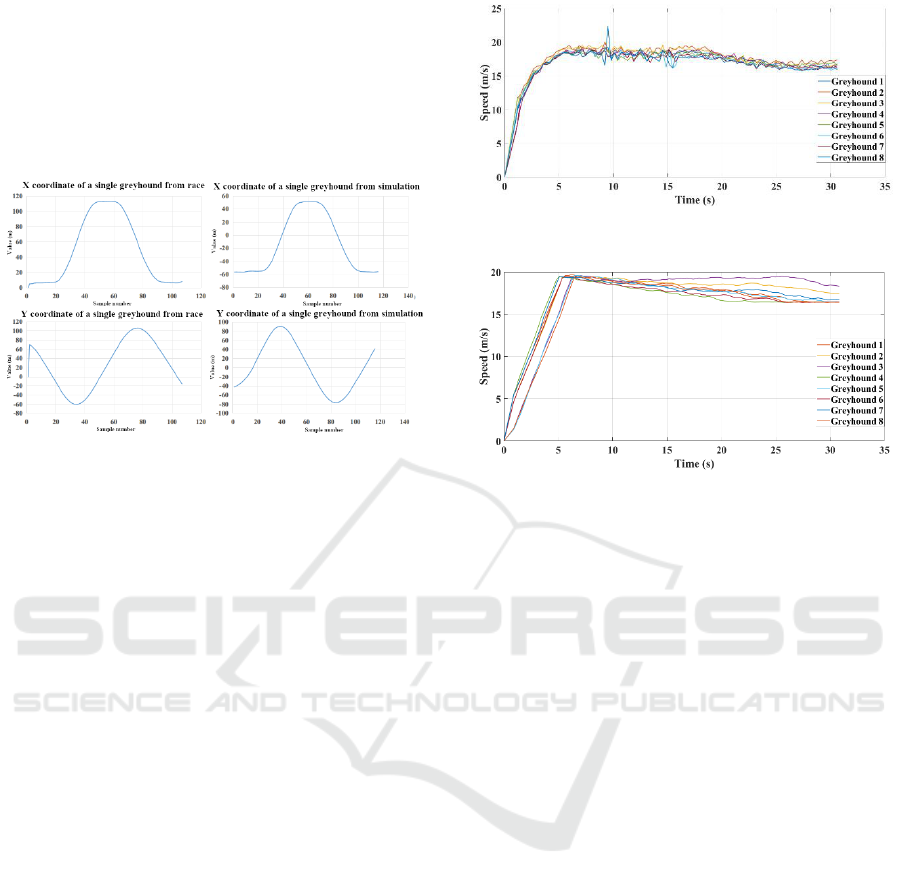
percentage differences between simulation and race
for Y coordinates are 4% and 15% respectively. This
shows simulated models resulted in a highly accurate
path following while percentages differences can be
attributed to slightly different race configurations
between simulation and actual race and varying
nature of each race.
Figure 1: Greyhound coordinate data as produced from
simulation and race.
4.1.2 Speed and Acceleration
During a race a greyhound’s speed remains variable
and has different phases as found from simulation and
race data. The following graphs depict greyhound’s
instantaneous speeds versus time for both simulated
and actual races. As shown in Figures 2 and 3, the
greyhound has an initial high acceleration phase
which puts a greyhound into its maximum speed limit
of roughly 19.5 m/s where the overall duration of this
phase depends on race distance, track shape and
starting box location in the track. Both simulated and
actual race data show initial acceleration continues
for 5 s where the rate change of this initial
acceleration is highly variable for actual race whereas
for simulation it is fixed as the greyhound model
functions use a constant average maximum
acceleration for greyhounds. After an initial
acceleration phase reaching maximum speed
greyhounds tend to lose speed as the time passes as
shown in the Figures 2 and 3. The average
deceleration of greyhound in this phase is
approximately 0.13 m/s
2
as found from both
simulation and race. Finally, the local fluctuations in
greyhounds speed can be attributed to factors
including track surface effects, bumping and
checking of greyhounds, and specific individual
greyhound behaviour.
Figure 2: Greyhound speed during a race.
Figure 3: Greyhound speed during a race from simulation.
4.1.3 Yaw Rate
Yaw rate is an important aspect in greyhound
kinematics as it defines how quickly a greyhound is
turning its heading. Also, veering performance during
a race as well as the lateral force magnitude acting on
a greyhound can be traced from the yaw rates.
Figures 4 and 5 illustrate instantaneous yaw rate of a
greyhound as derived from simulated and actual races
data. For the race distance selected, there are two bends
of constant radius in the track which are visible in the
yaw rates Figure 4 (red regions) where a yaw rate of
approximately 0.37 rad/s means the greyhound is
having a turning of radius roughly 50.5 m while
traversing through the bends with a speed roughly 18.8
m/s. Also, it is noticeable there is an initial spike in the
yaw rate of about 0.4 rad/s at 2.84 s and 1.49 s for
simulation and race data respectively. This is because
race distance start box location is not perfectly aligned
with the track path which causes the greyhound to
make an initial sharp turn for transitioning into the
track. The local fluctuations in the yaw rates can be
caused by greyhound path deviation because of
bumping and checking or collision avoiding. Overall,
the simulated race shows an excellent agreement with
the actual race data.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
52
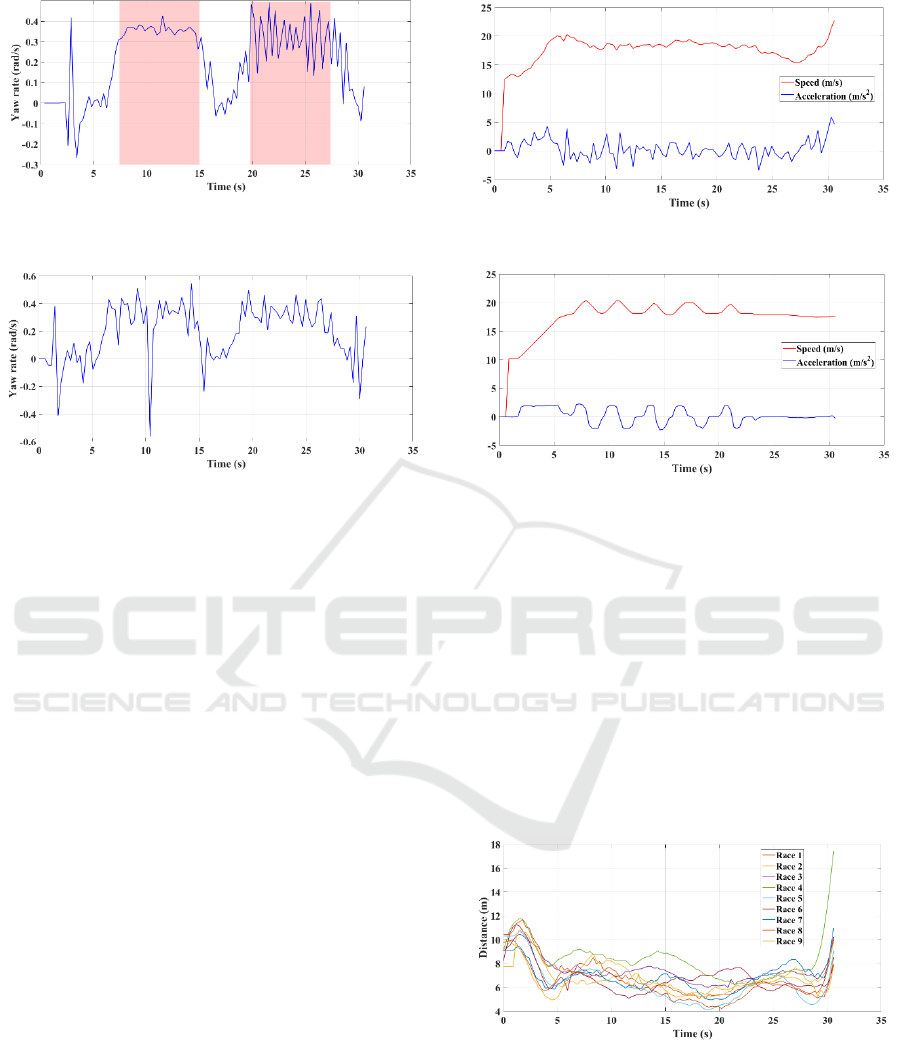
Figure 4: A greyhound’s yaw rate during a race from
simulation.
Figure 5: A greyhound’s yaw rate during a race.
4.2 Lure Performance Indicators
The following major lure performance variables were
analysed.
4.2.1 Speed
Lure driving condition was analysed between
simulation lure model and the actual race. The
simulation model yielded better lure driving
performance than the actual race as shown in Figures 6
and 7. The overall rate change of lure speed is higher
in the actual race and lower in the simulation model.
Furthermore, in actual race lure speed was affected by
track shape such as around the bends the overall speed
was slightly lower whereas no such trends are
noticeable in the simulation model other than
fluctuations from overall speed.
Finally, it is expected that both simulation model and
actual race lure driving would be slightly different
from each other as every race is unique in terms of
greyhound kinematics which lure highly depended on.
Figure 6: Lure driving speed during a race.
Figure 7: Lure driving speed during a race from simulation.
4.2.2 Lure Separation Distance
Maintaining a safe distance from the leading
greyhound in the race is also a performance indicator
for lure driving condition. The following figures
shows the simulation model and actual race lure
separation distance from leading greyhound during
races. As can be seen, in the actual race lure
separation distance tend to become lower and lower
until 20 s into the race where it was increased and
lowered again. In the simulation model, lure
separation distance is steadier after initial phase and
was increased after approximately 21 s into the race.
Figure 8: Lure separation distance from different races.
Simulation of Racing Greyhound Kinematics
53
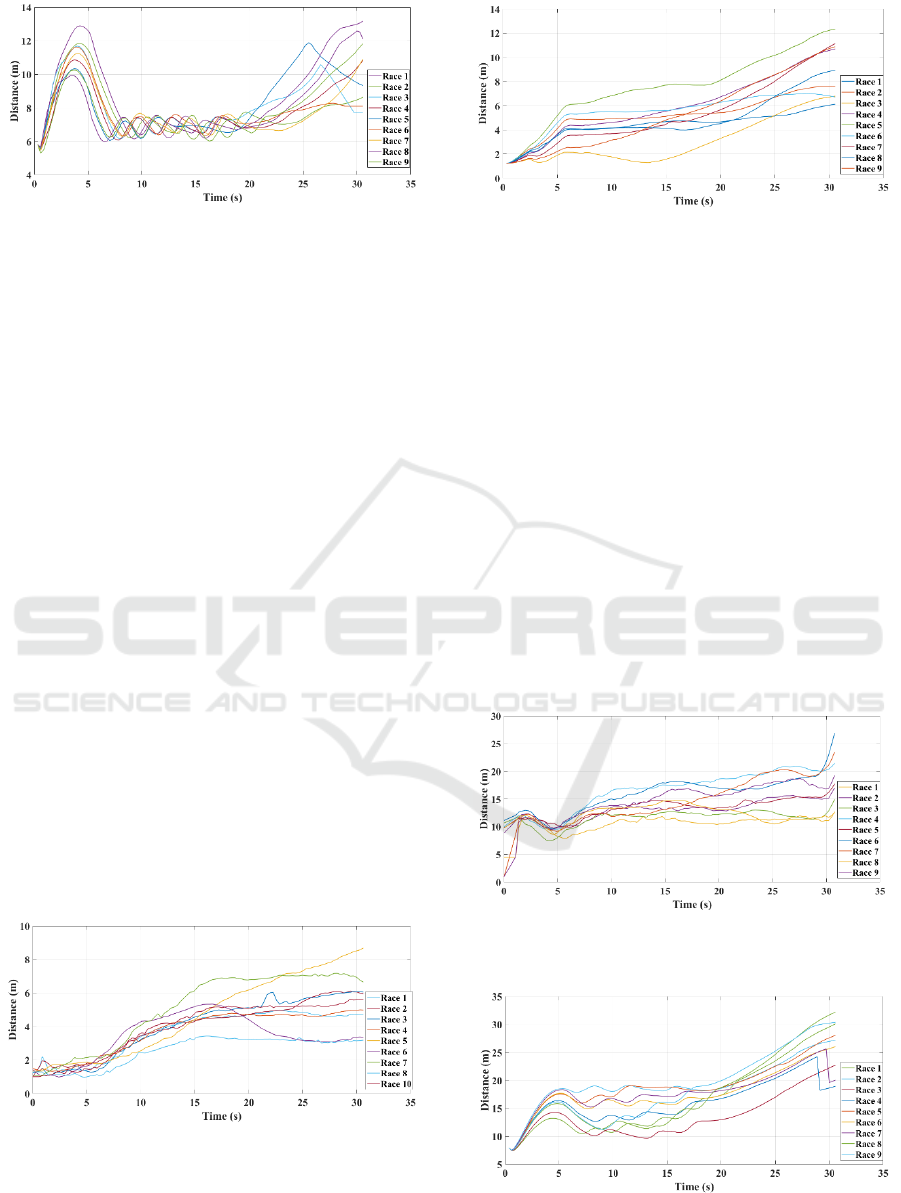
Figure 9: Lure separation distance from different simulated
races.
4.3 Greyhound Racing Performance
Indicators
To measure the racing performance the following
major variables were analysed.
4.3.1 Mean Distance from Cluster Centroid
In the race, greyhounds pack can be considered as a
cluster where the distances of each individual
greyhound from the cluster centroid can be averaged
to calculate the mean distance from cluster centroid.
Mean distance from cluster centroid can be used as a
measure to identify greyhounds pack formation and
resulting pack density. Figures 10 and 11 show
differences between simulated and actual race mean
distance from cluster centroid. Evidently, in actual
race greyhounds pack remained tightly packed as
indicated by the low mean distance from cluster
centroid value of about 2 m until 7 s into the race and
then mean distance saw a gradual increase until the
end of the race. In simulation, greyhounds pack
density was reduced more rapidly in the first 5 s into
the race and then it saw a slow and gradual increase
until the end of the race. Overall, both simulation and
actual race showed a similar trend in the greyhound
pack density.
Figure 10: Greyhounds mean distance from cluster centroid
for different races.
Figure 11: Greyhounds mean distance from cluster centroid
for different simulated races.
4.3.2 Mean Distance from Lure
Like lure separation distance, the mean distance from
lure is the average of all individual greyhound
distances from the lure during a race. A higher value
of the mean distance from lure indicates greyhounds
more spread out along the track while going through
different packs formations. As can be seen from the
Figure 12, in actual race mean distance from lure
slowly increases after initial greyhound acceleration
phase. In the simulation, after the initial acceleration
phase, the mean distance from lure remains mostly
steady until approximately 15 s into the race while
after this period it increases significantly. As a result,
both simulation and actual race show that mean
distance from lure increases with time during a race
which indicates that dispersing of greyhounds is
proportional to race time.
Figure 12: Greyhounds mean distance from lure for
different races.
Figure 13: Greyhounds mean distance from lure
for different simulated races.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
54
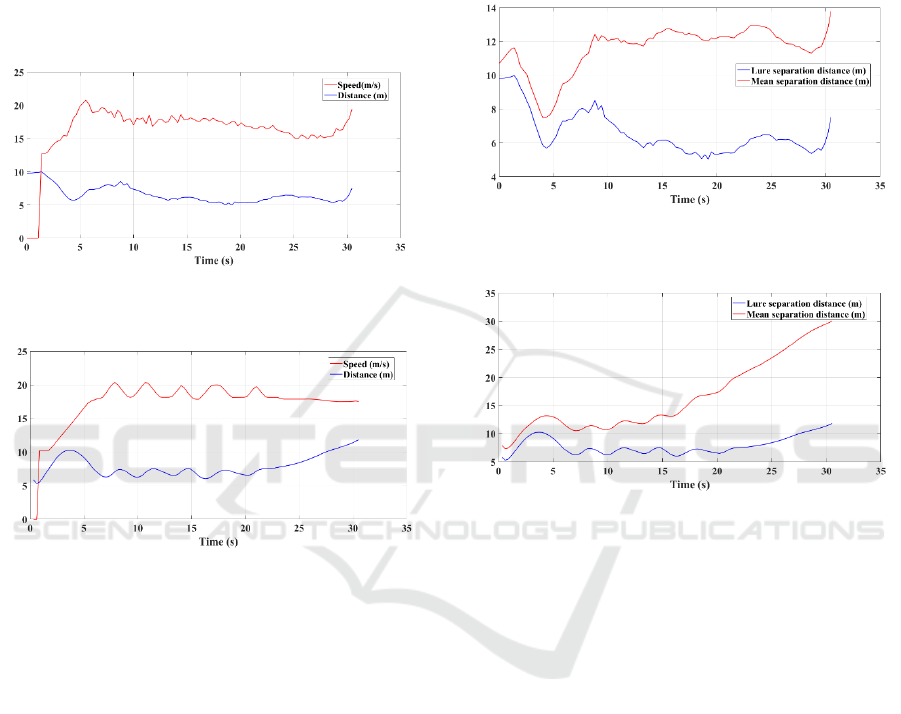
4.3.3 Speed vs. Separation Distance
Both simulation and actual race data showed that
there is an approximate inversely proportional
relationship between lure speed and lure separation
distance which is shown in Figures 14 and 15. The
instantaneous increase in lure speed decreases the lure
separation distance and vice versa. This observed race
dynamic nature can be utilised to design race dynamic
nature outcomes.
Figure 14: Lure speed vs. lure separation
distance during a race.
Figure 15: Lure speed vs. lure separation distance
during a race from simulation.
4.3.4 Lure Speed vs. Mean Distance from
Cluster Centroid
Both simulation and real race data indicated no
influence of instantaneous lure speed on mean
distance from cluster centroid dynamic results.
4.3.5 Lure Speed vs. Mean Distance from
Lure
Both simulation and real race data did not show any
direct relationship between instantaneous lure speed
and mean distance from lure variables.
4.3.6 Lure Separation Distance vs. Mean
Separation Distance
Simulation and actual race data pointed out that there
is an approximately proportional relationship
between instantaneous lure separation distance and
mean distance from lure which is depicted in
Figures 16 and 17. Also, the mean distance from lure
is always greater than lure separation distance. This
relationship suggests that the lure separation distance
can be used for managing greyhounds' congestions to
some extent as indicated by the mean distance from
lure variable.
Figure 16: Lure separation vs. mean separation distances
during a race.
Figure 17: Lure separation vs. mean separation distances
during a race from simulation.
5 CONCLUSIONS
The greyhound racing simulation models were
primarily developed to investigate various factors
affecting greyhound racing performance where
different racing factors were incorporated as different
numerical models to produce racing simulations. By
analysing field and racing data the models were
refined over time and reached a certain level of
maturity where the outputs from the models'
simulation showing comparable results to actual race
data. The findings from the greyhound racing models
simulation suggest trends which are existing in
greyhound racing as well as racing factors which
would require optimisations. Lastly, this paper
presents an approach for developing numerical
models for simulation of greyhound racing which can
be considered for simulating systems having multiple
factors and interacting elements.
Simulation of Racing Greyhound Kinematics
55

ACKNOWLEDGEMENTS
This work is sponsored by Greyhound Racing NSW,
Australia and Faculty of Engineering and Information
Technology at the University of Technology, Sydney,
Australia. Special Thanks to Greyhound Racing
Victoria, Australia for providing with real time race
data and track survey plan.
REFERENCES
Griebel, G., 2010. Numerical Simulation in Molecular
Dynamics: Numeric, Algorithms, Parallelization,
Applications, (s.n.).
Garcia, J., 2012. Kinematic and Dynamic Simulation of
Multibody Systems: The Real-Time Challenge. Springer-
Verlag New York, LLC.
Hayati H., Eager D., Jusufi A., Brown T., A novel approach
to analysing rapid tetrapod locomotion using inertia
measurement units and stride length as a speed indicator
in fast quadrupeds, International Society of
Biomechanics Conference, Brisbane, Australia, 23-27
July 2017.
Hayati H., Eager D., Stevenson R., Brown T., Arnott E., The
impact of track related parameters on catastrophic injury
rate of racing greyhounds, 9
th
Australian Congress on
Applied Mechanics ACAM9, Sydney Australia 27-29
November 2017.
Iddon, J., Lockyer, R. H., and Frean, S. P., 2014, “The effect
of season and track condition on injury rate in racing
greyhounds,” J Small Animal Practise, 55(8), pp. 399-
404.
Respondek, J.S. 2010, ‘Numerical simulation in the partial
differential equations: controllability analysis with
physically meaningful constraints’, Mathematics and
Computers in Simulation, 81 (1), pp. 120–132.
Respondek, J.S. 2005, ‘Controllability of dynamical systems
with constraints’, Systems & Control Letters, 54 (4), pp.
293-314.
Krasny, D.P. and Orin, D.E. 2004, ‘Generating high-speed
dynamic running gaits in a quadruped robot using an
evolutionary search’, IEEE Transactions on Systems,
Man, and Cybernetics, Part B: Cybernetics, 34, pp.
1685-1696.
Mahadavi F., Hossain I., Hayati H., Eager D., Kennedy P.,
Track shape, resulting dynamics and injury rates of
greyhounds, ASME-IEMCE 2018, Pittsburgh,
Pennsylvania, USA, 9-15 November, 2018.
Sicard, G., Short, K. and Manley, P. 1999, ‘A survey of
injuries at five greyhound racing tracks’, Journal of
Small Animal Practice, vol. 40, pp. 428-432.
APPENDIX
Simulation video links
Race 525 m run 1:
https://drive.google.com/open?id=10nm-
qZGX4ngWrrA3Wn44aU1OOO7V_ALx
Race 525 m run 2:
https://drive.google.com/open?id=1beipV48R5KI6VB8Q
Q2nmlWp6lvNhquoT
Race 525 m run 3:
https://drive.google.com/open?id=1qHftUiCULA0xnXG--
h-hZzL83XZSgxZe
Race 525 m run 4:
https://drive.google.com/open?id=1ellWXHoksw8M_bSP
saJCJv1IowFN1V-W
Race 525 m run 5:
https://drive.google.com/open?id=1FlXH0h2gk5nt33agQy
mJAfW2oto48xUK
Race 525 m run 6:
https://drive.google.com/open?id=1_EeYqArAOG2Le1uY
yeYHwMGXidoHx_Qe
Race 525 m run 7:
https://drive.google.com/open?id=1gs6EvbaZuCakKSg-
c6YGwixEAWBKXVPB
Race 525 m run 8:
https://drive.google.com/open?id=1ZZ_edPkhlY2_Ayubm
jsb7zXp9pTK7fHi
Race 525 m run 9:
https://drive.google.com/open?id=1zdAQ2KDky5g1ewVI
0yYfahH_2G3-ID5M
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
56
