Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV

using Super-Twisting Control Algorithm with Linear Correction Terms

Yassine Kali

, Jorge Rodas

, Maarouf Saad

, Raul Gregor

, Walid Alqaisi

and Khalid Benjelloun

EPCI Laboratory,

Ecole de Technologie Sup

erieure, Montreal, QC H3C 1K3, Canada

Laboratory of Power and Control Systems, Facultad de Ingenier

ıa, Universidad Nacional de Asunci

on, Paraguay

A2I Laboratory, Ecole Mohammadia d’Ing

enieurs, Mohammed V. University, Rabat, Morocco

Keywords:

Quadrotor, Unmanned Aerial Vehicle, Position and Attitude Tracking, Finite-time Convergence,

Super-Twisting Algorithm.

Abstract:

This work investigates the problem of ﬁnite-time position and attitude trajectory of quadrotor unmanned aerial

vehicle systems based on a modiﬁed second order sliding mode algorithm. The selected algorithm is a mod-

iﬁed super-twisting with both nonlinear and linear correction terms. It ensures robustness against unknown

dynamics and perturbations and allows fast ﬁnite-time convergence even when the trajectories of the consid-

ered system are far from the user-chosen switching surface. In addition, this algorithm is very attractive since it

solves the major problems of the ﬁrst and second order sliding mode, namely, the chattering phenomenon and

the required unavailable information for practical implementation. To show the effectiveness of the used mod-

iﬁed structure of the super-twisting algorithm, simulation results are presented for the considered quadrotor

system.

1 INTRODUCTION

Sliding Mode Control (SMC) is known to be one

of the most effective and powerful robust nonlinear

techniques that attracts the community of automa-

tion researcher (Utkin et al., 1999). Indeed, SMC

is well known for its three good features: insensitiv-

ity to a class of uncertainties, simplicity and ﬁnite-

time convergence. This controller uses switching in-

put signals to force the trajectories of the system

to reach in ﬁnite-time the so-called sliding surface

and then to move throughout this latter towards the

equilibrium point. SMC has been tested in simu-

lation and in real time on different nonlinear sys-

tems such as power systems (Kali et al., 2018a; Kali

et al., 2019), robotic manipulator systems (Feng et al.,

2002; Kali et al., 2015) and underactuated systems

as Unmanned Aerial Vehicles (UAVs) (Runcharoon

and Srichatrapimuk, 2013). Nevertheless, its real-

time implementation suffers from the chattering phe-

nomenon (Boiko and Fridman, 2005) caused by high

switching signals. This phenomenon is the major dis-

advantage of SMC since it can cause several problems

as bad performances and the degradation or/and dete-

rioration of the moving mechanical parts.

In literature, several published works tried to re-

duce or eliminate this problem (Tseng and Chen,

2010; Lee et al., 2009; Kali et al., 2018b; Besnard

et al., 2012). The most effective method is the pro-

posed Second Order Sliding Mode (SOSM) (Levant,

2003). Unlike the discontinuous classical SMC, the

SOSM control signals that fed into the system are

continuous (Kali et al., 2017a; Kali et al., 2017b)

since the the switching signals act on the derivative

of the control inputs. However, its real-time imple-

mentation still limited due to the lack of required

informations (measurement of the derivative of the

selected sliding surface). This problem has been

solved by the proposition of the Super-Twisting Al-

gorithm (STA) (Benallegue et al., 2008; Gonz

alez-

Hern

andez et al., 2017b; Gonz

alez-Hern

andez et al.,

2017a; Ibarra and Castillo, 2017; Kali et al., 2018).

In this paper, the modiﬁed STA (structure with

nonlinear and linear terms) will be designed and

tested by simulations on a quadrotor UAV system.

The choice of UAVs belongs to the fact that to the au-

thors’ best knowledge, unlike the standard STA, this

modiﬁed structure has never been studied, and conse-

quently, used for UAV systems. Moreover, control of

ﬂight robot systems is an attractive ﬁeld of research

since the number of applications where these systems

are used keeps growing. Among the most developed

Kali, Y., Rodas, J., Saad, M., Gregor, R., Alqaisi, W. and Benjelloun, K.

Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV using Super-Twisting Control Algorithm with Linear Correction Ter ms.

DOI: 10.5220/0007831202210228

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 221-228

ISBN: 978-989-758-380-3

221

applications, we cite exploration, construction, visual

inspection, transportation (Segales et al., 2016; Singh

and Frazier, 2018)... In addition, UAVs belong to

the class of nonlinear underactuated systems that suf-

fer from uncertainties due to the variation of the in-

ertia and mass that can happens during a transpora-

tion task (Yang and Xian, 2017) and external pertur-

bations due to environmental changes as wind (Cec-

carelli et al., 2007).

The rest of this article is organized as follows. In

Section 2, the mathematical model of the considered

quadrotor UAV system is described. In Section 3, the

used stucture of STA is studied for the position and

attitude tracking problem in the presence of uncer-

tainties. Simulation is conducted in Section 4 on the

considered system are provided to exhibit the effec-

tiveness of the used STA structure. The last section

concludes this article.

2 QUADROTOR UAV MODEL

AND PRELIMINARIES

The quadrotor UAVs are aerial robotic systems that

consist of four independent motors mounted on a rigid

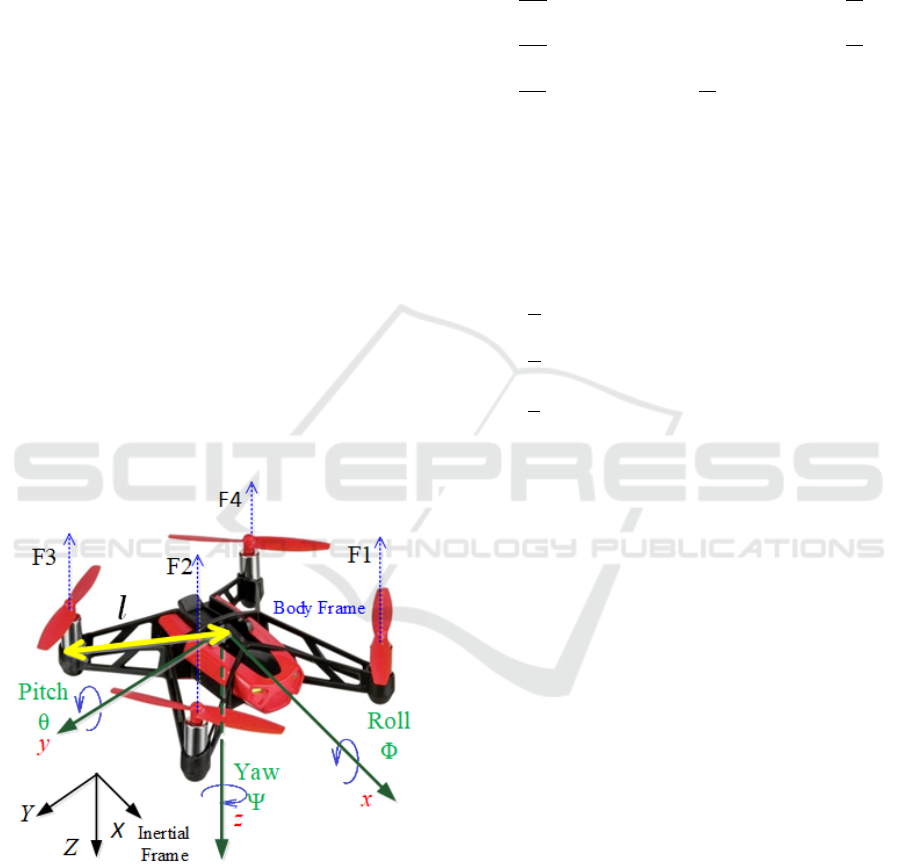
cross structure as shown in Fig. 1.

Figure 1: Quadrotor structure, forces, angles and frames.

2.1 Position and Attitude Dynamical

Model

The mathematical model of most of the UAV sys-

tems is based on 6-Degrees Of Freedom (DOF)

[x,y,z,φ,θ, ψ]

∈ R

. This latter contains the posi-

tion vector [x,y,z]

∈ R

that includes the altitude z

and the attitude or Euler angles vector [φ,θ, ψ]

∈ R

with φ represents the roll, θ represents the pitch and

ψ represents the yaw.

On the one hand, the position dynamic model is

given as in (Wu et al., 2017) by:

¨x = −

f tx

˙x + (cos(ψ)sin(θ)cos(φ) + sin(ψ)sin(φ))

+ d

¨y = −

f ty

˙y + (sin(ψ)sin(θ)cos(φ) − cos(ψ)sin(φ))

+ d

¨z = −

f tz

˙z − g + cos(θ)cos(φ)

+ d

(1)

where k

f tx

, k

f ty

and k

f tz

are drag coefﬁcients of trans-

lation, m denotes the quadrotor’s mass, g denotes the

constant of gravity, d

, d

and d

are uncertain func-

tions and u

is the vertical force.

On the other hand, the attitude dynamic model is

given as in (Wu et al., 2017) by:

φ =



−k

f ax

+ (I

− I

)

ψ − J

θ + u



+ d

θ =



−k

f ay

+ (I

− I

)

ψ + J

φ + u



+ d

ψ =



−k

f az

+ (I

− I

)

θ + u



+ d

(2)

where u

, u

and u

are respectively the roll, pitch and

yaw torques, k

f ax

, k

f ay

and k

f az

are the coefﬁcients of

the aerodynamic friction, I

, I

and I

denote the mo-

ments of inertia, J

denotes the motor inertia, d

, d

and d

are the uncertain functions and w

is the rotor

speed that is related to the torques by the following

equations:

= b(w

+ w

)

= b l(w

+ w

− w

)

= b l(w

+ w

− w

)

= c(w

+ w

− w

)

= w

− w

+ w

− w

(3)

where c, b and l represent respectively the drag co-

efﬁcient, the thrust coefﬁcient and the length of the

moment arm.

2.2 Problem Formulation

As said before, the objective of this work is to de-

sign a robust nonlinear control technique that en-

sures a ﬁnite-time convergence of the 6-DOF vec-

tor [x, y,z,φ, θ,ψ]

of the quadrotor system to the de-

sired known trajectory vector [x

,φ

,θ

,ψ

]

despite the presence of uncertainties and perturba-

tions. In the subsequent section, the used controller

will be derived based on the following assumptions:

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

222

• Assumption 1: The vectors [x,y, z,φ,θ, ψ]

and



˙x, ˙y, ˙z,

φ,

θ,



are available for measurements.

• Assumption 2: The reference vector

,φ

,θ

,ψ

]

and its time deriva-

tives are known. Moreover, the desired Euler

angles are limited to:

|φ

| < π/2,

|θ

| < π/2,

|ψ

| < π.

• Assumption 3: The Euler angles are limited to:

|φ| < π/2,

|θ| < π/2,

|ψ| < π.

• Assumption 4: The ﬁrst time derivative of uncer-

tain functions d

for j = x,y,z,φ, θ,ψ is bounded

such as:

| ≤ δd

1 j

+ δd

2 j

where δd

is a positive constants, δd

1 j

is chosen to

be equal to δd

, δd

2 j

is an arbitrary chosen posi-

tive constant and |S

| is the selected switching sur-

face for each trajectory that will be given in the

design procedure.

3 MODIFIED SUPER-TWISTING

ALGORITHM

In this section, the used STA structure for the ﬁnite-

time both position and attitude trajectory tracking of

uncertain quadrotor UAV systems will be designed in

two steps. The ﬁrst step consists on designing the

controller for the outer position loop while the sec-

ond step consists on generating the desired roll and

pitch angles and on designing the inner attitude loop.

3.1 Position Controller Design

The position dynamic model given in (1) can be

rewritten as follows:

χ = [ ¨x, ¨y, ¨z]

= F(

χ) +U

+ d

(4)

where F(

χ) =

−

f tx

˙x,−

f ty

˙y,−

f tz

˙z

represents

the known dynamics, d

= [d

]

represents the

vector of uncertainties and disturbances and U

]

with u

, u

and u

are virtual control in-

puts deﬁned as follows:

(cos(ψ)sin(θ)cos(φ) + sin(ψ)sin(φ))u

(sin(ψ)sin(θ)cos(φ) − cos(ψ)sin(φ))u

= g −

cos(θ)cos(φ)u

(5)

Now, let us select the sliding surface as follows:

= ˙e

+ λ

χ −

+ λ

(χ − χ

)

(6)

where e

∈ R

is the position tracking error vector

with χ

∈ R

is the vector of desired positions such

as χ

= x

, χ

= y

and χ

= z

and λ

is a diag-

onal matrix with strictly positive elements. The aim

of the SOSM is to ensure robustness, high precision

and lower chattering. To this end, the following STA

structure is selected:



= −M

0.5

sign(S

) − M

+ η

η = −M

sign(S

) − M

(7)

where |S

0.5

= diag



1χ

0.5

,|S

2χ

0.5

,|S

3χ

0.5



, M

and M

are (3 × 3) diagonal matrices

where the elements will be chosen to satisfy the

stability of the closed-loop system and sign(S

) =



sign(S

1χ

),sign(S

2χ

),sign(S

3χ

)



with:

sign(S

iχ

) =







1, i f S

iχ

> 0

0, i f S

iχ

= 0

−1, i f S

iχ

< 0

f or i = 1,2, 3 (8)

Now, let us calculate

based on (6) and using the

nominal position dynamic model (4) as follows:

= ¨e

+ λ

˙e

χ −

+ λ

˙e

=F(

χ) +U

−

+ λ

˙e

(9)

Therefore, solving (7) using (9) gives the follow-

ing proposed improved super-twisting control algo-

rithm:

= − F(

χ) +

− λ

˙e

− M

0.5

sign(S

)

− M

sign(S

)dt − M

(10)

Finally, the total thrust u

can be obtained using

the following formula (Zhao et al., 2015):

= m

+ u

+ (u

− g)

(11)

Theorem 3.1. (Wang et al., 2018) Consider the po-

sition model of the quadrotor system given in (4), the

Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV using Super-Twisting Control Algorithm with Linear Correction

Terms

223

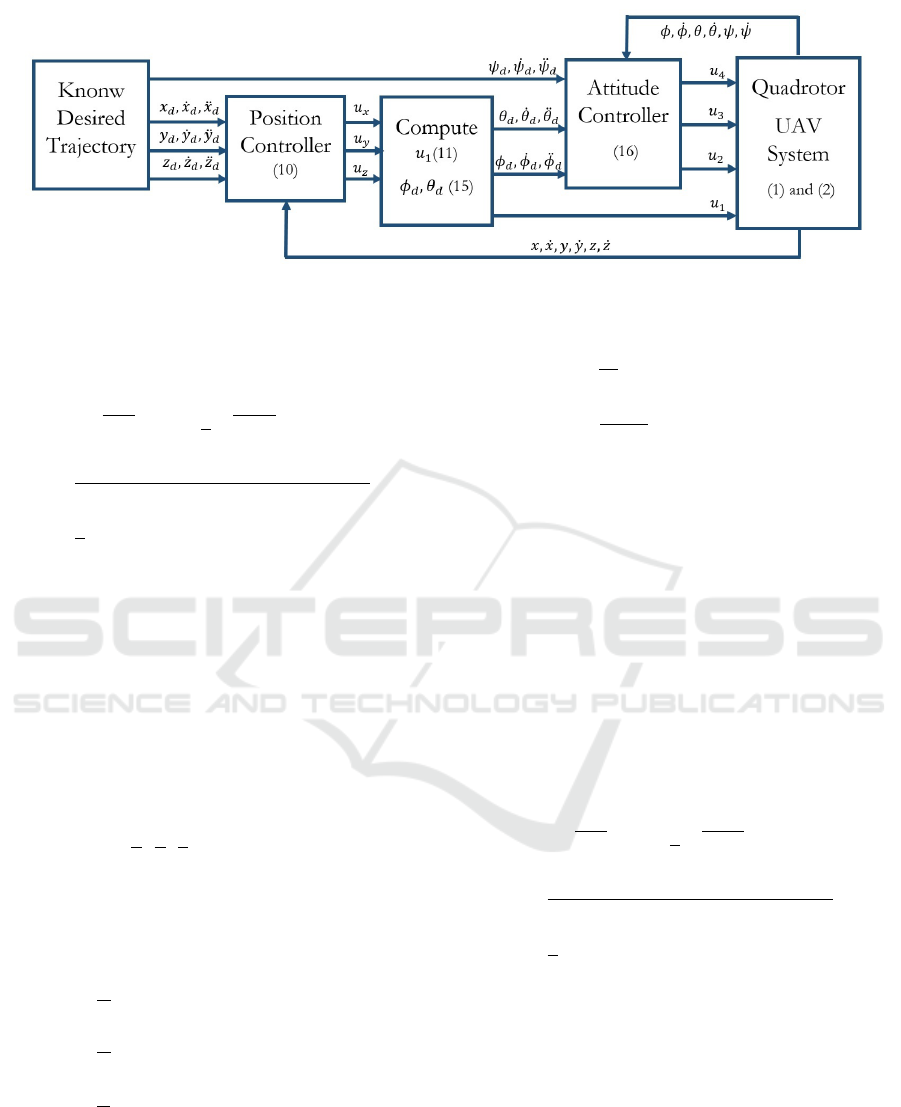
Figure 2: Block diagram of the closed-loop quadrotor UAV.

proposed controller in (11) ensures ﬁnite-time conver-

gence if the diagonal elements for i = 1,2, 3 of the

matrices M

, M

and M

in (10) are chosen as

follows:

> 2

δd

, M

2δd

, M

> δd

(2M

− δd

) + v



+ 2δd



− M

+ M

− δd

(12)

Proof. Refer to (Wang et al., 2018).

3.2 Attitude Controller Design

The same methodology used for the position tracking

will be adopted in this part. First of all, let us rewrite

the attitude dynamical model given in (2) as follows:

Θ = H(

Θ) + GU

+ d

(13)

where Θ = [φ,θ,ψ]

represents the attitude state vec-

tor, G = diag





is the non-singular control

matrix, d

= [d

]

is the vector of uncer-

tainties and disturbances and U

= [u

]

and

Θ) = [H

(

Θ),H

(

Θ),H

(

Θ)]

denotes the known

nonlinear dynamics with:

(

Θ) =



−k

f ax

+ (I

− I

)

ψ − J



(

Θ) =



−k

f ay

+ (I

− I

)

ψ + J



(

Θ) =



−k

f az

+ (I

− I

)



(14)

The objective of this part is to ensure the fast con-

verge to zero of the attitude tracking error e

Θ − Θ

where Θ

= [φ

,θ

,ψ

]

is the vector of the

known desired trajectories. Here, the desired roll

and pitch angles are generated from the virtual con-

trollers (Zhao et al., 2015) as follows:

= arcsin





sin(Θ

) − u

cos(Θ

)





= arctan



+ g



cos(Θ

) + u

sin(Θ

)





(15)

Theorem 3.2. (Wang et al., 2018) Consider the atti-

tude model of the quadrotor system given in (13), the

proposed control law is given by:

= − G

−1



Θ) −

+ λ

˙e

+ ζ



− G

−1



0.5

sign(S

) + N



ζ =

sign(S

)dt + N

(16)

where S

= ˙e

+ λ

is the classical switching sur-

face with λ

∈ R

3×3

is a diagonal positive matrix.

Moreover, The above controller ensures ﬁnite-time

convergence if the gains of the diagonal positive ma-

trices N

, N

and N

are chosen for i = 1, 2,3 as

follows:

> 2

δd

, N

2δd

, N

> δd

(2N

− δd

) + p



+ 2δd



− N

+ N

− δd

(17)

Proof. Refer to (Wang et al., 2018).

Finally, the architecture of the proposed control

system is represented in Fig. 2.

4 NUMERICAL SIMULATION

In this work, numerical simulation is performed us-

ing MATLAB/Simulink software to validate the used

improved super-twisting algorithm. The consid-

ered quadrotor is the parrot-rolling spider quadro-

tor (Mathworks, 2018) described by (1) and (2). The

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

224

used physical parameters given in Table 1 can be

found in (Mathworks, 2018).

Table 1: Physical parameters of the quadrotor UAV.

Parameter Value Unit

Mass, m 0.068 Kg

Moment of inertia, I

0.0686 10

−3

Kg.m

Moment of inertia, I

0.0920 10

−3

Kg.m

Moment of inertia, I

0.1366 10

−3

Kg.m

Motor inertia, J

1.0209 10

−7

Kg.m

Gravity, g 9.81 m/s

The simulation is performed such as the initial 6-

DOF vector is chosen to be [0,0,0,0, 0,0]. In addi-

tion, the desired scenario is given by choosing the fol-

lowing desired references:

(t) = 2 sin(0.5t) m

(t) = 2 cos(0.5t) m

(t) = 1 m

(t) = 0 rad

In addition, the disturbances are introduced at time

t = 8 s. The chosen proﬁle for the disturbances on the

position is given for j = x,y, z by:



0, i f t < 8

0.5 sin(2πt), i f t ≥ 8

while the disturbances on the Euler angles are given

for j = φ,θ, ψ by:



0, i f t < 8

0.2 sin(2πt), i f t ≥ 8

Moreover, for this scenario, the chosen sliding sur-

face and improved super-twisting gains are given in

Table 2.

Table 2: Proposed controller gains.

Gains Value

= diag(λ

χ1

,λ

χ2

,λ

χ3

) diag(5,5,5)

= diag(M

) diag(7.5,7.5,7.5)

= diag(M

) diag(6,10,10)

= diag(M

) diag(6, 6,6)

= diag(M

) diag(3, 3,3)

= diag(λ

Θ1

,λ

Θ2

,λ

Θ3

) diag(20,20,20)

= diag(N

) diag(5,7,10)

= diag(N

) diag(15,20,2)

= diag(N

) diag(4,5.5,5.5)

= diag(N

) diag(10,17,1)

The results obtained are given in ﬁgures 3-6. The

used nonlinear method ensures the high accuracy con-

vergence of the position and attitude trajectories to

their desired known references in ﬁnite-time as de-

picted in ﬁgures 3 and 4. These good performances

0.5

Z (m)

1.5

X (m)

Y (m)

-1

-2

Figure 3: Finite-time 3D tracking.

are due to the ability of the proposed controller to re-

ject the uncertain functions. Indeed, Fig. 5 conﬁrms

the good results since all the tracking error values are

very small. Finally, Fig. 6 shows that the chattering

is reduced in the control torque inputs. Moreover, the

obtained values of the control torque inputs are in the

range of acceptable torques for the considered parrot-

rolling spider quadrotor system.

5 CONCLUSIONS

In this paper, the robust super-twisting control algo-

rithm with nonlinear and linear correction terms has

been designed and simulated on a quadrotor UAV for

ﬁnite-time position and attitude tracking in the pres-

ence of unknown dynamics and perturbations. The

chosen controller has never been used for underac-

tuated systems such as the considered aerial robotic

systems. Moreover, this algorithm allows fast ﬁnite-

time convergence, reduces chattering and rejects the

effects of the unmodelled and unknown dynamics and

unexpected perturbations. The simulation has been

carried out on parrot-rolling spider quadrotor. The re-

sults obtained showed good performances even in the

presence of uncertainties. Future works will be con-

ducted to implement in real-time the proposed con-

troller and to make the convergence time faster during

the sliding phase.

ACKNOWLEDGEMENTS

This work received support from the Paraguayan Sci-

ence and Technology National Council - CONACYT

(PINV15-0136).

REFERENCES

Benallegue, A., Mokhtari, A., and Fridman, L. (2008).

High-order sliding-mode observer for a quadrotor

UAV. International Journal of Robust and Nonlinear

Control, 18(4-5):427–440.

Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV using Super-Twisting Control Algorithm with Linear Correction

Terms

225

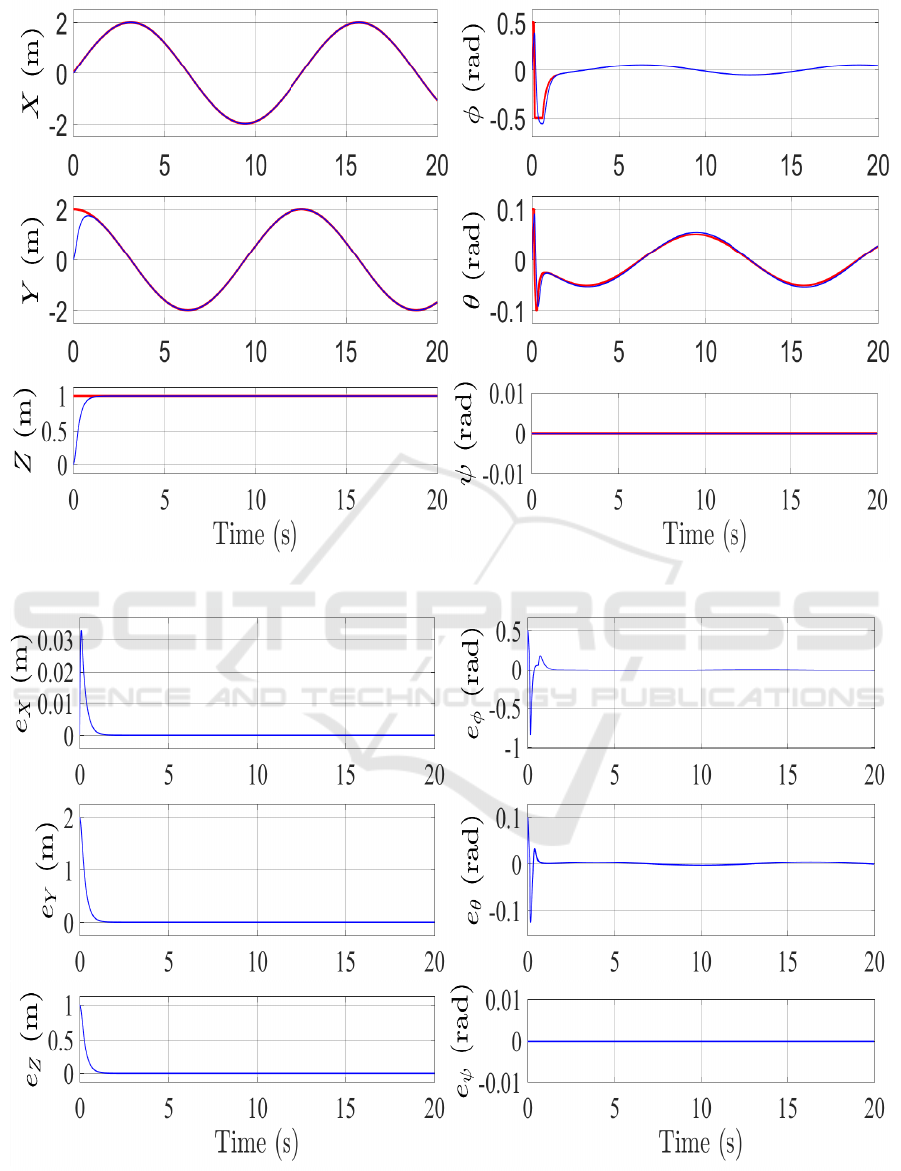
Figure 4: Finite-time position and attitude trajectory tracking.

Figure 5: Finite-time position and attitude tracking error.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

226

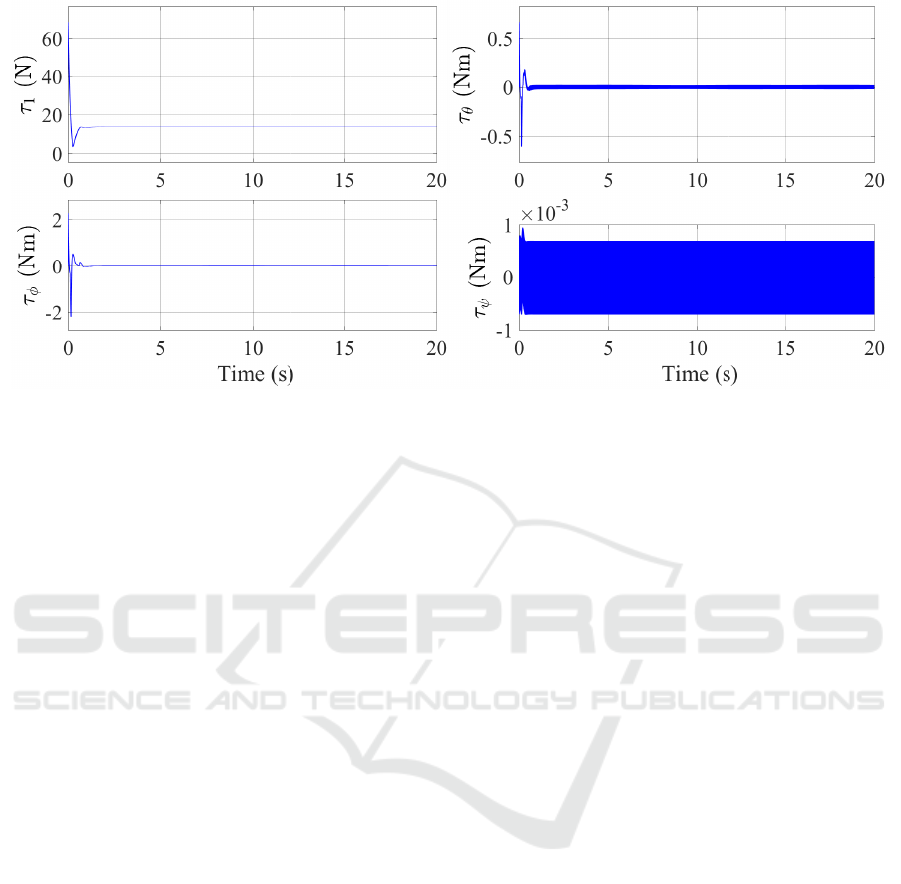
Figure 6: Computed control torque inputs.

Besnard, L., Shtessel, Y. B., and Landrum, B. (2012).

Quadrotor vehicle control via sliding mode controller

driven by sliding mode disturbance observer. Journal

of the Franklin Institute, 349(2):658 – 684.

Boiko, I. and Fridman, L. (2005). Analysis of chattering in

continuous sliding-mode controllers. IEEE Transac-

tions on Automatic Control, 50(9):1442–1446.

Ceccarelli, N., Enright, J. J., Frazzoli, E., Rasmussen, S. J.,

and Schumacher, C. J. (2007). Micro UAV path plan-

ning for reconnaissance in wind. In ACC, American

Control Conference, pages 5310–5315.

Feng, Y., Yu, X., and Man, Z. (2002). Non-singular terminal

sliding mode control of rigid manipulators. Automat-

ica, 38(12):2159 – 2167.

Gonz

alez-Hern

andez, I., Palacios, F. M., Cruz, S. S., Que-

sada, E. S. E., and Leal, R. L. (2017a). Real-time alti-

tude control for a quadrotor helicopter using a super-

twisting controller based on high-order sliding mode

observer. International Journal of Advanced Robotic

Systems, 14(1):1–15.

Gonz

alez-Hern

andez, I., Salazar, S., Munoz, F., and

Lozano, R. (2017b). Super-twisting control scheme

for a miniature quadrotor aircraft: Application to

trajectory-tracking problem. In ICUAS, International

Conference on Unmanned Aircraft Systems, pages

1547–1554.

Ibarra, E. and Castillo, P. (2017). Nonlinear super twisting

algorithm for UAV attitude stabilization. In ICUAS,

International Conference on Unmanned Aircraft Sys-

tems, pages 640–645.

Kali, Y., Ayala, M., Rodas, J., Saad, M., Doval-Gandoy, J.,

Gregor, R., and Benjelloun, K. (2019). Current con-

trol of a six-phase induction machine drive based on

discrete-time sliding mode with time delay estimation.

Energies, 12(1).

Kali, Y., Rodas, J., Ayala, M., Saad, M., Gregor, R., Benjel-

loun, K., Doval-Gandoy, J., and Goodwin, G. (2018a).

Discrete-time sliding mode with time delay estimation

of a six-phase induction motor drive. In IECON 2018

- 44th Annual Conference of the IEEE Industrial Elec-

tronics Society, pages 5807–5812.

Kali, Y., Rodas, J., Gregor, R., Saad, M., and Benjelloun,

K. (2018b). Attitude tracking of a tri-rotor uav based

on robust sliding mode with time delay estimation. In

2018 International Conference on Unmanned Aircraft

Systems (ICUAS), pages 346–351.

Kali, Y., Saad, M., and Benjelloun, K. (2017a). Non-

singular terminal second order sliding mode with time

delay estimation for uncertain robot manipulators. In

ICINCO, International Conference on Informatics in

Control, Automation and Robotics, pages 226–232.

Kali, Y., Saad, M., Benjelloun, K., and Benbrahim, M.

(2015). Sliding mode with time delay control for

mimo nonlinear systems with unknown dynamics. In

2015 International Workshop on Recent Advances in

Sliding Modes (RASM), pages 1–6.

Kali, Y., Saad, M., Benjelloun, K., and Fatemi, A. (2017b).

Discrete-time second order sliding mode with time de-

lay control for uncertain robot manipulators. Robotics

and Autonomous Systems, 94:53 – 60.

Kali, Y., Saad, M., Benjelloun, K., and Khairallah, C.

(2018). Super-twisting algorithm with time delay es-

timation for uncertain robot manipulators. Nonlinear

Dynamics, 93(2):557–569.

Lee, D., Jin Kim, H., and Sastry, S. (2009). Feedback

linearization vs. adaptive sliding mode control for a

quadrotor helicopter. International Journal of Con-

trol, Automation and Systems, 7(3):419–428.

Levant, A. (2003). Higher-order sliding modes, differentia-

tion and output-feedback control. International Jour-

nal of Control, 76(9-10):924–941.

Mathworks (2018). Parrot minidrones support

from simulink. https://www.mathworks.com/

hardware-support/parrot-minidrones.html.

Runcharoon, K. and Srichatrapimuk, V. (2013). Sliding

mode control of quadrotor. In TAEECE, International

Conference on Technological Advances in Electrical,

Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV using Super-Twisting Control Algorithm with Linear Correction

Terms

227

Electronics and Computer Engineering, pages 552–

557.

Segales, A., Gregor, R., Rodas, J., Gregor, D., and Toledo,

S. (2016). Implementation of a low cost UAV for pho-

togrammetry measurement applications. In ICUAS,

International Conference on Unmanned Aircraft Sys-

tems, pages 926–932.

Singh, K. K. and Frazier, A. E. (2018). A meta-analysis and

review of unmanned aircraft system (UAS) imagery

for terrestrial applications. International Journal of

Remote Sensing, 0(0):1–21.

Tseng, M. and Chen, M. (2010). Chattering reduction of

sliding mode control by low-pass ﬁltering the control

signal. Asian Journal of Control, 12(3):392–398.

Utkin, V., Guldner, J., and Shi, J. (1999). Sliding mode

control in electromechanical systems. Taylor-Francis.

Wang, Y., Yan, F., Chen, J., and Chen, B. (2018). Contin-

uous nonsingular fast terminal sliding mode control

of cable-driven manipulators with super-twisting al-

gorithm. IEEE Access, 6:49626–49636.

Wu, D., Du, H., and Zhu, W. (2017). Finite-time position

tracking control of a quadrotor aircraft. In 2017 36th

Chinese Control Conference (CCC), pages 737–742.

Yang, S. and Xian, B. (2017). Trajectory tracking control

design for the system of a quadrotor UAV with a sus-

pended payload. In CCC, Chinese Control Confer-

ence, pages 777–782.

Zhao, B., Xian, B., Zhang, Y., and Zhang, X. (2015). Non-

linear robust adaptive tracking control of a quadrotor

uav via immersion and invariance methodology. IEEE

Transactions on Industrial Electronics, 62(5):2891–

2902.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

228