
Modeling and Discretization of Hydraulic Actuated Telescopic Boom
System in Port-Hamiltonian Formulation
Lingchong Gao
1
, Wang Mei
2
, Michael Kleeberger
1
, Haijun Peng
3
and Johannes Fottner
1
1
Chair of Materials Handling, Material Flow, Logistics, Technical University of Munich,
Botlzmannstrasse15, 85748 Garching, Germany
2
Chair of Automatic Control, Technical University of Munich, Botlzmannstrasse15, 85748 Garching, Germany
3
Department of Engineering Mechanics, Dalian University of Technology,
Linggong Road No. 1, 116023 Dalian, P.R. China
Keywords:
Port-Hamiltonian System, Structure-preserving Discretization, Hydraulic Cylinder, Telescopic boom.
Abstract:
The hydraulic actuated telescopic boom system is the primary operation actuator of mobile cranes and aerial
platform vehicles. The purpose of this paper is to develope a unified mathematic model of such a boom
system which is a multi-domain system consisting of boom structure and hydraulic drive system. The model
is formulated within the port-Hamilton (PH) formalism using the definition of hydraulic system and elastic
boom structure as (Stokes-) Dirac structures. The Port-Hamiltonian systems can be easily interconnected thus
allowing the description of a complex system as a composition of subsystems. This property is especially
useful to model a multi-domain system with energy exchanges between subsystems. Considering the boom
structure as a Timoshenko beam, the luffing operation of boom system is simplified in a plane coordinate
system. The Port-Hamiltonian model of the hydraulic system and the boom structure are described with
details separately, a structure-preserving discretization is applied to transfer the distributed-parameter boom
model into a lumped-parameter model. Then the interconnections between the subsystems are illustrated and
a complete simulation including hydraulic system is accomplished in MATLAB/Simulink.
1 INTRODUCTION
Mobile cranes and aerial platform vehicles are con-
struction machineries designed to lift heavy loads
for construction operations and to assist high al-
titude operations respectively. They are generally
equipped with long boom systems. The boom sys-
tem can be considered as a long boom manipu-
lator that consists of single or multiple long and
lightweight booms, using hydraulic actuators along
with an electro-hydraulic servo system to control the
movements. Because of its high energy density, the
hydraulic system is suitable to actuate such large scale
boom systems with heavy loads. Due to the long
boom system, mobile cranes are suitable for lifting
tasks with large radius and height, whereas aerial plat-
form vehicle can transport persons and equipment to
high operation positions for installation, maintenance
or fire rescue missions. The longest boom system of
mobile cranes has reached the length of 250 meter and
the highest position that can be reached by aerial plat-
form vehicles is 114 meter.
In order to reduce the self-weight and to ensure the
mobility as well as transport-ability, the boom sys-
tems of mobile cranes and aerial platform vehicles
are designed as light as possible. The boom struc-
tures with limited stiffness are always performing a
strong flexible behavior, even though the strength of
the boom system is ensured. Due to the dynamic
behavior of hydraulic actuators (hydraulic cylinders
or motors) which derives from the elastic hydraulic
oil and flow characteristics of hydraulic components,
the output of the hydraulic system during start-up and
braking stages of the operations could fluctuate signif-
icantly. The combination of the elastic drive system
and the flexible boom structure leads to a hybrid sys-
tem with complex dynamic behavior. The flexibility
of the boom structure can cause an intense vibration
response when the loads applied on the boom struc-
ture or the motion statuses of boom system change.
The structure vibration will increase the maximum
dynamic stress which could cause structure fatigue or
even structure failure. The oscillation at the boom’s
tip could also increase the difficulty of load locat-
Gao, L., Mei, W., Kleeberger, M., Peng, H. and Fottner, J.
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation.
DOI: 10.5220/0007832100690079
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 69-79
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
69

ing or endanger the safety of the personnel on plat-
forms. The vibration suppression for these large scale
boom systems is essential for improving the structure
fatigue life-cycle, operation efficiency and personnel
safety.
Some researchers focus on the dynamic analysis
of the boom structure, some others have investigated
the analysis of the whole boom system including hy-
draulic system and use hydraulic actuators to control
the structure vibration. Sun combined the finite el-
ement calculation method with mathematical formu-
lations of hydraulic drive system including essential
hydraulic components, to obtain a new model which
describes the dynamic interaction between the boom
structure and the drive system of mobile crane. (Sun
and Kleeberger, 2003). The method has been applied
for the exemplary calculation of slewing, lifting and
luffing operations of lattice boom cranes (Sun et al.,
2005)(Sun and Liu, 2006). Both the load-bearing
structure and the drive system can be described in
details. The calculation of a telescopic boom crane
has also been studied. Similar long boom systems
are also used in fire-rescue turntable ladders. The
boom system of a fire-rescue turntable ladder is a
telescopic lattice boom actuated by a hydraulic cylin-
der. Sawodny described the long fire-rescue turntable
ladder as a flexible multi-body system (Zuyev and
Sawodny, 2005) and the dynamic behavior of the hy-
draulic drive system was included in the mathemat-
ical model equations (Sawodny et al., 2002). In the
work of Pertsch (Pertsch et al., 2009), a distributed-
parameter model for the fire-rescue turntable ladder
was derived, based on the Euler-Bernoulli beam the-
ory. The model of the ladder structure was transferred
into low dimensional model space. In their recent
work (Pertsch and Sawodny, 2016), a model for the
coupled bending-torsional vibration associated with
the rotational motion of an articulated aerial ladder
has been derived and an active vibration damping con-
trol has been developed and validated in real opera-
tion.
The hydraulic actuated telescopic boom can be re-
garded as a multi-physical system consisting of the
mechanical structure, hydraulic drives and electrical
control system. The interconnections between the
subsystems are achieved by hydraulic actuators and
electro-hydraulic servo systems. With the increas-
ing demands for more accurate control precision dur-
ing the operations of these long boom manipulators,
the dynamic analysis for such multi-physical systems
has been extended from the dynamic respond study
of separated subsystems to a coupling analysis of dif-
ferent domain subsystems. The bond-graph method
(Gawthrop and Bevan, 2007) is a graphical approach
in which the component energy ports are connected
by bonds using power-conjugate variables, efforts
and flows, to illustrate the energy transformation and
conversion between components and different phys-
ical systems. This port-based modeling method is
widely used to build a mathematical model of electro-
mechanical multi-domain systems (Guo et al., 2016)
(Cheng et al., 2016). The representation of a physi-
cal system as a bond graph can lead to a dynamical
system endowed with a geometric structure, which is
called a Port-Hamiltonian (PH) system. The geomet-
ric structure called Dirac structure is introduced as the
key mathematical concept to unify the description of
complex interactions in multi-physical systems. The
Hamiltonian function of the system energy which is
used to derive system state space equations, can also
be used as Lyapunov function for stability analysis.
Many researchers did a lot of work on the
system modeling and control design for flexible
beam systems based on their representation as Port-
Hamiltonian system. Macchelli also reformulated the
Timoshenko model of beam within the framework
of the Port-Hamiltonian system (Macchelli and Mel-
chiorri, 2004). The transitional and rotational deflec-
tions and momenta were chosen as state variables to
build the (Stokes-) Dirac structure. He also used Port-
Hamiltonian approach to describe the multi-body sys-
tem (rigid body, flexible links and kinematic pairs)
based on the power conserving interconnection (Mac-
chelli et al., 2009). In order to solve the infinite di-
mensional model in Port-Hamiltonian formulation, a
structure-preserving discretization method is needed.
So that the discretized finite-dimensional model still
has the property of (Stokes-) Dirac structure (Moulla
et al., 2012)(Vu et al., 2013). Wang applied a ge-
ometric pseudo-spectral discretization to obtain the
finite-dimensional Port-Hamiltonian framework of
linear Timoshenko beam model, and solved the feed-
forward motion control problem based on this lumped
model (Wang et al., 2017). For the hydraulic sys-
tems, Kugi designed a nonlinear controller for a clas-
sical hydraulic piston actuator system based on the
Port-Hamiltonian model (Kugi and Kemmetm
¨
uller,
2004). In his doctor thesis (Stadlmayr, 2009), Stadl-
mayr gave a Port-Hamiltonian representation of flex-
ible manipulator consisting a long boom with a mass
at the tip and a hydraulic system using hydraulic
cylinder to actuate the manipulator (Stadlmayr and
Schlacher, 2004). Combined with feed-forward and
feedback control system, a MIMO-control was de-
signed and used to accomplish path tracking and vi-
bration suppression for the flexible manipulator.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
70
2 SYSTEM DESCRIPTION
2.1 Port-Hamiltonian System
From the above research, it has shown that the Port-
Hamiltonian framework is a proper modeling method
for multi-domain systems because of its unique math-
ematical structure. To definite a Port-Hamiltonian
system, we start with the definition of a suitable space
of power variables which are strictly related to the ge-
ometry structure of the system. A Dirac structure de-
fined on this space of power variables will be used to
describe the internal and external interconnection of
the system. We consider a linear space F (space of
generalized velocities or flows) and its dual denotes
as E = F
∗
(space of generalized forces or efforts).
The space of the power variables is F ∗ E . Accord-
ing to the definition given by Duidam (Duindam et al.,
2009), there exists a canonically defined symmetric
bilinear form on F ∗ E
(f
1
,e
1
),(f
2
,e
2
) :=
h
e
1
| f
2
i
+
h
e
2
| f
1
i
, (1)
where f
i
⊂ F , e
i
⊂ E and .,. denotes the duality
product between F and its dual space E . A constant
Dirac structure on F is a linear subspace D ⊂ F ×E
with the property D = D
⊥
. A crucial property of the
Dirac structure is that the standard interconnection of
Dirac structures is again a Dirac structure (Duindam
et al., 2009). Thus the components of each system
will be described as energy-storing elements, resistive
elements with the formation of Dirac structure and
also called as internal ports. The energy exchanges
between the system and environment (other systems)
are described by external ports, interaction ports and
control ports specifically. So that the system con-
sisting of these components is still a Dirac structure,
so as a large-scale multi-domain system composed of
multiple subsystems which have the formulations of
Dirac structure.
The system energy function Hamiltonian H(x) is
used to build the mathematical model of the system.
The state space variables x reflect the system flow
variables by the definition of ˙x = f and the system
effort variables e are given by the co-energy variables
∂ H(x)/∂ x. All the subsystems can be described in the
form of
˙x = (J
J
J(x) − R
R
R(x))(
∂ H
∂ x
(x))
>
+ G
G
G(x)u
y = G
G
G(x)(
∂ H
∂ x
(x))
>
(2)
which is a useful formulation because the matrix
J
J
J(x) is a skew-symmetric matrix and the compo-
nents of J
J
J(x) are smooth functions of the state vari-
ables. The matrix R
R
R has to be symmetric and positive
semi-definite R
R
R = R
R
R
>
≥ 0. A dynamic system with
such formation is called a Port-Hamiltonian system.
In order to model the whole boom system as Port-
Hamiltonian system, the space of power variables of
hydraulic system and boom structure will be defined
with numerical Dirac structure. The representation of
the boom system is written as the combination of the
hydraulic system and the boom structure in the for-
mulations of a Port-Hamiltonian system. For the sake
of simplicity, the damping effect is momentarily ne-
glected in the following chapters.
2.2 Port-Hamiltonian Model of
Hydraulic System
2.2.1 Essential Equations and Assumptions
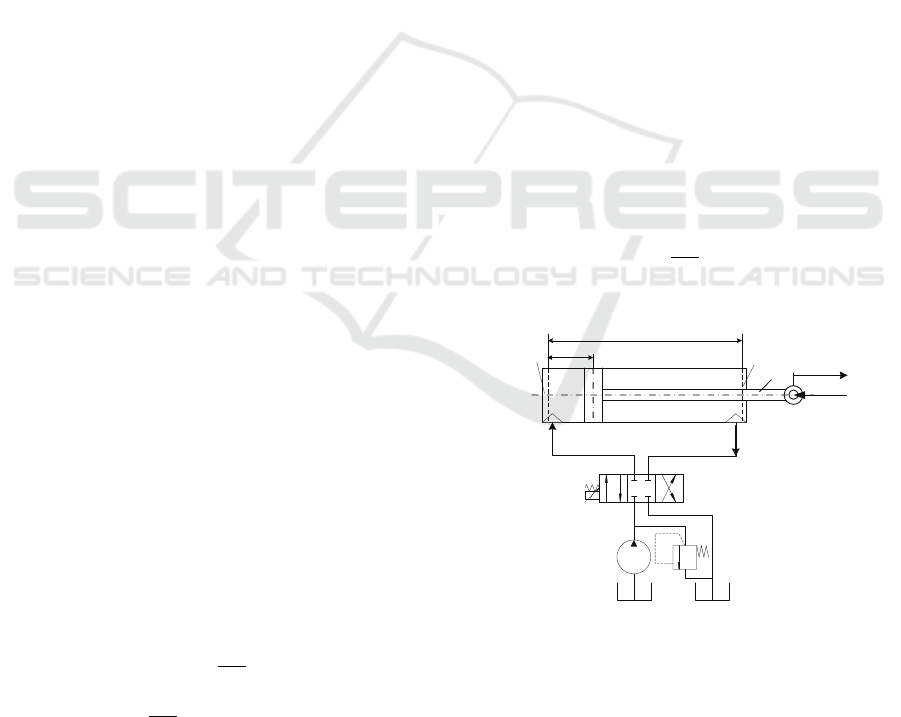
The luffing cylinder of the boom system can be simply
considered as the hydraulic cylinder actuator of Fig.
(1). A 4/3-way proportional directional valve controls
the movement of the asymmetric cylinder, which ac-
tuates the luffing movement of the boom system. The
directional valve is connected with a pressure pump
and a tank. The supply pressure p
S
is determined by
the relief valve, and the tank pressure is p
T
.
The volumetric flows through the directional
valve, Q
1
and Q
2
, are simply given by
Q
i
= k
v
p
∆p
i
x
v
,i = 1,2 (3)
1
Q
2
Q
l
s
1
p
2
p
A
A
D
m
P
F
T
p
S
p
01
: Minimal volume
in Chamber 1
V
01
V
02
V
02
: Minimal volume
in Chamber 2
V
Figure 1: Diagram of the hydraulic system of a hydraulic
cylinder.
with the position of the valve core x
v
, the pressure dif-
ference ∆p
i
and the valve coefficient k
v
, which can be
considered as constant when the properties of the flow
through the valve ports are constant and the type of
valve core is slide valve. Then, we assume that there
is no internal or external leakage flows and the tem-
perature remains constant. The continuity equations
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation
71

of the cylinder chambers can be described as
d
dt
(As) = Q
1
,
d
dt
(αA(l − s)) = Q
2
. (4)
Using the linearized constitutive law of the con-
stant (isothermal) bulk modulus E
oil
E
oil
= ρ
∂ p
∂ ρ
, (5)
we can rewrite Eq. (3) as a well-known formation
˙p
1
=
E
oil
V
01
+ As
−A
P
m
+ Q
1
˙p
2
=
E
oil
V
02
+ αA(l − s)
αA
P
m
− Q
2
(6)
with the piston’s momentum P and its mass m. And
the motion equations of the piston are considered as
the following form
˙
S =
P
m
˙
P = (p
1
A − p
2
αA − F).
(7)
Eq. (7) and (6) constitute a state model of the valve-
controlled hydraulic cylinder of Fig. (1) with the state
vector x
x
x = [s, P, p
1
, p
2
]
>
.
2.2.2 Energy Description of Isentropic Fluid
In the case of an isentropic process no heat transfer
between the environment and the considering system,
which performs only work of expansion. The system
energy can be simplified as
dU = −pdV. (8)
By defining the specific internal energy u = U/M
and the specific volume v = V /M, with M the mass of
the fluid in the system, we can get
du = −pdv =
p
ρ
2
dρ (9)
where ρ = 1/v is the density of the fluid.
Now we introduce another important thermody-
namic quantity, the enthalpy H = U + pV and the
mass specific enthalpy h = H/M = u + pv . Combin-
ing the definition of h with (9), we get the following
relations for the isentropic scenario
h = u +
1
ρ
p = u +
1
ρ
ρ
2
∂ u
∂ ρ
=
∂
∂ ρ
(uρ)
(10)
Based on the definition of isothermal bulk mod-
ules, integrating along an isentropic process, Eq. (5)
yields
p(ρ) = p
0
+ E
oil
ln
ρ
ρ
0
with p
0
= p(ρ
0
). (11)
Then, the specific energy of the fluid obeying the
constitutive law (5) can be obtained form (9) in the
form:
u(p) =
p
0
+E
oil
+u
0
ρ
0
−(p+E
oil
)e
((
p
0
−p
)
/E
oil
)
ρ
0
with u
0
= u (p
0
).
(12)
For the sake of convenience we will subsequently
choose p
0
= 0 and u
0
= 0. Hence the internal energy
results in
U(p) =
M
z }| {
V ρ(p)u(p) = V
E
oil
e
(p/E
oil
)
− 1
− p
.
(13)
Using the above formulation, we can acquire the
energy function of the fluid inside the hydraulic cylin-
der, which is essential to building the Hamiltonian
function of the system.
2.2.3 Port-Hamiltonian Representation of
Hydraulic Cylinder
The specific internal energy u(p) of the fluid in the
two chambers of the hydraulic cylinder can be deter-
mined by (12), then the energy stored in the hydraulic
cylinder of Fig. 1 is given by
U
Hydr
= V
1
ρ
1
u(p
1
) +V
2
ρ
2
u(p
2
)
= E
oil
∑
i=1,2
V
i
e
(p
i
/E
oli
)
−
p
i
E
oil
− 1
V
1
= V
01
+ As,V
2
= V
02
+ αA(l − s),
(14)
the subscripts refer to the corresponding quantities of
the chamber 1 and chamber 2 (rob side). Assuming
that the kinetic energy of fluid mass can be neglected
compared to the kinetic energy of the piston, the total
energy E
c
of the hydraulic cylinder is
E
c
= U
Hyd
+
P
2
2m
. (15)
We can use the total energy E
c
as the Hamilto-
nian function H
c
, then the Port-Hamiltonian model
of the hydraulic cylinder takes the form as (2) with
the state vector x
x
x = [s, P, p
1
, p
2
]
>
and the input vec-
tor u
u
u = [F,Q
1
,Q
2
]
>
, the hydraulic cylinder can be de-
scribed as
∑
0
Σ
0
:
˙
x
x
x = J
J
J(x)∂
x
H
c
+ g
g
g(x)u
u
u
y
y
y = g
g
g(x)
>
∂
x
H
c
(16)
The matrices J
J
J(x) and g
g
g(x) are
J
J
J(x) =
0 1 0 0
−1 0 E
oil
A/V
1
−E
oil
αA/V
2
0 −E
oil
A/V
1
0 0
0 E
oil
αA/V
2
0 0
(17)
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
72

g
g
g(x) =
0 0 0
−1 0 0
0 E
oil
/V
1
0
0 0 −E
oil
/V
2
(18)
In order to illustrate the system output y
y
y, more de-
tails of the model is given by
∂ H
c
∂ x
=
αA (Γ
2
) − A (Γ
2
)
P/m
V
1
e
(p
1
/E
oil
)
− 1
V
2
e
(p
2
/E
oil
)
− 1
,
with Γ
i
= p
i
− E
oil
e
(p
i
/E
oil
)
+ E
oil
,i = 1,2.
(19)
Then using the definition (13), the system output
is
y
y
y = g
g
g(x)
>
∂ H
c
∂ x
=
0 −1 0 0
0 0 E
oil
/V
1
0
0 0 0 −E
oil
/V
2
∂ H
c
∂ x
=
−p/m
E
oil
e
(p
1
/E
oil
)
− 1
−E
oil
e
(p
2
/E
oil
)
− 1
=
−v
ρ
1
h
1
−ρ
2
h
2
(20)
The change of the system energy can be obtained
by the product of input u
u
u and output y
y
y as
dE
c
dt
= y
y
y
>
u
u
u = h
1
ρ
1
Q
1
|{z}
˙
M
1
−h
2
ρ
2
Q
2
|{z}
˙
M
2
−v · F (21)
In Eq. (21), the first two parts represent the en-
ergy changed by the fluid mass flows to or from the
chambers respectively,
˙
M
1
or
˙
M
2
, and the third part
represents the work transferred to the boom structure
by cylinder force F.
2.3 Port-Hamiltonian Model of 2-D
Timoshenko Beam
2.3.1 A Rotation Homogeneous Timoshenko
Beam
The boom structure can be simplified as an ideal
beam model in a plane, when the lateral and axial
loads can be neglected. In order to obtain a suitable
Port-Hamiltonian representation of the boom struc-
ture, we start with the rotating homogeneous Timo-
shenko beam formulation to describe the dynamic be-
havior of the boom structure.
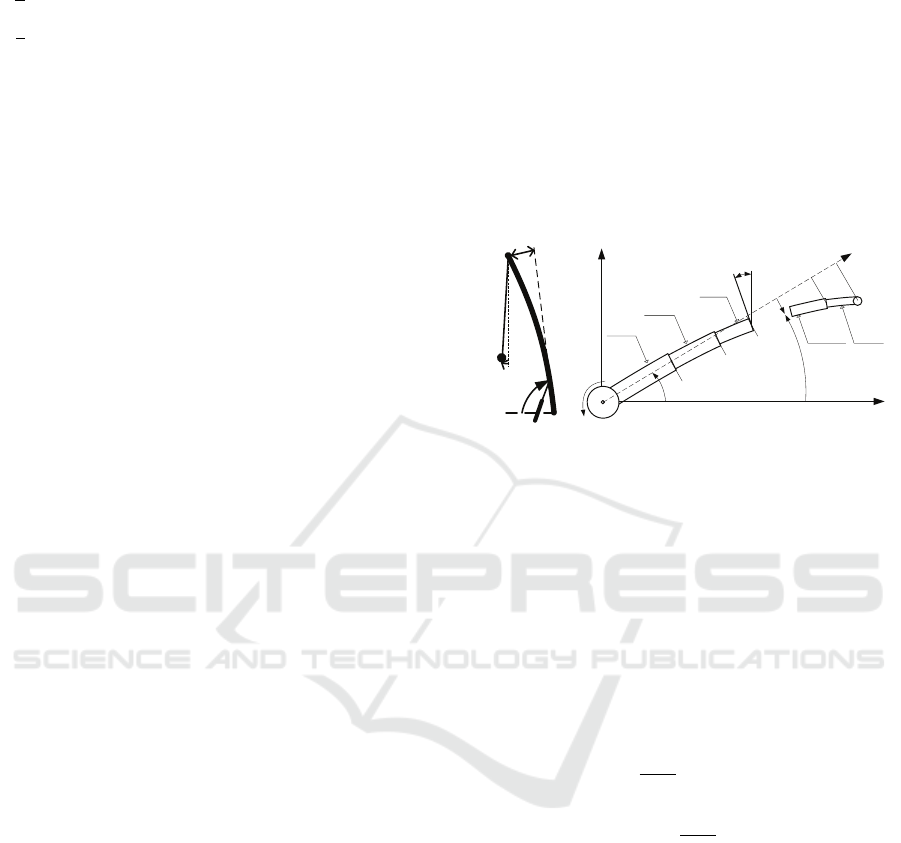
In Fig. 2. , t is the time variable and z is the spa-
tial coordinate along the equilibrium position of the
beam, and w
e
(z,t) is the deflection of the beam from
t
T
Z
e
Z
e
Y
Y
O
,
e
w t z
,
e
t z
\
Figure 2: A rotation homogeneous Timoshenko beam.
the equilibrium position and Ψ
e
(z,t) is the rotation of
the beam’s cross section.
The boundary condition of the boom structure can
be considered as a free tip with a fixed end, and the
fixed end rotates around a fixed axis with the angle
displacement θ (t). Then the original Timoshenko
beam model is transferred to a rotating Timoshenko
beam. New system variables are defined as
w(z,t) = w
e
(z,t) + z · θ(t)
ψ(z,t) = ψ
e
(z,t) + θ (t)
(22)
which still fulfill the original PDEs in a new form
ρ
∂
2
w
∂t
2
− K
∂
2
w
∂ z
2
+ K
∂ ψ
∂ z
= 0
I
ρ
∂
2
ψ
∂t
2
− EI
∂
2
ψ
∂ z
2
+ K
ψ −
∂ w
∂ z
= 0
(23)
In (23), the coefficients ρ, I
ρ
, E, I are the mass per
unit length, the mass moment of inertia of the cross
section, Young’s modulus and the moment of the in-
ertia of the cross section respectively. And in the co-
efficient K = kGA, G is the modulus of elasticity in
shear, A is the area of cross section and k is a constant
depending on the shape of the cross section.
2.3.2 Port-Hamiltionian Model of Timoshenko
Beam
For a homogeneous Timoshenko beam, the coeffi-
cients are constant and its mechanical energy is given
as following form:
H
B
(t) =
Z
L
0
Hdz
H =
1
2
ρ ˙w
2
+ I
ρ
˙
ψ
2
+ K (ψ − ∂
z
w)
2
+ EI (∂
z
ψ)
2
.
(24)
According to the mechanical energy formulation
(24) the potential elastic energy is the function of the
shear and bending deformations, which can be written
as:
ε
t
(z,t) = ∂
z
w(z,t) − ψ(z,t)
ε
r
(z,t) = ∂
z
ψ(z,t).
(25)
The associated co-energy variables are shear force
Kε
t
(z,t) and bending momentum EIε
r
(z,t). The ki-
netic energy is the function of the translational and
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation
73

rotational momenta which are given as
p
t
(z,t) = ρ ˙w(z,t),
p
r
(z,t) = I
ρ
˙
ψ(z,t),
(26)
and the co-energy variables are translational velocity
(p
t
(z,t))/ρ and rotational velocity p
r
(z,t)/I
ρ
.
According to the definition of new state variables,
the original PDEs can be rewritten in a form
˙p
t
˙p
r
˙
ε
t
˙
ε
r
=
0 0 ∂
z
0
0 0 1 ∂
z
∂
z
−1 0 0
0 ∂
z
0 0
δ
p
t
H
δ
p
r
H
δ
ε
t
H
δ
ε
r
H
. (27)
We denote e ∈ E , f ∈ F as the effort and flow
variables separately. They are related to the time
derivative of state variables f
f
f = −
˙
x
x
x and the associ-
ated co-energy variables as
f
f
f =
f
p
t
f
p
r
f
ε
t
f
ε
r
=−
˙p
t
˙p
r
˙
ε
t
˙
ε
r
,e
e
e =
e
p
t
e
p
r
e
ε
t
e
ε
r
=
δ
p
t
H
δ
p
r
H
δ
ε
t
H
δ
ε
r
H
. (28)
The total energy (we neglect the gravity potential
energy and just focus on the quadratic energy func-
tions) becomes the following formulation:
˙
H
B
=
Z
L
0
∂
x
H ·
˙
xdz = −
Z
L
0
e
>
· fdz. (29)
Applying integration by parts on Eq. (29), one
obtains
˙
H
B
= (e
p
t
e
ε
t
+ e
p
r
e
ε
r
)
|
L
0
. (30)
Defining the boundary flow and effort variables as
f
t
∂
f
r
∂
e
t
∂
e
r
∂
=
e
p
t
|
∂ Z
e
p
r
|
∂ Z
e
ε
t
|
∂ Z
e
ε
r
|
∂ Z
, (31)
where e
|
∂ Z
denotes the restriction on the border of the
domain Z = [0, L]. Comparing the right hand sides
of (29) and (30), it is clear that the increase of the
total energy is equal to the power through the borders.
And the power continuity and conservation equation
is fulfilled as
Z
Z
e
>
· fdz +
f
t
∂
· e
t
∂
+ f
r
∂
· e
r
∂
∂ Z
= 0. (32)
Finally, Eq. (27) can be rewrote shortly as
− f
f
f = J
J
J(z)∂
x
H = J
J
J(z)e
e
e, (33)
where J
J
J(z) is a skew-symmetric differential operator
as that in Eq.(2). Using the definition of flow, ef-
fort variables (28) and the system state equations (33),
one can define a bilinear geometric structure, a Dirac
structure D:
D =
{
( f
f
f , f
t
0
, f
r
∂
,e
e
e,e
t
∂
,e
r
∂
) ∈ F × E |
− f
f
f = J
J
J(z)e
e
e and Eq.(30) holds }.
(34)
2.3.3 Structure-preserving Spatial Discretization
In order to solve the distributed parameter model
of Timoshenko beam, we need to transfer its Port-
Hamiltonian model into a lumped-parameter model.
The skew-symmetric differential operator has to
be retained in the new discretized model, which
means that the discretization method should preserve
such certain (geometric or structural) property. In
(Moulla et al., 2012), a structure-preserving spa-
tial discretization method is applied to approximate
the infinite-dimensional Timoshenko model by the
pseudo-spectral method. The discretization of the
Port-Hamiltonian system is completed with the finite-
dimensional approximation of the energy and the con-
stitutive relations based on the discretization of the
(Stokes-) Dirac structure. Furthermore, the bound-
ary port variables are preserved and specified (inter-
connection) port variables (inputs and outputs) in the
resulting lumped Port-Hamiltonian model during the
whole process.
The geometric discretization has proven to pro-
vide a good approximation of system properties in
(Wang et al., 2017), such as the spectrum of the dif-
ferential operators. Some essential steps are reviewed
in this section.
Based on the formulation (27), we rewrote the
Dirac structure (34) as
−f =
1 0
0 1
1 0
0 1
∂
z
e+
0 0
1 0
0 −1
0 0
e
∗
(35)
so we can classify the effort vectors as e and e
∗
, de-
pending on whether it is subject to differentiation or
not.
According to the pseudo-spectral method pro-
posed for canonical systems of two conservation
laws, we define different approximation bases for
the flows f
v
∈
{
f
f
f
p
t
, f
f
f
p
r
, f
f
f
ε
t
, f
f
f
ε
r
}
and the efforts e
v
∈
{
e
e
e
p
t
,e
e
e
p
r
,e
e
e
ε
t
,e
e
e
ε
r
}
.
f
f
f
v
(t,z) ≈
N−1
∑
k=0
f
v
k
ϕ
k
(z), e
v
∗
(t,z) ≈
N−1
∑
k=0
e
v
∗,k
ϕ
k
(z),
e
v
(t,z) ≈
N
∑
i=0
e
v
i
φ
i
(z).
(36)
The time dependent coefficients are collected in
the vectors
f
f
f
v
,e
e
e
v
∗
∈ R
N
and e
v
∈ R
N+1
,v ∈
{
p
t
, p
r
,ε
t
,ε
r
}
(37)
ϕ
k
(z) and φ
i
(z) are the basis functions for flows
and efforts, and satisfying the exact differentiation or
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
74

compatibility condition (Vu et al., 2013):
E = span
{
φ
0
,... ,φ
N
}
F = span
{
ϕ
0
,... ,ϕ
N−1
}
∂
x
E = F .
(38)
Then we chose the interpolation Lagrange poly-
nomials of degree N and N −1 as suitable bases func-
tions for the efforts and flows:
ϕ
k
(z) =
N−1
∏
j=0, j6=k
z − z
j
z
k
− z
j
,φ
i
(z) =
N
∏
j=0, j6=i
z − ζ
j
ζ
i
− ζ
j
. (39)
z
k
∈ (0, L),k = 0,.. . ,N − 1 and ζ
i
∈ (0, L), i =
0,... ,N are the collocation points for ϕ
k
(z) and φ
i
(z)
respectively. In this paper, we choose the zeros of
Legendre polynomials to reduce the Runge’s phe-
nomenon (Cardoso-Ribeiro et al., 2016), i.e. the oc-
currence of numerical oscillations at the boundaries
of the interval with increasing number of collocation
points.
Denote φ
φ
φ = [φ
0
,... ,φ
N
]
>
the vector of effort basis
functions and
Φ
Φ
Φ =
φ
φ
φ(0)
>
φ
φ
φ(L)
>
. (40)
Let f
f
f
t/r
∂
=
h
f
t/r
0
, f
t/r
L
i
>
and e
e
e
t/r
∂
=
h
e
t/r
0
,e
t/r
L
i
>
be
the vectors of boundary flows and efforts correspond-
ing to translational or rotational motion. Inserting
(36) into (35) and (31), one obtains the linear system
of equations
−
f
f
f
p
t
f
f
f
p
r
f
f
f
ε
t
f
f
f
ε
r
=
D
D
D 0
0 D
D
D
D
D
D 0
0
0
0
0
0 D
D
D
e
e
e
p
t
e
e
e
p
r
e
e
e
ε
t
e
e
e
ε
r
+
0 0
I
I
I 0
0
0
0
0
0−I
I
I
0 0
e
e
e
p
t
∗
e
e
e
p
r
∗
e
e
e
ε
t
∗
e
e
e
ε
r
∗
f
f
f
t
∂
f
f
f
r
∂
e
e
e
t
∂
e
e
e
t
∂
=
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
e
e
e
p
t
e
e
e
p
r
e
e
e
ε
t
e
e
e
ε
r
.
(41)
The elements of the derivative matrix D
D
D ∈
R
N×(N+1)
are obtained from the spatial derivative
of the effort bases functions at the flow collocation
points:
D
k+1,i+1
= ∂
x
φ
i
(z
k
), (42)
with i = 0, ... ,N,k = 0, ... ,N −1. In accordance with
the distributed parameter model, an additional cou-
pling term with identity matrices I
I
I = I
I
I
N
appears on
the right hand side of (42).
Replacing the approximations of flows and efforts
in the energy balance, we obtain
˙
H ≈
∑
v∈
{
p
t
,p
r
,ε
t
,ε
r
}
(e
e
e
v
)
>
M
M
M f
f
f
v
(43)
with the elements of the non-square matrix M
M
M ∈
R
(N+1)×N
defined as
M
i+1,k+1
=
Z
L
0
φ
i
(z)ϕ
k
(z)dz. (44)
The right hand side of (43) consists of degen-
erated bilinear forms between the vectors of dis-
crete flows and efforts. Due to the degeneracy (the
kernel of M
M
M is non-empty), this bilinear form does
not qualify to define a Dirac structure on the finite-
dimensional bond space of reduced flows and efforts
F
r
× E
r
with
e
e
e
p
t
,e
e
e
p
r
,e
e
e
ε
t
,e
e
e
ε
r
,e
e
e
t
∂
,e
e
e
r
∂
∈ E
r
∈ R
4N+8
and
f
f
f
p
t
, f
f
f
p
r
, f
f
f
ε
t
, f
f
f
ε
r
, f
f
f
t
∂
, f
f
f
r
∂
∈ F
r
∈ R
4N+4
. It can,
however, be shown that the power continuity equation
(32) is approximated via
∑
v∈
{
p
t
,p
r
,ε
i
,ε
j
}
(e
e
e
v
)
>
M
M
M f
f
f
v
+
∑
u∈{t,r}
e
e
e
u
∂
>
M
M
M f
f
f
u
∂
= 0.
(45)
To obtain a non-degenerate power pairing, vectors of
reduced effort variables
˜
e
e
e
v
∈ R
N
are defined:
˜
e
e
e
v
= M
M
M
T
e
e
e
v
. (46)
These shall be, we discretize the constitutive equa-
tion e
e
e = (δ
x
H)
>
, derived from a discrete energy. Note
that
˙
x
x
x = − f
f
f holds, i.e. states and flows are discretized
with respect to the same basis. We can define
˙
x
x
x
v
=
− f
f
f
v
and replace the approximation in H =
R
Z
H dz
with Hamiltonian density. We obtain
H ≈
1
2
∑
v
c
v
(x
x
x
v
)
>
S
S
Sx
x
x
v
, c
v
∈
1
ρ
,
1
I
ρ
,K
s
,K
b
, (47)
where the elements of S
S
S ∈ R
N×N
are given by
S
i+1, j+1
=
Z
L
0
ϕ
i
(z)ϕ
j
(z)dz. (48)
The required discretized constitutive relation is
simply
˜
e
e
e
v
=
∂ H
∂ x
x
x
v
>
= c
v
S
S
Sx
x
x
v
, ∀v. (49)
On the other hand, the relation for the discretized
effort vectors e
e
e
v
∗
in the flow (or state) bases becomes
e
e
e
v
∗
= c
v
x
x
x
v
= S
S
S
−1
e
e
e
e
v
= S
S
S
−1
M
M
M
>
e
e
e
v
. (50)
According to (Moulla et al., 2012), the discretised
Timoshenko beam can be formulated into an input-
/output (I/O) representation:
f
f
f =
0 J
J
J
s
1
J
J
J
s
2
0
· e
e
e (51)
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation
75
with
f =
f
f
f
p
t
,−e
t
∂ 0
, f
f
f
p
r
,−e
r
∂ 0
, f
f
f
ε
t
, f
t
∂ L
, f
f
f
ε
r
, f
r
∂ L
>
e
e
e =
˜
e
e
e
p
r
, f
t
∂ 0
,
˜
e
e
e
p
r
, f
r
∂ 0
,
˜
e
e
e
ε
t
,e
t
∂ L
,
e
e
e
e
ε
r
,e
r
∂ L
>
J
J
J
s
1
=
−D
D
D
−φ
φ
φ
>
0
M
M
M
>
φ
φ
φ
>
L
−1
0
0
0
−S
S
S
−1
M
M
M
>
0
M
M
M
>
φ
φ
φ
>
L
−1
−D
D
D
−φ
φ
φ
>
0
M
M
M
>
φ
φ
φ
>
L
−1
J
J
J
s
2
=
−D
D
D
−φ
φ
φ
>
L
M
M
M
>
φ
φ
φ
0
>
−1
−S
S
S
−1
M
M
M
>
0
M
M
M
>
φ
φ
φ
>
L
−1
0
0
0
−D
D
D
−φ
φ
φ
>
L
M
M
M
>
φ
φ
φ
>
0
−1
Indeed, J
J
J
s
1
= J
J
J
>
s
2
, i.e. the interconnection matrix
J
J
J ∈ R
(4N+4)×(4N+4)
is skew-symmetric.
We obtain the explicit state space model in linear
Port-Hamiltonian form
˙
X
X
X = J
J
J
4N×4N
Q
Q
Q
4N×4N
X
X
X +G
G
G
4N×4
U
U
U
Y
Y
Y = G
G
G
>
4N×4
Q
Q
Q
4N×4N
+ D
D
D
4×4
U
U
U.
(52)
The vector x
x
x
v
∈ R
N
is merged in the
overall state vector X
X
X ∈ R
4N
, Q
Q
Q
4N×4N
=
blockdiag
S
S
S/ρ, S
S
S/I
ρ
,K
b
S
S
S,K
s
S
S
S
is the overall
energy (Hessian) matrix, and U
U
U ∈ R
4
, Y
Y
Y ∈ R
4
are
the vectors of boundary inputs and collocated, power
conjugated outputs. They are composed of the
elements of the boundary flow an effort vectors. In
the terms of the physical boundary variables we have
U
U
U(t) =
U
1
U
2
U
3
U
4
=
v(0)
ω(0)
Q(L)
M(L)
,
Y
Y
Y (t) =
Y
1
Y
2
Y
3
Y
4
=
−Q(0)
−M(0)
v(L)
ω(L)
.
2.4 Port-Hamiltonian Model of the
Hydraulic Actuated Telescopic
Boom System
2.4.1 Modeling of the Telescopic Boom Structure
Based on the Timoshenko assumption and its Port-
Hamiltonian representation, it is not difficult to build
a proper mathematical model for the structure of tele-
scopic boom. However there are some modifications
should be clarified. The coefficients ρ, I
ρ
, I of the
new beam model are not constant. Considering the
telescopic boom structure, its boom sections are de-
creasing so that all the other boom sections can be
pulled back into the first boom, it means that a ho-
mogeneous beam model is no longer suitable. The
boom structure will be modeled as a N-stepwise beam
with different coefficients for each boom section, a
non-homogeneous Timoshenko beam. However, each
boom section can be considered as a homogeneous
Timoshenko beam and the boundary conditions be-
tween each two sections are specified as fixed accord-
ing to the continuous conditions. The overlapping
parts of the boom sections and the telescopic mech-
anism are neglected in the purpose of simplification.
1
1
E
I
U
2
2
E
I
U
3
3
E
I
U
n
n
EI
U
1
1
n
n
EI
U
1
L
2
L
3
L
n
L
L
1n
L
t
T
, ( , ) ( )
e
w z t w z t z t
T
( )
M
t
Z
( , )
e
w z t
( , ) ( , )
e
z t z t t
\ \ T
0
0L
Y
T
I
Figure 3: Telescopic boom and its simplified model: the
rotating non-homogeneous Timoshenko beam.
According to the definition of power variables
(25) and (26), we can define the new power vari-
ables for the k
th
section of the N-stepwise beam in the
domain of D
k
:= [L
k−1
,L
k
] as p
t,k
, p
r,k
,ε
t,k
,ε
r,k
,k =
1,... ,n. For each part of the stepwise Timoshenko
beam, a Dirac structure D
k
can be acquired by using
the corresponding power variables.
According to the Port-Hamiltonian form (51), the
I/O represent of the kth boom is represented as system
∑
k
Σ
k
:
˙
X
X
X
k
= J
J
J
k
∂ H
k
∂ x
x
x
k
>
+ G
G
G
k
U
U
U
k
Y
Y
Y
k
=
G
G
G
k
>
∂ H
k
∂ x
x
x
k
>
+ D
D
D
k
U
U
U
k
U
U
U
k
=
v
k
k−1
ω
k
k−1
Q
k
k
M
k
k
>
Y
Y
Y
k
=
h
−Q
k
k−1
− M
k
k−1
v
k
k
ω
k
k
i
>
(53)
the superscripts indicate that the variables are belong
to the k
th
beam and the subscripts represent the con-
nection points.
2.4.2 Interconnection between Subsystem
Now we focus on the interconnection between sub-
systems. The telescopic boom structure can be con-
sidered as the combination of multiple subsystem and
each of them is a homogeneous Timoshenko beam.
Based on the geometrical and mechanical continu-
ous conditions, the flows and efforts of the k
th
and
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
76
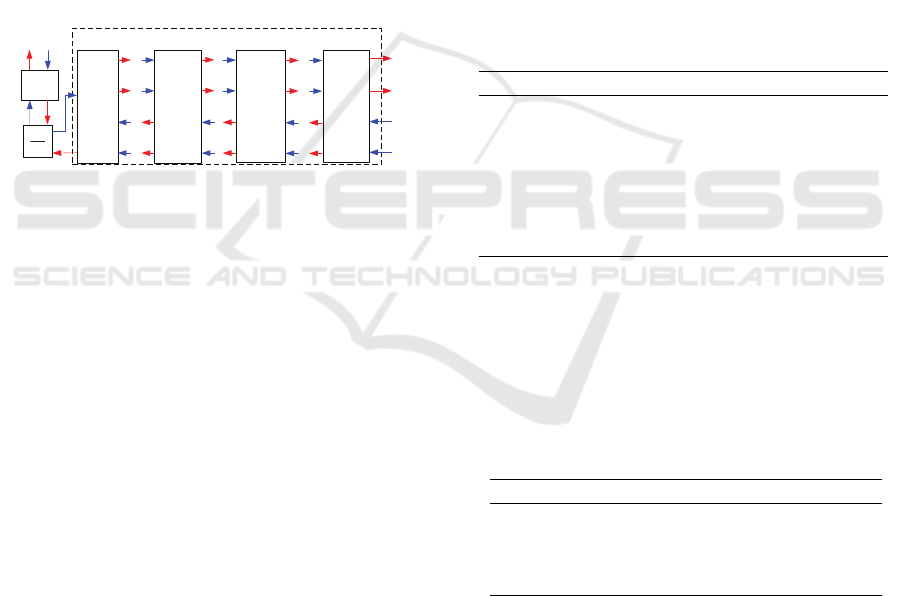
(k + 1)
th
beam sections through the connection point
L
k
have the following relations
f
t,k
∂
(L
k
,t) = f
t,k+1
∂
(L
k
,t)
f
r,k
∂
(L
k
,t) = f
r,k+1
∂
(L
k
,t)
e
t,k
∂
(L
k
,t) = e
t,k+1
∂
(L
n
,t)
e
r,k
∂
(L
k
,t) = e
r,k+1
∂
(L
k
,t)
(54)
which mean that the inputs and outputs of the adja-
cent two beams have similar relations at the connec-
tion point L
k
Y
Y
Y
k
k
= U
U
U
k+1
k
,Y
Y
Y
k+1
k
= −U
U
U
k
k
. (55)
According to the I/O representation (53) as Port-
Hamiltonian system and the transfer characteristics
(55) between outputs and inputs, the boom structure
can be built as a series system showed in Fig. 4.
1
0
v
1
0
Z
1
0
M
1
0
Q
1
1
v
1
1
Z
1
1
M
1
1
Q
1
k
k
v
1
k
k
Z
1
k
k
M
1
k
k
Q
k
k
v
k
k
Z
k
k
M
k
k
Q
1
1
k
k
v
1
1
k
k
Z
1
1
k
k
M
1
1
k
k
Q
1k
k
v
1k
k
Z
1k
k
M
1k
k
Q
1
n
n
v
1
n
n
Z
1
n
n
M
1
n
n
Q
n
n
v
n
n
Z
n
n
M
n
n
Q
1
L
1k
L
k
L
1k
L
1n
L
n
L
...
s
T
w
w
F
s
Hydraulic
Cylinder
Telescopic boom structure
Loads
Responds
...
...
...
...
-1
-1
1
1
...
...
...
...
...
k
L
i i
h
U
i
Q
1
6
k
6
1k
6
n
6
0
6
Figure 4: Interconnection of multiple beam and hydraulic
system.
The interconnection between the hydraulic sys-
tem and the boom structure is reflected by the luff-
ing mechanism, in which the hydraulic cylinder acts
as the actuator. The output of the hydraulic system,
the velocity of the piston, can be transferred to the
input angle velocity of the first beam at its boundary
(z = 0).
Based on the measurements of luffing mechanism
(the length of the cylinder and the positions of the
joints), the rotation of the boom can be expressed as
θ(t) = ∂
s
θ · s(t), the actuate force and moment have
the relation F = ∂
s
· θM. Therefor we have the I/O
transfer relation between the hydraulic system and the
boom structure as
U
r,1
0
= ω
1
0
= ∂
s
θ · ˙s = ∂
s
θ ·y
v
u
F
= F(t) = ∂
s
θ ·M
1
0
= ∂
s
θ ·Y
r,1
0
(56)
which illustrates the interconnection between the two
systems in different domains.
Finally, we have the complete model of the hy-
draulic actuated telescopic boom system. The load
at the boom’s tip and the hydraulic flows though the
cylinder are the system inputs, the velocity responds
at the boom’s tip and the enthalpy change of the hy-
draulic system are the system outputs.
3 SIMULATION AND RESULTS
In order to evaluate the performance of our complete
model, we firstly evaluate the approximation quality
of the finite-dimensional model of non-homogeneous
Timoshenko beam based on the geometric discretiza-
tion.
We define a stepped beam model with three sets
of parameters as Table 1. The model of each part
of the beam are built as a Port-Hamiltonian system,
discretized and implemented in MATLAB/Simulink
individually. Then connect these three I/O represen-
tations as a series system. A finite element model
using the given parameters (Table 1) is also built
in NODYA, a dynamic finite element analysis pro-
gramme developed by our institute. An eigenvalue
analysis is applied firstly to check the frequencies, and
the next step is to check the respond behaviors by the
dynamic analysis.
Table 1: System parameters.
Parameter Beam 1 Beam 2 Beam 3
Length 0.3m
Width 0.02m 0.015 0.01
Depth 0.005m 0.004m 0.003m
Density 7850kg
Yong’s modulus 210GPa
Poisson’s ratio 0.33
Shear factor 5/6
The results of eigenvalue analysis is listed in Ta-
ble 2, the deviations between the two models are less
than 4% . It means that the Port-Hamiltonian system
representation and the corresponding geometric dis-
cretization are still suitable for the non-homogeneous
Timoshenko beam.
Table 2: Eigenvalue analysis results.
Mode num. FE- PH Deviation
1 7.37Hz 7.54Hz 2%
2 27.5Hz 28.2Hz 3%
3 65.9Hz 67.9Hz 3%
4 136.4Hz 141Hz 3%
Fig. 5 (b) represents the transient responds of the
FE-model and the Port-Hamiltonian model, both have
the definition of input ω
1
0
as Fig. 5 (a) shows. The
amplitudes of the responding angle velocity at the
boom’s tip are very close. And the difference of the
eigenvalue is also reflected.
Next, we can evaluate the model of complete
telescopic boom system using the verified Port-
Hamiltonian model of boom structure. The model
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation
77
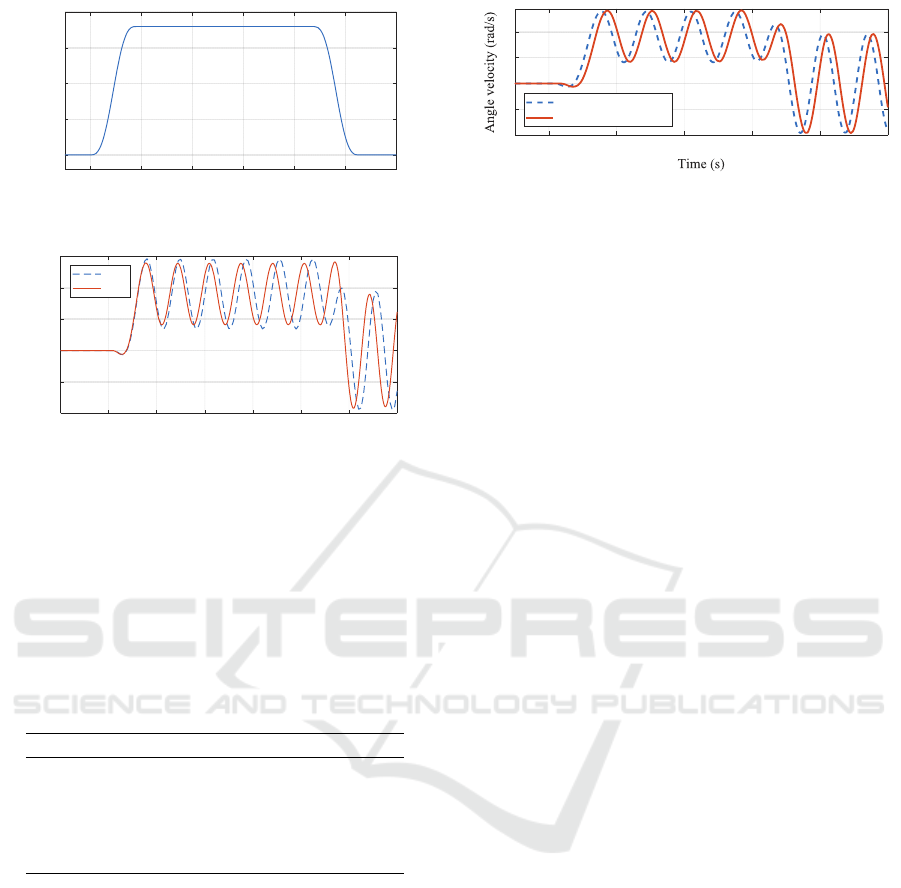
(a) Input angle velocity
(b) Output angle velocity
1 1.2 1.4 1.6 1.8 2 2.2
Time (s)
0
0.5
1
1.5
2
Angle velocity (rad/s)
0.8 1 1.2 1.4 1.6 1.8 2 2.2
Time (s)
-2
-1
0
1
2
3
Angle velocity (rad/s)
FEM
pH
Figure 5: Desired input and the transient responds of FE-
model and Port-Hamiltonian model.
of the hydraulic system with the parameter set as
in Table 3 is also implemented in Matlab/Simulink.
Then the model can be easily connected to the model
of boom structure by the specified input and output
ports.
Table 3: Parameters of hydraulic system.
Parameters Value
Supply pressure 10bar
Tank pressure 0bar
Piston Area and area ratio 0.0001m
2
, 0.75
Bulk modulus 1.2GPa
Piston stoke length 0.25m
In order to avoid the strong nonlinear characteris-
tic of luffing mechanism, we set the limit of the input
angle displacement to π/3. Fig. 6 shows the transient
responds of the boom structure model and the com-
plete model including the hydraulic system. In this
case, the influence of the hydraulic system is reflected
by the respond time delay.
4 CONCLUSION AND OUTLOOK
In this paper, we presented a modeling method and
a corresponding discretization method to describe the
hydraulic actuated telescopic boom system as a Port-
Hamiltonian system. The hydraulic cylinder and tele-
1 1.2 1.4 1.6 1.8 2
-2
-1
0
1
2
Beam only
With hydraulic system
Figure 6: Transient respond of the complete model of tele-
scopic boom, including hydraulic system.
scopic boom structure were modeled in PH formula-
tion respectively. A PH model of non-homogeneous
Timoshenko beam is proposed, in order to describe
the telescopic boom structure more accurately. The
model is proven by the comparison with finite element
model. Using the interconnection ports, these individ-
ual models could be integrated into a complete model,
which include the dynamic behavior of hydraulic sys-
tem in the dynamic simulation of telescopic boom
system. The future works are presented as following:
1. The complete model in this paper is still an open
loop system, the vibration responds of the boom
structure is not controlled. A closed loop system
will be developed. Some suitable controller will
be added to the hydraulic system for the purpose
of boom vibration suppression.
2. The 2-D bending vibration model of Timoshenko
beam is not good enough for the boom structure
modeling under some circumstances, especially
for the mobile cranes hoisting heavy loads. The
boom structure is bearing axial force when the
luffing angle is large, in such case the axial de-
formation cannot be neglected. A more complex
beam model will be investigated and its PH for-
mulation will be presented.
ACKNOWLEDGEMENTS
The research is supported by Deutsche Forschungs-
gemeinschaft (FO 1180 1-1) and National Science
Foundation of China (11761131005).
REFERENCES
Cardoso-Ribeiro, F. L., Matignon, D., and Pommier-
Budinger, V. (2016). A power-preserving discretiza-
tion using weak formulation of piezoelectric beam
with distributed control ports. IFAC-PapersOnLine,
49(8):290–297.
Cheng, L., Ye, Z., and Tong, Z., editors (2016). Bond graph
modeling and simulation analysis of direct drive vol-
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
78

ume control electro-hydraulic servo system with long
pipeline. IEEE.
Duindam, V., Macchelli, A., Stramigioli, S., and Bruyn-
inckx, H. (2009). Modeling and control of complex
physical systems: The port-Hamiltonian approach.
Springer Science & Business Media.
Gawthrop, P. J. and Bevan, G. P. (2007). Bond-graph mod-
eling. IEEE Control Systems Magazine, 27(2):24–45.
Guo, Y., Liu, D., Yang, S., Li, X., and Chen, J. (2016).
Hydraulic–mechanical coupling modeling by bond
graph for impact system of a high frequency rock drill
drifter with sleeve distributor. Automation in Con-
struction, 63:88–99.
Kugi, A. and Kemmetm
¨
uller, W. (2004). New energy-
based nonlinear controller for hydraulic piston actu-
ators. European journal of control, 10(2):163–173.
Macchelli, A. and Melchiorri, C. (2004). Modeling and
control of the timoshenko beam. the distributed port
hamiltonian approach. SIAM Journal on Control and
Optimization, 43(2):743–767.
Macchelli, A., Melchiorri, C., and Stramigioli, S. (2009).
Port-based modeling and simulation of mechanical
systems with rigid and flexible links. IEEE transac-
tions on robotics, 25(5):1016–1029.
Moulla, R., Lefevre, L., and Maschke, B. (2012). Pseudo-
spectral methods for the spatial symplectic reduction
of open systems of conservation laws. Journal of com-
putational Physics, 231(4):1272–1292.
Pertsch, A. and Sawodny, O. (2016). Modelling and con-
trol of coupled bending and torsional vibrations of an
articulated aerial ladder. Mechatronics, 33:34–48.
Pertsch, A., Zimmert, N., and Sawodny, O., editors (2009).
Modeling a fire-rescue turntable ladder as piecewise
Euler-Bernoulli beam with a tip mass. IEEE.
Sawodny, O., Aschemann, H., and Bulach, A. (2002).
Mechatronical designed control of fire-rescue
turntable-ladders as flexible link robots. IFAC
Proceedings Volumes, 35(1):509–514.
Stadlmayr, R. (2009). On a combination of feedforward and
feedback control for mechatronic systems. Shaker.
Stadlmayr, R. and Schlacher, K., editors (2004). Modelling
and Control of a Hydraulic Actuated Large Scale Ma-
nipulator, volume 1. Wiley Online Library.
Sun, G. and Kleeberger, M. (2003). Dynamic responses of
hydraulic mobile crane with consideration of the drive
system. 38(12):1489–1508.
Sun, G., Kleeberger, M., and Liu, J. (2005). Complete
dynamic calculation of lattice mobile crane during
hoisting motion. Mechanism and Machine Theory,
40(4):447–466.
Sun, G. and Liu, J. (2006). Dynamic responses of hydraulic
crane during luffing motion. Mechanism and Machine
Theory, 41(11):1273–1288.
Vu, N. M. T., Lefevre, L., Nouailletas, R., and Br
´
emond, S.
(2013). Geometric discretization for a plasma control
model. IFAC Proceedings Volumes, 46(2):755–760.
Wang, M., Bestler, A., and Kotyczka, P. (2017). Mod-
eling, discretization and motion control of a flexi-
ble beam in the port-hamiltonian framework. IFAC-
PapersOnLine, 50(1):6799–6806.
Zuyev, A. and Sawodny, O. (2005). Stabilization of a flexi-
ble manipulator model with passive joints. IFAC Pro-
ceedings Volumes, 38(1):784–789.
Modeling and Discretization of Hydraulic Actuated Telescopic Boom System in Port-Hamiltonian Formulation
79
