Manifold Learning to Identify Consumer Proﬁles in Real Consumption

Data

Diego Perez

, Marta Rivera-Alba

and Alberto Sanchez-Carralero

Research, Clarity AI, New York, U.S.A.

Keywords:

Manifold Learning, Big Data, Consumer Data, Econometrics, Consumption Proﬁles.

Abstract:

Precise and comprehensive analysis of individual consumption is key to marketers and policy makers. Tra-

ditionally, people’s consumption proﬁles have been approximated by household surveys. Although insightful

and complete, household surveys suffer from some biases and inaccuracies. To compensate for some of those

biases, we propose a new approach to compute and analyze consumer proﬁles based on millions of purchase

transactions collected by a personal ﬁnancial manager. Since this new kind of data sources requires new anal-

ysis methods, in this paper we propose the use of manifold learning techniques to visualize the whole data set

at once, demonstrating how these techniques can cluster consumers in more meaningful groups than demo-

graphics alone. These unsupervised behavior-based clusters allow us to draw more educated hypotheses that

we could otherwise miss. As an example, we will speciﬁcally discuss the characteristics of individuals with

high housing and recreation consumption in our sample.

1 INTRODUCTION

Understanding people’s priorities and desires has al-

ways been a challenge for marketers and policy mak-

ers. This knowledge guides marketers in their cam-

paigns and, perhaps more importantly, it guides policy

makers to come up with approaches catering to those

demographic groups more in need (Deaton, 2001;

Deaton et al., 1980). Because individuals rely on ex-

ternally supplied goods and services to satisfy their

needs, the analysis of consumption serves as rele-

vant approximation to people’s preferences and needs

(Deaton, 1997).

In order to estimate consumption data, researchers

have traditionally asked consumers directly through

household surveys (Deaton and Zaidi, 2002). These

surveys suffer from some biases, perhaps the most im-

portant one being the response bias—some groups are

more eager to respond than others—making parts of

the population invisible or underrepresented in house-

hold surveys (Groves, 2006; Christian, 2012; Furn-

ham, 1986). Moreover, these surveys focus on con-

sumption at the household level. Although this could

make sense for many analyses, it misses the individ-

https://orcid.org/0000-0002-1837-2270

https://orcid.org/0000-0002-8069-385X

https://orcid.org/0000-0002-1966-2800

ual preferences within the household. For example,

the behavior of non-emancipated young adults with

their own salary and expenses is diluted when aggre-

gating household consumption. Analyzing this popu-

lation segment is specially relevant when forecasting

future consumption trends.

An alternative to asking people directly about their

preferences through surveys is measuring their con-

sumption behavior. The global adoption of electronic

payment systems and mobile devices open new op-

portunities to collect behavioral data—after the nec-

essary anonymization protocols. Compared to house-

hold surveys, behavioral data shows increased indi-

vidual resolution, lower costs, and alternative pop-

ulation sampling–with complementary selection bi-

ases to surveys. In this paper we used a behavioral

data set collected from a Personal Financial Manager

in Spain. Our data set includes millions of transac-

tions from almost 50 thousand anonymous users. As

a comparison, the national Spanish consumption sur-

vey include less households for a larger cost (INE,

2017). From our transaction data set we computed the

complete consumer proﬁles in a given year. Although

anonymous, the data set includes some demographic

information about the users sampled, which allows us

to analyze the consumption patterns of thousands of

individuals with either individual or demographic res-

olutions.

Perez, D., Rivera-Alba, M. and Sanchez-Carralero, A.

Manifold Learning to Identify Consumer Proﬁles in Real Consumption Data.

DOI: 10.5220/0007832400230031

In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 23-31

ISBN: 978-989-758-377-3

Addressing the visualization and analysis of these

new large data sets challenges traditional statisti-

cal tools. Over the recent years, several research

groups have developed new supervised and unsuper-

vised machine-learning techniques to analyze them

(Di Clemente et al., 2018; Pentland, 2013). In this pa-

per we use an unsupervised method known as t-SNE

(Maaten and Hinton, 2008). t-SNE is an non-linear

embedding technique based on manifold learning able

to represent all of our high dimensional consumer

proﬁles in a two dimensional space, while aiming

to keep the original relative distance between users.

This embedded representation can be used as a basis

for more relevant clustering than demographic seg-

ments. In addition, unsupervised methods like t-SNE

can produce more meaningful and sometimes counter

intuitive insights from the data set that could be other-

wise missed. As an example, in this paper we used the

t-SNE embedding to identify two clusters of individ-

uals: one with above average housing consumption,

and other with above average recreation consumption.

We found middle-age individuals over-indexing in the

former, and younger, poorer males over-indexing in

the latter.

The remainder of this paper is structured as fol-

lows: section 2 describes the methods, including a

data overview and description of consumption cat-

egories, section 3 describes the results of the pa-

per, section 3.1 outlines our pipeline for construct-

ing consumption proﬁles from micro-transaction data

and explore the mean consumer proﬁle in our sample,

section 3.2 explores the differences in consumption

across demographics, section 3.3 shows the problems

of this traditional approach, section 3.4 shows how

manifold learning can serve as a basis for more rel-

evant clusters, allowing us to analyse independently

the consumers of speciﬁc categories, and ﬁnally we

discuss our results in section 4.

2 METHODS

2.1 Data Overview

The data set used is comprised of almost 24 million

banking transactions from 49965 users of a Spain-

based Personal Finance Management service. The

data set covers all transactions for those users in 2017

including inbound/outbound money transfers, card

payments and cash withdrawals. In this work we only

analyzed transactions that can be connected to a con-

sumption category (section 2.2 and Appendix). Each

user is described by its Region, Age range, Income

range, and Gender. Demographic slices are struc-

tured as follows:

• Region contains the Spanish region—Comunidad

Autonoma—where the user lives.

• Age range is divided in the following ranges: 18

to 25, 26 to 35, 36 to 45, 46 to 55 and Over 55.

• Income range encloses ranges divided by the an-

nualized average monthly income. The ranges

are the following: Under e584, e584 to e1,083,

e1,084 to e1,583, e1,584 to e2,416, e2,417 to

e3,333, e3,334 to e4,166, e4,167 to e5,000,

e5,001 to e5,834 and Over e5,834

• Gender: Male or female.

Since the main objective of this paper is not to an-

alyze the Spanish population, but to introduce novel

methods to analyze big data sources, data is not re-

sampled to mimic the Spanish population—as ex-

plained in the next sections this reduces the complex-

ity of the approach. The full description of the sample

distribution across regions, age ranges, income ranges

and gender can be found at Appendix. Signiﬁcance

is measured based on data sample. Users have given

express consent to research and commercial exploita-

tion of the data, in accordance with GDPR—General

Data Protection Regulation—(Council of European

Union, 2016) regulations. Data has been irreversibly

anonymized using differential privacy techniques.

2.2 Consumption Categories

We used our proprietary classiﬁcation on consump-

tion categories based on the COICOP standard (Clas-

siﬁcation of Individual Consumption according to

Purpose) for households developed by the United

Nations Statistics Division (United Nations, DESA,

2018). This standard classiﬁes consumption based on

the purpose of goods or services acquired. Our orig-

inal proprietary classiﬁcation includes 42 categories,

but the granularity of this data set allows us to map

our transactions to 27 of them (Appendix). Although

all calculations in this work include all 27 categories,

in the interest of clarity, most of the graphics on this

paper include only the 12 most relevant categories.

Transactions in the categories of loans and trans-

fers are reassigned to category Housing based on

amount, recurrence, and whether the corresponding

user has been identiﬁed as a loan or mortgage owner.

Transactions in low-frequency categories at the com-

merce level —those covering less than 4% of the

total—, were reassigned at random, keeping the rela-

tive proportions of the rest of categories for that com-

merce.

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

3 RESULTS

3.1 Consumption Proﬁles

Understanding people’s consumption proﬁles re-

quires a individual representation of that consump-

tion. To generate that representation we aggregated

the full list of annual transactions for each user in

27 different consumption categories (see section 2.2).

We then deﬁned the consumption vector of a given

user as a 27-dimensional vector including the relative

spent of each category.

Consumption vectors can be aggregated to obtain

the mean consumption vector of the total data set (Fig.

1), or subsets of the sample, as we will see in the next

sections. These aggregated consumption vectors al-

low us to analyze general consumption trends in our

sample and could allow other researchers to ﬁnd in-

sights on global patterns.

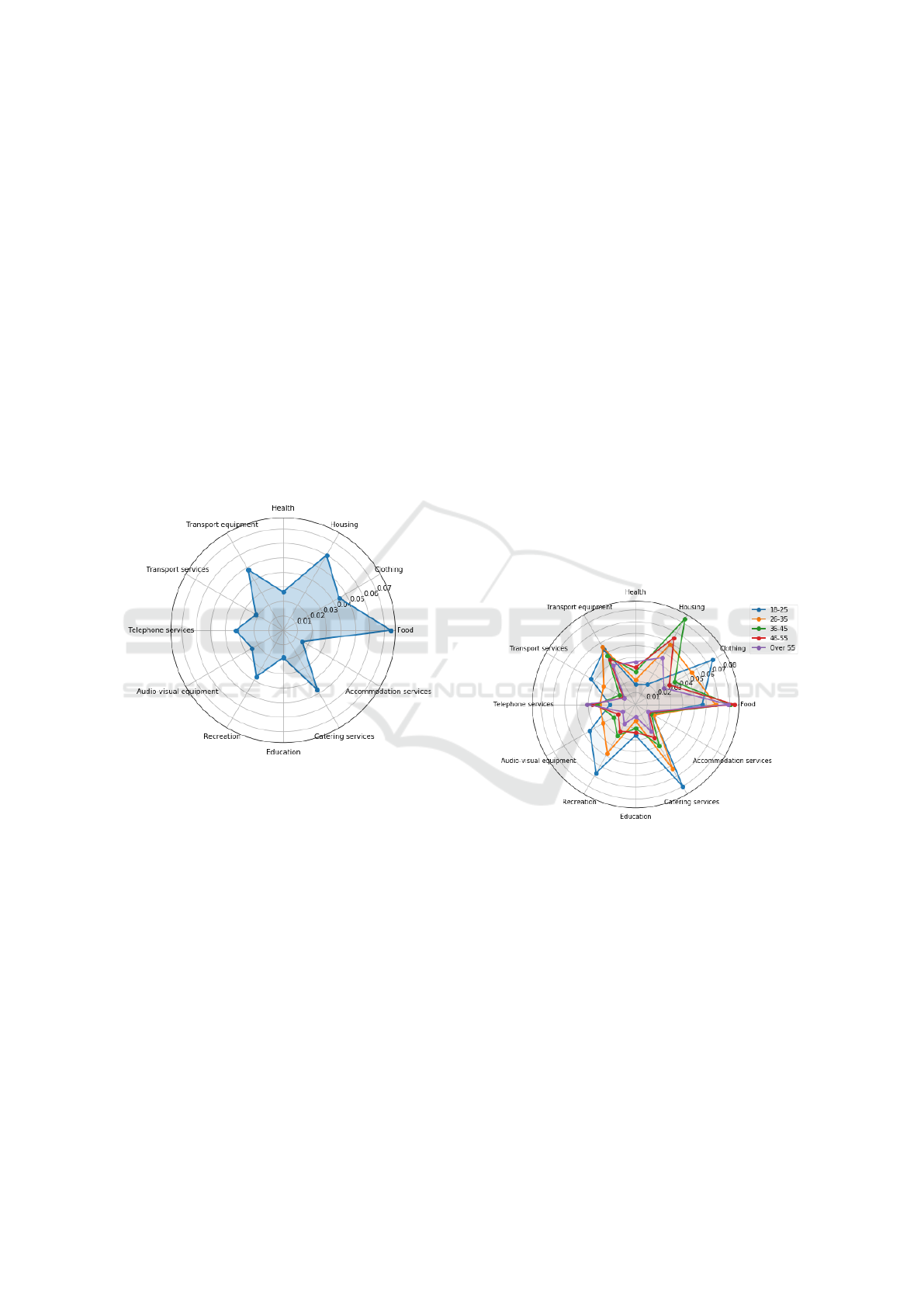
Figure 1: Average relative consumption on principal cate-

gories. Each point represents the mean relative spent in each

selected category for the total data set.

Among the 12 selected categories, we observed

the highest relative spent on Food, Housing, Trans-

port equipment and Catering services. In addition,

we also observed some particularities of the Spanish

population: for example, we found low spending on

Health and Education, as they are largely covered by

the public system (OECD/European Observatory on

Health Systems and Policies, 2017; Rogero-Garc

ıa

and Andr

es-Candelas, 2014).

Although averaging consumption vectors across

our entire sample gave us an idea about general pat-

terns of behavior, it lacks granularity. For example,

as we explored in the next sections, it is not feasible

to compare more than one demographic slice of the

sample at the same time.

3.2 Demographic Slices

Besides identifying global patterns, consumption pro-

ﬁle analysis is able to explore more granular and spe-

ciﬁc insights for target demographic slices. Splitting

the population in different groups allow us to analyze

different consumption proﬁles and study differences

and similarities between them.

Many studies have split the population by demo-

graphic proﬁles (Behrendt, 2005; Morris et al., 2006).

By way of illustration, we compare the mean con-

sumption vector across age ranges in Fig. 2. Re-

ﬂecting peculiarities of the Spanish population, these

age-based mean spending vectors vary widely across

age ranges: for example, the oldest range spends rela-

tively more than the rest on Health, and the youngest

range spends relatively more than other slices on

Clothing, Transport, and Recreation. This represen-

tation already suggests that younger population is less

likely to spend in Housing than middle-age ranges, as

we will explore deeper in future sections. In addi-

tion, the data also suggests that the younger you are,

the more you spend in Recreation and Transport Ser-

vices.

Figure 2: Average consumption proﬁle by age range. Each

line represents the mean consumption vector of the speciﬁc

age range.

Radar charts (Fig. 1 and Fig. 2) are a clear and

straightforward approach to represent consumption

vectors. Nevertheless, they can become complicated

to understand when comparing several demographic

dimensions at once. In those cases, we could use

pyramid plots. As an illustration, we split our sample

by age and gender in order to analyze the relative con-

sumption on Recreation. We observed that younger

users are the ones spending more in that category and

male users spend relatively more than females (Fig.

3).

A pyramid plot (Fig. 3) allowed us to add another

demographic dimension. However, it is still unable to

Manifold Learning to Identify Consumer Proﬁles in Real Consumption Data

Figure 3: Recreation budget share by age and gender. On

the left (red): females and on the right (blue): males. Age

ranges are ordered as vertical axis.

represent more than two slices of the sample or show-

ing different consumption categories at a time. As a

solution, we could stack those categories in the same

plot, but generated plots could be difﬁcult to interpret.

3.3 Problems of Demographic Slices

When splitting the population by demographic slices,

we implicitly assume that those slices are meaningful

for our analysis. In this section, we explore the valid-

ity of this hypothesis by measuring the behavioral ho-

mogeneity within each slice. We ﬁnd evidence to the

contrary in the form of consumption proﬁles hetero-

geneity even when restricting to a particular regional,

income, age, and gender bracket.

As an illustration of this heterogeneity, we se-

lected four male individuals from Madrid—Spanish

region—, with the same income range—from e1,584

to e2,416 per month—and within the same age

range—from 36 to 45—and we compared their con-

sumption vectors with the average consumption pro-

ﬁle from that speciﬁc demographic slice. We ob-

served that those users present notable behavioral dif-

ferences between them and the average consumption

of their demographic group (Fig. 4). For example, we

observed that individual 1 spends an important share

of his budget on Housing and almost nothing on Edu-

cation and Food. Whereas individual 3 spends a sig-

niﬁcant part of his budget on Education and Food.

In order to measure this heterogeneity in each de-

mographic slice, we measured the behavioral disper-

sion within each slice. We deﬁned dispersion as the

mean of the euclidean distances from every single

consumption proﬁle to the mean consumption pro-

ﬁle in a given sample slice. As a reference, we also

Figure 4: Comparison between 4 individuals with the same

demographic proﬁle. Each line (Blue, orange, green and

red) represents a single user selected from a certain de-

mographic slice—Same region, age, gender and income

range—whereas purple line represent the average consump-

tion proﬁle of this speciﬁc demographic slice.

computed the dispersion of the total sample obtain-

ing 0.22 ± 0.10 (mean ± std) (Fig 5, orange). We

found that the measured dispersion within each age

range (Fig 5A) and within income range (Fig 5B) are

largely overlapping with the dispersion of the total

sample. Also, the mean dispersion in each demo-

graphic groups is not systematically smaller than the

mean dispersion of the total sample (Fig 5, 1-sided

Student-t tests). Therefore, splitting the population

by demographic slices does not guarantee more ho-

mogeneous groups.

We have detected two fundamental problems in

the demographic analysis: ﬁrst, showing the infor-

mation for multiple dimensions at the same time is

confusing with standard plots, and second, even if

we could focus on one dimension at a a time, demo-

graphic slices are not necessarily a meaningful clas-

siﬁcation criterion. We therefore need new analysis

methods to treat this new kind of data sets.

In this work, we propose the application of un-

supervised manifold learning algorithms (Elgammal

and Lee, 2004; Cayton, 2005) to reduce the dimen-

sionality of our consumption data. The beneﬁt of

these algorithms is twofold: better visualization and

unbiased pattern discovery. Clustering on the new

lower-dimensional spaces can help us to further con-

ﬁrm that demographic slices are not meaningful and

to address the problem by suggesting more mean-

ingful behavior-based groups of individuals. Tradi-

tionally, dimensionality reduction has been performed

with linear approaches that look for the best pro-

jection of the n-dimensional data in a lower dimen-

sional space. A very wide spread example is Princi-

pal Component Analysis (PCA) (Wold et al., 1987;

Jolliffe, 2011) that looks for the projection of maxi-

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

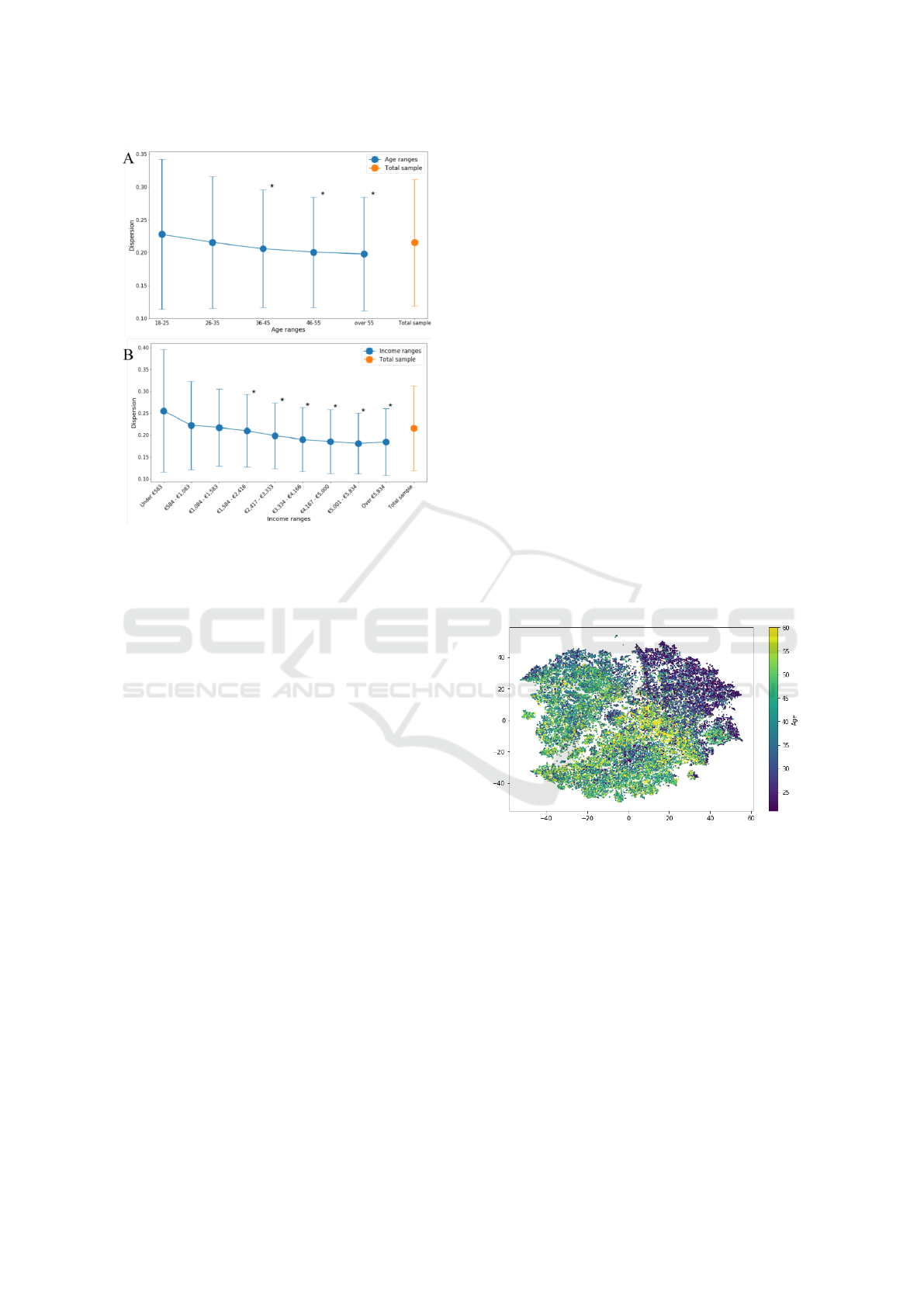
Figure 5: Distribution of dispersion within demographic

groups overlaps the distribution of dispersion of the total

sample. Dispersion measured as euclidean distance be-

tween all the users’ spending proﬁle to the average spend-

ing proﬁle. Orange: Dispersion of the total sample and

blue: dispersion within slices. A) Dispersion within age

ranges. B) Dispersion within income ranges. Error bars rep-

resent standard deviation. Signiﬁcance of statistical test—

one sided Student-t—denoted as follows: * p-value <0.05.

mum variance. This traditional approach may be not

ideal when data structure cannot be fully explained

by linear projections–spirals are paradigmatic cases

of this limitation. As an alternative manifold learning

algorithms are a non-linear approach to perform di-

mensionality reduction. Considering a n-dimensional

space, manifold learning ﬁnds sets of data points

which are close to each other at the original high-

dimensional space. Once these sets are identiﬁed,

manifold learning reduces the dimensionality by em-

bedding the points into a lower-dimensional space,

while keeping the original structure and distances of

the points within those groups.

In this paper we used a particular manifold learn-

ing technique called t-SNE (Maaten and Hinton,

2008). Compared to other manifold learning algo-

rithms, t-SNE do not overlap points in the embed-

ded space, generating representations that easier to vi-

sualize. This technique maps any large-dimensional

vector into a low dimensional space using embed-

dings aiming to preserve relative distances between

points, as mentioned before. Thus, manifold learn-

ing allowed us to represent our 27-dimensional con-

sumption vector for each user as x,y coordinates of a

2-dimensional space.

In order to further conﬁrm that demographic slices

are heterogeneous, we plotted the embedded x,y co-

ordinates as a 2D scatter plot. Since each point in

our plot represents each individual, we can color them

based on their age range (Fig. 6) or income range

(Fig. 7).

Although we can infer a larger concentration of

older individuals at the bottom left corner of the plot

and younger individuals at the top right corner, age

ranges are intertwined in this behavioral space (Fig.

6). The same is true when representing income ranges

age (Fig. 7). This representation visually conﬁrms

our previous calculations on the heterogeneity of de-

mographic slices.

Extrapolating conclusions to the actual population

when using unsupervised embeddings is not trivial

and out of the scope of this paper. To be able to do

that extrapolation the sample data should mimic the

Spanish population. To do so we could either ran-

domly select a sub-sample that mimics the original

demographics, but that could mean discarding a large

part of our dataset. Or alternatively, we could artiﬁ-

cially augment the under-sampled demographics, but

that would require a new set of assumptions about

those demographics.

Figure 6: t-SNE colored by age. Representation of the em-

bedding coordinates colored by user’s age range.

3.4 Using Manifold Learning to

Address the Problem

In previous sections, we conﬁrmed that demographic

slices can be heterogeneous in terms of consump-

tion proﬁles. We also introduced the use of manifold

learning methods like t-SNE to visualize the whole

large-dimensional behavioral space. In this section,

we will show how we used the same t-SNE em-

bedding to generate more meaningful behavior-based

groups of individuals.

In order to visualize the individual consumption

across categories, we colored them by the budget

Manifold Learning to Identify Consumer Proﬁles in Real Consumption Data

Figure 7: t-SNE colored by income. Representation of the

embedding coordinates colored by user’s income range.

share of each on a certain category (Fig 8) instead of

coloring the individual points by demographics slices.

As manifold learning tries to preserve relative dis-

tances between points, users who are close to each

other in this representation tend to have a similar con-

sumption proﬁle.

Our implementation of t-SNE avoids the problem-

atic heterogeneity within demographic slices by con-

struction, since every user is represented. Moreover,

as data points aims to preserve their relative distances,

we can select behavior-based groups of users just by

vicinity. The members of each group share spend-

ing patterns and lifestyles, regardless of their demo-

graphic slices.

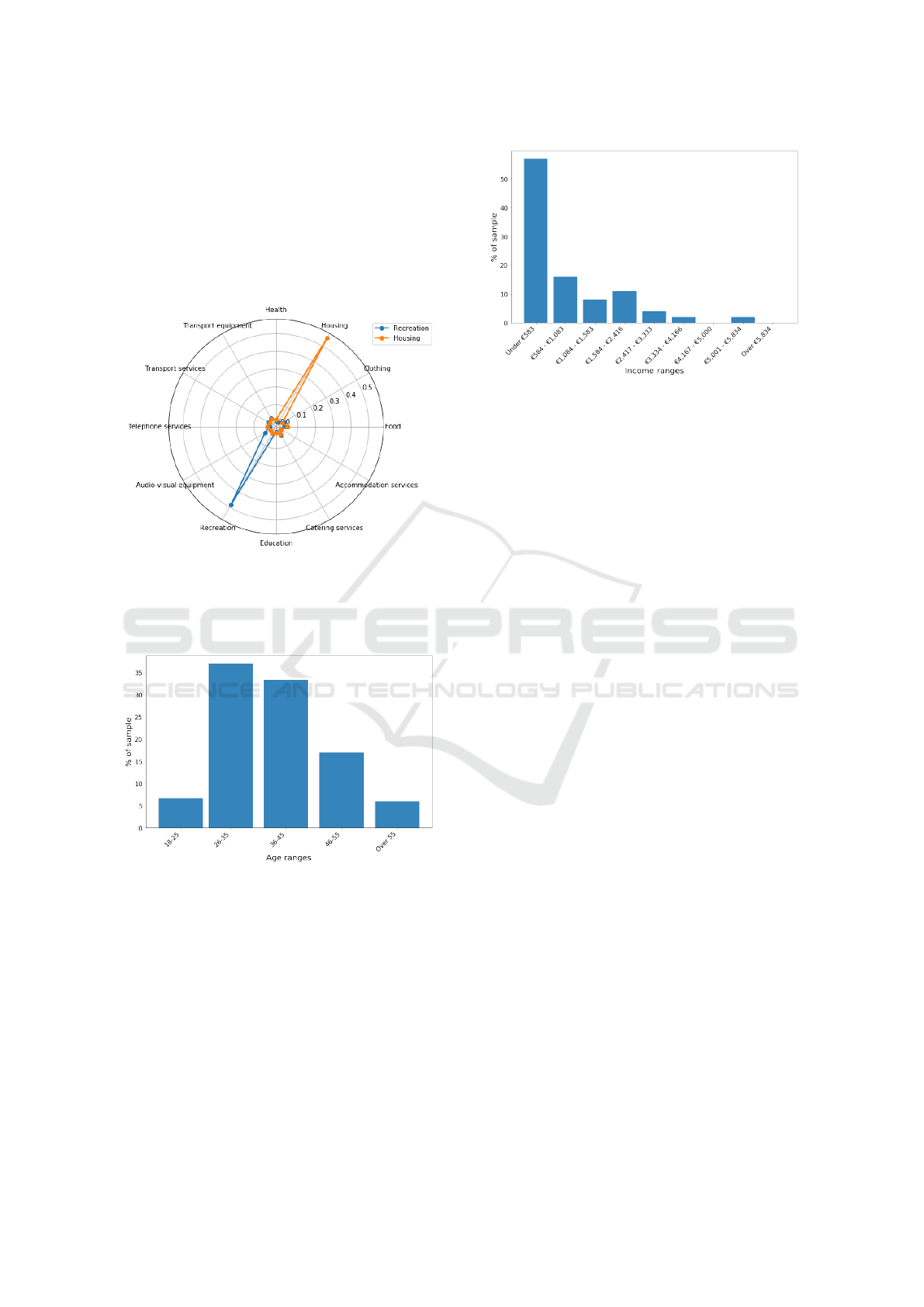
Following the strategy described above, we se-

lected two behavior-based groups from the embedded

space to further analyze them. We identiﬁed these

groups by selecting the nearest neighbours to some

relevant points—based on the euclidean distance be-

tween points in the embedded space. The ﬁrst group

explored contains 300 users close to the top left cor-

ner of the space and therefore who spent a large bud-

get share on Housing. The second group analyzed

contains the 100 users closer to the top center part of

the plot and therefore showing a large relative spent

in Recreation. Second group have less users because

we conﬁrmed graphical and analytically that due to

the density in the top center, 100 users are enough to

cover the area of interest. To conﬁrm that the users

selected are in fact behaving as expected, we calcu-

lated the average consumption vector for each group

(Fig. 9).

One of our goals when computing groups using t-

SNE was to generate more homogeneous groups than

demographic slices. In section 3.3 we showed that the

dispersion of demographic slices overlapped with the

dispersion for the entire sample. So to test whether

we had in fact generated more homogeneous groups

we computed the dispersion within those groups and

we compared to the dispersion for the whole sample.

Figure 8: t-SNE colored by category budget share. Each

subplot represents the consumption ratio of every user on

the speciﬁc category.

The mean dispersion for both groups is statistically

smaller than mean the dispersion of the total sample;

Housing group dispersion: 0.14± 0.07 and Recre-

ation group dispersion: 0.16 ± 0.08 (Student-t test

for comparison of means with different standard de-

viations p −value < 10

−9

in both cases). This proves

that we have generated more homogeneous groups

than the total sample.

Once we have seen that our groups are homoge-

neous, we can further explore the characteristics of

the individuals in each of those new behavior-based

groups. In particular, we compared their demograph-

ics to the demographics of the total sample (see Ap-

pendix) to assay whether they show a different de-

mographic proﬁle than the expected from the sample.

With this approach we found that individuals in the

Housing group are signiﬁcantly more often middle

age than the total sample and less often young (bino-

mial tests, p −value < 0.01) (Fig. 10), but we did not

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

observe relevant differences to the whole sample re-

garding income, region or gender. For the Recreation

group we also observed some statistical differences to

the sample. The members of this second group are

more often male (binomial test, p − value < 10

−6

at the youngest range (binomial test, p − value <

−19

) and at the lowest income range(binomial test,

p − value < 10

−20

) (Fig. 11).

Figure 9: Slices of population selected from t-SNE. Blue

represent the average consumption proﬁle of people who

mostly pay for Recreation and orange people who mostly

pay for Housing. Individuals were got from nearest neigh-

bours in the embedding matrix.

Figure 10: Age distribution from slice of individuals who

mostly pay for Housing. Bar height shows the percentage

of sample and horizontal axis the age range.

Although, the behavior-based groups derived from

the embedded visualizations could be composed

mostly of speciﬁc demographics, our unsupervised

method allow us to also include other individuals

that otherwise would be missed. Therefore, mani-

fold learning enhances on research by including data-

driven counter-intuitive insights into our analysis.

Figure 11: Income distribution from slice of individuals

who mostly pay for Recreation. Bar heights shows the per-

centage of the sample and horizontal axis the income range.

4 CONCLUSIONS

Precise analysis of people’s consumption can serve

as a basis to infer people’s preferences and needs.

To address this analysis, new technological develop-

ments open new opportunities for data collection al-

lowing us to generate new data sets as an alternative

to surveys. As these new data sets require new anal-

ysis methods, in this paper we propose the use of one

of these new methods—manifold learning—to embed

the multidimensional spaces of consumption proﬁles

into 2D spaces. This way, we generated meaningful

groups of individuals that transcends demographics.

The global adoption of electronic payments allow

the development of personal ﬁnancial apps. These

apps generate micro-transaction databases that serves

us to build and analyze people’s consumption patterns

addressing some biases of the traditional approach:

household surveys. Furthermore, micro-transaction

data has more granularity that surveys, allowing us

to analyze individual by individual instead of house-

holds. These kind of data sets open a new ﬁeld of

analysis opportunities to explore individual needs and

desires.

To analyze this new data set, we propose the use

of manifold learning to reduce the dimensionality of

consumption vectors in order to visualize the behav-

ior of thousands of individuals at the same time. This

visualization allowed us to ﬁnd new consumption pat-

terns and lifestyles regardless of demographic groups.

The same technique can be use by marketers to under-

stand their clients and by policy makers to better assay

people’s behaviors and needs.

On top of better visualizations using manifold

learning we grouped individuals based on their con-

sumption proﬁles instead of standard demographic

Manifold Learning to Identify Consumer Proﬁles in Real Consumption Data

segments. Standard demographic segmentation show

intra-group heterogeneities regarding consumption

proﬁles that we reduced with our more homogeneous

behavior-based groups. The use of manifold learning

avoid biases by its non-supervised nature.

In this paper we showed that modern data sets

in conjunction with smarter big data analysis create

a powerful synergy to analyze peoples consumption,

needs and desires. A better understanding of individ-

uals behavior puts a step closer to more efﬁcient poli-

cies towards a fairer world.

REFERENCES

Behrendt, C. E. (2005). Mild and moderate-to-severe copd

in nonsmokers: distinct demographic proﬁles. Chest,

128(3):1239–1244.

Cayton, L. (2005). Algorithms for manifold learning. Univ.

of California at San Diego Tech. Rep, 12(1-17):1.

Christian, L. (2012). Assessing the rep-

resentativeness of public opinion sur-

veys. Retrieved February 27th, 2019 from

http://www.people-press.org/2012/05/15/assessing-

the-representativeness-of-public-opinion-surveys/.

Council of European Union (2016). Regulation (eu)

2016/679 of the european parliament and of the coun-

cil of 27 april 2016 on the protection of natural per-

sons with regard to the processing of personal data and

on the free movement of such data, and repealing di-

rective 95/46/ec (general data protection regulation).

Ofﬁcial Journal of the European Union, L 119 (4 May

2016):1–88.

Deaton, A. (1997). The analysis of household surveys: a mi-

croeconometric approach to development policy. The

World Bank.

Deaton, A. (2001). Counting the world’s poor: problems

and possible solutions. The World Bank Research Ob-

server, 16(2):125–147.

Deaton, A., Muellbauer, J., et al. (1980). Economics and

consumer behavior. Cambridge university press, New

York, NY.

Deaton, A. and Zaidi, S. (2002). Guidelines for construct-

ing consumption aggregates for welfare analysis, vol-

ume 135. World Bank Publications.

Di Clemente, R., Luengo-Oroz, M., Travizano, M., Xu, S.,

Vaitla, B., and Gonz

alez, M. C. (2018). Sequences of

purchases in credit card data reveal lifestyles in urban

populations. Nature communications, 9.

Elgammal, A. and Lee, C.-S. (2004). Inferring 3d body pose

from silhouettes using activity manifold learning. In

Proceedings of the 2004 IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition,

2004. CVPR 2004., volume 2, pages II–II. IEEE.

Furnham, A. (1986). Response bias, social desirability and

dissimulation. Personality and individual differences,

7(3):385–400.

Groves, R. M. (2006). Nonresponse rates and nonresponse

bias in household surveys. Public opinion quarterly,

70(5):646–675.

INE (2017). Encuesta de Presupuestos Familiares. Madrid:

Instituto Nacional de Estadistica.

Jolliffe, I. (2011). Principal component analysis. Springer.

Maaten, L. v. d. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of machine learning research,

9(Nov):2579–2605.

Morris, M., Evans, D., Tangney, C., Bienias, J., and Wil-

son, R. (2006). Associations of vegetable and fruit

consumption with age-related cognitive change. Neu-

rology, 67(8):1370–1376.

OECD/European Observatory on Health Systems and

Policies (2017). Spain: Country health proﬁle

2017, state of health in the eu. Technical re-

port, OECD Publishing, Paris/European Observa-

tory on Health Systems and Policies, Brussels.

http://dx.doi.org/10.1787/9789264283565-en.

Pentland, A. S. (2013). The data-driven society. Scientiﬁc

American, 309(4):78–83.

Rogero-Garc

ıa, J. and Andr

es-Candelas, M. (2014). Fam-

ily and state spending on education in spain: Differ-

ences between public and publicly-funded private ed-

ucational institutions. Revista Espa

nola de Investiga-

ciones Sociol

ogicas, 147:121–132.

United Nations, DESA (2018). Classiﬁcation of Individ-

ual Consumption According to Purpose (COICOP)

2018. Statistical Papers, Series M No. 99,

ST/ESA/STAT/SER.M/99.

Wold, S., Esbensen, K., and Geladi, P. (1987). Principal

component analysis. Chemometrics and intelligent

laboratory systems, 2(1-3):37–52.

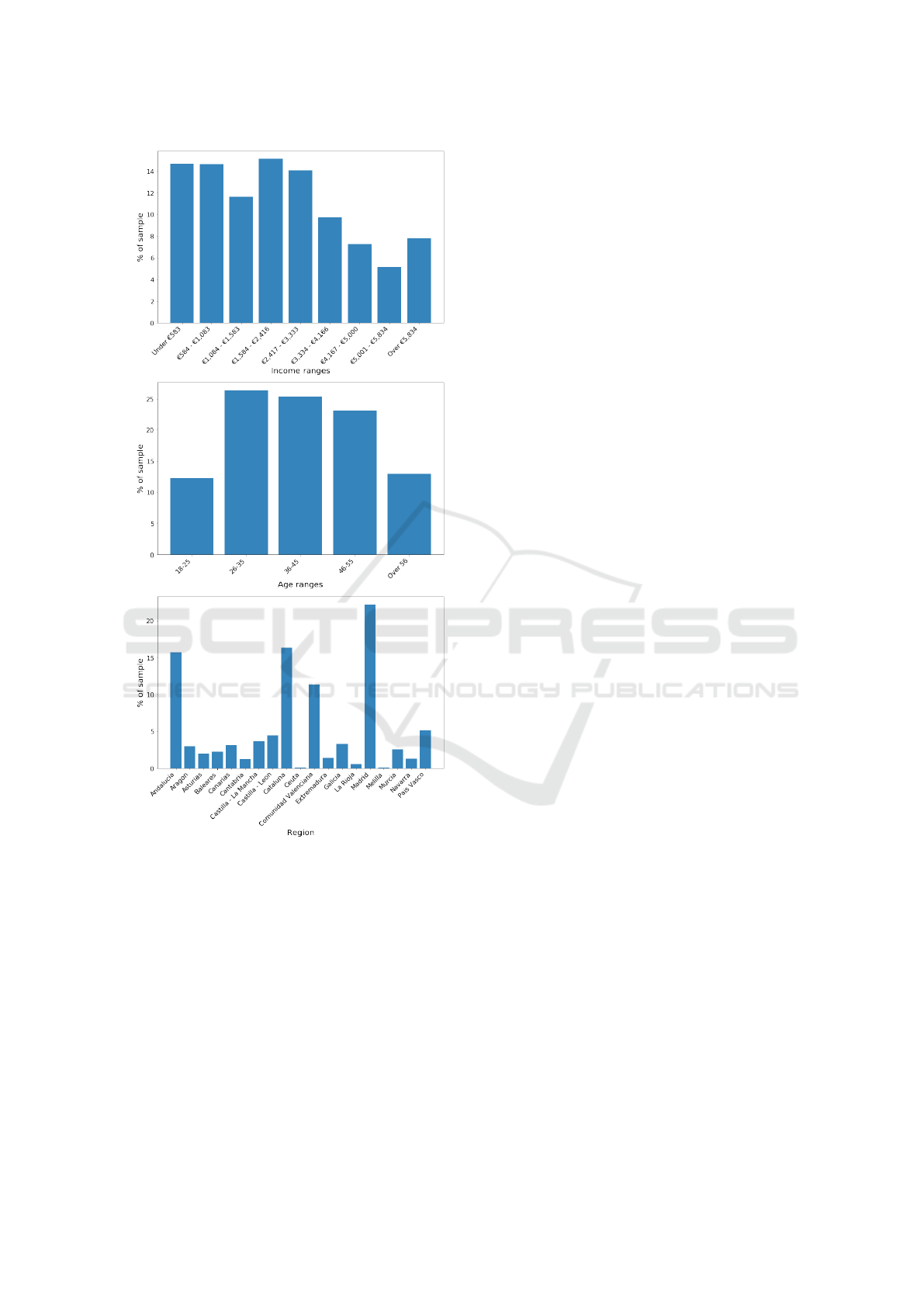
APPENDIX

Sample Demographics

Demographic distribution for the sample in the data

set for income ranges, age ranges and regions (Fig.

12). In addition, in our sample data we measured a

68% male ratio. These distributions are not meant to

be a representation of the Spanish population.

List of Categories

Complete list of 27 consumption categories. In bold

we highlighted the most relevant categories selected

for plotting through the paper:

• Health

• Housing

• Clothing

• Food

• Accommodation Services

DATA 2019 - 8th International Conference on Data Science, Technology and Applications

Figure 12: Demographic distributions of the sample. Bar

heights shows the percentage of the sample falling on a

given A) income-range, B) age-range or C) Region.

• Catering services—Restaurants and bars

• Education

• Recreation

• Audio-visual equipment

• Telephone Services

• Transport Services

• Transport Equipment

• Financial services

• Household appliances

• Other recreational items and equipment, gardens

and pets

• Personal care

• Insurance

• Electricity, gas and other fuels

• Water supply and miscellaneous services relating

to the dwelling

• Newspapers, books and stationery

• Other services n.e.c.

• Maintenance and repair of the dwelling

• Purchase of vehicles

• Tools and equipment for house and garden

• Goods and services for routine household mainte-

nance

• Social protection

• Furniture and furnishings, carpets and other ﬂoor

coverings

Manifold Learning to Identify Consumer Proﬁles in Real Consumption Data