
Reliability Analysis of the Kalman Filter for INS/GPS Integrated
Navigation System Applied to Train
Seong Yun Cho
1a
, Chang Ho Kang
2b
and Kyung Ho Shin
3c
1
Department of Robotics Engineering, Kyungil University, Gyeongsan, South Korea
2
Research Institute of Engineering and Technology, Korea University, Seoul, South Korea
3
Railroad Control & Communication Research Team, Korea Railroad Research Institute, Uiwang, South Korea
Keywords: INS/GPS, Train Application, Kalman Filter, Observability, RMSE.
Abstract: This paper aims to analyse the navigation performance that can be provided by the navigation system when
applying the INS/GPS integrated navigation system to the train. The performance of the Kalman filter
integrating INS and GPS can be summarized by the integrity of the measurement and the observability of the
filter. Assuming the integrity of the GPS information used as a measurement is always satisfied, the
performance of the filter can eventually be analysed by the observability. The observability of the filter
depends on the dynamic trajectory of the train. Because the train has a non-holonomic constraint and one-
dimensional motion, the filter design and the performance analysis are carried out considering this. We
analyse the observability of the filter through simulation and explain the limit of the filter and the flaw of the
observability. We also analyse the reliability of the navigation system and present additional research
directions.
1 INTRODUCTION
Accurate navigation information of a train must be
provided to control the train. Generally, trains are
detected on the basis of a fixed infrastructure installed
along the railway to track the position of trains. If the
train detection fails, the location information of the
train will not be provided. When new railways are
built, therefore, new infrastructure must be installed
at a high cost, infrastructure faults must be detected,
and infrastructure must be maintained periodically.
To overcome this realistic problem, in this paper, the
application of the inertial navigation system (INS)
/global positioning system (GPS) integrated
navigation system to trains is considered. That is, a
system that estimates the position of a train with only
INS and GPS receiver mounted on a train without any
additional infrastructure is dealt (Presti and Sabina,
2018).
The INS uses an inertial measurement unit (IMU)
consisting of 3-axis accelerometers and gyros. If the
sensor outputs are processed by the INS algorithm,
a
https://orcid.org/0000-0002-4284-2156
b
https://orcid.org/0000-0002-9899-3076
c
https://orcid.org/0000-0002-4700-5955
the position, velocity, and attitude information is
provided at a frequency faster than 100Hz. However,
INS errors gradually increas over time due to the
errors included in the sensor outputs, the initial
attitude errors, the non-commutative errors occurring
in the digital computer, and so on. This is a bigger
problem if the low-level IMU is used (Titterton and
Weston, 1997; Cho, 2014). This error can be
estimated and compensated using the information
provided by the GPS receiver. This system is called
the INS/GPS integrated navigation system (Liu et al.,
2010; Miller and Campbell, 2012; Cho, 2014). INS
and GPS are integrated using a Kalman filter.
Integration types can be divided into loosely coupling,
tightly coupling, and ultra-tightly coupling depending
on the type of measurement. In this paper, we discuss
loosely coupling method considering simplicity of
implementation.
The performance of INS/GPS integrated
navigation system depends on the specifications of
the IMU and GPS receiver and the performance of the
integration filter. In this paper, it is assumed that 2.0
Cho, S., Kang, C. and Shin, K.
Reliability Analysis of the Kalman Filter for INS/GPS Integrated Navigation System Applied to Train.
DOI: 10.5220/0007832602370242
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 237-242
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
237

deg/hr grade MEMS type IMU and integrity
guaranteed GPS receiver are used. Therefore, the
performance of INS/ GPS integrated navigation can
be predicted through the performance analysis of the
integration filter.
The filter used in INS/GPS integration can be
selected from nonlinear Kalman filters such as
extended Kallman filter (EKF), unscented Kalman
filter (UKF), cubature Kalman filter (CKF), etc.
considering the nonlinearity of INS (Reif et al., 1990;
Julier et al., 2000; Cho et al., 2017). In this paper,
EKF is used in consideration of small initial attitude
error. The performance of the filter can be explained
by the observability. The observability of the INS/
GPS integration filter is determined by the trajectory
of the trains. In this paper, considering the trajectory
of trains, we analyze the observability of the filter
through the estimation error covariance of the filter
state variables (Cho et al., 2007). Since the train has
a non-holonomic constraint and moves in one
dimension, the filter is designed considering this. In
this case, the observability is analyzed through
covariance analysis. Also, the limitation of the filter
and the loopholes in the analysis of the observability
are discussed by analyzing the covariance of the filter
and the root mean squared errors (RMSE) based on
Monte-Carlo simulation results.
All this analysis is done through simulation. The
information provided in this paper can be used to
analyze the reliability of the location information
provided by the INS/GPS integrated navigation
system installed on trains without infrastructure.
2 INS/GPS INTEGRATION
FILTER AND ANALYSIS
In this section, we design a loosely coupled INS/GPS
integration filter based on EKF using the position and
velocity information of GPS as a measurement, and
analyse the navigation performance when it is applied
to the train.
2.1 INS Algorithm
For INS, initial alignment is performed in the stopped
state first. In the case of train application, the final
navigation information can be stored in memory
when the train operation is finished. This information
can be used at the next operation. Therefore, INS can
be performed without initial alignment.
INS calculates the navigation information in
synchronization with the output period of the sensor
data output from the IMU. First, the attitude is
updated based on the following quaternion
differential equation using the gyro output (Titterton
and Weston, 1997).
1
()
2
bbnn
ib n ie en
qq C
(1)
where
q
is the quaternion,
is the quaternion
product,
b
ib
is the gyro output,
n
ie
is the Earth
rotation angular velocity, and
n
en
is the rotation
angular velocity of the navigation frame. And
b
n
C
is
the direction cosine matrix (DCM) from the
navigation frame to the body frame, and the
quaternion, DCM, and Euler angles are mutually
convertible.
The velocity is updated using the updated attitude
information and accelerometer output, and the
position is update by integrating the velocity.
(2 )
nnb nn nn
bieen
VCf Vg
(2)
/( )
/( )cos
Nm
Et
D
LvRh
lvRhL
hv
(3)
where
[]
nT
NED
Vvvv
is the velocity on the
navigation frame,
b
f
is the accelerometer output,
n
g
is the gravitational acceleration vector,
[]
T
P
Llh
is the position (latitude, longitude,
and altitude), and
m
R and
t
R are the Earth radii
calculated in the latitude and longitude directions,
respectively.
2.2 Filter Design
The integration filter is driven in synchronization
with the GPS signal output. First, the error state
variables are set as follows for EKF-based filter
design.
[]
nn bbT
XPV
(4)
where
P
is the position error,
n
V
is the velocity
error,
n
is the attitude error shown in the navigation
frame, and
b
and
b
are the accelerometer bias and
gyro bias, respectively.
The discrete-time system and measurement
equations of the filter are expressed as follows:
1
,~(0,)
,~(0,)
kkkk
k kkk
X
XwwNQ
Z
HX vvN R
(5)
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
238

The systems matrix is derived by applying the
linear perturbation method to (1) to (3) (Titterton and
Weston, 1997). In case of using the position and
velocity information of GPS, the measurement matrix
can be denoted as follows:
66 69
[0]
k
HI
(6)
Table 1: Specification of the sensors used in simulation.
Sensor Error Spec.
Accelerometer
Bias Repeatability 3.0 mg
Noise 0.05 mg/√hr
Gyro
Bias Repeatability 2.0 deg/hr
Noise 0.07 deg/√hr
GPS
Position Noise 5.0 m (1σ)
Velocity Noise 0.1 m/s (1σ)
2.3 Simulation Analysis
Simulation is performed to analyse the navigation
performance considering the application of the INS/
GPS integrated navigation system to the train. The
specifications of the IMU and GPS used in the
simulation are set as shown in Table 1. The model of
IMU is Northrop Grumman’s MEMS type μIMU-I,
and the model of GPS receiver is u-blox.
The maximum speed of the train is 200
km/hr
and the moving trajectory is set as shown in Fig. 1.
The train accelerates first and then runs at constant
Figure 1: Moving trajectory.
speed and the total driving time is 2 hours. After 10
minutes of straight running, rotate 30.0 degrees at a
rotational angular velocity of 1.0
deg/s for 30 seconds.
And repeat this. There are three tunnels, which cannot
receive GPS signals. The Monte-Carlo simulation
was performed on this trajectory, and the number of
simulations was 10 times. Fig. 2 shows the RMSE and
standard deviation (SD) obtained through the
covariance matrix of the filter. In the section where
the GPS signal can be received, it is seen that the
RMSE and SD are similar, and it is confirmed that the
Monte-Carlo simulation is performed normally. It can
be seen that accelerometer bias and gyro bias can be
estimated according to time and train rotation.
However, when the GPS signal cannot be received,
the RMSE values of the position and velocity of the
horizontal axis increase greatly. Therefore, it can be
Figure 2: RMSE and standard deviation in INS/GPS.
Reliability Analysis of the Kalman Filter for INS/GPS Integrated Navigation System Applied to Train
239
confirmed that there is a limitation of INS/GPS
integrated navigation in the section where the tunnel
exists.
3 NON-HOLONOMIC
CONSTRAINT FILTER AND
ANALYSIS
3.1 Filter Design
Trains have six degree of freedom movement.
However, it only moves on railways with non-
holonomic constraints. In other words, there is
velocity only in the longitudinal direction on the body
frame, and the velocities are zero in the lateral and
vertical directions. Using this information as an
additional measurement, a new measurement matrix
for the filter can be constructed. To do this, the
velocity on the body frame is calculated.
bbn
n
VCV
(7)
The linear perturbation method is applied to this
equation.
()( )
bbb n nn
n
VVCI VV
(8)
Therefore, the velocity error model on the y and z
axis of the body frame can be approximated as
follows:
(:) (:)( )
y
bnbnn
nn
z
v
CyzV CyzV
v
(9)
where
010
(:)
001
bb
nn
Cyz C
(10)
Based on this equation, the following two
measurement matrices can be derived.
33 33 33 36
33 33 33 36
23 26
000
000
0(:)(:)()0
k
bbn
nn
I
HI
Cyz CyzV
(11)
23 26
0(:)(:)()0
bbn
knn
HCyzCyzV
(12)
We define two filters as follows.
- INS/GPS with NHC-1: The measurement matrix (16)
is used where GPS signals can be received and the
measurement matrix (12) is used where GPS signals
cannot be received.
- INS/GPS with NHC-2: (11) is used in an open space
where GPS signals can be received, and (12) is used
in places where GPS signals cannot be received like
a tunnel.
3.2 Simulation Analysis
Three types of INS/GPS integrated navigation were
performed: INS/GPS, INS/GPS with NHC-1, and
INS/GPS with NHC-2. Fig. 3 shows the RMSE for
each type as a result of Monte-Carlo simulations.
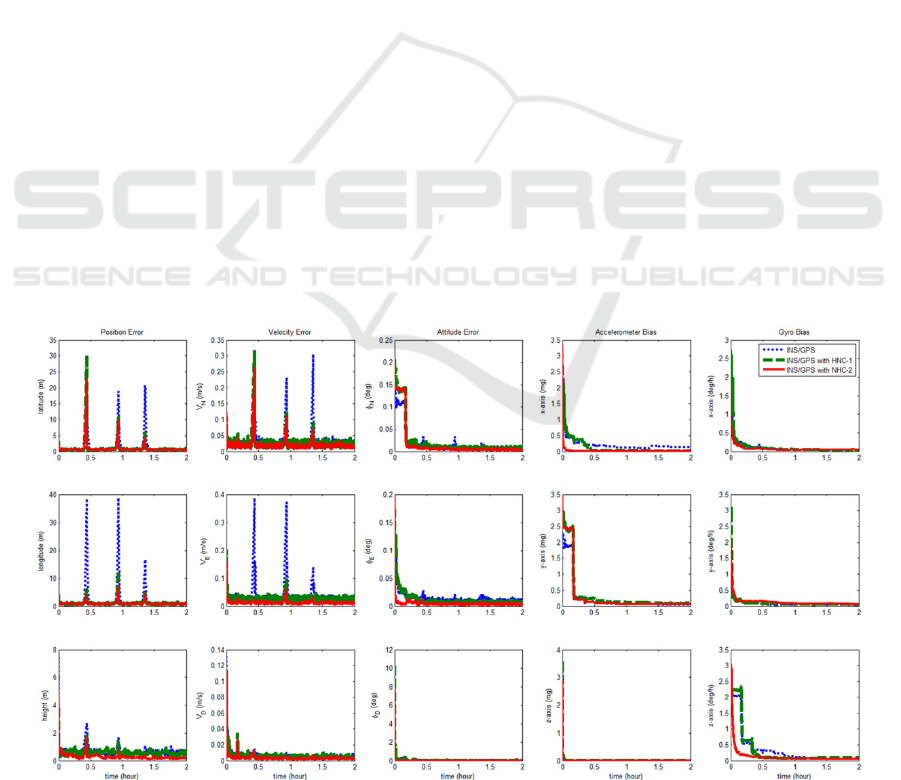
Figure 3: RMSEs according to the filters.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
240
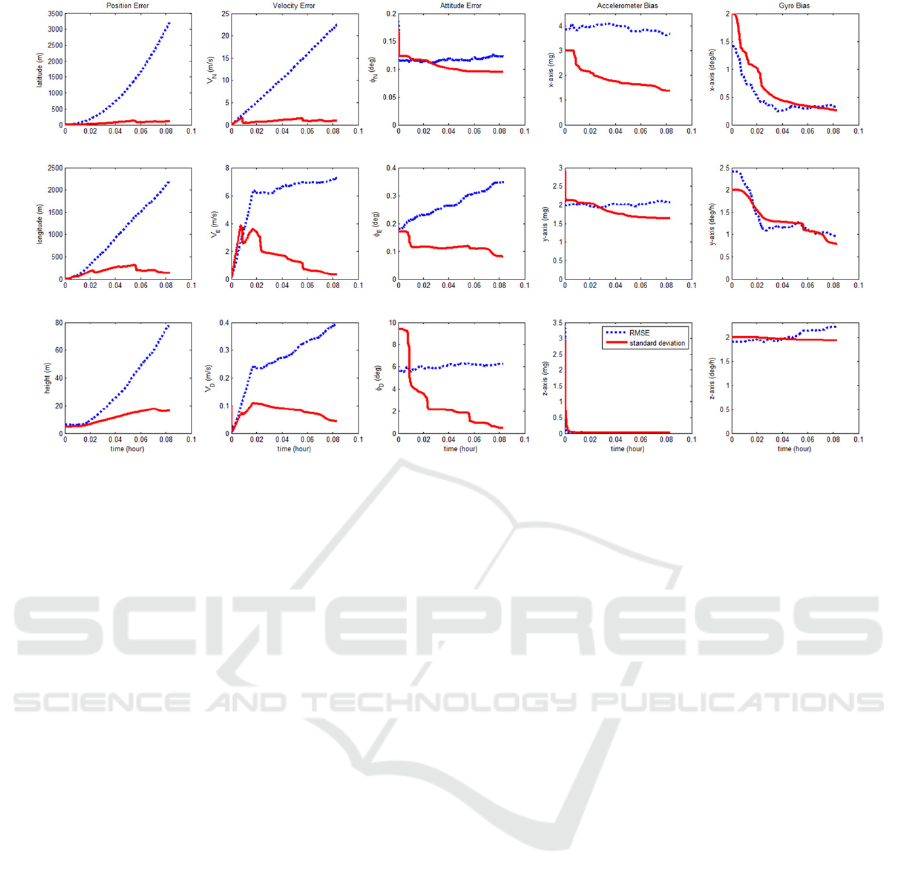
Figure 4: RMSE and standard deviation in INS with NHC.
First, in the case of NHC-2, the x-axis
accelerometer bias is estimated faster than other
methods. As a result, the E-axis attitude error is also
estimated quickly. And the z-axis gyro bias
estimation speed is increased. Based on this effect,
the horizontal-axis velocity and position error
estimation performance is improved. In particular, the
increase in the error is also reduced in tunnels because
the filter can be driven through the NHC.
In case of NHC-1, the sensor bias estimation
performance is not significantly different from
INS/GPS. However, overall performance is better
than INS/GPS because it has the advantage of driving
the filter even in tunnels.
What should be considered here is that until the
train meets the tunnel after departure, the errors are
reduced by driving the filter sufficiently through the
GPS signal. Therefore, the errors in tunnels relatively
small.
To further analyse this problem, the NHC filter
was driven without a GPS signal for the first 5
minutes after departure and the results are shown in
Fig. 4. Comparing RMSE and SD, we can see that the
accuracy of the actual estimate of the gyro bias is
within the covariance of the filter, which is the
performance index of the filter. In the case of the
horizontal-axis accelerometer bias, however, the two
values seem to be somewhat different. The horizontal
–axis attitude errors also has the same tendency. A
problem lies in the D-axis attitude error. In the NHC
filter, the covariance of the D-axis attitude error falls
to a value close to zero. In other words, it is ensured
that the observability is obtained. However, when
starting with a relatively large initial attitude
estimation error, the estimates do not converge to true
values. This is a crucial factor, which results in
velocity and position estimation errors. This is a hoe
in the NHC filter.
3.3 Reliability Analysis
The performance of the filter can be expressed in
terms of observability. In a time-varying system such
as INS/GPS, the observability of the filter can be
confirmed by covariance analysis rather than rank-
based analysis. It is determined that the state variable
having the covariance converging to a value close to
0 according to the filter update is estimable. However,
the important point is that estimability does not
always mean convergence to true values. As shown in
Fig. 4, the state variables converge but may converge
to the wrong values.
Therefore, it is difficult to judge the performance
of the filter only by the observability. In this case, it
is necessary to set various environments and judge the
performance of the filter based on the RMSE analysis
through Monte-Carlo simulations. It is important to
carry out simulations using various trajectories for
trains. In addition, reliability analysis of GPS signal
and INS/GPS performance analysis according to IMU
specification must be done.
Reliability Analysis of the Kalman Filter for INS/GPS Integrated Navigation System Applied to Train
241

4 CONCLUSION
In this paper, we designed the navigation filters and
analysed its performance when applying the INS/GPS
integrated navigation system to the train. NHC filters
for NHC-based trains were designed and Monte-
Carlo simulations were performed to performance
analysis. Tunnels were set on a trajectory and
simulations were performed. Here, the case of
performing pure INS in the tunnels and the case of
driving the NHC filter were considered, respectively.
By analysing covariance and RMSE together, it was
verified that the use of NHC filter regardless of GPS
signal availability is good for filter performance. And
the loophole in covariance analysis was point out.
Based on this, it can be concluded that it is necessary
to analyse covariance and RMSE together based on
the Monte-Carlo simulations performed under
various environment settings to analyse the reliability
of the filter, therefore.
ACKNOWLEDGEMENTS
This research was supported by a grant from R&D
Program (PK1904A1) of the Korea Railroad
Research Institute, Republic of Korea.
REFERENCES
Cho, S. Y., 2014, IM-filter for INS/GPS-integrated
navigation system containing low-cost gyros, IEEE
Trans. Aerospace and Electronic Systems, vol. 50, pp.
2619-2629.
Cho, S. Y., Ju, H. J., Park, C. G., Cho, H., and Hwang, J.,
2017, Simplified cubature Kalman filter for reducing
the computational burden and its application to the
shipboard INS transfer alignment, Journal of
Positioning, Navigation, and Timing, vol. 6, pp. 167-
179.
Cho, S. Y., and Kim, B. D., Cho, Y. S., and Choi, W. S.,
2007, Multi-model switching for car navigation
containing low-grade IMU and GPS receiver, ETRI
Journal, vol. 29, pp. 688-690.
Julier, S., Jhlmann, J., and Durrant-Whyte, D. G., 2000, A
new method for the nonlinear transformation of means
and covariances in filters and estimators, IEEE Trans.
Automatic Control, vol. 45, pp. 477-482.
Liu, H., Nassar, S., and El-Sheimy, N., 2010, Two-filter
smoothing for accurate INS/GPS land-vehicle
navigation in urban centers, IEEE Trans. Vehicular
Technology, vol. 59, pp. 4256-4267.
Miller, I., and Campbell, M., 2012, Sensitivity analysis of a
tightly-coupled GPS/INS system for autonomous
navigation, IEEE Trans. Aerospace and Electronic
Systems, vol. 48, pp. 1115-1135.
Presti, L. L, and Sabina, S., 2018, GNSS for Rail
Transportation: Challenges and Opportunities, Cham,
Switzerland: Springer.
Reif, K., Gunther, S., Yaz, E., and Unbehauen, R., 1990,
Stochastic stability of the discrete-time extended
Kalman filter, IEEE Trans. Automatic Control, vol. 44,
pp. 714-728.
Titterton, D. H., and Weston, J. L. 1997, Strapdown Inertial
Navigation Technology, London: Peregrinus.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
242
