Singularity Analysis for Redundant Manipulators of Arbitrary

Kinematic Structure

Ahmad A. Almarkhi

and Anthony A. Maciejewski

Department of Electrical and Computer Engineering, Colorado State University, Fort Collins, CO 80523-1373, U.S.A.

Keywords:

Redundant Robots, Singularities, Kinematics.

Abstract:

This paper presents a technique to identify singularities of any rank for a robot of any kinematic structure.

The technique is based on computing the gradient of singular values of the robot Jacobian. The algorithm

deals with the situations when two or more singular values become nearly equal and their corresponding

singular vectors are ill-deﬁned. Also, an algorithm is developed to identify the physically meaningful singular

directions from the high dimensional singular subspaces of high-rank singularities. The suggested technique

is applied to a 4-DoF and a 7-DoF robot to show its efﬁcacy at identifying robot singularities of all ranks and

dealing with the ill-deﬁned singular directions.

1 INTRODUCTION

A robot singular conﬁguration is a conﬁguration in

which the robot’s end effector loses the ability to

move in one (or more) direction(s), i.e., singular

direction(s). Such singular conﬁgurations are usu-

ally called singularities (Baker and Wampler, 1988).

Robot singularities are also called critical points

(Burdick, 1989) or special conﬁgurations (Hunt,

1986). At a singularity, there is no joint velocity that

can result in an end-effector velocity in a singular di-

rection(s). Singularities result from having the cor-

responding Jacobian (J) columns be linearly depen-

dent. The singular value decomposition (SVD) of J

can reveal immediate information about singularities.

At a singularity, one (or more) singular value(s) of

the robot Jacobian are zero. Robot singularities can

offer mechanical advantages (Kieffer and Lenarcic,

1994), however, they require more sophisticated in-

verse kinematics solutions (Nakamura and Hanafusa,

1986).

Identifying robot singularities has been exten-

sively studied. For non-redundant manipulators,

where J is square, singularities can be found by sym-

bolically solving for conditions when the determinant

of J equals zero (|J|= 0) (Waldron et al., 1985). For

redundant manipulators, where |J| does not exist, the

conditions that make |JJ

| = 0 can be computed,

https://orcid.org/0000-0002-5767-6103

https://orcid.org/0000-0002-1376-5825

but this is usually difﬁcult to solve. In this case, one

viable approach is to solve for conditions that make

all the 6 ×6 sub-Jacobians singular, i.e., the determi-

nants of all sub-Jacobians equal zero (Litvin et al.,

1986), but this also becomes infeasible for robots with

a large number of degrees of freedom (DoF). For ex-

ample, an 8-DoF manipulator requires computing the

determinants of 28 sub-Jacobians. In addition, these

techniques typically lack the ability to provide infor-

mation about the singular vector(s) associated with a

singularity.

To more easily identify singularities and ﬁnd sin-

gular directions, (Sugimoto et al., 1982) suggested

using the fact that at a singularity, there must be

a screw reciprocal to all screws that represent the

columns of the robot Jacobian. This technique has

been used to identify the rank-1 singularity condi-

tions and the singular directions for 7-DoF manip-

ulators (Boudreau and Podhorodeski, 2010). The

reciprocity-based methodology has also been used to

ﬁnd the rank-1 singularities of an 8-DoF manipula-

tor (Nokleby and Podhorodeski, 2004b). In addition,

it was extended to identify the rank-2 singularities

of a 7-DoF manipulator (Nokleby and Podhorodeski,

2004a). This technique shows its merit of being rel-

atively easy and extendable, but it is highly depen-

dent on selecting a reference frame that simpliﬁes

the computation of J. Building on the reciprocity-

based approach, researchers have suggested further

simpliﬁcations of the Jacobian by performing elemen-

tary transformations on the Jacobian before solving

Almarkhi, A. and Maciejewski, A.

Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure.

DOI: 10.5220/0007833100420049

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 42-49

ISBN: 978-989-758-380-3

for the singularity conditions as in (Xu et al., 2013).

This approach has been further employed in perform-

ing singularity avoidance for manipulators with non-

spherical wrists (Xu et al., 2016). All these techniques

work well for simple classes of kinematically redun-

dant manipulators and for rank-1 singularities. Such

manipulators have their successive joint axes either

perpendicular or parallel, which makes computing J

relatively easy.

In this paper we suggest a technique to ﬁnd the

singularities of a manipulator with an arbitrary degree

of redundancy and arbitrary kinematic structure. This

can be achieved by driving a certain singular value,

, of J to zero by following the gradient descent of

that singular value, i.e., −∇σ

. The complexity of this

technique is independent of the rank of the singularity.

In addition, we present an algorithm to identify the

singular directions at high-rank singularities.

The rest of this paper is organized as follows.

Methodologies to identify robot singularities and their

corresponding singular directions are presented in

section 2. In section 3, the results of applying the

methodologies to a 4-DoF robot and a 7-DoF robot

are discussed. Finally, the conclusions of this work

are presented in section 4.

2 SINGULARITY ANALYSIS

2.1 Background

The forward kinematics of an n-DoF robot that is act-

ing in an m-dimensional workspace can be written as

˙x = J

θ (1)

where ˙x is an m ×1 vector representing the end-

effector velocity, J is the m ×n robot Jacobian, and

is an n ×1 vector that represents the joint angle rates.

For redundant robots, n > m, where n −m is the de-

gree of redundancy. For a redundant manipulator, J is

not a square matrix, and thus not invertible, however,

an inverse kinematics solution can be found using

θ = J

˙x + n

(2)

where J

is the pseudoinverse of J and n

is an ar-

bitrary vector in the null space of the Jacobian.

The singular value decomposition of J can be rep-

resented as

J =

∑

i=1

(3)

where r is the rank of J, the σ

’s are the ordered sin-

gular values, i.e., σ

≥ σ

≥ ··· ≥ σ

≥ 0, the unit

vectors u

represent the output singular vectors, and

are the input singular vectors. For a robot at a

rank-n singularity, there are n singular values, σ

’s,

that become zero. Thus, employing a technique that

minimizes singular values of J can be used to identify

robot singular conﬁgurations.

2.2 Identifying Robot Singularities

In this section, we explain how to employ the gradient

descent of a singular value of J to drive a robot of

an arbitrary kinematic structure to a singularity. This

technique is not limited by the rank of the singularity.

The singular value σ

in (3) can be expressed as

= u

. (4)

Differentiating (4) with respect to time results in

= ˙u

+ u

J ˙v

. (5)

One can note that u

and v

are zero for i 6= j

and that the derivative of a unit vector is orthogonal to

that vector. So, (5) can be further simpliﬁed to (Ma-

ciejewski, 1988)

= u

. (6)

The partial derivative of σ

with respect to some θ

can be expressed as

∂σ

∂θ

= u

∂J

∂θ

(7)

where

∂J

∂θ



∂j

∂θ

∂j

∂θ

,··· ,

∂j

∂θ



. (8)

The partial derivative of the i

column of the Jaco-

bian is given by (Klein and Chu, 1997), (Groom et al.,

1999)

∂j

∂θ











−(z

×z

, k < i

−(z

, k ≥i

(9)

Then, the gradient of σ

for any J can be simply com-

puted from (7), (8), and (9), as

∇σ



∂σ

∂θ

∂σ

∂θ

,··· ,

∂σ

∂θ



. (10)

Now that one can compute ∇σ

, it is possible to

employ the gradient descent technique to locate a

minima for any singular value σ

. In the following, we

explain an algorithm to ﬁnd rank-1 and higher rank

singularities.

Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure

2.2.1 Identifying Rank-1 Singularities

For rank-1 singularities, one can employ the general

equation

(k+1)

= θ

(k)

−α

∇σ

(k)

(11)

where, θ

(k+1)

is a vector that represents the new joint

angles of a robot, the vector θ

(k)

is the current joint

angles, α

is an adaptive step size, and ∇σ

(k)

is the

gradient of σ

(σ

= σ

for rank-1 singularities). In

order to identify all rank-1 robot singular conﬁgura-

tions, one can start by generating random conﬁgura-

tions that span the robot joint space. Then, from each

random conﬁguration, one can move the robot along

the gradient descent of σ

as in (11). For faster con-

vergence to a singularity, one can use the steepest de-

scent method, in which α

needs to be adaptive, i.e., it

is chosen at each iteration to achieve a maximum de-

crease in σ

. This can be done by conducting a one-

dimensional search along the −∇σ

(k)

direction until a

minimizer, θ

(k+1)

, is found.

2.2.2 Identifying Rank-2 Singularities

A robot is said to be in a rank-2 singularity if ε >

m−1

≥ σ

, where ε is a small threshold (virtually

zero). To identify rank-2 singularities, one can start

with a population of random joint conﬁgurations and

employ (11) by moving along the −∇σ

(k)

m−1

direction

until the σ

m−1

< ε condition is satisﬁed. However,

it is not uncommon for an undesirable behavior to

occur, that results from having the two singular val-

ues σ

m−1

and σ

become nearly equal before they

reach zero, i.e., σ

m−1

≈ σ

> ε. In this case, the

two singular values are not distinct, which means that

their corresponding singular vectors are ill-deﬁned. In

other words, any singular vectors (u and v) in the

m−1

} and {v

m−1

} subspaces are valid for

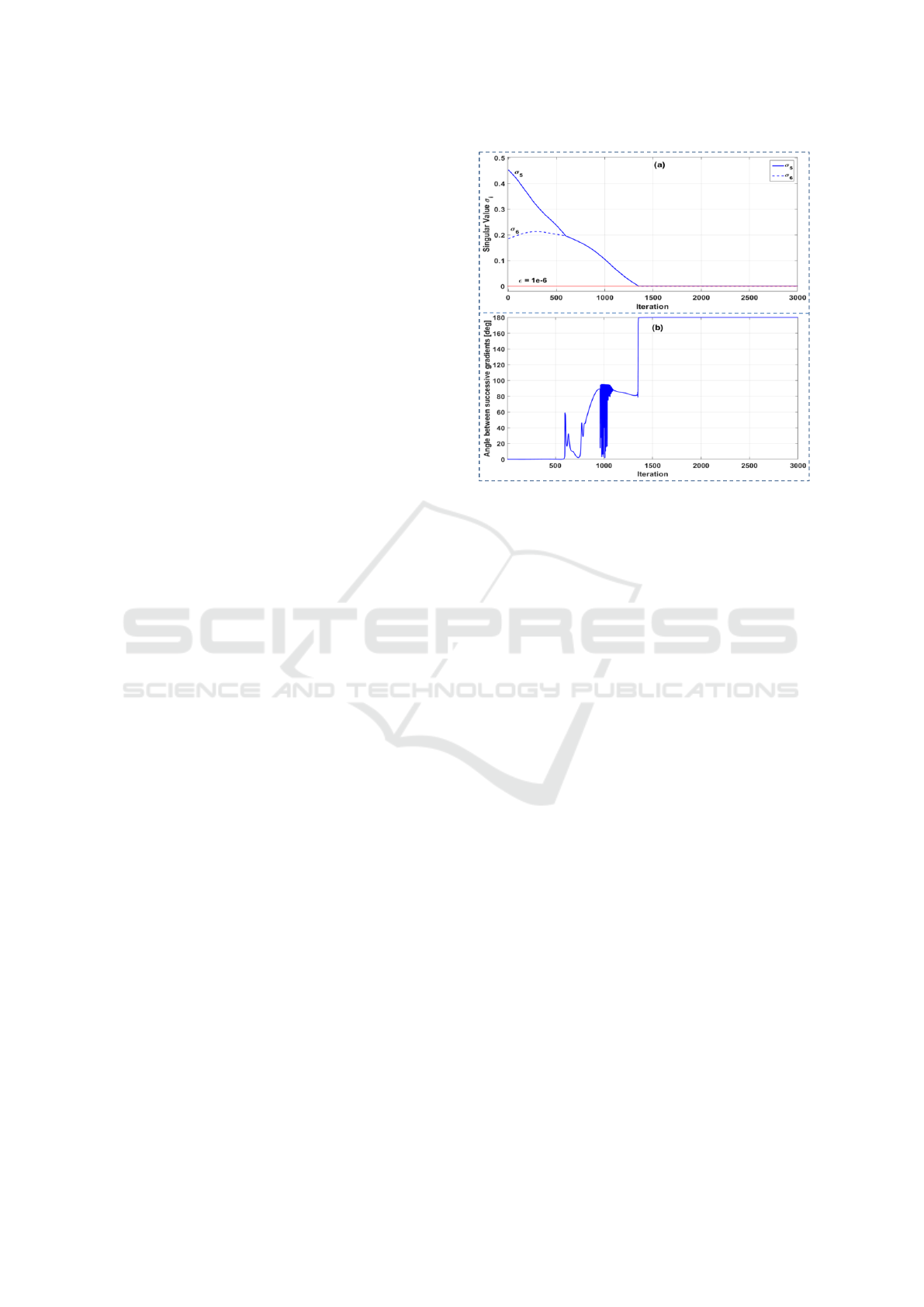
solving (6). Figure 1, shows the behavior of the algo-

rithm when the two smaller singular values become

nearly equal through the process of driving a robot

into a rank-2 singularity. In this case, σ

≈ σ

(at

around iteration 600), which makes them indistinct

and their corresponding singular vectors ill-deﬁned.

The direction of ∇σ

can completely change direc-

tion from one iteration to another, which affects the

rate of convergence.

To overcome this unwanted effect, one can start

with moving the robot along the −∇σ

(k)

m−1

direction

until σ

and σ

become very close in value. Then,

a combination between the two gradients is com-

puted. Because the singular value decomposition is

not unique in these cases, any singular vectors u and

v in the subspace associated with the equal singular

Figure 1: In subplot (a), the evolution of σ

and σ

is shown

as the standard gradient descent algorithm is employed. The

singular value σ

is minimized until σ

≈ σ

at around it-

eration 600. When they become nearly equal, the angle be-

tween the gradients in successive iterations becomes large.

These angles are plotted in (b), where the change in the an-

gles reaches 180

◦

. It is clear that the convergence requires

a long time (about 3000 iterations) due to the large change

in the gradient direction. In this case, the convergence time

is approximately 40 seconds. The threshold, ε = 10

−6

, is

indicated with a red horizontal line.

values are valid. One can rotate the singular subspace

such that the angle between ∇σ

(k)

and ∇σ

(k)

is mini-

mized, i.e.,

5(new)

= u

cosφ + u

sinφ

6(new)

= u

cosφ −u

sinφ

5(new)

= v

cosφ + v

sinφ

6(new)

= v

cosφ −v

sinφ

(12)

where φ is the angle of rotation. It should be noted

that the angle between the gradients of σ

and σ

can

vary from 0 to π based on the angle of rotation φ. A

suitable selection of the rotation angle for the singu-

lar subspaces is crucial in minimizing the change in

the gradient direction from one iteration to another.

Once the ∇σ

(k)

and ∇σ

(k)

that have the minimum an-

gle between them are computed, a combination that

minimizes σ

can be found

∇σ

(k)

= γ∇σ

(k)

+ (1 −γ)∇σ

(k)

(13)

where ∇σ

(k)

is the desired gradient and γ is a posi-

tive scalar where 0 ≤ γ ≤ 1. This linear search will

minimize the change in the gradient direction from

one iteration to another. After ∇σ

(k)

is computed, the

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

steepest descent method is applied to ﬁnd an optimal

value of α

in (11) that minimizes σ

. An analogous

process can be employed for identifying higher rank

singularities.

2.2.3 Identifying High-rank Singularities

To identify high-rank singularities, i.e., where three

or more singular values become zero, one can em-

ploy a similar approach to that applied for identifying

rank-2 singularities. For a robot in a singular conﬁg-

uration, J is of rank r if σ

= 0 for i > r, which also

means the robot is in a rank-(m −r) singularity. To

ﬁnd high-rank singularities, one can move the robot

by iteratively solving (11) until a desired σ

reaches

zero. While moving along the −∇σ

direction, it is

possible that σ

and σ

i+1

become nearly equal. In this

case, the procedure in the previous section can be ap-

plied.

In some cases, more than two singular values be-

come nearly equal but larger than the threshold, i.e.,

≈ σ

i+1

≈ ··· ≈ σ

> ε. For the purpose of illus-

tration, we will consider the case where a robot is be-

ing driven to a rank-3 singularity when the situation

≈ σ

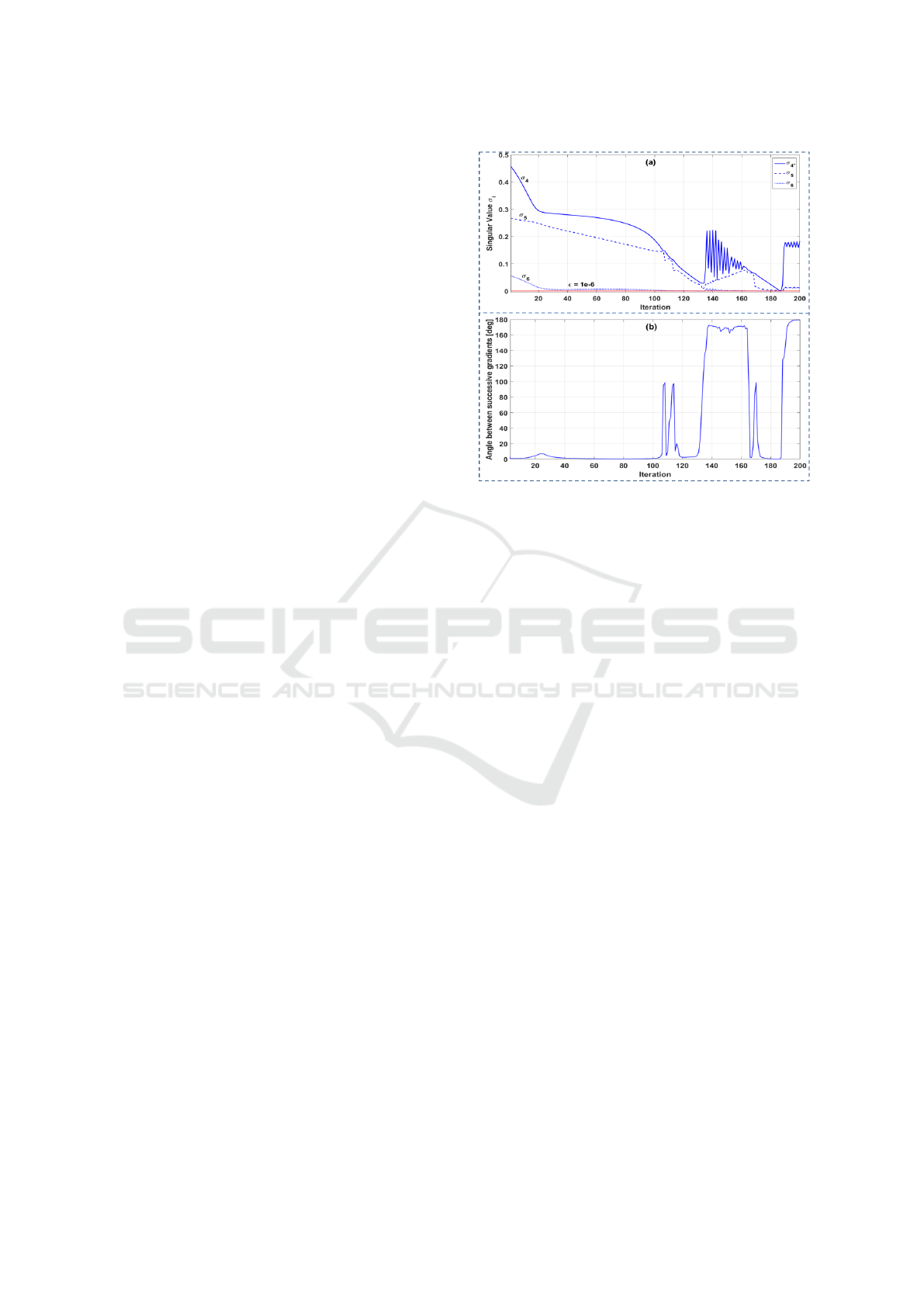
> ε occurs, as illustrated in Figure 2.

One can note that around iteration 186 in Figure 2

all three singular values became very close in value.

At this point, the angle between the gradient of σ

in successive iterations (the angles between ∇σ

(k−1)

and ∇σ

(k)

) became 170

◦

, which resulted from having

the singular values indistinct and their correspond-

ing singular vectors ill-deﬁned. This also contributed

to an unwanted increase in σ

because the gradients

switched direction. In this case, one can rotate their

corresponding singular subspaces to ﬁnd a suitable ro-

tation that minimizes the sum of the angles between

the three gradients. The solution is to minimize an

objective function H, where

H =

∑

(i=r+1)

∑

( j=i+1)

i, j

(14)

and θ

i, j

is the angle between ∇σ

and ∇σ

. The ro-

tation of the singular subspaces can be done by iter-

atively employing (12). That is, because the singular

subspaces are three-dimensional (or higher), one can

iteratively rotate one plane at a time, i.e., in this case,

} and {v

}, then {u

} and {v

and so on. This iterative rotation should be done until

the sum of the angles between all gradients is mini-

mized. After ﬁnding the gradients of the singular val-

ues, one can use (13) to compute a combination be-

tween the ﬁrst two gradients,∇σ

and ∇σ

, that min-

imize σ

. Then, using (13) again to compute a com-

bination between the resulting gradient and ∇σ

that

Figure 2: In (a), the singular value σ

is minimized until it-

eration 106, where (σ

≈σ

). At iterations 135 and 186 the

singular values σ

, σ

, and σ

become nearly equal. Subﬁg-

ure (b) shows the change in the angle between the gradients

in successive iterations. The change of angle reaches 170

◦

when the three singular values become nearly equal. In this

case, the singular values σ

, σ

, and σ

never converge to

zero. The threshold, ε = 10

−6

, is indicated with a red hori-

zontal line.

minimizes σ

. This approach guarantees achieving

a minimum amount of gradient direction change and

thus a shorter convergence time.

This process can continue until the algorithm can-

not converge to any higher rank singularities. This al-

gorithm, along with an adaptive step size, was applied

to the same robot that resulted in Figure 2 and the re-

sults are shown in Figure 3. It is clear that the conver-

gence is faster and the change in the gradient angle is

smaller. The average convergence time was improved

from 40 seconds to less than 2 seconds when the pro-

posed technique is employed.

If one applies the above algorithm to an initial

population of random conﬁgurations then one can

identify all the singular conﬁgurations of various

ranks. It is then possible to analyze the resulting sin-

gularities to determine the singularity conditions for

the robot. Some singularity conditions depend on the

values of a few joints while other joints can take any

value. One may observe that a singularity can be sat-

isﬁed by an inﬁnite number of joint conﬁgurations. In

the next section, we discuss a mathematical approach

to identify singular directions associated with the sin-

gularities that are physically meaningful.

Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure

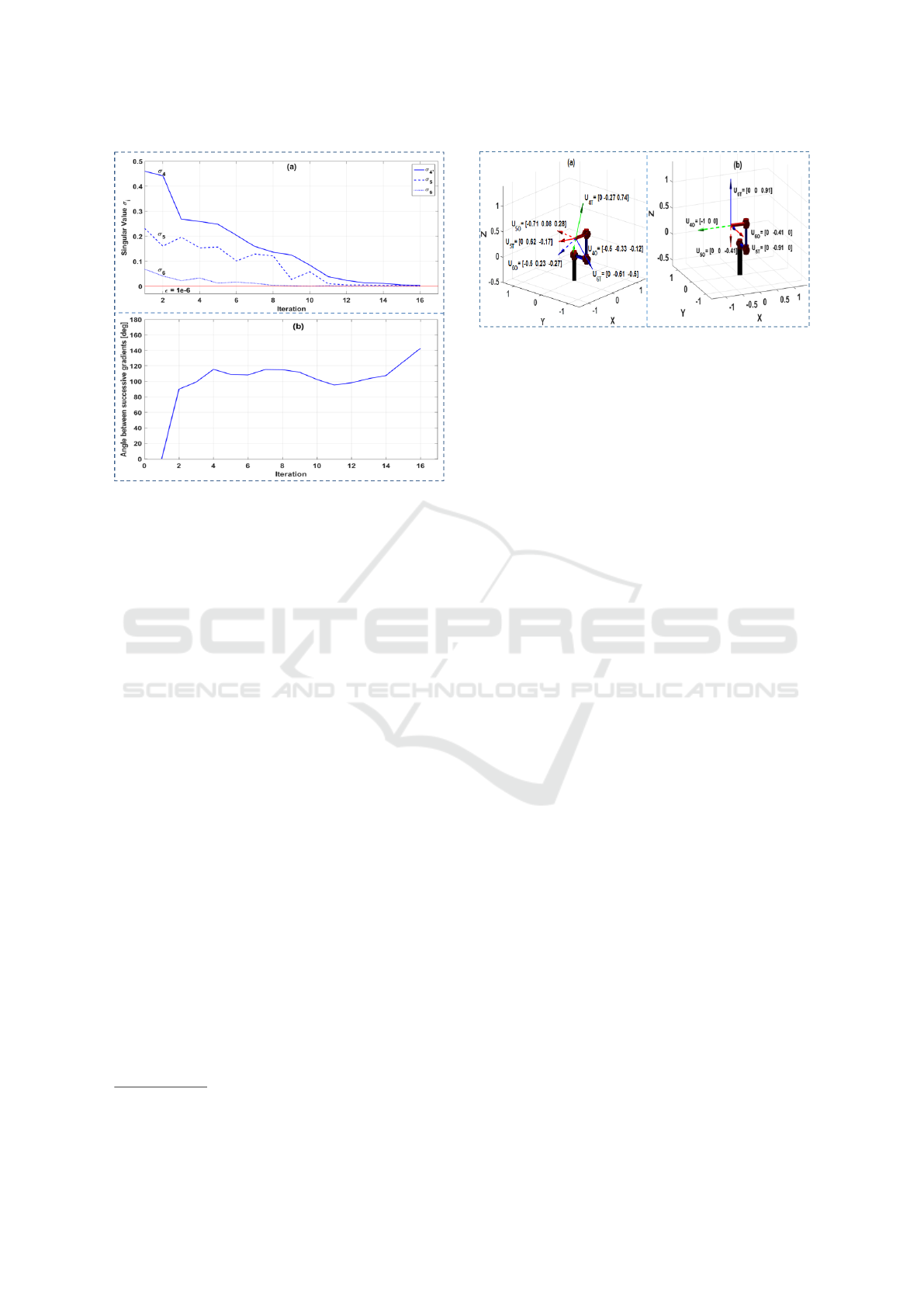
Figure 3: This ﬁgure shows the behavior of the singular

values when the proposed algorithm is applied to a robot to

ﬁnd a rank-3 singularity. This is the same robot as shown

in Figure 2. Subﬁgure (a) shows the values of the three

smaller singular values, σ

, σ

, and σ

, while applying the

algorithm with an adaptive step size α

. In subﬁgure (b),

the angles between the gradients in successive iterations are

shown. The angles average around 120

◦

. The algorithm

converges in 16 iterations. The convergence time in this

case is less than two seconds. The threshold, ε = 10

−6

, is

indicated with a red horizontal line.

2.3 Identifying Singular Directions

For a robot Jacobian J with rank r, the last m −r out-

put singular vectors, i.e., u

’s, span the directions of

lost end-effector motion. For spatial manipulators,

these singular vectors are 6-dimensional and repre-

sent a simultaneous translational and rotational ve-

locity. For rank-1 singularities, there is only one

unique singular direction, u

, and it is easy to vi-

sualize. At higher rank singularities, the singular

value decomposition is not unique. Thus, the singu-

lar vectors corresponding to the zero singular values

(σ

r+1

,σ

r+2

,··· ,σ

) are ill deﬁned and will likely not

be well aligned with the world (or task) frame of the

robot. However, one can apply Givens rotations to

these vectors in order to identify an intuitive repre-

sentation for the lost end effector motion. Consider

Figure 4, that shows a 7-DoF robot in a rank-3 singu-

larity, where both subﬁgures correspond to the same

robot in the same singular conﬁguration. The origi-

nal singular vectors, identiﬁed by employing the sin-

gular value decomposition, can be rotated to a more

Figure 4, 6, 7, 8, and 9 are produced using the Robotics

Toolbox (Corke, 2017).

Figure 4: A 7-DoF robot in the same rank-3 singularity is

presented.

In subﬁgure (a), the three SVD-generated singu-

lar directions are indicated. In subﬁgure (b), the singular di-

rections are plotted after they are properly rotated. The sin-

gular directions, u

, u

, and u

are represented by green,

red, and blue respectively. Dotted arrows represent rota-

tional velocity and solid arrows represent translational ve-

locity.

intuitive set that is aligned with the world coordinate

frame as follows:







0 0 0

−0.27 0.62 −0.61

0.74 −0.17 −0.50

−0.50 −0.71 −0.50

−0.33 0.08 0.23

−0.12 0.28 −0.27







⇒







0 0 0

0 −0.91 0

0 0 0.91

−1 0 0

0 0 −0.41

0 −0.41 0







Using the rotated subspace above (shown in Fig-

ure 4(b)), one can easily determine that there is no

joint velocity that can generate any rotational veloc-

ity around the −X direction (green). In addition, the

robot cannot have a simultaneous velocity with the il-

lustrated components of −Y translational motion with

−Z rotational motion (red). Likewise, there are no

joint rates that can generate a simultaneous velocity

with the illustrated components of Y translational mo-

tion with −Z rotational motion (blue). In the next sec-

tion, we illustrate the results of applying the proposed

algorithms to robots of different kinematic structures.

3 CASE STUDIES

3.1 Introduction

Our algorithm to identify robot singularities is neither

limited by the kinematic structure of the robot, nor

by the rank of the singularity. We employed it on

several 4-DoF regional and 7-DoF spatial robots and

present the results of one 4-DoF and one 7-DoF robot

here. For each robot we start with 10, 000 random

conﬁgurations in the joint space. From each point, we

apply the gradient-based algorithm to ﬁnd rank-1 and

all higher rank singularities. The resulting singular

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

vectors are then rotated to the most intuitive

representation of the lost directions of motion.

3.2 4-DoF Regional Robot

We study a locally optimal fault-tolerant 4-DoF robot

presented in (Ben-Gharbia et al., 2013) with the DH

parameters given in Table 1. This robot is a spa-

tial positioning (regional) manipulator, i.e., it has a

3-dimensional workspace. Our focus is on identify-

ing the singular conﬁgurations of this manipulator.

Table 1: DH parameters of an example 4-DoF manipulator.

Link

[radians] a

[m] d

[m] θ

[radians]

1 π/2

√

2 0 θ

2 -π/2

√

2 1 θ

3 π/2

√

2 -1 θ

4 0

3/2 1/2 θ

It was found that this robot has only rank-1 singu-

larities as presented in Figure 5. These singularities

are arranged along continuous manifolds in the joint

space. This means that the robot can continuously

move while staying in a singular conﬁguration. Note

that these are not the same as the self-motion mani-

folds.

Because the robot does not have any high-rank

singularities, the presentation of the singular direc-

tions is straightforward. The singular direction, u

gives the actual direction of the loss of the end-

effector velocity. Figure 6 shows the 4-DoF robot in

two different rank-1 singularities along with the sin-

gular directions with respect to the world frame.

3.3 Mitsubishi PA-10 Robot

3.3.1 Introduction

The Mitsubishi PA-10 is a 7-DoF manipulator with a

6-dimensional work space. Its kinematic structure is

similar to the human arm with three spherical joints in

the shoulder, one joint in the elbow, and three spher-

ical joints in the wrist. The DH parameters of the

PA-10 are listed in Table 2. The singularity analy-

sis on the PA-10 resulted in rank-1, rank-2, and rank-

3 singularities being identiﬁed. We were able to ﬁnd

singularity conditions for each singularity rank. The

singular directions, u

’s, were also identiﬁed and ap-

propriately rotated. In all ﬁgures, loss of directional

velocity is indicated with a solid arrow, while the loss

of rotational velocity is indicated with a dotted arrow.

Blue arrows indicate u

, red arrows indicate u

, and

green arrows indicate u

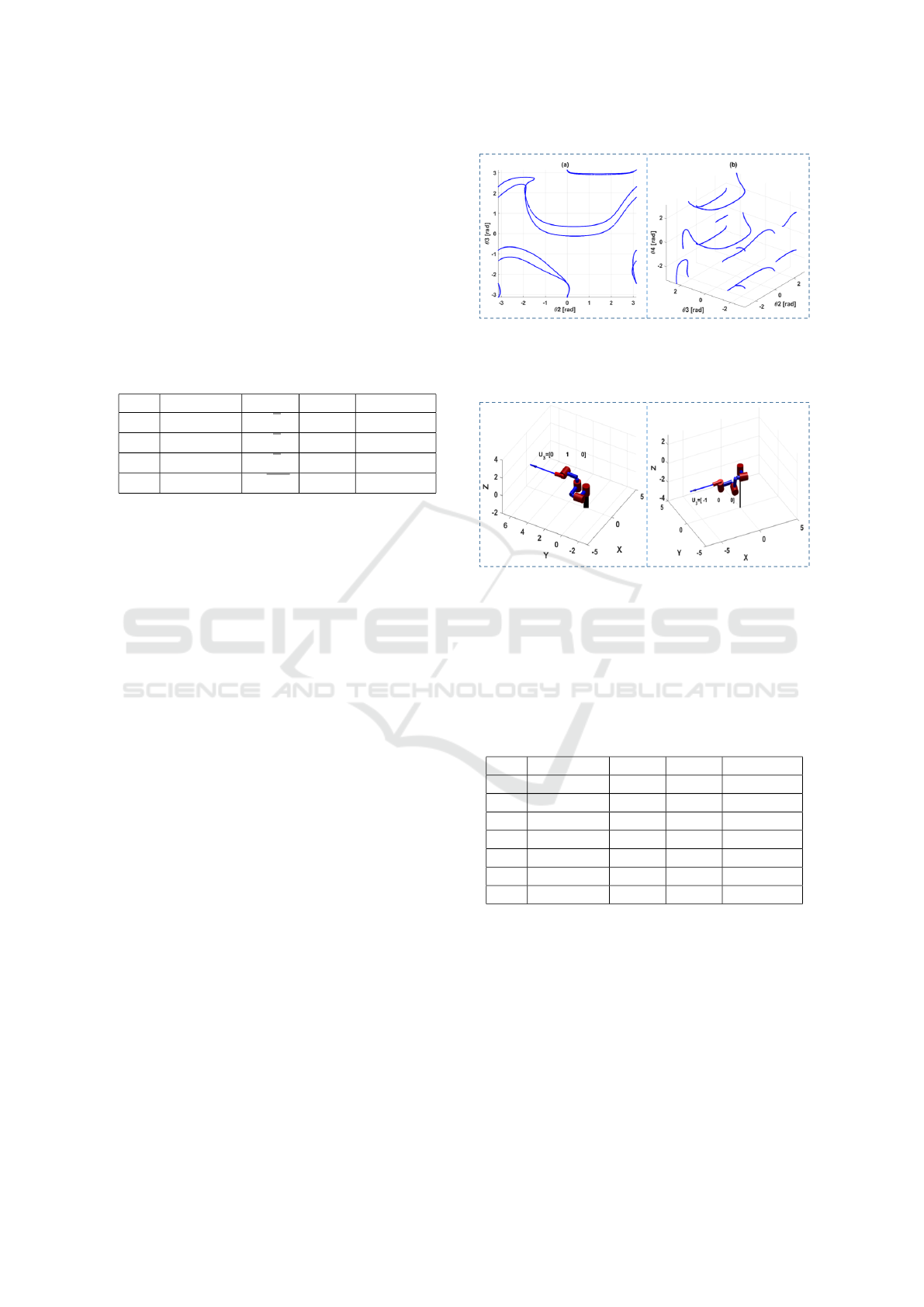
Figure 5: This ﬁgure illustrates the 4-DoF robot rank-1 sin-

gularities. In (a) the singular conﬁgurations are shown us-

ing a 2-D projection in [θ

,θ

]. In (b) a 3-D projection in

[θ

,θ

] is shown.

Figure 6: This ﬁgure shows the 4-DoF robot in two dif-

ferent rank-1 singular conﬁgurations. In (a) the robot is

shown in the conﬁguration θ = [−3.11,3.02,−1.53,0.15]

rad. The singular direction corresponding to the singularity

is u

= [0,1,0]

, which indicates that the singular direction

is aligned with the Y direction. In (b) the robot is shown in

the conﬁguration θ = [−1.76,−1.85,−1.39, 0.02] rad. The

singular direction is u

= [−1,0, 0]

, which indicates that

the singular direction is aligned with the −X direction.

Table 2: DH parameters of the PA-10 robot.

Link

[radians] a

[m] d

[m] θ

[radians]

1 -π/2 0 0 θ

2 π/2 0 0 θ

3 -π/2 0 0.45 θ

4 π/2 0 0 θ

5 -π/2 0 0.50 θ

6 π/2 0 0 θ

7 0 0 0.45 θ

3.3.2 Rank-1 Singularities

All rank-1 singularities are summarized in Table 3.

Joint 4 is critical in that the robot will be singular if

is equal to ±π or 0. One can observe that joint 4

is the only joint that can change the distance between

the shoulder and the wrist.

The robot singular directions that indicate the loss

of the end-effector velocity are all shown in Figure 7.

Because these are rank-1 singularities, their corre-

sponding singular directions are well deﬁned.

Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure

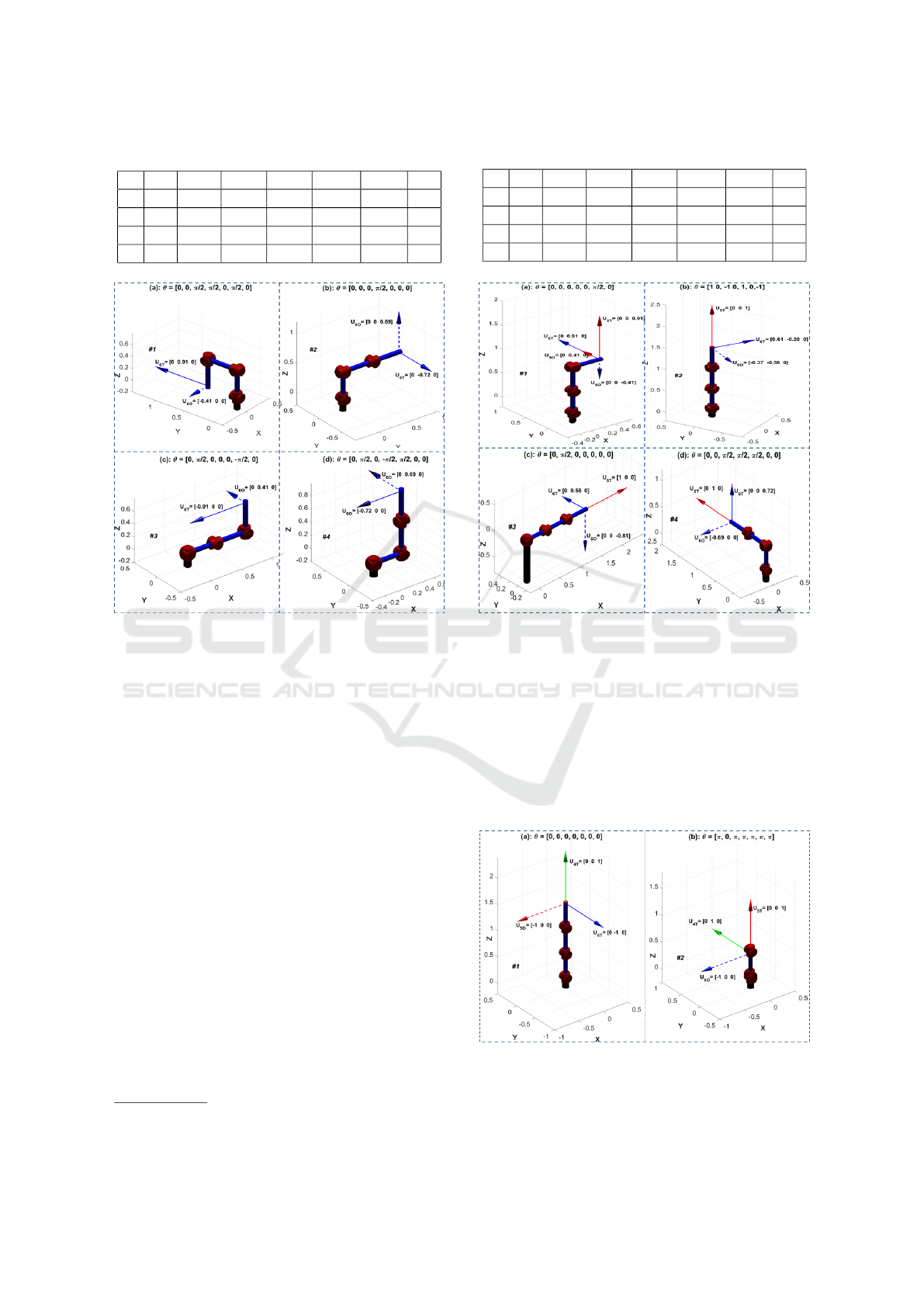
Table 3: PA-10 robot’s rank-1 singular conﬁgurations

i θ

1 x ±π,0 ±π/2 x x x x

2 x ±π,0 x x x ±π,0 x

3 x x x ±π,0 x x x

4 x x x x ±π/2 ±π, 0 x

Figure 7: The PA-10 robot is shown in rank-1 singular con-

ﬁgurations. The singular direction, u

, is also plotted for

each singularity. The singularity conditions, 1, 2, 3, and 4,

in Table 3 are satisﬁed in subﬁgures (a), (b), (c), and (d),

respectively.

3.3.3 Rank-2 Singularities

The PA-10’s rank-2 singularity conditions are shown

in Table 4. The common feature between these condi-

tions is that they do not depend on the value of θ

. We employed Givens rotation to make sure that

the two singular vectors, u

and u

, are rotated to

represent the most intuitive set of singular directions.

Figure 8 shows the four singular conditions listed in

Table 4.

3.3.4 Rank-3 Singularities

It was found that the PA-10 robot can have rank-3 sin-

gularities by aligning the axes of joints 1, 3, 5, and

7 so that their columns of the Jacobian are linearly

dependent. The conditions for these rank-3 singular-

ity conﬁgurations are listed in Table 5. As before,

we have used Givens rotations to make the singular

vectors, u

, u

as intuitive as possible. Figure 9

shows the manipulator in two different rank-3 singu-

In all tables, “x” means the angle value does not matter.

Table 4: PA-10 robot’s rank-2 singular conﬁgurations.

i θ

1 x ±π,0 ±π,0 ±π, 0 x x x

2 x ±π,0 x ±π,0 x ±π, 0 x

3 x x x ±π,0 ±π, 0 ±π,0 x

4 x ±π,0 ±π/2 x ±π/2 ±π,0 x

Figure 8: The PA-10 robot is shown in rank-2 singular con-

ﬁgurations. The singular directions u

and u

are plotted

for each singularity condition. The singularity conditions,

1, 2, 3, and 4, in Table 4 are represented in the subﬁgues (a),

(b), (c), and (d), respectively.

lar conﬁgurations. One can observe that the rank-

3 singularities occur for the PA-10 when it is com-

pletely stretched out (workspace boundary singular-

ity) or when it is folded back on itself.

In general, our approach for identifying robot sin-

gularities does not consider physical joint limits. One

Figure 9: The PA-10 robot is shown in rank-3 singular con-

ﬁgurations. The singular directions, u

, u

, and u

are in-

dicted in green, red, and blue respectively. In (a), the robot

is in conﬁguration θ = [0, 0,0,0, 0, 0,0] and in (b) the robot

is in θ = [π, 0,π,π, π, π,π].

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

Table 5: PA-10 robot’s rank-3 singular conﬁgurations.

i θ

1 x ±π,0 ±π,0 ±π, 0 ±π, 0 ±π,0 x

can employ our technique to ﬁnd any robot singular

conﬁguration but one must exclude infeasible angles

due to mechanical limits.

4 CONCLUSIONS

This work has proposed a procedure based on com-

puting the gradient of a singular value to drive a robot

into a singular conﬁguration. This algorithm is able

to: (1) identify the singularities of any rank for any

robot and (2) deal with ill-deﬁned singular vectors

when their corresponding singular values are equal.

A second algorithm was presented to obtain the most

intuitive representation of the singular vectors associ-

ated with conﬁgurations that correspond to high-rank

singularities. Both algorithms are applicable to robots

with an arbitrary number of degrees of freedom and of

arbitrary kinematic structure These algorithms were

illustrated on a 4-DoF redundant positioning robot

and on a 7-DoF redundant PA-10 robot.

REFERENCES

Baker, D. R. and Wampler, C. W. (1988). On the inverse

kinematics of redundant manipulators. The Interna-

tional Journal of Robotics Research, 7(2):3–21.

Ben-Gharbia, K. M., Maciejewski, A. A., and Roberts,

R. G. (2013). Kinematic design of redundant robotic

manipulators for spatial positioning that are opti-

mally fault tolerant. IEEE Transactions on Robotics,

29(5):1300–1307.

Boudreau, R. and Podhorodeski, R. P. (2010). Singularity

analysis of a kinematically simple class of 7-jointed

revolute manipulators. Transactions of the Canadian

Society for Mechanical Engineering, 34(1):105–117.

Burdick, J. W. (1989). On the inverse kinematics of re-

dundant manipulators: Characterization of the self-

motion manifolds. International Conference on

Robotics and Automation, 1(2):264–270.

Corke, P. (2017). Robotics, vision and control: Fundamen-

tal algorithms in MATLAB

, volume 118. Springer.

Groom, K. N., Maciejewski, A. A., and Balakrishnan, V.

(1999). Real-time failure-tolerant control of kinemat-

ically redundant manipulators. IEEE Transactions on

Robotics and Automation, 15(6):1109–1115.

Hunt, K. H. (1986). Special conﬁgurations of robot-arms

via screw theory. Robotica, 4(3):171–179.

Kieffer, J. and Lenarcic, J. (1994). On the exploitation of

mechanical advantage near robot singularities. Infor-

matica, 18(3):315–323.

Klein, C. A. and Chu, L.-C. (1997). Comparison of ex-

tended Jacobian and Lagrange multiplier based meth-

ods for resolving kinematic redundancy. Journal of

Intelligent & Robotic Systems, 19(1):39–54.

Litvin, F., Yi, Z., Castelli, V. P., and Innocenti, C. (1986).

Singularities, conﬁgurations, and displacement func-

tions for manipulators. The International Journal of

Robotics Research, 5(2):52–65.

Maciejewski, A. A. (1988). The analysis and control of

robotic manipulators operating at or near kinemati-

cally singular conﬁgurations. PhD thesis, The Ohio

State University.

Nakamura, Y. and Hanafusa, H. (1986). Inverse kinematic

solutions with singularity robustness for robot manip-

ulator control. Journal of Dynamic Systems, Measure-

ment, and Control, 108(3):163–171.

Nokleby, S. B. and Podhorodeski, R. P. (2004a). Iden-

tifying multi-DOF-loss velocity degeneracies in

kinematically-redundant manipulators. Mechanism

and Machine Theory, 39(2):201–213.

Nokleby, S. B. and Podhorodeski, R. P. (2004b). Identi-

fying the 1-DOF-loss velocity-degenerate (singular)

conﬁgurations of an 8-joint manipulator. Transactions

of the Canadian Society for Mechanical Engineering,

28(2A):109–124.

Sugimoto, K., Duffy, J., and Hunt, K. (1982). Special

conﬁgurations of spatial mechanisms and robot arms.

Mechanism and Machine Theory, 17(2):119–132.

Waldron, K., Wang, S.-L., and Bolin, S. (1985). A study of

the Jacobian matrix of serial manipulators. Journal of

Mechanisms, Transmissions, and Automation in De-

sign, 107(2):230–237.

Xu, W., Zhang, J., Liang, B., and Li, B. (2016). Singular-

ity analysis and avoidance for robot manipulators with

nonspherical wrists. IEEE Transactions on Industrial

Electronics, 63(1):277–290.

Xu, W., Zhang, J., Qian, H., Chen, Y., and Xu, Y.

(2013). Identifying the singularity conditions of

Canadarm2 based on elementary Jacobian transforma-

tion. 2013 IEEE/RSJ International Conference on In-

telligent Robots and Systems, pages 795–800.

Singularity Analysis for Redundant Manipulators of Arbitrary Kinematic Structure