Experimental Implementation of Time-varying Input Shaping on UR

Robots

∗

Dan Kielsholm Thomsen

1,2

, Rune Søe-Knudsen

, David Brandt

and Xuping Zhang

Aarhus University Dept. of Engineering, Inge Lehmanns Gade 10, DK-8000 Aarhus C, Denmark

Universal Robots A/S, Energivej 25, DK-5260 Odense S, Denmark

Keywords:

Input Shaping, Industrial Robots, Time-varying Input Shaping, Conﬁguration Dependency, Fractional Delay

Finite Impulse Response.

Abstract:

Lightweight design leads to the unwanted vibration of industrial robot manipulators. Input Shaping (IS)

has been proven to be an effective vibration suppression method. However, applying IS to suppress the

vibration of industrial robots faces a challenging problem: time-varying dynamics. To address the time-varying

dynamics of robot manipulators, this paper presents a novel and practical solution to vibration suppression

based on Time-Varying Input Shaping Technology (TVIST). Our focus in this paper is to develop a practical

implementation strategy that can be applied in discrete time. A Fractional Delay Finite Impulse Response ﬁlter

is employed to design and implement TVIST. This solution makes TVIST more useful in practice because it can

be combined with online and discrete-time trajectory generation. It can also be implemented in combination

with position control using feed-forward velocity and torque. The performance of the new approach is validated

through experimental implementation on a lightweight robot from Universal Robots A/S. Experimental results

are analyzed to demonstrate signiﬁcant vibration suppression and increased productivity of the robot with

the proposed solution. The proposed method can be extended to the vibration suppression of other types of

industrial robotic manipulators with serial links as well as other time-varying dynamic systems.

1 INTRODUCTION

In order to meet the requirements of increased pro-

ductivity, safety and energy efﬁciency, manufacturers

tend to develop robots with light weight design com-

pared to traditional robots. Light weight design leads

to mechanical ﬂexibility of the robotic system due

to reduced stiffness and damping. A visualization of

primary mechanical ﬂexibility in a light weight col-

laborative robot from Universal Robots A/S (UR) is

presented in Figure 1.

As shown in the Figure 1, mechanical ﬂexibility

comes primarily from gear ﬂexibility in the joints

(strain wave gears) and link ﬂexibility in the two long

links. In addition to mechanical ﬂexibility, reduced

impedance resulting from control algorithms and elec-

trodynamics decreases the total system stiffness. The

mechanical and the electrical ﬂexibility cause the robot

manipulator to be subject to unwanted mechanical vi-

brations during motions with high acceleration. These

mechanical vibrations are unwanted, because they af-

∗

Patent pending, PCT/EP2018/068934

Figure 1: Mechanical ﬂexibility visualized in a UR3 robot.

fect robot precision, accuracy, wear, power consump-

tion and productivity in a negative way.

In the recent decades, many different strategies have

been investigated to reduce the unwanted mechanical

vibrations in light weight robotic systems. Generally,

the different strategies can be divided into hardware

design, trajectory optimization, feedback control, and

feed-forward control methods.

One type of feed-forward vibration suppression is

Input Shaping (IS) (Singer and Seering, 1990). IS has

gained a lot of attention for its simplicity and efﬁciency.

488

Thomsen, D., Søe-Knudsen, R., Brandt, D. and Zhang, X.

Experimental Implementation of Time-varying Input Shaping on UR Robots.

DOI: 10.5220/0007834504880498

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 488-498

ISBN: 978-989-758-380-3

The basic principle of IS is to convolve a reference

signal with a well-designed impulse train to generate a

modiﬁed (shaped) reference signal, that introduces a

reduced amount of unwanted mechanical vibrations in

the robotic system.

The conventional IS assumes that the system is

time invariant, i.e. the system frequency and damping

do not change with time. Applying IS to an industrial

robot manipulator faces a signiﬁcant challenge as in-

dustrial robots have conﬁguration dependent dynamics

(time-varying dynamics), i.e. the natural frequency

and damping of an industrial robot often vary with

conﬁguration and payload. This behavior arises mainly

from time-varying mass distribution, i.e. inertia, as

illustrated in Figure 2. Here, the actuator of the illus-

trated 1DOF robot will experience a position dependent

mass moment of inertia, which will result in position

dependent natural frequency and damping ratio of the

system.

q = 150

◦

Decreased

inertia

q = 90

◦

q = 30

◦

Increased

inertia

Actuator with

ﬂexibility

Figure 2: 1DOF manipulator with conﬁguration dependent

inertia.

Taking a UR5e robot as an example, the damped

natural frequency varies as much as from 6Hz to 15Hz

with a constant 5kg payload. The Robust IS method

was developed to accommodate slight deviations in sys-

tem frequencies and damping (Singh and Vadali, 1993;

Kim and Croft, 2018), but it is not capable of handling

the large deviation of the frequencies and damping in

industrial robot manipulators (Thomsen et al., 2018).

The Time-Varying Input Shaping Technology (TVIST)

is a promising method for handling the time-varying

dynamics and providing efﬁcient vibration suppression

throughout the workspace of the robot for any desired

motion (Cho and Park, 1995; Chang and Park, 2005;

Kivila, 2017). However, TVIST methods in existing

literature on are not directly applicable in commercial-

ized industrial robots, since the reported research is

limited to very ﬂexible robot manipulators, or have no

practical implementation strategies.

A new type of TVIST, which utilizes Fractional

Delay FIR ﬁltering has been suggested for industrial

robots (Thomsen et al., 2019). While simulations have

been published to support the new principles, practical

implementation and experimental validation have not

yet been presented.

The main contribution of this paper is to develop

and validate the practical and effective implementation

strategy of TVIST on typical industrial robots with six

joints. The detailed principles and procedures of imple-

menting TVIST on a UR robot are presented together

with preliminary experimental results. A set of test

motions are performed, and the experimental results

are analyzed. The experimental results validate the ef-

ﬁciency of the proposed experimental implementation

strategy.

2 OVERVIEW ON INPUT

SHAPING

Input Shaping (IS) is a vibration suppression method,

which aims to avoid introducing vibrations in a dy-

namic system by convolving the reference signal with a

set of vibration free impulses in order to obtain a modi-

ﬁed (shaped) reference signal. The shaped reference

signal will solve the desired task without introducing

vibrations in the system.

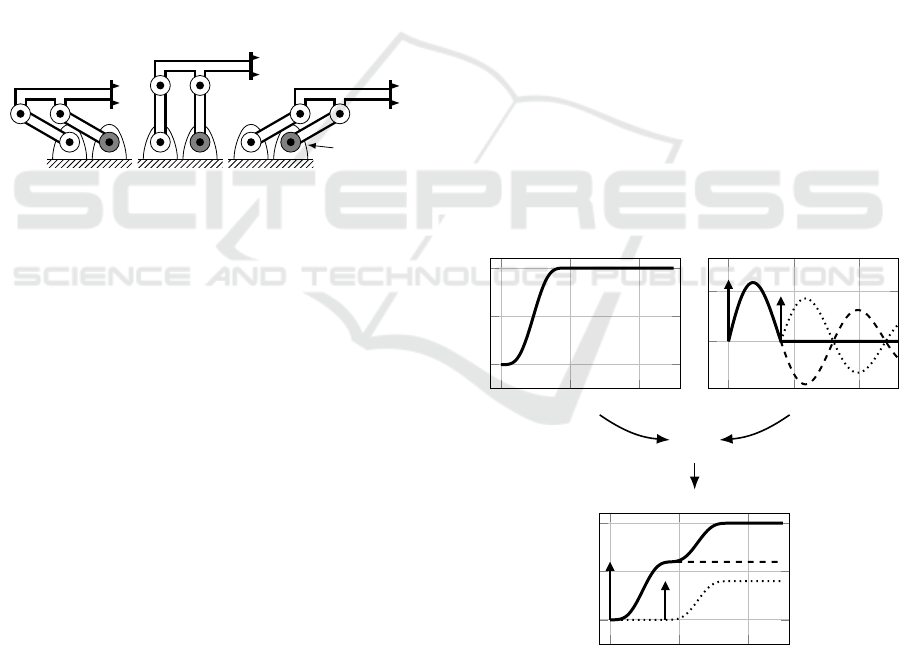
The fundamental principle of input shaping is illus-

trated in Figure 3. Here it is shown how an impulse,

, will cause a dynamic response in the system, and

how the response of a second impulse,

, will cancel

out this response if applied with the correct timing and

amplitude.

∗

Time,

System response

Impulse sequence, I(

∆

Time, t

Reference signal

Reference, x(t)

Total

From A

Time, t

Reference signal

Shaped reference, x

∗

(t)

∆

Figure 3: Convolution of Zero Vibration (ZV) shaper.

In general, the impulse sequence,

, can be ex-

pressed as shown in

(1)

(3)

, where

is internal ﬁlter

time,

is impulse amplitudes, and

∆

is impulse timings

for a shaper with N impulses.

Experimental Implementation of Time-varying Input Shaping on UR Robots

489

A =



··· A



(1)

∆ =



∆

··· ∆



(2)

t) =

(

t = ∆

0 otherwise

(3)

For the Zero Vibration (ZV) shaper,

and

∆

can

be determined as described by

(4)

(7)

, where

is a

helping constant,

is damping ratio,

is natural

frequency in rad/s, and

is damped frequency in Hz

(Singer and Seering, 1990).

K = e

ζπ

√

1−ζ

(4)

2π

1 −ζ

(5)

A =



1 + K



(6)

∆ =



0 0.5/ f



(7)

Once all parameters of

are known, the shaped

reference command,

∗

(t)

, can be obtained by convolv-

ing the reference command,

x(t)

, and

as presented

in (8). This operation is called shaping.

∗

(t) = (x ∗I)(t) ≡

∑

j=1

·x(t −∆

)) (8)

The shaping can be performed on any reference

signal for the controlled system, such as a position,

velocity, acceleration, torque, or current reference sig-

nal. The convolution of a position reference is also

illustrated in Figure 3. Here it is seen that convolving

x(t)

with

corresponds to splitting

x(t)

into two

parts, which are scaled by

and

and delayed by

∆

and

∆

, respectively, before being added together

∗

(t)

. If

∗

(t)

is given to the system as reference,

this will result in zero vibration in the system.

3 TIME-VARYING INPUT

SHAPING

While IS has proved efﬁcient for suppressing vibrations

system with time-invariant dynamics, it is not robust

enough to variations in

and

to provide acceptable

vibration suppression for time-varying dynamic sys-

tems such as serial link robots. This is clearly seen, by

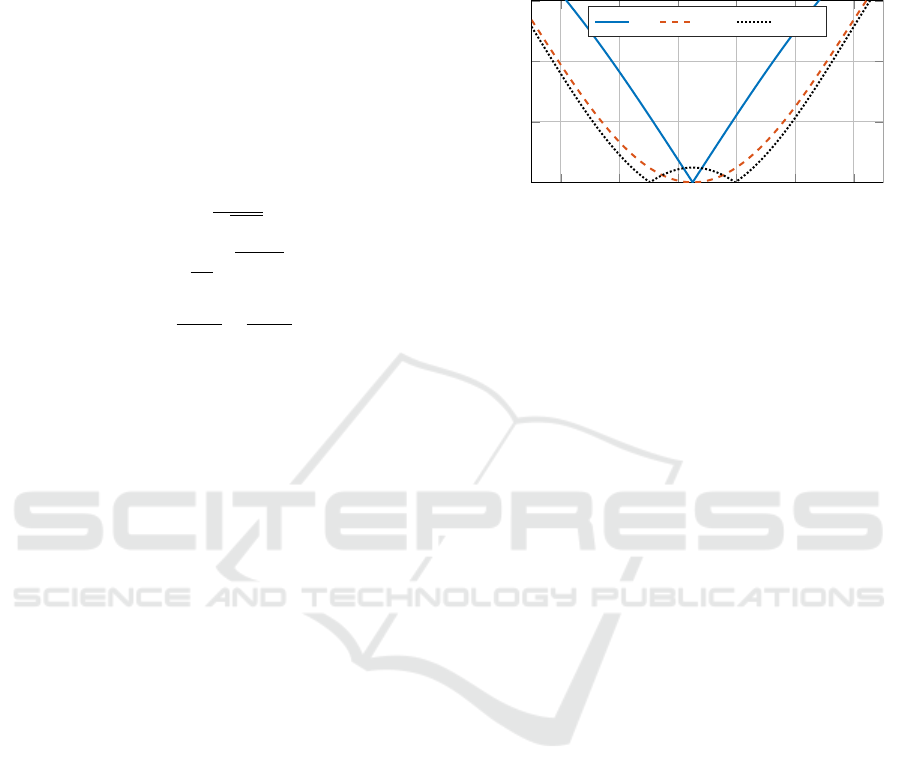
inspecting a sensitivity curve for the Zero Vibration

Derivative (ZVD) and Extra Insensitive (EI) shapers as

presented in Figure 4. It is seen, that an EI shaper can

not guarantee vibration suppression to a level of less

than 36% for the span of

from 6 to 15Hz, which

is seen in a UR5e robot. This is even without taking

damping variations into account.

8 10 12 14

Frequency (Hz)

Percent Residual Vibration (%)

ZV ZVD

EI 5%

Figure 4: Sensitivity plot of ZV, ZVD, and EI shapers.

It is possible to increase robustness, but this comes

at the expense of increased shaper delay, which is unde-

sirable. It is desired to increase vibration suppression

capabilities and decrease shaper delay for systems with

time-varying dynamics. Thus, a demand for taking

time-varying dynamics into account exists for light

weight robots. This section elaborates on how to extend

the IS methods to TVIST.

For a system with time-varying dynamics, i.e. time-

varying damping ratio,

ζ(t)

, and damped frequency,

(t)

, the impulse train can be updated as presented in

(9)

, which is an expansion of

(3)

. Here

t, f

(t),ζ(t))

is updated continuously as

(t)

and

ζ(t)

varies with

time.

t, f

(t),ζ(t)) =

(

(ζ(t)) if

t = ∆

( f

(t))

0 otherwise

(9)

When introducing the impulse sequence as

t, f

(t),ζ(t))

, it is necessary to expand

(8)

as pre-

sented in (10).

∗

(t) =

∑

j=1

(ζ(t)) ·x (t −∆

( f

(t)))) (10)

The formulation of TVIST in

(10)

is the idealized

principle, which can be used in systems, where: 1)

The analytical description of the reference signal is

known, and 2) The system does not have multiple

reference signals, which are dependent on each other,

such as position and velocity signals. The next section

elaborates on the shortcomings of this formulation, and

propose a way to overcome them in the implementation

in UR robots.

3.1 Implementation of TVIST

This section elaborates on the implementation of

TVIST in the control structure of a UR robot. The

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

490

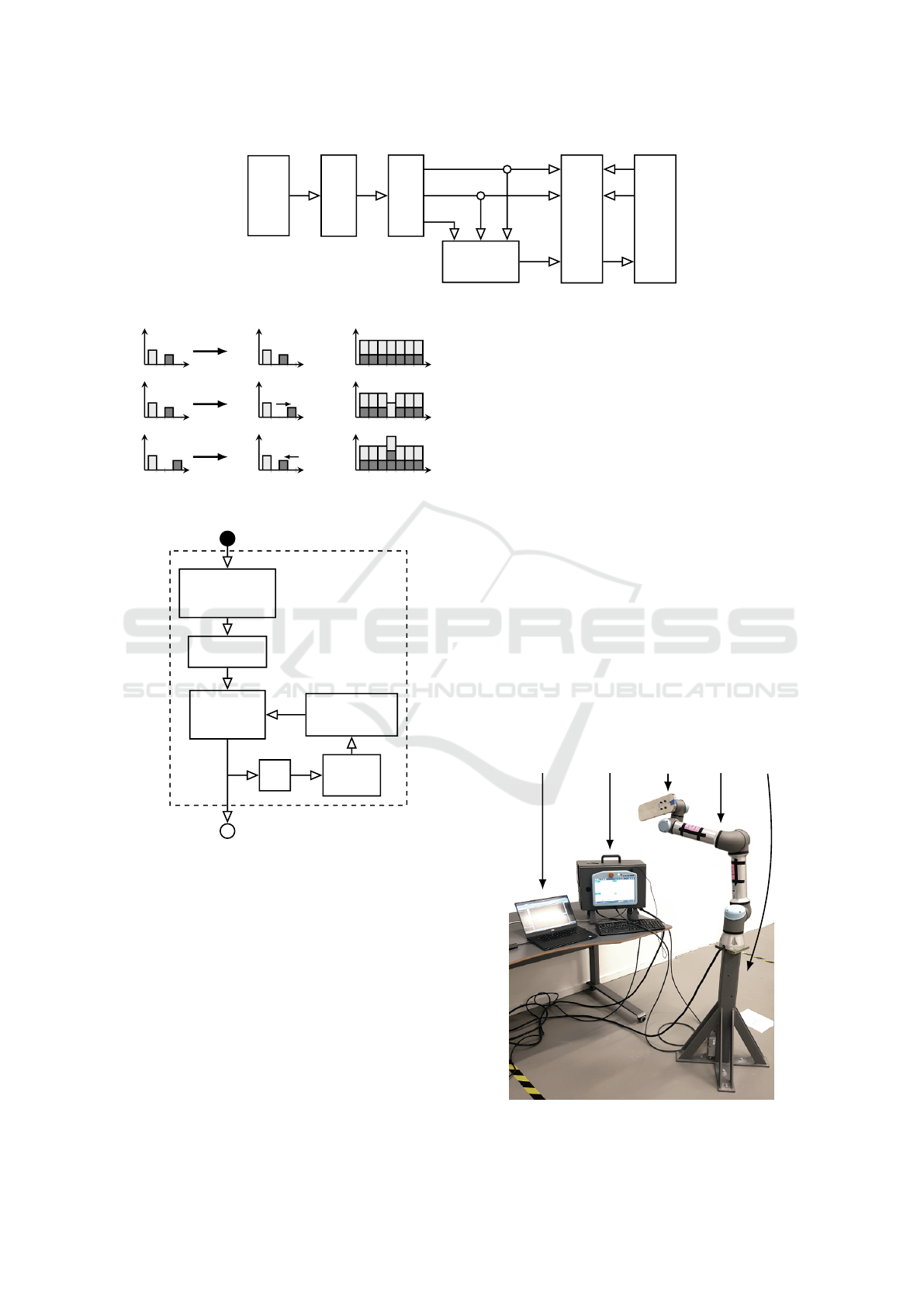
original control structure is illustrated in Figure 5. As il-

lustrated, a trajectory generator provides reference joint

positions,

, reference joint velocities,

, and reference

joint accelerations,

, to an inverse dynamic model,

which computes reference joint torques,

. Then

and

are provided to the joint controllers, which also

utilize sensor feedback about actual joint positions,

and actual joint velocities,

, to generate actual motor

voltages,

, which are applied in the joints. Thus

each joint controller should be seen as a feedforward-

feedback controller with 3 reference inputs, 2 feedback

measurements and 1 controller output.

Trajectory

generator

Inverse

dynamics

Joint

controllers

Electro-mechanical

dynamic system

Figure 5: Control structure of a UR robot.

By shaping

, and

simultaneously, it would be

possible to handle the multiple reference inputs in the

classic time-invariant shaper presented in

(8)

. However,

once introducing time-varying shaping, as presented in

(10)

, the relation between

and its derivatives becomes

non-linear.

Thus it is not an option to shape

, and

simulta-

neously using identical shapers. Others (Beazel, 2004;

Chatlatanagulchai et al., 2006) suggest averaging the

non-linear dynamics of the robot over the motion and

treat them like linear dynamics. Then

is shaped, and

weighted to ﬁt the linearized dynamics. Then

is de-

termined and integrated twice to obtain

and

. This

process requires that the analytic description of the

whole motion is known in advance, and that the motion

is completed before starting a new motion. Hence this

method does not suit a system with online trajectory

generation. Also, the method is computationally ex-

pensive because complex dynamic models need to be

evaluated.

Instead it is proposed to implement the method

in discrete time and to shape

while performing nu-

merical differentiation in order to obtain

and

, like

illustrated in Figure 6.

By implementing the TVIST ﬁlter as a discrete

time ﬁlter, the robot will be able to perform ﬁltering on

any trajectory, which can be generated online or even

provided by a 3

party PC or software, which sends

discrete reference commands to the robot.

3.2 TVIST in Discrete Time

When IS is implemented in discrete time, it is nec-

essary to use a discrete time impulse sequence,

I [i]

i.e. to discretize

from continuous time to discrete

time domain (Rappole, 1992; Murphy and Watanabe,

1992; Cole, 2011). The traditional method of imple-

menting IS in discrete time is to use a Finite Impulse

Response (FIR) ﬁlter to convolve the discrete time

reference signal

x [i]

with

I [i]

(Singer, 1989). However,

a major challenge in Discrete Time Time-Varying In-

put Shaping Technology (DT-TVIST) is that the FIR

convolution operation results in signiﬁcant defects in

∗

, when

is varying such that the position of an im-

pulse is moving from one discrete time step to another

(Magee and Book, 1992; Magee, 1996).

The discretization problem is illustrated in Figure 7.

Here it is seen how a change in

results in a time shift

of the second impulse. When the time shift becomes

large enough, the impulse will jump from one discrete

time step to the next, and this will cause defects in

the convolved signal (Murphy and Watanabe, 1992;

Magee, 1996).

In the proposed implementation, the described chal-

lenges are handled by maintaining a buffer of previous

ﬁlter inputs and perform an interpolation in order the

obtain an estimate of

x(t)

, as illustrated in Figure 8.

The ﬁgure illustrates that at time step

, the reference

command,

, is stored in a buffer of length

. An esti-

mate of

x(t)

is established through interpolation of the

buffered reference commands. Then

x(t)

is convolved

with the impulse sequence of current time step,

(

to compute the shaped reference command,

∗

(

established based on an estimate of

and

based on

the shaped reference command of the previous time

step, x

∗

i−1

, as described in section 3.3.

This type of convolution ﬁlter, which includes in-

terpolation of discrete reference commands, is called a

Fractional Delay Finite Impulse Response (FD-FIR) ﬁl-

ter (Laakso et al., 1996). The option to utilize FD-FIR

ﬁlters in IS has recently been presented and analyzed

(Thomsen et al., 2019).

3.3 Estimating Time-varying Dynamics

In order to validate the effect of the proposed TVIST

design, it is required to have a method of estimating

the robot dynamics, i.e.

(t)

and

ζ(t)

. This can be

achieved using different types of dynamic modeling

(Book, 1993; Chang and Park, 2005; Sayahkarajy et al.,

2016; Kivila, 2017), system identiﬁcation (Pham et al.,

2002; Khalil and Dombre, 2004), or lookup tables

(Hearne, 2009).

The most accurate estimate seems to be achieved

Experimental Implementation of Time-varying Input Shaping on UR Robots

491

Trajectory

generator

TVIST ﬁlter

Differentiator

Inverse

dynamics

Joint

controllers

Electro-mechanical

dynamic system

~q ~q

∗

Figure 6: Control structure of a UR robot with TVIST.

0 1 2 3

I[n]

0 1 2 3

I[n]

Constant

⇒

∗

[n]

0 1 2 3

I[n]

0 1 2 3

I[n]

Decrease

⇒

∗

[n]

0 1

2 3

I[n]

0 1 2 3

I[n]

Increase

⇒

∗

[n]

Figure 7: The discretization problem of TVIST.

Input buffer

i−M

··· x

]

Interpolation

Convolution

Estimated x(t)

Update

A(ζ) and

∆( f

)

Estimate

and ζ

(

∗

−1

∗

i−1

TVIST ﬁlter

Figure 8: UR TVIST ﬁlter design.

from a combination of dynamic modeling and sys-

tems identiﬁcation. However, a representative dynamic

model would need to include a large number of param-

eters in describing mechanical, electrical and software

non-linear dynamics.

Before engaging in developing such a complex and

computationally intensive estimator, it seems reason-

able to try a simple method and see, if this can provide

a useful estimate for the given application.

Thus, for this work it was decided to make a lookup

table based on measurements in multiple different

conﬁgurations over the workspace of the robot. This

lookup table was ﬁtted to two multi-variable polyno-

mials, which are evaluated to estimate

(~q(t))

and

ζ(~q(t)).

4 EXPERIMENT

To validate the performance of the proposed TVIST im-

plementation in UR robots, experiments are performed

on a UR5e robot. Section 4.1 presents the experimental

setup, section 4.2 presents the results of the experiment

together with the performance parameters of interest,

and section 4.3 presents a discussion on the results.

4.1 Experimental Setup

In the experimental setup, a UR5e robot is mounted on

a steel stand, which is deemed very rigid compared to

the ﬂexibility of the robot itself. A rigid steel payload

of 5kg is installed on the robot tool ﬂange. This corre-

sponds to the rated payload of the robot. The test setup

is illustrated in Figure 9.

5kg

payload

PC for data

logging

UR robot

controller

UR5e

robot

Steel

stand

Figure 9: Test setup with UR5e robot on stand.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

492

All test data is logged from the robot’s Real Time

Client (Universal Robots A/S Support, 2018) at 500Hz.

This includes reference joint positions,

, reference

joint accelerations,

, actual joint positions,

, and

tool accelerometer readings,

α .

It has been chosen to use a ZV shaper for evaluating

the performance of the proposed TVIST implementa-

tion. There are two reasons for this choice, 1) The ZV

shaper has a short time-delay, 2) The ZV is sensitive,

i.e. not robust, to errors in estimated

and

. Both of

these characteristics are seen as strengths, when it is

sought to validate the performance and applicability

of the method. In practice, it would probably make

sense to implement a Zero Vibration Derivative (ZVD)

shaper for increased robustness, but this depends on

the application.

Test motions are performed with and without shap-

ing for evaluating the TVIST method. Motions are

performed between conﬁgurations

, and

which are listed in Table 1.

Between these conﬁgurations, three different joint

space motions are used for evaluation, namely

→Q

, and

→Q

. Visualizations of these mo-

tions are presented in Figure 10 and Figure 11. The

conﬁgurations and motions are chosen such that the

→Q

motion will have non-varying dynamic prop-

erties, while

→Q

and

→Q

motions will have

varying dynamic properties.

Figure 10: Q

→ Q

motion.

By varying dynamic properties, it is understood

that

→Q

yields increasing

and decreasing

while

→Q

goes in the opposite direction and yields

decreasing

and increasing

. In the test motions, the

kinematic limitations of the double S velocity proﬁle

trajectory (Biagiotti and Melchiorri, 2008), is set as

max(

~q) = 1.5

rad/s,

max(

~q) = 2.0

rad/s

, and a jerk

time, i.e. acceleration ramp up time, of 20ms.

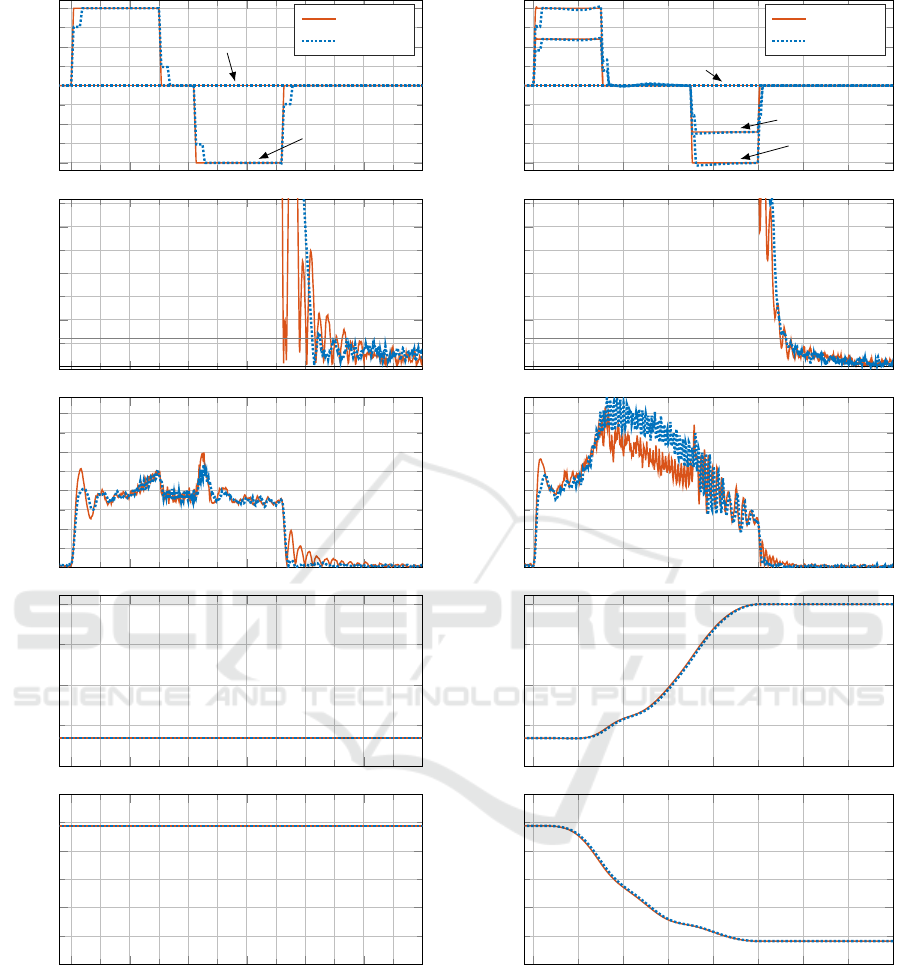
4.2 Experimental Results

The results of performing the three different motions

are presented in Figures 12-14. Here it has been chosen

to present shaped reference accelerations

(

∗

(t))

, Carte-

sian distance to attained position (

), tool accelerome-

ter amplitude (

α|

), estimated damped frequency in Hz

( f

), and estimated damping ratio (ζ).

Figure 11: Q

→ Q

motion.

is interesting because it is used to determine a set

of key performance parameters in (ISO 9283, 1998),

such as stabilization time (

stb

) and overshoot (

The attained position is the actual Tool Center Point

(TCP) position after the motion has ﬁnished, and after

the position has been stabilized.

is deﬁned as the

Cartesian distance from actual TCP position to the

attained position. Actual TCP position should ideally

be measured by external 3D tracking equipment. How-

ever, for the scope of this paper, which is to determine

the relative impact of TVIST on mechanical vibrations,

it has been chosen to use

and perform a calibrated

forward kinematics to determine actual TCP position.

This makes it possible to obtain all data from the robot

itself.

In this work, three performance parameters are

established based on

, namely

stb

, and

cycle

. The

deﬁnition of these parameters will be given here.

In this work, cycle time,

cycle

, denotes the time

span from when the reference motion starts, until the

last time, where

takes value higher than the repeata-

bility of the robot. For the UR5e robot, the repeatability

is speciﬁed as 0.03mm. The stabilization time,

stb

is the time span from the ﬁrst time, where

takes

value lower then the repeatability of the robot (

enter

until

cycle

(ISO 9283, 1998). The overshoot,

, is the

maximum value of

after

enter

(ISO 9283, 1998). If

this value is lower than the repeatability, the overshoot

is 0. Another metric of interest is the shaper delay

(

∆

stb

enter

, and

cycle

are all illustrated in

Figure 15, and the actual values for the test motions

are listed in Table 2. Here the listed values are average

values from 10 runs of the test motions.

Experimental Implementation of Time-varying Input Shaping on UR Robots

493

Table 1: Listed test conﬁgurations.

Conf. q

(rad) q

(rad) f

(Hz) ζ (-)

0 −π 0 −π/2 0 0 6.7 0.34

π/2 −π 0 −π/2 0 0 6.7 0.34

π/2 −π/2 5π/6 −π/2 0 0 15.0 0.14

Table 2: Performance evaluation of TVIST, average of 10 repetitions.

Delay (ms) Stabil. Time (ms) Cycle Time (ms) Overshoot (m) Res. Vibration (m/s

)

∆

stb

cycle

→ Q

Unshaped 0 548.8 2368.9 5.5E-04 1.11

Shaped 74.1 167.0 2229.5 3.1E-05 0.13

Impact - -69.6% -5.9% -94.3% -88.6%

→ Q

Unshaped 0 70.8 2821.4 3.7E-05 0.80

Shaped 33.6 7.2 2820.4 1.0E-05 0.17

Impact - -89.8% 0.0% -72.4% -78.5%

→ Q

Unshaped 0 1049.2 3707.8 1.3E-04 1.14

Shaped 74.2 816.7 3596.0 6.4E-05 0.22

Impact - -22.2% -3.0% -50.3% -80.8%

The UR5e robot has an accelerometer in the tool

ﬂange. Analyzing the measured accelerations is consid-

ered the most reliable way of quantifying the amount

of residual vibrations in of the motion without using

external 3D tracking equipment. When determining

the amount of residual vibration, the amplitude of the

total acceleration

α|

with gravity compensation is con-

sidered. Then the amount of Residual Vibration (RV)

is found by identifying the peaks of the acceleration

signal and ﬁtting them to an exponential decay. RV

is the amplitude of the ﬁtted curve at the time, where

the reference motion stops (Kozak et al., 2006). RV is

also listed in Table 2. Figure 16 is introduced for easy

comparison of |

α| with and without IS.

4.3 Discussion on Results

From the

→Q

motion presented in Figure 12 it

is seen that the estimated dynamics are constant at

= 6.7Hz

and

ζ = 0.34

during the motion. It is seen

from

α|

that mechanical vibrations are present dur-

ing and after the unshaped motion. When comparing

with the shaped motion, it is seen, how oscillations

are clearly reduced during the motion, while residual

vibrations are practically eliminated. It appears that IS

is performing well, but there are other contributions

to mechanical vibrations, which can not be eliminated

by IS. This is believed to be a result of mechanical

imperfections, such as kinematic error in the gears

(Tuttle, 1992) and bearing imperfections.

The same tendency for residual vibration is seen

for

. When comparing the shaped and unshaped

motions, it may be noticed how the introduced de-

lay seems to pay off well, as the TCP comes to rest

faster than originally. The promising results for the

→Q

motion tells us that IS can provide effective

vibration suppression in the system, when dynamics

are invariant.

By inspecting the

→Q

motion in Figure 13

and

→Q

in Figure 14. It is found that effective

vibration suppression is also possible, when

and

vary over time. These are really good results, especially

since the TVIST is implemented with the simple ZV

shaper. Achieving good vibration suppression using a

time-invariant robust shaper would require two or three

times more delay and would not give as good results.

is varying between 15Hz and 6.7Hz, while

varies

between 0.14 and 0.34. This huge span would not be

possible to cover appropriately with one robust shaper.

Table 2 lists the performance metrics for the shaped

and unshaped motions, as well as the relative impact

from shaping. Here, it is seen that

stb

, and residual

vibration are reduced for all three test motions. This

was also expected from introducing IS. However, it

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

494

−2

−1

¨q

, ¨q

~q (rad/s

)

Unshaped

Shaped

0.5

1.5

·10

−4

E (m)

α| (m/s

)

Estimated f

(Hz)

0.5

1.5

2.5

0.1

0.2

0.3

0.4

Time (s)

Estimated ζ (-)

Figure 12: Recorded data from Q

→ Q

motion.

is impressive to see, that the absolute reduction in

stabilization time is larger, than the introduced time

delay, meaning that the total cycle time can be reduced

by up to 5.9%. In other words, the productivity of the

robot can be increased by up to 6.3%.

−2

−1

¨q

, ¨q

¨q

, ¨q

~q (rad/s

)

Unshaped

Shaped

0.5

1.5

·10

−4

E (m)

α| (m/s

)

Estimated f

(Hz)

0 1 2 3 4

0.1

0.2

0.3

0.4

Time (s)

Estimated ζ (-)

Figure 13: Recorded data from Q

→ Q

motion.

5 CONCLUSIONS

In this paper, a need for efﬁcient vibration reduction

methods in light weight robots has been identiﬁed.

It was found that Input Shaping (IS) had great po-

tential, but lacked on the ability to handle the time-

varying dynamics of industrial robots with the serial

Experimental Implementation of Time-varying Input Shaping on UR Robots

495

−2

−1

¨q

, ¨q

¨q

, ¨q

~q (rad/s

)

Unshaped

Shaped

0.5

1.5

·10

−4

E (m)

α| (m/s

)

Estimated f

(Hz)

0 1 2 3 4

0.1

0.2

0.3

0.4

Time (s)

Estimated ζ (-)

Figure 14: Recorded data from Q

→ Q

motion.

link conﬁguration. IS has previously been extended

to Time-Varying Input Shaping Technology (TVIST),

for dealing with time varying dynamics. This paper

focuses on the strategy of implementing TVIST on

a UR5e robot from Universal Robots A/S (UR). It

was found that it is necessary to change its present for-

mulation to implement TVIST on an industrial robot

manipulator.

stb

Limit

Time, t

Distance from attained position, E

∗

cycle

∗

enter

∆

Figure 15: Visualization of delay (

∆

), stabilization time

stb

), cycle time (t

cycle

), and overshoot (e

1.8 2 2.2 2.4

2.6

0.5

1.5

RV: 1.16 m/s

RV: 0.09 m/s

α| (m/s

)

→ Q

Unshaped

Shaped

∗

2.6

2.8 3 3.2

0.5

RV: 0.78 m/s

RV: 0.22 m/s

α| (m/s

)

→ Q

∗

2.6

2.8 3 3.2

0.5

1.5

RV: 1.15 m/s

RV: 0.17 m/s

Time (s)

α| (m/s

)

→ Q

∗

Figure 16: Tool accelerometer amplitude.

We proposed a new and practical implementation

strategy of TVIST on a UR robot. The new implemen-

tation of TVIST is a discrete time ﬁlter that performs

IS in a reference position signal and numerically dif-

ferentiates the shaped position reference in order to

obtain shaped reference velocity and acceleration be-

fore performing inverse dynamics to compute shaped

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

496

reference torques. Experiments are conducted on a

UR5e robot with the proposed TVIST implementation

to validate its effectiveness.

Preliminary experimental results demonstrate that

the new TVIST implementation yields effective vibra-

tion suppression in the UR5e robot, and reduces the

residual vibrations by 78.5-88.6% in the tested cases.

In addition, experimental results show that it is possible

to increase the productivity of the robot by up to 6.3%

because the stabilization time is signiﬁcantly reduced

through the proposed TVIST implementation strategy.

We can conclude that the proposed method facili-

tates practical implementation of TVIST for vibration

suppression on commercial industrial robots that has

online trajectory generation and position control with

feed-forward velocity and torque.

ACKNOWLEDGEMENTS

This work was supported by Universal Robots A/S

and Innovation Fund Denmark, through the Industrial

PhD program. We wish to thank Anders Skovgaard

Knudsen from Universal Robots A/S for his valuable

help in proofreading.

REFERENCES

Beazel, V. M. (2004). Command shaping applied to nonlin-

ear systems with conﬁguration-dependent resonance.

PhD thesis, Purdue University.

Biagiotti, L. and Melchiorri, C. (2008). Trajectory Planning

for Automatic Machines and Robots. Springer-Verlag

Berlin Heidelberg.

Book, W. (1993). Controlled motion in an elastic world.

Journal of Dynamic Systems, Measurement and Control,

Transactions of the ASME, 115(2B):252–261.

Chang, P. H. and Park, H.-S. (2005). Time-varying input

shaping technique applied to vibration reduction of

an industrial robot. Control Engineering Practice,

13(1):121 – 130.

Chatlatanagulchai, W., Beazel, V. M., and Meckl, P. H.

(2006). Command shaping applied to a ﬂexible robot

with conﬁguration-dependent resonance. In 2006 Amer-

ican Control Conference.

Cho, J.-K. and Park, Y.-S. (1995). Vibration reduction in

ﬂexible systems using a time-varying impulse sequence.

Robotica, 13(3):305–313.

Cole, M. O. (2011). A discrete-time approach to impulse-

based adaptive input shaping for motion control without

residual vibration. Automatica, 47(11):2504 – 2510.

Hearne, J. (2009). Posture dependent vibration resistance of

serial robot manipulators to applied oscillating loads.

Master’s thesis, University of Waterloo.

ISO 9283 (1998). Manipulating industrial robots - perfor-

mance criteria and related test methods.

Khalil, W. and Dombre, E. (2004). Modeling Identiﬁcation

and Control of Robots. Butterworth-Heinemann.

Kim, J. and Croft, E. A. (2018). Preshaping input trajectories

of industrial robots for vibration suppression. Robotics

and Computer-Integrated Manufacturing, 54:35 – 44.

Kivila, A. (2017). Modeling, estimation and control for

serial ﬂexible robot arms. PhD thesis, Georgia Institute

of Technology.

Kozak, K., Singhose, W., and Ebert-Uphoff, I. (2006). Per-

formance measures for input shaping and command

generation. Journal of Dynamic Systems, Measurement

and Control, Transactions of the ASME, 128(3):731–

736.

Laakso, T. I., Valimaki, V., Karjalainen, M., and Laine, U. K.

(1996). Splitting the unit delay - tools for the fractional

delay ﬁlter design. IEEE Signal Processing Magazine,

13(1):30–60.

Magee, D. P. (1996). Optimal arbitrary time-delay ﬁltering

to minimize vibration in elastic manipulator systems.

PhD thesis.

Magee, D. P. and Book, W. J. (1992). The application

of input shaping to a system with varying parameters.

In Japan/USA Symposium on Flexible Automation,

volume 1, pages 519–526.

Murphy, B. R. and Watanabe, I. (1992). Digital shaping ﬁl-

ters for reducing machine vibration. IEEE Transactions

on Robotics and Automation, 8(2):285–289.

Pham, M. T., Gautier, M., and Poignet, P. (2002). Ac-

celerometer based identiﬁcation of mechanical systems.

In Proceedings 2002 IEEE International Conference

on Robotics and Automation (Cat. No.02CH37292),

volume 4, pages 4293–4298 vol.4.

Rappole, B. W. (1992). Minimizing residual vibrations

in ﬂexible systems. Master’s thesis, MIT Artiﬁcial

Intelligence Laboratory.

Sayahkarajy, M., Mohamed, Z., and Faudzi, A. A. M. (2016).

Review of modelling and control of ﬂexible-link manip-

ulators. Proceedings of the Institution of Mechanical

Engineers, Part I: Journal of Systems and Control

Engineering, 230(8):861–873.

Singer, N. C. (1989). Residual vibration reduction in com-

puter controlled machines. PhD thesis, Massachusetts

Institute of Technology. Dept. of Mechanical Engineer-

ing.

Singer, N. C. and Seering, W. P. (1990). Preshaping

command inputs to reduce system vibration. Jour-

nal of Dynamic Systems, Measurement, and Control,

112(1):76–82.

Singh, T. and Vadali, S. (1993). Robust time-delay control.

Journal of dynamic systems, measurement, and control,

115(2A):303–306.

Thomsen, D. K., Søe-Knudsen, R., Brandt, D., Balling, O.,

and Zhang, X. (2018). Generating vibration free rest-to-

rest trajectories for conﬁguration dependent dynamic

systems via 3-segmented input shaping. In IEEE

International Conference on Robotics and Automation.

Thomsen, D. K., Søe-Knudsen, R., Brandt, D., Balling, O.,

and Zhang, X. (2019). Smooth online time-varying in-

put shaping with fractional delay FIR ﬁltering. Control

Engineering Practice, 88:21–37.

Experimental Implementation of Time-varying Input Shaping on UR Robots

497

Tuttle, T. D. (1992). Understanding and modeling the behav-

ior of a harmonic drive gear transmission. Technical

report, Massachusetts Inst of Tech Cambridge Artiﬁcial

Intelligence Lab.

Universal Robots A/S Support (2018). Overview of

client interfaces. Last accessed: 16/04/2018. URL:

https://www.universal-robots.com/how-tos-and-

faqs/how-to/ur-how-tos/overview-of-client-interfaces-

21744/.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

498