BEARZ Attack FALCON: Implementation Attacks with Countermeasures

on the FALCON Signature Scheme

Sarah McCarthy

, James Howe

2,†

, Neil Smyth

3,‡

, Séamus Brannigan

and Máire O’Neill

Centre for Secure Information Technologies (CSIT), Queen’s University Belfast, U.K.

PQShield Ltd., Oxford, U.K.

Allstate NI, Belfast, U.K.

Keywords:

Lattice-based Cryptography, Fault Attacks, FALCON, Digital Signatures, Post-quantum Cryptography,

BEARZ, Countermeasures.

Abstract:

Post-quantum cryptography is an important and growing area of research due to the threat of quantum comput-

ers, as recognised by the National Institute of Standards and Technology (NIST) recent call for standardisation.

FALCON is a lattice-based signature candidate submitted to NIST, which has good performance but lacks in

research with respect to implementation attacks and resistance. This research proposes the ﬁrst fault attack

analysis of FALCON and ﬁnds its lattice trapdoor sampler is as vulnerable to fault attacks as the GPV sampler

used in alternative signature schemes. We simulate the post-processing component of this fault attack and

achieve a 100% success rate at retrieving the private-key. This research then proposes an evaluation of coun-

termeasures to prevent this fault attack and timing attacks of FALCON. We provide cost evaluations on the

overheads of the proposed countermeasures which shows that FALCON has only up to 30% deterioration in

performance of its key generation, and only 5% in signing, compared to runtimes without countermeasures.

1 INTRODUCTION

Digital signature schemes are an important crypto-

graphic primitive, used for data authentication, in-

tegrity, and non-repudiation across the Internet and

in secure computer systems. However, the discov-

ery of Shor’s algorithm (Shor, 1999) has the potential

to break all currently used signature schemes, such

as ECDSA. This threat has led to a new era of cryp-

tography which is built to withstand quantum com-

puting attacks, known as post-quantum, or quantum-

safe, cryptography. This threat has also prompted a

standardisation effort by NIST (2016a) through their

call for quantum-safe primitives. One of the most

promising types of post-quantum solutions is lattice-

based cryptography, which makes up almost half of

the round 2 candidates. Many problems based on

lattice assumptions provide the appealing property

of worst-case to average-case hardness (Ajtai and

Dwork, 1997) and lattices have yet to be hindered by

†

Most of this research was completed while the author was

at the University of Bristol.

‡

Most of this research was completed while the author was

at the Centre for Secure Information Technologies (CSIT),

Queen’s University Belfast.

a serious cryptanalytic break. They also beneﬁt from

extended functionality, with primitives such as fully-

homomorphic encryption (Gentry and Boneh, 2009)

and identity-based encryption (Ducas et al., 2014).

This research focuses on lattice-based signatures,

which have been shown to perform well in com-

parison to classical signature schemes (Howe et al.,

2015). They also have relatively small key sizes, offer

cryptographic agility, and most importantly offer pro-

tection from quantum attacks. There are three lattice-

based signatures in round 2 of the NIST standardisa-

tion process, and we analyse the performance and at-

tack resistance of one of these, FALCON (Prest et al.,

2017).

Despite being resistant to quantum computing at-

tacks, lattice-based cryptographic schemes are sus-

ceptible to the same side-channel attacks as alterna-

tive primitives used today, as summarised by Hodgers

et al. (2016) and Khalid et al. (2018). Thus, consider-

ing attacks and possible countermeasures is important

during standardisation and implementation. This re-

search focuses on countermeasures of types of attack

that have been considered to date for lattice-based

signatures, namely timing and fault analysis attacks.

Examples of these types of attacks and countermea-

McCarthy, S., Howe, J., Smyth, N., Brannigan, S. and O’Neill, M.

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme.

DOI: 10.5220/0007834800610071

In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 61-71

ISBN: 978-989-758-378-0

sures are given in (Roy et al., 2014; Bruinderink et al.,

2016; Howe et al., 2016; Espitau et al., 2016; Bindel

et al., 2016; Karmakar et al., 2018).

This research considers timing and fault attacks

and countermeasures of the lattice-based signature

FALCON, including the ﬁrst fault attack on the

scheme. This is an important contribution to the NIST

standardisation effort, as NIST (2016b) have stressed

for the need for side-channel analysis (SCA) and ef-

ﬁcient countermeasures. In NIST’s report on the sec-

ond round candidates (Alagic et al., 2019), their com-

ments for FALCON were that “more work is needed

to ensure that the signing algorithm is secure against

side-channel attacks” and this is the gap we hope to

address in this paper. We review existing implemen-

tation attacks, propose the ﬁrst fault attack on FAL-

CON, and implement the signature scheme with ap-

propriate countermeasures in place. The impact on

performance with these countermeasures is thus also

provided. The proposed attack, BEARZ, is a modiﬁ-

cation of the attack on the DLP (Ducas et al., 2014)

hash-and-sign scheme by Espitau et al. (Espitau et al.,

2016) (Espitau et al., 2018). The origins of FALCON

are somewhat based on DLP, but it employs a novel

recursive form of the GPV sampler in the FFT do-

main. We ﬁnd that the FALCON sampler is still vul-

nerable to fault attacks and we are able to retrieve the

private-key; however we show that it still performs

competitively with countermeasures in place, incur-

ring only a 5% decrease in performance. The zero-

check countermeasure is effective against the pro-

posed fault attack, and causes a 16% decrease in per-

formance on the high security parameter set. Fur-

thermore, we compare our results to those of signa-

ture schemes Dilithium (Lyubashevsky et al., 2017)

and BLISS-B (Ducas, 2014) with similar countermea-

sures applied.

The contributions of this paper are as follows:

• The ﬁrst fault attack on FALCON using a Ba-

sis Extraction by Aborting Recursion or Zeroing

(BEARZ) technique.

• Novel portable ANSI C design of FALCON, with

competitive performance (as part of libSAFE-

crypto

). Features include constant-time compo-

nents and use of the CDT (Gaussian) sampler.

• The ﬁrst proposed design of FALCON with coun-

termeasures against known side-channel attacks.

• A thorough overhead bench marking and com-

parison of FALCON with alternative state of the

art signature schemes incorporating side-channel

countermeasures.

https://github.com/safecrypto/libsafecrypto

The structure of the paper is as follows. Section 2 in-

troduces lattice-based cryptography and describes the

signature schemes discussed in this research. Section

3 outlines timing attacks on FALCON and proposed

countermeasures. Section 4 presents the ﬁrst fault at-

tack on FALCON, followed by appropriate counter-

measures to prevent this attack. Section 5 presents

performance ﬁgures for our software implementa-

tions of the signature scheme, with and without attack

countermeasures, followed by evaluations. The paper

is then concluded in Section 6.

2 LATTICE-BASED DIGITAL

SIGNATURE SCHEMES

This section describes preliminaries on lattice-based

cryptography and introduces the FALCON signature

scheme (Prest et al., 2017) and its relation to the DLP

IBE (Ducas et al., 2014) scheme.

2.1 Preliminaries

Lattices are speciﬁed by a collection of vectors,

, which form their basis, B, which can be de-

ﬁned as: L(B) =

{

∑

∈ Z, x

∈ B,1 ≤i ≤ n

}

Computationally hard lattice problems, such as the

Shortest Vector Problem (SVP), Short Integer Solu-

tion (SIS), and Learning With Errors (LWE) (Regev,

2005, 2009) can form security assumptions for cryp-

tographic primitives. In this research, we examine

schemes which use module or ideal lattices, which

progressively add more structure to the basis. The

hardness assumption of FALCON’s key generation is

based on a variant of the NTRU problem, which states

that, given polynomial ring element A = g · f

−1

, it is

difﬁcult to recover f and g. The hardness of the sign-

ing procedure depends on the SVP, which states that

if we are given the public basis of the lattice, it is a

hard to ﬁnd a short vector in the lattice.

We denote by N the dimension of the ring, q the

modulus, and we operate in the polynomial ring R

[x]/(x

+1). The elements in R

can be represented

as polynomials of degree N or vectors of dimension

N. These parameters for FALCON are given in Table

1, as well as the (equivalent) security levels of each

parameter set.

2.2 The FALCON Signature Scheme

The FALCON signature scheme was proposed by Prest

et al. (Prest et al., 2017). Its notable character-

istics are that it is a hash-and-sign type signature

SECRYPT 2019 - 16th International Conference on Security and Cryptography

Table 1: The proposed parameters (Prest et al., 2017) for the FALCON signature scheme.

Parameter NIST Security Dimension Modulus

Set Level Level (N) (q)

Set 1 Level 1 AES128 512 12289

Set 2

Level 4 SHA384 1024 12289

Level 5 AES256 1024 12289

scheme (in contrast to Dilithium, a Fiat-Shamir sig-

nature scheme) and is secure in the random oracle

model. It is based on the DLP identity-based en-

cryption scheme proposed by Ducas et al. (2014),

together with fast Fourier sampling techniques pro-

posed Ducas and Prest (2016). These techniques im-

prove the compactness of the private key and speed of

the sampling procedure. The key generation process,

shown in Algorithm 1, produces NTRU polynomials,

where f and g become the private keys, and h = g f

−1

is the public key. For the signing process, shown in

Algorithm 2, the f f Sampling algorithm (Algorithm

3) ﬁnds a short vector in the NTRU lattice, using the

private key. The public key is used to verify the sig-

nature by checking the modulus lies beneath the re-

quired bound β in the veriﬁcation algorithm, given in

Algorithm 4.

2.3 The DLP Signature Scheme

Espitau et al. (2016, 2018) present an attack on the

GPV-based DLP hash-and-sign signature scheme. In

their fault model, the attacker is able to abort a loop

early in the GPV Gaussian lattice-sampling stage in

the signing algorithm. Whilst sampling vector coef-

ﬁcients of a signature polynomial of degree 2n, they

force the process to terminate at some iteration m ≤n,

and obtain a faulty signature in the sub-lattice of rank

m. After producing around m + 3 faulty signatures,

they can generate the original lattice and recover a

short vector with probability 86%, thereby recovering

enough of the NTRU lattice structure to obtain the pri-

vate key. Espitau et al. recommend checking the va-

lidity of the DLP signature before sending, by running

the veriﬁcation algorithm. In Section 4, we construct

a variant of this attack which targets the FALCON sig-

nature scheme.

3 TIMING ATTACKS ON

FALCON

3.1 Gaussian Sampler

Gaussian samplers are used in FALCON to sam-

ple short lattice vectors. Generally in lattice-based

Algorithm 1: FALCON key generation (adapted

from (Prest et al., 2017)).

Data: N,q

Result: B ∈ Z

2N×2N

, h ∈ R

1 σ

= 1.17

2 f ,g,← D

N,σ

3 Norm

← max



||g,−f ||,





f ∗

f +g∗¯g

q ¯g

f ∗

f +g∗¯g







4 if Norm > 1.17

√

q then go to Step 2;

5 Compute ρ

,ρ

∈ R and R

∈ Z such

that: ρ

· f = R

and ρ

·g = R

6 if GC D(R

) 6= 1 or GCD(R

,q) 6= 1 then

go to Step 2;

7 Compute u,v ∈ Z such that:

u ·R

+ v ·R

= 1

8 F ← qvρ

and Q ← −quρ

9 k =

F∗

f +G∗¯g

f ∗

f +g∗¯g

∈ R

10 F ← F −k ∗ f and G ← G −k ∗g

11 h = g ∗ f

−1

mod q

12 B =



g −f

G −F



B =



FFT (g) −F FT ( f )

FFT (G) −FFT (F)



14 T=ffLDL*(G)

15 σ ← 1.55

√

16 for each leaf of T, leaf.value = σ/

√

leaf.value

17 sk ← (

B,T),pk = h

18 return sk, pk

cryptography, Gaussian samplers are known to be vul-

nerable to timing analysis attacks and constant-time

samplers can be expensive. Bruinderink et al. (Bruin-

derink et al., 2016) proposed the ﬁrst timing attack on

a lattice-based signature scheme, BLISS, and recov-

ered the private key by targeting the scheme’s Gaus-

sian sampler. Because of this, there has been signif-

icant research on designing the Gaussian sampler to

operate in independent time (Saarinen, 2015; Khalid

et al., 2016; Howe et al., 2016; Micciancio and Wal-

ter, 2017).

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme

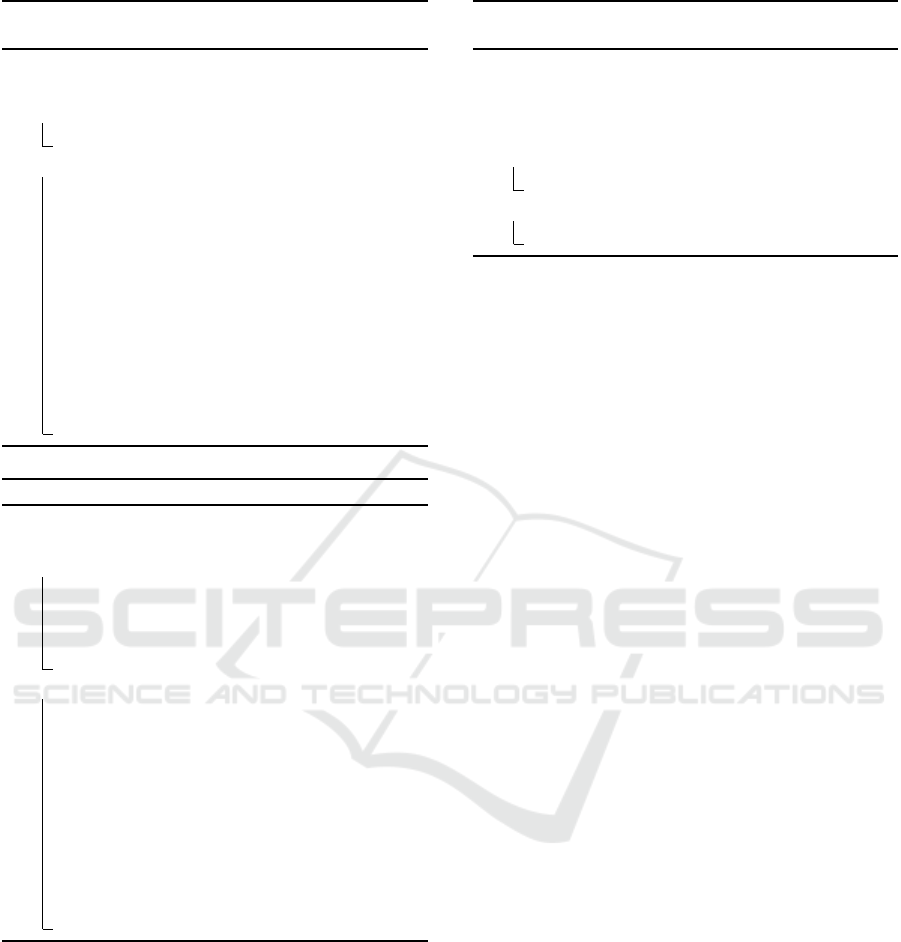
Algorithm 2: FALCON signing (adapted from (Prest

et al., 2017)).

Data: sk, H : {0, 1}

∗

→ Z

, m, β

Result: SIG

1 if SK

is in local storage then

2 return Output SIG

to message m

3 else

4 r ← Unif({0,1}

320

)

5 c ← H(r||m) ;

6 t ← (FFT (c),FFT (0)) ·

−1

z ← ffSampling(t,T )

7 s = (t −z)

8 while ||s|| > β

9 (s

) ← invFFT (s)

10 s

= Compress(s

)

11 SIG

← (r,s

)

12 return Output SIG

associated to

message m and keep in local storage

Algorithm 3: ffSampling (Prest et al., 2017).

Data: t = (t

) in FFT format , T

Result: z = (z

) in FFT format

1 if n = 1 then

2 σ

← T.value

3 z

← D

Z,t

,σ

4 z

← D

Z,t

,σ

5 return z = (z

)

6 else

7 (l, T

) ←

(T.value,T.leftchild,T.rightchild)

8 t

← splitfft(t

)

9 z

← ffSampling(t

)

10 z

← mergefft(z

)

11 t

←t

+ (t

−z

) ·l

12 t

← splitfft(t

)

13 z

← ffSampling(t

)

14 z

← mergefft(z

)

15 return z = (z

)

3.2 Number Theoretic Transform

The NTT is commonly used in lattice-based cryptog-

raphy, such as FALCON, to speed up multiplication

of ring polynomials. However, it involves a lot of

modular arithmetic, which is difﬁcult to implement

in constant-time, as described by Scott (2017), and

so is a potential risk. There has also been signiﬁ-

cant research on attacking the NTT, as well as making

the module run in constant-time (Longa and Naehrig,

2016; Alkim et al., 2016; Primas, 2017).

Algorithm 4: FALCON verifying (adapted from

(Prest et al., 2017)).

Data: pk = h ∈ R

, (SIG

,m), β

Result: Accept or Reject

1 c ← H(r||m)

2 s

= Decompress(s

),s

← c −s

h mod q

3 if ||(s

)|| < β and H(r||m) = c then

4 return Accept

5 else

6 return Reject

3.3 HashtoPoint

The HashtoPoint function hashes the message to a

point in the polynomial ring. The authors of FALCON

note that this “may be difﬁcult to efﬁciently imple-

ment in a constant-time way”. If the message is to be

kept secret, this could pose a problem.

3.4 Proposed Countermeasures to

Timing Attacks

We now discuss existing countermeasures in the liter-

ature which we incorporate into our FALCON imple-

mentation, as well as novel designs of constant-time

components.

Roy et al. (2014) introduced shufﬂing of the

Gaussian-distributed vector as a countermeasure to

timing attacks, which was also extended by Howe

et al. (2016). The Fisher-Yates shufﬂing algorithm

(Fisher et al., 1938) is typically used to effectively

randomly permute these vector coefﬁcients. How-

ever, Pessl (2016) suggested that this countermea-

sure is not sufﬁcient on its own. The BlindVector al-

gorithm introduced by Saarinen (2017) extended the

use of the Fisher-Yates shufﬂing procedure to en-

hance random shufﬂes for side-channel protection.

We utilise this algorithm and ensure a constant-time

implementation to further increase the attack com-

plexity. The algorithmic loops are not data dependent

and the operations are such that regardless of whether

a value is swapped or not they are always performed.

We introduce sample discard, the process whereby

extra cache reads from random addresses are per-

formed, in an attempt to distort statistics used in SCA.

These extra reads are then thrown away. In this imple-

mentation, where it has been added as an extra pre-

ventative layer, we have used a range of discard rates

at 6.25%, 12.5%, and 25%.

Our designs use a novel, efﬁcient constant-time

design of the CDT Gaussian sampling technique as

this is much more simple to adapt for multiple param-

eter sets than other contenders. An exact number of

SECRYPT 2019 - 16th International Conference on Security and Cryptography

look-up reads are performed each time, with the com-

parison being computed using arithmetic logic using

the same operations regardless of the branch which

we want to take according to the CDT algorithm. The

upper bound for the number of look-ups required is

dlog

Ne and so each call of the sampler is padded out

to the nearest power-of-two to take this same amount

of clock cycles. For the required values of the stan-

dard deviation, this CDT sampler gives better per-

formance than the Knuth-Yao, discrete Ziggurat, and

Bernoulli samplers when operated in constant-time.

The NTT and FFT functions are also made

constant-time in our designs. The modular reduction

part of NTT can leak timing information (Scott, 2017)

and so our implementation is made constant-time by

avoiding branch operations at the cost of some per-

formance. This is done by processing all required

branch variables and eschewing logic for more time

consuming arithmetic operations. Performance is in-

creased by employing lazy reduction to reduce the

number of modular reductions that occur and using

SIMD vectorisation. Point-wise modulo multiplica-

tion computes each element independently, allowing

a multiplication of two polynomial rings in the NTT

domain. As the operations are sequential and uncon-

ditional, it is constant-time.

The transform routinely utilises the Cooley-Tukey

NTT algorithm with some small optimisations de-

signed to increase performance, enable automatic

vectorisation, and ensures that no conditional branch

operations are used. The inverse NTT operation is

the mirrored operation of the forward NTT, but ad-

ditionally requires shufﬂing of the output coefﬁcients

and the use of both forward and inverse roots of unity

coefﬁcient tables. Automatic vectorisation of the ﬁ-

nal shufﬂe of the inverse NTT was not possible as

the loop conditions were considered too complex and

therefore it is performed separately to the modular re-

duction in order to improve performance. Our mod-

ular reduction design is a simpliﬁed range restriction

that avoids the use of logical operations and instead

opts to use arithmetic operations, in particular the

constant time less than comparison function.

4 BEARZ ATTACK FALCON

This section proposes a new fault attack on the FAL-

CON digital signature scheme, which uses Basis Ex-

traction by Aborting Recursion or Zeroing, named

BEARZ. The attack exerts and then exploits faults in

the FALCON signature scheme in order to learn pri-

vate key information, following a similar attack used

on DLP. We utilise a different attack model, assuming

that the attacker is able to skip instructions and to zero

variables as assumed by Bindel et al. (2016, 2017).

The original attack is on the GPV sampling compo-

nent in DLP, however there are two major differences

between this sampler and the FALCON sampler: re-

cursion and FFT domain.

4.1 DLP Attack

We begin with a recap of the attack on DLP by Es-

pitau et al. (2016). In the GPV lattice trapdoor sam-

pler, coefﬁcients of the n-dimensional vectors (R,r)

are sampled in a 2n-length loop in reverse, from the

last coefﬁcient r

to the ﬁrst coefﬁcient R

. This is

converted to a short Gaussian-distributed lattice vec-

tor by multiplying the vector (R,r) by the basis:

B =



A(g) −A( f )

A(G) −A(F)



where A(F) is the anti-circulant matrix associated

with the degree-n polynomial, F. We are con-

cerned with second half of the signature, denoted

= (R, r) (−A( f ),−A(F)) = R. f + r.F, which is a

2n-dimensional vector.

The fault attack is a loop abort on the 2n-loop

which samples the (R, r) coefﬁcients. It causes

the loop to abort at the m

iteration, where m ≤

n. This effectively eradicates the vector R, so s

becomes: s

= (0,.. .,0,r

,.. .,r

m−n

)F, or alterna-

tively the polynomial s

= r

n−1

F + r

n−2

F + ···+

m−1

n−m

F, which is in the sub-lattice of L(A(F)).

With a certain number of faulty signatures, l ≈m, one

will obtain a set spanning the lattice. From this, lat-

tice reduction can be used to ﬁnd a short vector, which

should be one of the signed shifts of F, from which

the private basis can be recovered. We now propose a

similar attack which works for FALCON.

4.2 Recursion of FALCON

The FALCON sampling algorithm, shown in Algo-

rithm 3, can be viewed as a recursive form of the GPV

sampler. We change the attack notation to match that

in FALCON’s speciﬁcations (Prest et al., 2017), where

(R,r) in the DLP scheme becomes z = (z

). The

DLP attack inserts a loop abort fault at some itera-

tion, m, of the 2n loop (Espitau et al., 2016, Fig. 2),

however in FALCON this translates to aborting the re-

cursive call early (Prest et al., 2017, Alg. 18). To do

this, we need to examine the structure of the recur-

sion. There are two recursive calls in the top level

of the f f Sampling algorithm, given the target vec-

tor (t

), it acts ﬁrst on t

, recursively, from right

to left, and then on t

. Each of t

, and then t

, con-

tinuously splits into two vectors of length n := n/2

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme

until n = 2, and then samples the coefﬁcients from a

Gaussian distribution, before building back up to give

sample vector (z

). Hence, there are two recursive

branches within the top level algorithm. Also, this is

all performed within the FFT domain. For a vector

of length n, the ﬁrst n/2 values represent the real co-

efﬁcients and the second n/2 represent the imaginary

coefﬁcients. So, the initial approach would be to ter-

minate the recursive call at the required point so that

only m −n spaces would be ﬁlled, but this would not

work due to the nature of the FFT functions.

4.3 FFT: Merging and Splitting

The sampling algorithm calls merging and splitting

functions as subroutines. These functions do not sim-

ply break up and concatenate the polynomial ring ele-

ments. The split function separates a polynomial into

its even and odd coefﬁcients and is performed in the

FFT domain. Operating in the FFT domain causes is-

sues for the fault attack, since a zero input does not

translate to zero in the FFT domain. Thus, we have

to track the coefﬁcients of the samples as they move

up through the recursive tree of the algorithm. This is

done by manually examining the pseudocode. Once

the lattice vector has been obtained from the Gaus-

sian sample, the FFT

−1

function is applied to it, and

the signing and verifying procedures are the same as

in DLP. This means the same post-processing can be

used from the DLP attack, however we need to ensure

that the signature is not in the FFT domain by apply-

ing the inverse FFT function.

We now present different methods of attack, dif-

ferentiated by the point at which the abortion occurs,

this being the m positions from the end of the vector.

This depends on where the attacker decides to abort

the sample generation. All attack methods lead to the

same output vector format for z; the ﬁrst (2n −m) co-

efﬁcients of z = (z

) are forced to zero.

4.3.1 Abort Second Recursion (for m = n)

This attack can be performed in a straightforward

manner. Simply abort at the top sampling algorithm

call, after the ﬁrst recursive call, after Line 10 of Al-

gorithm 3. Therefore z

gets ﬁlled with sampled co-

efﬁcients, yet z

remains all zeros. This fault abortion

is also performed for the case where m ≤ n, in order

to zero the ﬁrst n coefﬁcients.

4.3.2 Zeroing or Skipping Attack (for m ≤ n)

There are two options for this attack. First, at the

penultimate merge (n = 256 to 512), set the required

coefﬁcients (e.g., the ﬁrst half if m = n/2) of the out-

put coefﬁcients to zero by skipping operations or later

zeroing the corresponding coefﬁcients. The skipped

operations are f [(u << 1) + 0] = t_re and f [(u <<

1) + 1] = t_re, from the reference code

(Prest et al.,

2017). Otherwise, one can set the ﬁrst required num-

ber of coefﬁcients of z

to zero before computing

the corresponding lattice vector, that is, overwrite the

sampler output z

4.3.3 Aborting Mid-recursion (m ≤ n)

dimension This attack is more sophisticated, as we

must track the coefﬁcients throughout the tree. Al-

though this requires a prior one-off computation, it

allows the fault to be applied at the one-dimensional

Gaussian sampler stage, which is an easier point to

physically exploit.

Suppose the target is m = n/2; we want the left

half of z

to be zero. For this to occur, the left-hand

side (LHS) vector in the ﬁnal merge_fft() call has to

have its ﬁrst half equal to zero, and the right-hand side

(RHS) vector has to have the ﬁrst half of its coefﬁ-

cients equal to the second half. We generate each real

coefﬁcient (the ﬁrst half) of the z

vector by z

[2u] =

[u] + ( f

[u] − f

[u + n/4]) andz

[2u + 1] = f

[u] −

( f

[u] − f

[u + n/4]), where n is the dimension of the

higher-level vector, and u ∈ {0,.. .,n/4 −1). Note

that constants have been removed from the equations

as they are irrelevant for the result.

For z

[2u] and z

[2u + 1] to be zero, we can

set f

[u] = 0 and f

[u] = f

[u + n/4] for each u ∈

{0,.. .,n/4 −1). So for n = 512, the ﬁrst n/4 = 128

coefﬁcients of the LHS 256-dimension vector are set

to equal zero, and the ﬁrst 128 coefﬁcients of the RHS

256-dimension vector are set to equal the second 128

coefﬁcients.

For the LHS 256-dimension vector, the ﬁrst half

of its coefﬁcients must equal zero. The LHS 128-

dimension vector must have its ﬁrst half equal to zero,

and the RHS 128-dimension vector must have the ﬁrst

half of its values equal to the second half of its values.

This process is repeated on the LHS. The RHS 256-

dimension vector must have the ﬁrst half coefﬁcients

equal to the second half. For this to occur, the LHS

128-dimension vector must have the real values equal

to the imaginary values, and the RHS 128-dimension

vector must equal zero.

Speciﬁcally, the merge_fft() function in falcon_fft.c

SECRYPT 2019 - 16th International Conference on Security and Cryptography

This conclusion is reached by considering the fact

we want f [2u] = f [2u + n/2] (ﬁrst real/imaginary

computation per iteration) and f [2u + 1] = f [2u +1 +

] (second real/imaginary) equal for each iteration of

From the merge_fft() function, this

means f

[u] + ( f

[u] − f

[u + n/4]) =

[u + n/4] + ( f

[u] + f

[u + n/4]) and f

[u] −

( f

[u] − f

[u + n/4]) = f

[u + n/4] −

( f

[u] + f

[u + n/4]). To satisfy the components

of the equations, we can set f

[u] = f

[u + n/4],

that is the ﬁrst half of coefﬁcients equal to second

half, and for the second component, we can set

[u] = f

[u + n/4] = 0. Therefore the equations will

simply depend on the LHS feed-in vector.

For the RHS, every branch below can be set equal

to zero. Take the LHS 128-dimension vector. It fol-

lows the same conditions as the level above, that is

the LHS 64-dimension vector must have its real and

imaginary values equal, and the RHS must be zero.

Any vector equalling zero must have both feed-in vec-

tors equalling zero, so the branches below this can be

zeroed. This method can be applied for any m such

that m = 2

, where k ∈ Z.

4.4 Post-attack Processing

The ﬁnal step of the attack involves recovery of the

private basis from the faulty signatures. Suppose we

have the ﬁrst 2n −m coefﬁcients of vector (z

)

equal to zero. Then, according to the signing algo-

rithm (Algorithm 2) of FALCON, we compute the sig-

nature s

as:

s = t −z

where

B is the basis matrix in the FFT domain. But

we only need the second half of s, that is s

, where

= t

−z



−A( f )

−A(F)



and since t

is set to zero,

= −z



−A( f )

−A(F)



Furthermore, the ﬁrst m −n coefﬁcients of z are zero,

which further implies:

= −z

(−A(F)) ,

and since some of the coefﬁcients of z

are zero, we

ﬁnally have:

= (z

[m −1]x

n−m

F + ···+ z

[0]x

n−1

F).

This leaves us with a sub-lattice of the lattice gener-

ated by F, akin to that obtained in the DLP attack.

The only difference is that we are in the FFT do-

main, which we overcome by applying the inverse

FFT function to the output. Thus, with multiple faulty

signatures, the lattice spanned by F (where F is a

short vector in this lattice) can be found, where the

BKZ algorithm can be used to retrieve it. Then G, f ,

and g can be deduced from the public key h, and thus

the private NTRU lattice basis can be found.

4.5 Attack Results

The aim of this research is to show that if this fault at-

tack is applied successfully, the the output can reveal

the private key. The technicalities of the fault injec-

tion are left as future work. Thus, to verify this attack

model, we ﬁrst tested each method of attack through

software simulation and ensured the output signature

gave the expected number of zeros. This was success-

ful for all attack methods and parameter sets. We then

collected l faulty signatures for the values of m zeros

given in Table 2, and ran the BKZ algorithm (FPLLL

Development Team, 2016) to obtain the private key

polynomial F. The timings in seconds for the BKZ

algorithm to obtain F are given in Table 2. The as-

sumptions and attack model are similar to that used

by Espitau et al. (2016), in particular for estimating

the number of faults required.

4.6 Fault Model

The physical attack methods required for BEARZ are

early abortion and zeroing. Side-channel analysis

may be used to detect the window between the ﬁrst

call and the second recursive call, within which the

algorithm can be aborted, as in the original DLP at-

tack. A zeroing attack can be performed as a memory-

based attack, during storage of the vector in RAM,

by setting the required bits to zero (Naccache et al.,

2005). Alternatively, skipping lines of code can be

performed by CPU clock glitching (Blömer et al.,

2014). With respect to the fault models guide (Ver-

bauwhede et al., 2011), we can classify the BEARZ

fault attack models as being on the processing part

(for zeroing) and program ﬂow (for skipping and

aborting). These are high precision attacks, where the

adversary has the ability to bit ﬂip/set, and targets the

cryptographic primitive.

4.7 Countermeasures to BEARZ

Bindel et al. (2017) discuss countermeasures rele-

vant to BEARZ. A straightforward method of detect-

ing fault attacks (such as by Bruinderink and Pessl

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme

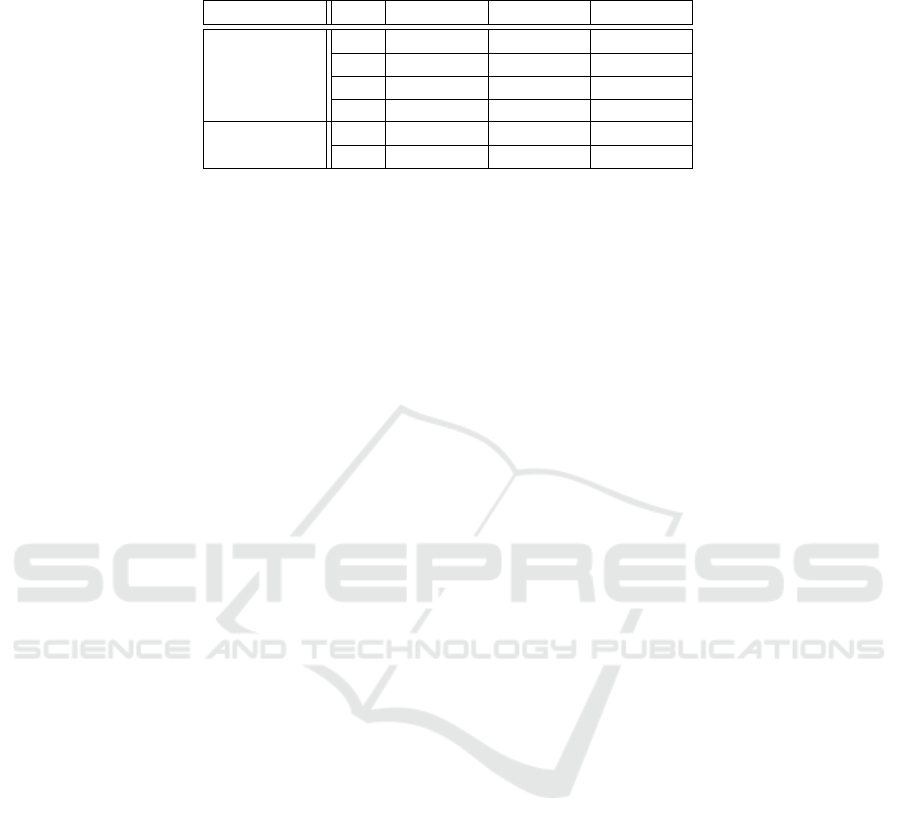
Table 2: Timings (in seconds) to run the BKZ algorithm on l faulty signatures to obtain the basis polynomial F running on a

single core of an Intel Core i7-6700HQ CPU at 2.60 GHz.

Parameters m l = m + 1 l = m +2 l = m + 3

Set 1

64 0.07 0.07 0.08

128 0.35 0.30 0.36

256 2.17 2.80 2.36

385 10.9 12.8 11.8

Set 2

128 0.28 0.29 0.35

256 2.24 2.55 2.67

(2018)) is to compute the signature twice. The dou-

ble computation method works for non-deterministic

schemes by ﬁxing the randomness. A conservative

estimate of this is doubling the signing time. Run-

ning the veriﬁcation process immediately after sign-

ing can give the signer conﬁdence that their hardware

has not been subject to fault attacks (Bruinderink and

Pessl, 2018). A simple, efﬁcient method of detecting

the BEARZ attack is checking that the sampled vector

does not go to zero at some point along its length at

the end of the f f Sampler algorithm.

5 RESULTS AND EVALUATION

This section analyses the performance results of the

optimised software design of the FALCON signature

scheme, as well as the three countermeasures dis-

cussed in the previous section. Clearly, as with any

attack countermeasure, we expect some performance

degradation, however we are more concerned with

their relative impacts on performance. Unless oth-

erwise stated, performance ﬁgures were obtained on

Intel E5-1620 CPU @ 3.7GHz, with hyperthreading

disabled, running on a single CPU. The platform of

the reference ﬁgures are also stated. Any results with

“-” mean the results are unchanged, thus not being af-

fected by the countermeasure(s).

Our libSAFEcrypto implementation consists of

portable C code that is written to permit a compiler

(gcc) to generate AVX-2 assembler (or any other type

of SIMD code) without having to revert to writing

assembler code by hand. It can also be ported to

other target processors (like ARM) without having

to re-write the code; this portability was set out as

one of our major design goals in the project to pro-

vide for wide adoption. This portability comes at a

performance cost, but is advantageous if one wants

to support various systems (embedded or server),

quickly adapt to changing algorithms (like a NIST

post-quantum scheme), or are looking for wide sup-

port. Therefore our performance is lower than the ref-

erence implementation by Prest et al. (2017).

5.1 FALCON with Countermeasures

Results for our FALCON optimised designs and the

effects of our countermeasures are shown in Table 3.

Parameter sets for FALCON slightly changed for the

second round of NIST’s post-quantum standardisa-

tion. Speciﬁcally, the second set of parameters, thus

we have omitted these from our results and perfor-

mance analysis and focus on parameter sets 1 and 2.

Interestingly, FALCON’s performance is not

largely affected by the countermeasures. Applying

verify-after-sign to protect against BEARZ does not

signiﬁcantly slow performance (∼ 5%), and the key

generation only drops signiﬁcantly with a high sam-

ple discard rate. The recommended combination of

countermeasures together slow the key generation and

signing down by less than 5% for Parameter Set 1.

Sample discard has less than a 5% effect on key gen-

eration, and the effect of the 6.5% rate on Parameter

Set 1 is so minimal that the effect of ﬂuctuation causes

an increase from the rate without discard. This small

effect on performance is due to the sampling and ver-

iﬁcation processes being efﬁcient.

5.2 Effectiveness of Countermeasures

5.2.1 Timing Attacks

To verify our timing attack countermeasure, we ran

the signing procedure 100 times and found for Set 1,

it fell within a range of 50 operations per second, and

for Set 2 within 20 operations per second. This sug-

gests it is effective against timing attacks.

5.2.2 BEARZ Attack

If the same fault is successfully implemented twice,

then double computation will not sufﬁce. The verify-

after-sign may not detect a fault attack which targets

the sampling, this has been shown previously by Espi-

tau et al. (2016), thus it still may produce a valid sig-

nature and go undetected. However, the zero-check

countermeasure should detect the attack with 100%

SECRYPT 2019 - 16th International Conference on Security and Cryptography

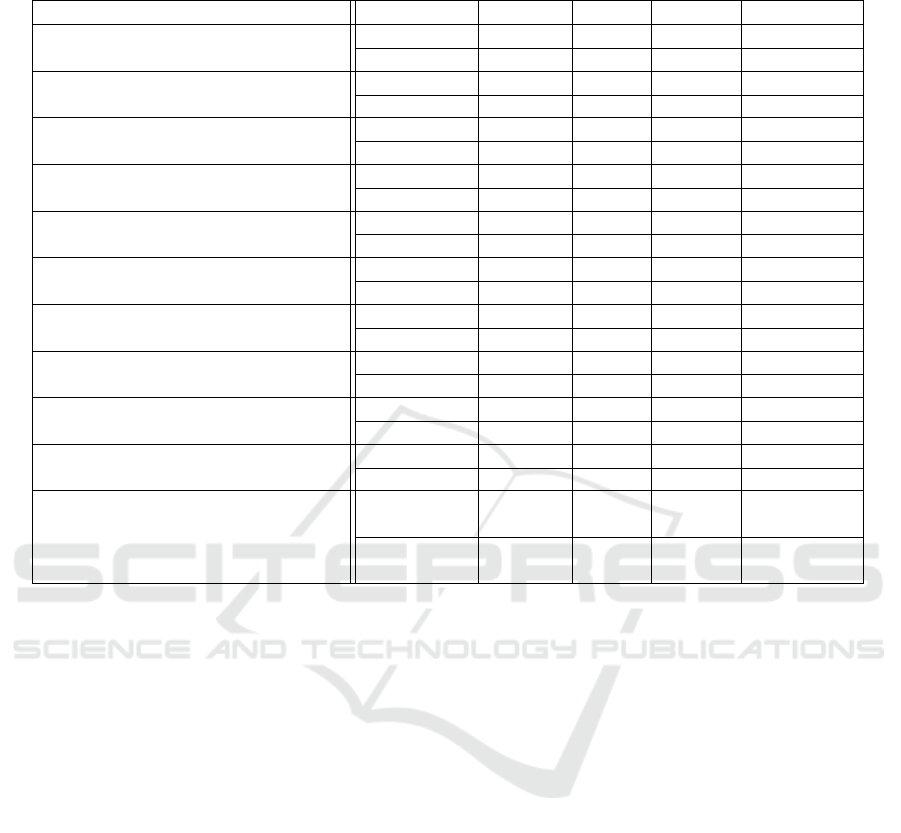
Table 3: Performance results (ops/sec) for FALCON with SCA countermeasures, including % decrease in affected components,

on Intel E5-1620 @ 3.7GHz unless otherwise stated.

Implementation Parameters KeyGen Sign Verify % decrease

Reference (Prest et al., 2017)

Intel Core i7-6567U @ 3.3GHz

Set 1 143 6081.9 37175.3 -

Set 2 50.9 3072.5 17697.4 -

Baseline

+constant-time NTT

Set 1 29.8 1484 29002 -

Set 2 11.1 734 14366 -

+Verify-after-sign

Set 1 - 1412 - 5

Set 2 - 699 - 5

+Zero-check

Set 1 - 1006 - 32

Set 2 - 489 - 16

+Double Computation

+Verify after sign

Set 1 - 706 - 52

Set 2 - 350 - 76

+Sample Discard (Low) (6.25%)

Set 1 26.3 - - 12

Set 2 12.0 - - +8

+Sample Discard (Medium) (12.5%)

Set 1 24.9 - - 16

Set 2 10.2 - - 8

+Sample Discard (High) (25%)

Set 1 27.7 - - 7

Set 2 8.0 - - 28

+Fisher-Yates Shufﬂing

Set 1 23.87 - - 20

Set 2 10.9 - - 2

+BlindVector

Set 1 27.03 - - 9

Set 2 8.7 - - 49

+Verify-after-sign

+Sample Discard (Low) (6.25%)

+Fisher-Yates Shufﬂing

Set 1 29.0 1426 - 4

Set 2 10.7 706 - 4

success rate. We therefore recommend this as a mini-

mum, sufﬁcient countermeasure.

5.3 Comparison to Other Lattice-based

Signature Schemes

We compare our results to our implementation of

Dilithium (Lyubashevsky et al., 2017) and Bliss-B

(Ducas, 2014) signature schemes with countermea-

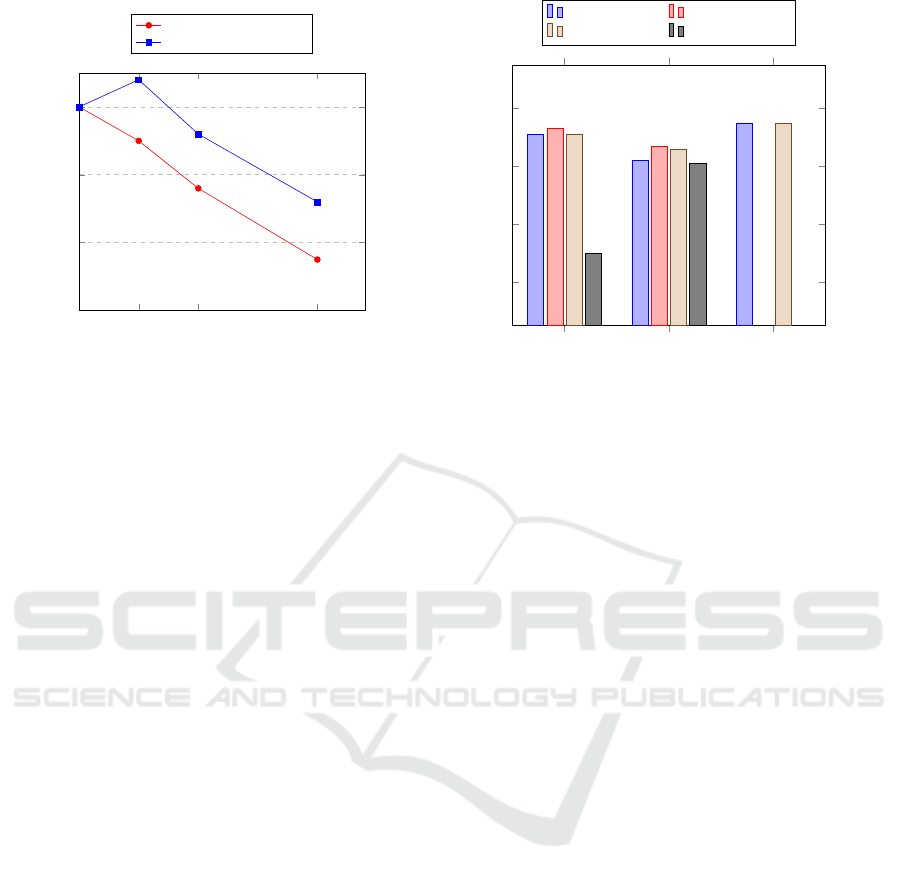
sures in place. Interestingly, the performance of FAL-

CON is not as adversely affected as much as its NIST

competitor scheme Dilithium when the verify-after-

sign countermeasure is added, as shown in Figure

1b. Even at high security levels, it does not suffer

as much of a slowdown as BLISS-B, shown in Fig-

ure 1a. This is due to the efﬁciency of the FALCON

components. Similar countermeasures on Dilithium

that prevent the fault attack proposed by Bruinderink

and Pessl (2018), cause its performance to deterio-

rate by almost 20%. BLISS-B has a larger range of

countermeasures available in order to protect against

those proposed by Pessl et al. (2017), meaning the ef-

fect on performance can range between an additional

10% and 50%, depending on the instance. Dilithium

has the advantage of being immune to Gaussian sam-

pler attacks, however its protection from the fault at-

tacks by Bruinderink and Pessl (2018) remain an open

problem. Its performance is slowed down by nearly

20% with countermeasures in place and has greater

degradation than BLISS-B with a protected Gaussian

sampler.

6 CONCLUSION

In this research, we have proposed a new attack on

the FALCON signature scheme, BEARZ. We have

shown that FALCON is vulnerable to fault attacks on

its Gaussian sampler and so consideration of physical

attacks should be addressed when implementing for

real world use. We also provide possible countermea-

sures, including the verify-after-sign countermeasure,

as the faulty signature will not pass the norm bound

test, and the zero-check. Furthermore, we implement

double computation, a costly but reliable method, as-

suming the attacker only has access to the hardware

during one of the signing processes. Additionally,

we review timing attack vulnerabilities and counter-

measures and compare the impact on performance to

other lattice-based schemes, deducing that FALCON is

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme

6.25 12.5 25

100

110

Sample discard rate (%)

Degredation of performance (%)

BLISS-B Signing (Set-IV)

FALCON KeyGen (Set 2)

(a) Sample Discard countermeasure effect

on BLISS-B and FALCON for equivalent

(192-bit) security levels.

BLISS-B Dilithium

FALCON

100

Degredation of performance (%)

Parameter Set-I Parameter Set-II

Parameter Set-III Parameter Set-IV

(b) Verify-after-sign effect on BLISS-B,

Dilithium, and FALCON.

Figure 1: Performance analysis of the proposed SCA countermeasures for the FALCON, Dilithium, and BLISS-B signatures.

a still a competitive second-round candidate.

ACKNOWLEDGEMENTS

The authors would like to thank Thomas Prest and the

anonymous reviewers of T-CHES 2019 and COSADE

2019 for their careful reading of the paper and their

diligent comments. The authors would also like to

acknowledge that this work was supported in part

by the European Union Horizon 2020 SAFEcrypto

project (grant no. 644729) and the EPSRC via grant

EP/N011635/1.

REFERENCES

Ajtai, M. and Dwork, C. (1997). A public-key cryptosystem

with worst-case/average-case equivalence. In STOC

’97 Proceedings of the twenty-ninth annual ACM sym-

posium on Theory of computing, pages 284–293.

Alagic, G., Alperin-Sheriff, J., Apon, D., Cooper, D., Dang,

Q., Liu, Y.-K., Miller, C., Moody, D., Peralta, R.,

Perlner, R., Robinson, A., and Smith-Tone, D. (2019).

Status Report on the First Round of the NIST Post-

Quantum Cryptography Standardization Process.

http://aiweb.techfak.uni-bielefeld.de/content/bworld-

robot-control-software/. [Online; accessed February

2019].

Alkim, E., Ducas, L., Pöppelmann, T., and Schwabe, P.

(2016). Post-quantum key exchange-a new hope. In

USENIX Security Symposium, volume 2016.

Bindel, N., Buchmann, J., and Krämer, J. (2016). Lattice-

based signature schemes and their sensitivity to fault

attacks. In Fault Diagnosis and Tolerance in Cryp-

tography (FDTC), 2016 Workshop on, pages 63–77.

IEEE.

Bindel, N., Kramer, J., and Schreiber, J. (2017). Special ses-

sion: hampering fault attacks against lattice-based sig-

nature schemes-countermeasures and their efﬁciency.

In Hardware/Software Codesign and System Synthe-

sis (CODES+ ISSS), 2017 International Conference

on, pages 1–3. IEEE.

Blömer, J., Silva, R. G. D., Günther, P., Krämer, J., and

Seifert, J.-P. (2014). A practical second-order fault

attack against a real-world pairing implementation.

In Fault Diagnosis and Tolerance in Cryptography

(FDTC), 2014 Workshop on, pages 123–136. IEEE.

Bruinderink, L. G., Hülsing, A., Lange, T., and Yarom, Y.

(2016). Flush, Gauss, and reload-a cache attack on

the BLISS lattice-based signature scheme. In Inter-

national Conference on Cryptographic Hardware and

Embedded Systems, pages 323–345. Springer.

Bruinderink, L. G. and Pessl, P. (2018). Differential fault at-

tacks on deterministic lattice signatures. IACR Trans-

actions on Cryptographic Hardware and Embedded

Systems, pages 21–43.

Ducas, L. (2014). Accelerating BLISS: the geometry of

ternary polynomials. Cryptology ePrint Archive, Re-

port 2014/874. https://eprint.iacr.org/2014/874.

Ducas, L., Lyubashevsky, V., and Prest, T. (2014). Efﬁcient

identity-based encryption over ntru lattices. In Inter-

national Conference on the Theory and Application

of Cryptology and Information Security, pages 22–41.

Springer.

Ducas, L. and Prest, T. (2016). Fast fourier orthogonal-

ization. In Proceedings of the ACM on International

Symposium on Symbolic and Algebraic Computation,

pages 191–198. ACM.

Espitau, T., Fouque, P., G’erard, B., and Tibouchi, M.

(2018). Loop-abort faults on lattice-based signature

SECRYPT 2019 - 16th International Conference on Security and Cryptography

schemes and key exchange protocols. IEEE Transac-

tions on Computers, 67(11):1535–1549.

Espitau, T., Fouque, P.-A., Gérard, B., and Tibouchi, M.

(2016). Loop-abort faults on lattice-based ﬁat-shamir

and hash-and-sign signatures. In International Con-

ference on Selected Areas in Cryptography, pages

140–158. Springer.

Fisher, R. A., Yates, F., et al. (1938). Statistical tables for

biological, agricultural and medical research. Statis-

tical tables for biological, agricultural and medical

research.

FPLLL Development Team, O. T. (2016). fplll,

a lattice reduction library. Available at

https://github.com/fplll/fplll.

Gentry, C. and Boneh, D. (2009). A fully homomorphic

encryption scheme, volume 20. Stanford University

Stanford.

Hodgers, P., Regazzoni, F., Gilmore, R., Moore, C., and

Oder, T. (2016). State-of-the-art in physical side-

channel attacks and resistant technologies. Technical

report.

Howe, J., Khalid, A., Rafferty, C., Regazzoni, F., and

O’Neill, M. (2016). On practical discrete Gaussian

samplers for lattice-based cryptography. IEEE Trans-

actions on Computers.

Howe, J., Pöppelmann, T., O’Neill, M., O’Sullivan, E.,

and Güneysu, T. (2015). Practical lattice-based digital

signature schemes. ACM Transactions on Embedded

Computing Systems (TECS), 14(3):41.

Karmakar, A., Roy, S. S., Reparaz, O., Vercauteren, F., and

Verbauwhede, I. (2018). Constant-time discrete gaus-

sian sampling. IEEE Transactions on Computers.

Khalid, A., Howe, J., Rafferty, C., and O’Neill, M.

(2016). Time-independent discrete gaussian sampling

for post-quantum cryptography. In 2016 Interna-

tional Conference on Field-Programmable Technol-

ogy (FPT), pages 241–244. IEEE.

Khalid, A., Oder, T., Valencia, F., O’Neill, M., Güneysu,

T., and Regazzoni, F. (2018). Physical protection of

lattice-based cryptography: Challenges and solutions.

In Proceedings of the 2018 on Great Lakes Symposium

on VLSI, pages 365–370. ACM.

Longa, P. and Naehrig, M. (2016). Speeding up the number

theoretic transform for faster ideal lattice-based cryp-

tography. In International Conference on Cryptology

and Network Security, pages 124–139. Springer.

Lyubashevsky, V., Ducas, L., Kiltz, E., Lepoint, T.,

Schwabe, P., Seiler, G., and Stehle, D. (2017).

CRYSTALS-Dilithium. Technical report, National

Institute of Standards and Technology. avail-

able at https://csrc.nist.gov/projects/post-quantum-

cryptography/round-1-submissions.

Micciancio, D. and Walter, M. (2017). Gaussian sampling

over the integers: Efﬁcient, generic, constant-time. In

Annual International Cryptology Conference, pages

455–485. Springer.

Naccache, D., Nguyen, P. Q., Tunstall, M., and Whelan,

C. (2005). Experimenting with Faults, Lattices and

the DSA. In International Workshop on Public Key

Cryptography, pages 16–28. Springer.

NIST (2016a). Post-quantum crypto project.

http://csrc.nist.gov/groups/ST/post-quantum-crypto/.

NIST (2016b). Submission requirements and

evaluation criteria for the post-quantum

cryptography standardization process.

https://csrc.nist.gov/csrc/media/projects/post-

quantum-cryptography/documents/call-for-proposals-

ﬁnal-dec-2016.pdf.

Pessl, P. (2016). Analyzing the shufﬂing side-channel coun-

termeasure for lattice-based signatures. In Interna-

tional Conference in Cryptology in India, pages 153–

170. Springer.

Pessl, P., Bruinderink, L. G., and Yarom, Y. (2017). To

BLISS-B or not to be: Attacking strongSwan’s Imple-

mentation of Post-Quantum Signatures. In Proceed-

ings of the 2017 ACM SIGSAC Conference on Com-

puter and Communications Security, pages 1843–

1855. ACM.

Prest, T., Fouque, P.-A., Hoffstein, J., Kirchner, P., Lyuba-

shevsky, V., Pornin, T., Ricosset, T., Seiler, G., Whyte,

W., and Zhang, Z. (2017). Falcon. Technical re-

port, National Institute of Standards and Technol-

ogy. available at https://csrc.nist.gov/projects/post-

quantum-cryptography/round-1-submissions.

Primas, R. (2017). Side-channel attacks on efﬁcient lattice-

based encryption. Master’s thesis, Graz University of

Technology, Graz.

Regev, O. (2005). On lattices, learning with errors, ran-

dom linear codes, and cryptography. In Proceedings of

the 37th Annual ACM Symposium on Theory of Com-

puting, Baltimore, MD, USA, May 22-24, 2005, pages

84–93.

Regev, O. (2009). On lattices, learning with errors, random

linear codes, and cryptography. Journal of the ACM

(JACM), 56(6):34:1–34:40.

Roy, S. S., Reparaz, O., Vercauteren, F., and Verbauwhede,

I. (2014). Compact and side channel secure discrete

Gaussian sampling. IACR Cryptology ePrint Archive,

2014:591.

Saarinen, M.-J. O. (2015). Gaussian sampling precision

and information leakage in lattice cryptography. IACR

Cryptology ePrint Archive, 2015:953.

Saarinen, M.-J. O. (2017). Arithmetic coding and blind-

ing countermeasures for lattice signatures. Journal of

Cryptographic Engineering, pages 1–14.

Scott, M. (2017). A note on the implementation of the num-

ber theoretic transform. In IMA International Confer-

ence on Cryptography and Coding, pages 247–258.

Springer.

Shor, P. W. (1999). Polynomial-time algorithms for prime

factorization and discrete logarithms on a quantum

computer. SIAM Review, 41(2):303–332.

Verbauwhede, I., Karaklajic, D., and Schmidt, J.-M. (2011).

The fault attack jungle-a classiﬁcation model to guide

you. In 2011 Workshop on Fault Diagnosis and Toler-

ance in Cryptography, pages 3–8. IEEE.

BEARZ Attack FALCON: Implementation Attacks with Countermeasures on the FALCON Signature Scheme