Deriving Programs by Reliability Enhancement
Marwa Benabdelali and Lamia Labed Jilani
Universit
´
e de Tunis, Institut Sup
´
erieur de Gestion de Tunis, Lab. RIADI-GDL, Bardo, Tunisia
Keywords:
Specification, Formal Approach, Program Derivation Process, Refinement, Relative Correctness, Reliable
Software.
Abstract:
This paper concerns the exploration of an approach that deals with formal program derivation in contrast to the
traditional approach that begins with a formal specification, derive different refinements of that specification
until generating the final correct program code. Hence, we use a rigorous theoretical framework which is based
on the concept of relative correctness; the property of a program to be more correct than another program with
respect to a specification. Program derivation process by relative correctness presents several advantages as
for example deriving reliable software. In fact, for most software products, as for products in general, perfect
correctness is not necessary; very often, adequate reliability threshold is sufficient. Our aim is to continue
experimenting with the discipline of reliable program derivation by correctness enhancement by conducting
an analytical and empirical study of this approach as a proof of concept. Then, to analyze the results and
compare them (give feedback) to what is predicted and proposed by the analytical approach and decide on the
usability of the approach and/or adjust/complete it. Finally, we propose a mechanism that helps and guides
developer in the program derivation process using relative correctness.
1 INTRODUCTION
As we know, deriving programs from specifications
by using a formal approach assures program correct-
ness and better quality. Reuse based software engi-
neering is essential nowadays where lot of software
artifacts are available. Deriving programs from other
existing programs can also be envisaged, more specif-
ically, we can construct programs by successive pro-
gram transformations. We are working on the pro-
gram derivation process by correctness enhancement
that was introduced by (Diallo et al., 2015) and re-
fined by (Benabdelali et al., 2018). This process is
orthogonal to traditional refinement-based program
derivation processes (Back, 1978; Morgan, 1990) in
the sense that instead of preserving correctness and
enhancing executability (as traditional processes do),
it preserves executability (i.e. proceeds from one ex-
ecutable program to the next) while enhancing cor-
rectness until it achieves absolute correctness. In this
paper, we observe that the sequence of programs de-
rived in the correctness enhancement process are in-
creasingly reliable, and we argue that this process can
be used to derive programs that are sufficiently reli-
able (for a given reliability threshold) even if they are
not necessarily (absolutely) correct. Therefore, we
are conducting an analytical and empirical study as a
proof of concept about deriving programs by enhanc-
ing correctness. We are going to present a set of rel-
atively simple programs as a first sample. This latter
will permit to illustrate the approach and to find mech-
anisms or guidelines that permit the transformation
of a program to another. The paper is structured as
follows: Section 2 discusses both approaches of pro-
gram construction process according to a given speci-
fication. Section 3 presents the analytical and empiri-
cal analysis of the program derivation by correctness-
enhancing transformations and describes the program
derivation mechanism that our empirical study leads
us to highlight. This mechanism will permit to guide
how transformations can be done in program deriva-
tion by relative correctness process. Section 4 sum-
marizes our findings and presents the future directions
of our research.
2 PROGRAM DERIVATION
PROCESS FROM
SPECIFICATIONS
In computer science, program derivation aims to pro-
duce an executable and correct program from its
210
Benabdelali, M. and Jilani, L.
Deriving Programs by Reliability Enhancement.
DOI: 10.5220/0007835402100217
In Proceedings of the 14th Inter national Conference on Software Technologies (ICSOFT 2019), pages 210-217
ISBN: 978-989-758-379-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

specification by applying mathematical correct rules.
So, we are concerned with transformation process
that takes a formal specification of what the com-
puter is to do and produces a program which will
cause the computer to do it. The program thus ob-
tained is then correct by stepwise derivation. In the
present paper, we are interested to explore a for-
mal approach of program derivation that is based
on relative correctness and consists in successive
correctness-enhancing transformations in contrast to
the traditional refinement-based process of successive
correctness-preserving transformations. Before em-
barking on the study of the programs derivation pro-
cess, we briefly introduce some elements of relational
mathematics (Chris Brink and Schmidt, 1997) that we
use throughout the paper to represent the specifica-
tions and programs functions. To represent specifi-
cations and programs, we need sets and relations. A
set is the space S of the program and its elements is
the states of the program. Indeed, given a program
p that operates on space S, we let P be the function
that defines the program, this function is represented
as a set of pairs (s, s
0
) where s is the start execution
state of P and s
0
is the end execution state. A rela-
tion R on a set S is a subset of the cartesian product
S × S. Relations on a set S include the identity re-
lation denoted by I = {(s, s
0
)|s
0
= s}, empty relation
denoted by ø = {} and the universal relation denoted
by L = S × S.
2.1 Refinement-based Program
Derivation
A program is a sequence of different operations and
calculations. The difficulty in developing such a pro-
gram is usually proportional to the size of the spec-
ification. It is often difficult to write the final ver-
sion at the first shot. Traditionally, to solve this prob-
lem we proceed in stages using the refinement ap-
proach. The latter, was first introduced by (Back,
1978), (Morgan, 1990) and (Back and Wright, 1998)
and is defined as a notation and a set of rules for de-
riving programs from their specifications. The basic
idea behind this approach is to derive a correct pro-
gram through a sequence of refinement steps, begins
with a formal specification until generating the final
correct program meeting the specification.
Definition 1: Given two programs P and P
0
, we write
P v P
0
when P
0
is an effective program, meeting the
specification more than P. The relation v is called
re f inement and we say that P
0
refines P. To respond
such definition, (Morgan, 1990) presents a catalogue
of lemmas that determines how specification may be
refined to an executable code. As an illustration of
this definition, we would like to construct a program
that manipulates three variables of type float, say, u,
v, w where v, w are positive. The program must give
log(v) in u and any positive value in v.
Space, S = f loat u, v, w;
{(s, s
0
)|v > 0 ∧ w ≥ 0 ∧ u
0
= log(v) ∧ v
0
> 0 ∧ w
0
> 0}
v
{(s, s
0
)|v > 0 ∧ w ≥ 0 ∧ u
0
= log(v) ∧ v
0
> 0 ∧ w
0
= w}
v
{(s, s
0
)|v > 0 ∧ w ≥ 0 ∧ u
0
= log(v) ∧ v
0
= sqrt(w) ∧
w
0
= w}
= [u := log(v); v := sqrt(w);]= a piece of the program
that is conformed with the first specification.
Although refinement is a well-known approach
for developing correct-by-derivation software that has
proven its value in software development, nowadays
the issues become no longer to construct applica-
tions from scratch and achieving the correctness, but
rather to maintain and evolve them. Therefore, as for
products in general, perfect correctness is not neces-
sary; very often, adequate reliability (depending on
the level of criticality of the application) is sufficient.
2.2 Relative Correctness-based
Program Derivation
With the Relative Correctness-based program deriva-
tion approach, the objective becomes no longer to de-
velop a program that is absolutely correct in relation
to the specification but rather to achieve a satisfactory
reliability threshold. The term reliability according
to (O’Regan, 2017) is the probability that the pro-
gram works without failure for a specified length of
time, and it is a statement of the future behaviour of
the software. So, in this context and while most ap-
proaches deal with informal program derivation tech-
niques, the approach underlying this present work is
based on a formal approach. Hence, we use a rigorous
theoretical framework which is based on the concept
of relative correctness. This latter, was introduced by
(Diallo et al., 2015) as a viable alternative approach to
the traditional refinement-based process of successive
correctness-preserving transformations starting from
the specification and culminating in a correct program
(see Figure 1).
Among the many properties of relative correct-
ness, the most intriguing is the property that program
P
0
refines program P if and only if P
0
is more-correct
than P with respect to a specification. This yield to
reconsider program derivation by successive refine-
ments: each step of this process mandates that we
transform a program P into a program P
0
that refines
P.
Definition 2: due to (Diallo et al., 2015) given two
Deriving Programs by Reliability Enhancement
211

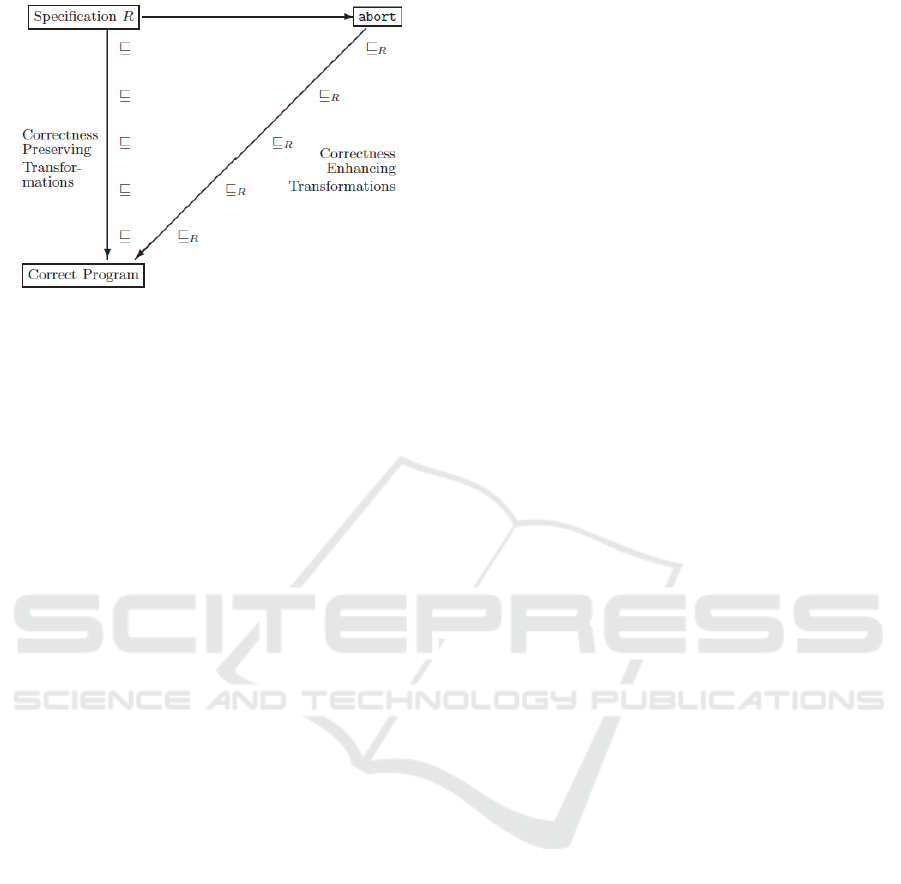
Figure 1: Program Derivation process (Diallo et al., 2015).
programs P, P
0
and a specification R; we say that
P
0
is more − correct than P if and only if P
0
obeys
R for a larger set of inputs than P. This relation is
denoted by P v
R
P
0
which is equivalent to the rela-
tion: (R ∩ P)oL ⊆ (R ∩ P
0
)oL. Also, we say that P
0
is strictly more − correct than P with respect to R if
and only if P @
R
P
0
which is equivalent to the relation
(R ∩ P)oL ⊂ (R ∩ P
0
)oL. o is the relative product of
two relations.
The relation (R ∩ P)oL refers to the set of initial
states on which the behavior of P satisfies specifica-
tion R. This set is denoted the competence domain of
P with respect to R. Relative correctness of P
0
over
P with respect to R simply means that P
0
has a larger
competence domain than P. We illustrate this defi-
nition by a simple example; given a specification R
defined on space S={a,b,c,d,e,1,2,3,4,5}
R = {(a,2),(b,4),(c,5),(d,1),(a,3)}
Where for the input a it gives the output 2 and 3, for
the input b it gives the output 4, for the input c it gives
the output 5 and for the input d it gives the output 1.
And let P and P
0
be the following candidates pro-
grams: P={(a,2), (c,5)}. P
0
={(a,2),(b,4),(c,5) }
(R ∩ P)oL = {a, c} × S. (R ∩ P
0
)oL = {a, b, c} × S
Hence P
0
is more-correct than P with respect to R.
(Khaireddine et al., 2017) defined program relia-
bility as the probability that a randomly element of the
specification domain (dom(R)=initial states on which
candidate program must behaves according to R) se-
lected according to the probability distribution ((θ))
falls within the competence domain of the program
with respect to the specification. It can be written as:
ρ
θ
R
=
∑
s∈dom(R∩P)
θ(s).
Definition 3: P
0
is more correct than P implies that P
0
has higher reliability than P. Hence, P v
R
P
0
⇔ (∀θ :
ρ
θ
R
(P) ≤ ρ
θ
R
(P
0
). So, the more the program is correct
(P
0
), the more it is reliable compared to P.
With the absence of strong analytical and empir-
ical evidence, (Diallo et al., 2015) have presented
some advantages of relative correctness based pro-
gram derivation that may complement those of re-
finement. Indeed, the underlying approach is com-
petent to model not only program development from
scratch but also several software engineering activi-
ties including the development of sufficiently reliable
programs, software upgrade, adaptive maintenance,
program merger, corrective maintenance and software
evolution. Table 1 present a comparison between the
two programs derivation approaches. The table high-
lights the contributions of relative correctness concept
in the program derivation process.
3 RELATIVE CORRECTNESS
BASED PROGRAM
DERIVATION: PROOF OF
CONCEPT
This section presents our contributions. In fact, we
discuss the feasibility of the relative correctness ap-
proach as an alternative to the refinement approach
in the program derivation process. This, allows us
to identify the strengths and weaknesses of such ap-
proach and may lead us to decide on the usability of
the approach and/or adjust/complete it.
3.1 Analytical Study
The analytical study deals with the relational math-
ematics(Chris Brink and Schmidt, 1997) to proceed
to the development process using relative correctness.
Therefore, we present in the following a set of illus-
trative examples. In each example, we start with an
abort program that fails to capture any functionality
of the specification and we apply the relative correct-
ness formula until reaching either a correct program
or a program with a satisfying reliability threshold ac-
cording to the specification.
3.1.1 MedianIndex
Let S be the space defined by; variable x of type
itemtype, variable a[1..N]for some constant N ≥ 0,
and variable k of type indextype, used as an index
variable into array a. And let R be the following spec-
ification on S:
R = {(s, s
0
)|a
0
= a ∧ 1 ≤ k
0
≤ N ∧ a[k
0
] = x∧
|(#h : 1 ≤ h < k
0
: a[h] = x) − (#h : k
0
< h ≤ N :
a[h] = x)| ≤ 1} ∪{(s,s
0
)|a
0
= a ∧
(∀h : 1 ≤ h ≤ N : a[h] 6= x) ∧ k
0
= −1}.
The operator # means we count the number of times
the condition is verified.
ICSOFT 2019 - 14th International Conference on Software Technologies
212

Table 1: Comparison between refinement and relative correctness.
Criterion Refinement-based program deriva-
tion
Relative correctness-based program
derivation
Starting condition Client specification. Program that does not meet the specifi-
cation.
Ending condition Correct program. Reliable program.
Transformation process In each transformation step, We have a
partially defined program.
In each transforation step, we have an
executable program that satisfies R in
some initial sates.
Designer decision Determined/ restricted Undetermined/ expanded
Goal Derives executable and correct program
from its specification.
Models various software engineering
activities.
Development; cost and
complexity
High cost and complexity because it
aims to produce an absolutely correct
program.
Low cost and complexity because we
are not trying to produce all the
program functionalities but rather to
achieve a sufficiently reliability level.
Fault removal When an error occurs, it can easily
propagates in the development process
which generates a defective program
that does not satisfying the client spec-
ification.
Since each transformation step repre-
sents a program that is more correct to
the previous one, it is easy to detect its
defaults and correct them immediately.
Correctness and exe-
cutability
Correctness preservation and exe-
cutability enhancement.
Correctness enhancement and exe-
cutability preservation.
The specification mandates to return in k’ a me-
dian index where x occurs (i.e. if x occurs three times
in a, return in k’ the second position; and if x oc-
curs for example six times then return in k’ the 3rd
or fourth index where x occurs)if x is in a[1..N]. else
(if x does not occur in a[1..N]) to return -1 in k’. In
addition, the specification mandates to preserve a. We
start from the initial program P
0
whose competence
domain is the empty set and we let the next program
P
1
be the program that assigns the value -1 to variable
k’. In fact, remember that k’=-1 is the value men-
tioned in the specification R when x is not in the array
a.
P1: int main ()
{int K; k=-1; return k;}
We compute the function of this program and we find:
P
1
= {(s, s
0
)|k
0
= −1 ∧ a
0
= a ∧ x
0
= x}.
Whence, we compute the competence domain of P
1
with respect to R:
(R ∩ P
1
)oL
= {substitution, simplification}
{(s, s
0
)|(∀h : 1 ≤ h ≤ N : a[h] 6= x) ∧ k
0
= −1 ∧ a
0
=
a ∧ x
0
= x}oL.
= {taking the domain}
{(s, s
0
)|(∀h : 1 ≤ h ≤ N : a[h] 6= x)}.
program P
1
satisfies specification R for all initial
states that have no instance of x in a. We now con-
sider the case where the number of instances of x in
a[1..N] does not exceed 2. This yields the program P
2
which is derived from P
1
.
P2:int main ()
{loaddata(); // loads a and x
int a[N+1]; int x; int k; int N; k = N;
while ((a[k] != x)&&(k >= 0)) {k = k - 1;}
return k;}
The program preserves a, and returns in k’ the largest
index where x occurs if x is in a[1..N]. else (if x does
not occurs in a[1..N]) it return -1 in k’. We write its
function as follows:
P
2
= {(s, s
0
)|a
0
= a ∧ x
0
= x∧ a[k
0
] = x ∧ 1 ≤ k
0
≤ N ∧
(∀h : k
0
< h ≤ N : a[h] 6= x)} ∪{(s, s
0
)a
0
= a ∧
x
0
= x ∧ (∀h : 1 ≤ h ≤ N : a[h] 6= x)∧ k
0
= −1}.
We compute the competence domain of P2 with re-
spect to R:
(R ∩ P2) {(s, s
0
)|a
0
= a ∧ x
0
= x ∧ a[k
0
] = x ∧ 1 ≤ k
0
≤
N∧ (#h : 1 ≤ h < k
0
: a[h] = x) ≤ 1∧ (∀h : k
0
< h ≤ N :
a[h] 6= x)} ∪{(s, s
0
)|(∀h : 1 ≤ h ≤ N : a[h] 6= x) ∧ a
0
=
a ∧ x
0
= x ∧ k
0
= −1}.
Whence
(R ∩ P
2
)oL
= {Domain of a union}
{(s, s
0
)|(#h : 1 ≤ h ≤ N : a[h] = x) ≤ 2} ∪ {(s, s
0
)|(∀h :
1 ≤ h ≤ N : a[h] 6= x)}.
= {The first term is a superset of the second}
{(s, s
0
)|(#h : 1 ≤ h ≤ N : a[h] = x) ≤ 2}.
R mandates to return the median index when x is
found in a[1..N] whereas P
2
returns the largest index;
hence P
2
satisfies R for all initial states in which the
number of instances of x in a[1..N] does not exceed
2. For the third program, we want to satisfy the spec-
ification R for any initial state s in S. We consider the
following program:
P3: int main ()
{loaddata(); // loads a and x
Deriving Programs by Reliability Enhancement
213

int a[N+1]; int x; int k; int N; int k2;
k = N + 1; k2 = N + 1;
while (k2 > 0) { k = k - 1; k2 = k2 - 1;
while ((a[k] != x)&&(k >= 0))
{k = k - 1;};while ((a[k2] != x)
&&(k2 >= 0)){k2 = k2 - 1;};if ((k2 >= 0))
{k2 = k2 - 1;};while ((a[k2] != x)
&&(k2 >= 0)){k2 = k2 - 1;};} return k;}
\end{verbatim}
We write the function of P
3
as follows:
P
3
= {(s, s
0
)|a
0
= a ∧ x
0
= x ∧ 1 ≤ k
0
≤ N ∧ a[k
0
] = x∧
|(#h : 1 ≤ h < k
0
: a[h] = x) − (#h : k
0
< h ≤ N :
a[h] = x)| ≤ 1} ∪{(s,s
0
)|a
0
= a ∧ x
0
= x ∧
(∀h : 1 ≤ h ≤ N : a[h] 6= x) ∧ k
0
= −1}.
We compute the competence domain of P
3
with re-
spect to R and we find that (R ∩ P
3
)oL = RL = S
So, it’s easy to see that the competence domain of
P
3
is S, since it may satisfies R for any initial state s in
S. Therefore we conclude that P
3
is the more correct
program with respect to R. Hence P
3
is correct with
respect to R hence it is more-correct than P
2
with re-
spect to R. So we do have: P
0
v
R
P
1
v
R
P
2
v
R
P
3
. Fur-
thermore, we find that P
3
is correct with respect to R;
this concludes the derivation.
3.1.2 BinaryCode
We let space S be defined by a natural variable n and
we let specification R be the following relation on S.
R = {(s, s
0
)|n
0
= binary(n) ∧ n ≤ 1024 ∧ n
0
= n}.
with binary(n); a function that represents natural
numbers as sequences of digits 0 or 1 in the usual
way(binary representation). Thereby, our specifica-
tion R mandates to return in n
0
the binary code of a
given natural number n between 0 and 1024. Start-
ing from the initial program P
0
that is always false
according to R, and we let the next program P
1
be the
program that returns the binary code of given n that
must be ≤ 100.
P1: int main ()
{ int n; long long binaryNumber = 0;
if (n <= 100) { binaryNumber = binary(n);}
return binaryNumber;}
The function of this program and its competence
domain are given as:
P1 = {(s, s
0
)|n
0
= binary(n) ∧ n ≤ 100 ∧ n
0
= n}
∪{(s, s
0
)|n
0
= 0 ∧ n > 100 ∧ n
0
= n}.
(R ∩ P
1
)oL
= {(s, s
0
)|n ≤ 100 ∧ n
0
= binary(n) ∧ n
0
= n}oL.
= {taking the domain} = {(s, s
0
)|n ≤ 100}.
P
1
works only when n ≤ 100, and when it does, it
returns the binary code of the given n. Therefore,
the competence domain of P
1
, is the set of n whose
value does not exceed 100. For the next programs;
P
2
,P
3
, P
4
and P
5
we do the same thing as P
1
only,
at each transition from one program to another we
keep the same functionalities of the program then
we increase the domain of n until it reaches 1024.
Therefore, we obtain in the end of derivation a
program P
5
({(s, s
0
)|n
0
= binary(n) ∧ n ≤ 1024 ∧ n
0
=
n}∪{(s, s
0
)|n
0
= 0 ∧ n > 1024 ∧ n
0
= n}.) that works
on the whole interval of n defined by the specification
R. Hence we do have: P
0
v
R
P
1
v
R
P
2
v
R
P
3
v
R
P
4
v
R
P
5
.
Furthermore, we find that P
5
is correct with respect
to R; this concludes the derivation.
3.1.3 StringCombinations
Let space S be defined by; str: string of char, a and
b: char. Also, we let R be the following specification:
R = {(s, s
0
)|str
0
= (a ∨ b)
∗
∨ epsilon}.
With str
0
; a string formed of epsilon or any combi-
nation of ”a” and/or ”b”. The specification mandates
to return all string formed from {a, b} or epsilon. We
start with P
0
whose competence domain is the empty
set. For the next program, we choose:
string P1(string str)
{string r = ""; if (str == "a") {r = str;}
return r;}
The function of this program and its competence do-
main are given as:
P
1
= {(s, s
0
)|str
0
= a ∨ epsilon}.
(R ∩ P
1
)oL = {(s, s
0
) = |str
0
= a ∨ epsilon}.
The competence domain of P
1
is the set of string
that are constructed only from one a and also from
epsilon. For the next programs; P
2
, P
3
and P
4
, at each
transition from one program to another we improve
the output of the string str
0
by adding some function-
alities to the next program compared to its predeces-
sor. For P
2
, it satisfies the specification R only for the
string that are formed from either one a or one b or
epsilon ({(s, s
0
)|str
0
= a ∨ b ∨ epsilon}.) For P
3
it sat-
isfies R for the string that are constructed only from
multiple a or multiple b or epsilon ({(s, s
0
)|str
0
=
a
∗
∨ b
∗
∨ epsilon}.). And for P
4
it satisfies our R for
all the string that are formed from either a or b or
epsilon ({(s,s
0
)|str
0
= (a ∨ b)
∗
∨ epsilon}.). Hence
we do have: P
0
v
R
P
1
v
R
P
2
v
R
P
3
v
R
P
4
. Therefore we
conclude that P
4
is the more correct program with re-
spect to R.
Due to the lack of space, we find in (Benabdelali,
2019) the detailed development of the example Bina-
ryCode and StringCombinations. We find also various
other examples that illustrate the program derivation
by correctness enhancement.
ICSOFT 2019 - 14th International Conference on Software Technologies
214

3.2 Empirical Study
In this section, we conduct an empirical experimen-
tation using c++ language of the examples presented
in the previous section and some others examples that
have been presented in (Benabdelali et al., 2018). To
implement the specifications, we use the concept of
test oracle that checks the programs reliability thresh-
old according to specification R. Therefore, in all ex-
amples implementations, our test oracle always con-
tains the c ++ code source of our specifications. We
define a general format, which we instantiate it for
each example to calculate the reliability of programs
with respect to given specification:
typedef struct {int n, x, y;}state;
state sinitial;state sfinal;
//--------------------------------------------
bool domR (state sinitial)
{ }// domain of specification
//--------------------------------------------
bool R (state sinitial, state sfinal)
{ }// specification
//--------------------------------------------
bool oracle (state sinitial, state sfinal)
{ }//oracle of correctness with respect to R
//--------------------------------------------
state p1(int n)
{ }// The candidates programs p1, p2, p3, etc...
//--------------------------------------------
int randomgeneration(int n)
{}//random generator
//--------------------------------------------
void tesdriver(int testdatasize)
{int counters1=0;int counters2=0;..//initialize
for(int testindex=1; testindex <= testdatasize;
++testindex){sinitial.n=randomgeneration(10000);
....}// run the test oracle on our programs
std::cout << "reliability of p1 : " <<
(counters1/static_cast<double>(testdatasize))
<< std::endl;
std::cout << "reliability of p2 : " <<
(counters2/static_cast<double>(testdatasize))
<< std::endl;
....}// check the reliability of each program
int main(){tesdriver();}
// run the tesdriver function n number times
So, for each experimentation, we just instantiate
domR, R and oracle, redefine our variables, and of
course write the programs. we define a test driver and
a random test data generator. Then we apply each test
driver to the programs generated in the corresponding
derivation. We take the example of Fermat Decompo-
sition, we generate 4 000 random numbers (as a test
data size) between 1 and 10 000. For each random
number, we execute the programs P
0
, P
1
, P
2
, P
3
and
we see which satisfies the specification R (with the or-
acle test that translates the specification R). For each
random number, if the program is correct with respect
to R, the program counter is incremented and at the
end (until we finished the generation of 4000 random
number) the counter sum of each program is divided
on test data size. As a result, for each program we
obtain a probability that will be the reliability thresh-
old according to R. Table 2 summarizes the reliability
results of the examples that we have used for the pro-
gram derivation based relative correctness.
The results obtained in each example, shows that
the reliability evolves from one program to another.
We start from a program abort that never runs suc-
cessfully since, it always gives 0 for reliability with
respect to R(it’s useless to mention it in the table),
and we enhance the transforation until we reach a cor-
rect program, or a sufficiently reliable program. Note
when we obtain reliability percentage strictly greater
than 0 and strictly less than 1 the program is partially
correct with respect to R. Furthermore, in the program
derivation process by correctness enhancement, de-
riving a reliable program follows the same process as
deriving a correct program, except that the derivation
terminates as soon as the required reliability thresh-
old matches or exceeds the selected threshold. Ac-
cording to the programs reliability results obtained in
each example, we argue that for most software prod-
ucts, as for products in general, absolute correctness
is not necessary; often, a high reliability threshold is
sufficient. This could greatly reduce the development
costs and complexity.
3.3 Towards a Mechanism for Program
Derivation Process
In the previous sections and with samples examples,
we have realized a proof of concept regarding the
program derivation process using relative correctness.
We have showed that when going from P
i
to P
i+1
we
improved the reliability of the latter according to the
specification R and we end the derivation where the
desired level of reliability has been achieved and/or
when we attain program correctness. However, un-
til there, we have reasoned as if the programs that
we have derived are at our disposal in some way or
other. Therefore, the objective of this section is to
find a mechanism that helps and guides the developer
in his program derivation process. So, we propose
three possible attempts.
3.3.1 Different Possible Scenarios
The various examples presented above and in (Ben-
abdelali et al., 2018), lead us to conclude that we can
use the program derivation process using relative cor-
rectness in at least four scenarios that will show how
Deriving Programs by Reliability Enhancement
215

Table 2: Programs reliability results.
Output of each program according to R
Programs Test
Data
Size
Input Data P
1
P
2
P
3
P
4
P
5
Median Index 3000 Random array with a size N
between 5 and 10 and with
cells between 0 and 50. Ran-
dom variable x between 60
and 80. An occurrence num-
ber of x between 0 and 4.
0.2620 0.5803 1.0000
Even number (Benabdelali,
2019)
1000 Random array of size between
1 and 5 and with value be-
tween 1 and 20.
0.2140 0.6050 0.7480
BinaryCode (Benabdelali,
2019)
4000 Random natural number n be-
tween 0 and 1024.
0.0985 0.2917 0.4860 0.8790 1.0000
StringCombinations (Benab-
delali, 2019)
5000 File of strings formed from{a,
b}.
0.2486 0.3 0.5078 1.0000
MinMax (Benabdelali, 2019) 3000 Random array of size between
5 and 25 and with value be-
tween 0 and 20. Random vari-
able z between 1 and 30.
0.0593 0.1103 1.0000
Decimal number (Benabde-
lali, 2019)
5000 Random binary numbers (n)
range between 0 and 10.
0.1782 0.7248 0.9068
Palindrome stringAB (Ben-
abdelali, 2019)
5000 Random string formed
from{a, b}.
0.2022 0.3898 0.5034
Fermat Decomposition (Ben-
abdelali et al., 2018)
4000 Random natural variable range
between 1 and 10 000.
0.2535 0.3445 1.0000
The Ceiling of the Square
Root (Benabdelali et al.,
2018)
4000 Random natural variable range
between 1 and 10 000.
≈0.00000.0102 1.0000
Analyzing a String (Benab-
delali et al., 2018)
100 ASCII file (for example: the
latex source of an article, with
symbols and numbers).
0.0057 0.2790 0.2917 1.0000
Word Wrap (Benabdelali
et al., 2018)
3000 ASCII file file (for example:
the latex source of an article,
with symbols and numbers.
0.0363 0.0873 0.1023 0.8990 1.0000
to derive a program that is more correct than another:
Domain Enlargement: using this scenario, we keep
the same program functionalities but at each transi-
tion from one program to another, we increase the do-
main of P (dom(P)) with respect to the domain of R
(dom(R))(as our binary code example).
Particular Case: the program does something else
but in particular cases, it does what the specification
R requires (e.g in the MedianIndex example, the spec-
ification mandates to return the median index where x
is found whereas P2 does something else indeed, it
returns the largest index where x is found hence P2
satisfies R only in particular cases which are the ini-
tial states in which the number of instances of x does
not exceed 2. beyond this, P2 no longer satisfies R.
Changing Behavior: the behavior of the program
changes depending on the type of input data(e.g; Fer-
mat decomposition).
Improve Program Functionality: improve the pro-
gram functionalities from one program to another
with respect to the specification(from one program to
another, we add a little bit of code to the program
until we reach a program that is absolutely correct
with respect to R or we reach a sufficiency reliabil-
ity threshold. (as string analysis, StringAB, Palin-
dromeStringAB).
Hence, the transformation from one program to
another which is more correct according to a given
specification can be done as mentioned by the differ-
ent scenarios. The only calculus to be done is about
the competence domains between the programs and
the specification R. These scenarios help the devel-
oper to decide from the beginning about the strategy
adopted in the program derivation process using rela-
tive correctness.
3.3.2 Reusable Programs Stored in a Repository
The program derivation process starts with an abort
program and then we search in the repository for pro-
ICSOFT 2019 - 14th International Conference on Software Technologies
216

grams that are more and more correct according to the
specification R by competence domain calculations.
The process finishes when a reliability threshold is
reached. It seems to be very interesting because it
encourages reuse-based development in one hand and
it capitalizes the multitude of existing programs that
can be reused.
3.3.3 Test Driven Development as an Instance of
Relative Correctness
The idea of Test Driven Development (commonly
shortened to TDD) was popularized by (Beck and
Andres, 2004) in the Extreme Programming (XP)
method. This agile software development methodol-
ogy is considered as a short iterative software devel-
opment process. It starts by developing the test before
writing the code source which specifies and validates
what the code will do (Beck, 2002). The TDD pro-
cess revolves around five simple steps: 1) write the
first test, 2) confirm the test fails because the code he
is testing does not exist, 3) write write enough code to
pass the test, 4) confirm the test passes, and 5) refac-
tor: that is to say improve it while keeping the same
functionalities.
Despite the fact that the program derivation pro-
cess using TDD is different to that of relative correct-
ness, the results obtained by both processes are the
same, where we obtain a sequence of programs that
are respectively more-correct with respect to a speci-
fication R. Our aim is to draw inspiration from TDD
process to derive programs using relative correctness.
So with a series of tests
∑
n
i=1
T
i
, we create a list of pro-
grams
∑
n
i=1
P
i
such as each P
i
is an upgrade of P
i−1
.As
a result, the competence domain increases from one
program to another. Note that to create P
n
programs,
we need T
n−1
tests. So, the notion of testing before
coding can be a way that helps the developer to derive
programs by using the approach of relative correct-
ness. In a short term research perspective, we will
better focus on developing this idea with illustrative
examples.
4 CONCLUSION
Program derivation or construction by relative cor-
rectness enhancement seems to be another way to pro-
duce executable programs sufficiently reliable but not
necessary correct for a given specification. As men-
tioned previously in this paper, this can be very at-
tractive in a world where people don’t develop from
scratch but reuse existing reliable programs. This pa-
per tried first to present concrete programs and speci-
fications used to illustrate the analytical aspect of rel-
ative correctness. Second, an empirical approach was
conducted in order to establish a proof of concept and
demonstrates the viability of the approach. Now, we
think that development based on relative correctness
is a promising tentative for constructing reliable pro-
grams. As a short term perspective, we are going to
continue the experimentation by cases from the real
world. Also, we try to find other mechanisms and sce-
narios for the program transformation process based
on relative correctness. In fact, we are conscious that
this latter process is not efficient as program deriva-
tion by refinement calculus which is older and more
mature. Hence, we still need to investigate if we can
find a kind of calculus or a set of more sophisticated
guidelines for program transformations in the Rela-
tive Correctness- based reliable program construction
approach. Furthermore, we would like to use this lat-
ter concept in the context of software maintenance
and test driven development.
REFERENCES
Back, R.-J. (1978). On the Correctness of Refinement Steps
in Program Development. PhD thesis.
Back, R.-J. and Wright, J. V. (1998). Refinement Calcu-
lus: A Systematic Introduction. Springer-Verlag New
York.
Beck, K. (2002). Test Driven Development. By Example
(Addison-Wesley Signature). Addison-Wesley Long-
man, Amsterdam.
Beck, K. and Andres, C. (2004). Extreme Programming
Explained: Embrace Change (2Nd Edition). Addison-
Wesley Professional.
Benabdelali, M. (2019). Deriving programs by reliability
enhancement appendix. https://drive.google.com/file/
d/1jW7B0mvqndIX tS-Cqla3wXu Hpoe 0H/view?
usp=sharing.
Benabdelali, M., Labed Jilani, L., Ghardallou, W., and Mili,
A. (2018). Programming without refining. Electronic
Proceedings in Theoretical Computer Science.
Chris Brink, W. K. and Schmidt, G. (1997). Relational
Methods in Computer Science. Advances in Computer
Science. Springer Verlag, Berlin, Germany.
Diallo, N., Ghardallou, W., Desharnais, J., and Mili, A.
(2015). Program derivation by correctness enhace-
ments. In In Proceedings, Refinement 2015.
Khaireddine, B., Zakharchenko, A., and Mili, A. (2017).
Correctness enhancement,a pervasive software engi-
neering paradigm. In Third Spring Festival Workshop.
Morgan, C. (1990). Programming from specifications.
Prentice-Hall.
O’Regan, G. (2017). Software Reliability and Dependabil-
ity. In book: Concise Guide to Formal Methods.
Deriving Programs by Reliability Enhancement
217