Assessment of Extreme Surge Simulation Accuracy in the Sea of Azov

for Various Types of Atmospheric Forcing and Ocean Model

Parameters

Vladimir Fomin

, Nikolay Diansky

1,2,3 b

, Evgeniya Korshenko

and Irina Panasenkova

Department of Numerical Modelling of Hydrophysical processes, Zubov State Oceanographic Institute, Moscow, Russia

Faculty of Physics, M. V. Lomonosov Moscow State University, Moscow, Russia

Institute of Numerical Mathematics, Russian Academy of Sciences, Moscow, Russia

Keywords: Azov Sea, Numerical Modelling, Atmospheric and Marine Circulation Models, Storm Surge.

Abstract: This paper focuses on numerical modelling of an extreme surge in the Taganrog Gulf on March 24, 2013 to

study its formation features and identify the requirements for an accurate reproduction of atmospheric and

marine circulation in the Sea of Azov. Two versions of the three-dimensional σ-model of marine circulation

INMOM (Institute of Numerical Mathematics Ocean Model) with different spatial resolutions of ~4 km and

~250 m were originally used. Additionally, two types of atmospheric forcing were used during the simulations

of these models: Era-Interim reanalysis and WRF (Weather Research and Forecast Model) model data. The

paper shows that, according to the obtained results, the accuracy of an extreme surge reproduction in the Sea

of Azov was more dependent on the quality of atmospheric forcing than on the spatial resolution of the marine

circulation model. Additional simulations were performed with three different configurations within the

INMOM version with a spatial resolution of ~250 m and with the use of the WRF atmospheric forcing.

Configurations varied in types of the model: baroclinic, barotropic and shallow water approximation.

However, simulation results of the models with different configurations were practically identical to each

other.

1 INTRODUCTION

The Sea of Azov with its coastal cities, intensive

navigation, developed fishing and recreational

potential has great economic importance. Therefore,

forecasting of extreme storms in it is especially

valuable. It should be noted that the strongest impact

of the storm on economic activities is connected to

the sea level fluctuations in the Sea of Azov due to

surges. Nowadays, numerical modelling is a widely

applied approach for their simulation. Although it has

reached high level of accuracy for the Sea of Azov

(Popov and Lobov, 2016; Filippov, 2012), further

attempts to improve the accuracy of simulation results

should still be made. Numerical modeling results

depend on various factors, especially on the use of

https://orcid.org/0000-0001-8857-1518

https://orcid.org/0000-0002-6785-1956

https://orcid.org/0000-0003-2310-9730

https://orcid.org/0000-0002-8338-4825

atmospheric forcing and a configuration of the marine

hydrodynamics model with its physical

parametrizations and spatial resolution. This article

examines these factors and their influence on the

simulation results with numerical modelling of an

extreme surge that occurred on March 24, 2013.

According to the data from a series of observations

for 1881-2013, this surge is the second strongest after

the historical surge of 1997. Observational data for

the surge of 2013 is available and can be used for the

appropriate setting up and verification of models. In

the present study, several versions of the three-

dimensional σ-model of marine circulation INMOM

(Institute of Numerical Mathematics Ocean Model)

with different spatial resolution and various types of

model configurations are used as models of sea

340

Fomin, V., Diansky, N., Korshenko, E. and Panasenkova, I.

Assessment of Extreme Surge Simulation Accuracy in the Sea of Azov for Various Types of Atmospheric Forcing and Ocean Model Parameters.

DOI: 10.5220/0007836603400344

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 340-344

ISBN: 978-989-758-371-1

dynamics. During simulations of these models two

types of atmospheric forcing are used.

2 METHODOLOGY

Three-dimensional σ-coordinate model of marine

circulation INMOM is used to calculate the

circulation in the Sea of Azov. It was developed at the

INM RAS (Institute of Numerical Mathematics of the

Russian Academy of Sciences) (Diansky, 2013). The

model is based on so called system of primitive

equations in approximations of hydrostatics and

Boussinesq expressed in the generalized orthogonal

coordinates in horizontal direction and in σ-system of

coordinates in vertical direction. Such system with an

additional applied linearization is of the following

form:





−

(

+

)

 = −



























−



















+

(1)





+

(

+

)

 = −



























−



















+

(2)





+













(3)







=















++





(4)







=















+

(5)

=

(

,+35‰,



)

−

(

0,0,





)

(6)

Here  – depth of the ocean being at rest; 



and 



–

metrical coefficients, =(,) – horizontal

velocity vector,  and  – zonal and meridional

components of the current velocity;  – vertical

velocity in the  – system of coordinates;  –

deviation of the ocean level from its undisturbed

state;  – potential temperature;  – penetrating solar

radiation flow;  – salinity net of the constant value

of 35‰;  – deviation of the water density from a

certain average density profile which depends only on

the hydrostatic pressure 



 with the average

density in the ocean 



= 1.025/



at the depth

= . Non-linear state equation 

(

, +

35‰,



)

for the water density computation,

considering compressibility due to the hydrostatic

pressure 



, is taken from (Brydon, 1999). Coriolis

parameter is =2Ω



, where Ω



– angular rate of

the Earth rotation considering the annual rotation

around the Sun, and  – geographical latitude;  –

summand which describes the additional pulse

transfer in curvilinear coordinates;



- atmospheric

pressure on the ocean surface; .



,



– coefficients

of vertical turbulent viscosity and diffusion; 



and





– components of the horizontal pressure gradient;





, 





– operators of transfer;  – operator of lateral

diffusion of heat and salt which is chosen to be equal

for  and .

Various versions of this model were successfully

used in numerical simulations of the World Ocean

circulation (Gusev and Diansky, 2014; Diansky, 2013),

as well as for the circulation in the western seas of the

Russian Arctic (Diansky et al., 2014, Diansky et al.,

2015), the Black, Caspian, Japanese and Baltic Seas

(Diansky et al., 2012; Zakharchuk et al., 2016;

Stepanov et al., 2014; Zalesny et al., 2012). The global

version of INMOM serves as an oceanic block of the

Earth system model created at INM RAS, participating

in international programs for research and prediction of

climate change (Volodin et al., 2013).

This paper used two versions of the INMOM

model for reproducing the Sea of Azov circulation:

the BAMS model, which includes basins of the Black,

Azov and Marmara Seas with a horizontal resolution

of ~ 4 km, and the AS model, which includes the Sea

of Azov basin with the Kerch Strait and the adjacent

waters of the Black Sea (up to about 100 m) with a

horizontal resolution of ~250 m. Fomin and Diansky

(2018) provide a detailed description of BAMS and

AS models’ configurations and physical

parametrizations.

3 RESULTS AND DISCUSSION

3.1 Analysis of the Impact of the

Atmospheric Forcing and the

Spatial Resolution of the INMOM

Model on the Sea of Azov

Circulation

The quality of atmospheric forcing is one of the key

factors affecting the accuracy of marine dynamics’

calculation. Therefore, two different types of an atmos-

pheric forcing were used to calculate the atmospheric

impact: one was from the Era-Interim global

atmospheric reanalysis with spatial resolution of 80 km

Assessment of Extreme Surge Simulation Accuracy in the Sea of Azov for Various Types of Atmospheric Forcing and Ocean Model

Parameters

341

and the other one was from the regional atmospheric

model WRF with spatial resolution of 10 km,

calculated at the Zubov State Oceanographic Institute.

Module and components of wind speed with a

resolution of 6 hours from the coastal weather stations

in Taganrog and Kerch were used to validate obtained

results of calculations using the WRF model and the

Era-Interim reanalysis. Detailed results of this

verification were discussed in the work of Fomin and

Diansky (2018). Verification results of

meteorological characteristics showed that, in

comparison with the Era-Interim reanalysis, the data

in the WRF model reproduced meteorological

characteristics over the Sea of Azov Sea more

accurately, especially during storms.

We used both versions of the INMOM model,

BAMS and AS models, for the simulation of the 2013

surge in the Taganrog Gulf with meteorological

parameters from the Era-Interium reanalysis, as well

as the WRF model. Experiments were carried out for

the period from January 1 till March 31, 2013. We

used January climatic fields of temperature and

salinity, and zero current velocity fields as initial

conditions. Moreover, it was assumed that there was

no ice field in the Sea of Azov.

The AS model with a spatial resolution of 250 m

was applied for simulation of the Sea of Azov

dynamics using Era-Interium reanalysis, as well as

WRF atmospheric characteristics. We only used the

WRF data in the numerical experiments with the

BAMS model with a spatial resolution of 4 km. We

used sea level observations at the Taganrog station in

order to estimate the accuracy of simulated sea level,

especially during the storm situations, using AS and

BAMS models.

At first, we analysed the results from the AS

model, as an a priori more accurate model because of

its higher spatial resolution, and assessed the impact

of the atmospheric forcing type on the reproduction

of the storm surge in the Sea of Azov. Hereinafter, the

analysis was carried out for the sea level deviation

from the average value. The average value was

calculated for the period of 01.02 - 03.31.2013.

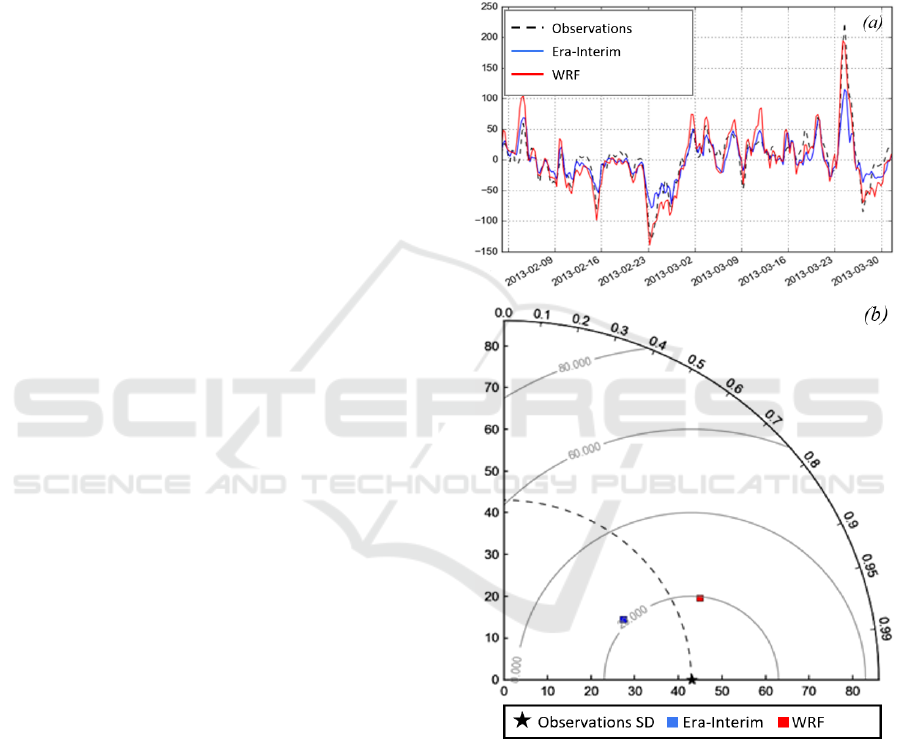
Figure 1 shows verification results of the

modelled sea level using the AS model with

atmospheric characteristics from the Era-Interim

reanalysis and from the WRF model, as well as the

observation data from the Taganrog station.

According to the calculation results, sea level during

the extreme surge on 24.03.2013 was more accurately

reproduced with the WRF model data. The maximum

value of the sea level using WRF forcing for the

Taganrog station was 194.7 cm. At the same time, the

maximum sea level according to the observations

reached 223.4 cm. The correlation coefficient

reached 0.92 for the WRF data, and equaled 0.88 for

the data from the Era-Interim reanalysis. However,

the standard deviation of the sea level was smaller for

the WRF data than for the Era-Interim data: 19.8 cm

and 21.3 cm, respectively.

Thus, calculations using WRF forcing made it

possible to improve the storm surge simulation and

the quality of the sea level variability.

Figure 1: a) Comparison between the sea level observations

from the Taganrog station (black line) and the sea level

simulated by the AS model using Era-Interium reanalysis

(blue line) and the WRF data (red line); b) the Taylor

diagram for the experiments. Black star corresponds to the

standard deviation for measurement data; blue square – Era-

Interium reanalysis; red square – WRF model.

Therefore, WRF forcing was more suitable for the

simulation of the storm surge in 2013. For this reason,

the research of the horizontal resolution of two

versions of the INMOM model (AS and BAMS

ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics

342

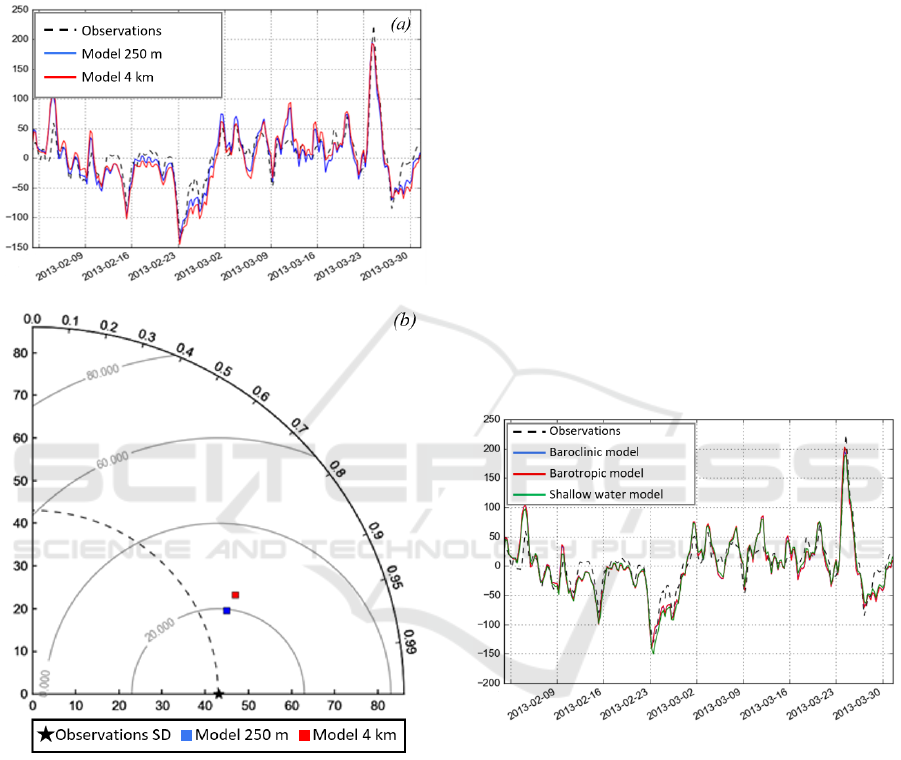
models) was carried out using meteorological

parameters from the WRF model. Results of the

verification of the simulated data with observation

data showed that the AS model with horizontal

resolution of 250 m reproduced sea level slightly

better (Figure 2).

Figure 2: a) Comparison between the sea level observations

from the Taganrog station (black line) and sea level

simulated by the AS model (blue line) and by the BAMS

model (red line); b) the Taylor diagram for the considered

experiments. Black star corresponds to the standard

deviation for measurement data; blue square –for the AS

model; red square – for the BAMS model.

3.2 Effects of the INMOM

Configuration on the Azov Sea

Circulation

One more experiment was conducted in order to

estimate the influence of the INMOM model

configuration on the quality of simulated

hydrodynamical parameters.

We conducted a comparative analysis of the sea

level calculated for the period from February 1 until

March 31, 2013, using three methods of numerical

modelling: three-dimensional baroclinic version of

the INMOM model, three-dimensional barotropic

version of the INMOM model and shallow water

model implemented in the INMOM. In the barotropic

model prognostic variables included current velocity

and sea level. It was also assumed that the density

gradients did not vary.

Figure 3 shows the results of the sea level

calculations using three versions of the INMOM

model with a spatial resolution of 250 m.

Meteorological characteristics were taken from the

WRF model. According to the Figure 3, the results of

calculations were almost identical. All models

realistically described main trends in the sea level

variability. In general, the three model versions

adequately reproduced the sea levels. Although the

storm surge on the March 24, 2013 in the Taganrog

Bay was underestimated by all of them, the shallow

water model performed worse than other models.

Figure 3: Sea level calculated using baroclinic INMOM

model (blue line), barotropic INMOM model (red line) and

shallow water model (green lone) from 01.02.2013 till

31.03.2013 in the Taganrog Bay of the Sea of Azov.

The experiments’ results showed that the non-

hydrostatic WRF model calculations of the

atmospheric forcing allowed reproducing extreme

storm situations with higher accuracy than the Era-

Interim reanalysis. A comparison of the results with

observational data demonstrated that both the

meteorological characteristics, including wind speed

and direction, and the sea level variability were

reproduced well. Therefore, the proposed approach

can be used in the future to predict and prevent

emergencies in the studied area of the Sea of Azov.

Assessment of Extreme Surge Simulation Accuracy in the Sea of Azov for Various Types of Atmospheric Forcing and Ocean Model

Parameters

343

4 CONCLUSIONS

We examined the basic features of an extreme surge

in the Taganrog Gulf on March 24, 2013 using two

versions of the INMOM model with different spatial

resolutions of ~4 km and ~250 m. Two types of

meteorological parameters were used to study the

impact of the atmospheric forcing on the Sea of Azov

dynamics: Era-Interim reanalysis with horizontal

resolution of 80 km and WRF model data with

horizontal resolution of 10 km.

We demonstrated that the simulation based on

the WRF atmospheric forcing with a higher spatial

resolution reproduced the extreme surge with higher

accuracy than the simulation based on the Era-

Interim reanalysis. At the same time, the results of

the sea level simulation during the non-extreme

period did not depend much on the type of

atmospheric forcing.

For the area of the Taganrog Gulf, increased

spatial resolution of the marine circulation model

slightly improved the quality of the extreme surge

reproduction, particularly in the coastal areas.

However, this improvement of the model amounted

to no more than 3-5%. Therefore, the formation of the

surge was mainly determined by the response of the

circulation in the entire Sea of Azov basin to the

atmospheric forcing.

Additionally, we carried out the experiments

with various configurations of the INMOM model to

study the effect of baroclinicity on the storm surge

reproduction in 2013. Three versions of the INMOM

model with spatial resolution of 250 m were used for

these experiments: the baroclinic model, the

barotropic model and shallow water model. As

expected, for such a shallow basin as the Sea of

Azov, the baroclinic factor had a negligible impact

on the storm surges reproduction. Thus, simplified

models would be suitable for calculating surge

levels only. However, if the task was to reproduce

the full hydrodynamics of the Sea of Azov,

including sea ice, then it was necessary to use

complex models of the sea circulation with high

quality atmospheric forcing.

ACKNOWLEDGEMENTS

This work was supported by the Russian Foundation

for Basic Research according to the research project

№17-05-41089.

REFERENCES

Brydon D., San S., Bleck R., 1999. A new approximation

of the equation of state for sea water, suitable for

numerical ocean models. J. Geophys. Res., 104(C1):

1537–1540.

Diansky, N. A., 2013. Modelling of the ocean circulation

and study of its response to short-term and long-term

atmospheric forcing. 1

ed. Physmatlit, Moscow. (in

Russian)

Diansky, N. A., Gusev A. V., Fomin V. V., 2012. The

Specific Features of Pollution Spread in the North west

Pacific Ocean. Izvestiya, Atmospheric and Oceanic

Physics, 48(2): 222-240.

Diansky, N. A., Fomin, V. V., Kabatchenko, I. M.,

Gruzinov, V. M., 2014. Simulation of Circulation in the

Kara and Pechora Seas with the System for Operational

Diagnosis and Forecasting of Marine Dynamics.Arctic:

Ecology and Economy, 1(13): 57-73. (in Russian)

Diansky, N. A., Kabatchenko, I. M., Fomin, V. V.,

Arkhipov, V. V., Tsvetsinskii, A. S., 2015. Simulation

of Hydrometeorological Characteristics in the Kara and

Pechora Seas and Computation of Sediments near the

Western Coast of the Yamal Peninsula. Vesti Gazovoi

Nauki, 2(22): 98-105. (in Russian)

Filippov, Yu. G, 2012. Natural fluctuations of the Sea of

Azov level. Russian meteorology and hydrology,-2:

126-129. doi: 10.3103/S1068373912020082

Fomin, V. V., Diansky, N. A., 2018. Simulation of Extreme

Surges in the Taganrog Bay with Atmosphere and

Ocean Circulation Models. Russian Meteorology and

Hydrology, 43(12): 843-851.

Gusev, A. V., Diansky, N. A, 2014. Numerical Simulation

of the World Ocean Circulation and Its Climatic

Variability for 1948–2007 Using the INMOM.

Izvestiya, Atmospheric and Oceanic Physics, 50: 1-12.

Popov, S. K., Lobov, A. L., 2016. Diagnosis and

Forecasting of the Flood in Taganrog Using an

Operational Hydrodynamic Model. Trudy

Gidromettsentra Rossii, 362: 92-108. (n Russian)

Stepanov, D. V., Diansky, N. A, Novotryasov, V. V., 2014.

Numerical Simulation of Water Circulation in the

Central Part of the Sea of Japan and Study of Its Long-

term Variability in 1958–2006. Izvestiya, Atmospheric

and Oceanic Physics, 50(1): 73-84.

Volodin, E. M., Diansky, N. A., Gusev, A. V., 2013.

Simulation and Prediction of Climate Changes in the

19th to 21st Centuries with the Institute of Numerical

Mathematics, Russian Academy of Sciences, Model of

the Earth’s Climate System. Izvestiya, Atmospheric and

Oceanic Physics, 49(4): 347-366.

Zakharchuk, E. A., Tikhonova, N. A, Gusev, A. V.,

Diansky, N. A., 2016. Comparison of Methods for

Numerical Hydrodynamic Modeling of the Baltic Sea

Level Fluctuations. Trudy GOIN, 217. (in Russian).

Zalesny, V. B., Diansky, N. A, Fomin, V. V., Moshonkin,

S.N., Demyshev, S.G., 2012. Numerical Model of the

Circulation of the Black Sea and the Sea of Azov. Russ.

J. Num. Anal. and Math. Model, 27(1): 95-112.

ONM-CozD 2019 - Special Session on Observations and Numerical Modeling of the Coastal Ocean Zone Dynamics

344