Exploiting Physical Contacts for Robustness Improvement of a

Dot-painting Mission by a Micro Air Vehicle

Thomas Chaffre

, Kevin Tudal

, Sylvain Bertrand

and Lionel Prevost

Learning, Data and Robotics Lab, ESIEA, Paris, France

ONERA - The French Aerospace Lab, Palaiseau, France

Keywords:

Aerial Robotics, Contact based Navigation, Dot-painting.

Abstract:

In this paper we address the problem of dot painting on a wall by a quadrotor Micro Air Vehicle (MAV), using

on-board low cost sensors (monocular camera and IMU) for localization. A method is proposed to cope with

uncertainties on the initial positioning of the MAV with respect to the wall and to deal with walls composed

of multiple segments. This method is based on an online estimation algorithm that makes use of information

of physical contacts detected by the drone during the ﬂight to improve the positioning accuracy of the painted

dots. Simulation results are presented to assess quantitatively the efﬁciency of the proposed approaches.

1 INTRODUCTION

Robotics has experienced an outstanding growth and

gained focus in recent years both from research and

industry. Nowadays, use of robots in everyday life is

becoming more and more usual. Researchers, teach-

ers, students and artists are trying to use robotic plat-

forms for creation, expression and sharing, bridging

the gap between arts and engineering. As a mat-

ter of fact, Science, Technology, Engineering, Art

and Mathematics (STEAM) are now considered as a

whole in education or research, and in close relation-

ship to robotics.

The ﬁrst cybernetic sculpture of history, named

CYSP1, was created in 1956 by Nicolas Sch

offer

(Pagliarini and Hautop Lund, 2009). An electronic

“brain” attached to it allowed its sensors (photocells

and microphone) to catch all natural variations in

colour, light and noise intensity in its surroundings or

made by the audience and therefore react to it. Ever

since this period, a lot of attempts have been made

to use robotic systems in the process of artistic cre-

ation, either autonomously or teleoperated by artists.

Designing and disposing of a robot with drawing or

painting capability is a challenge from a technical

point of view, but it is also very interesting for artists

in terms of creativity.

If the robotic system is supposed to duplicate a

given drawing, painting is a process that requires mul-

tiple abilities: being able to perform precise move-

ments, stay in contact with a surface and adapt to

the environment changes. Aerial robots with Verti-

cal Take-Off and Landing (VTOL) capabilities are ap-

pealing platforms thanks to the size of the operating

volume enabled by aerial capacity and their low-speed

and stationary ﬂight capabilities. The term “Paint-

ing Drone” appeared in the early 2014s (Handy-Paint-

Products, 2014). From this time forth, several paint-

ing drone projects where a quadcopter is equipped

with a remotely activated spray-paint have been de-

veloped. One of the ﬁrst to do that was the artist

KATSU in 2015 who used a quadcopter to draw on

a public billboard in the city of New-York. The ﬁrsts

tangible projects of drone painting then emerged in

2016 with (Leigh et al., 2016) where an AR Drone

2.0 quadrotor was used to reproduce in real time the

movements made by an user with a pen, and with

(Galea and Kry, 2017) (Galea et al., 2016) where a

small quadrotor robot was utilized for stippling. A

motion capture system was used to measure the posi-

tion of the robot and the canvas, and a robust control

algorithm to drive the robot to different stipple posi-

tions and make contact with the canvas using an ink

soaked sponge. In 2017, the exhibition “Evolution

2.1” by Misha Most at the Winzavod Cultural Center

in Moscow presented a fresco realized by a painting

drone (Most, 2017). The quadcopter robot was able to

precisely and autonomously paint on wide facades in-

door and outdoor which can be considered as the best

performance with a painting drone known to date.

In all the aforementioned works, the painting

drones were either remotely controlled by the artist,

Chaffre, T., Tudal, K., Bertrand, S. and Prevost, L.

Exploiting Physical Contacts for Robustness Improvement of a Dot-painting Mission by a Micro Air Vehicle.

DOI: 10.5220/0007838900510060

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 51-60

ISBN: 978-989-758-380-3

or made use of an external motion capture system

to localize themselves and perform the painting au-

tonomously. This kind of setup can be expensive and

restricts the use of these robots to known and ade-

quately equipped environments. The problem investi-

gated in this paper is therefore the one of autonomous

dot-painting by a quadrotor using on-board sensors

for localization.

In the process of dot-painting, contacts have to be

made with the support to be painted (eg. wall, facade).

Contrary to classical mobile robotics, where collision

avoidance with the environment is a major concern,

contact is here imposed by the mission. Use of col-

lisions for the navigation of a ﬂying robot has been

addressed by some works of the literature. In (Briod

et al., 2013) a contact-based navigation method has

been developed using a ﬂying robot that can sus-

tain collisions and that can self-recover once on the

ground thanks to active legs. Random exploration is

performed by the robot which taking advantage of

the information from contact sensors to correct its

direction after every collision with obstacles (walls,

ceiling, ﬂoor). More recently, (Y

uksel et al., 2019)

and (Ollero et al., 2018) have proposed control ap-

proaches to ensure physical interactions between a

multi-rotor micro aerial vehicle and its environment

for industrial use cases.

In this paper, an estimation and control strategy

is proposed to enable autonomous and accurate dot-

painting missions by a quadrotor robot using only on-

board low-cost sensors (monocular camera and IMU).

The main contribution consists in the design of an on-

line estimation procedure taking advantage of colli-

sions to ensure robustness of the mission with respect

to two types of uncertainties: uncertainty on the ini-

tial positioning of the robot with respect to the support

that has to be painted; uncertainty on the knowledge

of the shape of the support. Implementation and per-

formance analysis of the proposed approach are real-

ized through realistic simulations (ROS+Gazebo) by

considering scenarios with both types of uncertain-

ties.

The paper is organized as follows. Section 2 is

devoted to notations and problem deﬁnition. Section

3 presents the navigation system and the dot-painting

strategy. Section 4 presents the proposed estimation

and control approach exploiting contact information

and illustrate its efﬁciency on the scenario of dot-

painting on a ﬂat wall. Section 5 is devoted to its ex-

tension to deal with walls composed of multiple seg-

ments. Finally, Section 6 concludes this work.

2 NOTATIONS AND PROBLEM

DEFINITION

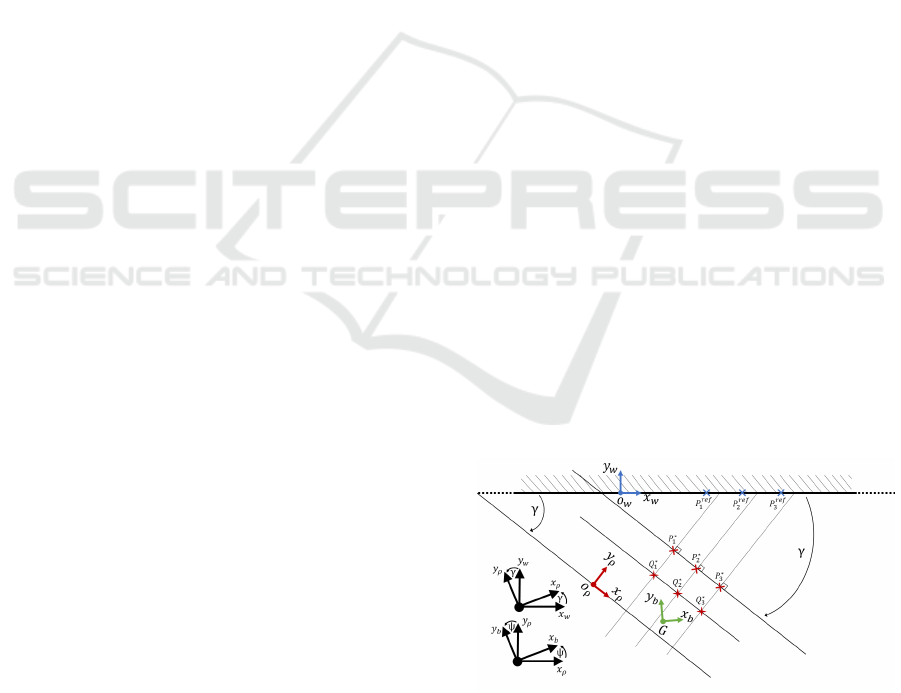
2.1 Reference Frames

Three reference frames that will be used in the

problem description are introduced in this section.

They are presented in Figure 1.

The ﬁrst one is a ﬁxed reference frame

: (O

, y

, z

) attached to the wall. Paint

dots to be applied will be deﬁned in this frame.

The second frame is deﬁned by R

, y

, z

) and corresponds to the frame in

which the localization of the robot is performed

by its on-board navigation system. Its origin O

corresponds to the initial position of the quadrotor,

before take-off, and its orientation is deﬁned by the

initial directions of the main axis of the quadrotor,

before take-off. Assuming a 2D representation of

the problem, the transformation R

→ R

is deﬁned

by the translation vector δ =

−−−→

and the rotation

matrix R(γ) parameterized by the angle γ.

The third frame to be deﬁned is the body frame

: (G;x

, y

, z

) attached to the center of gravity G

of the quadrotor robot and oriented along its main

axis. The current position vector of the drone is de-

noted by ξ =

−−→

G. The on-board navigation system

of the drone will provide its position coordinates ξ

(ρ)

in R

. Assuming quasi-stationary ﬂight (low speed

and small attitude angles), and for simpliﬁcation of

the dot-painting problem, only the yaw angle ψ of

the quadrotor will be considered. The transformation

→ R

is therefore determined by the translation

vector ξ and the rotation matrix R(ψ) parametrized

by the angle ψ. Note that, before take-off the two

frames R

and R

coincide.

Figure 1: Dot-painting problem formalization.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

2.2 Deﬁnition of Paint Dots

The objective is to apply a set of n ∈ N

∗

paint dots

re f (w)

, i = 1, .., n, whose coordinates are deﬁned

in R

re f (w)







re f (w)







, i = 1, . . . , n

At the initial instant t = 0, it is assumed that the drone

disposes of a list of these points. Since localization

information on the drone is available in R

, the co-

ordinates of these points must therefore be deﬁned in

this frame. They are denoted by P

∗(ρ)

and deﬁned by

∗(ρ)







∗(ρ)







= R(γ)



re f (w)

− δ

(w)



, i = 1, .., n

(1)

Note that this deﬁnition requires a perfect knowledge

of (δ, γ). Uncertainties on these parameters will lead

to errors in the resulting positions of the paint dots.

Although the whole dot-painting mission will be re-

alized autonomously by the quadrotor, the initial po-

sitioning of the robot with respect to the wall is as-

sumed to be done by a human operator. Knowing the

desired location on the wall of the paint dots, the op-

erator will be asked to place the drone facing the wall

and at a given distance d from the origin O

. If the

accuracy of this initial positioning was perfect, one

would have at t = 0: δ

(w)

= ξ

(w)

(0) = [0, −d, 0]

and

γ = ψ(0) = 0. Since in practice this initial position-

ing will suffer from uncertainties, an estimate of the

value of (δ, γ) has to be performed and used to update

the deﬁnition of the points P

∗(ρ)

so that the pattern

obtained by the paint dots matches the desired one as

much as possible.

This paper aims at proposing such a method to

compute an online estimate (

(w)

γ) of (δ

(w)

, γ), along

with the corresponding updates of the P

∗(ρ)

, by ex-

ploiting information of physical contacts of the MAV

with the wall. This information consists in the coor-

dinates of the contact points denoted

c(ρ)







c(ρ)







, i = 1, . . . , n

which correspond to the coordinates of the MAV pro-

vided in R

by the on-board localization system when

can be deﬁned for example as the ground projection

of the ﬁrst point to be painted.

a contact with the wall is detected (see Section 3.2).

At the initial instant t = 0, the initial value

of the estimates are deﬁned as (

(w)

(0),

γ(0)) =

([0, −d, 0]

, 0) which corresponds to the instruction

given to the operator for the quadrotor initial posi-

tioning. Instead of using (1) which requires a perfect

knowledge of (δ

(w)

, γ) and which is not available, the

list of paint dots given to the quadrotor at t = 0 is

computed using

∗(ρ)

= R(

γ(0))



re f (w)

−

(w)

(0)



, i = 1, .., n (2)

As will be described later in the paper, accumulating

information as contacts occur will improve the esti-

mation process and the accuracy of the positioning of

the next points to be painted. Detection of the contacts

is explained in the next section along with localization

and control strategy for the drone.

3 CONTROL AND ESTIMATION

ARCHITECTURE FOR

DOT-PAINTING

This section describes the localization and control ar-

chitecture of the drone as well as the simulation tools

used for implementation and validation of the pro-

posed approach.

3.1 Simulation Environment

The proposed methods have been implemented us-

ing the ROS (Robot Operating System) middleware

and the Gazebo simulator. The drone simulated is

an AR Drone 2.0 and the ardrone autonomy (Mon-

ajjemi, 2014) and tum ardrone (Engel et al., 2014b)

packages are used. Gazebo is a 3D dynamic simula-

tor which offers physics simulation with a high degree

of ﬁdelity and a large suite of robot and sensor mod-

els. The model used to simulate the quadrotor robot is

representative of the true robot dynamics but does not

account for external perturbations. In reality, the air

ﬂow generated by the rotors acts as an external pertur-

bation that can disturb the quadcopter ﬂight when it is

operating close to a facade. This is not included in our

simulations and will be addressed in future work.

To mimic the act of dot-painting in Gazebo, we

decided to make the quadcopter touch the facade and

then to make a dot appears (represented by the yellow

dots in Figure 3) at the collision coordinates.

3.2 Contact Painting Strategy

To perform dot-painting, the quadcopter must impact

the wall at each dot coordinates. To do so, for each

Exploiting Physical Contacts for Robustness Improvement of a Dot-painting Mission by a Micro Air Vehicle

paint dot P

∗(ρ)

to be applied, the chosen strategy is to

make use of a PID position controller to ﬁrst stabilize

the quadrotor at a ”waiting” position Q

∗(ρ)

located at

a given offset distance ∆ from P

∗(ρ)

(see Figure 1):

∗(ρ)

= P

∗(ρ)

− [0 ∆ 0]

Following this, a velocity controller is then used to

move the quadcopter along the y

direction towards

the wall, until contact.

Collisions between the robot and the wall are

detected by monitoring the acceleration measurement

along the y

axis provided by the IMU. If the absolute

value of this acceleration measurement



exceeds

a predeﬁned threshold (which was chosen to be

0.25g), it is assumed that the robot just touched the

facade. An example of acceleration measurements

and contact detections is given in Figure 2.

Figure 2: Contact detection from acceleration measure-

ments.

Once a contact is detected, the position controller

is used again to assign the robot back to the Q

∗

”waiting” point. Using the information of contact, the

estimation process of (δ

(w)

, γ) is run and the updated

coordinates of the next paint dot are computed along

with the new yaw reference to align the drone with

the wall. The whole process is repeated until the last

paint dot is applied onto the wall.

3.3 MAV Localization

For applications in GPS-denied or GPS-perturbed en-

vironments, such as in close proximity to facades,

speciﬁc methods have to be used for localization of

the drone. Different kinds of Simultaneous Localiza-

tion And Mapping (SLAM) methods allow to deter-

mine the position of a robot from IMU measurements

and vision (Mei and Rives, 2007).

In this paper, the AR Drone 2.0 quadcopter has

been chosen as test platform. This choice is moti-

vated by the fact that it is equipped with an IMU and

a monocular camera, which are the sensor suite of in-

terest, and by the availability of software drivers and

simulation packages for this drone. Indeed, a monoc-

ular SLAM based on the Parallel Tracking and Map-

ping (PTAM) algorithm (Engel et al., 2014a)(Engel

et al., 2012a)(Engel et al., 2012b) is provided in the

tum ardrone package used for simulation and is there-

fore used as localization algorithm. It provides an es-

timate of the pose of the robot in R

which will be

considered in the control algorithm. This estimate is

accurate enough for small speed and short term tra-

jectories but may suffer a drift when used over a long

period of time.

If the number of paint dots is large, the mission

will indeed have a long duration. To account for the

energetic endurance of the robot, it has been chosen

to make the quadcopter land after every ∼ 8 min-

utes of ﬂight. It is assumed that landing is realized

at the same location as take-off (automatic return to

a home battery charging or changing station for ex-

ample, equipped with a visual tag so that the drone is

able to automatically land on the same point). This

”break” in the mission can also be used to reﬁll the

painting system, and is ﬁnally taken as an opportu-

nity to reset the PTAM algorithm so that the localiza-

tion of the drone will not be affected by the long-term

drift. Of course the estimation process is not reset and

the current value obtained for the estimate (

(w)

γ) is

maintained.

The monocular PTAM algorithm used in this nav-

igation system also provides a 3D point cloud of the

environment. An intuitive idea would be to use it

to make a 3D reconstruction of the wall, but in our

use case, it is not possible. The PTAM method es-

timates the position of the camera for mapping posi-

tions of points of interest in the space by analyzing

and processing the image provided by the camera in

real time. To do that, the algorithm needs various tex-

tured elements to be present in the image. Because of

the very close proximity and contacts to the wall, it

is not possible to make the camera of the drone face

the wall. In addition, looking at low textured walls

would not enable us to get enough points of interest

for the computer vision algorithm. To overcome this

problem, an angular offset of 90deg has been chosen

between the optical axis of the camera and the normal

to the wall. In other terms, and according to the no-

tations used in the deﬁnition of the reference frames

(see Figure 1), the camera is directed along the x

axis

of the robot, and the painting system along y

to be

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

facing the wall. Therefore the camera is not looking

directly at the wall. By doing this, the PTAM method

is able to detect enough points for localization but the

3D mapping capability of the algorithm may not be

used anymore to get 3D information on the wall. This

motivates the proposed strategy of using collisions to

generate information about the wall without bother-

ing the PTAM method in its process of tracking and

mapping.

4 DOT PAINTING ON A FLAT

WALL

4.1 Scenario Description

In this scenario, the goal is to apply a set of 140 dots

re f

0:140

) on the ﬂat wall visible in Figure 4, forming

a predeﬁned drawing that is 3.5 meters wide and 2.1

meters high (see Figure 3). The application order of

the dots has been arbitrarily chosen to be from the

right to the left and from the top to the bottom. To

improve the estimation process of (δ

(w)

, γ), an addi-

tional point is introduced just before the ﬁrst dot of the

drawing and far enough from it. Therefore, contact in-

formation from these two ﬁrst distant points will lead

to a rather good ﬁrst estimate, that will be improved

then after collecting more and more contact informa-

tion. This process is described in more details in the

next subsection.

Figure 3: Reference positions of the paint dots to be applied

used for the different simulations.

Figure 4: The Gazebo world used for the ﬂat wall scenario.

4.2 Estimation from Contact

Information

The objective here is to compute an estimate (

(w)

γ)

of (δ

(w)

, γ) by making use of the information on

the discrepancy between the reference coordinates

re f (w)

of the points to be painted and the obtained

coordinates P

c(ρ)

of the collision points.

Let us denote by i the index of the last collision

point achieved. The estimation process is run after

each collision, for i ≥ 2. For i < 2, the initial value

(

(w)

(0),

δ(0)) is used instead.

The estimate (

(w)

) is computed, after the i-th con-

tact, as the solution of the optimization problem

min

(

(w)

γ)

∑

j=1



γ)P

c(ρ)

(w)

− P

re f (w)



(3)

where the coefﬁcients ω

are some strictly positive

weights. Note that a 2D problem is considered here by

deﬁning the reference points and contact points used

in (3) by two-dimensional vectors from the x and y

components of the 3D points. Other choices, eg. val-

ues of ω

depending on the localization accuracy at

the time of contact j, will be investigated in future

work.

This is the classical problem of ﬁnding the

best-ﬁtting rigid transformation between two sets of

matching points and for which an analytical solution

exists. To compute this solution, a method based on

Singular Value Decomposition (SVD) is used. The

different steps of this method are the one presented in

(Sorkine-Hornung and Rabinovich, 2017):

1. Compute the centroids of both point sets:

c(ρ)

∑

j=1

c(ρ)

∑

j=1

(4)

Exploiting Physical Contacts for Robustness Improvement of a Dot-painting Mission by a Micro Air Vehicle

re f (w)

∑

j=1

re f (w)

∑

j=1

(5)

2. Compute the centered vectors ( j = 1, .., i):

= P

c(ρ)

−

c(ρ)

(6)

= P

re f (w)

−

re f (w)

(7)

3. Compute the 2 × 2 covariance matrix:

S = XWY

(8)

where X and Y are the 2 × i matrices that have

and y

as their columns, respectively, and

W = diag(ω

, ω

, . . . , ω

). In our case, the weights ω

have all been set to 1.

4. Compute the Singular Value Decomposition

S = U ΣV

. The rotation matrix solution of (3) is

given by:

) = V







det(VU

)







(9)

The angle estimate

is directly determined from the

knowledge of R(

5. The translation vector solution of (3) is given by:

(w)

re f (w)

− R(

)

c(ρ)

(10)

From the obtained estimate (

(w)

), the coordi-

nates of the next points P

∗(ρ)

, k > i, can be updated,

as well as the yaw reference ψ

to be applied to the

MAV so that its painting system faces the wall:

∗(ρ)

= R(

)(P

re f (w)

−

(w)

) (11)

= −

(12)

4.3 Results

Simulation results are provided in this section on

the ﬂat wall scenario. The approach proposed in

the previous subsection has been applied to differ-

ent set ups corresponding to several values of the

angular offset γ. Results are ﬁrst presented for the

case γ =10deg, and performance is then analyzed for

γ ∈

{

−15, −10, 0, 10, 15

}

deg. In all cases, the posi-

tion offset is chosen as δ

(w)

= [0 − 1.1 0]

To assess of the performance of the proposed ap-

proach, a comparison is provided between the follow-

ing cases:

• online estimation of the offsets (δ

, γ), and local-

ization of the drone based on the PTAM algorithm

(”offset estimation and PTAM”)

• online estimation of the offsets (δ

, γ), and local-

ization of the drone based on ground truth (”offset

estimation and GT”)

• no estimation of the offsets (δ

, γ), and localiza-

tion of the drone based on ground truth (”no offset

estimation and GT”)

Comparison between the ﬁrst two cases enable to

identify the inﬂuence of the localization algorithm.

Comparison to the third case enable to analyze the in-

ﬂuence of the proposed offset estimation method. In

the third case the robot is therefore sent directed to the

wall toward the y

direction, whatever the value of γ.

The ﬁrst case, ”offset estimation and PTAM”, is the

one corresponding to ”real” conditions and is the sole

for which the multiple take-off and landing procedure

presented in Section 3.3 is realized.

Figure 5 to 11 correspond to the particular case

γ = 10 deg. Figures 5, 6, 7 present a comparison be-

tween the desired and the obtained drawings respec-

tively for the three aforementioned cases. Compari-

son of these ﬁgures clearly demonstrates the improve-

ment of the drawing accuracy obtained when applying

the proposed estimation method. Inﬂuence of the lo-

calization precision is also clearly visible, when com-

paring Figures 5 and 6, showing a degradation when

using the on-board localization algorithm compared

to a theoretical localization based on ground truth.

Nevertheless, the ”offset estimation and PTAM” case

which corresponds to conditions close to reality re-

sults in a good drawing.

Figures 8 and 9 present the time evolution of the

estimates

(w)

and

γ respectively, for the case ”offset

estimation and PTAM”. As can be seen, the computed

estimates converge close to the true values. The evo-

lution of the yaw angle ψ of the robot is therefore

well compensated to make the painting system face

the wall. This can be seen on Figure 10 where the yaw

angle of the robot is controlled so as to compensate

for the angular deviation γ. Chattering on the curve

is due to contacts with the wall and the points ψ = 0

that are visible every each ∼8 minutes correspond to

successive take-offs and landings as explained in Sec-

tion 3.3. As can be seen on Figure 11, the online es-

timation hence enables to decrease the distance error

between desired and obtained dots as the estimation

improves over time.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

Figure 5: Desired and obtained drawings for the case ”offset

estimation and PTAM” (γ=10deg).

Figure 6: Desired and obtained drawings for the case ”offset

estimation and GT” (γ=10deg).

Figure 7: Desired and obtained drawings for the case ”no

offset estimation and GT” (γ=10deg).

Figure 8: Estimates of δ

and δ

for the case ”offset estima-

tion and PTAM” (γ=10deg).

Figure 9: Estimate of γ for the case ”offset estimation and

PTAM” (γ=10deg).

Figure 10: Quadcopter yaw angle for the case ”offset esti-

mation and PTAM” (γ=10deg).

Exploiting Physical Contacts for Robustness Improvement of a Dot-painting Mission by a Micro Air Vehicle

Figure 11: Evolution of the distance error between desired

and obtained dot positions for the case ”offset estimation

and PTAM” (γ=10deg).

Accuracy of the obtained drawings is ﬁnally as-

sessed and compared in terms of Root Mean Square

Error of the dot positions over the whole mission.

These results are provided in Table 1 for the three

cases and the different tested values of γ. As can be

seen the theoretical and ideal case (”offset estimation

and GT”) shows the best accuracy and the improve-

ment obtained by the proposed approach is clearly

visible when compared to the case without online es-

timation (”no offset estimation and GT”). The prac-

tical case which relies on PTAM localization intro-

duces more errors, but within an acceptable order of

magnitude. As was shown on Figure 5, the largest er-

rors occur at the ﬁrst applied points, due to the time

of convergence of this estimation process, and are re-

sponsible of these RMSE values.

Table 1: RMSE (in centimeters) on dot positions.

With estimation Without

γ (degrees) PTAM GT GT

0 8,09 5,67 4,81

+10 15,71 4,67 15,79

-10 15,51 7,71 14,49

+15 22,68 7,71 18,89

-15 23,37 11,49 17,34

It can be concluded that the proposed approach en-

ables to obtain a good drawing, despite uncertainty on

the initial positioning of the robot. A 3D visualization

of such drawing is provided for illustration purpose on

Figure 12 for this ﬂat wall scenario.

Figure 12: 3D illustration of a drawing obtained by the pro-

posed approach.

5 DOT PAINTING ON MULTIPLE

SEGMENTS WALL

5.1 Scenario Description

In this scenario, the goal is to apply the same set of

paint dots P

re f

as in the previous ﬂat wall scenario

but on a multiple segments wall this time. Each of

them is associated with an offset γ

which character-

izes the orientation difference between the facade and

the theoretical position of the quadcopter (see Figure

13). An extension of the previous approach is pro-

posed, and tested on a scenario with a wall consisting

of three segments (Figure 14).

Figure 13: Example of a 3 segments wall with angular off-

sets γ

{

−10, 0, +10

}

deg (A) and

{

+10, 0, +10

}

deg (B).

5.2 Proposed Approach

This approach consists of estimating the shape of the

surface by online computing, as previously, the angle

offset between the surface and the quadcopter after

each dot application. It is then possible to determine

the optimal command to make the robot orthogonal to

the surface model for the next dots.

From the above point of view, we consider the

shape Σ of a multiple segments wall as a set of

lines L

Σ = {L

, L

, . . . , L

}, with L

: y

(ρ)

= a

(ρ)

(13)

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

After applying the ﬁrst two dots, we start by com-

puting the ﬁrst line L

that goes through them. This

gives an initial estimate of the shape of the wall. For

each new dot i applied, the discrepancy is computed

between the real coordinates of where the contact

point actually occurred (P

c(ρ)

) and the predicted one

corresponding to (P

re f (ρ)

) by using the previously es-

timated shape of the wall:



i−1

re f (ρ)

+ b

i−1

− y

c(ρ)



(14)

where L

i−1

: y

(ρ)

= a

i−1

(ρ)

+ b

i−1

corresponds to

the the shape model of the current part of the facade

on which the robot is working, as estimated from

previous contacts. If the discrepancy ε

exceeds a

predetermined threshold

ε, it is considered that the

current dot was applied on a different segment of

the facade with an offset in the γ angle compared

to the previous segment. In this case, a new line

: y

(ρ)

= a

(ρ)

+ b

is computed by using the

coordinates of the contact point i and the ones of the

previous contact point i − 1. This line is added to

Σ. If ε

is lower than the threshold

ε, the new line

added to Σ is computed by performing a linear

regression including all previous contact points ﬁtting

this model.

As for the ﬂat wall case, once this estimation pro-

cess has been done, the coordinates of the next contact

point is updated by taking into account the estimate

of the current wall segment. This time, the update is

done only for the y

∗(ρ)

i+1

coordinate of the next point

∗(ρ)

i+1

∗(ρ)

i+1

:= a

∗(ρ)

i+1

+ b

(15)

This choice is made arbitrarily to ensure no ”longitu-

dinal” deformation of the drawing (i.e. no deforma-

tion along the width), meaning that someone standing

in front of the symmetry axis of the wall (if any) and

starring at the drawing would not notice any deforma-

tion. On the contrary, the observed deformation will

increase with the distance to this speciﬁc observation

position. This is different from a fresco application

where all parts of the drawing should be projected

normally to each corresponding wall segment.

5.3 Results

Simulation results are provided in this section on the

multiple segments wall scenario. The approach pro-

posed in the previous subsection has been applied

to different setups corresponding to several values of

wall angular offsets γ. Results are ﬁrst presented for

the case γ = −10

deg

| + 10

deg

Figure 14: The Gazebo world used for this scenario.

Figure 15: Desired and obtained drawings for the case ”off-

set estimation and PTAM” (γ = −10

deg

| + 10

deg

Figure 16: Model of the wall made from contact informa-

tion and using the localization based on PTAM.

Accuracy of the obtained drawings is assessed

and compared again in terms of Root Mean Square

Error of the dot positions over the whole mission.

These results are provided in Table 2 for the three

cases and the different values of γ. As shown on

Figure 16, the wall model generated is very similar

to the real one and a good drawing is obtained (see

Figure 17).

Exploiting Physical Contacts for Robustness Improvement of a Dot-painting Mission by a Micro Air Vehicle

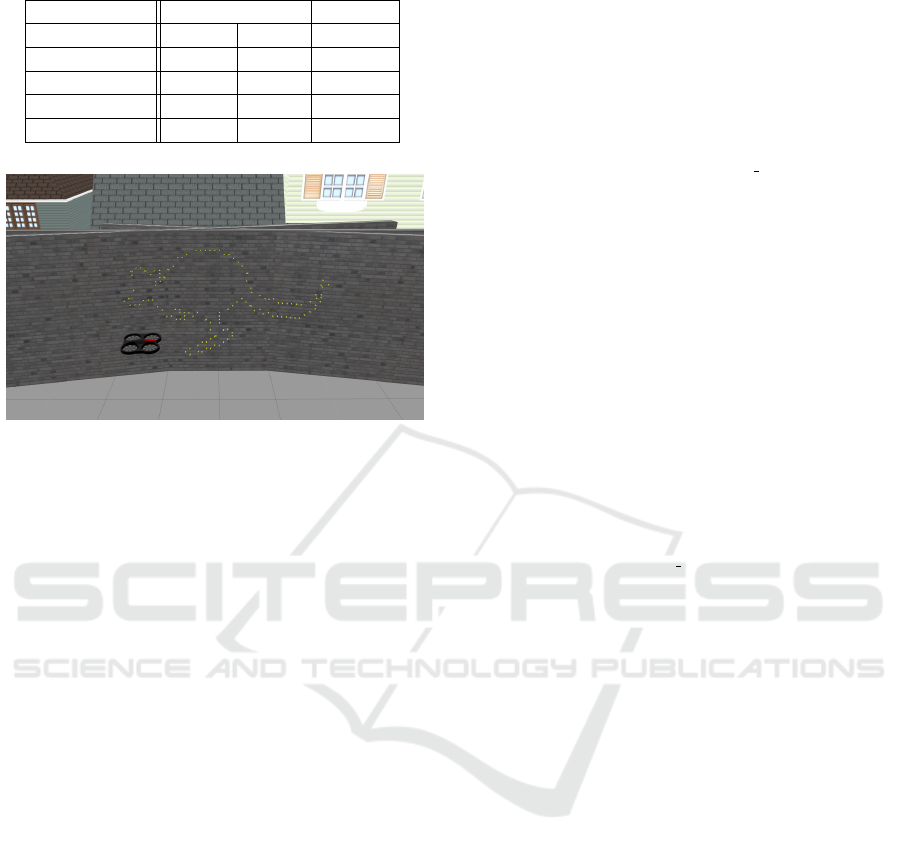
Table 2: RMSE (in centimeters) on dot positions.

With estimation Without

γ (degrees) PTAM GT GT

-10 | 0 | +10 3,74 4,96 4,68

-15 | 0 | +15 6,75 5,91 4,59

+10 | 0 | +10 7,70 5,85 5,03

-10 | 0 | -10 5,01 5,72 4,63

Figure 17: 3D illustration of a drawing obtained by the pro-

posed approach.

6 CONCLUSION

In this paper, an estimation and control method has

been proposed for the problem of dot painting by a

quadrotor Micro Air Vehicle. Based only on on-board

sensors, this method enables us to deal with uncertain-

ties on the initial positioning of the drone with respect

to the wall and with uncertainties on the shape of the

wall. Making use of information of contacts between

the MAV and the wall, the proposed online estima-

tion procedure compensates for positioning errors due

to such uncertainties and results in an improvement

of the positioning accuracy of the paint dots. Perfor-

mance analysis has been proposed in terms of accu-

racy of the drawings obtained for different simulation

scenarios.

Future work will focus on ﬂight experiments of the

proposed approach.

REFERENCES

Briod, A., Kornatowski, P., Klaptocz, A., Garnier, A., Pag-

namenta, M., Zufferey, J.-C., and Floreano, D. (2013).

Contact-based navigation for an autonomous ﬂying

robot. In IEEE/RSJ Int. Conf. on Intelligent Robots

and Systems.

Engel, J., Sturm, J., and Cremers, D. (2012a). Accurate ﬁg-

ure ﬂying with a quadrocopter using onboard visual

and inertial sensing. In Workshop on Visual Control of

Mobile Robots, at the IEEE/RSJ Int. Conf. on Intelli-

gent Robot Systems.

Engel, J., Sturm, J., and Cremers, D. (2012b). Camera-

based navigation of a low-cost quadrocopter. In

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems.

Engel, J., Sturm, J., and Cremers, D. (2014a). Scale-

aware navigation of a low-cost quadcopter with a

monocular camera. Robotics and Autonomous Sys-

tems, 62(11):1646–1656.

Engel, J., Sturm, J., and Cremers, D. (2014b). TUM

ARDrone. http://wiki.ros.org/tum ardrone.

Galea, B., Kia, E., Aird, N., and Kry, P. G. (2016). Stip-

pling with aerial robots. Symposium on Computa-

tional Aesthetics / Expressive, 2016.

Galea, B. and Kry, P. G. (2017). Tethered ﬂight control of a

small quadrotor robot for stippling. In IEEE/RSJ Int.

Conf. on Intelligent Robots and Systems.

Handy-Paint-Products (2014). The World’s

First Drone Painting Company.

https://diydrones.com/proﬁles/blogs/the-world-s-

ﬁrst-drone-painting-company.

Leigh, S., Agrawal, H., and Maes, P. (2016). A ﬂying pan-

tograph: Interleaving expressivity of human and ma-

chine. In 10th Conf. on Tangible Embedded and Em-

bodied Interaction.

Mei, C. and Rives, P. (2007). Cartographie et localisation

simultan

ee avec un capteur de vision. In Journ

ees Na-

tionales de la Recherche en Robotique.

Monajjemi, M. (2014). AR Drone Autonomy.

http://wiki.ros.org/tum ardrone.

Most, M. (2017). Evolution2.1.

http://www.mishamost.com/exhibitions-

1/2017/10/10/evolution21.

Ollero, A., Heredia, G., Franchi, A., Antonelli, G., Kondak,

K., Sanfeliu, A., Viguria, A., de Dios, J. M., Pierri,

F., Cort

es, J., Santamaria-Navarro, A., Trujillo, M.,

Balachandran, R., Andralde-Cetto, J., and Rodriguez,

A. (2018). The aeroarms project: Aerial robots with

advanced manipulation capabilities for inspection and

maintenance. IEEE Robotics and Automation Maga-

zine, 25(4).

Pagliarini, L. and Hautop Lund, H. (2009). The devel-

opment of robot art. Artiﬁcial Life and Robotics,

13(2):401–405.

Sorkine-Hornung, O. and Rabinovich, M. (2017). Least-

squares rigid motion using svd. Technical report, De-

partment of Computer Science, ETH Zurich.

uksel, B., Secchi, C., B

ulthoff, H. H., and Franchi, A.

(2019). Aerial physical interaction via ida-pbc. Inter-

national Journal of Robotics Research.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics