
Fractional Controller for Thin Plate Surface Temperature Control
Dan S. Necsulescu
1
, Bilal A. Jarrah
1
and Jurek Z. Sasiadek
2
1
Department of Mechanical Engineering, Ottawa University, 161 Louis Pasteur, Ottawa, Canada
2
Department of Mechanical and Aerospace Engineering, Carleton University, Ottawa, Canada
Keywords: Direct Problem, Inverse Problem, Zero-Pole Expansion, Laplace Transform, Fractional Order Controllers.
Abstract: Surface temperature control of a thin aluminium plate were investigated using closed loop control approach
implemented using inverse problem. The one-dimensional model with periodic boundary condition was
solved using the Laplace transform and both direct problem and inverse problem transfer functions were
obtained. The resulting transfer functions were expanded using Zero-Pole expansion to obtain a finite order
polynomial transfer function. Simulation results for closed loop control using fractional controllers (FOPI
λ
,
FOPD
μ
, and FOPID
μ
) were evaluated.
1 INTRODUCTION
Fractional order controllers start to be used more
often recently with the purpose to obtain better
performance of the system.
A heat conduction modelling for both steady state
and unsteady state using periodic boundary
conditions was presented in (Gebhart, 1971). Phase
angle and magnitude of transfer functions of different
order were provided (Ogata, 2010).
Inverse heat transfer problems of a metal plate
have several solution methods, were presented in
(Maillet, 2000). A detailed method was formulated
for the design of FOPI, FOPD, and FOPID controllers
(Monje, 2010). The heat flux and the temperature
control on front surface using the measurement on the
back surface of a finite slab, which is a standard
problem, was estimated. The Laplace transform was
used to get a solution of the resulting heat conduction
equation to obtain the transfer functions, and then was
expanded using Zero-Pole expansion (Feng, 2010).
A controller was designed with respect to gain and
phase margin criteria to satisfy the robustness
property for PID controller for the case of a ceramic
infrared heater (Shekher, 2016). A detailed design of
fractional order PID (FOPID) controller was
proposed and the parameters of the controller were
obtained according to the model characteristics and
design specifications (Zheng, 2018). A stability
regions study based on specified gain and phase
margin of the fractional order PI controller to control
integrating process was presented in (Cokmez, 2018).
For FOPD controller design, a new tuning method of
typical class of second order system was proposed
and can ensure given gain crossover frequency and
phase margin (Li, 2010 and Li, 2008). Smith predictor
combined a fractional order controller is proposed to
control the temperature of a steel slab reheating
furnace, they introduce a simulation results for a
fractional order proportional integrator controller
(Batlle, 2013).
Laplace transform was used to get a solution for
the one dimensional heat conduction equation, this
done to obtain the transfer functions representing both
problems resulted, direct problem and inverse
problem of the system. Both Zero-Pole expansion and
Taylor expansion were investigated using root locus
plots. The number of terms used in the inverse
transfer function was investigated to see the effect on
the ill posedness of the problem. Zero-Pole expansion
was adopted and simulations were done for a thin
aluminium plate to control surface temperature of the
plate on one side using inverse problem in closed loop
control approach (Necsulescu, 2017). An approach
was introduced to design a fractional order PI
controller for controlling a DC motor speed and
experimental results proved the efficiency of using
such controller (Muresan, 2013). A fractional order
controller that is able to deal with non-modelled
dynamics was proposed for the cooperative cruise
control (Flores, 2016). Interactive tools like Matlab
and Labiew are used to teach fractional order control
methods and how they can introduced in classical
control course ( Tan, 2016). A hybrid fractional order
Necsulescu, D., Jarrah, B. and Sasiadek, J.
Fractional Controller for Thin Plate Surface Temperature Control.
DOI: 10.5220/0007839406410647
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 641-647
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
641

controller were optimized for a proportional
derivative controller (Maurya, 2016).
In the current paper we compare several fractional
order controller types (FOPI
λ
, FOPD
μ
, and FOPID
μ
)
to control the surface temperature of a thin plate on
one side using the inverse problem in closed loop
control approach; this was achieved by using the
Laplace transform to solve the 1D heat conduction
equation with periodic boundary conditions to get the
transfer functions for both direct and inverse problem.
We use periodic boundary conditions because of the
possibility to represent temperature changing with
time using Fourier series.
2 THEORY
2.1 Transfer Functions
The 1D heat conduction equation is given by:
∂
2
θ
∂z
2
=
1
α
∂θ
∂
t
(1
)
where z is the 1D position variable 0 < z < L for a
plate of thickness L.
Boundary conditions are the following for this
study were:
θ
1
0,
t
=A sin⍵t, θ
2
L,
t
=free
(2)
∅
1
0,t
= free, ∅
2
L,t
= 0
(3)
where stand for the temperature, ∅ stand for the
heat flux, α stand for thermal diffusivity, and
subscript 1 and 2 indicate faces 1 and 2 of the plate.
Equation (1) can be written in complex domain as:
d
2
θ(z,s)
d
z
2
=
s
α
θ
z,s
(4)
Boundary conditions in s-domain become:
θ
1
0,s
=A
⍵
S
2
+⍵
2
, θ
2
L,s
=free
(5)
∅
1
0,s
= free , ∅
2
L,s
= 0
(6)
Equations (5) and (6) define the thermal
quadrupole ends, θ
and∅
for input and
θ
and∅
for output.
The solution of (4), is:
θ
z,s
=A
1
cosh
Kz
+ A
2
sinh
Kz
(7)
The heat flux is given by
∅
z,s
= -Ks
dθ
ds
(7.1)
where
K=
s
α
(8
)
Applying boundary conditions, (5) and (6), to (7),
gives the following results for A
1
and A
2
(Gebhart,
1971 and Maillet, 2000).
A
1
=A
⍵
S
2
+⍵
2
, A
2
=-A
⍵
S
2
+⍵
2
tanh
KL
(9
)
For the aboveA
andA
,the solutions become:
,
⍵
⍵
(10
)
∅
z,s
=-KsA
⍵
S
2
+⍵
2
∗
cosh
Kz
-tanh
KL
sinh
Kz
(11
)
The boundary temperatures θ
andθ
are:
θ
1
= θ
0,s
= A
⍵
S
2
+⍵
2
(12
)
,
(13)
⍵
⍵
⍵
1/
The transfer function of the direct problem linking
θ
toθ
is
G
1
=
θ
2
θ
1
=
1
cosh
KL
=sech(KL)
(14
)
The transfer function for the inverse problem is
G
2
=
1
G
1
= cosh(KL)
(15
)
Given (8) for K in this formulation, the hyperbolic
functions G
1
and G
2
depend on square root of s:
x=KL=
s
α
L
(16
)
To overcome the computation problem in case of
square root of s, Zero-Pole expansion is used to obtain
equations in integer powers of s.
Zero-Pole expansion Gives the following
equations:
G
1
s
=
p
1
p
2
p
3
p
4
p
5
p
6
…
s-p
1
s-p
2
s-p
3
s-p
4
s-p
5
s-p
6
…
(17
)
where
p
n
= -[
2k-1
π
2
*
√
∝
L
]
2
, n=1,2,3,… p
n
(18
)
and
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
642
G
2
s
=
s- z
1
s- z
2
s- z
3
s- z
4
…
z
1
z
2
z
3
z
4
…
(19)
where
z
n
-
2
k
-1
π
2
*
√
∝
L
2
,n1,2,3,…z
n
(20)
The above Zero-Pole expansions (17) and (19) of
G
1
=1/cosh(x) and G
2
=cosh(x) use integer number
powers polynomials in s for simulation. These
approximations proved appropriate for real-time
surface temperature control of a plate.
Simulations were carried out for a thin 6061T6
Aluminium plate of thickness L = 12.7 [mm] and
thermal diffusivity α= 6.9031e-5 [m
2
/sec].
Simulations were done with M=4 terms for an
inverse problem transfer function and N= 6 terms for
the direct problem transfer function.
where
N & M stand for the number of terms for direct
problem and inverse problem.
After we get the Transfer function to our plant:
G
1
=
.
.
.
.
.
..
G
2
=
s
4
+122.5s
3
+3450s
2
+2.497e4s+2.267e4
2.267e4
The resulting transfer function for the system is:
G=G
2
*G
1
=
22805
( S+178.5)( s+127.8)
(21)
2.2 Control Approach
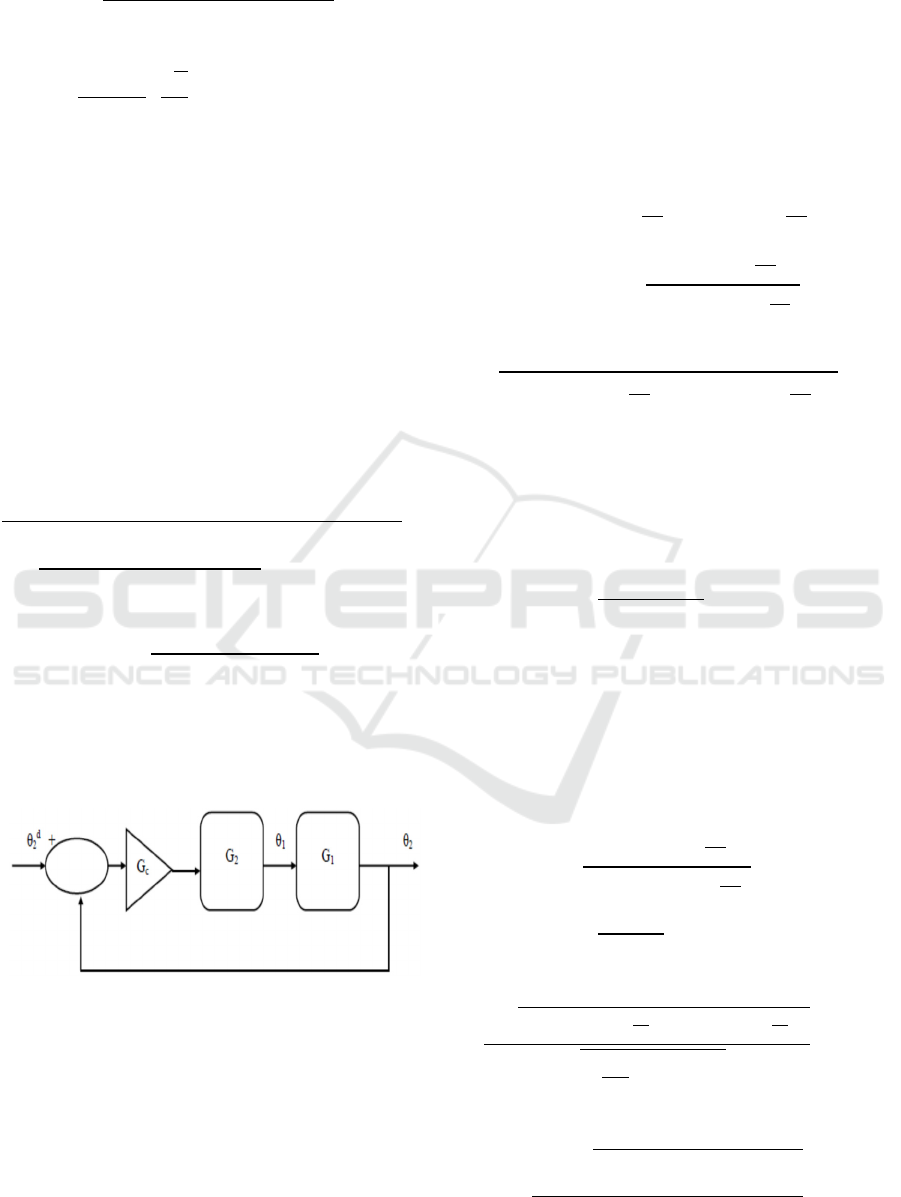
The block diagram for closed loop scheme is shown
in Fig. 1, where
Figure 1: Block diagram for closed loop scheme.
is the desired input temperature.
is the temperature output of the inverse
problem.
is the temperature output of the direct
problem.
G
c
is the transfer function of the controller.
G
1
is the direct transfer function.
G
2
is the inverse transfer function.
2.3 Controller Equations
The first controller is the fractional order proportional
integral controller (FOPI
λ
).
The fractional order PI controller formula is
(Cokmez, 2018):
C
jω
=k
p
[1+ k
i
(jω)
-λ
]
(22
)
C
jω
=
k
p
[1+k
i
(ω)
-λ
cos
μπ
2
+jk
i
(ω)
-λ
sin
μπ
2
(23
)
Arg
C(jω)
=tan
-1
[
k
I
(ω)
-λ
sin
μπ
2
1+ k
I
(ω)
-λ
cos
μπ
2
]
(24
)
|
C(jω)
|
=K
p
*
[1+ k
I
(ω)
-λ
cos
μπ
2
]
2
+[k
I
(ω)
-λ
sin
μπ
2
]
2
(25
)
The open loop transfer function is:
L() = C()G()
We want to satisfy three conditions to solve for
variables:
1 - Robustness:
d(Arg
L(jω)
dω
ω=ω
cg
=0
2 - Gain crossover frequency:
|
L(jω)
|
dB
=0
3 - Phase Margin:
Arg
L(jω)
|
ω=ω
cg
= -π+ φ
m
From criteria (3) we get:
tan
-1
k
I
(ω
cg
)
-λ
sin
μπ
2
1+ k
I
(ω
cg
)
-λ
cos
μπ
2
-
tan
-1
2ζω
cg
ω
n
ω
n
2
-ω
c
g
2
= -π+ φ
m
(26
)
From criteria (2) we get:
K
p
[1+ k
I
(ω
cg
)
-λ
cos
μπ
2
]
2
+[k
I
(ω
cg
)
-λ
sin
μπ
2
]
2
(1-
ω
cg
2
ω
n
2
)
2
+ 4ζ
2
ω
cg
2
/ω
n
2
=1
(27
)
From criteria (1) we get:
K
I
=
- B ±
B
2
- 4A[Aω
cg
-2λ
+λ(ω
cg
)
-2λ-1
]
2[Aω
cg
-2λ
+λ(ω
cg
)
-2λ-1
]
(28
)
Fractional Controller for Thin Plate Surface Temperature Control
643

where
A=
2ζω
n
ω
n
2
- ω
cg
2
+4ζω
n
ω
cg
2
(ω
n
2
- ω
cg
2
)
2
+(2ζω
n
ω
cg
)
2
and
B= 2Aω
cg
-λ
cos
λπ
2
+λω
cg
-λ-1
cos
λπ
2
The second controller is the fractional order
derivative controller (FOPD
μ
).
The system transfer function formula is (Ogata,
2010):
G=
ω
n
2
s
2
+2ζω
n
s+ω
n
2
(29)
we get:
|
G(jω)
|
=
1
(1-
ω
2
ω
n
2
)
2
+ 4ζ
2
ω
2
/ω
n
2
(30)
Arg
G(jω)
=- tan
-1
2ζωω
n
ω
n
2
- ω
2
(31)
The fractional order PD controller formula is
(Monje, 2010 and Li, 2010):
C
jω
=k
p
[1+ k
d
(jω)
μ
]
(32)
C
jω
=
k
p
[ 1+ k
d
(ω)
μ
cos
μπ
2
+jk
d
(ω)
μ
sin
μπ
2
]
(33)
Arg
C(jω)
=
tan
-1
[
sin
1- μ
π
2
+k
d
(ω)
μ
cos
1- μ
π
2
]-
1- μ
π
2
(34)
|
|
∗
1
cos
2
1
sin
2
(35)
were:
K
p
is the proportional gain.
K
d
is the derivative gain.
The open loop transfer function is:
L() = C()G()
We want to satisfy three conditions to solve for
variables:
1 - Robustness:
d(Arg
L(jω)
dω
ω=ω
cg
=0
2 - Gain crossover frequency:
|
L(jω)
|
dB
=0
3 - Phase Margin:
Arg
L(jω)
|
ω=ω
cg
= -π+ φ
m
From criteria (3) we get:
tan
-1
sin
1- μ
π
2
+k
d
(ω
cg
)
μ
cos
1- μ
π
2
-
1- μ
π
2
-
tan
-1
2ζω
cg
ω
n
ω
n
2
-ω
cg
2
= -π+ φ
m
(36
)
From criteria (2) we get:
1
cos
2
sin
2
1
4
1
(37
)
From criteria (1) we get:
μK
d
ω
cg
μ-1
cos
1- μ
π
2
cos
2
1- μ
π
2
+[sin
1- μ
π
2
+K
d
ω
cg
μ
]
2
-
2ζω
n
ω
n
2
- ω
cg
2
+4ζω
n
ω
cg
2
(ω
n
2
- ω
cg
2
)
2
+(2ζω
n
ω
cg
)
2
=0
(38
)
From criteria (3) we can get a relation between
and as follows:
K
d
=
- B ±
B
2
- 4A
2
ω
cg
2μ
2Aω
cg
2μ
(39
)
where:
A=
2ζω
n
ω
n
2
- ω
cg
2
+4ζω
n
ω
cg
2
(ω
n
2
- ω
cg
2
)
2
+(2ζω
n
ω
cg
)
2
B= 2Aω
cg
μ
sin
1- μ
π
2
- μω
cg
μ-1
cos
1- μ
π
2
The third controller is the fractional order
proportional derivative controller (FOPID
μ
).
The fractional order PID controller formula is
(Shekher, 2016 and Zheng, 2018):
C
s
=k
p
[1+
k
i
s
λ
+k
d
(s)
μ
]
(40
)
For the current controller we have 1, we get:
1
cos
2
sin
2
(41
)
Let:
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
644

P
ω
=1
+k
d
(ω)
μ
cos
μπ
2
and
Q(ω)=- k
i
ω
-1
+k
d
(ω)
μ
sin
μπ
2
Then
Arg
C(jω)
=tan
-1
[
Q(ω)
P(ω)
]
(42)
|
|
(43)
We want to satisfy four conditions to solve for
variables:
1 - Robustness:
d(Arg
L(jω)
dω
ω=ω
cg
=0
2 - Gain crossover frequency:
|
L(jω)
|
dB
=0
3 - Phase Margin:
Arg
L(jω)
|
ω=ω
cg
= -π+ φ
m
4 - Noise rejection:
T
jω
=
C
jω
G(jω)
1+C
jω
G(jω)
dB
≤A dB
were A is a designed value.
According to specification (2) we get:
k
p
P
2
(ω)+Q
2
(ω)
(1-
ω
cg
2
ω
n
2
)
2
+ 4ζ
2
ω
cg
2
/ω
n
2
=1
(44)
From specification (3) we get:
tan
-1
Q
ω
P
ω
-tan
-1
2ζωω
n
ω
n
2
- ω
2
= -π+φ
m
(45)
From specification (1) we get:
P
ω
*aa-Q
ω
*pp
P(ω)
2
+Q(ω)
2
-
2ζω
n
ω
n
2
- ω
cg
2
+4ζω
n
ω
cg
2
(ω
n
2
- ω
cg
2
)
2
+(2ζω
n
ω
cg
)
2
=0
(46)
From criteria (4) we get:
|
C
jω
G(jω)
|
|
1+C
jω
G(jω)
|
=
P
2
(ω)+Q
2
(ω)
[
(1-
ω
cg
2
ω
n
2
)
2
K
p
+P
w
]
2
+[Q
w
+2ζ
ω
cg
ω
n
K
p
]
2
≤A
(47
)
3 RESULTS AND DISCUSSION
For the design purpose, the crossover frequency was
set to be 20 (rad/sec) and the phase margin is set to be
65 degrees, all results had a one second of step time
to see a clear step response away from Y-axis.
After we solve (26, 27, and 28) for the fractional order
PI controller parameters, we get controller formula as
follows:
FOPI= 1.3862
+ 25.993(s)
-1.486
From Fig. 2, we see that the system reaches the
desired response after 1.5 seconds, but it has an
overshoot of 20%.
After we solve (37, 38, and 38) for the fractional order
PD controller parameters, we get controller formula
as follows:
FOPD= 1.5622
+ 0.0086842(s)
1.832
Figure 2: Step response using fractional order proportional
controller (FOPI
λ
).
Figure 3: Step response using fractional order proportional
derivative controller (FOPD
μ
).
Fractional Controller for Thin Plate Surface Temperature Control
645

From Fig. 3, we can see that the controller can't reach
the desired steady state value no matter how long time
we give the system.
After we solve (44, 45, 46, and 47) for the fractional
order PID controller parameter we get the controller
formula as follows:
FOPID= 0.9639
+
2.9379
-0.0862(s)
0.713
From Fig. 4, we can see that the system reaches the
desired response after 2.5 seconds, also with no
overshoot.
From Fig. (2, 3, and 4), we see that the best controller
is the fractional order proportional derivative
controller (FOPID
μ
), since it achieves the desired
response without overshoot.
Now we compare the results with the integer order
controller (IOPID). From Fig. 5, we can see that the
response is slower with an overshoot of about 8%,
and this favours the fractional order proportional
derivative controller (FOPID
μ
) over all other
controllers, this is due to the fact that for this
controller we have four parameters to change which
gives a better design over all other controllers were
only three parameters are available to change for
design. The results for integer order controller were
obtained by using Automatic Tuning Criteria in
Matlab
TM
.
Figure 4: Step response using fractional order proportional
derivative controller (FOPID
μ
).
Figure 5: Step response using integer order proportional
derivative controller (IOPID).
4 CONCLUSIONS
The fractional order controller has an advantages over
integer order controller with respect to overshoot
time, the fractional controller results show that we can
get a response without overshoot. Fractional order
controller design gives us more flexibility to choose
five controller parameters compare to three controller
parameters for integer order, which helps in control
response time, overshoot and system stability.
Surface temperature control for a metal thin plate has
still to be further investigated and verified
experimentally.
REFERENCES
Gebhart, B., 1971. Heat Transfer. McGraw Hill Inc. USA,
2
nd
edition.
Ogata, K., 2010. Modern Control Engineering. Prentice
Hall. New Jersey, 5
th
edition.
Maillet D., Andre, A., Batsale B., Degiovanni A., and
Moyne., 2000. Thermal quadrupoles: solving the heat
equation through integral transforms. John Willey &
Sons. Chichester, 1
st
edition.
Monje C., Chen Y., Vinagre B., Xue D., and Feliu V., 2010.
Fractional-order Systems and Controls: Fundamentals
and Applications. Springer-Verlag. London, 1
st
edition.
ch. 5, 6, and 7.
Feng, Z., Chen, J., and Zhang, Y., 2010, Real-time solution
of heat conduction in a finite slab for inverse analysis,
International Journal of Thermal Sciences. vol. 49,
issue 5 pp. 762-768
Shekher, V., Gupta, V., and Saroha, S., 2016, Analysis of
Fractional order PID controller for Ceramic Infrared
Heater, International Journal of Engineering
Development and Research. vol. 4, issue 1, pp. 43-52.
Zheng, W., Lou, Y., Chen, Y., Pi, Y., and Yu, W., 2018, An
Improved Frequency-domain Method for the
Fractional Order PI
λ
D
μ
Controller Optimal Design,
International Federation of Automatic control., 51-4,
pp. 681-686.
Cokmez, E., Atic, S., Peker, F., and Kaya, I., 2018,
Fractional-order PI Controller Design for Integrating
Process Based on Gain and Phase Margin
Specifications, International Federation of Automatic
control. 51-4, pp. 751-756.
Li, H., Lou, Y., and Chen, Y., 2010, A Fractional Order
Proportional and Derivative (FOPD) Controller:
Tuning Rule and Experiments, IEEE Transactions on
Control Systems Technology. vol. 18, no. 2, pp. 516-
520.
Li, H., and Chen, Y., 2008, A Fractional Order
Proportional and Derivative (FOPD) Controller
Tuning Algorithm, IEEE Chinese Control and Decision
Conference.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
646

Batlle, V., Perez, R., Garcia, and F., 2013, Simple
Fractional Order Controller Combined with a Smith
Predictor for Temperature control in a Steel Slab
Reheating Furnace, International Journal of Control,
Automation, and Systems. Vol. 11(3), pp. 533-544.
Necsulescu, N., and Jarrah, B., 2017, Real-Time
temperature control of a one dimensional metal plate,
21st International Conference on Control Systems and
Computer Science (CSCS21). Vol. 1, pp. 5-12.
Muresan, C., Folea, S., Mois, G., and Dulf, E., 2013,
Development and implementation of an FPGA based
fractional order controller for a DC motor,
Mechatronics., vol. 23, Issue 7, pp. 798-804.
Flores, C., Milanés, V., and Nashashibi, F., 2016, Using
Fractional Calculus for Cooperative Car-Following
Control, IEEE 19th International Conference on
Intelligent Transportation Systems (ITSC).
Tan, N., Yuce, A., and Deniz, F., 2016, Teaching
Fractional Order Control Systems Using Interactive
Tools, International Conference on Education in
Mathematics, Science & Technology(ICEMST). Vol. 4,
pp. 554-563.
Maurya, R., and Bhandari, M., 2016, Design of Optimal
PID[FOPID] controller for Linear System,
International Conference on Micro-Electronics and
Telecommunication Engineering (ICMETE).
Fractional Controller for Thin Plate Surface Temperature Control
647
